讲稿2附件(牛顿差分表及例题)
牛顿法代数插值ndash差商表的求法

牛顿法代数插值ndash 差商表的求法原文地址:牛顿法代数插值–差商表的求法作者:大关牛顿法代数插值–差商表的求法下面的求插商的方法并不是好的求插商的方式,因为他的效率并不是很高,不论是从空间效率还是时间效率,但是下面主要探讨的是一种将塔形的数据转换成一位数组的方式。
实际上求插商仅通过一个n个元素的一位数组就能解决,但本文强调的是一种思路,希望对大家有所借鉴。
牛顿插商公式:f[xi,xj]=(f(xj)– f(xi))/(xj– xi)f[xi,xj,xk]=(f[xj,xk]– f[xi,xj])/(xk– xi)….f[x0,x1,x2…,xn]=(f[x1,x2,…,xn]– f[x0,x1,…,xn-1])/(xn– x0)转换成均插表(或称差商表)形式如下:定义1:f[xi,xi+1,…xj]简记为f(i,j)其中i=0&&i=n&&j=0&&j=n&&i j;记f(xi)为f[xi,xi]即f(i,i)根据定义1可以推出:f[x0,x1]=f(0,1),f[x0,x1…xn]=f(0,n)….根据定义1:可以将插商表转换为如下形式。
根据上图,可以给出实际一维数组存储时的序列关系,如下图所示:此时f(0,0)位置是数组下标0,f(1,1)是数组下标为1….这样,我们从中找出相应的规律。
推论1:已知f(i,j),n为变量的数目,令k=j– i。
当k不等于0时,f(i,j)在数组中的下标通过计算得:Index=k*n–((k-1)*k)/2+i当k等于0时Index=i。
推论1很容易证明(实际就是一个等差数列求和问题)这里证明略。
推论2:n为变量的数目,则一维数组的长度可以计算得((1+n)*n)/2推论2可以通过等差数列求和得以证明。
证明略。
推论3:各阶插商就是f(0,k)k=1,2….n.推论3:根据插商的定义和定义1可以直接推出。
数值分析2-3(牛顿插值法)差商和与牛顿插值

确定插值多项式的次数
根据已知数据点的数量确定插值多项式的最高次 数。
计算插值多项式
利用差商表,通过拉格朗日插值公式计算插值多 项式。
3
进行插值
将需要插值的x值代入插值多项式中,得到对应 的y值。
05
牛顿插值法的优缺点分析
优点
计算简单
局部性质好
相比于其他多项式插值方法,牛顿插 值法的计算过程相对简单,不需要求 解高阶方程,降低了计算的复杂度。
数值分析2-3:牛顿 插值法、差商和
目录
• 引言 • 牛顿插值法的基本概念 • 差商的计算方法 • 牛顿插值法的实现步骤 • 牛顿插值法的优缺点分析 • 实际应用案例 • 总结与展望
01
引言
主题简介
数值分析是数学的一个重要分支,主 要研究如何用数值方法解决各种数学 问题。
本章节将介绍牛顿插值法、差商和的 概念及其应用。
03
差商的计算方法
差商的递推公式
差商的递推公式
$f[x_0, x_1, ldots, x_n] = frac{f[x_1, ldots, x_n] - f[x_0, x_1, ldots, x_{n-1}]}{x_n - x_0}$
应用
通过递推公式,我们可以计算任意点之间的差商,从而得到插值多项式的导数。
在数据点附近,牛顿插值具有较好的 局部性质,能够提供较为准确的插值 结果。
适用性强
牛顿插值法适用于各种数据分布情况, 无论是线性还是非线性数据,都能得 到较好的插值结果。
缺点
全局误差较大
由于牛顿插值多项式的构造方式, 其全局误差通常较大,尤其是在 数据点较少的情况下。
对数据点敏感
如果数据点发生微小的变动,牛 顿插值多项式可能会发生较大的 变化,导致插值结果不稳定。
讲稿2附件(牛顿差分表及例题)
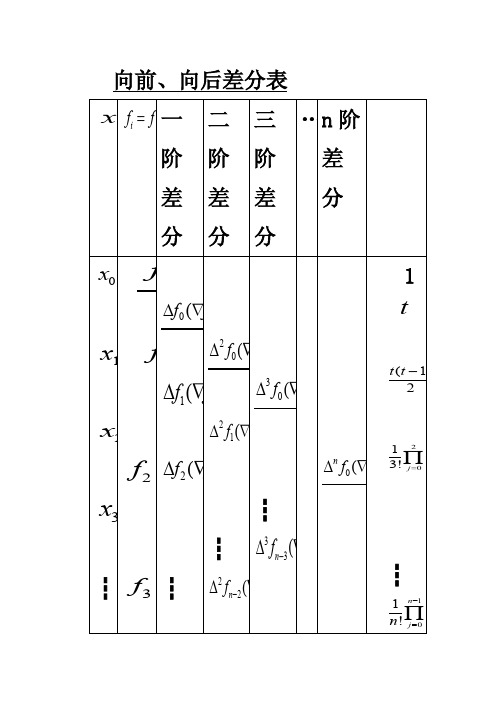
向前、向后差分表)j-)j-例:在微电机设计计算中需要查磁化曲线表,通常给出的表是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值,下面要解决B 从4000至11000区间的查表问题。
为节省计算机存储单元,采用每500高斯存入一个at值,在利用差分公式计算。
从差分表中看到三阶差分近似于0,计算时只需二阶差分。
当4000≤B≤10500时用牛顿前插公式;当10500≤B ≤11000时用牛顿后插公式;例如,求f (5200)时取200005000, 1.58,0.11,B f f f ==∆=∆=,h=500,B=5200,t=0.4,取n=2,由公式000(1)()2!n t t N x th f t f -+=+∆+计算得:(0.4)(0.(5200) 1.58(0.4)(0.11)2f -≈++这个结果与直接查表得到的值相同,说明用此算法在计算机上求值是可行的。
(0210)《古代散文》复习思考题一、填空题1.甲骨卜辞、和《易经》中的卦、爻辞是我国古代散文的萌芽。
2.深于比兴、,是先秦散文的突出特点。
3.《》长于描写外交辞令。
4.《国语》的突出特点是长于。
5.“兼爱”、“非攻”是思想的核心。
6.先秦诸子中,善养“浩然之气”。
7.先秦诸子中,提出了“言不尽意”、“得意忘言”的观点。
8.荀子的《》是我国最早以“赋”名篇的作品。
9.《鵩鸟赋》是的骚体赋。
10.枚乘的《》标志着散体赋的正式形成。
11.“破釜沉舟”出自《》。
12.对偶、辞藻、用典和声律是的主要特征。
13.被鲁迅誉为“改造文章的祖师”。
14.“文以气为主”、“诗赋欲丽”是提出的著名观点。
15.《大人先生传》的作者是。
16.嵇康的代表作是《》。
17.西晋作家中,“善为哀诔之文”。
18.《归去来兮辞》可以说是辞仕归隐的宣言书。
19.《别赋》、《恨赋》的作者是。
20.孔稚圭的《》以山灵的口吻,讽刺了“身居江海之上,心存魏阙之下”的假隐士。
21.唐代古文运动发生在时期,是一次提倡散文、的文体改革运动。
牛顿流体 讲稿

第三求出总截面的流量。Q 为截面 S 内,距轴心不同 r 处,各流 层流量之和。
其实这是一类非常普通的疾病冠心病或者心绞痛冠心病是冠状动脉粥样硬化性心脏病的简称冠状动脉供应心脏自身血液当发生严重粥样硬化或痉挛使冠状动脉狭窄或闭塞导致心肌缺血缺氧或梗塞的一种心脏病冠心病的主要临床表现就是心肌缺血缺氧而导致的心绞痛心律失常严重者可发生心肌梗塞使心肌大面积坏死危及生命
讲稿 人们经常可以在电视上看到这样的镜头:一个情绪激动的老人手 捂胸口,表情非常痛苦,服用药丸后,几分钟内,症状就得到极大的 缓解,那么这个老人究竟得了什么病症?吃的又是什么药,以及为什 么如此有效? 其实这是一类非常普通的疾病,冠心病或者心绞痛,冠心病是冠 状动脉粥样硬化性心脏病的简称,冠状动脉供应心脏自身血液,当发 生严重粥样硬化或痉挛,使冠状动脉狭窄或闭塞,导致心肌缺血,缺 氧或梗塞的一种心脏病,冠心病的主要临床表现就是心肌缺血、缺氧 而导致的心绞痛,心律失常,严重者可发生心肌梗塞,使心肌大面积 坏死,危及生命。 病人吃的药物通常就是速效救心丸。 2018 年 2 月 24 日,河北石家庄市火车站东广场,突发紧急情况, 一名旅客突发心脏病,吐血并瘫坐在地上,幸好被巡逻的警察及时发 现,喂食一颗速效救心丸才转危为安。 再有网上流传这样的段子,告诫陪娃儿做作业的家长常备速效救 心丸,以防气急火攻心,血压升高,危及生命,虽然这只是把你的痛 苦说出来,让大家快乐一下的调侃,但是也并不无道理 速效救心丸具有舒张血管,镇静止痛,改善微循环降低外周血管 阻力,减轻心脏负荷,改善心肌缺血的作用。 下面我们就通过推导泊肃叶定律定量分析心血管疾病的发病及 急救原理。
当 t=0 时,同时抽开 2 块隔板,流体在重力的作用下,向下做变 加速运动。
牛顿均差差值

f ( n ) (ξ ) f [ x 0 , ... , x n ] = , ξ ∈ ( x min , x max ) n!
的函数表如下, 例 f(x)的函数表如下,用三次牛顿插值计算 的函数表如下 用三次牛顿插值计算f(0.596)的近似值 的近似值
←
y ← y+t*A(k,k) k ← k+1
N
k>N
Y
输出y 输出
§2 Newton’s Interpolation
等距节点公式 /* Formulae with Equal Spacing */ 牛顿基本插值公式对结点是否等距没有限制. 牛顿基本插值公式对结点是否等距没有限制.不过当 结点等距时前述牛顿插值公式可进行简化.首先介绍 结点等距时前述牛顿插值公式可进行简化. 差分概念. 差分概念. x −x 当节点等距分布时: 等距分布时 当节点等距分布时 x i = x 0 + i h ( i = 0 , ... , n ) h =
0.62)+0.21303(x-0.55)(x-0.65)(x-0.80) f(0.596) ≈N3(0.596)=0.63192
牛顿插值算法设计
N n ( x ) = f ( x0 ) + f [ x0 , x1 ]( x − x0 ) + f [ x0 , x1 , x2 ]( x − x0 )( x − x1 ) + ...
f [ x 0 , x 1 , x 2 ,⋯ , x n] =
参考资料-牛顿差分

S ince f(>i)g, the functio has Y 1 p,{z;), fo rR»u e's T heor er n ïm Pplt ;yät a numb er } in (o.in [O, b j. The G e ner alïZ6dg‹•)(})0, SO0 f'n' f J•"(*)•pol ynomi al of de$fe•riwhose l eaöin g cœffic ie nt is f 1x0!>i!- •pin) ) = ri! f lx‹,• l , ... , x n1›J O,¡31vd t es of x.ASäC O fl S q l e 'l G-e. .z,J,Newton’s interpolat o fÿn!d iv id ed-dif f erence form ula can be ex pressed in * *Pform when <o. <i. -p, are arranged co nsec uöv ely with equ¥spacing• J»*****-•* inœoduc e the notaüon h = =‹+—x¡, f or each im 0, 1, . • • › n 1 and let x = >o +-* Then the diff erenc e x- x, can be wrineng, p q, (s —i)ù. S o @. (3.10) b ecomesP,(x) ——P,(/ -i- ›) ,J[ x0] + sh f r i o! ul +S * )2* 0' * ^2’-j-- --j- s{s Uf(s —* + )h‘/$^ ' ^ ' ' ‘•A=OUsing bin O mia l-Cœ Ncient notaöon,s s{s - 1) $ — k -I- 1)k k!wc can express P>‹x) c ompactly asSn x} m P,(x$ -J- sh} f{x9} 3- k)*!*This formula is called the Newton forseard divid ed-difference fomu+•fom, called the Newtonthe forward difference notation A introduced in Aitken’s A2 me@od.fp g :l *h - f(*o)0›*i — <o12h 2/t2‘2*(* )'Aj°(x ) —Ö f{y )tt Since Pn{ z)ïs a3 2 Divided £//,t/gFg/jCand, in general,127Then, Eq. (3.11) has the following formula.Newton For war d-Dif ference F ormula£f (<o)(3.12)If the i nterpolating nodes are reordered as z… z,—i, ... , = . a for mu la sil nildf tO Eq. (3.10) results:+ - j- f[xz, ... , x o] • - xz){x —x.—i) ‹x — xi).H the nodes are equally spaced wilx xz + sh and x xi -i- ( S 3- n —i)h, thenPz{x) ——P,{x, -i- sh)f{x n + SP f[xz, xz-i1 -1- s(s -¥1)h2J f<n. <.—i. *n—2] +-J- s{s -1- 1)- - (S + Zt I)h‘ [ n• -• . , x o]-This form is called the Newton backward divided-dNerence formula. It is used to derive a more com monly applied formula known as the Newton backward-dNerenceformul a . T O di SC uss thi s f O rmula, we need the following d efinition.Definition $.T Given the se quence {p•! n=o• define the backward difference 4 pz (read nabla p,) by"Up. ——p. —p.-i. for n ¿; 1.Higher powers are define d recwsively bypn '!!!- °'p»), for k 2i 2.De finit ion 3.7 i mplies fatf xz, x,-ifand, i n ge ner&,2h2Con sequently,f[xz, x z-;, ... •='k!h*k f••)pp g) f g n ] 3- s4 f{xz) +1'( n)•n 1)2 n!2) • '('-c H A P T L R 3 • intet polaiion anö PoJyn p NJa ï Appro ximat loH ’’’I f we e X t e fl d the b1Il Or»ial co effic ient no tatio n to includ e all real values o › by l ( -J- 1-)- - (J + k - 1 "- • — — 3— i (——* k + 1)— _ •)’ . ).thenP,[x} == j"[gq] —b(— 1)1—sQjf(y q )-ÿ(—1)2 2)-ÿ = •-f(—1)‘whieh gives the following result.Newton Back ward- DiHere nce For mul aP n {x } —— j"[x,](— 1) kkm IXAMPLE 2The divided-difference Table 3.9 eorresponds to the data in Example 1.bbte 3.91.00.76519771.30.6200860First divided differences—0.4837057Second Third ,F divided divided di differencesdiserencesdiff—0.1087339 —0.5489460 0.0658784 . 1.60.4554022—0.0494433 0.&l—0.57861200.0680685 1.90.28181860.0118183 **” ”***”*—0.5715210****””””*”Only one in t er pol ati n g poly nom ial of de gree £tt m O s t 4 u S we will organize the data QOlfltS tO O btai n t hebest eS thèsefive data po 1, 2, and 3. T his will give us a sense the given value of x. i 'l t°'P l £t u O n £f pproximation s O I of aceuracy O f t he f t 3 ll rth-deg ree approxim äIf a n a p r O xiIR t i O n t f( . ) is req uir e d, the re il s o nab le e hoiew ^o = 1 0, x i = 1.3, a:2 = 1.6, 3 = 1.9, ande for the nodes possible use of the data poiEtS cl os est to xp. 1, and alsO m ake s dif ference. This impli es that ù 0.3 and s o the Newuse of the fourtb form ll l il l S u S e d with the d ivide d dif fe re nc es fhàt ÏÎt C n f orward divided-diä…,, ave ä SO lid un derscore in T able 3•4 ( -1) = P 4 (1.0 -j- (0.3))= 0.7651997 -p (p)(—0.4837057)"* Z ( 2) (0.3)°( —0. 1087332J-s=i.3.2 f/ivJded Difi erencœ+ 31+ 30.7196480.(0.3)3(0.0658784)(0.3)4(0.0018251)To app r oz¡i » £f te a value when x is close to the end of the tabulate d V alues, s £f y, x = 2.0, we would l g • llk t o ma ke ie earliest use of ie data p O i fl tS closest to z. This requires using Öe N ewt O n backwa rd d ivided-diä erence formula w 1Î S = 2 and the divided d if feren ces in Tabl e 3.9 that have a dashed underscore: 4(2.0)4 2.2 — 2(0.3))= 0.1103623 — 2 (0.3)(—0.5715210) — 2) (0.3)2(0.0118183)3 3J)4) (0.3)3(0.0680685) — 3 J) 4-) J) (0.3)4(0.0018251)0.2238754.The Newton formulas are not appropriate for approximating f(x) when z lies near the center of ie table since employing either ie backward or forward method in such a way that the highest-order difference is involved will not allow <o to be close to x. A number of divided-diYerence formulas are available for this case, each of which has situations when it can be used to maximum advantage. These methods are Aown as centered-difference formulas. There are a number of such melods, but we will present only one, Stirling’s melod, and again refer ie interested reader to [Hild] for a more complete presentation.For the centered-difference f or mulas, we choose =0 near the point being approxi- mated and label the nodes direcXy below =o as x… x 2. . and those directly above asx _… x _2, ....With thi s co n vention, S tirling’s formu l il i s given by s/i p x) P;w p (x) f{x o] if[x -i. •o1 + J [x o. <il) + s 2h 2(3.14) nl+ 2g21)J 3.fIx —2. x-;. <o.=il + Cf=-i.=o. xz])21*—i, *o, *i5-p ... 3- s 2 (s21)(s 2 — 4) • • • ls - [ttt - l )2)h f $x ,z, ... , x,z)J(i 2 — 1-)- - (s 2 — 2)h**+'** 2(/t=— -i. . , xp! -t- f ïx q, ... , <q+,]),«» = 2« -)- 1 is o dd. If ü- 2m is even, we use the same formula but delete the last line. The entri es used for this f ormu la are underûned in Table 3.10 on page 130. c o fl s i d erl e tabl e O f d£t W °* given in the previous examples. To use Stirling’s formula to ap proxi fna te J ’(1.5) wi1*o = 1.6, we use the underlined entries in the difference Table3.11.c H A P T E R 3- lnte‹polai ion an0 P ol y nomial Appro xima tionTable 3.10First Secon ddivided divide dd if ferenc es dis erenc esThirddi videddifferen ces diffepggf{x-i, x-i. zoJfi«-i. x0l f'•- 2°-' °0’"x0 /l›0l/[ 0› lJ f lx- . x0.•ff[x-i,x0. x; , >2!x2 /lx213bble 3.JJ1.0 0.76519770.62008601.6 0.45540221.9 0,28181862.2 0.1103623 —0.5786120-0.57152100.01181830.0680685Th e f O rmul il , with A = 0.3, Up = 1.6, and s =j"(1.5) 4 1.6 -j- —} ) (0.3))3'beco mes= 0.4554022 -F0.3((—0.5489460) -j- (—0.5786120)) .(0.3)2(—0.04 94433)(0.3)3(0.0658784 + 0.0680685)= 0.51l820g. (0.3)4(0.0018251)divided diYerencesSeconddivideddifferencesThirddivideddifferences—0.48370J7—0.1087339—0.5489 460 0.0658784—0.0494433。
牛顿定律PPT课件

同一性质的力; 4. 两个物体相互作用,可以接
触也可不接触。
弹性力
永磁体悬浮在超导体上方
磁场力
四、力的概念 力 一个物体所受的力必为其他物体所施予
▪ 自然界的四种基本力:
引力、电磁力、强相互作用和弱相互作用
1. 万有引力 两个物体之间的相互吸引力
F
各个力分别作用时所 产生的加速度的叠加
ai
Fi m
3. 第二定律 F m a 为瞬时关系 力与加速度同时存在、同时改变和同时消失
4. 第二定律表达 式为d矢2r量关系
F
i
Fi mdt2
y
解题时常用分量式
▪ 直角坐标系中的分量形式
m ax Fx
r
Fy
ay
a
F
Fx mxamdd2tx2
O
x
Fy may mdd2t2y 力和加速度的直角坐标分解
例题2-2 m1= 3 kg,m2= 2 kg,m1与m2间的静
摩擦系数0 = 0.3,m1与水平桌面间的滑动摩擦系 数 = 0.2, 受与水平面的夹角为30º的拉力F 作
用。求:(1)两物体不发生相对滑动时,拉力 F 与
系统的加速度 a 的关系,并考察 a = 0 时的情形;
(2)两物体不发生相对滑动时,系统的最大加速度
Fco3sm 01m s2ign 30 25
(2) 两物体无相对运动时,m2 受 m1的静摩擦力作 用,当加速度为最大时,摩擦力为最大静摩擦力,
取物体m2为研究对象,坐标系的选取与(1)相同。
根据牛顿第二定律列出m2的运动方程:
x 方向: y 方向:
Ffm2a F N 2m 2g0
第二讲牛顿插值与分段线性插值

四、分段线性插值
我们已经知道插值有多种方法, 我们已经知道插值有多种方法 例 插值、 插值等. 如, Lagrange插值、 Newton插值等 插值 插值 插值等 的目的就是数值逼近的一种手段, 而数值逼近为 的目的就是数值逼近的一种手段 的是得到一个数学问题的精确解或足够的精确解, 的是得到一个数学问题的精确解或足够的精确解 那么是否插值多项式的次数越高, 那么是否插值多项式的次数越高 越能达到这个目 的呢? 观察n次插值多项式的余项 的呢 观察 次插值多项式的余项 f ( n +1) (ξ ) n
差商表
xi x0 x1 x2 x3 x4 ┊ f(xi) f(x0) f(x1) f(x2) f(x3) f(x4) ┊ f(x0,x1) f(x1,x2 ) f(x2,x3 ) f(x3,x4 ) ┊ f(x0,x1,x2) f(x1,x2,x3 ) f(x2,x3,x4 ) ┊ 1阶 阶 2阶 阶 3阶 阶 4阶 阶
∆ 3 f ( x1 ) = ∆(∆ 2 f ( x1 )) = ∆ 2 f ( x2 ) − ∆ 2 f ( x1 )
∆3f(x0) ∆3f(x1) ┊ ∆4f(x0) ┊
……
计算规律: 任一个k(≥1) 阶差分的数值等于所求 计算规律 任一个 差分左侧的数减去左上侧的数. 差分左侧的数减去左上侧的数 注意: 差分表中, 注意 差分表中 对角线上的差分是构造差分形 式的牛顿插值公式的重要数据. 式的牛顿插值公式的重要数据
+ an ( x − x0 )( x − x1 ) ⋅⋅⋅ ( x − xn−1 ).
它满足递推性: 它满足递推性
Pn ( x ) = Pn −1 ( x ) + an ( x − x0 )( x − x1 )L ( x − xn −1 ).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向前、向后差分表
-
)j
-
)j
例:在微电机设计计算中需要查磁化曲线表,通常给出的表是磁密B每间隔100高斯磁路每厘米长所需安匝数at的值,下面要解决B 从4000至11000区间的查表问题。
为节省计算机存储单元,采用每
500高斯存入一个at值,在利用差分公式计算。
从差分表中看到三阶差分近似于0,计算时只需二阶差分。
当4000≤B≤10500时用牛顿前插公
式;当10500≤B ≤11000时用牛顿后插公式;
例如,求f (5200)时取
2
00005000, 1.58,0.11,B f f f ==∆=∆=
,h=500,B=5200,t=0.4,取n=2,由公式
000(1)
()2!
n t t N x th f t f -+=+∆+
计算得:
(0.4)(0.
(5200) 1.58(0.4)(0.11)2
f -≈++
这个结果与直接查表得到的值相同,说明用此算法在计算机上求值是可行的。
