代换法及二进制
二进制的规律

二進制的規律二进制的规律在计算机科学领域中,二进制是一种十分重要的数制形式。
二进制由0和1两个数字组成,可以表示各种信息。
本文将介绍二进制的基本规律和相关概念。
二、二进制的表示方法二进制使用0和1两个数字来表示数值。
其中,0被表示为低电压或低信号,1被表示为高电压或高信号。
通过这种方式,计算机可以轻松识别和处理二进制数。
三、二进制的转换方法将十进制数转换为二进制数时,可以采用除2取余法。
具体步骤如下:1. 将十进制数不断除以2,一直除到商为0为止;2. 将每次的余数倒序排列,即为对应的二进制数。
四、二进制的运算规则二进制数除了可以进行转换,还可以进行基本的运算。
常见的二进制运算规则包括:1. 二进制的加法:按位相加,进位则向高位进;2. 二进制的减法:按位相减,借位则向高位借;3. 二进制的乘法:按位相乘,进位则向高位进;4. 二进制的除法:按位相除,商则向低位取。
五、二进制的应用领域由于计算机内部运算采用二进制表示,二进制在计算机科学中有着广泛的应用。
以下是一些常见的二进制应用领域:1. 数据存储和传输:计算机中的文件和数据都是以二进制的形式存储和传输的;2. 图像和音频处理:二进制可以用于表示图像和音频,通过对二进制数据的处理可以实现图像和音频的编辑和压缩;3. 计算机编程:计算机程序中的指令和数据都是以二进制形式存在的,编程语言通常提供了二进制操作的支持。
本文介绍了二进制的基本规律,包括二进制的表示方法、转换方法、运算规则以及应用领域。
二进制在计算机科学中扮演着重要的角色,深入理解二进制对于理解计算机原理和编程技术具有重要意义。
通过学习和应用二进制的知识,有助于提升对计算机的认识和运用能力。
文档创作者:百度文库用户。
二进制的换算方法

二进制的换算方法二进制是一种数制系统,使用两个数字0和1来表示数值。
在计算机科学和电子通信领域广泛使用,因为计算机使用的是二进制逻辑电路。
二进制转换方法有多种,下面将详细介绍常见的二进制换算方法。
十进制到二进制的转换:要将一个十进制数转换为二进制,可以使用除2取余法。
具体步骤如下:1.将十进制数除以2,得到商和余数。
2.将得到的余数写在一张表格中的右侧。
3.将商再次除以2,继续得到商和余数,将余数写在表格的下一列。
4.重复这个过程,直到商为0为止。
5.从上到下依次读取表格中的余数,即为二进制数。
例如,将十进制数25转换为二进制,按照上述步骤进行计算:25÷2=12 (1)12÷2=6 06÷2=3 03÷2=1 (1)1÷2=0 (1)十六进制到二进制的转换:十六进制是一种基数为16的进位制数,使用0-9和A-F来表示10-15的数。
为了将十六进制转换为二进制,可以将每个十六进制数转换为4位二进制数。
例如,十六进制数3A的二进制表示如下:3=0011A=1010八进制到二进制的转换:八进制是一种基数为8的进位制数,使用0-7来表示数值。
将每个八进制数转换为3位二进制数可以实现八进制到二进制的转换。
例如,八进制数57的二进制表示如下:5=1017=111二进制到十进制的转换:要将一个二进制数转换为十进制,可以使用权值法。
从最右边的位开始,每个位都乘以2的指数,指数从0开始递增。
然后将所有乘积相加,得到十进制数。
1*2^4+1*2^3+0*2^2+0*2^1+1*2^0=16+8+0+0+1=25二进制到十六进制的转换:为了将二进制转换为十六进制,可以将每四位二进制数转换为一个十六进制数。
从右到左每四位进行分组,然后根据二进制到十六进制的对应关系进行转换。
1101=D1101=D二进制到八进制的转换:要将一个二进制数转换为八进制,可以将每个三位二进制数转换为一个八进制数。
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
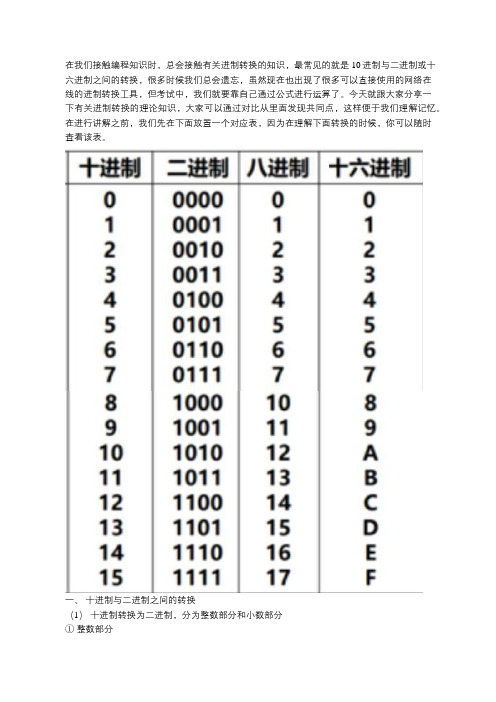
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
经典密码

一、经典密码
⑴.单表代换密码
只使用一个密文字母表,并且用密文字母表中的一 个字母来代换明文字母表中的一个字母。 明文字母表:A ={ a0 , a1 ,..., an-1 }
密文字母表:B ={ b0 , b1 ,..., bn-1 } 定义一个由A到 B的映射:f:A→B
–因此,单表代换密码可用统计分 析攻破。
三、经典密码的统计分析
• 英语的统计规律
–每个单字母出现的频率稳定。
最高频率字母
E
次高频率字母
TAOINSHR
中高频率字母
DL
低频率字母
CUMWFGYPB
最低频率字母 V K J X Q Z
三、经典密码的统计分析
• 英语的统计规律
–频率最高的双字母组: TH HE IN ER AN RE ED ON ES ST EN AT TO NT HA ND OU EA NG AS OR TI IS ET IT AR TE SE HI OF
三、经典密码的统计分析
• 英语的统计规律
–频率最高的三字母组: THE ING AND HER ERE ENT THA WAS ETH FOR DHT HAT SHE ION HIS ERS VER
其中THE的频率是ING的3倍!
三、经典密码的统计分析
• 英语的统计规律
–英字母的约占一
半。
–还有其它统计规律!
三、经典密码的统计分析
经得起统计分析是对近代 密码的基本要求!
一、经典密码
•(2)把明文按某一顺序排成一个矩阵, 然后
按另一顺序选出矩阵中的字母以形成密文, 最后截成固定长度的字母组作为密文。
例如:
简述不同进制之间的转换方法

简述不同进制之间的转换方法一、进制的概念进制是计算机科学中一个非常重要的概念,它是用来表示数字的一种方法。
我们常用的十进制是基于10个数字0-9,而其他进制则是基于不同数量的数字。
二、二进制和十进制的转换方法二进制是计算机中最基本的进制,它只包含两个数字0和1。
而十进制是我们平常生活中使用的进制,包含0-9这十个数字。
1. 二进制转换为十进制二进制转换为十进制的方法很简单,只需要根据权重相加即可。
例如,二进制数1101转换为十进制的计算方法是:1x2^3 + 1x2^2 + 0x2^1 + 1x2^0 = 13。
2. 十进制转换为二进制十进制转换为二进制的方法是不断除以2,直到商为0为止。
将每一步的余数倒序排列即可得到二进制数。
例如,十进制数13转换为二进制的计算方法是:13÷2=6余1,6÷2=3余0,3÷2=1余1,1÷2=0余1,所以13的二进制表示为1101。
三、八进制和十进制的转换方法八进制是基于8个数字0-7的进制,常常用于计算机中的文件权限。
八进制数的每一位表示3个二进制位。
1. 八进制转换为十进制八进制转换为十进制的方法也是根据权重相加。
例如,八进制数17转换为十进制的计算方法是:1x8^1 + 7x8^0 = 15。
2. 十进制转换为八进制十进制转换为八进制的方法是不断除以8,直到商为0为止。
将每一步的余数倒序排列即可得到八进制数。
例如,十进制数15转换为八进制的计算方法是:15÷8=1余7,1÷8=0余1,所以15的八进制表示为17。
四、十六进制和十进制的转换方法十六进制是基于16个数字0-9和字母A-F的进制,常常用于表示颜色、内存地址等。
1. 十六进制转换为十进制十六进制转换为十进制的方法同样是根据权重相加。
其中,字母A-F分别表示10-15。
例如,十六进制数1A转换为十进制的计算方法是:1x16^1 + 10x16^0 = 26。
进制转换规则

进制转换规则一、求余法。
适用范围:十进制转换为→二进制、八进制、十六进制。
要将十进制转换为多少进制,那么就对几求余。
例如:①、23转换为二进制,就是不停的对2求余数(第一次用本数对2求余,从第二次开始都用上一次的商除以2,直到商的值为0为止)。
23除以2的商为11 余数为111除以2的商为5 余数为15除以2的商为2 余数为12除以2的商为1 余数为01除以2的商为0 余数为1将余数从下到上写就可以得到23的二进制为10111;②、23转换为八进制,就是不停的对8求余(第一次用本数对8求余,从第二次开始都用上一次的商除以8,直到商的值为0为止。
)23除以8的商为2 余数为72除以8的商为0 余数为2同理将余数从下到上写可以得到23的八进制数位27③、27转换为十六进制,就是不停的对16求余(第一次用本数对16求余,从第二次开始都用上一次的商除以16,直到商的值为0为止。
)27除以16的商为1 余数为111除以16的商为0 余数为1同理将余数从下到上写可以得到27的十六进制数位1B(11在十六进制数中用字母B表示)。
二、乘方。
N制数的右边第一位为N的0次方,前一位为N的1次方,依次类推。
例如:2进制的右边第一位就为2的0次方,前一位2的1次方,依次类推。
适用范围:将二进制、八进制、十六进制转换为十进制。
例如:①、将27O转换为十进制。
右边第一位表示8的0次方,该位上的数位7,就表示有7个8的0次方。
右边第二位表示8的1次方,该位上的数位2,就表示有2个8的1次方。
所以这个八进制数就等于7个8的0次方与2个8的1次方之和即为:7×81082⨯+=7+16=23,所以八进制的23O转换为十进制就为23。
(数字后有字母O表示八进制。
)②、将1BH转换为十进制。
右边第一位表示16的0次方,该位上的数位B,就表示有B,十六进制B表示11即是说有11个8的0次方。
右边第二位表示16的1次方,该位上的数位1,就表示有1个16的1次方。
二进制转换算法

一、概念1.十进制十进制使用十个数字( 0、1、2、3、4、5、6、7、8、9)记数,基数为 10,逢十进一。
历史上第一台电子数字计算机 ENIAC是一台十进制机器,其数字以十进制表示,并以十进制形式运算。
设计十进制机器比设计二进制机器复杂得多。
而自然界具有两种稳定状态的组件普遍存在,如开关的开和关,电路的通和断,电压的高和低等,非常适合表示计算机中的数。
设计过程简单,可靠性高。
因此,现在改为二进制计算机。
2.二进制二进制以 2 为基数,只用 0 和 1 两个数字表示数,逢 2 进一。
二进制与遵循十进制数遵循一样的运算规则,但显得比十进制更简单。
例如:(1)加法: 0+0=0 0+1=1 1+0=1 1+1=0(2)减法: 0-0=0 1-1=0 1-0=1 0-1=1(3)乘法: 0*0=0 0*1=0 1*0=0 1*1=1(4)除法: 0/1=0 1/1=1 ,除数不能为 0二、进制转换1.二进制与十进制数间的转换(1)二进制转换为十进制将每个二进制数按权展开后求和即可。
请看例题:把二进制数( 101.101 )2=1*2 2+0*2 1+1*20+1*2-1 +0*2-2 +1*2-3 =(5.625 ) 10二进制数转换为十进制数:二进制数第 0 位的权值是 2 的 0 次方,第 1 位的权值是 2 的 1 次方⋯⋯所以,设有一个二进制数: 0110 0100 ,转换为 10 进制为:下面是竖式:0110 0100 换算成十进制第0位0*2 = 01第1位0*2 = 02第2位1*2 = 43第3位0*2 = 04第4位0*2 = 05第5位1*2 =326第6位1*2 =647第7位0*2 = 0+---------------------------100用横式计算为:0 1 2 3 4 5 6 70 * 2+0*2 +1*2 +1*2 +0*2 +1*2 +1*2 +0*2 = 100 0 乘以多少都是0,所以我们也可以直接跳过值为0 的位:2 3 5 61*2 +1*2 + 1*2 +1*2 = 100(2)十进制转换为二进制一般需要将十进制数的整数部分与小数部分分开处理。
各种进制之间的转换方法

各种进制之间的转换方法进制是数学中用来表示数字的一种方法。
常见的进制包括二进制、八进制、十进制和十六进制。
不同进制之间的转换可以用以下方法实现。
一、二进制与八进制的互相转换:二进制转换为八进制:将二进制数从右到左按照三位一组进行分组,然后将每组转换为对应的八进制数即可。
从右到左分组得到:(1)(011)(101)(011)。
将每组转换为对应的八进制数:(1)(3)(5)(3)。
八进制转换为二进制:将八进制数的每个位转换为对应的三位二进制数即可。
例如:将八进制数652转换为二进制数。
将八进制数的每个位转换为对应的三位二进制数:(6)(5)(2)=(110)(101)(010)。
二、二进制与十进制的互相转换:二进制转换为十进制:将二进制数的每个位与其对应的权重相乘,再将乘积相加即可得到十进制数。
例如:将二进制数1101转换为十进制数。
将二进制数的每个位与其对应的权重相乘,并将乘积相加:1×2³+1×2²+0×2¹+1×2⁰=13因此,二进制数1101转换为十进制数为13十进制转换为二进制:将十进制数不断除以二,将余数从下到上排列即可得到二进制数。
例如:将十进制数25转换为二进制数。
将十进制数25不断除以二,将余数从下到上排列:25/2=12余1、12/2=6余0、6/2=3余0、3/2=1余1、1/2=0余1三、二进制与十六进制的互相转换:二进制转换为十六进制:将二进制数从右到左按照四位一组进行分组,然后将每组转换为对应的十六进制数即可。
从右到左分组得到:(1)(0110)(0110)。
将每组转换为对应的十六进制数:(1)(6)(6)。
十六进制转换为二进制:将十六进制数的每个位转换为对应的四位二进制数即可。
例如:将十六进制数F8转换为二进制数。
将十六进制数的每个位转换为对应的四位二进制数:F=1111、8=1000。
四、八进制与十进制的互相转换:八进制转换为十进制:将八进制数的每个位与其对应的权重相乘,再将乘积相加即可得到十进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代换法及二进制
代换法:
1、建筑工地用3辆卡车和9辆马车一次运来720袋水泥,已知3辆马车和1辆卡车装的水泥袋数同样多,请你算一算,1辆卡车和1辆马车每次各运水泥多少袋?
2、甲、乙两人共同生产一种零件,甲生产了8小时,乙生产了6小时,一共生产312个零件,已知乙5小时的工作量等于甲粘时的工作量。
甲生产了多少个零件?乙生产了多少个零件?
3、粮店用10辆汽车和20辆板车一次把42吨粮食运往仓库,每辆汽车比每辆板车多运2.4吨,每辆汽车和每辆板车各装运了多少吨粮食?
4、一批石油,如果用甲种油车装运需要20辆,如果用乙种油车装有25辆,已知甲种油车比乙种油车每辆多装2吨,求这批石油重多少吨?
5、古时候人们买东西时不用钱,而是用东西去换,设换的标准是20只兔子可以换2只羊,9只羊可以换3头猪,8头猪可以换2头牛,如果一个人伤脑筋1头牛去换兔子,可以换多少只?
6、一笔奖金分一等奖、二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的2倍,每个二等奖的奖金是每个三等奖奖金的2倍,如果评一、二、三等奖各两人,那么两个一等奖奖金是308元,如果评1个一等奖,2个二等奖,3个三等奖,那么一等奖的奖金是多少元?
二进制:
1、加法:(1)10110+1101 (2)1110+101011
2、减法:(1)110101-11110 (2)10001-1011
3、加减混合运算:(1)110101+1101-11111 (2)101101-11011+11011
4、乘法:(1)1001 ⨯101 (2)11001 ⨯1010
5、除法:(1)10100010 ÷1001 (2)10010011 ÷111
6、二进制化十进制:(1)(2)110101=
(10)。
(2)(2)1011001=
(10)。
7、十进制化二进制:(1)317(10)= (2)
(2)509(10)= (2)
8、计算:(1)(2)(2)(2)11011(10111)⨯+
(2)(2)(2)(2)(100100101101101)101+÷。
