政和一中2010—2011学年(上)高三第二次月考数学试卷(文科)
政和一中2010—2011学年(上)高三第二次月考数学试卷(文科)

政和一中2010—2011学年(上)高三第二次月考数学试卷(文科)(时间:120分种,满分150分)一、选择题。
(每小题5分,共60分)1、若集合A={x ∣x >0} B={ x ∣<3},则A ⋂B 等于( )A 、{x ∣x >0}B 、{x ∣0<x <3}C 、{ x ∣x >3}D 、R2、“tana=1”是“a=4π”的( )A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分也不必要条件3、下列函数中,与函数y=x1有相同定义域是( )A 、f(x)=lnxB 、f(x)=x1C 、f(x)=xD 、f(x)=e x4、已知锐角△ABC 的面积为33,BC=4,CA=3则角C 大小为( )A 、75°B 、60°C 、45°D 、30° 5、函数f(x)=x 3+sinx+1(x ∈R)若f(a)=2则f(-a)的值是( )A 、3B 、0C 、-1D 、-26、已知曲线y=24x 的一条切线的斜率为21,则切点的横坐标为( )A 、1B 、2C 、-1D 、-27、若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x),在区间[a,b]上的图象可能是( )A B C D8、已知函数f(x)=⎩⎨⎧+-+22x x ()0)0(>≤x x 则不等式f(x)≥x 2的解集( )A 、[-1,1]B 、[-2,2]C 、[-2,1]D 、[-1,2] 9、定义在R 上的函数f(x)对任意两个不等实数a,b 总有ba b f a f --)()(>0成立,则必有( )A 、函数f(x)是先增后减函数B 、函数f(x)是先减后增函数C 、f(x)在R 上是增函数D 、f(x)在R 上是减函数10、若函数f(x)=x 3+ax 2+bx-7在R 上单调递增,则实数a,b 一定满足条件是( )A 、a 2-3b ≤0B 、a 2-3b >0C 、a 2-3b=0D 、a 2-3b <111、将函数f (x )=sin(ax+φ)的图象向左平移2π个单位,若所得图象与原图象重合,则a 的值不可能等于( )A 、4B 、6C 、8D 、1212、已知f(x)是周期为2的奇函数,当0<x <1时,f(x)=lgx ,设a=f(56) b=f(23) c=f(25)则( )A 、a <b <cB 、b <a <cC 、c <b <aD 、c <a <b二、填空题(每小题4分,共16分)13、设集合A={1,3,a},B={1,a 2-a+1}且A ⊇B ,则a 的值为 14、方程2-x +x 2=3的零点个数为 15、函数y=3x 2-2lnx 的单调递减区间是16、已知tan α,tan β是方程x 2+33x+4=0的两个根,且α,β∈(0,2π)则α+β的值为三、解答题(共74分)17、命题p :关于x 的不等式x 2+2ax+4>0,对一切x ∈R 恒成立,q :函数f(x)=(3-2a )x 是增函数,若p 或q 为真,p 且q 为假,求实数a 的取值范围。
2010~2011学年上学期政和一中高二期末考
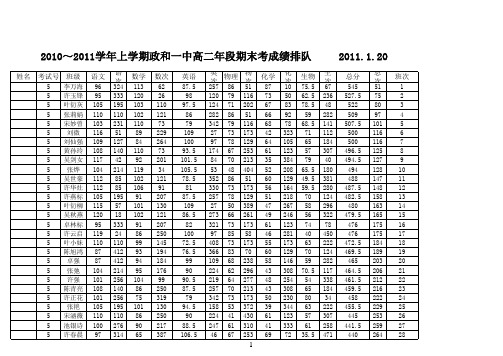
总次
266 271 275 295 297 304 325 326 326 335 338 357 362 366 366 368 376 383 390 401 412 413 416 418 428 433 444 445 451 459
班次
29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58
总分
307.5 297.5 295 241.5
总次
466 474 476 494
班次
59 60 61 62
平均分 及格人数 及格率 优秀人数
0
62 99.3 51 82% 1
62 80.0 24 39% 1
61 81.7 22 36% 0
62 60.3 36 58% 7
62 45.9 14 23% 1
语文 语次 数学
104 106 97 93 102 106 93 96 91 111 97 86 91 92 89 105 78 102 88 93 105 91 92 95 104 114 99 115 92 66 214 179 314 352 249 179 352 324 374 95 314 419 374 362 394 195 469 249 409 352 195 374 362 333 214 68 285 57 362 490 49 40 99 77 75 75 102 65 102 72 87 63 60 68 75 64 59 88 77 67 44 77 55 53 52 18 63 63 54 82
总次
51 75 80 97 101 116 116 125 127 128 147 148 158 163 165 175 175 184 189 203 206 212 216 222 229 253 259 264
政和一中2011届_9

政和一中2011届高三第二次月考政治试题(非答案卷)(总分:100分考试时间:90分钟)一、单项选择题:(请将正确的答案填涂到答题卡上,每小题2分,30题,共60分)1.某生产部门去年的劳动生产率是每小时生产1件商品,价值用货币表示为65元。
该部门今年的劳动生产率提高了30%。
假定甲生产者今年的劳动生产率是每小时生产2件商品,在其他条件不变的情况下,甲生产者1小时内创造的价值总量用货币表示为()A. 91元B. 100元C. 130元D. 194元2.近年来,一些地方名贵特产在商家疯狂炒作下,价格一路飙升,频频刷新“天价”。
江苏名产阳澄湖大闸蟹运至北京超市,卖到每斤328元;在青海,一公斤上等冬虫夏草,价格已达20万元,每克价格超过黄金;新疆和田玉中仔玉以克论价,精品每克高达数万元,真正演绎了“疯狂的石头”。
如此离谱的商业炒作实在应当“悬崖勒马”。
“天价商品”之所以要“悬崖勒马”,根本原因在于()A. “天价”商品扰乱了正常的市场秩序B. 违背市场规律的“天价”商品会影响其价值的实现C. 商品的价格必须要考虑消费者的承受能力D. 商品的价格尽管会受供求关系的影响,但最终由其价值决定3.国家统计局2009年10月22日发布的数据显示,前三季度我国居民消费价格指数(CPI)同比下降1.1%。
在其他条件不变的前提下,CPI指数下降可能会()①提高居民购买力②刺激企业提高劳动生产率③急剧降低人们消费水平④促使企业生产适销对路的高质量产品A. ①②③B. ①②④C. ①③④D. ②③④4.2009年央视春晚人气最旺的节目是赵本山和小沈阳的小品《不差钱》。
这个小品推出的几句台词随后已成为人们茶余饭后的谈资,尤其那句“人最痛苦的事是人死了钱没花完了”成为新的流行语。
从消费的角度看,这句经典台词告诫我们的是 ( )A. 要量入为出,适度消费B. 要避免盲从,理性消费C. 要保护环境,绿色消费D. 要勤俭节约,艰苦奋斗2009年7月23日,中共中央政治局召开会议,研究了当前经济形势和经济工作。
高三年级文科数学第二次月考试题

高三年级文科数学第二次月考试题总分:150分 考试时刻:120分钟第Ⅰ卷(选择题 共50分)一、选择题(本大题共12小题,每小题5分,共60分,每小题中给出四个选项,只有一项是符合题目要求的) 1.2sin210°的值是 ( )A .1B .-1C .3D .-3 2.不等式x x >2的解集是( )A .(-∞,0)B .(0,1)C .(1,+∞)D .(-∞,0) (1,+∞)3.等差数列n a a a a a n n 则已知中,10,7,1,}{521==+=为 ( )A .8B .9C .10D .114.命题, “若a>b ,则88->-b a ”的逆否命题是( ) A .若a>b ,则88-<-b a B .若88->-b a ,则a>b C .若a ≤b ,则88-≥-b a D .若88-≤-b a ,则a ≤b 5.若奇函数=+-==∈)1(),2()2()(,1)2())((f f x f x f f R x x f 则满足 ( )A .0B .1C .-21D .21 6.下列各式中,值为23的是( )A .︒⋅︒15cos 15sin 2B .︒-︒15sin 15cos 22C .115sin 22-︒D . ︒+︒15sin 15cos 227.在等比数列435421,27,1,}{a a a a a a a n +=+=+则中 ( )A .3B .18C .9D .81 21 )9.设)4tan(,41)4tan(,52)tan(ππ+=-=+x y y x 则的值为 ( )A .223 B .183 C .1813D .221310.将函数)1,6()32sin(3--=+=ππa x y 的图象按向量平移后所得函数的图象的解析式是( )A .1)322sin(3-+=πx y B .1)322sin(3++=πx yC .12sin 3+=x yD .1)32sin(3-+=πx y11.函数⎪⎭⎫⎝⎛-=32sin 3)(πx x f 的图像为C ,以下三个论断中,正确论断的个数是 ( )①图像C 关于直线π1211=x 对称;②函数⎪⎭⎫⎝⎛-125,12)(ππ在区间x f 内是增函数; ③由32sin 3π的图像向右平移x y =个单位长度能够得到图像C.A .0B .1C .2D .312.已知函数),2[)2(log 22+∞∈+-=x ax x y 在上恒为正,则a 的取值范畴是 ( ) A .(-2,2) B .]4,(-∞C .)25,(-∞D .),22()22,(+∞--∞二、填空题(本大题共4个小题,每小题4分,共16分)13.已知ααα则角,0tan ,0sin <>的终边在第 象限.14.已知数列}{n a 的前n 项和n n a n n S 则其通项,2+== .15.已知等比数列的公比10099531,60,21S a a a a q 则且=++++== . 16.函数x x y sin 2cos -=的最小为 .三、解答题(本大题共6小题,满分74分,解承诺写出文字说明、证明过程或演算步骤)17.(13分)已知数列}{n a 为等差数列,n S 为其前n 项和,且.4,3422S S a == (1)求证:数列}2{n a是等比数列; (2)求使得n n S S 22>+成立的n 的集合.18.(13分)已知α为第二象限角,βα,53sin =为第三象限角,.34tan =β (1)求)tan(βα+的值; (2)求)2cos(βα-的值.19.(12分)已知函数)0(,2cos26sin 6sin )(2>∈-⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛+=ωωπωπωR x x x x x f (1)求函数)(x f 的值域;(2)若函数y=)(x f 的图象与直线y=-1的两个相邻交点的距离为2π,求函数y=)(x f 的单调递增区间.20.(12分)已知数列}{n a 的前n 项的和为S n ,且 3,2,1,21,111===+n S a a n n 求:(1)数列}{n a 的通项公式; (2)n a a a a 2642++++ 的值.21.(12分)某商品每件成本9元,售价30元,每星期卖出432件.假如降低价格,销售量能够增加,且每星期多卖出的商品件数与商品单价的降低值x (单位:元,300≤≤x )的平方成正比,已知商品单价降低2元时,一星期多卖出24件. (1)将一个星期的商品销售利润表示成x 的函数; (2)如何定价才能使一个星期的商品销售利润最大?22.(12分)已知α为锐角,且,12tan -=α函数),42sin(2tan )(2παα+⋅+=x x x f 数列}{n a 的首项)(,2111n n a f a a ==+. (1)求函数)(x f 的表达式; (2)求证:;1n n a a >+ (3)求证:*),2(2111111121N n n a a a n∈≥<++++++<参考答案一、选择题1.B 2.D 3.C 4.D 5.D 6.B 7.C 8.D 9.A 10.A 11.C 12.C 二、填空题13.三 14.2n 15.90 16.-2 三、解答题17.(1)由题,⎩⎨⎧+=+⨯=+d a d a d a 64)2(43111(3分)故122,11-=∴==n a d a n (5分,4222232121==∴---n n a a n n 即数列为等比数列 (7分)(2)由21,12,2,1n S n a d a n n =-===得 (9分)8)2(2)2(22222<-⇒>+⇒>∴+n n n S S n n (11分)4,3,2,1=∴n (12分)故n 的集合为:{1,2,3,4}(13分) 18.解:(1)因为α是第二象限的角,,53sin =α 54sin 1cos 2=--=αα所以 (2分) 43cos sin tan -==ααα (3分) 247tan tan 1tan tan )tan(=++=+∴βαβαβα (6分)(2)因为β为第三象限的角,34tan =β 53cos ,54sin -=-=∴ββ (9分)又,2524cos sin 22sin -==ααα257sin 12cos 2=-=αα (11分) 53sin 2sin cos 2cos )2cos(=+=-∴βαβαβα(13分)19.(1)解:)1(cos cos 21sin 23cos 21sin 23)(+--++=x x x x x x f ωωωωω(2分) 1cos 21sin 232-⎪⎪⎭⎫ ⎝⎛-=x x ωω .16sin 2-⎪⎭⎫ ⎝⎛-=πωx (5分)由.116sin 23,16sin 1≤-⎪⎭⎫ ⎝⎛-≤-≤⎪⎭⎫⎝⎛-≤-πωπωx x 得 可知函数)(x f 的值域为[-3,1].(7分)(2)解:由题设条件及三角函数图象和性质可知,)(x f y =的周期为π, 又由2,2,0==>w w即得得ππω(9分) 因此有)(222221)62sin(2)(z k k x k x x f ∈+≤≤---=πππππ再由解得)(36Z k kx x k ∈+≤≤-πππ(11分)因此)(x f y =的单调增区间为)(3,6Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ (12分) 20.(1)由题,)2(23)2(1212111≥=⇒≥⎪⎪⎩⎪⎪⎨⎧-==++n a a n S a S a n n n n nn (3分) 即2}{a a n 是以为首项,以23为公比的等比数列(4分) 又212121112===a S a (5分) 故)2(2322≥⎪⎭⎫⎝⎛⨯=-n a a n n (6分)⎪⎩⎪⎨⎧≥⎪⎭⎫ ⎝⎛⋅==∴-2,23211,12n n a n n (8分)(2)n a a a a 2642++++⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=-nn 491522323231212242 (12分)21.解:(1)设商品降价x 元,则多卖的商品数为2kx ,若记商品在一个星期的获利为)(x f ,则依题意有)432)(21()432)(930()(22kx x kx x x f +-=+--= (4分)又由已知条件,2224⋅=k ,因此有k=6(5分)因此]30,0[,90724321266)(23∈+-+-=x x x x x f (6分)(2)依照(1),我们有).12)(2(1843225218)(2---=-+-='x x x x x f (8分)故)(,12x f x 时=达到极大值,因为,11264)12(,9072)0(==f f 因此定价为30-12=18元能使一个星期的商品销售利润最大.(12分) 22.(13分)解:(1)1)12(1)12(2tan 1tan 22tan 22=---=-=ααα 又α 是锐角 42πα=∴1)42sin(=+∴πα x x x f +=2)( (4分)(2)n n n a a a +=+21n a a a a ,,21321∴=都大于0 n n n a a a >∴>∴+120(6分)(3)nn n n n n n a a a a a a a +-=+=+=+111)1(1112111111+-=+∴n n n a a a1322121111111111111+-++-+-=++++++∴n n n a a a a a a a a a 1111211++-=-=n n a a a (9分)143)43(,4321)21(2322>+==+=a a又n n a a n >≥+1,221211131<-<∴>≥∴++n n a a a2111111121<++++++<∴na a a (12分)。
福建省南平市政和一中2015-2016学年高二下学期第二次

2015-2016学年福建省南平市政和一中高二(下)第二次月考数学试卷(文科)一、选择题(本大题共12小题,共60.0分)1.已知集合A={﹣1,0,1,2,3}B={x|x2>1},则A∩∁R B=()A.{0}B.{﹣1,0,1}C.{﹣1,1,2,3} D.{﹣1,0,1,2,3}2.命题“若∠C=90°,则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是()A.0 B.1 C.2 D.33.已知函数f(x)=,则f(1)+f(﹣1)的值是()A.0 B.2 C.3 D.44.已知条件p:x2﹣3x﹣4≤0,条件q:x2﹣6x+9﹣m2≤0.若p是q的充分不必要条件,则m的取值范围是()A.[﹣1,1]B.[﹣4,4]C.(﹣∞,﹣4]∪[4,+∞)D.(﹣∞,﹣1]∪[4,+∞)5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是()A.B.C.D.6.函数f(x)=的定义域为()A .(﹣∞,﹣2)∪(1,+∞)B .(﹣2,1)C .(﹣∞,﹣1)∪(2,+∞)D .(1,2)7.若函数f (x )是定义在R 上的奇函数,则函数F (x )=|f (x )|+f (|x |)的图象一定关于( ) A .x 轴对称B .y 轴对称C .原点对称D .直线y=x 对称8.设a=0.23,b=log 20.3,c=log 0.32,则( ) A .b <a <c B .b <c <a C .c <b <a D .a <b <c9.已知定义在R 上的奇函数f (x )满足f (2+x )=f (﹣x ),当0≤x ≤1时,f (x )=x 2,则f A .﹣1 B .1C .0D .2015210.下面是函数f (x )在区间[1,2]上的一些点的函数值由此可判断:方程f (x )=0在[1,2]解的个数( ) A .至少5个B .5个C .至多5个D .4个11.设函数f (x )=x +(0≤x ≤2),若当x=0时函数值最大,则实数a 的取值范围是( ) A .a ≥1B .a ≤1C .a ≥3D .a≤312.已知函数f (x )=lnx ﹣x﹣1,g (x )=x 2﹣2bx +4,若对任意x 1∈(0,2),存在x 2∈[1,2],使f (x 1)≥g (x 2),则实数b 的取值范围是( ) A .(2,]B .[1,+∞)C .[,+∞) D .[2,+∞)二、填空题(本大题共4小题,共20.0分)13.命题“存在 x >1,x 2+(m ﹣3)x +3﹣m <0”的否定是 . 14.计算:0.25×(﹣)﹣4+lg8+3lg5= . 15.函数y=log(x 2﹣3x +2)的递增区间是 .16.若函数f(x)=的部分图象如图所示,则b=.三、解答题(本大题共7小题,共84.0分)17.已知集合A={x|x2+ax+12b=0},集合B={x|x2﹣ax+b=0},满足2∈(∁U A)∩B,4∈A∩(∁U B),U=R,求实数a,b的值.18.设函数的定义域为集合A,函数的定义域为集合B.(I)求的值;(II)求证:a≥2是A∩B=∅的充分非必要条件.19.设函数f(x)=e x+ax+b在点(0,f(0))处的切线方程为x+y+1=0.(Ⅰ)求a,b值,并求f(x)的单调区间;(Ⅱ)证明:当x≥0时,f(x)>x2﹣4.20.已知某厂每天的固定成本是20000元,每天最大规模的产品量是350件.每生产一件产品,成本增加100元,生产x件产品的收入函数是R(x)=﹣x2+400x,记L(x),P(x)分别为每天的生产x件产品的利润和平均利润(平均利润=).(1)每天生产量x为多少时,利润L(x)有最大值?;(2)每天生产量x为多少时,平均利润P(x)有最大值?若该厂每天生产的最大规模为180件,那么每天生产量x为多少时,平均利润P(x)有最大值?21.已知函数f(x)=x 3﹣bx 2+2cx的导函数的图象关于直线x=2对称.(1)求b的值;(2)若函数f(x)无极值,求c的取值范围;(3)若f(x)在x=t处取得极小值,求此极小值为g(t)的取值范围.22.如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,弦BD∥MN,AC与BD相交于点E.(Ⅰ)求证:△ABE≌△ACD;(Ⅱ)若AB=6,BC=4,求的值.23.极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为(t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ.(1)求C的直角坐标方程;(2)设直线l与曲线C交于A,B两点,求弦长|AB|.2015-2016学年福建省南平市政和一中高二(下)第二次月考数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,共60.0分)1.已知集合A={﹣1,0,1,2,3}B={x|x2>1},则A∩∁R B=()A.{0}B.{﹣1,0,1}C.{﹣1,1,2,3} D.{﹣1,0,1,2,3}【考点】交、并、补集的混合运算.【分析】根据集合的运算法则求解即可.【解答】解:∵B={x|x2>1}={x|x<﹣1或x>1},∴∁R B={x|﹣1≤x≤1},∴A∩∁R B={﹣1,0,1},故选B.2.命题“若∠C=90°,则△ABC是直角三角形”与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数是()A.0 B.1 C.2 D.3【考点】四种命题的真假关系.【分析】直接判断原命题真假,写出原命题的逆命题,判断其真假,然后结合原命题的逆命题与否命题互为逆否命题,再根据互为逆否命题的两个命题共真假加以判断.【解答】解:命题“若∠C=90°,则△ABC是直角三角形”是真命题,∴其逆否命题也为真命题.原命题的逆命题为:“若△ABC是直角三角形,则∠C=90°”是假命题(△ABC是直角三角形不一定角C为直角),∴原命题的否命题也是假命题.∴真命题的个数是2.故选:C.3.已知函数f(x)=,则f(1)+f(﹣1)的值是()A.0 B.2 C.3 D.4【考点】函数的值.【分析】根据f(x)=,将x=1,和x=﹣1代入可得答案.【解答】解:∵函数f(x)=,∴f(1)=1,f(﹣1)=3,∴f(1)+f(﹣1)=4,故选:D.4.已知条件p:x2﹣3x﹣4≤0,条件q:x2﹣6x+9﹣m2≤0.若p是q的充分不必要条件,则m的取值范围是()A.[﹣1,1]B.[﹣4,4]C.(﹣∞,﹣4]∪[4,+∞)D.(﹣∞,﹣1]∪[4,+∞)【考点】必要条件、充分条件与充要条件的判断.【分析】先将条件p,q化简,然后利用p是q的充分不必要条件,确定参数a的取值范围.【解答】解:由x2﹣3x﹣4≤0得﹣1≤x≤4,即p:﹣1≤x≤4,由x2﹣6x+9﹣m2≤0得[x﹣(3﹣m)][x﹣(3+m)]≤0,①若m≥0,则不等式等价为3﹣m≤x≤3+m,若p是q的充分不必要条件,则,即,解得m≥4.②若m<0,则不等式等价为3+m≤x≤3﹣m,若p是q的充分不必要条件,则,即,解得m≤﹣4.综上m≥4或m≤﹣4,故m的取值范围是(﹣∞,﹣4]∪[4,+∞).故选:C5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是()A.B.C.D.【考点】函数的表示方法.【分析】解答本题,可先研究四个选项中图象的特征,再对照小明上学路上的运动特征,两者对应即可选出正确选项【解答】解:考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图象一定是下降的,由此排除A;再由小明骑车上学,开始时匀速行驶可得出图象开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图象与x轴平行,由此排除D,之后为了赶时间加快速度行驶,此一段时间段内函数图象下降的比较快,由此可确定C正确,B不正确.故选:C6.函数f(x)=的定义域为()A.(﹣∞,﹣2)∪(1,+∞)B.(﹣2,1)C.(﹣∞,﹣1)∪(2,+∞)D.(1,2)【考点】函数的定义域及其求法.【分析】根据函数f(x)的解析式,列出不等式组求出解集即可.【解答】解:函数f(x)=,∴,解得,即x<﹣1或x>2;∴f(x)的定义域为(﹣∞,﹣1)∪(2,+∞).故选:C.7.若函数f(x)是定义在R上的奇函数,则函数F(x)=|f(x)|+f(|x|)的图象一定关于()A.x轴对称B.y轴对称C.原点对称D.直线y=x对称【考点】函数奇偶性的判断.【分析】根据函数奇偶性的定义和性质进行判断即可.【解答】解:∵函数f(x)是定义在R上的奇函数,∴F(﹣x)=|f(﹣x)|+f(|﹣x|)=|﹣f(x)|+f(|x|)=|f(x)|+f(|x|)=F(x),即函数F(x)是偶函数,则图象关于y轴对称,故选:B8.设a=0.23,b=log20.3,c=log0.32,则()A.b<a<c B.b<c<a C.c<b<a D.a<b<c【考点】对数值大小的比较.【分析】根据对数函数和指数函数比较a,b,c与0,﹣1,的关系,即可得到答案【解答】解:∵0<0.23<1,b=log20.3<log20.5=﹣1,log0.32>log0.3=﹣1,∴b<c<a,故选:B.9.已知定义在R上的奇函数f(x)满足f(2+x)=f(﹣x),当0≤x≤1时,f(x)=x2,则fA.﹣1 B.1 C.0 D.20152【考点】函数奇偶性的性质.【分析】由奇函数的性质和f(2+x)=f(﹣x),求出函数的最小正周期,利用函数的周期性和奇偶性将f,再代入已知的解析式求值.【解答】解:由题意得,f(x)是定义在R上的奇函数,所以f(2+x)=f(﹣x)=﹣f(x),则f(x+4)=﹣f(x+2)=f(x),所以函数f(x)是以4为最小正周期的周期函数,因为当0≤x≤1时,f(x)=x2,则f=f(3)=f(﹣1)=﹣f(1)=﹣1,故选:A.10.下面是函数f(x)在区间[1,2]上的一些点的函数值由此可判断:方程f(x)=0在[1,2]解的个数()A.至少5个B.5个 C.至多5个D.4个【考点】二分法求方程的近似解.【分析】利用表格中的函数值,即可确定方程f(x)=0的近似解.【解答】解:由所给的函数值的表格可以看出,在x=1.25与x=1.375这两个数字对应的函数值的符号不同,即f(1.25)f(1.375)<0,∴函数的一个零点在(1.25,1.375)上,同理:函数的一个零点在(1.375,1.4065)上,函数的一个零点在(1.4065,1.438)上,函数的一个零点在(1.5,1.61)上,函数的一个零点在(1.61,1.875)上,故答案为:A.11.设函数f(x)=x+(0≤x≤2),若当x=0时函数值最大,则实数a的取值范围是()A.a≥1 B.a≤1 C.a≥3 D.a≤3【考点】函数的最值及其几何意义.【分析】根据条件确定f(0)≥f(2),可得a≥2+,即可求出实数a的取值范围.【解答】解:设x+1=t,则1≤t≤3,∴y=t+﹣1,∴y′=1﹣,∵当x=0时函数值最大,∴当t=1时函数值最大,∴f(0)≥f(2),∴a≥2+,∴a≥3,故选:C.12.已知函数f(x)=lnx﹣x﹣1,g(x)=x2﹣2bx+4,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),则实数b的取值范围是()A.(2,]B.[1,+∞)C.[,+∞) D.[2,+∞)【考点】利用导数求闭区间上函数的最值.【分析】首先对f(x)进行求导,利用导数研究函数f(x)的最值问题,根据题意对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),只要f(x)的最小值大于等于g(x)的最小值即可,对g(x)的图象进行讨论根据对称轴研究g(x)的最值问题,从而进行求解;【解答】解:∵函数f(x)=lnx﹣x﹣1,(x>0)∴f′(x)=﹣+==,若f′(x)>0,1<x<3,f(x)为增函数;若f′(x)<0,x>3或0<x<1,f(x)为减函数;f(x)在x∈(0,2)上有极值,f(x)在x=1处取极小值也是最小值f(x)min=f(1)=﹣+﹣1=﹣;∵g(x)=x2﹣2bx+4=(x﹣b)2+4﹣b2,对称轴x=b,x∈[1,2],当b<1时,g(x)在x=1处取最小值g(x)min=g(1)=1﹣2b=4=5﹣2b;当1<b<2时,g(x)在x=b处取最小值g(x)min=g(b)=4﹣b2;当b>2时,g(x)在[1,2]上是减函数,g(x)min=g(2)=4﹣4b+4=8﹣4b;∵对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),∴只要f(x)的最小值大于等于g(x)的最小值即可,当b<1时,≥5﹣2b,解得b≥,故b无解;当b>2时,≥8﹣4b,解得b≥,综上:b≥,故选C;二、填空题(本大题共4小题,共20.0分)13.命题“存在x>1,x2+(m﹣3)x+3﹣m<0”的否定是∀x>1,x2+(m﹣3)x+3﹣m≥0.【考点】命题的否定.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以命题”存在x>1,x2+(m﹣3)x+3﹣m<0”的否定是:∀x>1,x2+(m﹣3)x+3﹣m≥0.故答案为:∀x>1,x2+(m﹣3)x+3﹣m≥014.计算:0.25×(﹣)﹣4+lg8+3lg5=7.【考点】对数的运算性质.【分析】由题,直接根据指数的运算法则与对数的运算法则进行化简即可得到答案【解答】解:原式=×24+3lg 2+3lg 5=4+3=7.故答案为7.15.函数y=log(x2﹣3x+2)的递增区间是(﹣∞,1).【考点】对数函数的单调区间.【分析】由x2﹣3x+2>0得x<1或x>2,由于当x∈(﹣∞,1)时,f(x)=x2﹣3x+2单调递减,由复合函数单调性可知y=log 0.5(x2﹣3x+2)在(﹣∞,1)上是单调递增的,在(2,+∞)上是单调递减的.【解答】解:由x2﹣3x+2>0得x<1或x>2,当x∈(﹣∞,1)时,f(x)=x2﹣3x+2单调递减,而0<<1,由复合函数单调性可知y=log 0.5(x2﹣3x+2)在(﹣∞,1)上是单调递增的,在(2,+∞)上是单调递减的.故答案为:(﹣∞,1)16.若函数f(x)=的部分图象如图所示,则b=﹣4.【考点】函数的图象.【分析】由题意可得函数y=ax2+bx+c的图象与x轴的两个交点为(1,0)、(3,0),a>0,它的最小值为=﹣1,再利用韦达定理求得b的值.【解答】解:由函数f(x)=的部分图象,可得函数y=ax2+bx+c的图象与x轴的两个交点为(1,0)、(3,0),a>0,函数y=ax2+bx+c的最小值为=﹣1①.利用韦达定理可得1+3=﹣②,1×3=③.由①②③求得b=﹣4,故答案为:﹣4.三、解答题(本大题共7小题,共84.0分)17.已知集合A={x|x2+ax+12b=0},集合B={x|x2﹣ax+b=0},满足2∈(∁U A)∩B,4∈A∩(∁U B),U=R,求实数a,b的值.【考点】交、并、补集的混合运算.【分析】利用(C U A)∩B={2},A∩(C U B)={4},判断2,4与集合A、B的关系,得到方程组求出a,b即可.【解答】解:因为2∈(∁U A)∩B,4∈A∩(∁U B),所以2∈B,4∈A,∴,解得.18.设函数的定义域为集合A,函数的定义域为集合B.(I)求的值;(II)求证:a≥2是A∩B=∅的充分非必要条件.【考点】充要条件;函数的值.【分析】(I)判断函数f(x)的奇偶性,进而根据奇偶性可得的值;(II)分别求出A,B,分别讨论是a≥2⇒A∩B=∅与A∩B=∅⇒a≥2的真假,进而根据充要条件的定义可证得结论.【解答】解:(I)由题意得A={x|>0}={x|}=(﹣1,1)又∵=,∴f(﹣x)===﹣=﹣f(x)∴f(x)是奇函数∴=0(II)B={x|1﹣a2﹣2ax﹣x2≥0}=[﹣1﹣a,1﹣a]当a≥2时,1﹣a≤﹣1,此时A∩B=∅当A∩B=∅时,1﹣a≤﹣1,或﹣1﹣a≥1,即a≥2,或a≤﹣2故a≥2是A∩B=∅的充分非必要条件19.设函数f(x)=e x+ax+b在点(0,f(0))处的切线方程为x+y+1=0.(Ⅰ)求a,b值,并求f(x)的单调区间;(Ⅱ)证明:当x≥0时,f(x)>x2﹣4.【考点】利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求函数的导数,利用导数的几何意义以及切线方程建立方程关系即可求a,b值以及f(x)的单调区间;(Ⅱ)构造函数,利用导数研究函数的单调性和最值关系即可证明不等式.【解答】解:(Ⅰ)f′(x)=e x+a,由已知,f′(0)=﹣1,f(0)=﹣1,故a=﹣2,b=﹣2,f′(x)=e x﹣2,当x∈(﹣∞,ln2)时,f′(x)<0,当x∈(ln2,+∞)时,f′(x)>0,故f(x)在(﹣∞,ln2)单调递减,在(ln2,+∞)单调递增;…(Ⅱ)设g(x)=f(x)﹣(x2﹣4)=e x﹣x2﹣2x+2,g′(x)=e x﹣2x﹣2=f(x)在(ln2,+∞)单调递减,在(﹣∞,ln2)单调递增,因为g′(0)=﹣1<0,g′(2)=e2﹣6>0,0<ln2<2,所以g′(x)在[0,+∞)只有一个零点x0,且x0∈(0,2),=2x0+2,当x∈[0,x0)时,g′(x)<0,当x∈(x0,+∞)时,g′(x)>0,即g(x)在[0,x0)调递减,在(x0,+∞)时,单调递增,当x≥0时,g(x)≥g(x0)==4﹣>0,即f(x)>x2﹣4,…20.已知某厂每天的固定成本是20000元,每天最大规模的产品量是350件.每生产一件产品,成本增加100元,生产x件产品的收入函数是R(x)=﹣x2+400x,记L(x),P(x)分别为每天的生产x件产品的利润和平均利润(平均利润=).(1)每天生产量x为多少时,利润L(x)有最大值?;(2)每天生产量x为多少时,平均利润P(x)有最大值?若该厂每天生产的最大规模为180件,那么每天生产量x为多少时,平均利润P(x)有最大值?【考点】函数模型的选择与应用.【分析】(1)根据利润=销售收入﹣成本,结合销售收入函数,利用配方法,即可得出结论;(2)求出平均利润P(x),利用导数知识,确定函数的单调性,即可求出最大值.【解答】解:(1)依题意得利润,x∈(0,320]……∵x∈(0,320],∴当x=300时,L(x)有最大值…(2)依题意得,x∈(0,320]…,当x∈(0,200)时,P'(x)>0,P(x)在(0,200)递增,当x∈时,P'(x)>0,P(x)在(0,200)递增…∴当x=200时,P(x)有最大值…若x∈(0,180],由上可知P(x)在(0,180]上为增函数,∴当x=180,平均利润P(x)有最大值…答:(1)当产量为300件时,L(x)有最大值;(2)当产量为200时,P(x)有最大值,若该最大产量为180件时,则当产量为180时,P(x)有最大值…21.已知函数f(x)=x 3﹣bx 2+2cx的导函数的图象关于直线x=2对称.(1)求b的值;(2)若函数f(x)无极值,求c的取值范围;(3)若f(x)在x=t处取得极小值,求此极小值为g(t)的取值范围.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(1)先求导函数,根据导函数的图象关于直线x=2对称,可知﹣=2,从而可求b的值;(2)函数f(x)无极值,即导函数为0的方程至多有一解,从而可求c的取值范围;(3)由(2)知,c<6,f'(x)=0有两个异实根x1,x2,不妨设x1<x2,则x1<2<x2,易得f(x)在x=x1处取极大值,在x=x2处取极小值,且x2>2,可知函数g (t)的定义域为(2,+∞),根据f'(t)=3t2﹣12t+2c=0得2c=﹣3t2+12t.从而可得g(t)=f(t)=t3﹣6t2+(﹣3t2+12t)t=﹣2t3+6t2,再利用函数g(t)在区间(2,+∞)内是减函数,可求函数g(t)的取值范围.【解答】解:(1)f'(x)=3 x 2﹣2 bx+2 c,∵f'(x)关于直线x=2对称,∴=2,即b=6.(2)由(1)知f(x)=x 3﹣6 x 2+2 cx,f'(x)=3 x 2﹣12 x+2 c=3(x﹣2)2+2 c﹣12,当2 c﹣12≥0,即c≥6时,f'(x)≥0,此时f(x)无极值.(3)当c<6时,f'(x)=0有两个相异实根为x 1,x 2,不妨设x 1<x 2,则x 1<2<x 2,当x<x 1时,f'(x)>0,f(x)在(﹣∞,x 1)上单调递增,当x 1<x<x 2时,f'(x)<0,f(x)在(x 1,x 2)上单调递减,当x>x 2时,f'(x)>0,f(x)在(x 2,+∞)上单调递增,∴f(x)在x=x 1处取得极大值,在x=x 2处取得极小值,所以t=x 2>2,∴f'(t)=3 t 2﹣12 t+2 c=0得2 c=﹣3 t 2+12 t,∴g(t)=f(t)=t 3﹣6 t 2+(﹣3 t 2+12 t)t=﹣2 t 3+6 t 2,t∈(2,+∞),而g'(t)=﹣6 t 2+12 t=﹣6 t(t﹣2)<0,∴g(t)在(2,+∞)上单调递减,∴g(t)<g(2)=﹣2•2 3+6﹣2 2=8,∴g(t)<8.22.如图△ABC内接于圆O,AB=AC,直线MN切圆O于点C,弦BD∥MN,AC与BD相交于点E.(Ⅰ)求证:△ABE≌△ACD;(Ⅱ)若AB=6,BC=4,求的值.【考点】与圆有关的比例线段.【分析】(Ⅰ)在两个三角形中,证明两个三角形全等,找出三角形全等的条件,根据同弧所对的圆周角相等,根据所给的边长相等,由边角边确定两个三角形是全等三角形.(Ⅱ)证明△ABE与△DEC相似,得到对应边成比例,利用BD∥MNDC=BC=4,即可求的值.【解答】(Ⅰ)证明:由题意∠BAE=∠EDC∵BD∥MN∴∠EDC=∠DCN∵直线是圆的切线,∴∠DCN=∠CAD∴∠BAE=∠CAD在△ABE和△ACD中,∵AB=AC,∠ABE=∠ACD,∠BAE=∠CAD,∴△ABE≌△ACD(Ⅱ)解:∵∠ABE=∠DCE,∠AEB=∠DEC∴△ABE∽△DEC∴∵BD∥MN,∴DC=BC=4,∴=.23.极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为(t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ.(1)求C的直角坐标方程;(2)设直线l与曲线C交于A,B两点,求弦长|AB|.【考点】简单曲线的极坐标方程.【分析】(1)对极坐标方程两边同乘ρ即可得到普通方程;(2)将直线参数方程代入曲线普通方程解出A,B两点对应的参数关系,利用参数得几何意义得出|AB|.【解答】解:(1)∵ρsin2θ=8cosθ,∴ρ2sin2θ=8ρcosθ,∴曲线C的直角坐标方程是:y2=8x.(2)直线的参数方程标准形式为,代入y2=8x得3t2=8(2+t),即3t2﹣16t﹣64=0.设AB对应的参数分别为t1,t2,则t1+t2=,t1t2=﹣.∴|AB|=|t1﹣t2|==.2017年4月17日。
福建省南平市政和一中、周宁一中联考高三上学期第二次月考(数学文).doc

福建省南平市政和一中、周宁一中联考高三上学期第二次月考(数学文)(时间:1,满分150分)一、选择题。
(每小题5分,共60分)1、若集合A={x ∣x >0} B={ x ∣<3},则A ⋂B 等于( )A 、{x ∣x >0}B 、{x ∣0<x <3}C 、{ x ∣x >3}D 、R2、“tana=1”是“a=4π”的( ) A 、充分而不必要条件 B 、必要而不充分条件 C 、充要条件D 、既不充分也不必要条件3、下列函数中,与函数y=x1有相同定义域是( )A 、f(x)=lnxB 、f(x)=x1C 、f(x)=xD 、f(x)=ex4、已知锐角△ABC 的面积为33,BC=4,CA=3则角C 大小为( )A 、75°B 、60°C 、45°D 、30°5、函数f(x)=x 3+sinx+1(x ∈R)若f(a)=2则f(-a)的值是( )A 、3B 、0C 、-1D 、-26、已知曲线y=24x 的一条切线的斜率为21,则切点的横坐标为( )A 、1B 、2C 、-1D 、-27、若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x),在区间[a,b]上的图象可能是( )A B C D8、已知函数f(x)=⎩⎨⎧+-+22x x ()0)0(>≤x x 则不等式f(x)≥x 2的解集( )A 、[-1,1]B 、[-2,2]C 、[-2,1]D 、[-1,2] 9、定义在R 上的函数f(x)对任意两个不等实数a,b 总有ba b f a f --)()(>0成立,则必有( )A 、函数f(x)是先增后减函数B 、函数f(x)是先减后增函数C 、f(x)在R 上是增函数D 、f(x)在R 上是减函数10、若函数f(x)=x 3+ax 2+bx-7在R 上单调递增,则实数a,b 一定满足条件是( )A 、a 2-3b ≤0 B 、a 2-3b >0C 、a 2-3b=0D 、a 2-3b <111、将函数f (x )=sin(ax+φ)的图象向左平移2π个单位,若所得图象与原图象重合,则a 的值不可能等于( )A 、4B 、6C 、8D 、1212、已知f(x)是周期为2的奇函数,当0<x <1时,f(x)=lgx ,设a=f(56) b=f(23) c=f(25)则( )A 、a <b <cB 、b <a <cC 、c <b <aD 、c <a <b二、填空题(每小题4分,共16分)13、设集合A={1,3,a},B={1,a 2-a+1}且A ⊇B ,则a 的值为 14、方程2-x +x 2=3的零点个数为 15、函数y=3x 2-2lnx 的单调递减区间是16、已知tan α,tan β是方程x 2+33x+4=0的两个根,且α,β∈(0,2π)则α+β的值为三、解答题(共74分)17、命题p :关于x 的不等式x 2+2ax+4>0,对一切x ∈R 恒成立,q :函数f(x)=(3-2a )x 是增函数,若p 或q 为真,p 且q 为假,求实数a 的取值范围。
政和一中20102011学年高三第二次月考

政和一中2010—2011学年高三第二次月考数学试卷(理科)((时间:120分种,满分150分)一、选择题。
(每小题5分,共计50分)1、设三集合A=φ,B={φ},C={X >2}的元素个数依次为a 、b 、c ,则以下关系正确的是( )。
A 、a=b <cB 、a <b <cC 、a=b=cD 、a <b=c2、设p :a=1;q :方程ax 2+2ax-3a=o(a ≠o)的两根为1和-3,则p 是q 的( )。
A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件3、下列命题中假命题的个数是( )。
①∀x ∈R ,x 2-x >0的否定是∀x ∈R ,x 2-x ≤0 ②am 2<bm 2,则a <b 的逆命题为真③对∀x ∈N ,2x 2+1是奇数A 、0B 、1C 、2D 、34、计算:C 51+C 52+C 53+C 54的值是( )。
A 、29B 、30C 、31D 、325、函数y=2x-1+log 2x 的零点所在区间是( )。
A 、(41,81) B 、(21,41) C 、(21,1) D 、(1,2)6、有三个男同学和3个女同学排成一排,若女同学不相邻,则不同排种数是( )。
A 、24B 、36C 、144D 、7207、设f (x )=141-x +21,则它是( )A 、奇函数B 、偶函数C 、既是奇函数又是偶函数D 、非奇非偶函数8、给出四个函数,分别满足是:①f(x+y)=f(x)+f(y)②g(x+y)=g(x)g(y)③h(x ·y)=h(x)+h(y)④t(x ·y)=t (x)·t(y),又给出四个函数图象:它们的正确匹配方案是( )A 、①-a,②-b,③-c,④-dB 、①-b,②-c,③-a,④-dC 、①-c,②-a,③-b,④-dD 、①-d,②-a,③-b,④-c9、若函数y=f(x)是定义在R 上偶函数,在[0,8]上单调递减且f(x+8)=-f(x),则以下判断正确的是( )A 、f(7) >f(-6)B 、f(7) <f(14)C 、f(-7)=f(24)D 、f(-16)=f(24)10、设x ,y 都是整数,且xy+2=2x+2y ,则x 2+y 2的最大可能值为( )A 、32B 、25C 、18D 、16二、填空题(每小题5分,共计25分)11、若f(x)=⎪⎩⎪⎨⎧>≤-0,2log 0|,1|x x x x ,则f{f[f(-1)]}= 12、函数y=x x 222+-的值域是13、函数f(x)=-3log a (1-2x)+1(a >0且a ≠1)的图象必过的定点坐标是14、函数y=2x 4-x 2+1的递减区间是15、函数f(x)=12++x x ,则f(1)+f(2)+f(3)+…+f(100)+f(21)+f(31)+……+f(1001)= 三、解答题(共计75分)16(12分),求函数f(x)=142+x x 值域 17(12分)记关于x 的不等式1+-x a x <0的解集为P ,不等式1-x <1的解集为Q , (1)若a =3,求集合P ,(2)若Q ⊆P ,求正数a 的取值范围。
福建省南平市政和一中、周宁一中联考2011届高三上学期第二次月考化学试题

政和一中2010—2011学年(上)高三第二次月考(满分:100分 时间:90分)相对原子质量:H —1 C-12 N —14 O-16 Na —23 Mg-24 Cl —35.5 Fe —56卷Ⅰ 共48分一、选择题(每小题只有一个正确答案,每小题2分,共48分)1、下列说法错误的是( )A 、实验室中少量金属钠通常保存在煤油中。
B 、光线通过时,胶体可产生丁达尔效应.C 、氧气、液氯是单质,氯水、氯化氢、纯碱是化合物。
D 、“只要工夫深,铁杵磨成针” 只涉及物理变化。
2、下列类型的反应,一定没有发生电子转移的是( )A .化合反应B .分解反应C .置换反应D .复分解反应3、 向饱和石灰水中不断通入二氧化碳,其溶液导电性的变化是( )A 、由弱变强B 、由强变弱C 、由强变弱,再变强D 、由弱变强,再变弱4.下列叙述正确的是( )A .盐酸和食醋既是化合物又是酸B .凡是生成两种或两种以上物质的反应都是分解反应C .氯化钠和HCl 溶于水都发生电离,克服粒子间作用力的类型相同D .一种元素可能有多种氧化物,且一种化合价可能不止对应一种氧化物5.N A 为阿伏加德罗常数,下列叙述正确的是( )A .80g 硝酸铵中含有氮原子数为N AB .1molC 3H 8分子中共价键总数为11N A C .5。
6g 铁与足量盐酸反应转移的电子数为0.3N AD .0。
1molN 5+离子中所含的电子数为3。
4N A 6.在80g 密度为dg/cm 3的硫酸铁溶液中,含有2.8gFe 3+离子,则此溶液中SO 42-的物质的量浓度为( )mol/LA .d 1615B .d 165C .d 83D .d 857.同温同压下,等体积的两容器内分别充满由14N、13C、18O三种原子构成的一氧化氮和一氧化碳,两容器含有的()A.分子数和气体质量均不同B.分子数和电子数均相同C.质子数和中子数均相同D.分子数、原子数和中子数均相同8.下列变化中,必须加入氧化剂才能发生的是()A.Cl2→HCl B.NaCl→Cl2C.Fe2+→Fe3+D.NaHCO3→CO29.在一定温度下,向饱和的烧碱溶液中放入一定量的Na2O2,充分反应后恢复到原来的温度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
政和一中2010—2011学年(上)高三第二次月考数学试卷(文科)(时间:120分种,满分150分)一、选择题。
(每小题5分,共60分)1、若集合A={x ∣x >0} B={ x ∣<3},则A ⋂B 等于( )A 、{x ∣x >0}B 、{x ∣0<x <3}C 、{ x ∣x >3}D 、R2、“tana=1”是“a=4π”的( )A 、充分而不必要条件B 、必要而不充分条件C 、充要条件D 、既不充分也不必要条件3、下列函数中,与函数y=x 1有相同定义域是( ) A 、f(x)=lnx B 、f(x)=x1C 、f(x)=xD 、f(x)=e x4、已知锐角△ABC 的面积为33,BC=4,CA=3则角C 大小为( )A 、75°B 、60°C 、45°D 、30° 5、函数f(x)=x 3+sinx+1(x ∈R)若f(a)=2则f(-a)的值是( )A 、3B 、0C 、-1D 、-26、已知曲线y=24x 的一条切线的斜率为21,则切点的横坐标为( )A 、1B 、2C 、-1D 、-27、若函数y=f(x)的导函数在区间[a,b]上是增函数,则函数y=f(x),在区间[a,b]上的图象可能是( )A B C D8、已知函数f(x)=⎩⎨⎧+-+22x x ()0)0(>≤x x 则不等式f(x)≥x 2的解集( )A 、[-1,1]B 、[-2,2]C 、[-2,1]D 、[-1,2] 9、定义在R 上的函数f(x)对任意两个不等实数a,b 总有ba b f a f --)()(>0成立,则必有( )A 、函数f(x)是先增后减函数B 、函数f(x)是先减后增函数C 、f(x)在R 上是增函数D 、f(x)在R 上是减函数10、若函数f(x)=x 3+ax 2+bx-7在R 上单调递增,则实数a,b 一定满足条件是( )A 、a 2-3b ≤0B 、a 2-3b >0C 、a 2-3b=0D 、a 2-3b <111、将函数f (x )=sin(ax+φ)的图象向左平移2π个单位,若所得图象与原图象重合,则a 的值不可能等于( )A 、4B 、6C 、8D 、1212、已知f(x)是周期为2的奇函数,当0<x <1时,f(x)=lgx ,设a=f(56) b=f(23) c=f(25)则( ) A 、a <b <cB 、b <a <cC 、c <b <aD 、c <a <b二、填空题(每小题4分,共16分)13、设集合A={1,3,a},B={1,a 2-a+1}且A ⊇B ,则a 的值为 14、方程2-x +x 2=3的零点个数为 15、函数y=3x 2-2lnx 的单调递减区间是16、已知tan α,tan β是方程x 2+33x+4=0的两个根,且α,β∈(0,2π)则α+β的值为 三、解答题(共74分)17、命题p :关于x 的不等式x 2+2ax+4>0,对一切x ∈R 恒成立,q :函数f(x)=(3-2a )x 是增函数,若p 或q 为真,p 且q 为假,求实数a 的取值范围。
18、(12分)已知函数f(x)=x 3+mx 2+nx-2的图象过点(-1,-6)且函数p (x )=f /(x) +6x 的图象关于y 轴对称(1)求m ,n 的值 (2)求y=f(x)的单调区间19、(12分)已知函数f(x)=sin 2x+3sinxcosx ,x ∈R (1)求函数f(x)的最小正周期和单调增区间(2)函数f(x)的图象可以由函数y=sin2x(x ∈R)的图象经过怎样的变换得到?20、(12分)在锐角△ABC 中,a,b.c 分别为角A ,B ,C 所对的边且3a=2csinA (1)确定角C 的大小 (2)若c=7且△ABC 的面积为233,求a+b 的值21、(12分)某化工厂引进一条选进生产线生产某化工产品,其生产的总成本y (万元)与年产量x(吨)之间的函数关系式可以近似地表示为y=52x -48x+8000,已知此生产线产量最大为210吨。
(1)求年产量为多少时,生产每吨产品的平均成本最低,并求最低成本。
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?22、(14分)已知函数f(x)=x3+3ax-1,a R(1)若函数y=f(x)的图象在x=1处的切线与直线y=6x+6平行,求实数a的值。
(2)设函数g(x)=f/(x)-6,对满足-1≤a≤1的一切a的值,都有g(x) <0恒成立,求实数x的取值范围。
(3)当a≤0时,请问:是否在整数a的值,使方程f(x)=15有且只有一个实根?若存在,求出整数a 的值,否则,说明理由。
政和一中2010—2011学年高三第二次月考答题卷(文科)(考试时间:120分钟总分:150分)二.填空题(每小题4分,共16分)13 14.15. 16. 三.解答题(共75分)17.(本小题满分12分)18. (本小题满分12分)19. (本小题满分12分)20. (本小题满分12分)21.(本小题满分12分)22.(本小题满分14分)高三文科数学标准答案13、2或-1 14、2 15、(0,33) 16、3π三、解答题17、解设g(x)=x 2+2ax+4由于x 2+2ax+4>0对一切x ∈R 成立∴△=4a 2-16<0 ∴-2<a <2由于f(x)=(3-2a )x是增函数 ∴3-2a >1 ∴ a <1由p 或q 为真,p 且q 为假可知p 和q 一真一假∴①若p 真q 假时⎩⎨⎧≥〈〈-122a a ∴1≤a <2②若p 假q 真时⎩⎨⎧≥-≤ a a a 122 或∴a ≤-2 综上实数a 的取值范围为{a ∣1≤a <2或a ≤-2} 18、解①由于f(x)图象过点(-1,-6)∴m-n=-3又p (x )= f /(x)+6x=3x 2+2mx+n 的图象关于y 轴对称 ∴-662+m =0 m=-3 ∴m=-3 n=0②因为f /(x)=3x 2-6x ,由3x 2-6x=0得x 1=0 , x 2=2∴f /(x)>0得x >2或x <0 , f /(x)<0得0<x <2 ∴f(x)的单调增区间是(-∞,0),(2,+∞)减区间是(0,2) 19、解①f(x)=22cos 1x -+23sin2x=23sin2x-21cos2x+21=sin(2x-6π)+21∴f(x)的最小正周期T=π由2k π-2π≤2x-6π≤2k+2π , K ∈Z 得f(x)单调增区间为[k π-6π,k π+3π],K ∈Z ②将y=sin2x 图象上所有的点向右平移12π个单位长度,得y=sin(2x-6π)的图象,再把图象上所有的点向上平移21个单位长度就得到y=sin(2x-6π)+21的图象。
20、解①因为3a=2csinA∴c a =3sin 2A =CA sin sin 又sinA ≠0 ∴sinC=23 又△ABC 是锐角三角形∴C=3π ②因为s=21absinC ∴21absin 3π=23π ∴ab=6 又c 2=a 2+b 2-2abcos3π ∴a 2+b 2-ab=7即(a+b )2=3ab+7 ∴a+b=521、解设每吨平均成本为xy (万元) ∴x y =5x +x 8000-48≥2xx 80005∙-48=32 当且仅当5x +x8000即x=200时取得等号。
∴年产量为200吨时每吨平均成本最低为32万元②设年获得点利润为R (x )万元。
∴R (X )=40x-y=40x-52x +48x-8000=-52x +88x-800=-51(x-220)2 +1680(0≤x ≤210)R(x)在[0,210]上是增函数 ∴x=210时R (x )有最大值为-51(210-220)2+1680=1660 ∴年产量为210吨时可获得最大利润1660万元。
22、解①因为f /(x)=3x 2+3a依题意f /(1)=6 即3+3a=6 a=1②g(x)=3x 2+3a-6∴由g(x)<0得3x 2+3a-b <0 令h(a)=3x 2+3a-b 即h(a)=3a+(3x 2-6)满足-1≤a ≤1的一切a 的值都有h(a)<0∴⎩⎨⎧〈-〈0)1(0)1(h h 即⎪⎩⎪⎨⎧--09303322<x < x =-1<x <1 ③f /(x)=3x 2+3a ∴若a=0时,f /(x)≥0 ∴f(x)在R 上单调递增此时y=f(x)与y=15只有一个公共点若a <0则f /(x)=3(x+a -)(x-a -)列表如下y 极大值=f(-a -)=(-a -)3+3a(-a -)-1=-2a a --1y极小值=f(-a)=(+a--1<0-)-1=2a a-)3+3a(ay=f(x)与y=15有且只有一个实数根=f(-a-)<15即3)-<8=-4<a<0(a综上-4<a≤0,a为整数∴a可取-3,-2,-1,0∴存在整数a的值为-3,-2,-1,0使方程f(x)=15有且只有一个实根。
