工程测量竖曲线程序及公式
学习之竖曲线
隧道内竖曲线计算当正线相邻坡段坡度差≥1‰，应设置竖曲线，竖曲线形式为圆曲线。
竖曲线计算公式如下：L=Rsh×λ/2000（L为竖曲线全长的一半，单位：m）y=x2/2R（y为竖曲线高度，单位：m）其中：Rsh—竖曲线半径（m），10000～20000m；x—竖曲线始点至计算纵距之距离，单位m；λ—为相邻竖曲线的代数差。
在设计图中，竖曲线的位置的标高应表示为：括号内的标高为未考虑竖曲线影响的标高，括号外的标高为已考虑竖曲线影响的标高。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1 ω为正时，是凹曲线；ω为负，是凸曲线。
1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m=k5+000-k4+940=60m 桩号k5+000处：x1切线高程＝423.18+60*0.05=426.18m 2/2R=602/2*2000=0.90mh1=x1设计高程＝426.18 - 0.90=425.28m=k5+100-k4+940=160m 桩号k5+100处：x2切线高程＝423.18+160*0.05=431.18m 2/2R=1602/2*2000=6.40mh2=x2设计高程＝431.18 - 6.40=424.78m。
竖曲线高程计算公式推导过程及计算流程
竖曲线⾼程计算公式推导过程及计算流程竖曲线⾼程计算公式推导及计算流程1. 竖曲线介绍竖曲线是指在纵断⾯内，两个坡线之间为了延长⾏车视距或者减⼩⾏车的冲击⼒，⽽设计的⼀段曲线。
⼀般可以⽤圆曲线和抛物线来充当竖曲线。
由于圆曲线的计算量较⼤，所以，通常采⽤抛物线作为竖曲线，以减少计算量。
2. 竖曲线⾼程计算流程竖曲线计算的⽬的是确定设计纵坡上指定桩号的路基设计标⾼，其计算步骤如下：a. 计算竖曲线的基本要素：竖曲线长L ；切线长T ；外失距Eb. 计算竖曲线起终点的桩号：竖曲线起点的桩号=变坡点的桩号－Tc. 计算竖曲线上任意点切线标⾼及改正值：切线标⾼=变坡点的标⾼±（x T -）?i 改正值：221x Ry =d. 计算竖曲线上任意点设计标⾼某桩号在凹形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼+ y 某桩号在凸形竖曲线的设计标⾼ = 该桩号在切线上的设计标⾼－y3. 竖曲线⾼程计算公式推导已知条件：第⼀条直线的坡度为1i ，下坡为负值，第⼀条直线的坡度为2i ，上坡为正值，变坡点的⾥程为K ，⾼程为H ，竖曲线的切线长为B A T T T ==, 待求点的⾥程为X K 曲线半径R竖曲线特点：抛物线的对称轴始终保持竖直，即：X 轴沿⽔平⽅向，Y 轴沿竖直⽅向，从⽽保证了X 代表平距，Y 代表⾼程。
抛物线与相邻两条坡度线相切，抛物线变坡点两侧⼀般不对称，但两切线长相等。
竖曲线⾼程改正数计算公式推导设抛物线⽅程为：()021≠++=a c bx ax y设直线⽅程为：()02≠+=k b kx y由图可知，抛物线与直线都经过坐标系222Y O X 的原点2O ,所以可得：00==b c ；分别对21y y 、求导可得：b ax y +=2'1k y ='2当0=x 时，由图可得：b i y ==1'1k i y ==1'2当L x =时，由图可得：12'12i aL i y +==由上式可得：RL L i i a 212212==-=ω所以抛物线⽅程为：x i x Ry 12121+=直线⽅程为：x i y 12=对于竖曲线上任意⼀点P ，到其切线上Q 点处的竖直距离,即⾼程改正数y 为：21122121X RX i X i X R y y y P Q =-+=-= 竖曲线曲线元素推导竖曲线元素有切线长T 、外失距E 和竖曲线长L 三个元素，推导过程如下：由图可知：2tan ω=R T 由于转⾓ω很⼩，所以可近似认为22tan ωω=，因此可得：2ωR T = 由图易得：ωR L =将切线长T 带⼊到221x Ry =中可得外失距RT E 22=4. 曲线⾼程计算⽰例已知：某条道路变坡点桩号为K25+460.00，⾼程为780.72.m ，i1＝0.8％，i2＝5％，竖曲线半径为5000m 。
测量各类计算程序
程序名称：SQX “竖曲线计算主程序”IA“⊿I1”B“⊿I2”C“BP”F“HP”RTD=C－T：E=C+TLbl 0：{K}KD= >X=C－K：N=A：Goto 1⊿K≥E= >X=C－K：N=B：Goto 1⊿K≤C= >X=K－D：Y=C-K：N=A：Goto 2：≠>X=E－K：Y=C－K：N=B：Goto 2⊿Lbl 1：H“HS”=F-XN◢Goto 0Lbl 2：H“HS”=F－YN－I X2÷2÷R◢Goto 0注：I——竖曲线为凹型时输入-1，为凸型时输入1；⊿I1、⊿I2——输入格式为0.###BP——为变坡点里程HP——为变坡点高程R——半径T——切线K——输入待计算桩号HS——计算输出结果Re:各种常用程序集.doc极座标放样LBI 1:{EF}:A”XO”:B”YO”:C”X1”:D”Y1”:E”XA”:F”YA’G”X1A”=E-A:H”Y1A”=F-B:I’X12’=C-A:J”Y12”=D-BK”A1A”=tan-1(H÷G):L”A12”= tan-1(J÷I)M”JN”=√(G2+H2) ▲T”JD”=180-Abs(L-K) ▲POL(A-E,B-F) ▲J<0=>J=360+J△Z=J▲GOTO 1注:O为仪点,A为放点偏角法LBI 0:R:A:Q”QD”{G}I=Abs(G-Q)A[1]=90×I÷(πR) ▲C[1]=2RsinA[1] ▲GOTO 0直线座标Q”QD”:E”XA”:F’YA’:A”QHJ”:O”L=-90,R=+90”:G”FXD”:B”KD”I=Abs(G-Q)X=E+IcosA▲Y=F+IsinA▲P=A+OX”LR”=X+BcosP▲Y”LR”=Y+BsinP▲注:KD,:为向左右的宽度左为-90,右为90QD,为起点桩号XA,YA为起点桩号座标QHJ;方位角直线计算高程LBI 0:{XE}:Y”QD”:D”QDGC”:U”MD”:X”FDLC”:C”PD”;F”SZDGC”:A”HS’:E”QS”:U<X=>GOTO 0△X<Y=>GOTO 0△LBI 1:B=Abs(X-Y)L”SJGC”=B×C+D▲R”SXG”=A+F▲E=0=>M”DS”=R-L▲GOTO 0≠>N”GC”=R-E▲GOTO 0注: QS:为前视为0时到读数闭合导线座标计算LBI 0:{CE}:X”XO”:Y”YO”:D”FVJ”:C”JN”:E”L,R=360-L”GOTO 1LBI 1:E=0=>F=D▲≠>F=D+E-180△GOTO 2LBI 2:G=Rec(C,F) ▲D=F▲GOTO3LBI 3:X=I+X▲Y=J+Y▲GOTO 0任意里程中边桩坐标正反算（CASIO fx-4800P计算器）程序一、源程序(SZ-XY-SZ)"1.SZ => XY"："2. XY => SZ"：NU"X0"V"Y0"O"S0"G"F0"Q：Q=0=>R=1E-45：≠>R△J=0：M=AbsQ：K=1-M：N=1=>Goto 1：≠>Goto 2△←┙Lbl 1：{SZ}：SZ：L=S-O：B=90QL÷π÷R：F=G+B：E=F+B+90：C=LK+2MRsinQB：X"XS"= U+Rec(C,F)+ZcosE◢Y"YS"=V+J+ZsinE◢Goto 1←┙Lbl 2：W=G+90Q：E=U+Rec(R,W)：F=V+J←┙Lbl 3：{XY}：XY：D=Pol(X-E,Y-F):T=J：J<0=>T=J+360△B=T-W-180M：P=Abs B：S"S"=O+ DKcosP+ MπRP÷180◢Z"Z"=DKsinB+MQ(R-D)◢Goto 3←┙二、使用说明1.由里程、中边桩计算坐标启动程序后按以下提示输入数据：N ？1 （N=1，由里程中边桩计算坐标；N≠1，由坐标反算里程及中边桩)X0 ？142.353 (直线或圆曲线起点的X坐标）Y0 ？368.166 (直线或圆曲线起点的Y坐标）S0 ？155.252 (直线或圆曲线起点的里程）F0 ？60°54′03″(直线或圆曲线起点的切线方位角）Q ？-1 (当线元为直线时Q=0；当线元为圆曲线且左偏时Q=-1；当线元为圆曲线且右偏时Q=1)R ？100 (圆曲线的半径)S ？194.016 (中线里程)Z ？-5.251 (中线左侧5.251m的边桩；在中线上Z=0，在左侧<0，在右侧Z>0)显示计算结果XS=172.7467767YS=395.23168072.由坐标反算里程、中边桩启动程序后按以下提示输入数据：N ？2 （N=1，由里程中边桩计算坐标；N≠1，由坐标反算里程及中边桩)X0 ？142.353 (直线或圆曲线起点的X坐标）Y0 ？368.166 (直线或圆曲线起点的Y坐标）S0 ？155.252 (直线或圆曲线起点的里程）F0 ？60°54′03″(直线或圆曲线起点的切线方位角）Q ？-1 (当线元为直线时Q=0；当线元为圆曲线且左偏时Q=-1；当线元为圆曲线且右偏时Q=1)R ？100 (圆曲线的半径)X ？172.7467767 (待求里程及中边桩的点的X坐标)Y ？395.2316807 (待求里程及中边桩的点的Y坐标)显示计算结果S=194.016 Z=-5.251三、注意事项1.本程序主要是针对市政道路工程中的直线和圆曲线而编制的，未考虑缓和曲线等曲线的计算；2.程序中“R=1E-45”的意思为10的-45次方，输入程序时切莫输错。
竖曲线计算公式
竖曲线计算公式竖曲线计算公式是指在数学中用来计算竖曲线的公式，它是由多个变量组成的函数，可以用来表示曲线上的变化情况，并用来计算曲线的特定点的坐标值。
竖曲线计算公式是数学上非常重要的公式，它可以用来解决复杂的竖曲线数学问题，如求解曲线中的极值点、求解曲线的交点以及在曲线上定位特定点的坐标等。
竖曲线计算公式主要包括基本竖曲线计算公式、椭圆形竖曲线计算公式以及抛物形竖曲线计算公式，它们都是数学中用来计算竖曲线的公式。
1、基本竖曲线的计算公式基本竖曲线的计算公式为y=f(x)，它由一元一次方程组成，一般用来描述折线图上的变化状况，可以用来求解折线图上的特定点的坐标值。
2、椭圆形竖曲线计算公式椭圆形竖曲线的计算公式为y=f(x)，它由双曲线方程组成，它可以用来描述椭圆形曲线上变化的状况，可以用来求解椭圆形曲线上的特定点的坐标值。
3、抛物形竖曲线计算公式抛物形竖曲线的计算公式为y=f(x)，它由二次曲线方程组成，它可以用来描述抛物线形曲线上变化的状况，可以用来求解抛物线形曲线上的特定点的坐标值。
在实际的应用中，竖曲线计算公式有着广泛的用途，比如可以应用于物理学、工程学、经济学、社会学等诸多领域，它可以让我们准确无误地得出预测结果，是大量问题解决的重要手段。
竖曲线计算公式在学术研究中也有着重要的作用，诸如数学分析、微分方程等科学技术领域，准确求解曲线上各点的位置关系，是进行准确的数学研究和问题解决的前提条件。
因此，竖曲线计算公式一方面可以在实际应用中起到重要的作用，另一方面，它也有着重要的学术价值，可以帮助我们更好地进行数学研究和问题解决，因此，竖曲线计算公式是数学上非常重要的公式。
总之，竖曲线计算公式是数学中用来计算竖曲线的公式，它有基本的竖曲线计算公式、椭圆形竖曲线计算公式以及抛物形竖曲线计算公式，它在实际应用中有着重要的作用，在学术研究中也有着重要的价值，因此，竖曲线计算公式是数学上非常重要的公式。
竖曲线计算示意图及说明
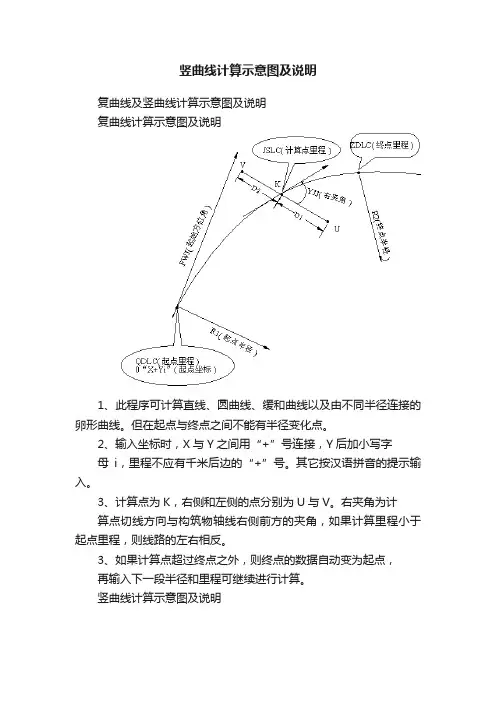
竖曲线计算示意图及说明
复曲线及竖曲线计算示意图及说明
复曲线计算示意图及说明
1、此程序可计算直线、圆曲线、缓和曲线以及由不同半径连接的卵形曲线。
但在起点与终点之间不能有半径变化点。
2、输入坐标时，X与Y之间用“+”号连接，Y后加小写字
母i，里程不应有千米后边的“+”号。
其它按汉语拼音的提示输入。
3、计算点为K，右侧和左侧的点分别为U与V。
右夹角为计
算点切线方向与构筑物轴线右侧前方的夹角，如果计算里程小于起点里程，则线路的左右相反。
3、如果计算点超过终点之外，则终点的数据自动变为起点，
再输入下一段半径和里程可继续进行计算。
竖曲线计算示意图及说明
1、竖曲线只能计算两个变坡点之间的高程。
按上图中所示的汉语拼音提示输入数据。
2、如果计算里程超过终点里程，则终点自动变为起点，然后再按提示输入下一个变坡点的数据，继续进行计算。
线路竖曲线测量
yE
i2
D
A
B
x
F
R α 2 O
第六部分
竖曲线测设计算案例
竖曲线测设计算案例
例：设i1= -1.114%，i2= +0.154%，为凹曲线，变坡点的桩号
为K1+670,高程为48.60，欲设置R=5000m的竖曲线
求：各测设元素、起点、终点的桩号和高程、曲线上每隔10间
距里程桩的标高改正数和设计高程
如图为竖曲线两种形式
凸竖曲线 凹竖曲线
i1(+) 凸形竖曲线
i2(-) 凹形竖曲线 i3(+)
第二部分
竖曲线测设元素计算
竖曲线测设元素计算
由于 i 较小，所以
tan1 i1 tan1 i2
( i1 i2 )
T
1 2
R( i1
i2
)
L R( i1 i2 )
E T2 2R
Cα
T i1
第七部分
竖曲线测设
竖曲线测设计算案例
按照一定的距离，先标定每一个桩的平面位置，根据每 一个桩的坡道高程和该桩的竖曲线高程标定工作标高。
Cα
T
i1
y
E
i2
D
A
B
x
F
R
谢谢观看
yE
i2
D
A
B
x
F
R α 2 O
第三部分
竖曲线主点里程计算
竖曲线主点里程计算
竖曲线起点里程
变坡点里程-T
竖曲线终点里程
变坡点里程+T
Cα
T i1
yE
i2
D
A
B
x
F
R α 2 O
工程测量常用计算公式
工程测量常用计算公式一、 方位角的计算公式二、 平曲线转角点偏角计算公式三、 平曲线直缓、缓直点的坐标计算公式 四、 平曲线上任意点的坐标计算公式 五、 竖曲线上点的高程计算公式 六、 超高计算公式七、 地基承载力计算公式 八、 标准差计算公式一、 方位角的计算公式1. 字母所代表的意义：x 1：QD 的X 坐标 y 1：QD 的Y 坐标 x 2：ZD 的X 坐标 y 2：ZD 的Y 坐标 S：QD～ZD 的距离 α：QD～ZD 的方位角 2. 计算公式：212212y y x x S1）当y 2- y 1>0，x 2- x 1>0时：1212x x y y arctg2）当y 2- y 1<0，x 2- x 1>0时：1212360x x y y arctg3）当x 2- x 1<0时：1212180x x y y arctg二、 平曲线转角点偏角计算公式 1. 字母所代表的意义：α1：QD～JD 的方位角 α2：JD～ZD 的方位角 β：JD 处的偏角β＝α2-α1（负值为左偏、正值为右偏）三、 平曲线直缓、缓直点的坐标计算公式1. 字母所代表的意义：U：JD 的X 坐标 V：JD 的Y 坐标A：方位角（ZH～JD）T：曲线的切线长，2322402224R L L D tg R L R T s s sD：JD 偏角，左偏为-、右偏为+ 2. 计算公式：直缓（直圆）点的国家坐标：X′=U+Tcos(A+180°)Y′=V+Tsin(A+180°)缓直（圆直）点的国家坐标：X″=U+Tcos(A+D)Y″=V+Tsin(A+D)四、 平曲线上任意点的坐标计算公式1. 字母所代表的意义：P：所求点的桩号B：所求边桩～中桩距离，左-、右+ M：左偏-1，右偏+1 C：JD 桩号 D：JD 偏角 L s ：缓和曲线长A：方位角（ZH～JD） U：JD 的X 坐标 V：JD 的Y 坐标T：曲线的切线长，2322402224R L L D tg R L R T s s sI=C-T：直缓桩号J=I+L：缓圆桩号s L DRJ H 180：圆缓桩号K=H+L：缓直桩号1）当P<I 时中桩坐标：X m =U+(C-P)cos(A+180°) Y m =V+(C-P)sin(A+180°) 边桩坐标：X b =X m +Bcos(A+90°) Y b =Y m +Bsin(A+90°)2）当I<P<J 时s230RL I P MA O 2390R I P I P G中桩坐标：X m =U+Tcos(A+180°)+GcosOY m =V+Tsin(A+180°)+GsinOs290RL I P W边桩坐标：X b =X m +Bcos(A+MW+90°) Y b =Y m +Bsin(A+MW+90°)3）当J<P<H 时R J P L M A R J P R L M A O s s909090 RJ P R G 90sin2 中桩坐标： O G R L M A R L L A T U X s ss m cos 30cos 90180cos 23O G R L M A R L L A T V Y s ss m sin 30sin 90180sin 23RJ P W90边桩坐标：X b =X m +Bcos(O+MW+90°) Y b =Y m +Bsin(O+MW+90°)4）当H<P<K 时sRL K P MMD A O 230180 2390R P K P K G中桩坐标：X m =U+Tcos(A+MD)+GcosOY m =V+Tsin(A+MD)+GsinOs290RL K P W边桩坐标：X b =X m +Bcos(A+MD-MW+90°) Y b =Y m +Bsin(A+MD-MW+90°)5）当P>K 时中桩坐标：X m =U+(T+P-K)cos(A+MD) Y m =V+(T+P-K)sin(A+MD) 边桩坐标：X b =X m +Bcos(A+MD+90°) Y b =Y m +Bsin(A+MD+90°)注：计算公式中距离、长度、桩号单位：“米”；角度测量单位：“度”；若要以“弧度”为角度测量单位，请将公式中带°的数字换算为弧度。
竖曲线高程计算公式
1竖曲线上点的高程计算公式1. 字母所代表的意义：R ：曲线半径i 1：ZY ～JD 方向的坡度 i 2：JD ～YZ 方向的坡度 T ：曲线的切线长 E ：外失距x ：竖曲线上的点到直圆或圆直的距离 y ：竖曲线上点的高程修正值2. 计算公式：212i i RT -=R T E 22=Rx y 22= 超高计算公式1. 字母所代表的意义：i 0：路拱坡度 i b ：超高坡度 L s ：缓和曲线长2b 1：所求点～路中线距离x 0：从直缓开始，到路左右坡度一致的距离，即图中C---C x ：所求点～直缓或缓直的距离 h b ：超高值X0LC=LS×i bb 1HY(YH)ZH(HZ)超高计算公式1相对于路中线超高值行车道外侧边缘行车道内侧边缘X0=2×i0/(i0＋ib)×LsX≤x0hb＝b1×(i0+ib)×X/Ls-b1×i0hb＝－（b1＋bx）×i0X≥x0hb＝－（b1＋bx）×X/LS×ib行车道外侧边缘行车道内侧边缘hb＝(-i0+(i0+ib)×X/Ls)×bhb＝(-i0-(ib-i0)×X/Ls)×bi0:路拱坡度ib:超高坡度L s :缓和曲线长b:到路中线距离X:所求点到ZH(HZ)距离超高计算公式22. 计算公式（公式1）：（绕中线旋转）()b si i L i x +=00021）当x ≤x 0时 行车道外侧边缘：()0101i b L xi i b h s b b -+=行车道内侧边缘：()01i b b h x b +-=2）当x≥x0时行车道外侧边缘：()11i bLxiibhsbb-+=行车道内侧边缘：()bsxbiLxbbh+-=13. 计算公式（公式2）：行车道外侧边缘：()1bLxiiihsbb⎪⎪⎭⎫⎝⎛++-=行车道内侧边缘：()1bLxiiihsbb⎪⎪⎭⎫⎝⎛---=3。
竖曲线运算步骤及公式讲解
竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。
竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。
（2）计算竖曲线起终点的桩号： 竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。
竖曲线高程计算公式
竖曲线高程计算公式
摘要：
一、竖曲线高程计算公式的简介
二、竖曲线高程计算公式的推导过程
三、竖曲线高程计算公式的应用实例
四、总结
正文：
竖曲线高程计算公式是测量学和地理信息系统中常用的一个公式，它用于计算在给定地球表面上的点的高程。
这个公式基于地球表面的曲率和测地线的概念，可以精确计算出给定点的高程。
竖曲线高程计算公式的推导过程涉及到一些复杂的几何和数学概念，包括椭球体、测地线、偏移量等。
具体的推导过程可以参考相关的测量学和地理信息系统教材。
在实际的应用中，竖曲线高程计算公式可以帮助我们精确地测量出地球表面上任意一点的高程，这对于地图制作、城市规划、资源勘探等领域都具有重要的意义。
例如，在地图制作中，我们需要知道地图上每个点的实际高程，以便更准确地反映出地形的变化。
总的来说，竖曲线高程计算公式是一个非常有用的工具，它可以帮助我们精确地理解和描述地球表面的形状和高程。
竖曲线高程计算公式
竖曲线高程计算公式竖曲线高程计算公式是道路工程设计中非常重要的一项内容，它用于确定道路纵向曲线的高程变化。
竖曲线的设计合理与否直接影响到道路的通行安全和舒适性。
竖曲线是指道路在纵向上的曲线形状，主要分为凸曲线和凹曲线。
在道路设计中，通常会根据实际需要选择合适的曲线形状，以满足车辆的行驶速度和舒适度要求。
竖曲线高程计算的目标是确定道路各个点的高程值，使其在竖曲线的路径上平稳过渡。
其计算公式主要包括三个要素：曲线的长度、曲线的半径和曲线的超幅。
曲线的长度是指道路在竖曲线路径上的长度，通常采用米为单位。
曲线长度的选择应综合考虑道路的几何形态、车辆的行驶速度和纵向坡度的要求等因素。
为了保证道路的通行安全和舒适性，曲线长度应尽量接近于所设计的数值。
曲线的半径是指曲线所画圆弧的半径，通常采用米为单位。
曲线半径的选择与车辆的行驶速度有关，车速越高，曲线半径应越大。
一般情况下，公路设计中常采用的最小曲线半径为150米。
曲线的超幅是指曲线路径两侧的高程变化。
超幅的选择应考虑到道路的实际需要以及地形条件等因素。
一般情况下，超幅的设计取决于道路的级别、纵向坡度和平均曲率等因素。
竖曲线高程计算公式可以用简洁的数学表达式表示，具体公式如下：高程（E）= 起点高程（E1）+ A1 + A2 + ... + An其中，A1、A2、...、An分别表示曲线路径上每个曲线段的高差值。
高差的计算可以通过使用切线方位角和曲线半径以及曲线长度来进行。
竖曲线高程计算公式的应用可以通过道路设计软件来实现。
根据实际的设计要求和数据输入，软件会自动生成曲线路径上的高程数值，以便进行进一步的设计工作。
总之，竖曲线高程计算公式在道路工程设计中具有重要的应用价值。
通过合理选择曲线的长度、半径和超幅，并利用计算公式进行高程的确定，可以保证道路的通行安全和驾驶舒适度。
因此，设计师在进行道路竖曲线设计时，应深入理解和掌握相关计算公式，并结合实际情况进行应用，以提升道路设计的质量和效果。
竖曲线高程计算公式
竖曲线上点的高程计算公式
1. 字母所代表的意义：
R：曲线半径
i1：ZY～JD方向的坡度
i2：JD～YZ方向的坡度
T：曲线的切线长
E：外失距
x：竖曲线上的点到直圆或圆直的距离
y：竖曲线上点的高程修正值
2. 计算公式：
超高计算公式
1. 字母所代表的意义：
i0：路拱坡度
i b：超高坡度
L s：缓和曲线长
b1：所求点～路中线距离
x0：从直缓开始，到路左右坡度一致的距离，即图中C---C
x：所求点～直缓或缓直的距离
h b：超高值
2. 计算公式（公式1）：（绕中线旋转）
1）当x≤x0时
行车道外侧边缘：()0101i b L x
i i b h s
b b -+=
行车道内侧边缘：()01i b b h x b +-= 2）当x ≥x0时
行车道外侧边缘：()0101i b L x
i i b h s b b -+= 行车道内侧边缘：()b s
x b i L x
b b h +-=
1 3. 计算公式（公式2）：
行车道外侧边缘：()100b L x i i i h s b b ⎪⎪⎭
⎫
⎝⎛++-= 行车道内侧边缘：()100b L x i i i h s
b b ⎪⎪
⎭
⎫
⎝
⎛
--
-=。
道路竖曲线高程计算公式
道路竖曲线高程计算公式在道路工程中，竖曲线高程的计算可是个相当重要的环节。
说起这竖曲线高程计算公式，那可真是让不少人头疼，但别怕，咱们一起来把它弄明白。
我还记得有一次在一个道路施工的现场，我亲眼目睹了因为竖曲线高程计算不准确而导致的问题。
当时，工人们正在铺设一段新的道路，一切看起来都有条不紊地进行着。
可是，当铺设到一处竖曲线的位置时，问题出现了。
原本应该顺滑过渡的路面，却出现了明显的高低差，车辆行驶在上面颠簸得厉害。
经过一番调查，发现就是因为竖曲线高程的计算出现了偏差。
那到底什么是竖曲线高程计算公式呢？简单来说，竖曲线是在道路纵断面上两个坡段的转折处，为了行车的平稳和安全而设置的一段曲线。
而计算竖曲线高程，就是要确定在这个曲线上不同位置的高度。
竖曲线高程的计算公式主要涉及到一些关键的参数，比如竖曲线的半径、切线长、外距等等。
其中，最常用的公式是：竖曲线高程 = 切线高程 ±竖距而切线高程 = 变坡点高程 ±坡度 ×坡长这里的“±”要根据竖曲线的凹凸情况来确定，如果是凸形竖曲线就用“-”，凹形竖曲线就用“+”。
比如说，我们有一个道路的变坡点高程为 100 米，坡度为 5%，坡长为 200 米，竖曲线半径为 5000 米。
首先计算切线高程，切线高程 = 100 + 0.05 × 200 = 110 米。
接下来计算竖距，竖距 = （坡长的平方）÷（2 ×竖曲线半径）= （200×200）÷（2×5000）= 4 米。
如果这是一个凸形竖曲线，那么竖曲线高程 = 110 - 4 = 106 米。
在实际应用中，可不能马虎。
就像我在前面提到的那个施工现场，一点点的偏差都可能导致严重的后果。
而且，不同的道路设计要求和地形条件，都会对竖曲线高程的计算产生影响。
有时候，计算竖曲线高程还需要考虑到一些特殊情况。
比如说，如果道路有多个变坡点，那就需要依次计算每个竖曲线的高程，确保整个路段的过渡都平稳顺畅。
竖曲线计算公式
第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。
1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：二、竖曲线最小半径（三个因素）1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验，a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时，Lmin = 2ST - 4/ω2.当L≥ST时，ST为停车视距。
以上两个公式，第二个公式计算值大，作为有效控制。
按缓和冲击、时间行程和视距要求（视距为最不利情况）计算各行车速度时的最小半径和最小长度，见表4-13。
表中：（1）一般最小半径为极限最小半径的1.5~2倍；（2）竖曲线最小长度为3s行程的长度。
（二）凹曲线最小半径和长度1.夜间行车前灯照射距离要求：1）L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例：设ω＝2%=0.02;则L＝ωＲ竖曲线最小长度Ｌ＝Ｖ/1.2速度Ｖ=120km/h V=40km/h 一般最小半径Ｒ凸17000 700一般最小半径Ｒ凹6000 700 L凸340 14Ｌ凹120 14 例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程＝431.18 - 6.40=424.78m。
竖曲线高程计算公式
竖曲线上点的高程计算公式1. 字母所代表的意义：R ：曲线半径i 1：ZY ～JD 方向的坡度 i 2：JD ～YZ 方向的坡度 T ：曲线的切线长 E ：外失距x ：竖曲线上的点到直圆或圆直的距离 y ：竖曲线上点的高程修正值2. 计算公式：212i i RT -=R T E 22=Rx y 22= 超高计算公式1. 字母所代表的意义：i 0：路拱坡度 i b ：超高坡度 L s ：缓和曲线长b 1：所求点～路中线距离x 0：从直缓开始，到路左右坡度一致的距离，即图中C---C x ：所求点～直缓或缓直的距离 h b ：超高值X0LC=LS1×i bb 1HY(YH)ZH(HZ)超高计算公式1相对于路中线超高值行车道外侧边缘行车道内侧边缘X0=2×i0/(i0＋ib)×LsX≤x0hb＝b1×(i0+ib)×X/Ls-b1×i0hb＝－（b1＋bx）×i0X≥x0hb＝－（b1＋bx）×X/LS×ib行车道外侧边缘行车道内侧边缘hb＝(-i0+(i0+ib)×X/Ls)×bhb＝(-i0-(ib-i0)×X/Ls)×bi0:路拱坡度ib:超高坡度L s :缓和曲线长b:到路中线距离X:所求点到ZH(HZ)距离超高计算公式22. 计算公式（公式1）：（绕中线旋转）()b si i L i x +=0002 1）当x ≤x 0时行车道外侧边缘：()0101i b L xi i b h sbb -+=行车道内侧边缘：()01i b b h x b +-=2）当x≥x0时行车道外侧边缘：()11i bLxiibhsbb-+=行车道内侧边缘：()bsxbiLxbbh+-=13. 计算公式（公式2）：行车道外侧边缘：()1bLxiiihsbb⎪⎪⎭⎫⎝⎛++-=行车道内侧边缘：()1bLxiiihsbb⎪⎪⎭⎫⎝⎛---=。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
竖曲线程序要素
已知要素
⏹ 1. 变坡点里程桩号 2. 变坡点高程3. 竖曲线半径4. 变坡点前坡度（上坡为正，下坡
为负） 5. 变坡点后坡度（上坡为正，下坡为负）6.待求点里程
计算公式
●凹凸型：当前坡度-后坡度为正，则为凸型，反之为凹型
●转坡角（曲折角）：前坡度–后坡度
●竖曲线长：半径* 转坡角
●切线长：竖曲线长/ 2
●外矢距：切线长的平方/ 2倍半径
●待求点到变坡点距离：待求点桩号–变坡点桩号（取绝对值）
●曲线起终点桩号：
起点：变坡点的桩号–切线长终点：变坡点的桩号+ 切线长
●任意点切线标高：变坡点的标高±测点与变坡点里程距离*该里程对应坡度
●任意点设计标高：
1. 凸型：该桩号在切线上的设计标高–修正值
2. 凹型：该桩号在切线上的设计标高+ 修正值
程序条件
◆条件：如果待求点≦变坡点，则待求点–起点=间距，反之待求点>变坡点，则终点–待
求点=间距
●曲线点间距：待求点–起点或终点–待求点
If K ≦Z:Then K - A→X:Else K > Z ＝＞B - K→X : IfEnd
●竖曲线上点的高程修正值：曲线点间距的平方/ 2倍半径
◆条件：凸型竖曲线（J>0）
如果待求点≦变坡点，则任意点设计标高=变坡点高程-（变坡点-待求点）* 前坡度(取绝对值)-修正值，反之待求点>变坡点，则变坡点任意点设计标高=变坡点高程-（待求点-变坡点）* 后坡度(取绝对值)-修正值
If K≦Z:Then H-Abs(U*I)-Y→G：Else K>Z＝＞H-Abs(U*L)-Y→G:IfEnd
◆条件：凹型竖曲线(J<0)
如果待求点≦变坡点，则任意点设计标高=变坡点高程+（待求点-变坡点）* 前坡度(取绝对值)+修正值，反之待求点>变坡点，则变坡点任意点设计标高=变坡点高程+（变坡点-待求点）* 后坡度(取绝对值)+修正值
If K≦Z:Then H+Abs(U*I)+Y→G：Else K>Z＝＞H+Abs(U*L)+Y→G:IfEnd。