2018中考冲刺专题(附答案)
2018中考语文冲刺专项小卷提升练案(2017真题)专题二十二 文言文 小卷狂练2 有答案 容美纪游 鱼我所欲也

2017中考语文全国真题分类专项练习小卷及反思提升练案总复习专题训练二十二阅读理解:文言文小卷狂练(二)2018年5月时间:40分钟总分:35分【真题演练】一、容美纪游(节选)①◆顾彩①二十九日,大雨。
龙江水涨,臵酒泛舟,观打鱼以为欢。
其渔者刻木一段为舟,牵巨网截江,度其中有鱼,则飞身倒跃入水,俄倾两手各持一鱼,口中复衔一鱼,分波跳浪登舟,百无一空 A 。
江面望见人在水中,扁阔如金虾蟆。
虽可笑,然亦奇观。
②云际庵亦名留云院,在山顶平处,每将雨则云铺地埋人肩,仅露其帽,电光煜爚②,走 B 下方,时发震雷撼墙壁。
大雨倏过,西风骤来,劈云为千百道,皆东走。
俄倾,屹立如奇峰,东西则霁矣。
当云行时急闭窗则留云一片挂窗牖③间不去徐徐放之最可娱玩。
③初五日,过长乐坪,览山景,路坦如康庄④,两边皆山,烟峦万变,应接不暇,如入画图。
草中多獐鹿,狎不避人, C 少亭台为点缀耳。
坪尽为三登坡,稍上复下者三,至底十二里,石礛⑤嶙峋,下马策杖而行,渡汉阳河,清浅可浴,然容之地界到此尽矣。
【注释】①《容美纪游》是清初戏曲作家顾彩游历鄂西容美土司地区的一部游记作品。
容美:地名,古有柘溪,容米,容阳诸称。
辖地甚广,今鹤峰、五峰,长阳大部,建始、石门、巴东、恩施局部均属之。
其地崇山峻岭,危关险隘,为古巴人后裔土家族聚居之地。
“纪”通“记”。
②煜爚:yù yuè光耀灿烂。
③牖:yǒu 窗户。
④康庄:平坦而四通八达。
⑤礛:jiān 磨玉的砺石。
6.请结合你所学过的文言文,解释文中加点词的意思。
(4分)度()霁()策()浴()7 .请将“于”“者”“但”三个虚词准确还原到原文的方框内。
(3分)(A) 百无一空 (B) 走下方 (C) 少亭台为点缀耳8.请用“/”为文中画波浪线的句子断句。
(2分)当云行时急闭窗则留云一片挂窗牖间不去徐徐放之最可娱玩。
9.翻译文中画横线的句子。
(2分)路坦如康庄,两边皆山,烟峦万变,应接不暇,如入画图。
2018中考备考三角函数专题复习归纳总结(最后冲刺 )
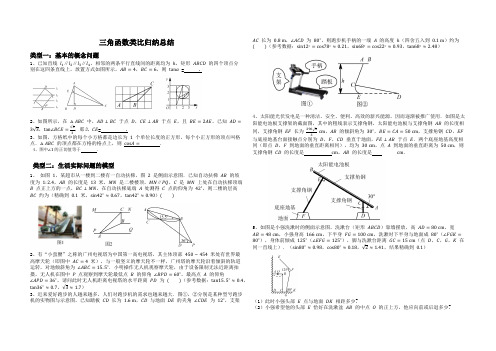
三角函数类比归纳总结类型一:基本的概念问题1、已知直线l1∥l2∥l3∥l4,相邻的两条平行直线间的距离均为ℎ,矩形ABCD的四个顶点分别在这四条直线上,放置方式如图所示,AB=4,BC=6,则tanα=.2、如图所示,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,且BE=2AE,已知AD=33,tan∠BCE=33,那么CE=.3、如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cos A=.4、图中∠1的正切值等于.类型二:生活实际问题的模型1、如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42∘,则二楼的层高BC约为(精确到0.1米,sin42∘≈0.67,tan42∘≈0.90) 2、有“小蛮腰”之称的广州电视塔为中国第一高电视塔,其主体顶部450∼454米处有世界最高摩天轮(即图中AC=4米),与一般竖立的摩天轮不一样,广州塔的摩天轮沿着倾斜的轨道运转,对地倾斜角为∠ABC=15.5∘.小明操作无人机观察摩天轮,由于设备限制无法近距离拍摄,无人机在图中P点观察到摩天轮最低点B的仰角∠BPD=60∘,最高点A的仰角∠APD=36∘,请问此时无人机距离电视塔的水平距离PD为 (参考数据:tan15.5∘≈0.4,tan36∘≈0.7,3≈1.7)3、近来爱好跑步的人越来越多,人们对跑步机的需求也越来越大.图①,②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为 1.6 m,CD与地面DE的夹角∠CDE为12∘,支架AC长为0.8 m,∠ACD为80∘,则跑步机手柄的一端A的高度ℎ(四舍五入到0.1 m)约为 (参考数据:sin12∘=cos78∘≈0.21,sin68∘=cos22∘≈0.93,tan68∘≈2.48)4、太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,支撑角钢EF长为29033cm,AB的倾斜角为30∘,BE=CA=50 cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30 cm,点A到地面的垂直距离为50 cm,则支撑角钢CD的长度是cm,AB的长度是cm.5、如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80 cm,宽AB=48 cm,小强身高166 cm,下半身FG=100 cm,洗漱时下半身与地面成80∘(∠FGK=80∘),身体前倾成125∘(∠EFG=125∘),脚与洗漱台距离GC=15 cm(点D,C,G,K在同一直线上).(sin80∘≈0.98,cos80∘≈0.18,2≈1.41,结果精确到0.1)(1)此时小强头部E点与地面DK相距多少?(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?6、如图是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2米,当车门打开角度∠AOB为40∘时,车门是否会碰到墙?请说明理由.(参考数据:sin40∘≈0.64,cos40∘≈0.77,tan40∘≈0.84)7、图1是小区常见的漫步机,人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高 1.7 m,AD长0.3 m,踏板静止时从侧面看与AE上点B重合,BE长0.2 m,当踏板旋转到C处时,测得∠CAB=42∘,求此时点C距离地面EF的高度.(结果精确到0.1 m)(参考数据:sin42∘≈0.67,cos42∘≈0.74,tan42∘≈0.90)8、如图1是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示,若坐板DF平行于地面MN,前支撑架AB与后支撑架AC分别与坐板DF交于点E,D,现测得DE=20 cm,DC=40 cm,∠AED=58∘,∠ADE=76∘.(1)求椅子的高度(即椅子的坐板DF与地面MN之间的距离);(2)求椅子两脚B,C之间的距离(精确到 1 cm)(参考数据:sin58∘≈0.85,cos58∘≈0.53,tan58∘≈1.60,sin76∘≈0.97,cos76∘≈0.24,tan76∘≈4.00).9、如图1为放置在水平桌面上的某创意可折叠台灯的平面示意图,将其抽象成图2,量得∠DCB=60∘,∠CDE=150∘,灯杆CD的长为40 cm,灯管DE的长为26 cm,底座AB的厚度为 2 cm,不考虑其他因素,分别求出DE与水平桌面(AB所在的直线)所成的夹角度数和台灯的高(点E到桌面的距离).(结果保留根号)10、每年的6至8月份是台风多发季节,某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15∘后折断倒在地上,树的顶部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15∘,大树被折断部分和地面所成的角∠ADC=60∘,AD=4米,求这棵大树AB原来的高度是多少米?(结果精确到个位,参考数据:2≈1.4,3≈1.7,6≈2.4)11、图1是太阳能热水器装置的示意图,利用玻璃吸热管可以把太阳能转化为热能.玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算.如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10 cm,DE=120 cm,FG⊥DE,垂足为点G.(1)若∠θ=37∘50ʹ,则AB的长约cm;(参考数据:sin37∘50ʹ≈0.61,cos37∘50ʹ≈0.79,tan37∘50ʹ≈0.78)(2)若FG=30 cm,∠θ=60∘,求CF的长.12、图1是一种新型自行车,将其放置在水平地面上,并简化结构得到图2测得自行车的后轮圆心A与中轴点B所在直线平行于地面,前后轮半径均为28 cm,且在同一平面内.车架由两个三角形构成:在△ABC中,AB=AC,BC=30 cm,∠A=40∘;在△BCD中,CD⊥BC,∠CDB=30∘.座子MN与地面平行,与座杆EC交于点E,E,C,B三点在同一直线上.(结果均精确到0.1 cm,参考数据:sin70∘≈0.94,cos70∘≈0.34,tan70∘≈2.75,3≈1.73)(1)若BC=EC,求自行车的高度(点E到地面的距离);(2)若前轮的圆心为F,连接BF,∠DFB=70∘,求自行车的长.13、某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72∘,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72∘≈0.95,cos72∘≈0.31,tan72∘≈3.08)类型三:方位角的问题1、在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60∘方向的C处,他先沿正东方向走了200 m到达B处,再沿北偏东30∘方向走,恰能到达目的地C,如图所示,可知B,C两地相距m.2、如图,在一笔直的沿湖道路l上有A,B两个游船码头,观光岛屿C在码头A北偏东60∘的方向,在码头B北偏西45∘的方向,AC=4 km.游客小张准备从观光岛屿C乘船沿CA回到码头A或沿CB回到码头B,设开往码头A,B的游船速度分别为v1,v2,若回到A,B所用时间相等,则v1v2=(结果保留根号).3、如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A,B两处,同时测得事发地点C在A的南偏东60∘且C在B的南偏东30∘上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)4、(2017焦作一模)某天,我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截了不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?(参考数据:cos75°≈0.2588,sin75°≈09659tan75°≈3.732,√2≈1.414,√3≈1.732)5、如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?参考数据:cos75°≈0.2588,sin75°≈09659tan75°≈3.732,√2≈1.414,√3≈1.732)6、小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30∘,他又继续走下台阶到达C处,测得树的顶端E的仰角是60∘,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45∘.已知A点离地面的高度AB=2米,∠BCA=30∘,且B,C,D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是.如图,AB是⊙O的弦、D为半径OA的中点,过点D作CD⊥OA交弦AB于点E交⊙O于点F,且CE=CB(1)求证:BC是⊙O的切线(2)连接AF,BF,求∠ABF的度数(3)如果CD=15,BE=10,sin A=513求⊙O的半径如图,直线PQ与⊙O相交于点A、B,BC是⊙O的直径,BD平分∠CBQ交⊙O于点D,过点D作DE⊥PQ,垂足为E.(1)求证:DE与⊙O相切;(2)连结AD,己知BC=10,BE=2,求sin∠BAD的值.如图,在△ABC中,∠C=90∘,D是BC边上一点,以DB为直径⊙O经过AB的中点E,交AD的延长线于点F,连接EF.(1)求证:∠1=∠F;(2)若sin B=55,EF=2CD的长.如图(1),线段AB=4,以线段AB为直径画⊙O,C为⊙O上的动点,连接OC,过点A作⊙O的切线与BC的延长线交于点D,E为AD的中点,连接CE.(1)求证:CE是⊙O的切线;(2)填空:①当CE=时,四边形AOCE为正方形;②如图(2),当CE=时,△CDE为等边三角形.。
中考冲刺:中考语文考点之散文阅读分析

中考冲刺中考语文考点之散文阅读分析作品的思想感情是作者通过人、事、景等外在的事物表达出的内涵,也就是散文的中心思想,它是散文的核心。
分析作品中作者的思想感情,实际上就是分析概括文章中作者对所写的人、事、景、物等表现的情感倾向,是对散文的核心内容和思想情感的整体把握。
一、阅读下面的文字,完成小题。
在我们去打酱油的那条路上陈思呈①说到打酱油,曾是我们的常规工作。
②八十年代的每个孩子都干过。
家里做菜要用到酱油,下面条要用到芝麻酱,早餐要用到下粥菜——都要派遣孩子到杂咸铺走一趟。
③打酱油有两种规格。
一是用瓶,一是用碟。
用碟的,几分钱就够了。
用瓶的可能要两毛钱。
两毛钱里,一毛八分钱用于打酱油,剩下两分钱买颗糖,神不知鬼不觉地吃掉。
这属于儿童打酱油业的潜规则。
④杂咸铺的前台,用几个脸盆装着橄榄、乌榄、腐乳、南姜……各种小菜,后面几个瓮,装着鱼露,酱油,醋……各种蘸料。
酱油就在后面某个瓮中,上面盖有木板。
量酱油的器具是竹做的筒状物,大小不同的竹筒对应不同的价格容量。
⑤打芝麻酱又不同。
装芝麻酱的不是瓮,而是玻璃缸。
上面盖着的也不是木板,而是大玻璃片。
通体透明的玻璃设施,是对芝麻酱本身的信心。
其姿色和形态确实值得展露,膏油柔腻的样子总能让人通感。
所以打芝麻酱的小孩,碟子里买了五分钱的芝麻酱,回到家一般只剩下三分。
有两分在路上舔进了肚子。
这也是打芝麻酱行业的潜规则。
⑥这些都是我和小夏,在这个人到中年的秋天里,共同回忆起来的。
但小夏记得比我更多,她早慧,五官开放程度更充分,听到看到感到的比普通的小孩多。
⑦小时候,我们分头居于那条街的南北两端。
南北两端各有个杂咸铺。
小夏打交道的杂威铺,店长是一个热情而瘦的女人,大家都喊她“三姨”。
早慧的小夏还能记得她招呼时慈眉善眼的微笑和声音:“妹啊,来啊。
”而我打交道的那个杂咸铺,店长却是一个脸色阴沉、面目模糊的老头,记忆中他从来没开口说话,听家里长辈叫他“铜锣伯”,但以我们几分钱酱油的交情,也没有到需要开口互相交谈的程度。
2018年山西省中考信息冲刺卷·第一次适应与模拟理综试卷及答案与评分标准

姓名______________________准考证号______________________注意事项:1.本试卷由化学部分和物理部分组成,分第Ⅰ卷和第Ⅱ卷两部分。
全卷共12页,满分150分,考试时间150分钟。
2.答卷前,考生务必将自己的姓名﹑准考证号填写在本试卷相应的位置。
3.答案全部在答题卡上完成,答在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷选择题(共50分)化学部分可能用到的相对原子质量:H—1C—12O—16Cl—35.5Cu—64Zn—65一、选择题(在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该选项涂黑。
每小题2分,共20分)1.化学使世界变得绚丽多彩,科学家为此作出了巨大贡献。
其中研究元素周期表的科学家是A.中国科学家侯德榜B.英国科学家道尔顿C.俄国科学家门捷列夫D.法国科学家拉瓦锡(第2题图)2.锂电池在手机和电脑中被广泛使用。
在元素周期表中,锂元素的信息如图所示,以下对图中信息解释正确的是A.元素符号为Li B.中子数为3C.锂原子的相对原子质量为6.94 g D.属于非金属元素3.青少年生长发育期,需要补充足量的蛋白质,以下食物富含蛋白质的是A.苹果B.豆浆C.面条D.青菜4.2017年世界环境日中国的主题是“绿水青山就是金山银山”,下列做法与这一主题不相符的是A.通过燃烧煤炭取暖B.尽量乘坐公交车或骑自行车出行C.去超市购物,自带布袋D.外出就餐,少用一次性筷子5.次氯酸(HClO)常用于消毒杀菌,其中氯元素的化合价为A.+7B.-1C.+5D.+16.规范的实验操作是实验成功的基本保障。
下列实验操作正确的是A.闻气体气味B.稀释浓硫酸C.倾倒液体D.读取液体体积7.消防安全是我们时刻关注的话题,下列属于“当心火灾”标志的是A B C D8.保鲜膜的主要成分为聚乙烯,是由乙烯经过化学反应合成,乙烯的化学式为C2H4。
下列关于乙烯的说法正确的是A.乙烯的相对分子质量为28 g B.乙烯中碳、氢元素的质量比为1∶1C.14 g乙烯中含有12 g碳元素D.乙烯由2个碳原子和4个氢原子构成9.除杂是将混合物中的指定成分消除且不增加新物质的一般方法,下表所列除杂过程错误的是10.化学上可用曲线表示物质间的相互联系和变化过程,其中对应关系正确的是①②③④A.图①是向一定量的稀盐酸和氯化钙的混合溶液中不断加入碳酸钠溶液至过量B.图②是向硫酸中不断加水,溶液pH的变化C.图③是向饱和食盐水中不断加水,溶液中溶质质量的变化D.图④是向一定量硫酸铜溶液中不断加入锌粉,溶液质量的变化物理部分二、选择题(在每小题给出的四个选项中只有一项符合题目要求,请选出并在答题卡上将该选项涂黑。
中考数学冲刺专题训练(附答案):三角形与四边形

精品基础教育教学资料,仅供参考,需要可下载使用!中考数学冲刺专题训练(附答案):三角形与四边形一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的)1.一个等腰三角形的底边长是6,腰长是一元二次方程28150x x -+=的一根,则此三角形的周长是( ) A .16 B .12C .14D .12或16【答案】A 【解析】解方程28150x x -+=,得:3x =或5x =,若腰长为3,则三角形的三边为3、3、6,显然不能构成三角形; 若腰长为5,则三角形三边长为5、5、6,此时三角形的周长为16, 故选:A .2.如图,在△ABC 中,BE 是∠ABC 的平分线,CE 是外角∠ACM 的平分线,BE 与CE 相交于点E ,若∠A =60°,则∠BEC 是( )A .15°B .30°C .45°D .60°【答案】B 【解析】∵BE 是∠ABC 的平分线, ∴∠EBM=12∠ABC , ∵CE 是外角∠ACM 的平分线, ∴∠ECM=12∠ACM , 则∠BEC=∠ECM-∠EBM=12×(∠ACM-∠ABC )=12∠A=30°, 故选:B .3.如图,在△ABC 中,∠C =90°,AC =12,AB 的垂直平分线EF 交AC 于点D ,连接BD ,若cos ∠BDC =57,则BC 的长是( )A .10B .8C .3D .6【答案】D 【解析】∵∠C =90°,cos ∠BDC =57, 设CD =5x ,BD =7x , ∴BC =6x ,∵AB 的垂直平分线EF 交AC 于点D , ∴AD =BD =7x , ∴AC =12x , ∵AC =12, ∴x =1, ∴BC =6; 故选D.4.一个菱形的边长为6,面积为28,则该菱形的两条对角线的长度之和为( ) A .8 B .12C .16D .32【答案】C 【解析】 如图所示:四边形ABCD 是菱形,12AO CO AC ∴==, 12DC BO BD ==,AC BD ⊥, 面积为28,∴12282AC BD OD AO ⋅=⋅=① 菱形的边长为6,2236OD OA ∴+=②,由①②两式可得:222()2362864OD AO OD OA OD AO +=++⋅=+=,8OD AO ∴+=,2()16OD AO ∴+=,即该菱形的两条对角线的长度之和为16, 故选C .5.如图,点B 、F 、C 、E 在一条直线上,AB ∥ED ,AC ∥FD ,那么添加下列一个条件后,仍无法判定△ABC ≌△DEF 的是( )A .AB =DE B .AC =DF C .∠A =∠D D .BF =EC【答案】C 【解析】解:选项A 、添加AB=DE 可用AAS 进行判定,故本选项错误; 选项B 、添加AC=DF 可用AAS 进行判定,故本选项错误; 选项C 、添加∠A=∠D 不能判定△ABC ≌△DEF ,故本选项正确;选项D 、添加BF=EC 可得出BC=EF ,然后可用ASA 进行判定,故本选项错误. 故选C .6.如图,ABCD 中,对角线AC 、BD 相交于点O ,OE BD ⊥交AD 于点E ,连接BE ,若ABCD 的周长为28,则ABE ∆的周长为( )A .28B .24C .21D .14【答案】D 【解析】∵四边形ABCD 是平行四边形, ∴OB OD =,AB CD =,AD BC =, ∵平行四边形的周长为28, ∴14AB AD += ∵OE BD ⊥,∴OE 是线段BD 的中垂线, ∴BE ED =,∴ABE ∆的周长14AB BE AE AB AD =++=+=, 故选:D .7.如图,在ABCD 中,将ADC ∆沿AC 折叠后,点D 恰好落在DC 的延长线上的点E 处.若=60B ︒∠,=3AB ,则ADE ∆的周长为( )A .12B .15C .18D .21【答案】C 【解析】由折叠可得,90ACD ACE ︒∠=∠=,90BAC ︒∴∠=,又60B ︒∠=,30ACB ︒∴∠=,26BC AB ∴==,6AD ∴=,由折叠可得,60E D B ︒∠=∠=∠=,60DAE ︒∴∠=,ADE ∴∆是等边三角形, ADE ∴∆的周长为6318⨯=,故选:C .8.如图,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,AE 、AF 分别交BD 于M 、N ,连按EN 、EF 、有以下结论:①AN =EN ,②当AE =AF 时,BEEC=2﹣2,③BE+DF =EF ,④存在点E 、F ,使得NF >DF ,其中正确的个数是( )A .1B .2C .3D .4【答案】B 【解析】 ①如图1,∵四边形ABCD 是正方形,∴∠EBM =∠ADM =∠FDN =∠ABD =45°,∵∠MAN=∠EBM=45°,∠AMN=∠BME,∴△AMN∽△BME,∴AM MN BM EM=,∵∠AMB=∠EMN,∴△AMB∽△NME,∴∠AEN=∠ABD=45°∴∠NAE=∠AEN=45°,∴△AEN是等腰直角三角形,∴AN=EN,故①正确;②在△ABE和△ADF中,∵AB ADABE ADF90 AE AF︒=⎧⎪∠=∠=⎨⎪=⎩,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=CD,∴CE=CF,假设正方形边长为1,设CE=x,则BE=1﹣x,如图2,连接AC,交EF于H,∵AE=AF,CE=CF,∴AC是EF的垂直平分线,∴AC⊥EF,OE=OF,Rt △CEF 中,OC =12EF =22x , △EAF 中,∠EAO =∠FAO =22.5°=∠BAE =22.5°, ∴OE =BE , ∵AE =AE ,∴Rt △ABE ≌Rt △AOE (HL ), ∴AO =AB =1, ∴AC =2=AO+OC ,∴1+22x =2, x =2﹣2,∴BE EC =1(22)22---=(21)(22)2-+=22; 故②不正确; ③如图3,∴将△ADF 绕点A 顺时针旋转90°得到△ABH ,则AF =AH ,∠DAF =∠BAH , ∵∠EAF =45°=∠DAF+∠BAE =∠HAE , ∵∠ABE =∠ABH =90°, ∴H 、B 、E 三点共线, 在△AEF 和△AEH 中,AE AE FAE HAE AF AH =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△AEH (SAS ), ∴EF =EH =BE+BH =BE+DF , 故③正确;④△ADN 中,∠FND =∠ADN+∠NAD >45°, ∠FDN =45°, ∴DF >FN ,故存在点E 、F ,使得NF >DF , 故④不正确; 故选B .二、填空题(本大题共4个小题,每小题6分,共24分)9.如图,在△ABC 中,以点B 为圆心,以BA 长为半径画弧交边BC 与点D ,连结AD ,若∠B =40°,∠C =36°,则∠DAC 的度数是____________.【答案】34° 【解析】由作图过程可知BD=BA , ∵∠B=40°, ∴∠BDA=∠BAD=12(180°-∠B)=70°, ∴∠DAC=∠BDA-∠C=70°-36°=34°. 故答案为34°. 10.如图,在矩形ABCD 中,1AB =,BC a =,点E 在边BC 上,且35BE α=.连接AE ,将ABE ∆沿AE 折叠,若点B 的对应点B '落在矩形ABCD 的边上,则 a 的值为________.【答案】53或53【解析】 分两种情况:①当点B '落在AD 边上时,如图1. 四边形ABCD 是矩形,90BAD B ︒∴∠=∠=,将ABE ∆沿AE 折叠,点B 的对应点B '落在AD 边上,1452BAE B AE BAD '︒∴∠=∠=∠=,AB BE ∴=,315a ∴=, 53a ∴=;②当点B '落在CD 边上时,如图2. ∵四边形ABCD 是矩形,90BAD B C D ︒∴∠=∠=∠=∠=,AD BC a ==.将ABE ∆沿AE 折叠,点B 的对应点B '落在CD 边上,90B AB E '︒∴∠=∠=,1AB AB '==,35EB EB a '==,2221DB B A AD a ''∴=-=-,3255EC BC BE a a =-=-=. 在ADB '∆与B CE '∆中,90A 90B AD EBC B DD C ︒︒⎧∠=∠=-∠'''⎨∠=∠=⎩, ADB B CE ''∴∆⋃∆,DB AB CE B E'''∴=,即2112355a a a -=,解得153a =,20a =(舍去). 综上,所求a 的值为53或53. 故答案为53或53. 11.如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分BAE ∠交BC 于点F ,将ADE ∆绕点A 顺时针旋转90°得ABG ∆,则CF 的长为_____.【答案】6-25 【解析】作FM AD M FN AG N ⊥⊥于,于 ,如图,易得四边形CFMD 为矩形,则4FM =∵正方形ABCD的边长为4,点是的中点,2DE ∴=,∴224225AE =+=∵△ADE 绕点A 顺时针旋转90°得△ABG ,∴252349090AG AE BG DE GAE ABG D ∠∠∠︒∠∠︒==,==,=,=,== 而90ABC ∠︒= , ∴点G 在CB 的延长线上,∵AF 平分∠BAE 交BC 于点F ,∴∠1=∠2,∴∠2+∠4=∠1+∠3,即F A 平分∠GAD , ∴FN =FM =4, ∵11••22AB GF FN AG =, ∴425254GF ⨯==, ∴4225625CF CG GF +=-=﹣=﹣ . 故答案为6-25.12.如图,在平面直角坐标系中,OA =1,以OA 为一边,在第一象限作菱形OAA 1B ,并使∠AOB =60°,再以对角线OA 1为一边,在如图所示的一侧作相同形状的菱形OA 1A 2B 1,再依次作菱形OA 2A 3B 2,OA 3A 4B 3,……,则过点B 2018,B 2019,A 2019的圆的圆心坐标为_____.【答案】(-32018,3)2019) 【解析】过A 1作A 1C ⊥x 轴于C ,∵四边形OAA1B是菱形,∴OA=AA1=1,∠A1AC=∠AOB=60°,∴A1C=32,AC=12,∴OC=OA+AC=32,在Rt△OA1C中,OA1=2213OC AC+=,∵∠OA2C=∠B1A2O=30°,∠A3A2O=120°,∴∠A3A2B1=90°,∴∠A2B1A3=60°,∴B1A3=23,A2A3=3,∴OA3=OB1+B1A3=33=(3)3∴菱形OA2A3B2的边长=3=(3)2,设B1A3的中点为O1,连接O1A2,O1B2,于是求得,O1A2=O1B2=O1B133)1,∴过点B1,B2,A2的圆的圆心坐标为O1(0,23,∵菱形OA3A4B3的边长为333,∴OA4=934,设B2A4的中点为O2,连接O2A3,O2B3,同理可得,O2A3=O2B3=O2B2=3=(3)2,∴过点B2,B3,A3的圆的圆心坐标为O2(﹣3,33),…以此类推,菱形OA2019A2020B2019的边长为(3)2019,OA2020=(3)2020,设B2018A2020的中点为O2018,连接O2018A2019,O2018B2019,求得,O2018A2019=O2018B2019=O2018B2018=(3)2018,∴点O2018是过点B2018,B2019,A2019的圆的圆心,∵2018÷12=168…2,∴点O2018在射线OB2上,则点O2018的坐标为(﹣(3)2018,(3)2019),即过点B2018,B2019,A2019的圆的圆心坐标为:(﹣(3)2018,(3)2019),故答案为:(﹣(3)2018,(3)2019).三、解答题(本大题共3个小题,每小题12分,共36分.解答应写出文字说明、证明过程或演算步骤)13.如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F、H在菱形ABCD的对角线BD上.=;(1)求证:BG DEFH=,求菱形ABCD的周长。
2018中考历史冲刺二轮复习 专题六 科学技术是第一生产力

专题三
材料三
科学技术是第一生产力
请回答: (1)材料一中把1492年看作全球化的开端,结合所学知识回答是何含义?
答:新航路的开辟使世界开始连成一个整体。
(2)结合材料一和所学知识,举两例 “世界近代民主思想实践”的史实。
答:美国独立战争和法国大革命。
(3)阅读材料一,使世界从中号“缩水”为小号的是什么历史事件?举例说明有哪些“硬 件的发明和革新成为这次全球化的主要推动力”?“3.0版本将这个世界从小号进一步缩小到 微型”,主要得益于什么的广泛运用?
① 计 算 机 技 术 的 广 ①推动了社会生产力空前发展,极 20 世 纪 第 三 次 科 技 革 命 电 子 四五十 计 经济实 算 年代 力 大 增 ,机 的 (首先 政局稳 广 泛 从美国 定 使 开始) 用 二战后 泛 使 用 是 第 三 次 科 大地改变了人类生产和生活的面貌。 计算机时 技革命的核心。 ②引起了世界政治格局和国际经济 代 ② 生 物 工 程 的 核心 : 格局的变化,尤其是推动了世界经 信息时代 基 因 工 程 。 在 基 因 济的全球化。 网络时代 工 程 的 发 展 中 , 克 ③大大加快了知识转化为生产力的 原子能时 隆 技 术 尤 为 引 人 注 速度,缩短了知识变为物质财富的 代 目。 过程。
谈谈人类应如何应对科学“潜在的危险”。
答:①例如:火车的出现,为人类的生产和生活带来了极大地便利,但煤炭的大量 使用也极大地污染了环境。②走可持续发展之路,各国协作应对环境、气候危机 (其它意思相近的表述即可)。
专题三
科学技术是第一生产力
材料四 卷土重来的PM2.5,不只是北京的烦恼。从华北到江浙再到四川盆地,普遍是一
第一、二、三次科技革命
名称 时间 主要条件 标 志 主要发明
2018年中考政治专题复习冲刺训练法律知识(有答案)

法律知识一、单项选择题1.据报道,曾两度辍学打工替过世的父亲还清 20 多万元债务的某大学在读生小张,创办公司专门帮助贫困生。
我们应学习像小张一样()①自觉承担责任②孝亲敬长、乐于助人③承担责任辍学持家④不轻言代价与回报A. ①②B. ②③ C. ①④ D. ③④【答案】A2.“一屋不扫何以扫天下”给我们的启示是()A. 小事不重要,国家大事才重要B. 做好自己的事,就能做好对社会的事C. 承担自己的责任,才能承担对他人的责任D. 对自己不负责任就是对别人不负责【答案】C3.现实生活中,总有这样的一些人:身为国家干部,有文化、懂政策,非常清楚哪些是自己该干的,哪些是自己不该干的,但最终还是走向违法犯罪的深渊。
其原因是多方面的,但就其自身而言,是因为他们()①缺少明辨是非善恶的能力②道德水平低下,私心重,贪心强③对自我行为的控制能力差④法制意识淡薄,不能用法律标准严格约束自己的行为A. ①②③B. ②③④ C. ②④ D. ①③【答案】B4.我国法律规定:“公民的合法私有财产不受侵犯。
国家依照法律规定保护公民的私有财产……”这样规定的意义在于()①有利于进一步调动人们创造财富的积极性②有利于缩小贫富差距,消除城乡差距③有利于维护公民的正常生活,保障其专心致志地从事生产、工作和学习④有利于人们积极参加社会主义现代化建设A. ①②③④B. ①②④C. ①③④D. ②③④【答案】C5.“你可以唱歌,但不能在午夜破坏我的美梦。
”与这句话意思不相符的是()A. 作为公民要增强法律意识 B. 权利是为自己的,义务是为他人的C. 公民的权利和义务是一致的 D. 公民要在法律允许的范围内行使权利【答案】B6.2017年2月24日,教育部公布《关于做好2017年普通高校招生工作的通知》。
要求继续实施重点高校招收农村和贫困地区学生的专项计划,进一步完善政策、优化服务,逐步形成长效机制。
教育部的这一做法能够()A. 平等对待每一位社会成员,促进社会更加和谐B. 杜绝社会不公平现象,维护社会正义C. 满足每一位公民享有绝对平等的教育权利D. 从根本上解决教育中存在的城乡、区域差距【答案】A7.下列侵犯公民人格尊严权的行为中,对应不正确的是()①小明因妒忌而诬陷小辉在考试中作弊──名誉权②小强同学参观历史博物馆,发现博物馆里安装了很多摄像头──肖像权③小迪同学长得矮胖,有人给他起了个“武大郎”的外号──姓名权④网站将其注册会员的信息卖给某信息公司──隐私权A. ①③B. ②④C. ②③D. ①④【答案】C8.某初中生热衷于利用黑客软件侵入他人的QQ加密空间,以获取他人私密信息为乐。
中考冲刺—名著阅读直通车(2018版)11、假如给我三天光明

内
容
梗
概
假如给我三天光明
父亲性格温和,仁慈而宽厚。他除了打猎的季节 外,他很少离开我们。他爱种花,很会讲故事,并常 听我复述他讲过的那些故事。 我常发脾气。父母亲忧心如焚又手足无措。父亲 带我去治眼睛。医生也无能为力,不过他建议带我接 受教育,于是我们全家启程去华盛顿。在华盛顿,我 见到贝尔博士,感到了他的温厚与热情。(第一次与 贝尔博士见面)贝尔博士建议父亲写信给波士顿柏金 斯学校校长安纳诺斯先生,请她物色一位启蒙老师。 几个星期后告知找到了老师。
首页 末页
假如给我三天光明
阅
读
导
航
第三, 毕业后踏入社会的生活。大学毕业后 她却遇到了悲伤的事:慈母的去世。海伦后来还介 绍了在生活中遇到的一些伟人,比如:爱迪生、马 克吐温等等。同时也介绍她体会不同的丰富多彩的 生活以及她的慈善活动等。 第四, 写了她参加慈善活动和莎莉文老师的 经历。
首页
末页
阅
首页 末页
创 作 背 景
假如给我三天光明
从1902年4月开始,她又在莎莉文老师的帮助下,开 始在美国的一家杂志上连载她的自传《我的一生》(又 译《我生活的故事》)。第二年结集出版后轰动了美国 文坛,甚至被誉为1902年世界文学上最重要的两大贡献 之一。海伦以真实、自然的笔触再现了自己生命之初21 年的生活,为世人留下了一首永难遗忘的生命之歌。在 中国出版时翻译者加入了海伦一篇优美的散文并以此为 书名《假如给我三天光明》。
首页
末页
内
容
梗
概
假如给我三天光明
全书主要有五卷: 第一卷:张开心灵的眼睛; 第二卷:信心与希望; 第三卷:走出黑暗与寂静; 第四卷:春风化雨——莎莉文老师的故事; 第五卷:假如给我三天光明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考冲刺专题(一)等腰三角形1.1抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,3)三点,直线L是抛物线的对称轴。
①求抛物线的函数关系式②设点P是直线L上的动点,当△PAC的周长最小时,求点P的坐标③在直线L上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,说明理由1.2如图点A在X轴上,OA=4,将线段OA绕点O顺时针旋转1200,至OB的位置①求点B的坐标②求经过A、O、B的抛物线的解析式。
③在此抛物线的对称轴上,是否存在点P,使得以P、O、B为顶点的三角形是等腰三角形?若存在,求P的坐标;若不存在,说明理由。
④在(3)的条件下,求△OBP的外接圆圆心M的坐标1.3平面直角坐标系中,已知A(5,0)、B(4,4)①求过O、A、B的抛物线解析式②在第一象限的抛物线上存在点M,使以O、A、B、M为顶点的四边形面积最大,求M的坐标③作直线X=m交抛物线于点P,交线段OB于点Q,当△PQB为等腰三角形时,求m的值1.4如图,在平面直角坐标系中,点A(m,m),点B(n,-n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y 轴于C,已知实数m、n(m<n)分别是方程X2-2X-3=0的两根①求抛物线的解析式②若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于点D、E(点D在y轴右侧),连接OD、BD,当△OPC为等腰三角形时,求P的坐标。
③求△BOD面积的最大值,并写出此时D的坐标。
④点F为x轴上的动点,当△FAB是以AB为斜边的直角三角形时,求F的坐标。
1.5如图,四边形ABCD是等腰梯形,AB在x轴上,点D在y轴上,直线AC与y轴交于E(0,1),点C(2,3)①求A、D的坐标②求经过A、D、C三点的抛物线解析式③在y轴上是否存在点P,使△ACP为等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由。
④⊙M是△ABC的外接圆,求M的坐标。
1.6抛物线y=x2-(m+n)x+mn(m>n)与x轴交于A、B(点A在B的右侧),与y轴交于点C。
①若m=2,n=1,求A、B的坐标②若A、B分别位于y轴的两侧,C(0,-1),求∠ACB的大小。
③若m=2,△ABC是等腰三角形,求n的值。
④在(2)的条件下,若m=2,D是抛物线上的点,使得以A、B、C、D为顶点的四边形为直角梯形?若存在,求D的坐标;若不存在,请说明理由。
中考冲刺专题(二)平行四边形2.1如图,抛物线y=-x 2+2x+3与x 轴交于A 、B (A 在B 的左侧),与y 轴交于点C ,顶点为D 。
(1)直接写出A 、B 、C 的坐标及抛物线的对称轴。
(2)连接BC ,与抛物线的对称轴交于点E ,点P 是线段BC 上的动点,过点P 作PF ∥DE 交抛物线于点F ,设点P 的横坐标为m,①用含m 的代数式表示PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系。
(3)⊙M 为△BCD 的外接圆,求圆心M 的坐标。
2.2已知抛物线y=23X 2+bX+63经过A(2,0),设顶点为P ,与x 轴另一交点为B ①求b 的值,求出点P 、点B 的坐标。
②如图,在直线y=3X 上是否存在点D ,使得四边形OPBD 为平行四边形?若存在,求出D 的坐标;若不存在,请说明理由。
③在x 轴下方的抛物线上是否存在点M ,使△AMP ≌△AMB ?如果存在,试举例验证你的猜想;如果不存在,请说明理由。
④在(2)的条件下,若⊙G 为△OBD 的外接圆,求出圆心G 的坐标.。
2.3如图,抛物线y=x 2-2x+c 的顶点A 在直线L:y=x-5上。
①求顶点A 的坐标。
②设抛物线与y 轴交于B ,与x 轴交于C 、D(C 在D 的左侧),判断△ABD 的形状。
③在直线L 上是否存在点P ,使以P 、A 、B 、D 为顶点的四边形是平行四边形?若存在,求出P 的坐标;若不存在,请说明理由。
④设直线L 与抛物线交于点G ,求四边形ABDG 的面积。
2.4抛物线:y 1=-21X 2+2X①求抛物线y 1的顶点坐标。
②将抛物线y 1向右平移2个单位,再向上平移1个单位,得到抛物线y 2,求抛物线y 2的解析式。
③如图,抛物线y 2的为P ,x 轴上有一动点M ,在抛物线y 1、y 2上是否存在点N ,使得O 、P 、M 、N 构成以OP 为一边的平行四边形,若存在,求N 的坐标;若不存在,请说明理由。
④将射线OP 绕O 点顺时针旋转45°,并与抛物线y 1交于点D ,求D 的坐标。
2.5如图,在矩形OABC中,OA=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上点E处,分别以OA、OC所在直线为x轴y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O、D、C,①求AD的长及抛物线解析式②一动点P从E出发,沿EC以每秒2个单位的速度向C运动,同时动点Q从C出发,沿CO以每秒1个单位的速度向O运动,当点P运动到点C时,两点同时停止运动。
设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?③点N在抛物线对称轴上,点M在抛物线上,是否存在这样的M、N,使以M、N、C、E为顶点的四边形是平行四边形?若存在,直接写出M、N的坐标;若不存在,请说明理由。
中考冲刺专题(三)直角三角形3.1平面直角坐标系中,反比例函数与二次函数y=k(x 2+x-1)的图像交于A (1,k)和B (-1,-k ). ①当k=-2时,求反比例函数的解析式。
②要使反比例函数与二次函数在各自象限内都是y 随x 增大儿增大,求k 应满足的条件以及x 的取值范围。
③设二次函数的图像的顶点为Q ,当△ABQ 是以AB 为斜边的直角三角形,求k 的值。
④点C 为x 轴上一动点,且点C 的坐标(2k,0),当△ABC 是以AB 为斜边的直角三角形,求k 的值。
3.2抛物线C 1:y=-3x 2+3沿x 轴翻折,得到抛物线C 2 。
(1)直接写出抛物线C 2的解析式;(2)将抛物线C 1向左平移m 个单位,平移后得到的新抛物线的顶点为M ,与x 轴的交点为A 、B(A 在B 的左边),将抛物线C 2向右平移m 个单位,平移后得到新抛物线的顶点为N ,与y 轴的 交点为D 、E ( D 在E 的左边) ①当B 、D 为线段AE 的三等分点时,求m 的值;②在平移的过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,求m 的值;若不存在,请说明理由。
3.3抛物线y=x2+px+q(p <0)的图像与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),△ABC 的面积为45。
①求抛物线的解析式; ②过y 轴上的点M (0,m )作y 轴的垂线,若该垂线与△ABC 的外接圆有交点,求m 的取值范围; ③在抛物线上是否存在点D ,使以A 、B 、C 、D 为顶点的四边形为直角梯形?若存在,求出D 的坐标;若不存在,说明理由。
3.4平面直角坐标系中,直线y=-31x+2交x 轴于点P ,交y 轴于点A ,抛物线y=-21x 2+bx+c 的图像过点E (-1,0),并与直线相交于A 、B ①求抛物线的解析式②过点A 作AC ⊥AB 交x 轴于点C ,求C 的坐标③除C 点外,在坐标轴上是否存在点M ,使得△MAB 是直角三角形?若存在,求出点M 的坐标;若不存在,说明理由。
3.5平面直角坐标系中,点P是抛物线y=x2上的动点(第一象限),连接OP,过点O作OP的垂线交抛物线于点Q,连接PQ,交y轴于点M,作PA⊥x轴于点A,QB⊥x轴于点B,设点P的横坐标为m(1)如图,当m=2时,①求线段OP的长和tan∠POM的值②在y轴上找点C,使△OCQ是以OQ为腰的等腰三角形,求C的坐标(3)连接AM、BM,分别与OP、OQ相交于点D、E①用含m的代数式表示点Q的坐标②求证:四边形ODME是矩形3.6平面直角坐标系,抛物线y=x2+(k-1)x-k与直线y=kx+1交于点A、B(A在B的左侧)①当k=1时,直接写出A、B的坐标②在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,求出△ABP面积的最大值及此时点P的坐标③抛物线y=x2+(k-1)x-k(k>0)与x轴交于点C、D(C在D的左侧),在直线y=kx+1上是否存在唯一的点Q,使得∠OQC=900?若存在,求出k的值;若不存在,说明理由中考冲刺专题(一)参考答案等腰三角形1①y=-x 2+2x+3 D(1,4) ②P(1,2)③M(1,6)M(1,-6)M(1,1)M(1,0) 2、①B(-2,-23) ②y=-63x 2+332x ③P(2,-23) ④M(0,-334) 3、①y=-x 2+5x ②M(2,6)③10m=2;m=4(舍);20m=1,m=4(舍)30m=2,m=4(舍)4、①y=-21x 2+21x ②P(423,-423)、P(43,-43、)P(23,-23)③D (23,-83) ④F(0,0)F(2,0) 5、①A(-1,0)D(0,3)②y=-x 2+2x+3③P(0,17)、P(0,-17)、P(0,3+14)、P(0,3-14)、P(0,2) ④M (1,1)6、①A(2,0)B(1,0)②900③∵m=2∴mn=2n ∴A(2,0)B(n,0),C(0,2n)分类讨论n=0(舍)n=-34;n=251+-、n=251--、n=-2、n=2(舍) ④D(25,23)、D(-25,9)中考冲刺专题(二)参考答案平行四边形1、(1)A(-1,0)、B(3,0)、C(0,3)对称轴x=1(2) ①PF=-m 2+3m m=2时, 四边形PEDF 是平行四边形②S=-23m2+29m(0≤m ≤3) (3)M(2,2)2、(1)p(4,-23)、B(6,0)(2)D(2,23)(3)∠BAP 的平分线与抛物线的交点(4)G(3,33) 3、(1)A (1,-4)(2)直角三角形(3)P(4,-1)(-2,-7)(4)44、(1)P (2,2)(2)y=-21x 2+4x-5或y=-21(x-4)2+3 (3)N(2-10,-3)(2+10,-3)(4-23,-3)(4+23,-3) (4)D(730,-4930) 5、(1)AD=3,y=-32x 2+316x (2)t=1340、t=725 (3)N1(4,-314),M1(4,332);N2(4,-38),M2(-4,-32);N3(4,-26),M3(12,-32)中考冲刺专题(三)参考答案直角三角形1(1)k=-2 (2)当k <0且x <-21时 (3)K=332,k=-332 (4)K=33,k=-33 2、(1)y=3x 2-3 (2)m=2,m=21 (3)m=1 3、(1)y=x 2-23x-1 (2)-45≤m ≤45 (3)D (25,23),D(-25,9) 4、(1)y=-21x2+23x+2 (2)C(-32,0) (3)M (66511+,0)M (66511-,0) 5、(1)OP=6,tan ∠POM=22(2)C(0,23)(0,-23)(0,1) (3)①Q(-m 1,21m )②矩形 6、①A(-1,0)、B(2,3)②t=21时,有最大值,S=827③k=552。
