河北省2018年中考数学总复习规律探索专题

合集下载

中考数学复习专题2 规律探索型问题数学课件

2．解图形规律探索题的方法：第一步：标序号：记每组图形的序数为“1，2，3，…，n”；第二步：数图形个数：在图形数量变化时，要记出每组图形的表示个数；第三步：寻找图形数量与序号数 n 的关系：针对寻找第 n 个图形表示的数量时，先将后一个图形的个数与前一个图形的个数进行比对，通常作差(商)来观察是否有恒定量的变化，然后按照定量变化推导出第 n 个图形的个数；函数法：若当图形变化规律不明显时，可把序号数 n 看作自变量，把第 n 个图形的个数看作函数，设函数解析式为 y＝an2＋bn＋c(初中阶段设二次函数完全可以解决)，再代入三组数值进行计算出函数解析式(若算出 a＝0 就是一次函数)即可．
【点评】本题考查了图形的变化类问题，解题的关键是能够仔细读题，找到图形内和图形外格点的数目．
[对应训练] 4．在由 m×n(m×n＞1)个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数 f， (1)当 m，n 互质(m，n 除 1 外无其他公因数)时，观察下列图形并完成下表：
[对应训练] 2．(2015·咸宁)古希腊数学家把数 1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为 a1，第二个三角数记为 a2…，第 n 个三角数记为 an，计算 a1＋ a2，a2＋a3，a3＋a4，…由此推算 a399＋a400＝__1.6×105 或 160_000__．
1．(2015·德州)一组数 1，1，2，x，5，y…满足“从第三个数起，每个数都等于它前面的两个数之和”，那么这组数中 y 表示的数为( A )
A．8 B．9 C．13 D．15 2．(2015·河南)如图所示，在平面直角坐标系中，半径均为 1 个单位长度的半圆 O1，O2，

2018届中考数学专题4 规律探索题 (共28张PPT)

考点·梳理自清
考题·体验感悟
考法·互动研析
类型一
类型二
解:(1)4 17 (2)猜想:(2n+1)2-4n2=2(2n+1)-1.证明如下: 左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1, 右边=2(2n+1)-1=4n+2-1=4n+1. 左边=右边, 故(2n+1)2-4n2=2(2n+1)-1.
考点·梳理自清
考题·体验感悟
考法·互动研析
类型一
类型二
例4(2012· 安徽,17)在由m×n(m×n>1)个小正方形组成的矩形网格中,研究它的一条对角线所穿过的小正方形个数f, (1)当m,n互质(m,n除1外无其他公因数)时,观察下列图形并完成下表:
考点·梳理自清考题·Fra bibliotek验感悟考法·互动研析
类型一
类型二
解析:(1)1+3+5+7=16=42, 设第n幅图中球的个数为an, 观察,发现规律:a1=1+3=22,a2=1+3+5=32,a3=1+3+5+7=42,…, 故an-1=1+3+5+…+(2n-1)=n2. (2)观察图形发现: 图中黑球可分三部分,1到n行,第n+1行,n+2行到2n+1行, 即1+3+5+…+(2n-1)+[2(n+1)-1]+(2n1)+…+5+3+1=1+3+5+…+(2n-1)+(2n+1)+(2n-1)+…+5+3+1=an2 2 2 1+(2n+1)+an-1=n +2n+1+n =2n +2n+1. 答案:(1)4 n2 (2)2n+1 2n2+2n+1

河北省2018年中考数学总复习第八章第一节

考点三方
差
(5年1考)
(2017·邯郸一模)在一次射击训练中，甲、乙两人各射击10次，两人10次射击成绩的平均数均是9.1环，
方差分别是s甲2＝1.2，s乙2＝1.6，则关于甲、乙两人在
这次射击训练中成绩稳定的描述正确的是( A．甲比乙稳定 C．甲和乙一样稳定 B．乙比甲稳定 D．甲、乙稳定性没法对比 )
(2)求众数时，注意次数与出现次数最多的数据的区别；
(3)求平均数时，注意是否“加权”；(4)中位数、平均数是唯一的，但众数不唯一．练：链接变式训练3，4，5
3．(2017·裕华区模拟)某校九年级(1)班全体学生2016年
初中毕业体育考试的成绩统计如表：
根据表中的信息判断，下列结论中错误的是( A．该班一共有40名同学 B．该班学生这次考试成绩的众数是45分 C．该班学生这次考试成绩的中位数是45分 D．该班学生这次考试成绩的平均数是45分 D
C选项的调查范围较大，费时、费力，不宜普查．故选C.
1．(2016·盐城)下列调查中，最适宜采用普查的是( ) B A．对我国中学生视力状况的调查
B．对量子科学通信卫星上某种零部件的调查
C．对一批节能灯管使用寿命的调查 D．对《最强大脑》节目收视率的调查
2．(2017·襄阳)下列调查中，调查方式选择合理的是( ) D A．为了解襄阳市初中生每天锻炼所用时间，选择全面调查
)
4．(2014·河北)五名学生投篮球，规定每人投20次，统计他们每人投中的次数，得到五个数据．若这五个数据的中位数是6，唯一众数是7，则他们投中次数的
总和可能是(
B A．20 B．28
)
C．30
D．31
5．(2016·潍坊)超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：

2018年河北中考数学总复习之规律探索专题(无答案)

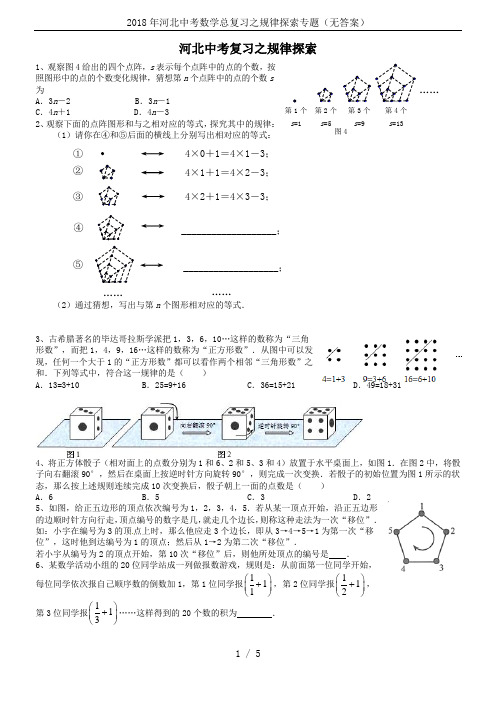
河北中考复习之规律探索1、观察图4给出的四个点阵，s 表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n 个点阵中的点的个数s 为 A ．3n －2 B ．3n －1C ．4n ＋1D ．4n －32、观察下面的点阵图形和与之相对应的等式，探究其中的规律：（1）请你在④和⑤后面的横线上分别写出相对应的等式：（2）通过猜想，写出与第n 个图形相对应的等式．3、古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（） A ．13=3+10 B ．25=9+16 C ．36=15+21 D ．49=18+314、将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90°，然后在桌面上按逆时针方向旋转90°，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是（） A ．6 B ．5 C ．3 D ．2 5、如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．……① ② ③ ⑤④ 4×0＋1＝4×1－3； 4×1＋1＝4×2－3； 4×2＋1＝4×3－3；___________________； ___________________； …… 图4 第2个 s =5 第1个 s=1第3个 s =9 …… 第4个 s =136、如图，∠BOC=9°，点A 在OB 上，且OA=1，按下列要求画图：以A 为圆心，1为半径向右画弧交OC 于点A 1，得第1条线段AA 1；再以A 1为圆心，1为半径向右画弧交OB 于点A 2，得第2条线段A 1A 2；再以A 2为圆心，1为半径向右画弧交OC 于点A 3，得第3条线段A 2A 3；…这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= ．7、观察下列各式及其验证过程：验证322322+=：()()3221221221222223232222233+=-+-=-+-==验证833833+=：()()8331331331333338383322233=-+-=-+-== （1）按照上述两个等式及其验证过程的基本思路，猜想1544的变形结果并进行验证；（2）针对上述各式反映的规律，写出用n （n 为任意自然数，且n ≥2）表示的等式，并给出证明。

2018年中考数学规律探索题(中考找规律题目_有答案解析)(最新整理)

中考规律探索1以下为全部整理类型.规律探索共两套试题.供参考学习使用一．选择题1．观察下列等式：31＝3.32＝9.33＝27.34＝81.35＝243.36＝729.37＝2187…解答下列问题：3＋32＋33＋34…＋32013的末位数字是（）A．0 B．1 C．3 D．72.把所有正奇数从小到大排列.并按如下规律分组：（1）.（3.5.7）.（9.11.13.15.17）.（19.21.23.25.27.29.31）.….现用等式A M=（i.j）表示正奇数M是第i组第j个数（从左往右数）.如A7=（2.3）.则A2013=（）A．（45.77） B．（45.39） C．（32.46） D．（32.23）3.下表中的数字是按一定规律填写的.表中a的值应是．1235813a…2358132134…4.下列图形都是由同样大小的矩形按一定的规律组成.其中第（1）个图形的面积为2cm2.第（2）个图形的面积为8 cm2.第（3）个图形的面积为18 cm2.…….第（10）个图形的面积为（）A．196 cm2B．200 cm2C．216 cm2D． 256 cm25．如图.动点P从（0.3）出发.沿所示的方向运动.每当碰到矩形的边时反弹.反弹时反射角等于入射角.当点P第2013次碰到矩形的边时.点P 的坐标为（）A、（1.4）B、（5.0）C、（6.4）D、（8.3）6．如图.下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是A． M=mn B． M=n(m+1) C．M=mn+1 D．M=m(n+1)7．我们知道.一元二次方程12-=x 没有实数根.即不存在一个实数的平方等于-1.若我们规定一个新数“”.使其满足12-=i (即方程12-=x 有一个根为).并且进一步规定: 一切实数可以与新数进行四则运算.且原有的运算律和运算法则仍然成立.于是有,1i i =12-=i .,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n.我们可得到,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么.20132012432i i i i i i +⋅⋅⋅++++的值为A ．0B ．1C ．-1D ．8．下列图形都是由同样大小的棋子按一定的规律组成.其中第①个图形有1颗棋子.第②个图形一共有6颗棋子.第③个图形一共有16颗棋子.….则第⑥个图形中棋子的颗数为（）图①图②图③··（第8题图）A ．51B ．70C ．76D ．81二．填空题1．观察下列图形中点的个数.若按其规律再画下去.可以得到第n 个图形中所有的个数为（用含n 的代数式表示）．2．如图.在直角坐标系中.已知点A （﹣3.0）、B （0.4）.对△OAB 连续作旋转变换.依次得到△1、△2、△3、△4….则△2013的直角顶点的坐标为．3．如图.正方形ABCD 的边长为1.顺次连接正方形ABCD 四边的中点得到第一个正方形A 1B 1C 1D 1.由顺次连接正方形A 1B 1C 1D 1四边的中点得到第二个正方形A 2B 2C 2D 2….以此类推.则第六个正方形A 6B 6C 6D 6周长是．4．直线上有2013个点.我们进行如下操作：在每相邻两点间插入1个点.经过3次这样的操作后.直线上共有个点．5．如图.古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1.5.12.22…为五边形数.则第6个五边形数是．6 ．如图.是用火柴棒拼成的图形.则第n个图形需根火柴棒．7．观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；….则1+3+5+…+2013的值是．8．如图12.一段抛物线：y＝－x(x－3)（0≤x≤3）.记为C1.它与x轴交于点O.A1；将C1绕点A1旋转180°得C2.交x 轴于点A2；将C2绕点A2旋转180°得C3.交x 轴于点A3；……如此进行下去.直至得C13．若P（37.m）在第13段抛物线C13上.则m =_________．9.直线上有2013个点.我们进行如下操作：在每相邻两点间插入1个点.经过3次这样的操作后.直线上共有个点. 10．观察下列各式的计算过程：5×5=0×1×100+25.15×15=1×2×100+25.25×25=2×3×100+25.35×35=3×4×100+25.…… ……请猜测.第n个算式(n为正整数)应表示为____________________________．11．将连续的正整数按以下规律排列.则位于第7行、第7列的数x是__ __．12、如下图.每一幅图中均含有若干个正方形.第①幅图中含有1个正方形；第②幅图中含有5个正方形；……按这样的规律下去.则第（6）幅图中含有个正方形；••••••①②③13．将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆. 第2个图形有10个小圆. 第3个图形有16个小圆. 第4个图形有24个小圆. …….依次规律.第6个图形有个小圆．14.已知一组数2.4.8.16.32.….按此规律.则第n个数是．15、我们知道.经过原点的抛物线的解析式可以是y＝ax2＋bx(a≠0)（1）对于这样的抛物线：当顶点坐标为（1.1）时.a＝__________；当顶点坐标为（m.m）.m≠0时.a与m之间的关系式是__________；（2）继续探究.如果b≠0.且过原点的抛物线顶点在直线y＝kx(k≠0)上.请用含k的代数式表示b；（3）现有一组过原点的抛物线.顶点A1.A2.….A n在直线y＝x上.横坐标依次为1.2.….n（为正整数.且n≤12）.分别过每个顶点作x轴的垂线.垂足记为B1.B2.….B n.以线段A n B n为边向右作正方形A n B n C n D n.若这组抛物线中有一条经过D n.求所有满足条件的正方形边长．16．如图.所有正三角形的一边平行于x轴.一顶点在y轴上.从内到外.它们的边长依次为2.4.6.8.….顶点依次用1A、2A、3A、4A、…表示.其中12A A与x轴、底边12A A与45A A、45A A与78A A、…均相距一个单位.则顶点3A的坐标是 .22A的坐标是．第16题图17．如图.已知直线l ：y=33x .过点A （0.1）作y 轴的垂线交直线l 于点B .过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线l 于点B 1.过点B 1作直线l 的垂线交y 轴于点A 2；……按此作法继续下去.则点A 2013的坐标为．18、如图.在平面直角坐标系中.一动点从原点O 出发.按向上.向右.向下.向右的方向不断地移动.每移动一个单位.得到点A 1（0.1）.A 2（1.1）.A 3（1.0）.A 4（2.0）.…那么点A 4n ＋1（n 为自然数）的坐标为（用n 表示）19．当白色小正方形个数n 等于1.2.3…时.由白色小正方形和和黑色小正方形组成的图形分别如图所示．则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________．（用n 表示.n 是正整数）20. （2013•衢州4分）如图.在菱形ABCD 中.边长为10.∠A=60°．顺次连结菱形ABCD 各边中点.可得四边形A 1B 1C 1D 1；顺次连结四边形A 1B 1C 1D 1各边中点.可得四边形A 2B 2C 2D 2；顺次连结四边形A 2B 2C 2D 2各边中点.可得四边形A 3B 3C 3D 3；按此规律继续下去…．则四边形A 2B 2C 2D 2的周长是；四边形A 2013B 2013C 2013D 2013的周长是．21.一组按规律排列的式子：ａ２.43a .65a ,87a,….则第n 个式子是________22.观察下面的单项式：a.﹣2a 2.4a 3.﹣8a 4.…根据你发现的规律.第8个式子是．23.如图.已知直线l：y=x.过点M（2.0）作x轴的垂线交直线l于点N.过点N作直线l的垂线交x轴于点M1；过点M1作x轴的垂线交直线l于N1.过点N1作直线l的垂线交x轴于点M2.…；按此作法继续下去.则点M10的坐标为　．24.为庆祝“六•一”儿童节.某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律.摆第（n）图.需用火柴棒的根数为．答案：选择题：1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C填空题：1、（n+1）2 2、（8052,0） 3、0.5 4、16097 5、51 6、2n+1 7、1014049 8、 2 9、16097 10、[10(n-1)+5]2=100n(n-1)+25 11、85 12、91 13、46 14、2n 15、（1）－1；a ＝－1m（或am ＋1＝0）；（2）解：∵a ≠0∴y ＝ax 2＋bx ＝a (x ＋2b a)2－24b a ∴顶点坐标为（－2ba .－24b a ）∵顶点在直线y ＝kx 上∴k (－2ba )＝－24b a ∵b ≠0∴b ＝2k（3）解：∵顶点A n 在直线y ＝x 上∴可设A n 的坐标为（n .n ）.点D n 所在的抛物线顶点坐标为（t .t ）由（1）（2）可得.点D n 所在的抛物线解析式为y ＝－1tx 2＋2x∵四边形A n B n C n D n 是正方形∴点D n 的坐标为（2n .n ）∴－1t(2n )2＋2×2n ＝n∴4n ＝3t∵t 、n 是正整数.且t ≤12.n ≤12∴n ＝3.6或9∴满足条件的正方形边长为3.6或916、（1）.（－8.－8）. 17、()()201340260,40,2或（注：以上两答案任选一个都对）18、（2n.1） 19、n 2+4n 20、20；21、221na n -（n 为正整数）22、-128a 8 23、（884736,0） 24、6n+2规律探索21、我们平常用的数是十进制数.如2639=2×103+6×102+3×101+9×100.表示十进制的数要用10个数码（又叫数字）：0.1.2.3.4.5.6.7.8.9。

【初中数学】河北省2018年中考数学总复习：精讲试题(91份) 人教版52

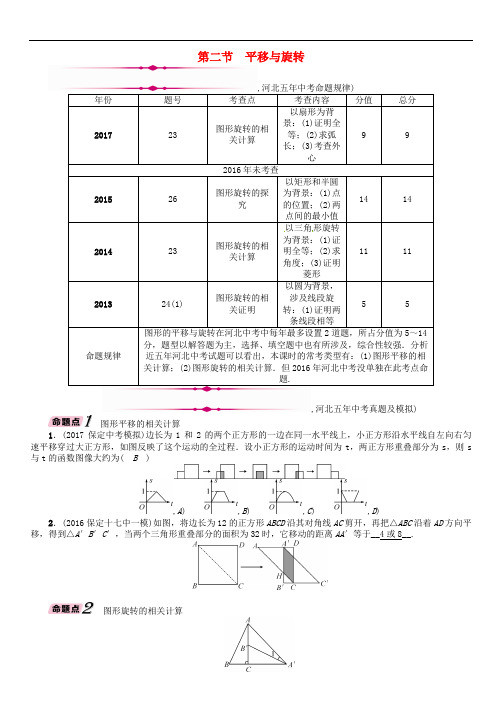
第二节平移与旋转以三角形旋转题.,河北五年中考真题及模拟)图形平移的相关计算1．(2017保定中考模拟)边长为1和2的两个正方形的一边在同一水平线上，小正方形沿水平线自左向右匀速平移穿过大正方形，如图反映了这个运动的全过程．设小正方形的运动时间为t ，两正方形重叠部分为s ，则s 与t 的函数图像大约为( B ),A ) ,B ) ,C ) ,D )2．(2016保定十七中一模)如图，将边长为12的正方形ABCD 沿其对角线AC 剪开，再把△ABC 沿着AD 方向平移，得到△A ′B ′C ′，当两个三角形重叠部分的面积为32时，它移动的距离AA ′等于__4或8__.图形旋转的相关计算3．(2016沧州十三中一模)如图，将Rt △ABC 绕直角顶点C 顺时针旋转90°，得到△A′B′C，连接AA′，若∠1＝20°，则∠B 的度数是( B )A ．70°B ．65°C ．60°D ．55°4．(2016张家口中考模拟)如图，线段OA 垂直射线OB 于点O ，OA ＝4，⊙A 的半径是2.将OB 绕点O 沿顺时针方向旋转，当OB 与⊙A 相切时，OB 旋转的角度为__60°或120°__．,(第4题图)) ,(第5题图))5．(2016邯郸中考模拟)如图所示，在正方形ABCD 中，AD ＝1，将△ABD 绕点B 顺时针旋转45°得到△A ′BD ′，此时A ′D ′与CD 交于点E ，则DE 的长度为．6．(2014河北中考)如图，△ABC 中，AB ＝AC 40°，将△ABC 绕点A 按逆时针方向旋转100°得到△ADE ，连接BD ，CE 交于点F .(1)求证：△ABD ≌△ACE ； (2)求∠ACE 的度数；(3)求证：四边形ABFE 是菱形．解：(1)根据图形旋转的性质可得△ABC ≌△ADE ，且AB ＝AC ，∴∠BAC ＝∠DAE ，AB ＝AC ＝AD ＝AE .∵∠BAC ＋∠CAD ＝∠DAE ＋∠CAD ，∴∠BAD ＝∠CAE ，在△ABD 和△ACE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△ABD ≌△ACE (SAS)；(2)根据图形旋转的性质可知，∠CAE ＝100°，且AC ＝AE ，∴∠ACE ＝∠AEC ＝(180°－100°)÷2＝40°，∴∠ACE 的度数为40°；(3)∵∠BAC ＝∠ACE ＝40°，∴BA ∥CE .由(1)知∠ABD ＝∠ACE ＝40°，∠BAE ＝∠BAC ＋∠CAE ＝140°，∴∠BAE ＋∠ABD ＝180°，∴AE ∥BD .∴四边形ABFE 是平行四边形．又∵AB ＝AE ，∴平行四边形ABFE 是菱形．,中考考点清单)图形的平移1．定义：在平面内，一个图形由一个位置沿某个方向移动到另一个位置，这样的图形运动叫做平移．平移不改变图形的形状和大小．2．三大要素：一是平移的起点，二是平移的方向，三是平移的距离． 3．性质：(1)平移前后，对应线段__平行且相等__、对应角相等； (2)各对应点所连接的线段平行(或在同一条直线上)且相等； (3)平移前后的图形全等． 4．作图步骤：(1)根据题意，确定平移的方向和平移的距离； (2)找出原图形的关键点；(3)按平移方向和平移距离、平移各个关键点，得到各关键点的对应点；(4)按原图形依次连接对应点，得到平移后的图形．图形的旋转5．定义：在平面内，一个图形绕一个定点沿某个方向(顺时针或逆时针)转过一个角度，这样的图形运动叫旋转．这个定点叫做旋转中心，转过的这个角叫做旋转角．6．三大要素：旋转中心、旋转方向和__旋转角度__． 7．性质：(1)对应点到旋转中心的距离相等；(2)每对对应点与旋转中心所连线段的夹角等于旋转角； (3)旋转前后的图形全等． 8．作图步骤：(1)根据题意，确定旋转中心、旋转方向及旋转角； (2)找出原图形的关键点；(3)连接关键点与旋转中心，按旋转方向与旋转角将它们旋转，得到各关键点的对应点； (4)按原图形依次连接对应点，得到旋转后的图形．【方法技巧】坐标系中的旋转问题：1．关于原点对称的点的坐标的应用．其基础知识为：点P (x ，y )关于原点对称点的坐标为(－x ，－y )，在具体问题中一般根据坐标特点构建方程组来求解，常用到的关系式：点P (a ，b )，P 1(m ，n )关于原点对称，则有⎩⎪⎨⎪⎧a ＋m ＝0，b ＋n ＝0. 2．坐标系内的旋转作图问题．与一般的旋转作图类似，其不同点在于若是作关于原点的中心对称图形，可以根据点的坐标规律，直接在坐标系内找到对应点的坐标，描点后连线．,中考重难点突破)图形平移的相关计算【例1】如图，已知△ABC 的面积为3，且AB ＝AC ，现将△ABC 沿CA 方向平移CA 长度得到△EFA.(1)求四边形CEFB 的面积；(2)试判断AF 与BE 的位置关系，并说明理由； (3)若∠BEC ＝15°，求AC 的长．【解析】(1)根据平移的性质和平行四边形的性质可得S △EFA ＝S △BAF ＝S △ABC ＝3，进而求即可；(2)容易证▱EFBA 为菱形，再据菱形的对角线的性质可得AF 与BE 的位置关系；(3)过点B 作高，用面积法求解即可．【答案】解：(1)由平移的性质得：AF∥BC 且AF ＝BC ，△EFA ≌△ABC ，∴四边形AFBC 为平行四边形．∴S △EFA＝S △BAF ＝S △ABC ＝3.∴四边形CEFB 的面积为9；(2)BE⊥AF.理由如下：由(1)知四边形AFBC 为平行四边形，∴BF ∥AC 且BF ＝CA.又∵AE＝CA ，∴BF ∥AE 且BF ＝AE.∴四边形EFBA 为平行四边形．又∵AB＝AC ，∴AB ＝AE.∴▱EFBA 为菱形，∴BE ⊥AF ；(3)过点B 作BD⊥AC 于点D ，∠BAC ＝∠ABE＋∠AEB＝15°×2＝30°.在Rt △ABD 中，sin 30°＝BD AB ＝12，故AB＝2BD ＝AC.S △ABC ＝12AC ·BD ＝12AC ·12AB ＝14AC 2＝3，∴AC ＝2 3.1．(泉州中考)如图，△ABC 沿着由点B 到E 的方向，平移到△DEF ，已知BC ＝5，EC ＝3，那么平移的距离为( A )A ．2B ．3C ．5D ．7图形旋转的相关计算【例2】如图①，在△ABC 中，AB ＝AC ，∠BAC ＝90°，D ，E 分别是AB ，AC 边的中点．将△ABC 绕点A 顺时针旋转α角(0°＜α＜180°)，得到△AB ′C ′(如图②)．(1)探究DB ′与EC ′的数量关系，并给予证明； (2)当DB ′∥AE 时，试求旋转角α的度数．【解析】(1)由于AB ＝AC ，∠BAC ＝90°，D ，E 分别是AB ，AC 边的中点，则AD ＝AE ＝12AB ，再根据旋转的性质得到∠B ′AD ＝∠C ′AE ＝α，AB ′＝AB ，AC ′＝AC ，则AB ′＝AC ′，根据三角形全等的判定方法可得到△B ′AD ≌△C ′AE (SAS)，则有DB ′＝EC ′；(2)由于DB ′∥AE ，根据平行线的性质得到∠B ′DA ＝∠DAE ＝90°，又因为AD ＝12AB ＝12AB ′，根据含30°的直角三角形三边的关系得到∠AB ′D ＝30°，利用互余即可得到旋转角∠B ′AD 的度数．【答案】解：(1)DB ′＝EC ′.证明如下：∵AB ＝AC ，∠BAC ＝90°，D ，E 分别是AB ，AC 边的中点，∴AD ＝AE ＝12AB .∵△ABC 绕点A 顺时针旋转α角(0°<α<180°)得到△AB ′C ′，∴∠B ′AD ＝∠C ′AE ＝α，AB ′＝AB ，AC ′＝AC ，∴AB ′＝AC ′，在△B ′AD 和△C ′AE 中，⎩⎪⎨⎪⎧AB ′＝AC ′，∠B ′AD ＝∠C ′AE ，AD ＝AE ，∴△B ′AD ≌△C ′AE (SAS)，∴DB ′＝EC ′；(2)∵DB ′∥AE ，∴∠B ′DA ＝∠DAE ＝90°.在Rt△B ′DA 中，∵AD ＝12AB ′，∴∠AB ′D ＝30°，∴∠B ′AD ＝90°－30°＝60°，即旋转角α的度数为60°.2．(2016石家庄四十二中三模)如图，在边长为1的正方形组成的网格中，△ABC 的顶点均在格点上，点A ，B ，C 的坐标分别是A(－2，3)，B(－1，2)，C(－3，1)，△ABC 绕点O 顺时针旋转90°后得到△A 1B 1C 1.(1)在正方形网格中作出△A 1B 1C 1；(2)在旋转过程中，点A 经过的路径AA 1︵的长度为________；(3)在y 轴上找一点D ，使DB ＋DB 1的值最小，并求出D 点的坐标．解：(1)如图所示；(2)132π； (3)∵点B ，B 1在y 轴两旁，连接BB 1交y 轴于点D ，设D′为y 轴上异于D 的点，显然D′B＋D′B 1>DB ＋DB 1，∴当点D 是BB 1与y 轴交点时，DB ＋DB 1最小．设直线BB 1的表达式为y ＝kx ＋b ，依据题意，得⎩⎪⎨⎪⎧－k ＋b ＝2，2k ＋b ＝1，解得⎩⎪⎨⎪⎧k ＝－13，b ＝53.1 3x＋53，∴D⎝⎛⎭⎪⎫0，53.∴y＝－。

中考数学专题复习— 探索规律问题完整版后附真题剖析

解:(1)观察图 1 可知:中间的每个正方形都对应了两个等腰直角三角形, 所以每增加一块正方形地砖,等腰直角三角形地砖就增加 2 块.故答案为 2. (2)观察图形 2 可知:中间一个正方形的左上、左边、左下共有 3 个等腰直角三角形,它右上和右下各对应了一个等腰直角三角形,右边还有 1 个等腰直角三角形,即 6=3+2×1+1=4+2×1;图 3 和图 1 中间正方形右上和右下都对应了两个等腰直角三角形,均有与图 2 一样的规律,图 3:8=3+2×2+1=4+2×2;归纳得:4+2n(即 2n+4); ∴若一条这样的人行道一共有 n(n 为正整数)块正方形地砖,则等腰直
中考数学专题复习
许多事物都存在着一定的规律性，只要我们善于观察、勤于思考，就可以发现它们，并利用它们来丰富我们的生活。
●解题思路
一、数字规律
例1
请你按照如下的数字规律,分别
写出第n个数字：（n为正整数）
① ②③ ④ ⑤
n
（1）2,4,6,8,10, … , _2_n__;
（2）1,3,5,7,9, … , 2n-1
一、选择题
1.平面上不重合的两点确定一条直线,不同三点最多可确定 3 条直线,
若平面上不同的 n 个点最多可确定 21 条直线,则 n 的值为 ( C )
A.5
B.6 C.7 D.8
2.(2021 山东临沂)实验证实,放射性物质在放出射线后,质量将减少,
减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某
•即时演练•
1.(2020 天水)观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2;…已

中考数学《规律探索》专题复习试题含解析

中考数学《规律(Lv)探索》专题复习试题含解析一(Yi)、选择题1. 如图，将一张等边(Bian)三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按(An)同样方式再剪成4个小三(San)角形，共得到7个小(Xiao)三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得(De)到10个小三角形，称为第三次操(Cao)作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（）A．25 B．33 C．34 D．50【考点】规律型：图形的变化类．【分析】由第一次操作后三角形共有4个、第二次操作后三角形共有（4+3）个、第三次操作后三角形共有（4+3+3）个，可得第n次操作后三角形共有4+3（n﹣1）=3n+1个，根据题意得3n+1=100，求得n的值即可．【解答】解：∵第一次操作后，三角形共有4个；第二次操作后，三角形共有4+3=7个；第三次操作后，三角形共有4+3+3=10个；…∴第n次操作后，三角形共有4+3（n﹣1）=3n+1个；当3n+1=100时，解得：n=33，故选：B．2.观察图中正方形四个顶点所标的数字规律，可知，数2016应标在（）A．第504个正方形的左下角B．第504个正方形的右下角C．第505个正方形的左上角D．第505个正方形的右下角【考点】规律型：点的坐标．【分(Fen)析】根据图形中对应的数字和各个(Ge)数字所在的位置，可以推出数2016在第多少个正方形和它所在的位置，本(Ben)题得以解决．【解(Jie)答】解(Jie)：∵2016÷4=504，又(You)∵由题目中给出的几个(Ge)正方形观察可知，每个正方形对应四个数，而第一个最小的数是0，0在(Zai)右下角，然后按逆时针由小变大，∴第504个正方形中最大的数是2015，∴数2016在第505个正方形的右下角，故选D．3．（2016.山东省临沂市，3分）用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是（）A．2n+1 B．n2﹣1 C．n2+2n D．5n﹣2【考点】规律型：图形的变化类．【分析】由第1个图形中小正方形的个数是22﹣1、第2个图形中小正方形的个数是32﹣1、第3个图形中小正方形的个数是42﹣1，可知第n个图形中小正方形的个数是（n+1）2﹣1，化简可得答案．【解答】解：∵第1个图形中，小正方形的个数是：22﹣1=3；第2个图形中，小正方形的个数是：32﹣1=8；第3个图形中，小正方形的个数是：42﹣1=15；…∴第n个图形中，小正方形的个数是：（n+1）2﹣1=n2+2n+1﹣1=n2+2n；故选：C．【点评】本题主要考查图形的变化规律，解决此类题目的方法是：从变化的图形中发现不变的部分和变化的部分及变化部分的特点是解题的关键．二、填空题1．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为4n﹣3 ．【考点】规律型：图形的变化类．【分析】结合题意，总结可知，每(Mei)个图中三角形个数比图形的编号的(De)4倍(Bei)少(Shao)3个三角形，即可(Ke)得出结果．【解(Jie)答】解：第(Di)①是(Shi)1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．【点评】此题主要考查了图形的变化，解决此题的关键是寻找三角形的个数与图形的编号之间的关系．2．如图，直线l：y=－x，点A1坐标为（－3，0）. 过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1长为半径画弧交x轴负半轴于点A2，再过点A2作x 轴的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴负半轴于点A 3，…，按此做法进行下去，点A2016的坐标为 .【考点】一次函数图像上点的坐标特征，规律型：图形的变化类．【分析】由直线l：y=－x的解析式求出A1B1的长，再根据勾股定理，求出OB1的长，从而得出A2的坐标；再把A2的横坐标代入y=－x的解析式求出A2B2的长，再根据勾股定理，求出OB2的长，从而得出A3的坐标；…，由此得出一般规律．【解(Jie)答】解(Jie)：∵点(Dian)A1坐(Zuo)标为（－3，0），知(Zhi)O A1=3，把(Ba)x=－3代入(Ru)直线(Xian)y=－x中，得y= 4 ，即A1B1=4.根据勾股定理，OB1===5，∴A2坐标为（－5，0），O A2=5；把x=－5代入直线y=－x中，得y=，即A2B2=.根据勾股定理，OB2====，∴A3坐标为（－3512，0），O A3=3512；把x=－3512代入直线y=－x中，得y=，即A3B3=.根据勾(Gou)股定理，OB 3====，∴A 4坐标(Biao)为（－3523，0），O A 4=3523；……同理(Li)可得(De)A n 坐(Zuo)标为（－，0），O A n =3521--n n ；∴A 2016坐(Zuo)标为（－，0）故(Gu)答案为：（− 3520142015，0）【点(Dian)评】本题是规律型图形的变化类题是全国各地的中考热点题型，考查了一次函数图像上点的坐标特征. 解题时，要注意数形结合思想的运用，总结规律是解题的关键. 解此类题时，要得到两三个结果后再比较、总结归纳，不要只求出一个结果就盲目的匆忙得出结论。

河北省中考数学总复习专题一探索规律问题课件.pptx

专题一探索规律问题
1
探索规律问题也是归纳猜想型问题，其特点是：给出一组具有某种特定关系的数、式、图形，或是给出与图形有关的操作变化过程，或某一具体的问题情境，要求通过观察分析推理，探究其中蕴含的规律，进而归纳或猜想出一般性的结论．探索规律问题涉及的知识面广，可以是代数领域也可以是几何领域，主要思想方法是从特殊到一般
18
这样画下去，直到得第n条线段，之后就不能再画出符合要求的线段了，则n＝ _9_ ．
19
4．(2017·邢台模拟)在矩形ABCD中，已知AB＝4，BC＝3，
矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位
置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2 017次后，顶点A在整个旋转过程中所经过的路程之和为 ________．
【分析】根据入射角等于反射角得出∠1，再由∠1是 △AA1O的外角即可得∠A度数．当MN⊥OA时，光线沿原路返回，分别根据入射角等于反射角和外角性质得出与∠A 具有相同位置的角的度数变化规律，即可解决问题．
15
【自主解答】 ①∵A1A2⊥AO，∠AOB＝7°， ∴∠1＝∠2＝90°－7°＝83°， ∴∠A＝∠1－∠AOB＝76°. ②如图，
特点，解答此类问题时，要将后一个图形与前一个图形进行比较，明确哪部分发生了变化，哪部分没有发生变化，分析其联系和区别，有时需要多画出几个图形进行观察，有时规律是循环性的，在归纳时要注意对应思想和数形结合思想．
12
(2016·河北)如图，已知∠AOB＝7°，一条光线
从点A出发后射向OB边．若光线与OB边垂直，则光线沿原
17
3．(2015·河北)如图，∠BOC＝9°，点A在OB上，且OA＝1.按下列要求画图：以A为圆心，1为半径向右画弧交OC于点A1，得第1条线段AA1；再以A1为圆心，1为半径向右画弧交OB于点A2，得第2条线段A1A2；再以A2为圆心，1为半径向右画弧交OC于点A3，得第3条线段A2A3； …

中考数学复习：规律探索

一．选择题（共27小题）1．按一定规律排列的单项式：a 2，4a 3，9a 4，16a 5，25a 6，…，第n 个单项式是中考数学复习：规律探索（）A ．n 2a n +1B ．n 2a n ﹣1C ．n n a n +1D ．（n +1）2a n2．把黑色三角形按如图所示的规律拼图案，其中第①个图案中有1个黑色三角形，第②个图案中有3个黑色三角形，第③个图案中有6个黑色三角形，…，按此规律排列下去，则第⑤个图案中黑色三角形的个数为（）A ．10B ．15C ．18D ．213．我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1，3，6，10…）和“正方形数”（如1，4，9，16…），在小于200的数中，设最大的“三角形数”为m ，最大的“正方形数”为n ，则m +n 的值为（）A ．33B ．301C ．386D ．5714．如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是（）A ．B ．C ．D ．5．根据图中数字的规律，若第n个图中出现数字396，则n＝（）A．17B．18C．19D．206．把菱形按照如图所示的规律拼图案，其中第①个图案中有1个菱形，第②个图案中有3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）A．15B．13C．11D．97．观察下列两行数：1，3，5，7，9，11，13，15，17，…1，4，7，10，13，16，19，22，25，…探究发现：第1个相同的数是1，第2个相同的数是7，…，若第n个相同的数是103，则n等于（）A．18B．19C．20D．218．将一列有理数﹣1，2，﹣3，4，﹣5，6，…，按如图所示有序排列．根据图中的排列规律可知，“峰1”中峰顶的位置（C的位置）是有理数4，那么，“峰6”中C的位置是有理数，2008应排在A、B、C、D、E中的位置．其中两个填空依次为（）A．﹣28，C B．﹣31，E C．﹣30，D D．﹣29，B9．用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第12个图案中共有小三角形的个数是（）A．34B．35C．37D．4010．观察下列算式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，…用你所发现的规律得出22022的末位数字是（）A．2B．4C．6D．811．用火柴棍按如图所示的方式摆大小不同的“E”，依此规律，摆出第n个“E”需要火柴棍的根数是（）A．2n+3B．4n+1C．3n+5D．3n+212．古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，它有一定的规律性，若把一个三角形数记为a1，第二个三角形数记为a2，…第n个三角形数记为a n，计算a2﹣a1，a3﹣a2，a4﹣a3，…，此推算，a100﹣a99＝（）A．99B．1C．101D．10013．将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A．2025B．2023C．2021D．201914．观察图中的“品”字形中个数之间的规律，根据观察到的规律得出a的值为（）A．75B．89C．103D．13915．用棋子摆出下列一组“口”字，按照这种方法摆，则摆第n个“口”字需用棋子（）A．4n枚B．（4n﹣4）枚C．（4n+4）枚D．n2枚16．在一列数：a1，a2，a3，…a n中，a1＝3，a2＝7，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这一列数中的第2019个数是（）A．1B．3C．7D．917．将一些完全相同的三角形按如图所示的规律排列，第①个图形中有2个三角形，第②个图形中有5个三角形，第③个图形中有10个三角形，第④个图形中有17个三角形，…，按此规律排列，则第⑥个图形中三角形的个数为（）A．26B．37C．50D．6518．我们把一些有理数按照一定的顺序排成一列，将第1个数记作a1，第2个数记作a2，…，第n个数记作a n．这样得到a1，a2，…，a n，如果这n个数满足：从第2个数开始，每个数都等于1与它前面的那个数的倒数的差，且a1＝﹣2，那么a2016＝（）A．B．C．﹣2D．19．如图，观察这组图形中五角星的个数，其中第①个图形中共有4个五角星，第②个图形中共有10个五角星，第③个图形中共有18个五角星…，按此规律，则第⑥个图形中五角星的个数为（）A．64B．34C．40D．5420．某公园里鲜花的摆放如图所示，第①个图形中有3盆鲜花，第②个图形中有6盆鲜花，第③个图形中有11盆鲜花，…，按此规律，则第⑥个图形中的鲜花盆数为（）A．26B．37C．38D．5121．观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑦中星星的颗数是（）A．24B．32C．41D．5122．下列图形都是由同样大小的★按照一定规律组成的，其中第①个图形中共有5个★，第②个图形中共有8个★，第③个图形中共有11个★，…，按此规律排列下去，第⑥个图形中的★个数为（）A．18个B．20C．22D．2423．如图，图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，按此规律，则第（6）个图形中面积为1的正方形的个数为（）A．14B．20C．24D．2724．将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，…，按此规律，则第11个图形中共有梅花的朵数是（）A．121B．125C．144D．14825．下列图形都是由三角形按一定规律组成的，其中第①个图形共有3个顶点，第②个图形共有6个顶点，第③个图形共有10个顶点，…，按此规律排列下去，第⑦个图形顶点的个数为（）A．66个B．55个C．45个D．36个26．下列各正方形中的四个数之间都有相同的规律，根据此规律，x的值为（）A．252B．209C．170D．13527．将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9B．10C．11D．12二．填空题（共11小题）28．观察下列各项：1，2，3，4，…，则第n项是．29．观察以下一列数：3，，，，，…则第20个数是．30．如图，将图1中的菱形剪开得到图2，图中共有4个菱形；将图2中的一个菱形剪开得到图3，图中共有7个菱形；如此剪下去，第5图中共有个菱形……，第n个图中共有个菱形．31．将一些圆按照如图方式摆放，从上向下有无数行，其中第一行有2个圆，第二行有4个圆，第三行有6个圆…按此规律排列下去，则前50行共有圆个．32．如图，用灰白两色正方形瓷砖铺设地面，则第10个图案中白色瓷砖块数为．33．将一些相同的“〇”按如图所示摆放，观察每个图形中的“〇”的个数，若第n个图形中“〇”的个数是78，则n的值是．34．用同样大小的小圆按下图所示的方式摆图形，第1个图形需要1个小圆，第2个图形需3个小圆，第3个图形需要6个小圆，第4个图形需要10个小圆，按照这样的规律摆下去，则第n个图形需要小圆个（用含n的代数式表示）．35．观察下列图形，第一个图形中有一个三角形；第二个图形中有5个三角形；第三个图形中有9个三角形；…，则第15个图形中有个三角形．36．按照下列图形反映出的规律，那么第8个图形中有个点．37．如图，是由相同的花盆按一定的规律组成的形如正多边形的图案，其中第1个图形一共有6个花盆，第2个图形一共有12个花盆，第3个图形一共有20个花盆，…则第98个图形中花盆的个数为．38．正偶数2，4，6，8，10，…，按如下规律排列，则第27行的第21个数是．三．解答题（共4小题）39．用火柴棒按图中的方式搭图形：按图示规律填空：图形标号①②③④⑤火柴棒根数5913a b（1）a＝，b＝；（2）按照这种方式搭下去，则搭第n个图形需要火柴棒的根数为；（用含n 的代数式来表示）（3）按照这种方式搭下去，用（2）中的代数式求第2021个图形需要的火柴棒根数．40．如图是一组有规律的图案，它们是由边长相等的等边三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形…照此规律摆下去：（1）摆成第4个图案需要个三角形，摆成第6个图案需要个三角形．（2）摆成第n个图案需要个三角形．（3）摆成第203个图案需要几个三角形？41．如图所示：搭1条、2条、3条“金鱼”各用几根火柴棒？（1）根据上面的图形填写如表：金鱼条数123…n火柴根数…（2）搭100条金鱼需要多少根火柴棒？（3）搭多少条金鱼需要500根火柴棒？42．用若干个“〇”与“▲”按如图方式进行拼图：（1）观察图形，寻找规律，并将下面的表格填写完整：图1图2图3图4〇的个数3921▲的个数1410（2）根据你所观察到的规律，分别写出图n中“〇”与“▲”的个数（用含n的代数式表示）．。

中考数学总复习第40课探索型问题

－ b ＝1，
2a
a＝－1，
∴ －b2＝1，解得 b＝2.
4a
即当顶点坐标为(1，1)时，a＝－1.
－ b ＝m， 2a
a＝－ 1 ，
当顶点坐标为 (m ，m )，m ≠0
时，
－b2＝m ， 4a
解得
b＝2.
m
∴a 与 m 之间的关系式是：a＝－m1 或 am＋1＝0.］
(2)∵a≠0，
∴y＝ax2＋bx＝a
专题解读
1．探索型问题：探索是人类认识客观世界过程中最生动，最活跃的思维活动．探索问题主要考查学生探究、发现、总结问题的能力，主要包括： (1)规律探索型问题； (2)结论探索型问题； (3)存在性探索型问题； (4)动态探索型问题． 2．解答探索型问题的注意事项：由于探索型问题的题型新颖，综合性强，思维能力要求高，结构独特，因此解题时并无固定模式，它要求解题者具有较扎实的基本功，较强的观察力，丰富的想象力及综合分析问题的能力．解题时要注意问题情境，注重思维的严密性，注意寻找问题解决的切入口．有时也可采用以下方法来寻找突破口：(1)利用特殊值(特殊点，特殊数量，特殊线段等)进行归纳，概括；(2) 反演推理法(反证法)；(3)分类讨论法；(4)类比猜想法．
3，4 3
3，
－2 P2 3
3，4 3
3
；当∠PAO＝90°时，P3
34 9
3，4 3
3 ；当∠POA＝90°时，
－16 3，4 3
P4 9
3.
名师点拨
存在性探索问题是运用几何计算进行探索的综合型问题，要注意相关的条件，可以先假设结论成立，然后通过计算求相应的值，再作存在性的判断．
【预测演练 3】如图 40－7，在△ABC 中，AB＝AC＝10 cm，BC＝12 cm，点 D 是 BC 边的中点．点 P 从点 B 出发，以 a(cm/s)(a>0)的速度沿 BA 匀速向点 A 运动；点 Q 同时以 1 cm/s 的速度从点 D 出发，沿 DB 匀速向点 B 运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为 t(s)． (1)若 a＝2，△BPQ∽△BDA (点 P 与点 D 对应)，求 t 的值； (2)设点 M 在边 AC 上，四边形 PQCM 为平行四边形． ①若 a＝5，求 PQ 的长； 2 ②是否存在实数 a，使得点 P 在∠ACB 的平分线上？若存在，请求出 a 的值；若不存在，请说明理由．

河北省2018年中考数学总复习第一编教材知识梳理篇第3章函数及其图像第4节反比例函数

第四节反比例函数的图像及性质河北五年中考真题及模拟反比例函数的图像及性质1．(2015河北中考)一台印刷机每年印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系，当x ＝2时，y ＝20，则y 与x 的函数图像大致是( C ),A ) ,B ),C ) ,D )2．(2014河北中考)定义新运算：a⊕b＝⎩⎪⎨⎪⎧a b ，（b ＞0）－ab ，（b ＜0）例如：4⊕5＝45，4⊕(－5)＝45.则函数y ＝2⊕x(x≠0)的图像大致是( D ),A ) ,B ) ,C ) ,D )3．(2013河北中考)反比例函数y ＝mx的图像如图所示，以下结论：①常数m ＜－1；②在每个象限内，y 随x 的增大而增大；③若A(－1，h)，B(2，k)在图像上，则h ＜k ；④若P(x ，y)在图像上，则P′(－x ，－y)也在图像上．其中正确的是( C )A ．①②B ．②③C ．③④D ．①④4．(2017沧州中考模拟)在同一直角坐标系中，一次函数y ＝kx －k 与反比例函数y ＝kx(k≠0)的图像大致是( A ),A ) ,B ),C ) ,D )5．(2016石家庄二十八中模拟)反比例函数y ＝2x的图像在( B )A ．第一、二象限B ．第一、三象限C ．第二、三象限D ．第二、四象限6．(2016沧州八中模拟)下列说法中不正确的是( D ) A ．函数y ＝2x 的图像经过原点B ．函数y ＝1x的图像位于第一、三象限C ．函数y ＝3x －1的图像不经过第二象限D ．函数y ＝－3x的值随x 的值的增大而增大7．(2016保定中考模拟)在反比例函数y ＝m x中，当x ＞0时，y 随x 的增大而增大，则二次函数y ＝mx 2＋mx 的图像大致是( A ),A ) ,B ) ,C ) ,D )8．(2016衡阳四中模拟)如图，函数y ＝－x 的图像是二、四象限的角平分线，将y ＝－x 的图像以点O 为中心旋转90°与函数y ＝1x的图像交于点A ，再将y ＝－x 的图像向右平移至点A ，与x 轴交于点B ，则点B 的坐标为__(2，0)__．(第8题图)(第9题图)9．(2016唐山九中模拟)如图，点A 是反比例函数y ＝kx图像上的一个动点，过点A 作AB⊥x 轴，AC ⊥y 轴，垂足分别为点B ，C ，矩形ABOC 的面积为4，则k ＝__－4__．10．(2017衡水中考模拟)如图，已知：点A(0，2)，动点P 从点A 出发，沿y 轴以每秒1个单位长度的速度向上移动，且过点P 的直线l ：y ＝－2x ＋b 也随之移动，并与x 轴交于点B ，设动点P 移动时间为t s .(1)当t ＝2 s 时，求直线l 的函数表达式；(2)如果点M(a ，3)，当OM 是Rt △OPB 斜边PB 上的中线时，在备用图中画出图形，并分别求出t 和a 的值；(3)直接写出t 为何值时，直线l 与双曲线y ＝4x(x ＞0)有且仅有一个公共点．解：(1)当t ＝2，AP ＝2×1＝2， ∵A(0，2)， ∴OA ＝2，∴OP ＝OA ＋AP ＝2＋2＝4， ∴y ＝－2x ＋4； (2)由题意可知 AP ＝t ，∴OP ＝OA ＋AP ＝t ＋2，∴直线l 的表达式为y ＝－2x ＋t ＋2，∴P(0，t ＋2)，B ⎝ ⎛⎭⎪⎫t ＋22，0，∵OM 是Rt △OPB 斜边PB 上的中线， ∴M(a ，3)是PB 的中点， ∴t ＋22＝2a ，t ＋2＝3×2，∴t ＝4，a ＝32；(3)t ＝－2＋4 2.,中考考点清单反比例函数的概念1．一般地，如果变量y 与变量x 之间的函数关系可以表示成__y ＝kx__(k 是常数，且k≠0)的形式，则称y 是x 的反比例函数，k 称为比例函数．反比例函数的图像和性质2．函数图像3.4.k设P(x ，y)是反比例函数y ＝kx图像上任一点，过点P 作PM⊥x 轴于M ，PN ⊥y 轴于N ，则S 矩形PNOM ＝PM·PN＝|y|·|x|＝|xy|＝|k|.【方法技巧】反比例函数与一次函数、几何图形结合： (1)反比例函数与一次函数图像的综合应用的四个方面： ①探求同一坐标系下两函数的图像常用排除法；②探求两函数表达式常利用两函数的图像的交点坐标；③探求两图像中点的坐标常利用解方程(组)来解决，这也是求两函数图像交点坐标的常用方法；④两个函数值比较大小的方法是以交点为界限，观察交点左、右两边区域的两个函数图像上、下位置关系，从而写出函数值的大小．(2)在平面直角坐标系中求三角形的面积时，通常以坐标轴上的边为底，相对顶点的横坐标(或纵坐标)的绝对值为高；如果没有坐标轴上的边，则用坐标轴将其分割后求解．反比例函数表达式的确定5．步骤：(1)设所求的反比例函数为y ＝kx(k≠0)；(2)根据已知条件列出含k 的方程； (3)由代入法求待定系数k 的值；(4)把k 代入函数表达式y ＝kx中．6．求表达式的两种途径：(1)根据问题中两个变量间的数量关系直接写出；(2)在已知两个变量x ，y 具有反比例关系y ＝kx(x≠0)的前提下，根据一对x ，y 的值，列出一个关于k 的方程，求得k 的值，确定出函数的表达式．反比例函数的应用7．利用反比例函数解决实际问题，首先是建立函数模型．一般地，建立函数模型有两种思路：一是通过问题提供的信息，知道变量之间的函数关系，在这种情况下，可先设出函数的表达式y ＝kx(k≠0)，再由已知条件确定表达式中k 的取值即可；二是问题本身的条件中不确定变量间是什么关系，此时要通过分析找出变量的关系并确定函数表达式．,中考重难点突破反比例函数的图像及性质【例1】(1)(黔东南中考)若ab<0，则正比例函数y ＝ax 与反比例函数y ＝bx在同一坐标系的大致图像可能是( B ),A ),B ),C ),D )(2)(安顺中考)如果点A(－2，y 1)，B(－1，y 2)，C(2，y 3)都在反比例函数y ＝kx(k>0)的图像上，那么y 1，y 2，y 3的大小关系是( B )A ．y 1<y 3<y 2B ．y 2<y 1<y 3C ．y 1<y 2<y 3D ．y 3<y 2<y 1【解析】(1)据ab ＜0及正比例函数与反比例函数图像的特点，可以从a ＞0，b ＜0和a ＜0，b ＞0两方面分类讨论，据反比例函数中k ＜0判断出函数所在的象限及增减性，再据各点横坐标特点即可得出结论；(2)本题主要考查反比例函数的图像与性质．【答案】(1)B ；(2)B1．(2017唐山中考模拟)若点A(a ，b)在反比例函数y ＝2x的图像上，则代数式ab －4的值为( B )A ．0B ．－2C ．2D ．－62．(2017石家庄中考模拟)如图，市煤气公司计划在地下修建一个容积为104 m 3的圆柱形煤气储存室，则储存室的底面积S(单位：m 2)与其深度d(单位：m )的函数图像大致是( A ),A ),B ),C ),D )3．在同一平面直角坐标系中，函数y ＝x －1与函数y ＝1x的图像可能是( C ),A ),B ) ,C ) ,D )反比例函数k 的几何意义【例2】(铁岭中考)如图，点A 在双曲线y ＝4x 上，点B 在双曲线y ＝kx(k≠0)上，AB ∥x 轴，分别过点A ，B 向x 轴作垂线，垂足分别为点D ，C.若矩形ABCD 的面积是8，则k 的值为( B )A ．12B ．10C ．8D ．6【解析】主要从矩形ABCD 的面积与双曲线中k 的关系考查．【答案】A4．(2017烟台中考)如图，点A 的坐标是(2，0)，△ABO 是等边三角形，点B 在第一象限．若反比例函数y ＝kx的图像经过点B ，则k 的值是( C ) A ．1 B ．2 C . 3 D ．2 3(第4题图)(第5题图)5．(2017河南中考)如图，在平面直角坐标系中，点P 在函数y ＝6x(x ＞0)的图像上，过点P 分别作x 轴、y轴的垂线，垂足分别为A ，B ，取线段OB 的中点C ，连接PC 并延长交x 轴于点D ，则△APD 的面积为__6__．反比例函数与一次函数结合【例3】(河北中考)如图，四边形ABCD 是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y ＝mx(x＞0)的图像经过点D ，点P 是一次函数y ＝kx ＋3－3k(k≠0)的图像与该反比例函数图像的一个公共点．(1)求反比例函数的表达式；(2)通过计算，说明一次函数y ＝kx ＋3－3k(k≠0)的图像一定过点C ；(3)对于一次函数y ＝kx ＋3－3k(k≠0)，当y 随x 的增大而增大时，确定点P 的横坐标的取值范围．(不必写出过程)【解析】(1)点B(3，1)，C(3，3)得BC⊥x 轴，BC ＝2，据平行四边形性质得AD ＝BC ＝2，而A 点坐标为(1，0)，可得D(1，2)．即易得解；(2)把x ＝3代入y ＝kx ＋3－3k ，得y ＝3即可说明；(3)设P 点横坐标为a ，由于一次函数过点C 且y 随x 的增大而增大时，P 点纵坐标要小于3，横坐标要小于3，故由y ＝2a ＜3得a ＞23.【答案】解：(1)y ＝2x；(2)当x ＝3时，y ＝3k ＋3－3k ＝3. ∴一次函数的图像一定过点C ；(3)设点P 的横坐标为a ，则23＜a ＜3.6．(郴州中考)如图，已知点A(1，2)是正比例函数y 1＝kx(k≠0)与反比例函数y 2＝mx(m≠0)的一个交点．(1)求正比例函数及反比例函数的表达式；(2)根据图像直接回答：在第一象限内，当x 取何值时，y 1<y 2? 解：(1)将A(1，2)代入正比例函数y 1＝kx 得，k ＝2，∴y 1＝2x ；将A(1，2)代入反比例函数y 2＝m x 得，m ＝2，∴y 2＝2x；(2)0<x<1.7．(济宁中考)在矩形AOBC 中，OB ＝6，OA ＝4，分别以OB ，OA 所在直线为x 轴和y 轴，建立如图所示的平面直角坐标系．F 是边BC 上一点，过点F 的反比例函数y ＝kx(k>0)的图像与AC 边交于点E.(1)请用k 表示点E ，F 的坐标；(2)若△OEF 的面积为9，求反比例函数的表达式．解：(1)∵E，F 是反比例函数y ＝kx(k>0)图像上的点，且OB ＝6，OA ＝4，∴点E 坐标为⎝ ⎛⎭⎪⎫k 4，4，点F 坐标为⎝ ⎛⎭⎪⎫6，k 6； (2)由题意知：S △ECF ＝12EC ×CF ＝12⎝ ⎛⎭⎪⎫6－14k ⎝ ⎛⎭⎪⎫4－16k ，∴S △EOF ＝S 矩形AOBC －S △AOE －S △BOF －S △ECF ＝24－12k －12k －12⎝ ⎛⎭⎪⎫6－14k ⎝ ⎛⎭⎪⎫4－16k ＝9.∴12－k248＝9，解得k ＝±12(负值舍去)．∴反比例函数的表达式为y ＝12x.。

2018年河北中考说明数学学科题型拓展拓展二代数式与规律探索

河北省2018年初中毕业生升学文化课考试说明数学学科题型拓展拓展二代数式与规律探索一、选择题1. 结果为a²的式子是A．a6÷a3B．a4∙a−2C．(a−1)2D．a4−a22. 把代数式ax²－4ax＋4a分解因式，下列结果中正确的是A．a(x−2)2B．a(x+2)2C．a(x−4)2D．a(x+2)(x−2)3. 如果ab =2，则a2−ab+b2a2+b2的值是A．45B．1C．35D．24. 某商品原价a元，因需求量大，经营者连续两次提价，每次提价10%，后因市场物价调整，又一次降价20%，降价后这种商品的价格是A．1.08a元B．0.88a元C．0.968a元D．a元5. 已知a＋b＝m，ab＝－4，化简(a－2)(b－2)的结果是A．6B．2m－8C．2m D．－2m6. 如图放置的△OAB1，△B1A1B2，△B2A2B3，…都是边长为2的等边三角形，边AO在y轴上，点B1，B2，B3，…都在直线y=√33x上，则A2018的坐标是A．(2018√3,2018)B．(2018√3,2020)C．(2018,2018√3)D．(2018,2016√3)7. 如图，阴影部分的面积是A．112xy B．132xy C．6xy D．3xy8. 已知4x²＋4mx＋36是完全平方式，则m的值为A．2B．±2C．－6D．±69. 若a²－b²＝14，a－b＝12，则a＋b＝A．−12B．12C．1D．210. 有一列数a1，a2，a3，…，a n，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a1=2，则a 2018为A ．2018B ．2C ．12D ．－111. 已知√20n 是整数，则满足条件的最小正整数n 为A ．10B ．6C ．5D ．3 二、填空题1. 若分式2x−4x+1的值为0，则x 的值为_____________． 2. 计算：a 2b ∙b a=__________． 3. 若代数式√x −3有意义，则实数x 的取值范围是_________________．4. 观察图形，若将一个正方形平均分成n ²个小正方形，则一条直线最多可穿越___________个这样的小正方形．5. 若−4x a y +x 2y b =−3x 2y ，则a ＋b ＝_____________．6. “数a 的2倍与10的和”用代数式表示为__________________．7. 一个长方形的面积是(x 2−9) m ²，其长为(x ＋3) m ，用含有x 的整式表示它的宽为_______．8. 计算：√153=_________．9. 一根钢筋长a m ，第一次用去了全长的13，第二次用去了余下的12，则剩余部分的长度为______m （结果要化简）．10. 如果正数m 的平方根为x ＋1和x －3，则m 的值是_____________．11. 计算：3x －5x ＝_________．12. 如果2018个整数a 1，a 2，a 3，…，a 2018满足下列条件：a 1=0，a 2=－|a 1+2|，a 3=－|a 2+2|，…，a 2018=－|a 2017+2|，则a 1+a 2+a 3+…+a 2018=_______________．13. 若代数式x ²－6x ＋b 可化为(x －a )²－1，则b －a 的值是___________．14. 试观察下列各式的规律，然后填空：（x －1）（x +1）=x 2－1（x －1）（x 2+x +1）=x 3－1（x －1）（x 3+x 2+x +1）=x 4－1……则（x －1）（x n +1+x n +…+x +1）=______．三、解答题1. 已知x ＝1是一元二次方程ax ²＋bx －40＝0的一个解，且a ≠b ，求a 2−b 22a−2b 的值． 2. 求值：(x ＋2)²＋(x ＋1)(x －5)，其中x ＝√2．3. 已知A ＝(a+b)2−4abab(a−b)2(a ,b ≠0，且a ≠b )．（1）化简A ；（2）若点P(a,b)在反比例函数y=−5的图象上，求A的值．x。

2018年河北省中考第22题的规律探究与拓展应用！

凭借猜测或者按照规律多写两个数字就可以得出答案但是个人感觉这种方法得出的答案虽然正确但是不会给满分其核心思想在这里考查列方程解决实际问题需要列一个简单的方程
2018年河北省中考第22题的规律探究与拓展应用！
本题主要考查图形的变化规律，解题的关键是根据相邻四个台阶上数的和都相等得出台阶上的数字是每4个一循环。但是非常有意思的一个问题，就是在尝试第二问中，很多同学可以凭借猜测或者按照规律多写两个数字就可以得出答案，但是个人感觉这种方法得出的答案虽然正确但是不会给满分，其核心思想在这里考查列方程解决实际问题，需要列一个简单的方程。

河北省2018年中考数学总复习 规律探索专题

中考数学复习 专题2 规律探索型问题数学课件