20.1.1《平均数》导学案1
20.1.1平均数(1)导学案.doc

20. 1. 1平均数(1)导学案学习目标:1、使学生理解数据的权和加权平均数的概念学习重难点:1、重点:会求加权平均数2、难点:对“权”的理解【自主学习】1、知识准备分中,去掉一个最高分,再去掉一个最低分,求出评分的平均数作为该选手的实际得分.已知评委给某选手的评分如下(单位:分):8, 9.1, 9.3, 9.2, 9.9,那么该选手的实际得分是()A. 9. 1 分B. 9.2 分C. 9.3 分D. 9. 18 分(2)一般地,若n个数Xi, x, , Xn,则2元 = 叫这n个数的平均数.元读作X拔2、阅读教材P111- 113页,了解加权平均数的概念及“权”的意义。
3、加权平均数的概念:若n个数Xi, X2, . , x n的权分别是Wi, w2. ,w”则叫做这n个数的加权平均数。
数据的权能够反映数据的相对__________________________________________________【探究实践】某校八(1)班有30名男生,20名女生,男生的平均身高为1.6米,女生的平均身高为1.4米;八(2)班有20名男生,30名女生,男生的平均身高为1.6 米,女生的平均身高为1.4米。
(1)猜猜看:八(1)班和八(2)班的平均身高相同吗?________________________(2)小组合作,思考计算平均身高的方法:八(1)班平均身高A(2)班平均身I W I____________________(3)说一说:是什么因素导致差别的产生?你怎样理解数据的权?【展示交流】1、一家公司打算招聘一名英文翻译,对甲、乙两名应试者实行了听、说、读、写的英语水平测试,他们各项的成绩(百分制)如下:应试者听说读写甲85837875乙73808582(1)如果这家公司想招一名口语水平较强的翻译,听、说、读、写成绩按3: 3:2: 2的比确定,计算两名应试者的平均成绩(百分制)。
从他们的成绩看,应该录取谁?(2)我来当主考官:如果现在要招一名笔译水平较强的翻译,你能给各数据制定一个合适的权吗?制定的依据是什么?谁将被录取?2、一次演讲比赛中,评委将从演讲内容、演讲水平、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲水平占40%、演讲效果占10%比例,计算选手的综合成绩(百分制)。
20.1.1平均数(第一课时) 导学案

20.1.1平均数(第一课时) 导学案〖学习目标〗1、认识和理解数据的权及其作用,学习统计的思想方法;2、通过实例了解加权平均数的意义,会根据加权平均数的计算公式进行有关计算;3、会利用加权平均数解决有关的实际问题;感受数学结论的确定性. 〖学习重点〗加权平均数的概念以及运用加权平均数解决实际问题. 〖学习难点〗对数据权的概念及其作用的理解. 〖学习过程〗一、【情境引入】 一般地,对于n 个数x 1,x 2,…,x n ,我们把x = ,叫做这n 个数据的算数平均数,简称平均数. 二、【自主学习】阅读课本124-125页,结合教材按顺序解答下列问题: 问题1:分析: 的耕地面积是0.15×15公顷,三个郊县的耕地总面积是 公顷,三个郊县的人口总数是 万人.人口总数总面积人均耕地面积=;解:(1)小明求得这个市郊县的人均耕地面积为: 你认为小明的解法对不对?为什么?(2)三个郊县的人数(单位:万)15、7、10在计算人均耕地面积时作用重要不重要? 这三县人数(单位:万)15、7、10分别叫0.15公顷、0.21公顷、0.18公顷三个数据的______;上面的平均数0.17称为0.15、0.21、0.18的 _______________;(3)若三个数x 1,x 2,x 3权分别是w 1,w 2…w 3,那么这3个数x 1,x 2,x 3的加权平均数就是 . (4)归纳: 加权平均数若n 个数x 1,x 2,……x n 的权分别是w 1,w 2…w n ,则叫做这n 个数的加权平均数.数据的权能够反映数据的相对“ ”.)(18.0318.021.015.0公顷=++=x问题2一家公司打算招聘一名英文翻译,对甲乙两名应试者进行了听、说、读、写的英语水2:2的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?(2)变一变:把第(1)问中“听、说、读、写成绩按照2:2:3:3的比”确定,改为“按照1:2:3:4的比”确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?问题2中,“权”是以一个比例的形式给出的,通过比较(1)、(2)两个问题的结果,你能体会到不同的“权”对最后结果的影响吗?问题3一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占30%、演讲效果占20%的比例,计算选手的综合成绩(百分制)。
2022年《《平均数1》导学案》优秀教案

平均数〔1〕导学案
【学习目标】
1.掌握平均数的计算方法;
2.掌握平均数在数据中所表示的意义。
重点:掌握平均数的计算方法。
【预习导学】
学一学:
仔细阅读教材、m 、m 、m –、m ,那么这组数据的平均数
= 。
6、假设1、2、3、、的平均数为2,且1、2、3、- 、的平均数为,
那么= ;= 。
探究:
互动探究一:
杨枫和李彪两位同学在本期的学习中的数学单元测试成绩如下表:
“议一议〞,到底定谁?谈谈你的看法。
杨枫的平均成绩是;
李彪的平均成绩是。
你认为谁参加比赛比拟适宜?
互动探究二:小明班上同学的平均身高是米,小强班上同学的平均身高是米小明一定比小强矮吗
【归纳总结】。
人教版八年级数学下册20.1.1平均数(第1课时)一等奖优秀教学设计

人教版义务教育课程标准实验教科书八年级下册20.1.1平均数(1) 教学设计一、内容和内容解析1.内容人教版八年级下册“20.1.1平均数”第一课时.2.内容解析统计活动的几个环节中,数据的分析是在对数据的收集、整理基础之上进行的,是统计活动中最重要的环节.平均数是最常用、最基本的数据分析方法,反映一组数据的“平均水平”,并与中位数、众数相结合,通过对数据集中趋势的描述,体现数据向其中心值靠拢或聚集的程度,因此平均数(尤其是加权平均数)是统计中的一个重要概念.本节着重研究加权平均数,“权”的重要性在于它反映的是数据的相对“重要程度”.尽管学生在以前的学习中已初步了解了平均数的意义,并会计算权数相等情况下的算术平均数,但对加权平均数的意义以及“权”的作用理解仍将非常困难,教学中应尽量列举典型的、贴近学生生活和具有现实意义的生活例子,在对实际问题的分析和解决中加深对“权”的理解和体会,渗透平均数和“权”的统计思想,为更好地进行数据的描述与分析,为实现后继统计知识的学习目标──建立统计观念、突出统计思想奠定基础.基于上述分析,确定本节教学重点是:以具体问题为载体,在实际问题情景中理解加权平均数的意义和作用,学会运用加权平均数解决实际问题.二、目标和目标解析1.通过本节教与学的活动,使学生了解平均数(加权平均数)的统计意义,理解“权”的意义和作用,学会计算加权平均数.教学中,以具体实例研究为载体,了解平均数可以描述一组数据的“平均水平”,理解“权”反映数据的相对“重要程度”,体会“权”的作用,使学生更全面的理解加权平均数,正确运用加权平均数解决实际问题.2.通过对加权平均数的学习,经历运用数据描述信息,作出推断的过程,体验统计与生活的联系,形成和发展统计观念,体会权的统计思想,养成用数据说话的习惯和实事求是的科学态度.3.通过具体问题的解决,培养学生严谨的统计精神,思维的深刻性.通过设计“我来决策”等教学活动,让学生学会从不同的侧面有侧重地对评价对象进行全面的客观的考察和评价,培养科学严谨的数学精神和思维的深刻性.三、教学问题诊断分析1.教师教学可能存在的问题:(1)就本论本,不能很恰当地列举典型的、贴近学生生活的现实例子,以具体的实际问题为载体,创设问题情景,揭示概念;(2)不能设计有效的数学问题,使学生通过有思维含量的数学活动,引导学生对“权”的意义和作用有深刻的理解;(3)过分强调知识的获得,忽略了统计思想的揭示和统计观念的建立;(4)对前两个学段中学生已经具有的相关平均数的知识经验了解不足,致使引入的问题太过简单或难度要求过高,导致学生的学习积极性不高.2.学生学习中可能出现的问题:(1)由于生活经验不足,同时受认知水平的影响,对抽象的“权”的意义和作用的理解会有所困难;(2)尽管在第一、第二学段已经学习了统计的简单知识,但对统计的意义和统计思想的理解尚处在最粗浅的认识层面,加之对“权”理解的困难,所以可能会感到这部分知识的学习比较抽象,缺少学习的激情.鉴于上述分析,确定本节的教学难点是:列举典型的、贴近学生生活的、和具有现实意义的生活例子,通过设计有效的、有思维含量的数学问题,激活学生的数学思维,深入理解数据的权的意义和作用.三、学准备:多媒体课件、导学案四、学过程。
人教版数学八年级下册20.1.1《平均数》导学案(无答案)
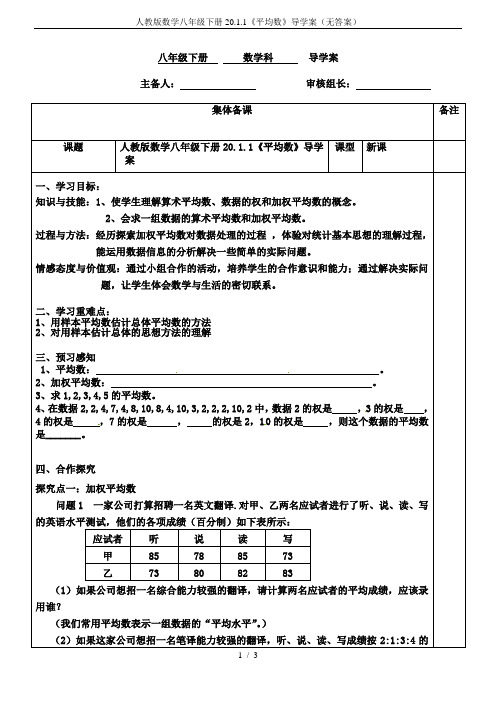
例1一次演讲比赛中,评委按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).试比较谁的成绩更好?
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
五、检查反馈:
1.(1)、如果一组数据是5,x,3,4的平均数是5,那么x=_______
八年级下册数学科导学案
主备人:审核组长:
集体备课
备注
课题
人教版数学八年级下册20.1.1《平均数》导学案
课型
新课
一、学习目标:
知识与技能:1、使学生理解算术平均数、数据的权和加权平均数的概念。
2、会求一组数据的算术平均数和加权平均数。
过程与方法:经历探索加权平均数对数据处理的过程,体验对统计基本思想的理解过程,能运用数据信息的分析解决一些简单的实际问题。
评委编号
1
2
3
4
5
6
7
8
9
10
评分
8.2
8.5
8.4
8.6
6.2
10
8.4
8.6
8.5
8.2
(1)该班的黑板报的得分是多少?此得分能否反映其设计水平?
(2)在这10个评委中,你认为哪几号评委给出了异常分?
六、感悟成功颗粒归仓
1、知识归纳:
2、感悟生成::
一般地,若数的加权平均数.
(3)如果公司想招一名口语能力较强的翻译,听、说、读、写成绩按3:3:2:2的比例确定,则应该录取谁?
(4)与问题(1)、(2)、(3)比较,你能体会到权的作用吗?
《平均数》导学案

精读
点拨
深化
理解
倾听思考理解
我们在求平均数时要找准总数量与总份数之间的对应关系
达标
测评
总结
提升
四(1)班平均身高135厘米,五(2)班平均身高137厘米,王民在四(1)班,张建在五(2)班,王民肯定比张建矮吗?
今天我们一起学习了什么?你有什么收获?
Hale Waihona Puke 确立目标自主探究
学路导航一:根据数据理解平均的含义,概括出平均数。
学路导航一:根据数据理解平均的含义,概括出平均数。
合作
交流
汇报
展示
1、探索其他方法吗?2、那平均数是不是就是以前学过的每份数呢?为什么?总数量4又表示什么呢?总份数,知道平均数可以怎么求吗?
学路导航二:我们一起来估算一下,平均数会是这么多吗?体验平均数。
《平均数》导学案
课题
平均数
课时
3
学科
数学
课型
新授
年级
三年
时间
4.3
主备人
王淑艳
执教人
王淑艳
学习
目标
1、使学生理解平均数的意义,初步学会简单的平均数的方法。
2、理解平均数在统计学上的意义。
3、培养应用所学知识合理、灵活解决简单的实际问题。
学习
重点
使学生理解平均数的意义,初步学会简单的平均数的方法。
学习
板书设计:
平均数
例1(14+12+11+15)÷4
=52÷4
=13(个)
教学反思:本节课我采用先理解什么是平均数,然后在解决平均问题,学生掌握的快又好。
《平均数》导学案

《10.1 平均数》导学案一、学习目标1、记住算术平均数、加权平均数的概念,会利用公式求一组数据的算术平均数和加权平均数。
2、体会算术平均数和加权平均数的联系和区别,并能利用他们解决一些实际问题,感受数学来源于生活,应用于生活。
3、极度热情,全力以赴,合作探究,参与到数学学习过程中去。
二、学习过程【实践探索,感悟新知】◆问题一:1、咱班甲乙二名同学在一次数学测验中的数学成绩分别是92分、85分,你能很快说出哪一位同学的数学成绩不错吗?根据是什么?2、咱班甲乙二个学习小组在一次数学测验中的数学成绩分别是85,89,90,80和86,85,92,81,81。
你知道应该如何衡量二个小组的数学成绩吗?你能列出算式并判断出结果吗?(要求:对第二个问题先独立思考,后在小组内交流)(此要求可在引出课题后再加)通过身边的事,体会:日常生活中,我们常用表示一组数据的“平均水平”。
◆问题二:1.如果你是中国女排的教练,想了解中国女排与俄罗斯女排哪个队更年青,应该收集什么数据?怎样判断?2、根据老师提供的数据,你能列出算式,得出判断结果吗?(要求:在小组内讨论并合作完成,说明思路)【合作交流,学习新知】◆ 算术平均数的定义一般地,对于n 个数,我们把叫做这n 个数的算术平均数,简称平均数,记作 ,读作 ,也就是。
初试身手:(要求:对以下问题先独立完成,后在小组内交流)⑴、七年级一班二组6名同学为“希望工程”捐款,每人捐款金额如下(单位:元):10,12.5,21,16.5,12,18,平均每人捐款 元。
⑵、有20个数据,它们的平均数是34,这20个数据的和是 。
⑶、如果一组数据:6,x ,2,5的平均数是5,那么数据x 的值是 。
⑷、七年级一班有学生50人,七年级二班有学生45人。
期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班所有学生的平均分是多少?(要求:列出算式,求出结果)◆ 加权平均数的定义一般地,在n 个数据中,如果数据x 1,x 2,…,x k 出现的次数分别为n 1,n 2,…,n k ,其中 =n ,那么这n 个数据的平均数为 。
平均数(导学案)

本单元的主要内容有认识平均数,用平均数解决实际问题和复式条形统计图。
本单元是在学生掌握了平均分,初步体验了数据的收集、整理、描述和分析过程,会用简单的统计图表表示统计的结果,能够根据统计图表提出一些简单问题的基础上进行教学的。
平均数是统计中的一个重要概念,由于学生已经具备了平均分的能力,所以应着重让学生理解平均数的意义,在此基础上学生能列出算式并进行计算。
在教学复式条形统计图时,应对第一学段统计的知识做比较系统的整理和复习,便于学生在已有知识和经验的基础上自主建构新的认知结构,让学生进一步体验数据的收集、整理、描述和分析的过程,认识复式条形统计图。
结合实际问题,进一步根据统计图表进行简单的分析,作出合理的判断和决策。
这样把数据分析与解决问题结合在一起,使学生更好地理解统计在解决问题中的作用,逐步形成统计观念。
1.体会平均数的作用,能计算平均数,能用自己的语言解释其实际意义。
2.认识复式条形统计图,了解复式条形统计图的特点,能根据收集的数据在提供的样图中完成相应的复式条形统计图。
3.能根据复式条形统计图提出并回答简单的问题,并进行简单的类推分析。
1.理解平均数的意义,学会简单的求平均数的方法。
2.认识两种复式条形统计图,能根据统计图回答并提出问题。
1.学会简单的求平均数的方法。
2.能根据统计图进行数据分析。
(1)平均数(2课时)(2)复式条形统计图(1课时)(3)练习课(1课时)本单元的教学中教师应注重引导学生理解平均数在统计学上的意义,还应注意让学生体会统计的意义和作用,初步学会利用统计结果进行合理的判断、预测和决策,并理解统计在实际生活中的作用。
平均数(1)课题平均数(1)课型新授课设计说明平均数对于四年级的学生来说是一个非常抽象的概念,教材的主要目的是让学生理解平均数的含义。
基于这一认识,将教学内容分为两部分:第一部分是让学生在具体情境中体会为什么要学习平均数;第二部分是在比较、观察中把握平均数的特征,进而运用平均数解决问题,了解它的价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2课时
1.加深对加权平均数的理解,会根据频数分布表、频数分布直方图求加权平均数.
2.能正确有效地应用平均数知识解决问题,提高分析问题的能力.
3.经历探索利用平均数对数据进行处理的过程,体验对统计基本思想的理解过程.
4.重点:根据频数分布表和频数分布直方图求加权平均数.
问题探究一求n个数的加权平均数
请你阅读教材“例2”上面一段至“探究”上面的内容,回答下列问题.
1.在一个班的40名学生中,14岁的有5人,15岁的有30人,16岁的有4人,17岁的有1人.求这个班学生的平均年龄.(精确到1岁)
解:=≈15.
答:这个班学生的平均年龄约是15岁.
【归纳总结】在求n个数据的简单算术平均数时,如果有k个数据多次重复出现,求这n个数据的算术平均数可以看作是求k个数据的加权平均数.
【预习自测】一组数据中,2出现了f1次,3出现了f2次,4出现了f3次,则这组数据的平均数是.
问题探究二根据频数分布表求加权平均数
1.依据统计表可以读出哪些信息?
5路公共汽车载客量在1≤x<21之间的班次有3次;载客量在21≤x<41之间的班次有5次等.
2.表中的组中值31指什么,它是怎么确定的?频数(班次)5可以看作是相应组中值31的什么?
一个小组的组中值是指这个小组的两个端点的数的平均数.频数5可看作是相应组中值31的权.
3.如果每组数据在本组中分布比较均匀,每组数据的平均值和组中值有什么关系?
当每组数据在本组中分布比较均匀时,每组数据的平均值恰好近似等于它的组中值.
【归纳总结】在上面的频数分布表中,不知原始数据的情况下,如何根据分组数据求加权平均数?
常用各组的组中值代表各组的实际数据,把各组频数看作相应组中的权.
【预习自测】某中学为了了解本校学生的身体发育情况,抽测了同年龄的40名女学生的身高情况,统计人员将上述数据整理后,列出了频数分布表如图所示,根据以上信息回答下列问题:
身高(cm)频数
144.5<x≤149.52
149.5<x≤154.5A
154.5<x≤159.514
159.5<x≤164.512
164.5<x≤169.56
合计40
(1)频数分布表中的A= 6 ;
(2)这40名女学生的平均身高是158.8 cm.(精确到0.1 cm)
问题探究三根据频数分布直方图求加权平均数
双语学校八年级同学进行知识竞赛后,李华将所得成绩进行了整理,结果如图所示:
1.从这个图中,你能算出有多少名同学参加这次知识竞赛吗?
10+25+35+25+5=100(名).
2.与前面所学过的频数分布表相比较,我们用什么代表各组的实际成绩,用什么代表相应组的权?
各组的组中值代表各组的实际成绩,把各组人数看作相应组中的权.
3.你能算出这次竞赛所有参赛选手成绩的平均数吗?
组中值分别为:=55,=65,=75,=85,=95.
=74(分).
4.根据3题中的计算结果,你知道大约有多少人的成绩在平均成绩以下吗?
10+25=35人.
【归纳总结】如何根据频数分布直方图求组中值的加权平均数?
(1)组中值=;(2)加权平均数=.
互动探究1:某单位举行歌咏比赛,分两场举行,第一场8名参赛选手的平均成绩为88分,第二场4名选手的平均成绩为94分.那么这12名参赛选手的平均成绩是多少?
解:=90,这12名参赛选手的平均成绩是90分.
[变式训练]在航天知识竞赛中,包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为71 分.
互动探究2:某班40名学生的身高情况如下图,请计算该班学生的平均身高.
解:=150,=160,=170,=180,
=165.5.
答:该班学生的平均身高为165.5 cm.
互动探究3:某个学习小组,期中考试的平均成绩是M,将M作为另一个同学的成绩,与原来小组同学的成绩合在一起算出平均成绩为N,求M∶N的值.
解:设原来的学习小组有x人,则加入一人后有(x+1)人,由题意得N===M,所以M∶N=1∶1.
见《导学测评》P46。
