小学奥数题——三角形
五年级奥数-图形问题练习及答案

图形问题练习及答案1、如图,在三角形ABC中,D是AB的中点,E是DB的中点,F是BC的中点,如果三角形ABC的面积是96cm2,那么三角形AEF的面积是多少平方厘米?CFA D E B解:三角形ABF与三角形ABC有公用的顶点A,并且它们的底BC和BF在同一条直线上,所以它们的高相等,而三角形ABF的底BF只有三角形ABC的底BC的一半,所以三角形ABF的面积等于三角形ABC的一半,是96÷2=48(cm2)。
同理,三角形AFD的面积是48÷2=24(cm2),三角形DEF的面积是24÷2=12(cm2),因此,三角形AEF的面积是24+12=36(cm2)。
答:三角形AEF的面积是36 cm2。
2、如图所示,大正方形的边长为12 cm,小正方形的边长为10 cm,求阴影部分的面积。
解:阴影三角形的面积无法直接求出,可以用两个正方形面积的和,减去阴影部分周围三个三角形的面积。
所以,阴影部分的面积是122+102-12×(12+10)÷2-102÷2-12×(12-10)÷2=144+100-132-50-12=50(cm2)。
答:阴影部分的面积是50 cm2。
3、把三角形ABC的边AB三等分,AC四等分,如图。
已知三角形ADE的面积是1 cm2,求三角形ABC的面积是多少平方厘米?AE DB C解:三角形AEC的面积是三角形AED的4倍,三角形ABC的面积是三角形AEC的3倍,所以三角形ABC的面积是三角形AED的4×3=12倍,是12(cm2)。
答:三角形ABC的面积是12 cm2。
4、如图所示,在直角梯形ABCD中,AD=8 cm,CD=10 cm,BC=12 cm,CG=GD。
阴影部分的面积是多少平方厘米?DGB C解:(8+12)×10÷2-8×(10÷2)÷2-12×(10÷2)÷2=50(平方厘米)。
【奥数题】人教版小学数学六年级上册三角形中的计算奥数思维拓展(试题)含答案与解析
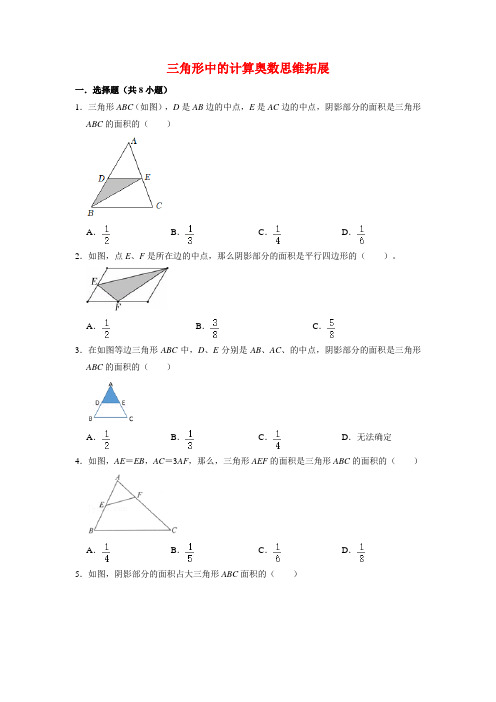
三角形中的计算奥数思维拓展一.选择题(共8小题)1.三角形ABC(如图),D是AB边的中点,E是AC边的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.2.如图,点E、F是所在边的中点,那么阴影部分的面积是平行四边形的()。
A.B.C.3.在如图等边三角形ABC中,D、E分别是AB、AC、的中点,阴影部分的面积是三角形ABC的面积的()A.B.C.D.无法确定4.如图,AE=EB,AC=3AF,那么,三角形AEF的面积是三角形ABC的面积的()A.B.C.D.5.如图,阴影部分的面积占大三角形ABC面积的()A.B.C.D.无法确定6.如图,把三角形ABC的一条边延长一倍到D,把它的另一条边延长2倍到E,得到一个较大的三角形,那么,三角形ABC的面积是三角形ADE的面积的()A.B.C.D.7.如图中,DE=2BE,那么阴影部分面积是长方形面积的()A.B.C.8.如图,在三角形ABC中,E、D、G分别是AB、BC、AD的中点,图中与三角形ADE面积相等的三角形还有()A.0个B.1个C.2个D.3个二.填空题(共8小题)9.如图中阴影部分的面积是12平方厘米,BD:CD=4:5,三角形ADC的面积是平方厘米。
10.如图,三角形ABC的面积27cm2,,三角形AED的面积是cm2。
11.如图,AD=DB,AE=EF=FC。
已知阴影部分的面积是5平方厘米,三角形ABC的面积是平方厘米。
12.如图,直角梯形ABCD的上底是5厘米,下底是7厘米,高是4厘米,且三角形ADE、ABF和四边形AECF的面积相等,则三角形AEF的面积是.13.如图每个小长方形的长2厘米,宽1厘米,阴影部分面积占长方形面积的%.14.在△ABC中,BD=2DC,AE=BE,已知△ABC的面积是18平方厘米,则四边形AEDC的面积等于平方厘米。
15.如图梯形中E是BC的中点,F是DC的中点,线段EF把梯形分成甲、乙两个部分,面积比是21:4,那么梯形的上底AB与下底CD的长度比是。
四年级数学三角形及其他奥数题

(一)、填空1.等腰三角形的两条边( ),它是( )图形,有( )条对称轴;等边三角形的( )相等,每个角都是( )度,它是( )图形,有( )条对称轴。
2.两条边相等的三角形叫( )三角形,已知它的底角为75°,那么顶角是( )度。
3.一个等腰三角形的一个底角是45°,顶角是( )度,它又叫( )三角形。
4.任何一个三角形三个内角的和是( )度。
5.三角形的一个内角为45°,另一个内角是它的2倍,第三个内角是( )度,这个三角形叫( )三角形。
(二)、判断,对的打“√”,错的打“×”6.∠1=75°,∠2=20°,∠3=85°,能组成三角形。
( )7.∠1=65°,∠2=76°,∠3=40°,不能组成三角形。
( )8.三条边分别为15厘米、7厘米、8厘米。
能组成三角形。
( )9.三条边分别为2.5厘米、4.5厘米、8厘米。
不能组成三角形。
( )10.一个三角形三条边的长度分别是6厘米、5厘米、6厘米,这个三角形是等腰三角形。
( )11.等腰三角形不可能是钝角三角形。
( )12.有两个角是锐角的三角形一定是锐角三角形。
( )13.等边三角形是等腰三角形,等腰三角形也是等边三角形。
( )(三)、等腰三角形的一个底角是75°,顶角是多少度?(四)、画出下面三角形底边上的高。
2.在一个等腰三角形中,底角的度数是顶角的2倍,求顶角和底角的度数。
3.计算9999×2222+3333×3334(用简便计算)4、父亲45岁,儿子23岁。
问几年前父亲年龄是儿子的2倍5.求1至100内所有不能被5或9整除的整数和。
6.A、B、C、D四个数,每次去掉一个数,将其余下的三个数求平均数,这样计算了4次,得到下面4个数.23, 26, 30, 33A、B、C、D 4个数的平均数是多少7.甲、乙两桶油共重30千克,如果把甲桶中6千克油倒入乙桶,那么两桶油重量相等,问甲、乙两桶原有多少油。
四年级下册数学奥数试题-培优拓展训练--第3讲:三角形(学生版)

第三讲三角形(1).三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形(2).三角形有三个顶点,三条边和三个角。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
为了表达方便,用字母A,B,C分别表示三角形的三个顶点,这个三角形可以表示成三角形ABC。
(3).三角形具有稳定的特性,这一特性在生活中有着广泛的应用(4).三角形边的关系:三角形任意两边的和大于第三边,如果用a,b,c表示三角形三条边的长度,则有:a+b>c;a+c>b;b+c>a。
(5).认识几种三角形锐角三角形:三个角都是锐角的三角形直角三角形:有一个角是直角的三角形钝角三角形:有一个角是钝角的三角形(6).三角形的分类:(1)按角分有:锐角三角形,直角三角形和钝角三角形。
(2)按边分有:不等边三角形和等腰三角形,其中等腰三角形中还包括三条边都相等的等边三角形。
(7).等腰三角形各部分的名称;在等腰三角形里,相等的两条边叫做腰;另一条边叫做底;两腰的夹角叫做顶角;底边上的两个角叫做底角。
等腰三角形的两个底角相等。
(8).三角形的内角和:任何三角形三个内角的和都是180度。
一个三角形,已知两个角的度数,可以根据“三角形的内角和是180度”求出第三个角的度数。
(9).用三角形拼四边形两个完全相同的三角形可以拼成一个平行四边形;两个完全相同的直角三角形可以拼成一个长方形;两个完全相同的等腰直角三角形可以拼成一个正方形;三个完全相同的三角形可以拼成一个梯形。
一:三角形内角和定理的应用。
二:三角形三边关系的应用,及画钝角三角形高。
1.两个椭圆圈重合的部分应是什么三角形?2.在能组成的三角形的三个角后面画“√”。
1. 900 500 400 ( )2. 500 500 500 ( )3. 1200 300 300 ( )4. 1000 320 190 ( )5. 600 600 600 ( )3.在能组成三角形的三条线段后面画“√”。
小学奥数题及答案:三角形面积

★这篇《⼩学奥数题及答案:三⾓形⾯积》,是⽆忧考特地为⼤家整理的,希望对⼤家有所帮助!
右图是由⼤、⼩两个正⽅形组成的,⼩正⽅形的边长是4厘⽶,求三⾓形ABC的⾯积.
三⾓形⾯积答案:
这道题似乎缺少⼤正⽅形的边长这个条件,实际上本题的结果与⼤正⽅形的边长没关系.连接AD(见右上图),可以看出,三⾓形ABD与三⾓形ACD 的底都等于⼩正⽅形的边长,⾼都等于⼤正⽅形的边长,所以⾯积相等.因为三⾓形AGD是三⾓形 ABD 与三⾓形 ACD的公共部分,所以去掉这个公共部分,根据差不变性质,剩下的两个部分,即三⾓形 ABG与三⾓形 GCD⾯积仍然相等.根据等量代换,求三⾓形ABC的⾯积等于求三⾓形BCD 的⾯积,等于4×4÷2=8。
三角形奥数题

三角形奥数题5.如图,△ABC中,DE∥BC,已知S△OBC=n2,S△=mn(n>m),其中O为BE和CD的交点,求S BCED BOD和S ADE 。
6.如图,D为等边△ABC的边BC上一点。
已知BD=1,CD=2,CH⊥AD于点H,连结BH。
试证:∠BHD=60°。
7.如图,平行四边形ABCD的面积是60,E、F分别是AB、BC的中点,AF与DE、DB分别交于G、H,求四边形EBHG的面积。
8.如图,在等边△ABC的BC边上有一点D,BD : DC=1 : 2,作CH⊥AD,H为垂足,连结BH,求证:△ADB∽△BDH。
9.如图,△ABC中,BC=2AC,D、E分别是BC、AB上的点,且∠1=∠2=∠3。
如果△ABC、△EBD、△ADC的周长为m、m1、m2,求12m mm的值。
10.如图,在直线l的同侧有三个相邻的等边三角形△ABC、△ADE、△AFG,且G、A、B都在直线l上,设这三个三角形边长分别为a 、b 、c ,连结GD 交AE 于N ,连BN 交AC 于L ,求AL 的长。
11.如图,△PQR 与△P'Q'R'是两个全等的等边三角形,六边形ABCDEF 的边长分别记为AB=a 1,BC=b 1,CD=a 2,DE=b 2,EF=a 3,FA=b 3,求证:a 12+a 12+a 12=b 12+b 12+b 1212.如图,设P 、Q 是线段BC上的两定点,且BP=CQ ,A 为BC 外一动点,当A 运动到使∠BAP=∠CAQ 时,△ABC是什么三角形?证明你的结论。
13.如图,△ABC的面积是其内接矩形△QRS面积的三倍,并且边BC与高AD的值是有理数,问矩形PQRS周长的值在什么情况下是有理数?在什么情况下是无理数?14.如图,在△ABC 中,∠BAC=60°,∠ACB=45°⑴求这个三角形三边之比AB : BC :AC ;⑵设P 为△ABC 内一点,且PA=62+,PB=326,PC=3226,求∠APB 、∠BPC 、∠CPA 。
四年级下册数学奥数试题-培优拓展训练--第3讲:三角形(教师版)

第三讲三角形(1).三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形(2).三角形有三个顶点,三条边和三个角。
从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
为了表达方便,用字母A,B,C分别表示三角形的三个顶点,这个三角形可以表示成三角形ABC。
(3).三角形具有稳定的特性,这一特性在生活中有着广泛的应用(4).三角形边的关系:三角形任意两边的和大于第三边,如果用a,b,c表示三角形三条边的长度,则有:a+b>c;a+c>b;b+c>a。
(5).认识几种三角形锐角三角形:三个角都是锐角的三角形直角三角形:有一个角是直角的三角形钝角三角形:有一个角是钝角的三角形(6).三角形的分类:(1)按角分有:锐角三角形,直角三角形和钝角三角形。
(2)按边分有:不等边三角形和等腰三角形,其中等腰三角形中还包括三条边都相等的等边三角形。
(7).等腰三角形各部分的名称;在等腰三角形里,相等的两条边叫做腰;另一条边叫做底;两腰的夹角叫做顶角;底边上的两个角叫做底角。
等腰三角形的两个底角相等。
(8).三角形的内角和:任何三角形三个内角的和都是180度。
一个三角形,已知两个角的度数,可以根据“三角形的内角和是180度”求出第三个角的度数。
(9).用三角形拼四边形两个完全相同的三角形可以拼成一个平行四边形;两个完全相同的直角三角形可以拼成一个长方形;两个完全相同的等腰直角三角形可以拼成一个正方形;三个完全相同的三角形可以拼成一个梯形。
一:三角形内角和定理的应用。
二:三角形三边关系的应用,及画钝角三角形高。
1.两个椭圆圈重合的部分应是什么三角形?答案:等腰直角三角形2.在能组成的三角形的三个角后面画“√”。
1. 900 500 400 ( )√2. 500 500 500 ( )3. 1200 300 300 ( )√4. 1000 320 190 ( )5. 600 600 600 ( )√3.在能组成三角形的三条线段后面画“√”。
小学奥数教程:三角形(一)全国通用(含答案)

小学奥数教程:三角形(一)全国通用(含答案)一、三角形的定义三角形是由三条线段组成的图形,每两条线段之间都有一个角。
二、三角形的分类根据边长关系,三角形可以分为以下几类:1. 等边三角形:三条边的长度都相等。
等边三角形:三条边的长度都相等。
2. 等腰三角形:两条边的长度相等,另一条边的长度不等。
等腰三角形:两条边的长度相等,另一条边的长度不等。
3. 直角三角形:其中一个角为直角,即90度。
直角三角形:其中一个角为直角,即90度。
4. 锐角三角形:三个角都是锐角,即小于90度的角。
锐角三角形:三个角都是锐角,即小于90度的角。
5. 钝角三角形:其中一个角是钝角,即大于90度的角。
钝角三角形:其中一个角是钝角,即大于90度的角。
三、三角形的性质三角形有一些特点和性质:1. 内角和:三角形的内角和等于180度。
内角和:三角形的内角和等于180度。
2. 外角和:三角形的外角和等于360度。
外角和:三角形的外角和等于360度。
3. 角平分线:三角形的内角的平分线相交于三角形的内心。
角平分线:三角形的内角的平分线相交于三角形的内心。
4. 中线:三角形的三条中线相交于三角形的重心。
中线:三角形的三条中线相交于三角形的重心。
5. 高线:三角形的三条高线相交于三角形的垂心。
高线:三角形的三条高线相交于三角形的垂心。
四、三角形的计算计算三角形的面积和周长时,可以根据不同类型的三角形采用不同的方法:1. 等边三角形:面积和周长可以直接计算。
等边三角形:面积和周长可以直接计算。
2. 等腰三角形:根据底边和腰的长度计算面积和周长。
等腰三角形:根据底边和腰的长度计算面积和周长。
3. 直角三角形:使用勾股定理和正弦、余弦、正切等三角函数计算面积和周长。
直角三角形:使用勾股定理和正弦、余弦、正切等三角函数计算面积和周长。
4. 一般三角形:使用海伦公式计算面积,根据边长计算周长。
一般三角形:使用海伦公式计算面积,根据边长计算周长。
