线性方程组求解Matlab程序
matlab求解方程组 整数解

一、概述MATLAB 是一种强大的科学计算软件,能够对各种数学问题进行求解和模拟。
其中,求解方程组是 MATLAB 的一项重要功能。
在实际的数学和工程问题中,需要求解多元方程组的整数解。
本文将介绍如何使用 MATLAB 来求解整数解的方程组。
二、方程组的表示在 MATLAB 中,方程组可以表示为矩阵的形式。
假设有一个包含 n 个变量和 n 个方程的方程组,可表示为以下形式:A * x = b其中,A 是一个n×n 的系数矩阵,x 是一个n×1 的未知数向量,b 是一个n×1 的常数向量。
三、MATLAB 求解整数解的方程组在 MATLAB 中,可以使用 linprog 函数来求解整数解的方程组。
该函数的语法如下所示:x = linprog(f, A, b, Aeq, beq, lb, ub, options)其中,f 是一个n×1 的目标函数系数向量,A 和 b 分别是n×n 和n×1 的不等式约束系数矩阵和常数向量,Aeq 和 beq 分别是n×n 和n×1 的等式约束系数矩阵和常数向量,lb 和 ub 分别是n×1 的下界和上界向量,options 是一个结构体用于指定求解器的参数。
四、实例演示为了更好地理解如何使用 MATLAB 求解整数解的方程组,下面举一个简单的实例进行演示。
假设有以下方程组:2x + 3y = 74x - 3y = 5需要将方程组表示为矩阵形式。
系数矩阵A 和常数向量b 如下所示:A = [2, 3; 4, -3]b = [7; 5]可以使用 linprog 函数进行求解。
假设目标函数为空,不需要约束条件和下界上界,即可直接使用如下命令进行求解:x = linprog([], -A, -b, [], [], zeros(2, 1))求解得到的 x 即为方程组的整数解。
五、注意事项在使用 MATLAB 求解整数解的方程组时,需要注意以下几点:1. 方程组必须为线性方程组。
matlab中用克拉默法则解n元方程

matlab中用克拉默法则解n元方程克拉默法则是一种解决n元线性方程组的方法,它通过使用行列式的性质,可以求解出方程组的解。
在MATLAB中,可以利用克拉默法则来解决n元线性方程组的问题。
克拉默法则的基本思想是,将n元线性方程组的解表示为各个未知数的比例关系,并通过计算行列式的值来求解未知数的值。
具体步骤如下:1. 将n元线性方程组写成矩阵形式。
假设方程组为A*X=B,其中A 是一个n阶矩阵,X是未知数向量,B是已知常数向量。
2. 计算系数矩阵A的行列式值det(A)。
如果det(A)=0,说明方程组无解;如果det(A)≠0,说明方程组有唯一解。
3. 对于方程组的每一个未知数Xi,将其系数矩阵A中第i列替换为常数向量B,得到矩阵Ai。
然后计算矩阵Ai的行列式值det(Ai)。
4. 未知数Xi的解为det(Ai)/det(A)。
将每个未知数的解代入原方程组中,可以验证解的正确性。
以一个具体的例子来说明克拉默法则在MATLAB中的应用。
假设有以下的3元线性方程组:2x + 3y - z = 14x - y + 2z = -23x + 2y - 3z = 3将方程组写成矩阵形式:A = [2, 3, -1; 4, -1, 2; 3, 2, -3]B = [1; -2; 3]接下来,计算系数矩阵A的行列式值:detA = det(A)然后,计算每个未知数的解:x = det([B, A(:,2:3)])/detAy = det([A(:,1), B, A(:,3)])/detAz = det([A(:,1:2), B])/detA将解代入原方程组中验证:eq1 = 2*x + 3*y - zeq2 = 4*x - y + 2*zeq3 = 3*x + 2*y - 3*z如果方程组有解,那么eq1、eq2和eq3的值应该分别为1、-2和3。
通过以上步骤,可以使用MATLAB中的克拉默法则来解决n元线性方程组的问题。
MATLAB程序设计第六讲

MATLAB程序设计杨凯2010 . 11主要内容自学))*MATLAB解方程与函数极值解方程与函数极值((自学(自学)自学)线性方程组求解(一、线性方程组求解二、非线性方程组求解三、函数极值四、常微分方程初值问题的数值解法*MATLAB符号计算一、符号计算基础二、微积分三、简化方程表达式四、解方程一、线性方程组求解(自学)1.1 直接解法1.利用左除运算符的直接解法对于线性方程组Ax=b,可以利用左除运算符“\”求可以利用左除运算符“解:x=A\b例*:用直接解法求解下列线性方程组用直接解法求解下列线性方程组。
命令如下命令如下::A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b2.利用矩阵的分解求解线性方程组矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积算法将一个矩阵分解成若干个矩阵的乘积。
常见的矩阵分解有LU 分解分解、、QR 分解分解、、Cholesky 分解分解,,以及Schur 分解分解、、Hessenberg 分解分解、、奇异分解等奇异分解等。
(1) LU 分解矩阵的LU 分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积形式角矩阵和一个上三角矩阵的乘积形式。
线性代数中已经证明,只要方阵A 是非奇异的是非奇异的,,LU 分解总是可以进行的分解总是可以进行的。
MATLAB 提供的lu 函数用于对矩阵进行LU 分解分解,,其调用格式为式为::[L,U]=lu(X):产生一个上三角阵U 和一个变换形式的下三角阵L(行交换),使之满足X=LU 。
注意注意,,这里的矩阵X 必须是方阵是方阵。
[L,U,P]=lu(X):产生一个上三角阵U 和一个下三角阵L 以及一个置换矩阵P ,使之满足PX=LU 。
当然矩阵X 同样必须是方阵方阵。
实现LU 分解后分解后,,线性方程组Ax=b 的解x=U\(L\b)或x=U\(L\Pb),这样可以大大提高运算速度这样可以大大提高运算速度。
线性方程组的直接解法及matlab的实现

本科毕业论文( 2010 届)题目线性方程组的直接解法及matlab的实现学院数学与信息工程学院专业数学与应用数学班级2006级数学1 班学号**********学生姓名胡婷婷指导教师王洁完成日期2010年5月摘要随着科技技术的发展及人类对自然界的不断探索模拟.在自然科学和工程问题中的很多问题的解决常常归结为线性代数问题!本文的主要内容是对线性方程组求解方法的探讨,主要介绍了四种求解线性方程组的方法,第一种是教科书上常见的消元法,我们称之为基本法.第二种方法是标准上三角形求解法,即将增广矩阵经过初等变换后化成标准上三角形,然后求解.它改进了一般教科书上的常见方法,与常见方法比较有如下优点:1)规范了自由未知量的选取;2)只用矩阵运算;3)减少了计算量.第三种方法是对特定的方程组(系数矩阵A为n阶对称正定矩阵,且A的顺序主子式均不为零.)的求解方法进行描述,并且为这种线性方程的求解提供了固定的公式化的方法.第四种方法是对现在实际问题中常常会遇到的系数矩阵为三对角矩阵的方程组的求解方法.同时给出这几种方法的数值解法(matlab程序),由于运用电脑软件求解,所以必须考虑计算方法的时间、空间上的效率以及算法的数值稳定性问题,所以针对不同类型的线性方程组有不同的解法.但是,基本的方法可以归结为两大类,即直接法和迭代法.关键词高斯消去法;三角分解法;乔莱斯基分解法;追赶法AbstractSystems of linear equations are associated with many problems in engineering and scinence ,as well as with applications of mathematics to the social sciences and the quantitative study of business and economic problems.The main content of this article is the method for solving linear equations, we introduce four methods for solving linear equations in this paper. The first is the elimination method which is commonly found in textbooks, and we call the Basic Law. The second method is Standard on the triangle Solution, that first change Augmented matrix into standards in primary triangle, and then solving. It improves the general textbook on common methods, compared with the common method has the following advantages:1) Specification of the free choice of unknowns; 2)Only matrix operations;3) Reduce the computation. The third method describes a way to solve a Specific equations(N coefficient matrix A is symmetric positive definite matrix, and A are not zero-order principal minor), And for this linear equation provides a fixed formulaic approach. The fourth method is to present practical problems often encountered in the coefficient matrix is tridiagonal matrix method for solving the equations. These methods are given numerical solution of (matlab program), As the use of computer software to solve, it is necessary to consider ways of computing time and space efficiency and numerical stability of algorithms, Therefore, different types of linear equations have a different solution. However, the basic method can be classified into two categories, namely direct methods and iterative methods.Key wordsGaussian elimination; Triangular decomposition; Cholesky decomposition method;Thomas algorithm目录1. 引言 (1)2.相关知识 (2)2.1 向量和矩阵 (2)2.2 特殊矩阵 (3)3.问题叙述 (3)4.问题分析 (4)4.1高斯分解法 (4)4.2三角分解法 (6)4.3乔莱斯基分解法 (6)4.4追赶法 (7)5. 举例说明与总结 (9)5.1举例说明 (9)5.1.1高斯分解的matlab程序方法 (9)5.1.2三角分解法的matlab程序方法 (10)5.1.3乔莱斯基分解法的matlab程序方法 (11)5.1.4追赶法的matlab程序方法 (13)5.2总结 (14)参考文献 (16)谢辞 (17)线性方程组的直接解法及matlab的实现Direct solution of linear equations and matlab implementation数学与信息工程学院数学与应用数学专业胡婷婷指导教师:王洁1.引言随着科技技术的发展及人类对自然界的不断探索模拟.在自然科学和工程问题中的很多问题的解决常常归结为线性代数问题!例如电学中的网络问题,用最小二乘法求实验数据拟合问题(如大地测量数据处理),解非线性方程组问题,用差分法或有限元法解常微分方程、偏微分方程边值问题等最终都归结于解线性代数方程组.从实际数据来看,这些方程组的系数矩阵大致分为两种,一种是低阶稠密矩阵(阶数不超过150).另一种是大型稀疏矩阵(矩阵阶数高且零元素较多).所以,现在我们需要对求线性方程组的方法进行探究,以便能够找到一些简便的方法来加以应用!本文主要就线性方程组的直接解法予以讨论.线性方程组是线性代数的主要内容,包括线性方程组有解性的判定、消元法解线性方程组和线性方程组解的结构. 它与矩阵、向量的内容密切相关,与矩阵、向量组相关的许多重要结论都是线性方程组有关结论的应用和推广. 如:一个向量是否可以由一个向量组线性表示、表示形式是否唯一往往与非齐次线性方程组是否有解、有唯一解还是无穷多解是等价的;一个向量组是否线性相关与齐次线性方程组是否有非零解是等价的等等.而且随着现代工业的发展,线性方程组的应用出现在各个领域,伴随着大量方程和多未知数的出现, 例如电学中的网络问题,用最小二乘法求实验数据拟合问题(如大地测量数据处理),解非线性方程组问题,用差分法或有限元法解常微分方程、偏微分方程边值问题等最终都归结于解线性代数方程组。
matlab最小二乘解方程

matlab最小二乘解方程最小二乘法是求解线性方程组的一种有效方法,可以通过最小化误差平方和来得到最优解。
在MATLAB中,我们可以使用“\”操作符或者使用“pinv”函数来求解一个线性方程组的最小二乘解。
以下是关于如何在MATLAB中使用最小二乘法来求解线性方程组的详细内容:1. 使用“\”操作符使用“\”操作符可以很方便地求解一个线性方程组的最小二乘解。
例如,假设我们有一个由n个方程组成的线性方程组:Ax = b其中,A是一个m ×n的矩阵,x是一个n维向量,b是一个m维向量。
则它的最小二乘解为:x = (A' A)^(-1) A' b在MATLAB中,我们可以通过以下代码实现最小二乘解:A = [1 1 1; 2 3 4; 4 5 7; 5 6 8];b = [1; 2; 3; 4];x = A \ b;其中,反斜杠符号“\”表示求解线性方程组的最小二乘解。
2. 使用“pinv”函数除了使用“\”操作符,我们也可以使用MATLAB中的“pinv”函数来求解一个线性方程组的最小二乘解。
例如,我们可以通过以下代码实现最小二乘解:A = [1 1 1; 2 3 4; 4 5 7; 5 6 8];b = [1; 2; 3; 4];x = pinv(A) * b;其中,pinv函数表示求矩阵A的伪逆矩阵。
使用“pinv”函数来求解线性方程组的最小二乘解与使用“\”操作符的结果是等价的。
需要注意的是,在使用最小二乘法来求解线性方程组时,矩阵A的列应该是线性无关的,否则可能会出现唯一最小二乘解不存在的情况。
综上所述,MATLAB中使用最小二乘法来求解线性方程组非常简单。
我们可以通过“\”操作符或者“pinv”函数来求解一个线性方程组的最小二乘解。
matlab多元一次方程组求解

MATLAB多元一次方程组求解在数学和工程领域,解决多元一次方程组是一个常见且重要的问题。
MATLAB作为一种高级的计算机编程语言和工具,提供了方便快捷的方法来解决这一类问题。
在本文中,我们将探讨MATLAB在解决多元一次方程组方面的应用和方法。
1. 了解多元一次方程组多元一次方程组是由多个未知数和这些未知数的线性关系组成的方程组。
一个包含两个未知数x和y的一次方程组可以表示为:a1x + b1y = c1a2x + b2y = c2其中a1、b1、c1、a2、b2、c2为已知常数。
2. MATBLAB的线性方程组求解函数MATLAB提供了几种用于求解线性方程组的函数,例如“linsolve”、“mldivide”、“inv”等。
其中,“linsolve”函数可以用于求解形如Ax=b的线性方程组,其中A为系数矩阵,b为常数向量。
而“mldivide”函数则可以直接求解形如Ax=b的线性方程组。
在MATLAB中,通过这些函数可以轻松求解多元一次方程组,无需手动推导和解答。
3. MATLAB求解多元一次方程组的示例下面我们通过一个具体的例子来演示MATLAB如何求解多元一次方程组。
假设我们有以下方程组:2x + 3y - z = 7-3x + 4y + 2z = -105x - 2y + 4z = 4我们可以使用MATLAB的“linsolve”函数来求解该方程组,具体代码如下:A = [2, 3, -1; -3, 4, 2; 5, -2, 4];B = [7; -10; 4];X = linsolve(A, B);通过运行以上代码,我们可以得到方程组的解X,即X = [1; 3; 2]。
这就是该多元一次方程组的解,即x=1,y=3,z=2。
4. 总结和回顾通过本文的介绍,我们了解了MATLAB如何求解多元一次方程组,以及其应用的方法和示例。
MATLAB提供的线性方程组求解函数可以帮助我们快速准确地求解复杂的方程组,为数学和工程问题的求解提供了便利。
数学实验“线性方程组的j迭代,gs迭代,sor迭代解法”实验报告(内含matlab程序代码)【最新精

西京学院数学软件实验任务书实验四实验报告一、实验名称:线性方程组的J-迭代,GS-迭代,SOR-迭代。
二、实验目的:熟悉线性方程组的J-迭代,GS-迭代,SOR-迭代,SSOR-迭代方法,编程实现雅可比方法和高斯-赛德尔方法求解非线性方程组12123123521064182514x x x x x x x x +=⎧⎪++=⎨⎪++=-⎩的根,提高matlab 编程能力。
三、实验要求:已知线性方程矩阵,利用迭代思想编程求解线性方程组的解。
四、实验原理:1、雅可比迭代法(J-迭代法):线性方程组b X A =*,可以转变为:迭代公式(0)(1)()k 0,1,2,....k k J XXB X f +⎧⎪⎨=+=⎪⎩ 其中b M f U L M A M I B J 111),(---=+=-=,称J B 为求解b X A =*的雅可比迭代法的迭代矩阵。
以下给出雅可比迭代的分量计算公式,令),....,()()(2)(1)(k n k k k X X X X =,由雅可比迭代公式有b XU L MXk k ++=+)()1()(,既有i ni j k i iji j k iij k iij b X aXa X a +--=∑∑+=-=+1)(11)()1(,于是,解b X A =*的雅可比迭代法的计算公式为⎪⎩⎪⎨⎧--==∑∑-=+=+)(1),....,(111)()()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 2、 高斯-赛德尔迭代法(GS-迭代法):GS-迭代法可以看作是雅可比迭代法的一种改进,给出了迭代公式:⎪⎩⎪⎨⎧--==∑∑-=+=+++)(1),....,(111)1()1()1()0()0(2)0(1)0(i j n i j k j ij k j ij i ii k iTn X a X a b a X X X X X 其余部分与雅克比迭代类似。
解线性方程组程序及流程图
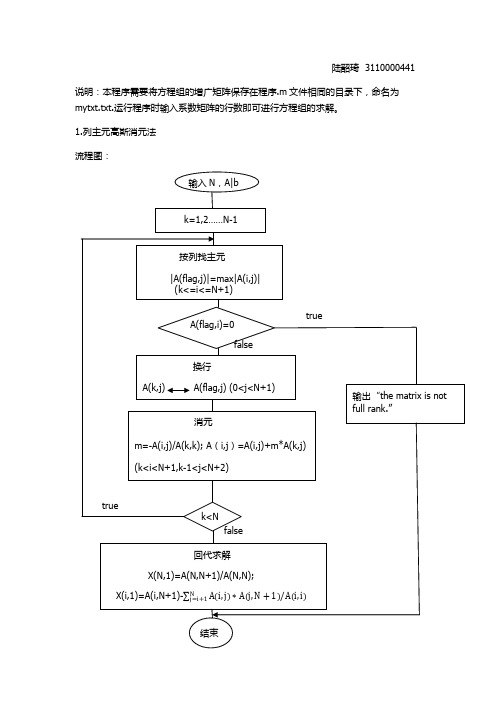
陆韶琦 3110000441说明:本程序需要将方程组的增广矩阵保存在程序.m文件相同的目录下,命名为mytxt.txt.运行程序时输入系数矩阵的行数即可进行方程组的求解。
1.列主元高斯消元法流程图:程序代码%列主元高斯消元法¨%控制输入增广矩阵行数N=input('what is the rank of the matrix:');%从mytxt.txt文件中读入增广矩阵f=fopen('mytxt.txt','r');A=fscanf(f,'%g',[N+1 N]);fclose(f);A=A';disp('A|b=');disp(A)%列主元的寻找for i=1:Nmax=abs(A(i,i));for j=i+1:Nif A(j,i)>maxflag=j;max=A(j,i);endend%判断矩阵是否满秩if A(flag,i)==0disp('the martrix is not full rank');flag=0;break;end;%实现两行的交换for k=i:N+1B=A(flag,k);A(flag,k)=A(i,k);A(i,k)=B;end%实现消元for kh=i+1:Nm=-A(kh,i)/A(i,i);A(kh,i)=0;for kl=i+1:N+1A(kh,kl)=A(kh,kl)+m*A(i,kl);endendendif flag~=0disp('U|b=');%输出此时得到的上三角矩阵disp(A);X=zeros(N,1);%回代得到解for i=N:-1:1for j=i-1:-1:1m=-A(j,i)/A(i,i);A(j,N+1)=A(j,N+1)+m*A(i,N+1);endX(i,1)=A(i,N+1)/A(i,i);end disp('X=');disp(X);end运行equation.m文件,结果如下:2.程序代码:%列主元三角分解法N=input('what is the rank of the matrix:');f=fopen('mytxt.txt','r');A=fscanf(f,'%g',[N+1 N]);fclose(f);A=A';disp('A|b=');disp(A);%形成Li1,U1jmax=A(1,1);flag1=1;for i=2:Nif A(i,1)>max;max=A(i,1);flag=i;endend%判断矩阵是否满秩if A(flag,1)==0flag1=0;disp('the matrix is not full rank');elsefor i=1:N+1m=A(1,i);A(1,i)=A(flag,i);A(flag,i)=m;endfor i=2:NA(i,1)=A(i,1)/A(1,1);end% 计算aij-∑Lij*Ujkfor k=2:Nfor i=k:Nfor j=1:k-1 A(i,k)=A(i,k)-A(i,j)*A(j,k);endend%寻找主元max=A(k,k);for i=k:Nif A(i,k)>max;max=A(i,k);flag=i;endend%判断矩阵是否满秩if A(flag,i)==0flag1=0;disp('the matrix is not full rank');break;else%换行for i=1:N+1m=A(k,i);A(k,i)=A(flag,i);A(flag,i)=m;end%形成Uijfor i=k+1:N+1for j=1:k-1A(k,i)=A(k,i)-A(k,j)*A(j,i);endend%形成Lijfor i=k+1:NA(i,k)=A(i,k)/A(k,k);endendendif flag1~=0disp('LU=');disp(A);X=zeros(N,1);%回代得到解for i=N:-1:1for j=i-1:-1:1m=-A(j,i)/A(i,i);A(j,N+1)=A(j,N+1)+m*A(i,N+1);endX(i,1)=A(i,N+1)/A(i,i);enddisp('X=');disp(X);endend运行equation2.m文件,结果如下:编程感想:本程序利用matlab平台,实现了线性方程组的求解,但是这是很底层的方法,如果将其中的语句稍加修改,就可以用c编译器进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性方程组求解 1.直接法 Gauss消元法: function x=DelGauss(a,b) % Gauss消去法 [n,m]=size(a); nb=length(b); det=1;%存储行列式值 x=zeros(n,1); for k=1:n-1 for i=k+1:n if a(k,k)==0 return end m=a(i,k)/a(k,k); for j=k+1:n a(i,j)=a(i,j)-m*a(k,j); end b(i)=b(i)-m*b(k); end det=det*a(k,k); end det=det*a(n,n); for k=n:-1:1 %回代 for j=k+1:n b(k)=b(k)-a(k,j)*x(j); end x(k)=b(k)/a(k,k); end Example: >> A=[1.0170 -0.0092 0.0095;-0.0092 0.9903 0.0136;0.0095 0.0136 0.9898]; >> b=[1 0 1]'; >> x=DelGauss(A,b)
x = 0.9739 -0.0047 1.0010 列主元Gauss消去法: function x=detGauss(a,b) % Gauss列主元消去法 [n,m]=size(a); nb=length(b); det=1;%存储行列式值 x=zeros(n,1); for k=1:n-1 amax=0;% 选主元 for i=k:n if abs(a(i,k))>amax amax=abs(a(i,k));r=i; end end if amax<1e-10 return; end
if r>k %交换两行 for j=k:n z=a(k,j);a(k,j)=a(r,j);a(r,j)=z; end z=b(k);b(k)=b(r);b(r)=z;det=-det; end for i=k+1:n %进行消元 m=a(i,k)/a(k,k); for j=k+1:n a(i,j)=a(i,j)-m*a(k,j); end b(i)=b(i)-m*b(k); end det=det*a(k,k); end det=det*a(n,n);
for k=n:-1:1 %回代 for j=k+1:n b(k)=b(k)-a(k,j)*x(j); end x(k)=b(k)/a(k,k); end Example: >> x=detGauss(A,b)
x = 0.9739 -0.0047 1.0010
Gauss-Jordan消去法: function x=GaussJacobi(a,b) % Gauss-Jacobi消去法 [n,m]=size(a); nb=length(b); x=zeros(n,1); for k=1:n amax=0;% 选主元 for i=k:n if abs(a(i,k))>amax amax=abs(a(i,k));r=i; end end if amax<1e-10 return; end if r>k %交换两行 for j=k:n z=a(k,j);a(k,j)=a(r,j);a(r,j)=z; end z=b(k);b(k)=b(r);b(r)=z; end %进行消元 b(k)=b(k)/a(k,k); for j=k+1:n a(k,j)=a(k,j)/a(k,k); end for i=1:n if i~=k for j=k+1:n a(i,j)=a(i,j)-a(i,k)*a(k,j); end b(i)=b(i)-a(i,k)*b(k); end end end for i=1:n x(i)=b(i); end Example: >> x=GaussJacobi(A,b)
x = 0.9739 -0.0047 1.0010 LU分解法: function [l,u]=lu(a) %LU分解 n=length(a); l=eye(n); u=zeros(n); for i=1:n u(1,i)=a(1,i); end for i=2:n l(i,1)=a(i,1)/u(1,1); end for r=2:n %%%% for i=r:n uu=0; for k=1:r-1 uu=uu+l(r,k)*u(k,i); end u(r,i)=a(r,i)-uu; end %%%% for i=r+1:n ll=0; for k=1:r-1 ll=ll+l(i,k)*u(k,r); end l(i,r)=(a(i,r)-ll)/u(r,r); end %%%% End function x=lusolv(a,b) %LU分解求解线性方程组aX=b if length(a)~=length(b) error('Error in inputing!') return; end n=length(a); [l,u]=lu(a); y(1)=b(1); for i=2:n z=0; for k=1:i-1 z=z+l(i,k)*y(k); end y(i)=b(i)-z; end
x(n)=y(n)/u(n,n); for i=n-1:-1:1 z=0; for k=i+1:n z=z+u(i,k)*x(k); end x(i)=(y(i)-z)/u(i,i); end Example: >> x=lusolv(A,b)
x = 0.9739 -0.0047 1.0010 对称正定矩阵之Cholesky分解法: function L=Cholesky(A) %对对称正定矩阵A进行Cholesky分解 n=length(A); L=zeros(n); for k=1:n delta=A(k,k); for j=1:k-1 delta=delta-L(k,j)^2; end if delta<1e-10 return; end L(k,k)=sqrt(delta); for i=k+1:n L(i,k)=A(i,k); for j=1:k-1 L(i,k)=L(i,k)-L(i,j)*L(k,j); end L(i,k)=L(i,k)/L(k,k); end end function x=Chol_Solve(A,b) %利用对称正定矩阵之Cholesky分解求解线性方程组Ax=b n=length(b); l=Cholesky(A); x=ones(1,n); y=ones(1,n); for i=1:n z=0; for k=1:i-1 z=z+l(i,k)*y(k); end y(i)=(b(i)-z)/l(i,i); end for i=n:-1:1 z=0; for k=i+1:n z=z+l(k,i)*x(k); end x(i)=(y(i)-z)/l(i,i); end Example: >> a=[9 -36 30 ;-36 192 -180;30 -180 180]; >> b=[1 1 1]'; >> x=Chol_Solve(a,b)
x = 1.8333 1.0833 0.7833 对称正定矩阵之LDL’分解法: function [L,D]=LDL_Factor(A) %对称正定矩阵A进行LDL'分解 n=length(A); L=eye(n); D=zeros(n); d=zeros(1,n); T=zeros(n); for k=1:n d(k)=A(k,k); for j=1:k-1 d(k)=d(k)-L(k,j)*T(k,j); end if abs(d(k))<1e-10 return; end for i=k+1:n T(i,k)=A(i,k); for j=1:k-1 T(i,k)=T(i,k)-T(i,j)*L(k,j); end L(i,k)=T(i,k)/d(k); end end D=diag(d);
function x=LDL_Solve(A,b) %利用对对称正定矩阵A进行LDL'分解法求解线性方程组Ax=b n=length(b);
