剪力和弯矩图关系_平衡微分方程
合集下载
用微分关系法绘制剪力图和弯矩图
CA段受向下均布荷载的作用，剪 力图为向右下倾斜的直线。
FSC = 0 FSLA = －qa
AB段受向下均布荷载的作用，
2qa
剪力图为向右下倾斜的直线。
＋
FSRB qa FA 2qa
FS图 qa
FSLB 3qa qa 2qa
并由 FSRA qx 2qa qx 0
得剪力为零的截面E的位置x=2a。
目录
弯曲内力\用微分关系法绘制剪力图和弯矩图
1. 2 弯矩、剪力、分布荷载集度之间的积分关系
由式
dFS (x) dx
q(x)
可以得出：在x＝a和x＝b处的两个横截间的
积分为
b
b
Байду номын сангаас
a dFS(x)
q( x)dx
a
它可写为
b
FSB FSA
q( x)dx
a
式中：FSA、 FSB——分别表示x＝a和x＝b两个横截面上的剪力。 该式表明：任何两个横截面上的剪力之差，等于这两个横截面
目录
弯曲内力\用微分关系法绘制剪力图和弯矩图
2）在均布荷载作用的一段梁上，q（x）=常数≠0。由
d2 M (x) d2 x
dFS (x） dx
q(x)
=常数可知，该梁段内各横截面上的剪力FS(x)
为x的一次函数，而弯矩M(x)为x的二次函数，故剪力图必然是斜直
线，而弯矩图是抛物线。
当q(x)＞0（荷载向上）时，剪力图为向上倾斜的直线，弯矩图 为向上凸的抛物线；
qa
－ 2qa
BD段受向下均布荷载的作用，剪力图为向右下倾斜的直线。
FSRB qa
FSD=0
目录
弯曲内力\用微分关系法绘制剪力图和弯矩图
剪力、弯矩方程与剪力、弯矩图
截面位置对剪力和弯矩的影响
总结词
截面位置对剪力和弯矩具有显著影响。不同的截面位置会导致剪力和弯矩的大小和方向发生变化。
详细描述
在结构分析中，截面位置是影响剪力和弯矩的重要因素之一。不同的截面位置会导致剪力和弯矩的大小和方向发 生变化，从而影响结构的整体受力性能。例如，在梁中选取不同的截面位置进行支撑或固定，会对梁的剪力和弯 矩产生显著影响。
05 剪力、弯矩与材料力学性 能的关系
材料弹性对剪力和弯矩的影响
弹性材料在剪力和弯矩作用下会发生弹性变形，变形量与外力成正比，当外力去 除后，材料能够恢复原状。
弹性材料的剪切模量和弯曲刚度决定了剪力和弯矩的大小，剪切模量越大，材料 抵抗剪切变形的能力越强；弯曲刚度越大，材料抵抗弯曲变形的能力越强。
根据绕顺时针方向观察确定，使上侧 纤维受拉时为正。
02 剪力方程与弯矩方程
剪力图与弯矩图的绘制
1
剪力图和弯矩图是表示梁上剪力和弯矩随截面位 置变化的图形。
2
这些图的绘制基于剪力方程和弯矩方程的计算结 果，通过将计算得到的剪力和弯矩值标在图中相 应的位置上，并连接成线。
3
剪力图和弯矩图的绘制有助于直观地了解梁在不 同截面位置的受力状态和应力分布情况。
弯矩
在梁或结构中，由于弯曲而产生 的力矩，表示弯曲变形的大小。
剪力与弯矩在力学中的作用
剪力
主要影响结构的剪切变形，对梁的剪切承载能力有重要影响 。
弯矩
主要影响结构的弯曲变形，对梁的弯曲承载能力有重要影响 。
剪力与弯矩的符号规定
剪力正方向
根据右手定则确定，从杆件的受压一 侧指向受拉一侧。
弯矩正方向
02
材料强度越高，抵抗剪力和弯矩等外力的能力越强， 所能承受的剪力和弯矩越大。
(剪力图与弯矩图)
3．建立剪力方程和弯矩方程
在AC和CB两段分别以坐标为x1 和x2的横截面将梁截开， 并在截开的横截面上，假设剪力FS(x1)、FS(x2)和弯矩M(x1)、 M(x2)都是正方向，然后考察截开的右边部分梁的平衡，由平 衡方程即可确定所需要的剪力方程和弯矩方程。
y
MO=2FPl
O A l x1 x2
例题5
悬臂梁在B、C两处分别承受集中力FP和集中力偶 M＝2FPl 的作用。梁的全长为2l。 试写出：梁的剪力方程和弯矩方程。
MO=2FPl
C
FP
B
A l
l
y
MO=2FPl
O A l
C
FP
x B
l
解：1．分段 本 例将 通 过 考察 截 开 截面 的右边部分平衡建立剪力方程 和弯矩方程，因此可以不必确 定左端的约束力。 由于梁在固定端A处 作 用 有约束力、自由端B处作用有 集中力、中点C处作用有集中 力偶，所以，因此，需要分为 AC和CB两段建立剪力和弯矩 方程。 2．建立Oxy坐标系 以梁的左端A为坐标原点， 建立Oxy坐标系。
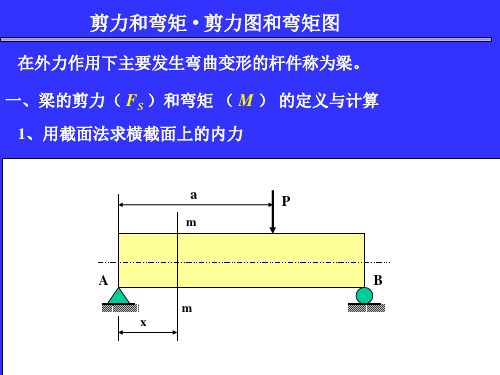
二、基本概念
1、弯曲变形 (1) 受力特征 外力（包括力偶）的作用线垂直于杆轴线. (2) 变形特征 变形前为直线的轴线,变形后成为曲线. 2、梁
三、 受弯杆件的简化
1. 杆件本身的简化：通常取梁的轴线代替梁。 2. 载荷简化 作用于梁上的载荷（包括支座反力）可简化为三种类型：
集中力、集中力偶和分布载荷。
例3 轴的计算简图如图所示，已知 F1 = F2 = F = 60kN ，
a = 230mm,b = 100 mm 和c = 1000 mm.求 C 、D 点处横截面 上的剪力和弯矩. F1=F
梁的剪力和弯矩概念讲解(剪力图弯矩图,含例题)
1
求下图所示简支梁1-1与2-2截面的剪力和弯矩。
F=8kN A 2m 1 1 q=12kN/m 2 2 3m B
例 题
1.5m FB
FA
1.5m
1.5m
解： 1、求支反力
M B 0 FA 6 F 4.5 q 3 F
y
0
3 0 FA 15kN 2 FA FB F q 3 0 FB 29kN
平衡剪力f下载文档收藏分享赏0您可能关注的文档文档评论
一、梁平面弯曲的概念
1、平面弯曲的概念
弯曲变形：作用于杆件上的外力垂直于杆件的轴线，使 杆的轴线由直线变为曲线。
平面弯曲：梁的外载荷都作用在纵向对称面内时，则梁的轴 线在纵向对称面内弯曲成一条平面曲线。 q Me 纵 向 F
对称面
B A
x
FAy FBy
6kN
1
2
q 2kN m
3
4
5
B
1 2 3 4 5
2m
A
3m
C
3m
FA 13kN
FB 5kN
例题
4.5
为使在锯开处两端面的开裂最小，应使锯口处的 弯矩为零，木料放在两只锯木架上，一只锯木架 放置在木料的一端，试问另一只锯木架放置何处 才能使木料锯口处的弯矩为零。
q
B
A
C
D
MD 0
q
a
a
qa 2
qa 2
qa 2
a2
qa 2
a2
qa2 8
qa2 8
F A F
F 2
F B
F 2
a
a
F 2
a
a
剪力以及弯矩剪力图以及弯矩图
剪力图和弯矩图在工程管理中的应用
结构设计：用于计 算结构受力确定结 构尺寸和材料
施工管理：用于 指导施工确保施 工质量和安全
维护管理：用于 评估结构状态制 定维护计划
优化设计：用于 优化结构设计降 低成本和能耗
剪力图和弯矩图的注意 事项
绘制剪力图和弯矩图时应注意的事项
确保数据准确无误 注意单位换算确保单位一致 绘制过程中注意比例尺和坐标轴的设置 绘制完成后检查图例、标题、标注等是否清晰明确
添加副标题
剪力和弯矩剪力图以及弯矩 图
汇报人：
目录
CONTENTS
01 添加目录标题
02 剪力和弯矩的基本 概念
03 剪力图和弯矩图的 绘制
04 剪力图和弯矩图的 解读
05 剪力图和弯矩图的 应用
06 剪力图和弯矩图的 注意事项
添加章节标题
剪力和弯矩的基本概念
剪力和弯矩的定义
剪力：作用在物体表面上的力使物体发生剪切变形 弯矩：作用在物体表面上的力使物体发生弯曲变形 剪力图：表示剪力在物体表面上的分布情况 弯矩图：表示弯矩在物体表面上的分布情况
剪力和弯矩的计算方法
剪力：作用在物体上的力使物体发生剪切变形 弯矩：作用在物体上的力使物体发生弯曲变形 剪力计算方法：根据力的平衡原理利用剪力公式进行计算 弯矩计算方法：根据力的平衡原理利用弯矩公式进行计算
剪力和弯矩的单位和符号
剪力：单位为牛顿（N） 符号为F
弯矩：单位为牛顿·米 （N·m）符号为M
证结构安全
剪力图和弯矩图在施工中的应用
确定结构受力情况： 通过剪力图和弯矩图 可以了解结构的受力 情况为施工提供依据。
优化施工方案：根据 剪力图和弯矩图可以 优化施工方案提高施 工效率和质量。
剪力图和弯矩图
绘剪力图和弯矩图的基本方法：首先分别写出梁 的剪力方程和弯矩方程，然后根据它们作图。
Fs(x)
o
x
o
x
Fs 图的坐标系
M(x) M 图的坐标系
不论在截面的 左侧 或 右侧 向上的外力均将引起 正值 的弯矩，而向下 的外力则引起 负值 的弯矩。
例题：图示简支梁 ，在全梁上受集度为 q 的均布荷载作用。 试作此梁的剪力图和弯矩图。
FA
2KN.m
FB
10KN//m
B
A
C
0.2m
0.4m
解: 求支座反力
F A 2KN (); F B 6KN ()
FA
A x
2KN.m
FB
10KN//m
B
C
0.2m
0.4m
F A 2KN (); F B 6KN ()
分段列剪力方程和弯矩方程
AC段 :
F S (x) F A 2 (0 x 0.2) M (x) F A x 2x (0 x 0.2)
剪力方程和弯矩方程 ：以梁的左端点为坐标原点，x 轴与梁的 轴线重合, 找出横截面上剪力和弯矩与横截面位置的关系 , 这种 关系称为剪力方程和弯矩方程。
即
Fs = Fs (x )
M = M（x）
剪力图和弯矩图
剪力 : 正值剪力画在 x 轴上侧，负值剪力画在 x 轴下侧。
** 弯矩 : 正值弯矩画在 x 轴的下侧；负值弯矩画在x 轴上侧。
不论在截面的 左侧 或 右侧 向上的外力均将引起
正值 的弯矩，而向下 的外力则引起 负值 的弯矩。
利用上述结论来计算某一截面上的内力是非常简便的， 此时不需画脱离体的受力图和列平衡方程，只要梁上的 外力已知，任一截面上的内力均可根据梁上的外力逐项 写出。因此，这种求解内力的方法称为简便法。
材料力学-5-弯矩图与剪力图
从所得到的剪力图和 弯矩图中不难看出:
在集中力作用点两 侧截面上的剪力是不相 等的，而在集中力偶作 用处两侧截面上的弯矩 是不相等的，其差值分 别为集中力与集中力偶 的数值。
例题5
q
A
4a FAy
梁由一个固定铰链支座和一个辊轴支座所
支承，但是梁的一端向外伸出，这种梁称为外 伸梁(overhanging beam)。梁的受力以及各部 分尺寸均示于图中。
工程中的弯曲构件
工程中可以看作梁的杆件是很多的:
桥式吊车的大梁 可以简化为两端饺支 的简支梁。在起吊重 量(集中力FP)及大梁自 身重量(均布载荷q)的 作用下,大梁将发生弯 曲。
工程中可以看作梁的杆件是很多的:
石油、化工设备中各种直立式反应塔，底部与地面固定 成一体，因此，可以简化为一端固定的悬臂梁。在风力载荷 作用下，反应塔将发生弯曲变形。
Nanjing University of Technology
材料力学 课堂教学(5)
2020年8月12日
第5章 梁的弯曲问题(1)－剪力图与弯矩图
杆件承受垂直于其轴线的外力或位于其轴线所在平面内的 力偶作用时，其轴线将弯曲成曲线，这种受力与变形形式称为 弯曲（bending）。
主要承受弯曲的杆件称为梁（beam）。
得到梁的剪力方程和弯 矩方程分别为：
M(x)
FQ x＝FRA qx＝ql－qx 0 x 2l
FRA x
M x＝qlx－qx2
0 x 2l
2
这一结果表明，梁上的剪力方程是x的线性函数；弯矩方程是x的 二次函数。
载荷集度、剪力、弯矩之间的 微分关系
绘制剪力图和弯矩图有两种方法：
第一种方法是：根据剪力方程和弯矩方程，在FQx和M-x坐标系中绘制出相应的图线，便得到所需要的 剪力图与弯矩图。
剪力和弯矩图关系平衡微分方程
5．确定控制面上的 x 弯矩值，并将其标在
M－x中。
目录
§4-5
A
FAy
9qa/4
Fs （+）
载荷集度、剪力和弯矩间的关系
q
D 解法2：1．确定约束力
B
4a
a FBy
qa
FAy＝
9 4
qa
,
FBy＝
3 4
qa
（-） qa
7qa/4
2．确定控制面，即A 、B、D两侧截面。
3．从A截面左测开始画
剪力图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
A CD EF B
FAY
1.5m
1.5m
2kN
1.5m FBY
例题4-6 简支梁受力的大 小和方向如图示。
试画出其剪力图和弯矩图。
解：1．确定约束力 根据力矩平衡方程
M A＝0， MB＝0
求得A、B 二处的约束力 FAy＝0.89 kN , FBy＝1.11 kN
从左到右，顺（逆）时针集中力偶作用处，弯矩图向上 （下）突变，突变幅度为集中力偶的大小。剪力图在该点没 有变化。
5、也可通过积分方法确定剪力、 弯矩图上各点处的数值。
dFS q dx
dFS qdx
b
b
a dFS
qdx
a
dM dx
FS
dM FSdx
b
b
dM a
a FSdx
FS
b
FS
a
B点的弯矩为
-1/2×7qa/4×7a/4 +81qa2/32=qa2
目录
作业
4-4 (a). (c) .(e). (g). (i). (k)
M－x中。
目录
§4-5
A
FAy
9qa/4
Fs （+）
载荷集度、剪力和弯矩间的关系
q
D 解法2：1．确定约束力
B
4a
a FBy
qa
FAy＝
9 4
qa
,
FBy＝
3 4
qa
（-） qa
7qa/4
2．确定控制面，即A 、B、D两侧截面。
3．从A截面左测开始画
剪力图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
A CD EF B
FAY
1.5m
1.5m
2kN
1.5m FBY
例题4-6 简支梁受力的大 小和方向如图示。
试画出其剪力图和弯矩图。
解：1．确定约束力 根据力矩平衡方程
M A＝0， MB＝0
求得A、B 二处的约束力 FAy＝0.89 kN , FBy＝1.11 kN
从左到右，顺（逆）时针集中力偶作用处，弯矩图向上 （下）突变，突变幅度为集中力偶的大小。剪力图在该点没 有变化。
5、也可通过积分方法确定剪力、 弯矩图上各点处的数值。
dFS q dx
dFS qdx
b
b
a dFS
qdx
a
dM dx
FS
dM FSdx
b
b
dM a
a FSdx
FS
b
FS
a
B点的弯矩为
-1/2×7qa/4×7a/4 +81qa2/32=qa2
目录
作业
4-4 (a). (c) .(e). (g). (i). (k)
剪力和弯矩图关系_平衡微分方程
1kN.m
A
CD E F B
3．建立坐标系
0.89 kN= FAY
FS (kN)
O
0.89
M (kN.m)
1.5m
2kN
1.5m
1.5m
1.11
(+)
(-)
建立 FS－x 和 M－x
FBY
坐标系
＝1.11 kN
4．应用截面法确定控
x 制面上的剪力和弯矩
值，并将其标在
FS－ x和 M－x 坐标
系中。
O (-)
的剪力和弯矩值标在相应的坐标系中。 应用平衡微分方程确定各段控制面之间 的剪力图和弯矩图的形状，进而画出剪力图 与弯矩图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
A CD EF B
FAY
1.5m
1.5m
2kN
1.5m FBY
例题4-6 简支梁受力的大 小和方向如图示。
试画出其剪力图和弯矩图。
解：1．确定约束力 根据力矩平衡方程
M A ＝ 0， M B ＝ 0
求得A、B 二处的约束力 FAy＝0.89 kN , FBy＝1.11 kN
2．确定控制面
在集中力和集中力偶作用处的两侧截面以及支座反力
内侧截面均为控制面。即A、C、D、E、F、B截面。
目录
§4-5 载荷集度、剪力和弯矩间的关系
0.89
3．从A截面左测开始画
剪力图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
4．从A截面左测开始画
A
C D B 弯矩图。
FAY
1.5m
1.5m
2kN
1.5m
材料力学课件4.(剪力弯矩图,微分关系)
§2.8 利用微分关系作剪力、弯矩图
例1
q
A
l
RA
ql
RA = RB = ql / 2
2
Fs
l/2
作图要点：
(1)计算支反力，标出其实际方向
B
(2)利用微分关系，确定形状
RB (3)考虑集中力、集中力偶的突变
自左向右剪力突变方向与集中 力方向相同
ql 顺时针转向的弯矩使弯矩图向下 2 突变
(4)计算控制截面值
RB
ql
2
Fs
l/2
ql
2
M
ql 2 8
§2.7 弯矩、剪力与载荷集度之间的 微分关系
例2
l / 3 F 2l / 3
A C
例3
C BA
a
m
b
B
RA
RB
l
2F
3
RA
RB
m
Fs
1 F Fs
am
l
3
l
M
2 Fl 9
M
bm l
哈尔滨工业大学本科生课
§2.8 利用M、Fs与q的微分关系作 剪力图和弯矩图
分布载荷、剪力图和弯矩图之间的规律
2.梁段上的分布载荷为不等于零的常数
M ( x ) 极值的位置在 Fs ( x ) 0 的截面
q( x )
0 M ( x ) 应有极小值
弯矩图为上凸曲线
0 M ( x ) 应有极大值
弯矩图为下凸曲线
§2.7 弯矩、剪力与载荷集度之间的 微分关系
例1
q
A
B
l
RA
d x2
集度 q 的正负
§2.7 弯矩、剪力与载荷集度之间的 微分关系
第3节 剪力图和弯矩图
第七章 直梁弯曲时的内力和应力
第三节 剪力图和弯矩图
一、剪力图和弯矩图 剪力方程和弯矩方程：为了描述剪力与弯矩沿梁 轴线变化的情况，沿梁轴线选取坐标 x 表示梁截 面位置，则剪力和弯矩是 x 的函数，函数的解析 表达式分别称为剪力方程和弯矩方程。
FQ FQ (x) M M (x)
剪力图和弯矩图：以梁轴线为横坐标，分别以剪 力值和弯矩值为纵坐标，按适当比例作出剪力和 弯矩沿轴线的变化曲线，称作剪力图和弯矩图。
第七章 直梁弯曲时的内力和应力
二、利用剪力、弯矩与载荷集度的微分关系作剪力图
和弯矩图
dFQ (x) dx
q(x)
剪力、弯矩与载荷 集度的微分关系
dM (x) dx
FQ
(x)
剪力图和弯矩图 的特点和规律
d2M (x) d2x
q(x)
1. q = 0的梁段：∵ dFQ / dx 0 ，∴ FQ为常数，剪力 图为水平直线；而 dM (x) / dx FQ 为常数，则 M (x) 是
n
FA
b l
F
MA (Fi ) 0 FB l F a 0
i1
2）求剪力方程和弯矩方程
FB
a l
F
C截面作用有集中力，AC 梁段和BC梁段的剪 力方程表达式不一样，需分段建立方程。
第七章 直梁弯曲时的内力和应力
分段建立方程：
AC段
FQ
(x)
b l
F
(0 x a)
x
M
(
x)
FA
x
b l
Fx
第七章 直梁弯曲时的内力和应力
2）作剪力图和弯矩图
剪力图中AC段的为一 水平线，CB段是斜直线，
x
如图b)所示；弯矩图中AC
第三节 剪力图和弯矩图
一、剪力图和弯矩图 剪力方程和弯矩方程：为了描述剪力与弯矩沿梁 轴线变化的情况，沿梁轴线选取坐标 x 表示梁截 面位置，则剪力和弯矩是 x 的函数，函数的解析 表达式分别称为剪力方程和弯矩方程。
FQ FQ (x) M M (x)
剪力图和弯矩图：以梁轴线为横坐标，分别以剪 力值和弯矩值为纵坐标，按适当比例作出剪力和 弯矩沿轴线的变化曲线，称作剪力图和弯矩图。
第七章 直梁弯曲时的内力和应力
二、利用剪力、弯矩与载荷集度的微分关系作剪力图
和弯矩图
dFQ (x) dx
q(x)
剪力、弯矩与载荷 集度的微分关系
dM (x) dx
FQ
(x)
剪力图和弯矩图 的特点和规律
d2M (x) d2x
q(x)
1. q = 0的梁段：∵ dFQ / dx 0 ，∴ FQ为常数，剪力 图为水平直线；而 dM (x) / dx FQ 为常数，则 M (x) 是
n
FA
b l
F
MA (Fi ) 0 FB l F a 0
i1
2）求剪力方程和弯矩方程
FB
a l
F
C截面作用有集中力，AC 梁段和BC梁段的剪 力方程表达式不一样，需分段建立方程。
第七章 直梁弯曲时的内力和应力
分段建立方程：
AC段
FQ
(x)
b l
F
(0 x a)
x
M
(
x)
FA
x
b l
Fx
第七章 直梁弯曲时的内力和应力
2）作剪力图和弯矩图
剪力图中AC段的为一 水平线，CB段是斜直线，
x
如图b)所示；弯矩图中AC
剪力图和弯矩图
剪力符号：当截面上的剪力使考虑的脱离体有顺时针转动 趋势时的剪力为正；反之为负。
◆ 横截面上的 弯矩 在数值上等于此横截面的 左侧 或 右侧 梁段上 的 外力（包括外力偶）对该截面形心的力矩之代数和 。外力矩的 正负号规定与弯矩的正负号规定相同。
弯矩符号：当横截面上的弯矩使考虑的脱离体凹向上弯曲（下 半部受拉，上半部受压）时，横截面上的弯矩为正；反之凹向 下弯曲（上半部受拉，下半部受压）为负。
x1 x2
l
该处弯矩值最大 。
Pb/l
+
-
Pa/l
+
Pab/l
例题：图示为一受均布荷载作用的悬臂梁。试作此梁的剪力图 和弯矩图。
q
x l
q
FS
M x
解: 将梁在任意 x 处用横截面截开, 取左段为研究对象 横截面上有剪力和弯矩 , 假设均为正值
q
x l
q
FS
M x
根据研究对象的平衡条件列剪力方程和弯矩方程
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS (0) 0 FS (l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
2
q
x l
FS
-
ql2/8
-
l/2
M
x ql
ql2/2
x
F S ,max ql
M max
1 ql 2 2
q
x l
FS
-
◆ 横截面上的 弯矩 在数值上等于此横截面的 左侧 或 右侧 梁段上 的 外力（包括外力偶）对该截面形心的力矩之代数和 。外力矩的 正负号规定与弯矩的正负号规定相同。
弯矩符号：当横截面上的弯矩使考虑的脱离体凹向上弯曲（下 半部受拉，上半部受压）时，横截面上的弯矩为正；反之凹向 下弯曲（上半部受拉，下半部受压）为负。
x1 x2
l
该处弯矩值最大 。
Pb/l
+
-
Pa/l
+
Pab/l
例题：图示为一受均布荷载作用的悬臂梁。试作此梁的剪力图 和弯矩图。
q
x l
q
FS
M x
解: 将梁在任意 x 处用横截面截开, 取左段为研究对象 横截面上有剪力和弯矩 , 假设均为正值
q
x l
q
FS
M x
根据研究对象的平衡条件列剪力方程和弯矩方程
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 括号里的不等式说明对应的内力方程所使用的区段。
FS(x)qx (0xl) M(x)1qx2 (0xl)
2 剪力图为一斜直线
FS (0) 0 FS (l) ql
弯矩图为二次抛物线
M (0) 0 M ( l 2 ) 1 ql 2
8 M ( l ) 1 ql 2
2
q
x l
FS
-
ql2/8
-
l/2
M
x ql
ql2/2
x
F S ,max ql
M max
1 ql 2 2
q
x l
FS
-
剪力图和弯矩图(史上最全面)
2 Q 0; M 3 qa2
2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q
A
B
RA qa
Q
qa/2
+
– qa/2
qa2 CD
RD
– qa/2
M qa2/2 +
–
3qa2/8 qa2/2
qa2/2
解：求支反力 左端点A：
RA
qa 2
;
RD
qa 2
Q qa ; M 0 2
解：
q — 均布力
10
一、弯曲内力：
§4–2
[举例]已知：如图，P，a，l。 求：距A端x处截面上内力。
解：①求外力
梁的剪力和弯矩
a A
l
X 0, XA 0
mA 0 ,
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
M
qa2/4
+
q
B
RA
qa 4
; RB
7qa 4
x
7qa/4
x
25
[例9] 已知Q图，求外载及M图（梁上无集中力偶）。
Q(kN)
2 +
–
3
1m
2m
5kN
1
+
x
1m 1kN
M(kN·m)
1.25 1
q=2kN/m
+
x
_
1
26
§4–5 按叠加原理作弯矩图
2
22
[例5] 用简易作图法画下列各图示梁的内力图。AB=BC=CD=a
q
A
B
RA qa
Q
qa/2
+
– qa/2
qa2 CD
RD
– qa/2
M qa2/2 +
–
3qa2/8 qa2/2
qa2/2
解：求支反力 左端点A：
RA
qa 2
;
RD
qa 2
Q qa ; M 0 2
解：
q — 均布力
10
一、弯曲内力：
§4–2
[举例]已知：如图，P，a，l。 求：距A端x处截面上内力。
解：①求外力
梁的剪力和弯矩
a A
l
X 0, XA 0
mA 0 ,
RB
Pa l
Y
0,
YA
P(l a) l
XA A YA
P B
P B
RB
11
②求内力——截面法
Y
0,
Q YA
P(l a) l
M
qa2/4
+
q
B
RA
qa 4
; RB
7qa 4
x
7qa/4
x
25
[例9] 已知Q图，求外载及M图（梁上无集中力偶）。
Q(kN)
2 +
–
3
1m
2m
5kN
1
+
x
1m 1kN
M(kN·m)
1.25 1
q=2kN/m
+
x
_
1
26
§4–5 按叠加原理作弯矩图
剪力弯矩微分关系
1 / 6
一、剪力、弯矩和载荷集度之间的关系
1.微分关系：)
()
(x q dx x dF Q =；)()(x F dx
x dM Q =。
2.积分关系：dx x q x F x F x x Q Q ⎰=-2
1)()()(12；dx x F x M x M x x Q ⎰=-2
1)()()(12。
（积分关系可以确定控制面的内力值） 二、梁内力（剪力、弯矩）分布规律的一些有用结论
三、应用
充分理解以上关系和结论，对常见静定梁熟练、准确作出其剪力和弯矩图。
一般的，可以按以下步骤进行：
1.外力分析：依据静力平衡关系求出约束反力。
2.确定控制面：即对梁进行分段的截面，一般有以下几种形式：①集中力作用截面；②集中力偶作用截面；③分布载荷作用的起始、终止截面；④中间铰处。
3.画剪力图：左→右，分段进行，确定控制面的剪力值（应用积分关系），绘出剪力图。
4.画弯矩图：左→右，分段进行，确定控制面的弯矩值（应用积分关系），绘出弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
FBY
坐标系
＝1.11 kN
4．应用截面法确定控
x 制面上的剪力和弯矩
值，并将其标在
FS－ x和 M－x 坐标
系中。
O (-)
(-)
0.335
1.335
1.67
x 5．根据微分关系连图 线
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
解法2：1．确定约束力
A
CD B
FAY
1.5m
1.5m
2kN
B点的弯矩为
-1/2×7qa/4×7a/4 +81qa2/32=qa2
目录
作业
4-4 (a). (c) .(e). (g). (i). (k)
4-16 (a). (c) .(d)
4-17 (a). (c) .(d)
在集中力和集中力偶作用处的两侧截面以及支座反力
内侧截面均为控制面。即A、C、D、E、F、B截面。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
A
CD E F B
3．建立坐标系
0.89 kN= FAY
FS (kN)
O
0.89
M (kN.m)
1.5m
2kN
1.5m
1.5m
1.11
(+)
(-)
建立 FS－x 和 M－x
1.5m
FBY
FAy＝0.89 kN FFy＝1.11 kN
Fs（ kN）
1.11
（+）
（-）
2．确定控制面为A、C 、D、B两侧截面。
0.89
3．从A截面左测开始画
剪力图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
1kN.m
4．从A截面左测开始画
A
C D B 弯矩图。
FAY
1.5m
1.5m
2kN
根据载荷及约束力的作用位置，确定控 制面。 应用截面法确定控制面上的剪力和弯 矩数值。
建立FS一x和M一x坐标系，并将控制面上
的剪力和弯矩值标在相应的坐标系中。 应用平衡微分方程确定各段控制面之间 的剪力图和弯矩图的形状，进的关系
1.5m
FBY
Fs（ kN）
0.89 M（ kN.m）
1.11
（+）
（-）
0.330
（-） （-）
1.330
1.665
从A左到A右 从A右到C左 从C左到C右 从C右到D左 从D左到D右 从D右到B左 从B左到B右
目录
§4-5 载荷集度、剪力和弯矩间的关系
A
FAy
q
例题4-7 试画出梁
C B
D 的剪力图和弯矩图。
剪力图。
目录
§4-5 载荷集度、剪力和弯矩间的关系
q
A
FAy
9qa/4
B
4a
a
FBy
Fs （+）
9a/ 4
（-） qa
7qa/4
81qa2/32 qa2
（+） M
4．求出剪力为零的点 D 到A的距离。
5．从A截面左测开始画弯
qa
矩图
AB段为上凸抛物线。且有 极大值。该点的弯矩为
1/2×9qa/4×9a/4 =81qa2/32
3. 剪力Fs=0处，弯矩取极值。
4. 集中力作用处，剪力图突变；
集中力偶作用处，弯矩图突变
目录
§4-5 载荷集度、剪力和弯矩间的关系
从左到右，向上（下）集中力作用处，剪力图向上（下） 突变，突变幅度为集中力的大小。弯矩图在该处为尖点。
从左到右，顺（逆）时针集中力偶作用处，弯矩图向上 （下）突变，突变幅度为集中力偶的大小。剪力图在该点没 有变化。
目录
§4-5 载荷集度、剪力和弯矩间的关系
q
C D 3．建立坐标系
A
9 qa 4
FAy
FS
9qa / 4
4a
（+）
O 9a/ 4
M
81qa2 /32
B
a qa
FBy＝ 3 qa 4
建立FS－x和M－x
坐标系 4．确定控制面上的
（-）
qa
7qa/ 4
x 剪力值，并将其标
在FS－x中。
O
（+）
qa 2
4a
a FBy
qa 解：1．确定约束力
根据梁的整体平衡，由 求得A、B 二处的约束力 2．确定控制面
M A ＝ 0， M B ＝ 0
FA＝ y 9 4q,aFB＝ y 4 3qa
由于AB段上作用有连续分布载荷，故A、B两个截
面为控制面，约束力FBy右侧的截面，以及集中力qa
左侧的截面，也都是控制面。
剪力和弯矩图关系_平衡微分方程
§4-5 载荷集度、剪力和弯矩间的关系
载荷集度、剪力和弯矩关系： d2dMx2(x)ddF s(xx)q(x)
1. q＝0，Fs=常数， 剪力图为水平直线； 2. M(x) 为 x 的一次函数，弯矩图为斜直线。
2.q＝常数，Fs(x) 为 x 的一次函数，剪力图为斜直线； M(x) 为 x 的二次函数，弯矩图为抛物线。 分布载荷向上（q > 0），抛物线呈凹形； 分布载荷向上（q < 0），抛物线呈凸形。
5、也可通过积分方法确定剪力、 弯矩图上各点处的数值。
dFS q dx
dFS qdx
b
b
a dFS a qdx
dM dx
FS
dMFSdx
b
b
a dM a FSdx
F SbF SaA qb a
M bM aA F Sb a
目录
§4-5 载荷集度、剪力和弯矩间的关系
微分关系绘制剪力图与弯矩图的方法：
5．确定控制面上的 x 弯矩值，并将其标在
M－x中。
目录
§4-5
A
FAy
9qa/4
Fs （+）
载荷集度、剪力和弯矩间的关系
q
D 解法2：1．确定约束力
B
4a
a FBy
qa
FA＝ y 9 4q,aFB＝ y 4 3qa
（-） qa
7qa/4
2．确定控制面，即A 、B、D两侧截面。
3．从A截面左测开始画
1kN.m
A CD EF B
FAY
1.5m
1.5m
2kN
1.5m FBY
例题4-6 简支梁受力的大 小和方向如图示。
试画出其剪力图和弯矩图。
解：1．确定约束力 根据力矩平衡方程
M A ＝ 0， M B ＝ 0
求得A、B 二处的约束力 FAy＝0.89 kN , FBy＝1.11 kN
2．确定控制面