截面法绘制梁结构的内力图
合集下载
梁的内力图—剪力图和弯矩图(23)
6kN
1
1
A 2mΒιβλιοθήκη 6kN m2 q 2kN m 3 4
5
B
2
34
5
C
3m
3m
FQ1 6kN M1 6 2 12kNm FQ2 6 13 7kN M 2 6 2 12kNm
FA 13kN
问题：最大内力的数
FB 5kN
FQ3 6 13 23 1kN
变化的（有的大、有的小）。
一、 梁的内力图—剪力图和弯矩图
1 、剪力方程和弯矩方程
由前面的知识可知：梁的剪力和弯矩是随截面位置
变化而变化的，如果将x轴建立在梁的轴线上，原点取 在梁左端，向右为正向, 坐标x表示截面位置，则FQ和M
就随x的变化而变化，V和M就是x的函数，这个函数式就 叫剪力方程和弯矩方程。
南充职业技术学院土木工程系建筑力学多媒体课件
任课 陈德先 教师
授课 12造价与建 班级 筑
授课 时间
2013/
学 时
4
课 剪力图和弯矩图 题
课型 新授课
教学 方法
讲练结合法
教学 熟练列出剪力方程和弯矩方程、并绘制剪力图和弯矩图； 目的 利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯
矩图.
教学 剪力图和弯矩图；剪力、弯矩和荷载集度的微分关系及其 重点 应用.
l，求梁剪力、弯矩方程的微分，并画剪力、弯矩图。
q
解 :1.建立剪力、弯矩方程
A x
B
l
FQ x
ql ql 2/2
FQ (x) qx M (x) qx x qx2
22
2.对剪力、弯矩方程取微分
dM (x) dx
02截面法求内力基本方法
例1. 求以下桁架各杆的内力
0 -33 34.8
19
19
Y 0 YNAD 11 kN YNAD CD 0.5 X NAD AC 1.5 X NAD 3YNAD 33 kN
X 0 FNAC 33 kN
0 -33
-33
34.8 -8
19
19
0 -33
-33
34.8
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
Mq
M+dM
dx
FN
dx
FN+d FN
FQ
FQ+dFQ
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
集中力
梁上 无外力 均布力作用 集中力作用 偶M作 铰处
情况
(q向下)
处(FP向下) 用处
斜直 剪力图 水平线 线(
)
为 零 处
有突 变(突 变值=
FP)
如 变 号
无 无变化 影
响
一般 抛物 有 有尖 有 有突变
弯矩图 为斜 线(
极 角(向 极 （突变 为零
直线 下凸) 值 下） 值 值=M）
曲杆微分关系
曲杆微段
dFN ds
=-qt+
FQ R
dFQ ds
=qn-
FN R
dM ds
=FQ-m
求内力基本方法：截面法
材料力学规定： 轴力FN --拉力为正 剪力FQ--绕隔离体顺时针方向转动者为正
弯矩M--使梁的下侧纤维受拉者为正
M
M+dM
0 -33 34.8
19
19
Y 0 YNAD 11 kN YNAD CD 0.5 X NAD AC 1.5 X NAD 3YNAD 33 kN
X 0 FNAC 33 kN
0 -33
-33
34.8 -8
19
19
0 -33
-33
34.8
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
Mq
M+dM
dx
FN
dx
FN+d FN
FQ
FQ+dFQ
dM dx
FQ ,
dFQ q( x), dx
dFN p( x) dx
集中力
梁上 无外力 均布力作用 集中力作用 偶M作 铰处
情况
(q向下)
处(FP向下) 用处
斜直 剪力图 水平线 线(
)
为 零 处
有突 变(突 变值=
FP)
如 变 号
无 无变化 影
响
一般 抛物 有 有尖 有 有突变
弯矩图 为斜 线(
极 角(向 极 （突变 为零
直线 下凸) 值 下） 值 值=M）
曲杆微分关系
曲杆微段
dFN ds
=-qt+
FQ R
dFQ ds
=qn-
FN R
dM ds
=FQ-m
求内力基本方法：截面法
材料力学规定： 轴力FN --拉力为正 剪力FQ--绕隔离体顺时针方向转动者为正
弯矩M--使梁的下侧纤维受拉者为正
M
M+dM
第十一讲 利用剪力方程、弯矩方程绘梁的内力图(之二)
ql FS ( x ) = FA − qx = − qx x ∈ (0, l ) 2
x ql q 2 q l ql 2 2 M ( x ) = FA ⋅ x − qx ⋅ = x − x = − ( − x ) + 2 2 2 2 2 8
x ∈ [0, l ]
3根据剪力方程作剪力图
§ 4.4 剪力方程和弯矩方程
§ 4.4 剪力方程和弯矩方程
例4—3
q
剪力图和弯矩图
x
FA qL/2 L FB (+) qL2 /8 M图 (+)
解：1求支反力 由对称性可知: 由对称性可知
FA = FB = ql 2
Mechanic of Materials of
Fs图
(-) qL/2 2建立坐标系如图所
示，求剪力、弯矩方 程（用截面法）
集中力处分荷的始末端杆端部集中力偶处1确定约束力4确定剪力和弯矩方程2确定控制截面和分段3建立坐标系44剪力方程和弯矩方程剪力图和弯矩图3步骤
第十一讲的内容、要求、 第十一讲的内容、要求、重难点 内容
Mechanic of Materials of 教学内容： 教学内容：
利用剪力方程、弯矩方程绘梁的内力图（ 利用剪力方程、弯矩方程绘梁的内力图（M，Fs图）。 图
在集中力偶处剪力图不突变、弯矩图要突变， 在集中力偶处剪力图不突变、弯矩图要突变，左到 顺势而上， 突变的大小为力偶矩的绝对值。 右：顺势而上， 突变的大小为力偶矩的绝对值。
§ 4.4 剪力方程和弯矩方程
练习1： 练习 ：
剪力图和弯矩图
x
P
D
m = Pa B E
Mechanic of Materials of
解：①求支反力 q0 x
x ql q 2 q l ql 2 2 M ( x ) = FA ⋅ x − qx ⋅ = x − x = − ( − x ) + 2 2 2 2 2 8
x ∈ [0, l ]
3根据剪力方程作剪力图
§ 4.4 剪力方程和弯矩方程
§ 4.4 剪力方程和弯矩方程
例4—3
q
剪力图和弯矩图
x
FA qL/2 L FB (+) qL2 /8 M图 (+)
解：1求支反力 由对称性可知: 由对称性可知
FA = FB = ql 2
Mechanic of Materials of
Fs图
(-) qL/2 2建立坐标系如图所
示，求剪力、弯矩方 程（用截面法）
集中力处分荷的始末端杆端部集中力偶处1确定约束力4确定剪力和弯矩方程2确定控制截面和分段3建立坐标系44剪力方程和弯矩方程剪力图和弯矩图3步骤
第十一讲的内容、要求、 第十一讲的内容、要求、重难点 内容
Mechanic of Materials of 教学内容： 教学内容：
利用剪力方程、弯矩方程绘梁的内力图（ 利用剪力方程、弯矩方程绘梁的内力图（M，Fs图）。 图
在集中力偶处剪力图不突变、弯矩图要突变， 在集中力偶处剪力图不突变、弯矩图要突变，左到 顺势而上， 突变的大小为力偶矩的绝对值。 右：顺势而上， 突变的大小为力偶矩的绝对值。
§ 4.4 剪力方程和弯矩方程
练习1： 练习 ：
剪力图和弯矩图
x
P
D
m = Pa B E
Mechanic of Materials of
解：①求支反力 q0 x
内力分析的基本方法-截面法
8kN 4kN E
4kN D C 4kN
C 4m n 1
A
D 4kN
N4
N1 N2 N3 N4
由结点E可知： N2 = -N3
取m-m截面以上为对象 由∑x= 0 得
解：取n-n截面以上为对象 ∑MD= 0 N1 ×6＋8×3＋4×4 = 0 得： N1 = －6.67 kN
N2=－6.67 kN
所以：
2、突变：在集中力作用处，剪力图有突变，弯矩图 有一尖角；在集中力偶作用处，弯矩图有突变，剪力 图无变化。 3、端值情况
详见教材p98表3-1
18
规律作图方法：
1、水平线图：段内任取截面求内力（一般取段端截面） 2、斜直线图：段内任取两截面求内力（一般取段两端 截面）
3、抛物线图：段内取两端截面及中间截面求弯矩
RA
RB 1、计算支座反力
得: QD= qL/2 Σmc= 0 MD–RA×L+qL×L/2 = 0 得: MD= qL2 取E--E截面右段为对象
ME
E
解得：RA=3qL/2 （竖直向上） RB=qL/2 （竖直向上）
2、取D--D截面左段为对象， 画出受力图 q D
MD
qL2
QE E
RA
D
ΣΎ= 0 Σmc= 0
2.5
=－2kNm（上拉） 静定平面刚架内力计算
一、刚架定义 刚架是由梁、柱等直杆组成的具有刚结点的结构， 其中全部或部分结点为刚结点。如图所示 D P C PC D
A
二、刚架的特点
B
A
B
1、结构内部空间较大，便于利用。 2、刚架的内力、变形峰值比用铰结点连接时小。
3、刚结点能传递力和力矩；而铰结点则只能传递力。
截面法计算内力的步骤
截面法计算内力的步骤截面法计算内力的步骤如下：1.确定截面：根据结构的几何形状和所需计算的截面位置，确定需要计算的截面。
2.建立截面坐标系：在确定的截面处，建立适当的坐标系，通常使用弯矩轴线和剪力轴线作为坐标轴。
3.计算剪力：在截面上计算受力情况，包括剪力和轴向力。
剪力可以通过受力平衡或应力分布方法进行计算。
4.计算弯矩：在截面上计算受力情况，包括弯矩和轴向力。
弯矩可以通过剪力和轴向力的计算结果进行进一步计算。
5.建立平衡方程：根据截面上的剪力和弯矩的计算结果，建立平衡方程。
平衡方程可以根据结构的具体情况建立，通常需要考虑截面上的所有力和力矩的平衡条件。
6.解平衡方程：解平衡方程以确定未知内力。
解方程时可能需要考虑结构的刚度和惯性等物理特性。
7.确定内力值：根据解出的未知内力和已知的剪力和弯矩的计算结果，确定内力值。
内力可以是拉力或压力，也可以是弯矩。
以上步骤可以帮助您使用截面法计算内力。
需要注意的是，具体的计算步骤可能会因结构的不同而有所差异，因此在进行内力分析时需要结合具体情况灵活运用各种方法。
截面法计算内力的优点和缺点如下：优点：1.简单易行：截面法是一种简单直观的方法，易于理解和计算。
2.可适用于多种结构形式：截面法可以适用于多种结构形式，如梁、板、柱等，因此在工程实践中得到广泛应用。
3.可以考虑多种内力：截面法不仅可以计算剪力和弯矩，还可以考虑拉力、压力等其他内力。
4.可用于静力分析和动力分析：截面法不仅可用于静力分析，即求结构在恒定载荷下的内力，还可用于动力分析，即求结构在动载荷下的内力。
缺点：1.精度有限：截面法是一种近似方法，其精度取决于所取的截面和所用的简化假定。
对于复杂结构，可能需要采用更精确的方法进行内力分析。
2.对经验要求高：使用截面法进行内力分析需要具备一定的工程经验和对结构的理解，否则可能会出现误差或遗漏。
3.对初始条件敏感：截面法的计算结果对初始条件（如初始剪力和弯矩）较为敏感，因此在进行内力分析时需要注意初始条件的设定。
截面法求内力讲解
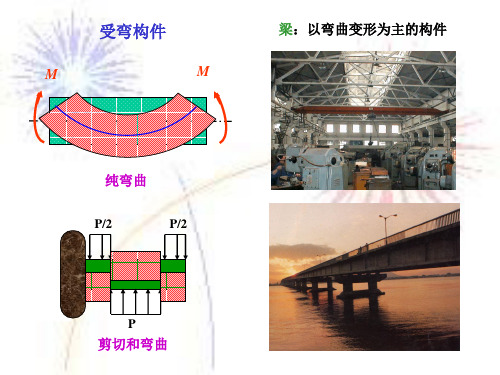
解： 1. 确定支座反力
B Fx 0 MA 0
FBy
Fy 0
FAx 0 2FPa FPa FBy 3a 0 FAy FBy 2FP 0
FBy
FP 3
FAy
5FP 3
2FP FQE
A 5FP
C E ME
3
Fy 0
2FP
FQE
5FP 3
0
C
a
FAy
b l
FPb l
+
FP a
-
l FQ图
FPab M图
l
B FBy
A FPb
l
FQ
M
MA 0
Fy 0
FBy
FP a l
FAy
FPb l
FQ
FQ
FPb l
(0 x a)
M
M FPb x (0 x a)
l
B
FQ
FP a l
(a x l)
FPa M FPa (l x)
平: 对留下部分写平衡方程求出内力的值
FQ(+)
FQ(+)
M(+)
M(+)
（1）平衡方程的正负和内力的正负是完全不同性质的两套符号系统。 （2）取简单部分作为隔离体，列平衡方程时，尽量使一个方程含有一个未知量
例1 求E截面内力
A FAx
FAy
2FP FPa
C
D
1.5a E
a
a
a
2. 用截面法研究内力
M JK J
F QJK
M JK J
梁的内力
MA=0
MC=FA×2=30×2kN·m=60kN·m
CD段：没有均布荷载作用，弯矩图是一条斜直线，需确定MC和MD左 MD左=FA×4-F×2=(30×4-20×2)kN·m=80kN·m
D截面：有逆时针方向的集中力偶M作用，弯矩图向上突变M=40kN·m
MD右=MD左-M=(80-40)kN·m=40kN·m
截面上必有弯矩M，且M=FAC。当左段梁若平衡，横截面 上必有两个内力分量：平行于横截面的竖向内力Fs以及位 于荷载作用面的内力偶M。内力Fs称梁横截面内的剪力， 而内力偶M称为梁横截面内的弯矩。
Fs
C
A
M
FA
x
若以右段梁为研究对象，由作用力与反作用力定律可知，
右段梁横截面上的内力值仍为Fs和M，指向与左段梁横截面
MBF0
F 6 M q 4 2 F A 8 0
解之得：
FA 30kN FB 30kN
（2）画剪力图
从左向右作图，全梁分为A端、AC段、C端、CD段、DB段和B端。
31
FA=30kN AC段：没有均布荷载作用，剪力图为一条水平线：FC左=FA右=30kN C端：有向下的集中力F作用，剪力图向下突变F=20kN
Mx=FA x-qx2/2= 81/32qa2
BC段：没有均布荷载作用，弯矩图是一条斜直线，需确定MB和MC。
MC 0
29
剪力图与弯矩图
30
[例] 如图所示，试画出该梁的剪力图和弯矩图。
F=20kN M=40kN
FA
FB
解：（1）计算支座反力 以整梁为研究对象，由平衡方程得：
MAF0
F B 8 M F 2 q 4 6 0
M144 kNm
材料力学第4讲-利用微分关系绘制梁内力图
（3）利用微分关系绘制多跨静定的内力图
求支座反力的顺序；中间铰接处和刚接处剪力图和弯矩图的特点。
（4）根据梁的内力图反推梁的荷载图
内力图与荷载图的对应关系；微分关系的应用。
2.4（1）梁的荷载集度函数、剪力 函数和弯矩函数之间的微分关系
设梁上作用有任意分布荷载，
其集度 q = q (x) 规定 q (x)向上为正. 将 x 轴的坐标原点取在梁的左端. 假想地用坐标为 x 和 x+dx的两
算出截面C上的剪力为 (3-
24)kN=-5kN,即可确定这条
4m
斜直线（如图所示）. FS/kN 3
M=10kN·m C 2m
F=2kN FRB
B
D
2m
2
x
截面C和B之间梁上无分布载荷,
剪力图为水平线.
5
截面B上有一集中力FRB,从B的左侧到B得右侧,建立了图发生突然变化, 变化的数值即等于FRB.故FRB右侧截面上的剪力为(-5+7)kN=2kN.
x1
等号右边积分的几何意义是x1 , x2两横截面间分布荷载图的面积.
dM ( x) dx
FS
(
x)
若横截面x= x1，x=x2 间无集中力偶作用则得
M ( x2 ) M ( x1 )
x2 x1
FS
(
x
)dx
等号右边积分的几何意义是 x1 , x2两个横截面间剪力图的面积.
例题3-4-1 一简支梁受两个力F作用,如图所示.已知 F= 25.3kN,
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
（3）内力的极值点位置的判断 1）最大剪力可能发生在集中力所在截面的一侧;或
求支座反力的顺序；中间铰接处和刚接处剪力图和弯矩图的特点。
（4）根据梁的内力图反推梁的荷载图
内力图与荷载图的对应关系；微分关系的应用。
2.4（1）梁的荷载集度函数、剪力 函数和弯矩函数之间的微分关系
设梁上作用有任意分布荷载，
其集度 q = q (x) 规定 q (x)向上为正. 将 x 轴的坐标原点取在梁的左端. 假想地用坐标为 x 和 x+dx的两
算出截面C上的剪力为 (3-
24)kN=-5kN,即可确定这条
4m
斜直线（如图所示）. FS/kN 3
M=10kN·m C 2m
F=2kN FRB
B
D
2m
2
x
截面C和B之间梁上无分布载荷,
剪力图为水平线.
5
截面B上有一集中力FRB,从B的左侧到B得右侧,建立了图发生突然变化, 变化的数值即等于FRB.故FRB右侧截面上的剪力为(-5+7)kN=2kN.
x1
等号右边积分的几何意义是x1 , x2两横截面间分布荷载图的面积.
dM ( x) dx
FS
(
x)
若横截面x= x1，x=x2 间无集中力偶作用则得
M ( x2 ) M ( x1 )
x2 x1
FS
(
x
)dx
等号右边积分的几何意义是 x1 , x2两个横截面间剪力图的面积.
例题3-4-1 一简支梁受两个力F作用,如图所示.已知 F= 25.3kN,
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
（3）内力的极值点位置的判断 1）最大剪力可能发生在集中力所在截面的一侧;或
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
用截面法计算任一截面上的弯矩和剪力。
计算步骤： 1. 截取：用假想平面沿垂直于轴线方向将杆件截成两部分， 保留一部分，去掉一部分（一般选择荷载较少的部分为研究 对象，以便于计算）；
2.代替：对保留的梁段进行受力分析，在其上画出已知外力， 在保留部分的截面上按正符号规定画出剪力和弯矩（设正 法）；
x 1 l, M 1 ql 2
2
8
工程力学
ql Qmax 2 M max pl
三.内力图的一般规律
1. M、Q图规律：
外力情况
有荷载段
q<0 (向下)
剪力图 ↘(向下斜直线) 上的特征
弯矩图 上的特征
(下凸抛物线)
最大弯矩 可 能的 截面位置
剪力为零的截面
无荷载段 水平线 斜直线
集中力F 作用处
有突变， 突变值为F
有尖点
剪力突变的 截面
集中力偶M 作用处 不变
有突变， 突变值为M 弯矩突变的
某一侧
2.其它规律：
①|M|max可能发生在剪力为零处、集中力作用处、集中力偶作用处； ②荷载图关于梁左右对称，则剪力图关于梁中点反对称，弯矩图左右对称； 荷载图关于梁中点反对称，则剪力图左右对称，弯矩图关于梁中点反对称。
3.平衡：列力的平衡方程求剪力；以截面形心为矩心列力矩 平衡方程求弯矩。
工程力学
一、学习任务
工程力学
Q(x) P ——剪力方程
M (x) Px 0 x l
——弯矩方程
剪力图 弯矩图
x 0, M 0 x l, M Pl
二．梁的内力图
1.剪力方程和弯矩方程 一般情况下，剪力和弯矩是随着截面的位
解：（1）计算支座反力
RA
RB
1 ql 2
（2）列剪力方程和弯矩方程
1 Q(x) RA qx 2 ql qx (0<x<l )
M (x)
RAx
1 qx2 2
1 qlx 2
1 qx2 2
(0≤x ≤l )
（3）绘剪力图和弯矩图
x 0, Q 1 ql 2
x l,Q 1 ql 2
x 0, M 0 x l, M 0
置不同而改变。如取梁的轴线为轴，以坐 标表示梁的横截面位置，则剪力和弯矩可 表示为的函数，即：
Q Q(x) ——剪力方程
M M (x) ——弯矩方程
工程力学
二．梁的内力图
2.剪力图和弯矩图 取横坐标代表截面的位置，纵坐标表示各
个横截面的剪力和弯矩的数值，表示剪力和 弯矩随截面位置变化而改变的图形称为剪力 图和弯矩图。
工程力学
四.利用规律作单跨梁的M图、Q图
M
M
l
l
bM l
aM
工程力学
l
Qmax
M l
M
max
aM l
四.利用规律作单跨梁的M图、Q图
工程力学
Qmax 12kNm M max 16kNm
• 阅读：P.111-P.114 • 习题：7-26.27.28.7-37(a)(b) • 预习：M(x)、Q(x)、q(x)间的微分关系
4.作图：根据剪力方程和弯矩方程分段画 出Q图和M图。
工程力学
三．用方程法绘制梁的内力图
• 例题分析1. 简支梁受集 中力作用如 图所示，求 梁的剪力方 程和弯矩方
程，画出Q、
M图并确定 最大剪力和 最大弯矩。
工程力学
例题分析2.简支梁受均布荷载作用如图所示，求梁的剪力方程和弯矩方程，
画Q、M图，确定最大剪力和最大弯矩。
规定：土建工程中习惯上把正的剪力画在轴的 上方，负的剪力画在轴的下方； 弯矩图规定把正的弯矩画在轴的下方。
工程力学
三．用方程法绘制梁的内力图
计算和作图步骤： 1.计算支座反力 2.分段：按集中力或集中力偶的作用点。 线分布荷载分布长度的端点来分；
3.列方程：在各段任取一截面按截面法求 Q(x)和M(x)得到剪力方程、弯矩方程；