梁的内力
合集下载
梁的内力分析
FQ 3 为负剪力， M 3 为正弯矩。
在计算梁的剪力和弯矩时，可以通过下面的结论直接计算： （1）某截面上的剪力等于该截面左侧（或右侧）梁段上所 有横向外力的代数和。（左上右下剪力为正；反之则为负） 以该截面左侧杆段上的外力进行计算时，则向上的外力产生 正剪力，反之为负。以该截面右侧杆段的外力计算时，则 向下的外力产生正剪力，反之为负。 (2)某截面上的弯矩等于该截面左侧（或右侧）所有外力对该 截面之矩的代数和。（左顺右逆弯矩为正；反之则为负） 以左侧的外力进行计算时，则绕截面顺转的外力产生正弯矩， 反之为负。以右侧的外力计算时，绕截面逆转的外力产生 正弯矩，反之为负。
F
Q1
、 M 1 为正值，表示该截面上剪力和弯矩与所设方向一致，故为正剪力，正弯矩。
例 7－ 1
（3）求 2-2 截面的内力。用截面法把梁从 2-2 截面处切成两段，取左段为研究对象，受 力如图 7－6c。图中剪力和弯矩都假设为正。由平衡方程得 ∑Fy＝0,
FA － F Q 2 ＝0, F Q 2 ＝ FA =2 kN
FQ1 FA 2kN M1 FA 2 2 2 4kN m
图
FQ2=FA－F＝2－3＝－1kN
M 2 FA 2 2 2 4kN m
(3)求3－3和4－4截面的剪力和弯矩，取右侧计算。
FQ 3 FB 1kN
M3 FB 4 m 1 4 2 2kN m
MA 0
MB ql ql 2 l 0 2 2 ql l q l ql 2 M C ( )2 2 2 2 2 8
当x ＝l 时
当x＝l/2时,
时将三点用一光滑曲线连成一抛物线即得梁的弯矩图，见图7－9c。
第四章 梁的内力
2.2
P =P FN + (− P ) = 0
第四章
梁 的 内 力
4.1 梁的计算简图
梁的约束条件及荷载千差万别，为便于计算，一般抓住主要因素对其 做出简化，得出计算简图。 首先是梁的简化，一般在计算简图中用梁的轴线代替梁。 另外，还需要对支座和荷载进行简化，下面分别讨论梁上支座和荷载 的简化。
2.3
由上述结果可见，该钢杆最大正应力发生在段内，大小为 176.84 MPa
2.19
A
第四章
二.斜截面上的应力
梁 的 内 力
4.3 梁的内力、剪力和弯矩
前面讨论了拉(压)杆横截面上的正应力，但实验表明，有些材料 拉(压)杆的破坏发生在斜截面上。为了全面研究杆件的强度，还需要 进一步讨论斜截面上的应力。 设直杆受到轴向拉力 P 的作用，其横截面面积为 A ，用任意斜截面将 杆件假想的切开，设该斜截面的外法线 x 与轴的夹角为 α ，如图 2.7(a)所示。设斜截面的面积为 Aα ，则
2.6
Qm
第四章
2. 载荷的简化
梁 的 内 力
4.1 梁的计算简图
梁上的载荷通常可以简化为以下三种形式。 (1) 集中力。作用在梁上 很小区域上的横向力，其 特点是分布范围远小于轮 轴或大梁的长度，因此可 以简化为集中力，如火车 轮轴上的P(图4.2)、吊车 大梁所挂的重物 Q (图 4.4(a))等，它的常用单位 为牛顿(N)或千牛顿(kN)。
常见的静定梁有以下三种形式:
2.11
y (tm + 1)
第四章
梁 的 内 力
4.1 梁的计算简图
(1)简支梁(simply supported beam)。一端为固定铰支座，另一端为可动 铰支座的梁，称为简支梁。如吊车大梁(图4.4(a))，两支座间的距离 称为跨度。 (2) 外伸梁(beam with an overhang)。当简支梁的一端或两端伸出支座 之外，称为外伸梁。如火车轮轴(图4.2)即为外伸梁。 (3) 悬臂梁(cantilever beam)。一端为固定端、另一端自由的梁称为悬 臂梁，如闸门立柱(图4.4(b))。 工程中另有一些梁，其支座反力的数目多于有效平衡方程的数目，这 样的梁称为静不定梁或者超静定梁 静不定梁或者超静定梁(图4.1)。为确定静不定梁的全部 静不定梁或者超静定梁 支反力，除静力平衡方程外，还需考虑梁的变形，这将在后面章节进 行介绍。
P =P FN + (− P ) = 0
第四章
梁 的 内 力
4.1 梁的计算简图
梁的约束条件及荷载千差万别，为便于计算，一般抓住主要因素对其 做出简化，得出计算简图。 首先是梁的简化，一般在计算简图中用梁的轴线代替梁。 另外，还需要对支座和荷载进行简化，下面分别讨论梁上支座和荷载 的简化。
2.3
由上述结果可见，该钢杆最大正应力发生在段内，大小为 176.84 MPa
2.19
A
第四章
二.斜截面上的应力
梁 的 内 力
4.3 梁的内力、剪力和弯矩
前面讨论了拉(压)杆横截面上的正应力，但实验表明，有些材料 拉(压)杆的破坏发生在斜截面上。为了全面研究杆件的强度，还需要 进一步讨论斜截面上的应力。 设直杆受到轴向拉力 P 的作用，其横截面面积为 A ，用任意斜截面将 杆件假想的切开，设该斜截面的外法线 x 与轴的夹角为 α ，如图 2.7(a)所示。设斜截面的面积为 Aα ，则
2.6
Qm
第四章
2. 载荷的简化
梁 的 内 力
4.1 梁的计算简图
梁上的载荷通常可以简化为以下三种形式。 (1) 集中力。作用在梁上 很小区域上的横向力，其 特点是分布范围远小于轮 轴或大梁的长度，因此可 以简化为集中力，如火车 轮轴上的P(图4.2)、吊车 大梁所挂的重物 Q (图 4.4(a))等，它的常用单位 为牛顿(N)或千牛顿(kN)。
常见的静定梁有以下三种形式:
2.11
y (tm + 1)
第四章
梁 的 内 力
4.1 梁的计算简图
(1)简支梁(simply supported beam)。一端为固定铰支座，另一端为可动 铰支座的梁，称为简支梁。如吊车大梁(图4.4(a))，两支座间的距离 称为跨度。 (2) 外伸梁(beam with an overhang)。当简支梁的一端或两端伸出支座 之外，称为外伸梁。如火车轮轴(图4.2)即为外伸梁。 (3) 悬臂梁(cantilever beam)。一端为固定端、另一端自由的梁称为悬 臂梁，如闸门立柱(图4.4(b))。 工程中另有一些梁，其支座反力的数目多于有效平衡方程的数目，这 样的梁称为静不定梁或者超静定梁 静不定梁或者超静定梁(图4.1)。为确定静不定梁的全部 静不定梁或者超静定梁 支反力，除静力平衡方程外，还需考虑梁的变形，这将在后面章节进 行介绍。
梁的内力与应力(图片版)
σ=FbA，其中F为作用在梁上的力，b 为梁的宽度，A为梁的横截面积。
描述
正应力表示梁在承受拉伸或压缩时， 截面上产生的应力。
剪应力
剪应力
与截面相切的应力，主要由于剪 切而产生。
描述
剪应力表示梁在承受剪切时，截面 上产生的应力。
公式
τ=FsA，其中Fs为作用在梁上的剪 力，A为梁的横截面积。
弯曲应力
致梁发生断裂或严重变形。
强度失效的原因可能包括材料缺 陷、设计不当或制造工艺问题等。
弯曲失稳
弯曲失稳是指梁在受到垂直于 轴线的横向力作用时，发生弯 曲变形并最终失去稳定性。
弯曲失稳通常发生在梁的长度、 跨度较大或支撑不足时，导致 梁发生过大弯曲和扭曲。
弯曲失稳的原因可能包括梁的 刚度不足、支撑条件不当或外 力过大等。
。
混凝土
适用于桥梁、房屋和基础设施 等需要承受较大荷载且稳定性
要求较高的场合。
木料
适用于临时建筑、小型建筑和 家庭装修等需要较低承载能力
的场合。
其他材料
如铝合金、玻璃钢等，适用于 特殊场合和特定需求。
优化设计
截面优化
根据梁的跨度、承载能力和稳定性要求，选择合适的截面尺寸和 形状，以减小材料用量和提高承载能力。
梁的内力与应力(图片 版)
目录 CONTENT
• 梁的简介 • 梁的内力 • 梁的应力 • 梁的强度与稳定性 • 梁的设计与优化 • 梁的案例分析
01
梁的简介
梁的种类
01
02
03
简支梁
简支梁是两端支撑在支座 上的单跨梁，其载荷作用 在跨中位置。
连续梁
连续梁是多跨梁，载荷可 以作用在任意位置。
悬臂梁
第五章 梁的内力
第五章 梁的内力§5−1 概述一、工程实际中的弯曲问题等直杆在其包含杆轴线的纵向平面内，承受垂直于杆轴线的横向外力或外力偶的作用，杆的轴线在变形后成为曲线，这种变形称为弯曲。
弯曲变形是构件的基本变形之一，这种以弯曲变形为主的杆件叫做受弯杆或简称为梁。
工程结构中经常用梁来承受荷载，例如图5−1a 所示房屋建筑中的楼板梁要受到由楼板传递来的均布荷载，图5−1b 所示的火车轮轴受到火车车厢的作用，这些杆件发生的主要变形都是弯曲变形。
梁发生弯曲变形后，梁的轴线成为一条平面曲线（图5−2），这种弯曲叫做对称弯曲，对称弯曲后，由于梁变形后的轴线所在平面与外力所在平面相重合，因此也称为平面弯曲。
这种弯曲统称为非对称弯曲。
二、梁的支座及支座反力1．可动铰支座这种支座如图5−3a 所示，它只限制梁在支承处沿垂直于支承面方向的位移，但不能限制梁在支承处沿平行于支承面的方向移动和转动。
故其只有一个垂直于支承面方向的支座反力F R y 。
2．固定铰支座这种支座如图5−3b 所示，它限制梁在支座处沿任何方向的移动，但不限制梁在支座处的转动。
故其反力一定通过铰中心，但大小和方向均未知，一般将其分解为两个相互垂直的分量：水平分量F R x 和坚向分量F R y ，即可认为该支座有两个支座反力。
3．固定端支座这种支座如图5−3c 所示，它既限制梁在支座处的线位移，也限制其角位移。
支座反力的大小、方向都是未知的，通常将该支座反力简化为三个分量F R x 、F R y 和M ，即可认为该支座有三个支座反力。
纵向对称面 A 图5−2 图 5−1（b ） （a ）三、静定梁的基本形式常见的简单静定梁有下列三种：1．简支梁。
这种梁的一端是固定铰支座，另一端是可动铰支座（图5−4a ）。
2．悬臂梁。
这种梁的一端是固定端支座，另一端是自由端（图5−4b ）。
3．外伸梁。
这种梁相当于简支梁的一端或两端伸出支座以外（图5−4c ）。
梁的内力
MA=0
MC=FA×2=30×2kN·m=60kN·m
CD段：没有均布荷载作用，弯矩图是一条斜直线，需确定MC和MD左 MD左=FA×4-F×2=(30×4-20×2)kN·m=80kN·m
D截面：有逆时针方向的集中力偶M作用，弯矩图向上突变M=40kN·m
MD右=MD左-M=(80-40)kN·m=40kN·m
截面上必有弯矩M，且M=FAC。当左段梁若平衡，横截面 上必有两个内力分量：平行于横截面的竖向内力Fs以及位 于荷载作用面的内力偶M。内力Fs称梁横截面内的剪力， 而内力偶M称为梁横截面内的弯矩。
Fs
C
A
M
FA
x
若以右段梁为研究对象，由作用力与反作用力定律可知，
右段梁横截面上的内力值仍为Fs和M，指向与左段梁横截面
MBF0
F 6 M q 4 2 F A 8 0
解之得：
FA 30kN FB 30kN
（2）画剪力图
从左向右作图，全梁分为A端、AC段、C端、CD段、DB段和B端。
31
FA=30kN AC段：没有均布荷载作用，剪力图为一条水平线：FC左=FA右=30kN C端：有向下的集中力F作用，剪力图向下突变F=20kN
Mx=FA x-qx2/2= 81/32qa2
BC段：没有均布荷载作用，弯矩图是一条斜直线，需确定MB和MC。
MC 0
29
剪力图与弯矩图
30
[例] 如图所示，试画出该梁的剪力图和弯矩图。
F=20kN M=40kN
FA
FB
解：（1）计算支座反力 以整梁为研究对象，由平衡方程得：
MAF0
F B 8 M F 2 q 4 6 0
M144 kNm
受静载荷梁的内力及变位计算公式
受静载荷梁的内力及变位计算公式1.集中力的作用下的受静载荷梁内力计算公式：(1)弯矩(M)的计算公式：M=F*x其中，M是梁的弯矩，F是集中力，x是集中力作用点到支点的距离。
(2)剪力(V)的计算公式：V=F其中，V是梁的剪力，F是集中力。
2.均布力的作用下的受静载荷梁内力计算公式：(1)弯矩(M)的计算公式：M=w*x^2/2其中，M是梁的弯矩，w是均布力的单位长度的大小，x是梁上的任意一点到支点的距离。
(2)剪力(V)的计算公式：V=w*x其中，V是梁的剪力，w是均布力的单位长度的大小，x是梁上的任意一点到支点的距离。
3.其他外力作用下的受静载荷梁内力计算公式：当存在多个外力作用在梁上时，我们可以将其分解为集中力和均布力的叠加。
然后可以使用前面提到的公式来计算相应的内力。
变位计算公式主要有两种方法，分别是力偏心法和位移法。
4.力偏心法：利用力偏心引起的弯矩和剪力，根据梁的弹性理论和材料的本构关系，可以计算出梁的变位。
其中，弯矩引起的变位可由以下公式计算：δ=M*l^2/(2*E*I)其中，δ是梁的变形，M是梁上弯矩的最大值，l是梁的长度，E是梁的弹性模量，I是梁的截面惯性矩。
剪力引起的变位可由以下公式计算：δ=V*l/(G*A)其中，δ是梁的变形，V是梁上剪力的最大值，l是梁的长度，G是梁的剪切模量，A是梁的截面面积。
5.位移法：利用位移函数法，将梁的各个节点的位移表示为节点位移和激励项的组合，可以通过解线性代数方程组得到梁的节点位移。
其中，节点位移可以用来计算梁的变位。
综上所述，受静载荷梁的内力和变位计算可以通过公式和方法进行求解。
具体的计算公式和方法取决于梁的受力情况和边界条件。
在实际工程中，通常会采用数值分析方法，如有限元法等，来计算受静载荷梁的内力和变位。
平面弯曲—梁的内力(建筑力学)
∑Fy=0 FQ1 ＋ FP=0 FQ1=－FP =－100kN (负剪力)
∑M1=0 M1＋FP×a=0 M1=－FP a= －100×1.5 =－150kN·m (负弯矩)
弯曲内力
（3）求2-2截面上的剪力和弯矩 ∑Fy=0 －FQ2－FP＋FAy =0 FQ2=25kN (正) ∑M2=0 M2＋FP×a=0 M2=－150kN·m (负)
弯曲内力
利用截面法求内力时应注意以下几点： １）为了简化计算，通常取外力比较少的一侧来研究。 ２）作所取隔离体的受力图时，在切开的截面上，未知 的剪力和弯矩通常均按正方向假定。 ３）在列梁段的静力平衡方程时，要把剪力、弯矩当作 隔离体上的外力来看待。因此，平衡方程中剪力、弯矩的 正负号应按静力计算的习惯而定，不要与剪力、弯矩本身 的正、负号相混淆。
=－15×1×2.5－30×3 =－127.5kN·m
计算结果为负，说明1-1截 面上弯矩的实际方向与图中 假定的方向相反，即1-1截面 上的弯矩为负值。
弯曲内力
（2）求2-2截面上的剪力和弯矩
取2-2截面的右侧为隔离体。
∑Fy =0 FQ2－FP－q×1=0 FQ2= FP＋q×1 =30＋15×1=45kN (正剪力)
弯曲内力
例10-3 直接用规律求图示简支梁指定截面上的剪力和弯矩。 已知：M=8kN·m，q=2kN/m
解 （1）求支座反力 FAy=1kN(↓) FBy=5kN(↑)
（2）求1-1截面上的剪力和弯矩。
取该截面的左侧为隔离体 FQ1=－FAy =－1kN
M1=8kN·m
弯曲内力
（3）求2-2截面上的剪力和弯矩。 取该截面的右侧为隔离体
FQ2=q×2－Fby =(2×2－5)kN=－1kN
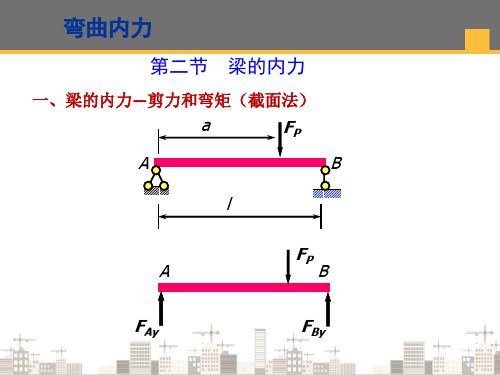
∑M1=0 M1＋FP×a=0 M1=－FP a= －100×1.5 =－150kN·m (负弯矩)
弯曲内力
（3）求2-2截面上的剪力和弯矩 ∑Fy=0 －FQ2－FP＋FAy =0 FQ2=25kN (正) ∑M2=0 M2＋FP×a=0 M2=－150kN·m (负)
弯曲内力
利用截面法求内力时应注意以下几点： １）为了简化计算，通常取外力比较少的一侧来研究。 ２）作所取隔离体的受力图时，在切开的截面上，未知 的剪力和弯矩通常均按正方向假定。 ３）在列梁段的静力平衡方程时，要把剪力、弯矩当作 隔离体上的外力来看待。因此，平衡方程中剪力、弯矩的 正负号应按静力计算的习惯而定，不要与剪力、弯矩本身 的正、负号相混淆。
=－15×1×2.5－30×3 =－127.5kN·m
计算结果为负，说明1-1截 面上弯矩的实际方向与图中 假定的方向相反，即1-1截面 上的弯矩为负值。
弯曲内力
（2）求2-2截面上的剪力和弯矩
取2-2截面的右侧为隔离体。
∑Fy =0 FQ2－FP－q×1=0 FQ2= FP＋q×1 =30＋15×1=45kN (正剪力)
弯曲内力
例10-3 直接用规律求图示简支梁指定截面上的剪力和弯矩。 已知：M=8kN·m，q=2kN/m
解 （1）求支座反力 FAy=1kN(↓) FBy=5kN(↑)
（2）求1-1截面上的剪力和弯矩。
取该截面的左侧为隔离体 FQ1=－FAy =－1kN
M1=8kN·m
弯曲内力
（3）求2-2截面上的剪力和弯矩。 取该截面的右侧为隔离体
FQ2=q×2－Fby =(2×2－5)kN=－1kN
梁的内力
均布荷载
§4-2 梁的荷载和支座反力
二、梁的支座及支座反力
1、固定铰支座
2、可动铰支座
FRx
FRy
FRy
3、固定支座
MA FRx
FRy
§4-2 梁的荷载和支座反力
三、静定梁的基本形式
FAx
FAy FAx
FAx MA
FAy FAy
简支梁
FBy
外伸梁 (伸臂梁)
FBy
悬臂梁 梁的支座反力可根据梁的平衡条件得到
CB
FS (x2 )＝− Fa / l (a ≤ x2 ≤ l) M(x2 )＝Fa(l − x2 )/ l (a ≤ x2 ≤ l)
3、作剪力图和弯矩图
例题3 图示简支梁C点受集中力偶作用。
例题4
a
b
M
试画出剪力图和弯矩图。
q
A
C
x1
FAy
l
B x2
FBy
解： 1、求支座反力 FAy＝M / l FBy＝ －M / l
dx Fs (x)+ dFs (x)
dM (x) dx
=
Fs (x)
dM 2(x) dx2
=
q(x)
弯矩图上某点处的曲率等于该点处荷载集度的大小
§4-5 剪力、弯矩与荷载集度的关系
§4-5 剪力、弯矩与荷载集度的关系
二、 剪力图、弯矩图的特征
dFs (x)
dx
=
q(x)
dM (x) dx
= Fs (x)
第4章 梁的内力
§4-1 工程中的弯曲问题
吊车大梁简化:
q F
§4-1 工程中的弯曲问题
火车轮轴简化：
§4-1 工程中的弯曲问题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
20
x=5.6
V (kN)
88 80
16
M C 72 2 144 kN.m
M (kN.m)
144
113.6
例7 作剪力图和弯矩图（用简捷法）
160kN.m A C 2m RA=72kN 72 20kN
20kN/m
B 8m 2m RB=148kN 60 D
弯矩极值的计算
E
x 5.6 m 88 80 16
(0 ≤ x≤a )
Fa l
V M
Fab l
CB段 Fa V FB (a＜x ＜ l ) l Fa M (l x) (a ≤ x≤l ) l
3. 画 V、 M 图
例4
Me A FA a
x
x
作图示梁的V 、M 图。 解： 支反力计算 1.
B b l FB
C
Me Me , FB l FA l
ql 2
V
ql 2
M
ql 2 8
3. 作V、M 图
例3
F A
Fb FA l
作图示梁的V、M 图 解： 支反力计算 1.
B b
a
x
Fb l
C l
Fb Fa FA , FB l l
Fa FB l
2. 列 V、 M 方程
AC段
Fb V FA Fb l M x l
x
(0＜x ＜ a )
V图
M图 Mmax
新课: 简捷法作V 、 M 图
分段——两面、两点 两面——集中力、集中力偶作用的截面 两点——分布荷载的起点和终点 求出各分点的内力，按微分关系作图。
简捷法绘制内力图的一般步骤：
(1）求支座反力。
（2）分段：凡外力不连续处均应作为分段点， 如集中力和集中力偶作用处，均布荷载两端点等。 （3）定点：据各梁段的内力图形状，选定控 制截面。如集中力和集中力偶作用点两侧的截面、 均布荷载起迄点等。用截面法求出这些截面的内力 值，按比例绘出相应的内力竖标，便定出了内力图 的各控制点。
（4）联线：据各梁段的内力图形状，分别用 直线和曲线将各控制点依次相联，即得内力图。
例5 作剪力图和弯矩图（用简捷法）
F
A
FA Fb l
解：
B b
Fa FB l
a
Fb l
C
l
Fb Fa FA , FB l l
Fa l
V
M
Fab l
例6
A FA
作图示梁的V、M 图（用简捷法）
q B l
解： 1. 支反力计算
1 、梁的内力
剪力 V 弯矩 M
F
A
x
B
M V x
剪力V 弯矩M
RA
2、 用简捷法绘制梁的剪力图和弯矩图 已知梁上的外力，根据梁上内力图的大致 形状，求出各控制段截面内力值便可绘 出全梁内力图。这种方法叫简捷法。 1）、 M 、V与 q 的微分关系
y
O x dx F q x
dV q dx
dM V dx
d2 M q 2 dx
根据梁的荷载集度 q 、剪力 Q 、弯矩 M 三者 间的微分关系得出梁内力图的规律：
据此，得直梁内力图的形状特征
梁上情况
q=0
水平线
⊕
⊖㊀
q=常数 q↓ q↑
斜直线
抛物线
P 作用处
有突变
铰或 作用处 自由端 (无m）
m
Q图
M图
Q=0 处 突变值为P 如变号 无变化 有极值 尖角指向同P 有极值 有突变 M=0 有尖角
V V
R
B
RA
x
M－RAx=0
M = RAx
内力总是成对的，大小相等，方向相反， 正负号如何规定？
3)剪力与弯矩的正负号规定 剪力的正负号规定
正的剪力
V V
负的剪力
V V
使脱离体顺时针为正
弯矩的正负号规定
正的弯矩
MM
上凹下凸
M
M
引起的变形 ——使梁下凸弯矩为正。
例1
求图示梁E截面的VE和ME 解：1.求支反力
下夹角亦向下； Q 图有一突变，荷载 向下突变亦向下。
3、均布荷载作用段 M图为抛物线，荷载向 下曲线亦向下凸；
Q 图没有变化。
Q 图为斜直线，荷载向
下直线由左向右下斜
作 业
P. 106 6.4
再见
3.联线
几点说明：
K
1.作EF段的弯矩图 用简支梁叠加法
RB
RA 38 8
1.6m x
Q图(kN)
K
20
12
M图(kN· m) Mk
Mmax=32.4kn· N
2.剪力等于零截面K 的位置 QK=QE－qx=8－5x=0 x=1.6m 3.K截面弯矩的计算
qx 2 MK=ME+QE x－ 2 2 5 1 6 =26+8×1.6－ 2
第六章 基本静定梁的内力分析
目的：用图示法形象地表示出剪力Q、 弯矩M沿梁长变化的情况，梁的内力图 绘制是材料力学教学中的一个重点和难 点内容，熟练、正确地绘制内力图有助 于对杆件自身的受力分析及杆件的强度、 刚度和稳定性计算。
绘制内力图方法： 绘制梁内力图的方法有静力法、简捷法和叠加 法，其中简捷法是利用剪力、弯矩和载荷集度 之间的微分关系作图的一种简便方法，通常是 用来确定梁的危险截面作为强度计算的依据， 因此熟练把握简捷法作梁的内力图是十分必要 的。
ql FA FB 2
V
ql 2
FB
2. 作V、M 图
ql 2
M
ql 2 8
例7 作剪力图和弯矩图（用简捷法）
R=200kN 160kN.m 20kN 20kN/m B 8m 2m RB=148kN
A
C 2m
RA=72kN
解：1. 支反力计算
M B 0, RA 10 160 20 10 3 20 2 0 M A 0, RB 10 160 20 10 7 20 12 0
2. 列 V , M 方程
V
Me l
Me V FA (0＜x＜ l ) l AC段
M ea l
Me M x l
(0 ≤ x < a )
CB段 M
M eb l
Me M (l x) (a < x≤l ) l
3. 画 V 、M 图
复
习
1、梁的内力（包括剪力和弯矩） 2、在已知梁外力的情况下，根据剪力、弯 矩、荷载三者之间的微分关系，掌握梁 内力图的大致形状。
RB=148kN （↑）
RA=72kN （↑）
例8 作剪力图和弯矩图（用简捷法）
160kN.m A C 2m RA=72kN 72 20kN
20kN/m
B 8m 2m RB=148kN 60 D
2.作剪力图和弯矩图
VB 72 20 8 88 kN VB 72 20 8 148 60 kN VD 20 kN
M A 0, RB 4 F1 1 F2 2.5 0 B 1 1.5m RB 24 1 80 2.5 56 kN 4 RB M B 0, RA 4 F1 3 F2 1.5 0
F1=24kN F2=80kN 1m
A
2m RA
F A B
x l V F
V =－F
（0 ＜ x＜l）
M =－F x
（0≤x＜l）
2. 作剪力图和弯矩图
注意：弯矩图画在受拉一侧 Fl
M
例2
q A B
作图示梁的V、M 图。 1. 解： 支反力计算
ql FA FB 2
x
FA l FB
2. 列 V、 M 方程
1 V ql qx (0＜x ＜ l ) 2 1 1 2 M qlx qx (0 ≤ x≤l ) 2 2
纵对称面
F1 F2
R1
轴线
R2
常见的三种静定梁
—— 简支梁
—— 悬臂梁
—— 外伸梁
二、梁的内力及计算
1）梁的内力 剪力 V
弯矩 M
F
Aபைடு நூலகம்
x
B
M V x
剪力V 弯矩M
RA
2)截面法计算梁的内力 F 剪力V ∑Fy=0, RA－V = 0 x V = RA RA RB 弯矩M y F O MM ∑MO=0,
斜直线
↓
↑
2）V 、M 图的若干规律 q=0 q=0
V﹥0 V= 0 V﹤0
V图
M图
V 、M 图的若干规律 q = 常数
q<0
q>0
V图 M图
抛物线
V、M 图的若干规律
集中力的影响
F
F ｛ F F ｛ 突变F
V图
M图
折角
V 、M 图的若干规律
集中力偶的影响
Me
Me
无影响
V图
M图
突变Me
V 、M 图的若干规律 V= 0的截面，必有Mmax 或 Mmin
M E RA 2 F1 1 48 2 24 1 72 kN.m
三、绘制梁的内力图——剪力图和弯矩图
1、静力法绘制剪力图和弯矩图
F
A B
x
l
剪力方程 弯矩方程
V=－F M =－F x （0≤x＜l）
坐标位置x的任意截面的剪力和弯矩 就是剪力方程和弯矩方程
1. 剪力方程和弯矩方程
Q图(kN) 由∑MB=0, 8 有 RA×8－20×9－30×7－5×4×4－10+16=0 12 得 20 RA=58kN（↑） 再由∑Y=0, 可得 20 RB MC=0,=20+30+5×4－58=12kN（↑） 16 m MA=－20×1=－20kN· 4 M图(kN· MD=－20×2+58×1=18kN· m) m 0 M =－20×3+58×2－30×1=26kN· m E 2 5 4 6 MF=12×2－16+10=18kN· 10m 8 MG左=12×1－16+10=6kN· m 18 18 MG右=12×1－16=－4kN· MB左=－16kN· m m 26