初二(上)数学作业纸
第一轮网课作数学作业纸
文通中学八年级数学作业纸（B） No.81班级姓名学号成绩课题：线段、角的对称性（3）命题人：卞洪波审核人：鲍兆清一、填空题：1. 如图1，BD平分∠ABC,E为射线BD上的点,EF⊥AB于F,若EF=3,则点E到边BC的距离为。
2. 如图2，已知CD⊥AB,BE⊥AC,垂足为D、E，BE、CD交与点O，且AO平分∠BAC,那么图中全等三角形共有对。
3. 如图3，在△ABC中，∠C=900，AD平分∠BAC,D到AB的距离为12，BD∶BC=3∶5，则BC的长为。
图44. 如图4，已知点C是∠AOB平分线上一点，点P、Q分别在OA、OB上。
如果要得到OP=OQ，需要添加以下条件：①∠OCP=∠OCQ ②∠OPC=∠OQC ③PC=QC ④PQ⊥OC 中的哪一个即可。
添加条件的可能为。
（填序号）5．（2014•四川遂宁）如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A．3B．4C．6D．5二、选择题：6.已知：在△ABC中，AD为∠BAC的角平分线，DE⊥AB，F为AC上一点，且∠DFA=1000，则（）A.DE>DF B.DE<DF C.DE=DF D.不能确定DE、DF的大小.7.下列说法中正确的有 ( ）①不在线段垂直平分线上的点，到线段两个端点的距离一定不相等②P是∠AOB平分线上的一点，C、D分别是OA、OB上的点，则PC=PD③角的平分线可以看成到角两边距离相等的点的集合④等腰三角形中，顶角的顶点一定在底边的垂直平分线上A.1个B.2个C. 3个D. 4个三、解答题：8. 利用网络线作图；（1）在BC 上找一点P ，使P 到AB 和AC 的距离相等；（2）在射线AP 上找一点Q ，使QB=QC 。
9.在课外活动中，小明发明了一个在直角三角形中画锐角的平分线的方法，他的方法是：如图所示，在斜边AB 上取一点E ，使BE=BC ，过点E 作ED ⊥AB ，交AC 于D ，那么DB 就是∠CDE 的平分线，BD 就是∠ABC 的平分线，你认为对吗？为什么？10.已知：在ΔABC 中，D 是BC 上一点,DF ⊥BA 于F,DE ⊥AC 于E,且DE=DF 。
北师大版八年级数学上寒假作业：7.3-7.4
FA B C D E G 图2初中数学试卷1.如图1，AB ∥CD ，则下列结论成立的是 ( ).A ．∠A+∠C=180°B ．∠A+∠B=180°C ．∠B+∠C=180°D ．∠B+∠D=180° 2.若两个角的一边在同一条直线上，另一边 互相平行，那么这两个角的关系是( )A ．相等B ．互补C ．相等或互补D ．相等且互补 3.如图2，E 、F 分别是AB 、AC 上的点，G 是BC 的延长线上一点，且∠B=∠DCG= ∠D ，则下列判断错误的是( ).A.∠ADF=∠DCGB.∠A=∠BCFC.∠AEF=∠EBCD.∠BEF+∠EFC=180o4.3，下列推理正确的是( ).A ．∵MA ∥NB ，∴∠1=∠3 B ．∵∠2=∠4，∴MC ∥ND C ．∵∠1=∠3，∴MA ∥NB D ．∵MC ∥ND ，∴∠1=∠3 5.如图4，a ∥b ，点B 在直线b 上，且AB ⊥ BC ，∠1=55°，则∠2的度数为 ( ). A ．35° B ．45° C ．55° D.125° 6.如图5，已知AB ∥CD ，∠1=65°，∠2=45°，则∠ADC=________．基础题1、如图6，已知∠1=∠2，∠BAD =57°，则 ∠B =________.A B CD4321N图321ACab图4231ABC D 图5图1 A CD 21A C DFABC DEABCDE 122.如图7，若AB ∥EF ，BC ∥DE ，则∠B + ∠E =________．3.如图8，由A 测B 的方向是________．4.已知：如图，∠B=∠C.（1）若AD ∥BC,求证：AD 平分∠EAC; (2)若∠B+∠C+∠ABC=180°,AD 平分 ∠EAC,求证AD ∥BC.5.已知：如图，∠1=∠B ，∠A =32°.求： ∠2的度数．6.如图，∠B+∠BCD+∠D=360o， 求证：∠1=∠2．7.现有下列命题，其中真命题的个数是（ ）①（-5）2的平方根是-5；②近似数3.14×103有3个有效数字；③单项式3x 2y 与单项式-2xy 2是同类项；④正方形既是轴对称图形，又是中心对称 图形． A ．1 B ．2 C ．3 D ．48.如图,在梯形ABCD 中,AD ∥BC,∠D= 120°,∠DCA=20°,求∠BCA 和∠DAC 的 度数.1ABCD2A BCD E 1 32 4FAEA B C DCBA9.如图，A 、B 之间是一座山，要修一条铁 路通过A 、B 两地，在A 地测得铁路走向 是北偏东58°11′．如果A 、B 两地同时 开工开隧道，那么在B 地按北偏西多少度 施工，才能使铁路隧道在山腹中准确接 通？7.5三角形内角和定理1已知，如图1，△ABC 中，∠B=∠DAC ，则 ∠BAC 和∠ADC 的关系是( ).A ．∠BAC ＜∠ADCB ．∠BAC=∠ADC C ．∠BAC ＞∠ADCD ．不能确定2.对于△ABC ( ) .A.若∠A+∠B=∠C ，则△ABC 是直角三角 形B.若∠A+∠B ＞∠C ，则△ABC 是锐角三角 形C.若∠A+∠B ＜∠C ，则△ABC 是钝角三角 形D.若∠A=∠B=∠C ，则△ABC 是斜三角形 3.在△ABC 中，已知∠A+∠C=2∠B ，∠C －∠A=80°，则∠C 的度数是( ). A ．60° B ．80° C ．100° D ．120°4.如图2，∠A 、∠DOE 和∠BEC 的大小关系是( ).A ．∠A ＞∠DOE ＞∠BECB ．∠DOE ＞∠A ＞∠BEC C ．∠BEC ＞∠DOE ＞∠AD ．∠DOE ＞∠BEC ＞∠A5.与∠AEB 的关系是( ).A ．∠ADC ＞∠AEB B.∠ADC=∠AEBC ．∠ADC ＜∠AEBD ．不能确定基础题 1.在△ABC 中，∠A ∶∠B ∶∠C=1∶2∶3，则∠C=________． 图3 A B CDE2.△ABC 中，若∠A=30°，∠B=21∠C ，则∠B=________，∠C=________． 3.△ABC 中，∠B=40°，∠C=60°，AD 是 ∠A 的平分线，则∠DAC 的度数为_____． 4.△ABC 中，∠C=90°，CD ⊥AB ，∠B=63°， 则∠DCA=________．5.如图4，点D 在△ABC 边BC 的延长线上， DE ⊥AB 于E ，交AC 于F ，∠B=50°， ∠CFD=60°，则∠ACB=________．6.已知：如图，AB ∥CD ，AD ∥BC ，∠1=50°，∠2=80°．求∠C 的度数．7.已知：如图，D 是△ABC 的∠C 的外角平 分线与BA 的延长线的交点．求证：∠BAC ＞∠B ．8.已知：如图，在△ABC 中，BD 、CE 是∠B 、∠C 的平分线，且相交于点O ．求证：∠BOC=90°+21∠A ．9.如图，已知DE ∥BC ，CD 是∠ACB 的平分 线，∠B ＝70°，∠ACB ＝50°， 10.求∠EDC和∠BDC 的度数.A BCDE11.如图，AB ∥CD ，EF ⊥AB 于O ，∠2＝135 °，求∠1的度数．下面提供三个思路： （1）过F 作FH ∥AB ，（2）延长EF 交CD 于I ； （3）延长GF 交AB 于K ．请你利用三个思路中的两个思路，求∠1的度数．21ABCDDABC E A BC DEO。
学校初二(上)数学作业纸
⒊ 已知：在△ABC中，AD为∠BAC的角平分线上，DE⊥AB，F为AC上一点，且∠ DFA=1000，则 A.DE>DF 二、填空题 ⒋如图,△ABC中，DE垂直平分AC，与AC交于E，与BC交于D，∠C=150, ∠BAD=600， 则△ABC是__________三角形. ⒌ 如图，△ABC中，∠C=900，DE是AB的垂直平分线，且∠BAD：∠CAD=3：1，则 ∠B＝_______. B.DE<DF C.DE=DF （ D.不能确定 DE、DF 的大小. ）
G C
E
a
b c
A
D E
B
C
⒏ 已知：如图，△ABC 中，BC 边中垂线 ED 交 BC 于 E，交 BA 延长线于 D，过 C 作 CF⊥BD 于 F，交 DE 于 G，DF=
1 1 BC，试说明∠FCB= ∠B 2 2
D
F A B
四、探究活动 如图，直线 a,b,c 表示三条相互交叉的公路，现要建一个货物中转站，要求它到三 条公路的距离相等，可供选择的地址有几处？如何选？
A E B
第 4 题图
C
D
A P
D
CAE第 5Fra bibliotek题图B O
第 6 题图
B
⒍如图，分别作出点P关于OA、OB的对称点P 1 、P 2 ，连结P 1 P 2 , 分别交OA、OB于点 M、N，若P 1 P 2 =5cm，则△PMN的周长为__________________.
三、解答题 ⒎如图， 己知 AB=AC， 垂直平分 AB 交 AC、 于 D、 两点， AB=12cm， DE AB E 若 BC=10cm, ∠A=49º，求△BCE 的周长和∠EBC 的度数.
学校初二（上）数学作业纸
4-9文通中学八年级数学作业纸
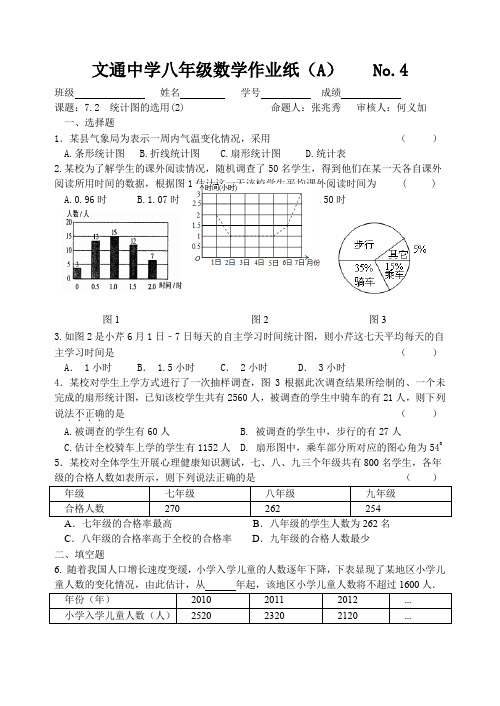
文通中学八年级数学作业纸（A ） No.4班级 姓名 学号 成绩 课题：7.2 统计图的选用(2) 命题人：张兆秀 审核人：何义加 一、选择题1．某县气象局为表示一周内气温变化情况，采用 （ ） A.条形统计图 B.折线统计图 C.扇形统计图 D.统计表2.某校为了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天各自课外阅读所用时间的数据，根据图1估计这一天该校学生平均课外阅读时间为 ( ) A.0.96时 B.1.07时 C.1.15时 D.1.50时3.如图2是小芹6月1日﹣7日每天的自主学习时间统计图，则小芹这七天平均每天的自主学习时间是 （ ） A ． 1小时 B ． 1.5小时 C ． 2小时 D ． 3小时4．某校对学生上学方式进行了一次抽样调查，图3根据此次调查结果所绘制的、一个未完成的扇形统计图，已知该校学生共有2560人，被调查的学生中骑车的有21人，则下列说法不正确．．．的是 （ ） A.被调查的学生有60人 B. 被调查的学生中，步行的有27人 C.估计全校骑车上学的学生有1152人 D. 扇形图中，乘车部分所对应的图心角为5405．某校对全体学生开展心理健康知识测试，七、八、九三个年级共有800名学生，各年级的合格人数如表所示，则下列说法正确的是 （ ）A ．七年级的合格率最高B ．八年级的学生人数为262名C ．八年级的合格率高于全校的合格率D ．九年级的合格人数最少 二、填空题6. 随着我国人口增长速度变缓，小学入学儿童的人数逐年下降，下表显现了某地区小学儿图1图2图37. 《中华人民共和国个人所得税法》规定，公民全月工资，薪金所得不超过800元的部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算某人三、解答题8.为了了解某市120000名初中学生的视力情况，某校数学兴趣小组调查、收集了相关数据，并进行了整理分析．（1）小明在眼镜店调查了1000名初中学生的视力，小刚在邻居中调查了20名初中学生的视力，他们的抽样是否合理？并说明理由．（2）该校数学兴趣小组从该市七、八、九年级各随机抽取了1000名学生进行调查，整理他们的视力情况数据，得到如下的折线统计图．请你根据抽样调查的结果，估计该市120000名初中学生视力不良的人数是多少？9. 某校根据课程设置要求,开设了数学类拓展性课程,为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整).请根据图中信息回答问题：(1)求m，n的值。
苏科版八年级数学上寒假作业(共8份)
第6题图图2A B F D E C 第7题图 第8题图 第9题图 初二数学寒假作业1（全等三角形）一、填空与选择1．已知△ABC≌△DEF，∠A=80°，∠E=50°，则∠F 的度数为（ ） A 、 30° B、 50° C、 80° D、 100°2．已知图中的两个三角形全等，则α∠的度数是（ ）A ．72°B ．60°C ．58°D ．50°3．如图，∠E=∠F=90°，∠B=∠C ，AE=AF ，给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN，其中正确的结论有（ ）A 、1个B 、2个C 、3个D 、4个4．△ABC 是格点三角形（顶点在网格线的交点），则在图中能够作出△ABC 全等且有一条公共边的格点三角形（不含△ABC）的个数是（ ）A 、1个B 、2个C 、3个D 、4个5．如图，AC 、BD 相交于点0，∠A=∠D，请补充一个条件，使△AOB≌△DOC，你补充的条件是 （填出一个即可）．6．已知，如图：∠ABC =∠DEF，AB =DE ，要说明△ABC ≌△DEF： 1）若以“SAS”为依据，还要添加的条件为______________； 2）若以“ASA”为依据，还要添加的条件为______________； 3）若以“AAS”为依据，还要添加的条件为______________．7．如图∠ACB ＝∠DFE ，BC ＝EF ，根据“ASA”,应补充一个直接条件___________，根据“AAS”，那么补充的条件为____________，才能使△ABC ≌△DEF ．8．如图，在Rt△ABC 中，∠C=90°，AC=10，BC=5，线段PQ=AB ，P 、Q 两点分别在AC 和过点A 且垂直于AC 的射线AO 上运动，当AP= 时，△ABC 和△PQA 全等.9．如右图示，△ABE 和△ADC 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠1∶∠2∶∠3=28∶5∶3，则∠α的度数为 。
数学作业本八年级上册北师大版
数学作业本八年级上册北师大版一、三角形。
1. 三角形的基本概念。
- 三角形的定义：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
- 三角形的表示方法：用符号“△”表示，如△ABC。
- 三角形的三边关系：三角形任意两边之和大于第三边，任意两边之差小于第三边。
- 三角形的分类。
- 按角分类：锐角三角形（三个角都是锐角）、直角三角形（有一个角是直角）、钝角三角形（有一个角是钝角）。
- 按边分类：不等边三角形（三边都不相等）、等腰三角形（有两边相等），其中等边三角形（三边都相等）是特殊的等腰三角形。
2. 三角形的内角和与外角。
- 三角形内角和定理：三角形三个内角的和等于180°。
- 三角形的外角：三角形的一边与另一边的延长线组成的角。
- 三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；三角形的一个外角大于任何一个与它不相邻的内角。
二、实数。
1. 平方根与算术平方根。
- 平方根：如果一个数的平方等于a，那么这个数叫做a的平方根，记作x = ±√(a)(a≥0)。
- 算术平方根：正数a的正的平方根叫做a的算术平方根，记作√(a)(a > 0)，0的算术平方根是0。
2. 立方根。
- 立方根的定义：如果一个数的立方等于a，那么这个数叫做a的立方根，记作x=sqrt[3]{a}。
- 立方根的性质：正数的立方根是正数，负数的立方根是负数，0的立方根是0。
3. 实数的概念与分类。
- 无理数：无限不循环小数叫做无理数，如π，√(2)等。
- 实数：有理数和无理数统称为实数。
实数可以分为正实数、0、负实数。
三、一次函数。
1. 函数的概念。
- 变量与常量：在一个变化过程中，数值发生变化的量称为变量，数值始终不变的量称为常量。
- 函数的定义：在一个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。
2022-2023学年人教新版八年级(上)数学寒假作业(1-5)
2022-2023学年人教新版八年级（上）数学寒假作业（一）一．选择题（共8小题）1．如图，△ABC中，AD是△ABC的角平分线，AE是△ABC高线，当∠B＝42°，∠C＝66°时，∠DAE的度数为（）A．6°B．8°C．10°D．12°2．如图，在Rt△ABC中，∠C＝90°，∠ABC的平分线BD交AC于点D，若AD＝5cm，CD＝4cm，则点D到直线AB的最小值是（）A．2cm B．3cm C．4cm D．5cm3．如图．已知在△ABC中，AC的垂直平分线交AC于点D，交BC于点E，连接AE．若△ABE的周长为13，则AB+BC的值为（）A．10B．13C．16D．184．下列等式从左到右的变形中，属于因式分解的是（）A．m（n﹣5）＝mn﹣5m B．m2﹣4m＝（m﹣2）2﹣4C．x2﹣81y2＝（x+9y）（x﹣9y）D．x2﹣y2﹣5＝（x+y）（x﹣y）﹣5 5．已知：32m＝4，32n＝8，则9m﹣n+1的值是（）A．﹣2B．C．4D．6．如图，在△ABC中，AC＝4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（）A．1cm B．2cm C．3cm D．4cm7．关于x的方程＝a﹣1无解，则a的值是（）A．a＝1B．a＝0或a＝﹣1C．a＝﹣1D．a＝1或a＝0 8．分式方程＝有增根，则m的值为（）A．0和3B．1C．1和﹣2D．3二．填空题（共6小题）9．已知m是关于x的方程x2﹣2x﹣3＝0的一个根，则2m2﹣4m＝．10．已知多项式x2﹣2（m﹣1）x+16是关于x的完全平方式，则m的值为．11．已知点P（m﹣1，n+2）与点Q（2m﹣4，2）关于x轴对称，则（m+n）2022的值是．12．如图，已知点O为△ABC的两条角平分线的交点，过点O作OD⊥BC于点D，且OD ＝4．若△ABC的周长是17，则△ABC的面积为．13．如图，∠ACD是△ABC的一个外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠DCE的大小是度．14．如图，已知∠ACB＝100°，OA平分∠BAC，OB平分∠ABC，则∠AOB＝°．三．解答题（共6小题）15．如图，FA⊥EC，垂足为E，∠C＝20°，∠F＝40°．求∠FBC的度数．16．如图，在△ABC中，D是AB上一点，CF∥AB，DF交AC于点E，DE＝EF．（1）求证：△ADE≌△CFE；（2）若AB＝5，CF＝3，求BD的长．17．如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC边上，且BE＝CF，BD＝CE．（1）求证：△DEF是等腰三角形；（2）当∠A＝40°时，求∠DEF的度数．18．把下列多项式进行因式分解（要写出必要的过程）：（1）﹣x2y+6xy﹣9y；（2）a2（x﹣y）+4b2（y﹣x）．19．先化简，再求值：，试从0，1，2，3四个数中选取一个你喜欢的数代入求值．20．计算：（1）﹣；（2）﹣÷．2022-2023学年人教新版八年级（上）数学寒假作业（二）一．选择题（共8小题）1．已知：a2﹣3a+1＝0，则a+﹣2的值为（）A．+1B．1C．﹣1D．﹣52．若分式的值为零，则x的值是（）A．1B．﹣1C．±1D．23．若x，y均为正整数，且2x+1•4y＝128，则x+y的值为（）A．3B．5C．4或5D．3或4或5 4．如图，△ABC中，BD平分∠ABC，BC的中垂线交BC于点E，交BD于点F，连接CF．若∠A＝60°，∠ABD＝24°，则∠ACF的度数为（）A．48°B．36°C．30°D．24°5．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD ＝8，则点P到BC的距离是（）A．8B．6C．4D．26．如图是由4个相同的小正方形组成的网格图，其中∠1+∠2等于（）A．150°B．180°C．210°D．225°7．如图，△ABC中，BO，CO分别是∠ABC，∠ACB的平分线，∠A＝50°，则∠BOC等于（）A．110°B．115°C．120°D．130°8．在△ABC中，∠A：∠B：∠C＝3：4：5，则∠C等于（）A．45°B．60°C．75°D．90°二．填空题（共6小题）9．如图，AB∥CD，∠1、∠2、∠3是五边形ABCDE的外角，若∠1+∠3＝70°，则∠2＝°．10．如图，在Rt△ABC中，∠C＝90°，AD是∠BAC的平分线，CD＝3，AB＝6，则△ABD 的面积是．11．等腰三角形一腰上的高与另一腰的夹角为30°，则它的顶角为．12．多项式x2+mx+5因式分解得（x+5）（x+n），则m＝，n＝．13．已知关于x的分式方程﹣＝1的解为负数，则k的取值范围是．14．若，则的值为．三．解答题（共6小题）15．先化简：，并从0，﹣1，2中选一个合适的数作为a的值代入求值．16．先化简，再求值：4（x﹣1）2﹣（2x+3）（2x﹣3），其中x＝﹣1．17．在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E，若AB＝5，求线段DE的长．18．如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF．求证：（1）AD平分∠BAC；（2）AC＝AB+2BE．19．如图，FA⊥EC，垂足为E，∠C＝20°，∠F＝40°．求∠FBC的度数．20．如图，在△ABC中，点D是边BC上一点，DE⊥AB于点E，连接CE，∠ACE＝∠BCE，∠ACB＝50°，∠B＝60°．求∠CED的度数．2022-2023学年人教新版八年级（上）数学寒假作业（三）一．选择题（共8小题）1．如图，将直尺与含30°角的三角尺摆放在一起，若∠1＝20°，则∠2的度数是（）A．30°B．40°C．50°D．60°2．小明把一副含45°，30°的直角三角板如图摆放，其中∠C＝∠F＝90°，∠A＝45°，∠D＝30°，则∠α+∠β等于（）A．180°B．210°C．360°D．270°3．如图，在△ABC中，∠B＝40°，∠A＝∠C，AF＝CD，AE＝CF，则∠EFD等于（）A．50°B．60°C．70°D．80°4．如图所示，有一池塘，要测池塘两端A、B的距离，可先在平地上取一个可以直接到达A 和B的点C，连结AC并延长到D，使CD＝CA．连结BC并延长到E，使CE＝CB，连结DE，那么量出DE的长就是A、B的距离．其中的依据是全等三角形的判定条件（）A．SSS B．SAS C．ASA D．AAS5．已知点P（a，3），Q（﹣2，b）关于x轴对称，则a+b的值为（）A．1B．−1C．5D．﹣56．下列计算正确的是（）A．a3+a3＝a6B．（3a﹣b）2＝9a2﹣b2C．a6b÷a2＝a4b D．（﹣ab3）2＝a2b3 7．分式中的a、b的值同时扩大到原来的10倍，则此分式的值（）A．是原来的20倍B．是原来的10倍C．是原来的D．不变8．下列式子：，，，，其中分式的共有（）A．2B．3C．4D．5二．填空题（共6小题）9．化简的结果是．10．代数式x2+4x+k是一个完全平方式，则k＝．11．等腰三角形一腰上的高与另一腰的夹角为36°，则该等腰三角形的底角的度数为．12．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝．13．一个n边形的每个内角都等于144°，则n＝．14．如图，工人师傅在安装木制门框时，为防止变形常常钉上两根木条，这样做的依据是．三．解答题（共6小题）15．如图是一个凹多边形，∠A＝90°，∠C＝106°，∠D＝116°，∠E＝100°；求∠1+∠2的值．16．如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F在AC上，BE ＝FC．求证：BD＝DF．17．如图，在△ABC中，AB＝AC，D为BC边上一点，∠B＝32°，∠BAD＝42°，求∠DAC的度数．18．因式分解（1）﹣2a3+12a2﹣18a（2）9a2（x﹣y）+4b2（y﹣x）19．计算：（﹣）﹣2+4×（﹣1）2019﹣|﹣23|+（π﹣5）020．化简：（﹣）÷．2022-2023学年人教新版八年级（上）数学寒假作业（四）一．选择题（共8小题）1．关于x的分式方程＝1的解为正数，则字母a的取值范围为（）A．a≥﹣1B．a＞﹣1C．a≤﹣1D．a＜﹣12．已知x+y﹣3＝0，则2y•2x的值是（）A．6B．﹣6C．D．83．下列四个图形中，轴对称图形有（）个．A．1B．2C．3D．44．如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于（）（4题）（5题）A．10B．7C．5D．45．如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论①AC＝AF，②∠FAB＝∠EAB，③EF＝BC，④∠EAB＝∠FAC，其中正确结论的个数是（）A．1个B．2个C．3个D．4个6．已知一个多边形的内角和是900°，则这个多边形是（）A．五边形B．六边形C．七边形D．八边形7．将一副直角三角尺如图放置，若∠AOD＝20°，则∠BOC的大小为（）A．140°B．160°C．170°D．150°8．如图，CE是△ABC的外角∠ACD的平分线，若∠B＝35°，∠ACE＝60°，则∠A＝（）A．35°B．95°C．85°D．75°二．填空题（共6小题）9．如图，点D在BC上，DE⊥AB于点E，DF⊥BC交AC于点F，BD＝CF，BE＝CD．若∠AFD＝145°，则∠EDF＝．10．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．11．如图所示，在△ABC中，DM、EN分别垂直平分AB和AC，交BC于D、E，若∠DAE ＝50°，则∠BAC＝度，若△ADE的周长为19cm，则BC＝cm．12．若a m＝6，a n＝2，则a m+2n的值为．13．若x2+kxy+49y2是一个完全平方式，则k＝．14．已知：，则＝．三．解答题（共6小题）15．先化简（x+3﹣）÷，再从0≤x≤4中选一个适合的整数代入求值．16．计算：（﹣1）2018﹣（π﹣3.14）0+（）﹣2．17．因式分解（1）﹣2a3+12a2﹣18a（2）9a2（x﹣y）+4b2（y﹣x）18．已知2a2+3a﹣6＝0．求代数式3a（2a+1）﹣（2a+1）（2a﹣1）的值．19．如图，在△ABC中，AC＜AB＜BC．（1）已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B．（2）以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ．若∠AQC ＝3∠B，求∠B的度数．20．如图，∠C＝∠E，AC＝AE，点D在BC边上，∠1＝∠2，AC和DE相交于点O．求证：△ABC≌△ADE．2022-2023学年人教新版八年级（上）数学寒假作业（五）一．选择题（共8小题）1．若一个多边形的每个外角都是72°，则这个多边形是（）A．四边形B．五边形C．六边形D．以上都有可能2．嘉嘉和淇淇到学校的直线距离分别是5km和3km，那么嘉嘉和淇淇的直线距离不可能是（）A．1km B．3km C．6km D．8km3．若一个正多边形的各个内角都是140°，则这个正多边形是（）A．正七边形B．正八边形C．正九边形D．正十边形4．下列各项长度的木棒首尾相接可以组成三角形的是（）A．1，2，3B．3，4，6C．2，3，5D．2，2，55．下列长度（单位：厘米）的三条线段，能组成三角形的是（）A．2，2，5B．4，3，8C．12，5，7D．3，4，56．下列各组数中，不可能成为一个三角形三边长的是（）A．3，7，11B．5，5，7C．3，4，5D．6，7，12 7．如图，在△ABC中，D，E，F分别是边AB，AC，BC的中点，G为线段EC的中点，下列四条线段中，是△ABC的中线的是（）A．线段DE B．线段BE C．线段EF D．线段FG8．如图，四根木条钉成一个四边形框架ABCD，要使框架稳固且不活动，至少还需要添加木条（）A．1根B．2根C．3根D．4根二．填空题（共6小题）9．已知一个多边形的内角和加上一个外角共2050°，这个多边形是边形，这个外角的度数是．10．如图，在五边形ABCDE中，∠A＝35°，去掉∠A后得到一个六边形BCDENM，则∠1+∠2的度数为．11．在△ABC中，∠A＝30°，∠B＝90°，则∠C＝度．12．如图，在正六边形ABCDEF中，延长AB，DC交于点O，则∠AOD的度数为．13．已知一个正多边形的外角为20°，则这个多边形的边数为．14．如图，工人师傅在安装木制门框时，为防止变形常常钉上两根木条，这样做的依据是．三．解答题（共6小题）15．如图是一个凹多边形，∠A＝90°，∠C＝106°，∠D＝116°，∠E＝100°；求∠1+∠2的值．16．如图，AD、BE分别是△ABC的高和角平分线，∠BAC＝86°，∠C＝58°，求∠AOB 的大小．17．如图，DE⊥AC于E，BF⊥AC于F，∠1+∠2＝180°，求证：∠AGF＝∠ABC．18．如图，△ABC中，AD是高，AE，BF是角平分线，它们相交于点O，∠CAB＝80°，∠C＝60°，求∠DAE和∠BOA的度数．19．已知一个多边形的内角和比外角和多900°，并且这个多边形各个内角的度数都相等．这个多边形的每个内角是多少度？20．已知一个正多边形的内角和比外角和的3倍多180°，求这个正多边形的边数和每个内角的度数．。
初二数学分式方程(1)作业纸和答案
小时多搬运 10kg，甲型机器人搬运 800kg 所用时间与乙型机器人搬运 600kg 所用时间相等．用
分式方程描述其中数量之间的相等关系。
（1）小华同学设乙型机器人每小时搬运 xkg 产品，可列方程为
．
（2）小惠同学设甲型机器人搬运 800kg 所用时间为 y 小时，可列方程为
．
7.解分式方程
(1) ﹣ ＝0
检验:当 x=2 时，
左边=右边=0 x＝﹣2 是原方程的解
左边=右边= x＝7 是原方程的解
左边=右边=1 x＝2 是原方程的解
二.能力提升 8.定义运算“※”：a※b=
，若 5※x=2，则 x 的值为 x=2.5 或 x=10 ．
A.1+（1－x）=x－2
B. 1－（1－x）=x－2
C. 1－（1－x）=1
D. 1+（1－x）=1
4. 方程 7 5 的解是________. x x4
5. 当 x=________时，分式 1 x 的值等于 1 .
5 x
2
6.某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品．甲型机器人比乙型机器人每
ax 4
(D)
A. 1
B. 3
C. －1
D. －3
3. 分式方程 1 － 1 x =1 的两边同乘以（x－2）,约去分母,得（ A ） x2 2x
A.1+（1－x）=x－2
B. 1－（1－x）=x－2
C. 1－（1－x）=1
D. 1+（1－x）=1
4. 方程 7 5 的解是 x=-14 x x4
5. 当 x=3 时，分式 1 x 的值等于 1 .
5 x
2
6.某危险品工厂采用甲型、乙型两种机器人代替人力搬运产品．甲型机器人比乙型机器人每
第一轮网课作业纸7.23八上数学作业纸(b)1-79(1) - 副本
文通中学八年级数学作业纸（B） No.81班级姓名学号成绩课题：线段、角的对称性（3）命题人：卞洪波审核人：鲍兆清一、填空题：1. 如图1，BD平分∠ABC,E为射线BD上的点,EF⊥AB于F,若EF=3,则点E到边BC的距离为。
2. 如图2，已知CD⊥AB,BE⊥AC,垂足为D、E，BE、CD交与点O，且AO平分∠BAC,那么图中全等三角形共有对。
3. 如图3，在△ABC中，∠C=900，AD平分∠BAC,D到AB的距离为12，BD∶BC=3∶5，则BC的长为。
图44. 如图4，已知点C是∠AOB平分线上一点，点P、Q分别在OA、OB上。
如果要得到OP=OQ，需要添加以下条件：①∠OCP=∠OCQ ②∠OPC=∠OQC ③PC=QC ④PQ⊥OC中的哪一个即可。
添加条件的可能为。
（填序号）5．（2014•四川遂宁）如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC=7，DE=2，AB=4，则AC长是（）A． 3 B． 4 C． 6 D． 5二、选择题：6.已知：在△ABC中，AD为∠BAC的角平分线，DE⊥AB，F为AC上一点，且∠DFA=1000，则（）A.DE>DF B.DE<DF C.DE=DF D.不能确定DE、DF的大小.7.下列说法中正确的有 ( ）①不在线段垂直平分线上的点，到线段两个端点的距离一定不相等②P是∠AOB平分线上的一点，C、D分别是OA、OB上的点，则PC=PD③角的平分线可以看成到角两边距离相等的点的集合④等腰三角形中，顶角的顶点一定在底边的垂直平分线上A.1个B.2个C. 3个D. 4个D EC AB 三、解答题：8. 利用网络线作图；（1）在BC 上找一点P ，使P 到AB 和AC 的距离相等； （2）在射线AP 上找一点Q ，使QB=QC 。
9.在课外活动中，小明发明了一个在直角三角形中画锐角 的平分线的方法，他的方法是：如图所示，在斜边AB 上取一点E ，使BE=BC ，过点E 作ED ⊥AB ，交AC 于D ，那么DB 就是∠CDE 的平分线，BD 就是∠ABC 的平分线，你认为对吗？为什么？10.已知：在ΔABC 中，D 是BC 上一点,DF ⊥BA 于F,DE ⊥AC 于E,且DE=DF 。
2019版八年级上册初二数学人教版全套课件作业本第十三章 第5课时画轴对称图形(2)
);
(3)△A₁B₁C₁的面积S=
.
作业本
解:(1)△A1B1C1如图所示; (2)A₁(0,﹣4);B₁(﹣2,﹣2); C₁(3,0); (3)S=5×4﹣ ×2×2﹣ ×3×4﹣ ×5×2 =20﹣2﹣6﹣5, =20﹣13, =7. 故答案为:(0,﹣4); (﹣2,﹣2); (3,0);7.
D.﹣2019
作业本
3.已知点A(a,5)与B(2,b)关于y轴对称,则 a+b= 3 .
作业本
4.若点P(﹣5,6)与点Q关于x轴对称,则点Q的坐标
为
(﹣5,.﹣6)
作业本
5.如图,在平面直角坐标系 中,A(﹣1,5),B(﹣1,0),C(﹣4,3). (1)求出△ABC的面积; (2)在图中作出△ABC关于y轴的对称图形△A₁B₁C₁; (3)写出点A₁,B₁,C₁的坐标.
作业本
解:(1)如图所示,A1(﹣4,1), B1(﹣3,4),C1(﹣1,2); (2)△ABC的面积=3×3﹣ ×1×3﹣ ×2×2﹣ ×1×3, =9﹣1.5﹣1.5﹣2, =9﹣5, =4.
谢谢！
作业本
7.如图,方格图中每个小正方形的边长为1,点A、B、 C都是格点. (1)画出△ABC关于直线MN对称的△A1B1C1; (2)写出AA1的长度.
作业本
解:(1)如图所示,△A1B1C1即为所求; (2)由图可得,AA1BC. (1)画出与△ABC关于x轴对称的图形,并写出各 顶点坐标; (2)直接写出△ABC的面积.
第十三章 轴对称
第5课时 画轴对称图形(2)
作业本
作业本
1.点M(1,2)关于y轴对称点的坐标为( ) A A.(﹣1,2) B.(﹣1,﹣2) C.(1,﹣2) D.(2,﹣1)
部编RJ人教版 初二八年级数学 上册第一学期秋季 精选寒假作业
八年级数学寒假作业(1)一、精心选一选⒈下列各组条件中,不能判定△ABC 与△DEF 全等的是 ( ) A. AB=DE ，∠B=∠E ，∠C=∠F B. AC=DF ，BC=DE ，BA=EF C. AB=EF ，∠A=∠E ，∠B=∠F D. ∠A=∠F ，∠B=∠E ，AC=EF⒉判定两个三角形全等必不可少的条件是 （ ） Ａ.至少有一边对应相等 B ．至少有一角对应相等 C ．至少有两边对应相等 D ．至少有两角对应相等⒊在△ABC 和△DEF 中，已知AB=DE ，∠A=∠D ，还需具备什么条件①AC=DF ；②BC=EF ；③∠B=∠E ；④∠C=∠F ，才能推出△ABC ≌△DEF ，其中符合条件有 （ ） A 、1个 B 、2个 C 、3个 D 、4个 二、细心填一填⒋ 如图1，AO 平分∠BAC ，AB=AC ，图中有__________________对三角形全等.⒌ 举例说明三角形稳定性在生活中的应用:_______________________________.⒍ 如图2，在△ABC 中，∠C=900，AD 是∠BAC 的平分线，交BC 于D ，BC=16，DC ：DB=3：5，则点D 到AB 的距离是___________. 三、用心做一做⒎如图,已知AD=AE,AC=AB,∠A=400, ∠B=350,求∠EOC 的度数图1 AC D OEBA图2B八年级数学寒假作业(2)一、精心选一选⒈下列说法中正确的是 ( ) Ａ.三个角对应相等的两个三角形全等. B ．面积相等的两个三角形全等.C ．全等三角形的面积相等.D ．两边和一角对应相等的两个三角形全等. ⒉在ΔABC 和ΔA ′B ′C ′中，AB=A ′B ′，∠B=∠B ′，补充一个条件后仍不一定能保证ΔABC 与ΔA ′B ′C ′全等，则补充的这个条件是 ( ) A ．BC=B ′C ′ B ．∠A=∠A ′ C ．AC=A ′C ′ D ．∠C=∠C ′⒊在△ABC 和ΔA ′B ′C ′中，AB= A ′B ′ ，∠A=∠A ′，∠C=∠C ′ ,可推出(1)∠B=∠B ′；(2)∠B 的平分线与∠B ′的平分线相等；(3)BC 边上的高与B ′C ′边上的高相等；(4) BC 边上的中线与B /C /边上的中线相等.其中正确的结论有 ( ) A. 1个 B. 2个 C. 3个 D. 4个 二、细心填一填⒋如图1： 在ΔABC 和ΔADC 中，下列三个论断：⑴AB=AD ，⑵∠BAC=∠DAC ，⑶BC=DC ，将其中两个论断作为条件，另一个论断作为结论，请你写出一个正确的推断：⒌如图2,在ΔABC 与ΔAED 中，AB=AE ，AC=AD ，请补充一个条件条件：____________(写一个即可)，使ΔABC ≌ΔAED.⒍如图3，在ΔABC 中，∠C=900，AC=BC ，AD 平分∠CAB ， 交BC 于D ，DE ⊥AB 于E ，且AB=6cm ，则ΔDEB 的周长为________. 三、用心做一做⒎如图，AC=BD ，AC ⊥AB ，DB ⊥CD ，则AB 与DC 相等吗？为什么？A图3图3B图1A DC⒏如图，ΔABC 中，BE 、CD 分别是AC 、AB 边上的高，BE 、CD 相交于点O ，若AO 平分∠BAC ，那么OB=OC 吗？为什么？八年级数学寒假作业(3)一、精心选一选⒈满足下列条件的两个等腰三角形，不能判定它们全等的是 ( ) A.两腰对应相等 B.一腰和顶角对应相等 C.一腰和底边对应相等 D.一腰与该腰上的中线对应相等⒉根据下列条件，能画出唯一的△ABC 的是 （ ） Ａ.AB=3，BC=4，AC=8 B ．AB =4，BC =3，∠A =300 C.∠A=600，∠B =450，AB =4 D ．∠C =900，AB =6⒊三角形的两条边的长分别为5和7，则第三边上中线的取值范围是 （ ） A.a<6B.a>1C.1<a<6D.1≤a ≤6二、细心填一填⒋如图1,已知AB ⊥BD 于B,ED ⊥BD 于D,AB=CD,BC=DE,则∠ACE=___________°.⒌如图2,已知AB ∥CF,E 为DF 的中点,若AB=9cm,CF=5cm,⒍如图3，在等腰△AOB 的腰OA 、OB 上截取OC=OD ，连结AD 、BC 交于点P ，下列结论：①△AOD ≌△BOC ；②△APC ≌△BPD ；③点P 在∠AOB 的平分线上；④AP=DP.其中正 确的有__________.(填序号) 三、用心做一做⒎如图，如果∠1=∠2，∠3=∠4，AC 、BD 相交于点O ，那么线段BD 与AC 有什么关系？为什C⒏如图，已知△ABC ，BE 、CF 为高，CP=AB ，BD=AC ，试判断AP 与AD 有什么关系？并说明你的理由.八年级数学寒假作业(4)一、精心选一选⒈在△ABC 与△A ′B ′C ′中，∠A+∠B=∠C ，∠B ′+∠C ′=∠A ′，且b －a=b ′－ c ′,b+a=b ′+c ′，则这两个三角形 （ ） A ．不一定全等 B ．不全等 C ．根据“SAS ”全等 D ．根据“ASA ”全等 ⒉下列图形中，一定全等的是 （ ） A ． 有一边相等的两个等腰三角形 B ．两个等边三角形 C ．有一个角是450，腰长都是3cm 的两个等腰三角形 D ．一个锐角和一条直角边对应相等的两个直角三角形⒊如图1，A 、B 、C 、D 在同一条直线上，AB=DC ，AE ∥DF ，在下列条件中，不能使 △AEC 与△DFB 全等的是A ．AE=DF B ．EC=FB C ．EC ∥BF D.∠E=∠F二、细心填一填⒋ 如图2，已知△ABC 中，∠C =900，点D 在AC 上，DE ⊥AB ，垂足为E ，且DC=DE ，∠CBD ：∠A=2：1，则∠A=______.图3PBCD 图2C⒌如图3，在不等边三角形△ABC 中，AQ=PQ ，PM ⊥AB ，PN ⊥AC ，PM=PN.①AN=AM ；②QP ∥AM ；③△BMP ≌△PNC.其中正确的是______________（填序号）．⒍如果两个等腰三角形_______________时，那么这两个等腰三角形全等.（只填一种能使结论成立的条件即可）. 三、用心做一做7.如图，点D 、E 分别是等边△ABC 的两边AB 、AC 上的点，且AD=CE ，BE 与CD 交于F ，求∠BFC 的度数.8.如图，在△ABC 、△AED 中，AB=AC ，AD=AE ，且∠CAB=∠DAE. ⑴问CE 与BD 有什么关系？为什么？⑵若将△AED 绕着点A 沿逆时针方向旋转，使D 、E 、B 在一条直线上，⑴的结论还成立吗？若成立，请说明理由.一、精心选一选1．(2011·泰安)下列等式不成立的是( )A ．m 2－16＝(m －4)(m ＋4)B ．m 2＋4m ＝m (m ＋4)C ．m 2－8m ＋16＝(m －4)2D ．m 2＋3m ＋9＝(m ＋3)2 2．(2011·无锡)分解因式2x 2－4x ＋2的最终结果是( )A ．2x (x －2)B ．2(x 2－2x ＋1)C ．2(x －1)2D ．(2x －2)2 3．(2011·济宁)把代数式 3x 3－6x 2y ＋3xy 2分解因式，结果正确的是( )A ．x (3x ＋y )(x －3y )B ．3x (x 2－2xy ＋y 2)C ．x (3x －y )2D ．3x (x －y )24．已知x 、y 满足等式2x ＋x 2＋x 2y 2＋2＝－2xy ，那么x ＋y 的值为( )A ．－1B ．0C ．2D ．1 5．(2011·台湾)下列四个多项式，哪一个是2x 2＋5x －3的因式？( )A ．2x －1B ．2x －3C ．x －1D ．x －3二、细心填一填6．(2011·绍兴)分解因式：x 2＋x ＝______________.7．(2011·枣庄)若m 2－n 2＝6，且m －n ＝2，则m ＋n ＝________. 8．(2011·威海)分解因式：16－8(x －y )＋(x －y )2＝______________.9．(2011·潍坊)分解因式：a 3＋a 2－a －1＝______________. 三、用心做一做10．(2011·湖州)因式分解：a 3－9a .11．(2011·宿迁)已知实数a 、b 满足ab ＝1，a ＋b ＝2，求代数式a 2b ＋ab 2的值．八年级数学寒假作业(6)一、精心选一选1．(2011年江苏盐城)已知a －b ＝1，则代数式2a －2b －3的值是( ) A ．－1 B ．1 C ．－5 D ．5 2．(2012年江苏无锡)分解因式(x －1)2－2(x －1)＋1的结果是( )A ．(x －1)(x －2)B ．x 2C ．(x ＋1)2D ．(x －2)2 3．(2012年山东济南)化简5(2x －3)＋4(3－2x )结果为( )A ．2x －3B ．2x ＋9C ．8x －3D ．18x －3二、细心填一填4．(2011年浙江杭州)当x ＝－7时，代数式(2x ＋5)(x ＋1)－(x －3)(x ＋1)的值为________． 5．(2012年江苏苏州)若a ＝2，a ＋b ＝3，则 a 2＋ab ＝______.6．已知⎩⎪⎨⎪⎧x ＋2y ＝4k ＋1，2x ＋y ＝k ＋2，且0<x ＋y <3，则k 的取值范围是 ______________.7．若买铅笔4支，日记本3本，圆珠笔2支，共需10元；若买铅笔9支，日记本7本，圆珠笔5支，共需25元，则购买铅笔、日记本、圆珠笔各一样共需______元．8．如右图, ∠1＋∠2＋∠3＋∠4＋∠5＋∠6＝________________. 三、用心做一做9.(2012年浙江丽水)已知A ＝2x ＋y ，B ＝2x －y ， 计算A 2－B 2的值．10．(2010年福建南安)已知y ＋2x ＝1，求代数式(y ＋1)2－(y 2－4x )的值．11.已知1x －1y ＝3，求代数式2x －14xy －2y x －2xy －y 的值．四、探索与创新 12. 已知a 1+b 1=61，b 1+c 1=91，a 1+c 1=151，求bcac ab abc++的值。
曹县博宇博雅中学初二数学作业纸3
曹县博宇博雅中学初二数学作业纸31、如图,已知: AD 是BC 上的中线 ,且DF=DE ． 求证:（1）△B ED ≌△CFD ．（2）BE ∥CF ．2、AE=AD ，AB=AC 。
求证：（1）DC=BE ；（2）CF=BF3、已知：AD 平分∠BAC ，AC=AB+BD ，AC=2DB 求证：∠B=2∠CCDB ACDFA4、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 的范围5、如图，已知∠1=∠2，∠3=∠4，求证：AB=CD6、如图，在四边形ABCD 中，E 是AC 上的一点，∠1=∠2，∠3=∠4，求证: ∠5=∠6．7、已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE.3421DCBAAADBC8、如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、 ∠BCD ，且点E 在AD 上。
求证：BC=AB+DC 。
9、如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =CF ．10、如图，OM 平分∠POQ ，MA ⊥OP ,MB ⊥OQ ，A 、B 为垂足，AB 交OM 于点N ．求证：∠OAB =∠OBAFE DC BA11、如图：在△ABC 中，BA=BC ，D 是AC 的中点。
求证：（1）∠ADB=∠BDC （2）BD ⊥AC 。
12、如图：AB=CD ，AE=DF ，CE=FB 。
求证：AF=DE 。
13、AB=AC ，DB=DC ，F 是AD 的延长线上的一点。
求证：BF=CFDCBAFEDC BAFDCBA。
初中八(上)数学国庆作业纸(1)
E DA宝应县画川初级中学八（上）数学国庆作业纸（1）班级________ 学号________ 姓名________1.等腰直角三角形三边长度之比为 （ ）A.1：1：2B. 1：1：2C. 1：2：3D.不确定2.若一个直角三角形的一条直角边长是7cm,另一条直角边比斜边短1cm,则斜边长为( )A.18 cmB.20 cmC.24 cmD.25 cm⒊一架2.5m 长的梯子斜靠在一竖直的墙上，这时梯脚距离墙角0.7m ，如果梯子的顶端沿墙下滑0.4m ，那么梯脚移动的距离是 （ ）A. 1.5mB. 0.9mC. 0.8mD. 0.5m4.下列说法不正确的是A.－0.064的立方根是－0.4;B.8的立方根是±2；C.立方根是5的数是125；D.271的立方根是31； 5.已知等腰三角形的一个外角等于100，则它的顶角是（ ）.（A ）80° （B ）20° （C ）80°或20° （D ）不能确定6.下列语句中正确的有（ ）句.①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③一个轴对称图形不一定只有一条对称轴；④两个轴对称图形的对应点一定在对称轴的两侧.（A ）1 （B ）2 （C ）3 （D ）47.下列语句错误的是（ ）.（A ）等腰三角形有一条对称轴 （B ）直线是轴对称图形（C ）任意等腰三角形只能有一条对称轴 （D ）直线的任意一条垂线都是它的对称轴8.如图，D 是ABC 中BC 边上一点，AB=AC=BD ，则∠1和∠2的关系是（ ）.（A ）∠1=2∠2 （B ）∠1+∠2=90° （C ）180°-∠1=3∠2 （D ）180°+∠2=3∠19.桌面上有A 、B 两球，若要将B 球射向桌面任意一边，使一次反弹后击中A 球，则如图所示8个点中，可以瞄准的点有（ ）个.（A ）1 （B ）2 （C ）4 （D ）611.如图，在锐角三角形ABC 中，AD ⊥BC ，AD=12， AC=13，BC=14. 则AB=_____.12.如图是一个育苗棚,棚宽a=6m,棚高b=2.5m,棚长d=10m,则覆盖在棚斜面上的塑料薄膜的面积为_____m 213.在高5m ，长13m的一段台阶上铺上地毯，台阶的剖面图如图所示，地毯的长度至少需要___________m ．14.⑴解方程：(x+1)2－169=0 ⑵4(x+1)2－9=0(3) 计算： 38-＋16；15. 如图，在△ABC 中，AB=AC=5，BC=4，AB 的垂直平分线DE 分别交AB 、AC 于点E 、D ．求△BCD的周长．∆AB C D (第11题)(第12题) 5m 第13题B AD C 16.甲、乙两人同时从同一地点匀速出发1h ，甲往东走了4km ，乙往南走了6km ．⑴这时甲、乙两人相距多少km ？⑵按这个速度，他们出发多少h 后相距13km ？17.如图，梯形ABCD 中，AD ∥BC ，∠A=90°，∠C=45°，BC=2AD ，CD=102，求这个梯形的面积．18.已知：如图，在△ABC 中，D 为边BC 上的一点，AB=13，AD=12，AC=15，BD=5.求△ABC 的面积.19.一张长方形纸片宽AB=8cm ，长BC=10cm.现将纸片折叠，使顶点D 落在BC 边上的点F 处(折痕为AE)，求EC 的长．20.如图，在直角三角形ABC 的斜边AB 上取两点D 、E ，使AD=AC ，BE=BC.当∠B 的度数变化时，试讨论∠DCE 如何变化？说明你的根据.命题人：汝夫恩 审核人：陈洪强AB C D A B C F E D。
数学人教版八年级上册全等三角形作业纸.1全等三角形作业纸
1.下列说法正确的是（ ）A ．全等三角形是指形状相同的两个三角形B ．全等三角形是面积相等的两个三角形C ．全等三角形的周长和面积分别相等D ．所有等边三角形都是全等三角形 2.两个三角形_______，就是全等三角形．3.全等三角形的性质是全等三角形的_______，全等三角形的________．4.记录两个全等三角形时,必须5.如图，∆ABC 与∆CDA 是全等三角形，则它的一组对应边是（ ）A ．AB ＝DC B ．AC ＝AC C ．CD ＝CB D ．AD ＝BC6.若∆MNP ≌∆NMQ 且MN ＝8cm ，NP ＝7cm ，PM ＝6cm ，则MQ 的长是（ ）A ．8cmB ．7cmC ．6cmD ．5cm7.如图所示，已知∆ADE ≌∆DBF ，DE ∥BF,DF ∥AE ，那么，这两个三角形的对应顶点为___ ____，对应边为_____ __，对应角为____ ____． 8.如图所示，在∆ABC 中,点A 、D 、C 、F 在同一条直线上，且∆FDE ≌∆CAB ，那么∠A=______，∠ACB ＝____，EF ∥________． 9.如图，△ABC ≌△ADE ， 若∠D=∠B ，∠C=∠AED ，则∠DAE= ，∠DAB= ．10．已知△ABC ≌△DEF ，且∠A=90°，AB=6，AC=8，BC=10，△DEF 中最大边长是 ，最大角是 度． 11. △ABE ≌△ACD ，AB 与AC ，AE 与AD 是对应边，∠A =40º，∠B =30º，求∠ADC 的大小。
12.已知ABC ∆≌∆DEF ，且∠A=52°，B ∠=31°，DE=10cm ，求∠F 的度数与AB 的长．13.如图所示，∆ABD ≌∆ACE ，求证：BE ＝CD ．D C BE AD CABE。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N
M A B C 初二（上）数学周测试题 08。
09。
06
班级________ 姓名________ 评价________
一、选择题
⒈图中的图形中是常见的安全标记，其中是轴对称图形的是 （ )
⒉下列图形中一定是轴对称图形的是 （ ）
A 、梯形
B 、直角三角形
C 、角
D 、平行四边形
⒊下列轴对称图形中，只有两条对称轴的图形是 （ ）
A ．
B ．
C ．
D ．
⒋下列说法不正确的是 （ ）
A.两个关于某直线对称的图形一定全等
B.对称图形的对称点一定在对称轴的两侧
C.两个轴对称的图形对应点的连线的垂直平分线是它们的对称轴
D.平面上两个全等的图形不一定关于某直线对称
二、填空题
5、右图是从镜中看到的一串数字，这串数字应为 .
6、线段的对称轴有__________条，是________________________________，
7、成轴对称的两个图形的对应线段___ ___、对应角__ __.
8、如果两个图形关于某直线对称，那么连结 的线段被 垂直平分. A
9、如图，在△ABC 中，AB 的垂直平分线DE
交BC
于点E ，交AB 于点D ，△ACE 的周长为11cm ， D
AB ＝4cm ，则△ABC 的周长为__________cm.
B E C
二、解答题
1．如图所示，画出△ABC 关于直线MN 的轴对称图形.
8题）
2、如图，在△ABC中，DE是边BC的垂直平分线，与边AB、BC交于点D、E，如果△ACD的周长为17cm，△ABC的周长是25cm，根据这些条件，你可以求出哪些线段的长？
A
D
B E C
3、以给定的两个圆、两个三角形、两条平行线为构件，请你尽可能多地构思出独特且有意义的轴对称图形，并写出一两句贴切、灰谐的解说词。
图中就是符合要流域的两个图形。
与同学比一比，谁构思的图形多而漂亮。