8-傅学怡、高颖等-杭州奥体博览城网球中心整体结构设计研究综述
大跨建筑可开启屋面技术要点浅析:杭州奥体博览城网球馆可开启屋面的设计

中图 分类号: U 3 T 21
( aa o aArn Z rg z e a. 1 8 年 .用 于澳 大利 亚 国家
网 球 中 心 ( t n l e ns C n r Nai a n i e t o T e. 1 8 年 ) , 日本 小 松 穹 顶 ( o t u 98 K ma s
至 此 大 跨 度 开 合 屋 盖 技 术 得 到 了 进 一步 的完 善 和发 展 ,世 界 上 对
其 前 景 和 建造 的 必 要 性逐 渐 看 好 。 之
后 ,世 界 上 相 继 建成 或 正 在 建设 的带 开 合屋 盖 的大 型 体 育场 有近 2 座 .面 0
近年来开合结 构建筑有 向大型化发
日本于 1 9 年建成 了跨度 1 6 91 3 m的阿瑞 卡 体 育场 ( r k le m ,用 于 网 A i e Coi u a s
屋 盖分为一个 或若干个 活动 单元 , 每个活动单 元沿着一定 的轨迹移动 .又
可细分 为:
球 及 其 它多 功能 用途 ) ,并 于 1 9 年 93
THESES 化 又
AN ANAL YSI S 文献标识码: A 文章编号: 483( 1) -146 10- 7 02 407- 0 5 2 0 ON THE ESSENTI AL TE CHNOL OGI S 可开启置面技术分析 E 1 .可开启屋面的概念简析 OFL ARGE— 开 合 屋 顶 ( t a t bl Re c a e ROo r f SP ANNI NG Srcue t tr )又称移 动开幕 ,是一种在短 u O PEN NABLE 时 间 内 ( 般 为 2 ~ 2 分 钟 )部 分 或 一 0 5 ROOF :DESI GN 全 部 屋 顶 可 以移 动 或 开 合 的结 构 形 式 , 它使建筑 物在屋顶 开启、关 闭和部 分开 OF THE 闭等状态 下都可 以使 用 ,是一种 动态建 OPEN NABLE 筑。 ROO F O F 1 61 9 年美 国建成 了用现 代 牵 引技 术驱动 的刚性开合结构 的匹兹堡 市民体 THE TENNI S 育场 ,跨度 为1 7 ,可 容纳 14 名观 2m .万 HAL L OF 众 的 圆形大 厅直 径1 5 2 m,由可 开 启的 OL YM PI CS AND 八瓣不锈 钢屋盖 组成 ,至今 仍具有开 拓 EXHI TI BI ON 性 的意义 。据 统计 .从2 世纪6 年代至 O 0 今 ,全 球 已建成2 0 座 开合结 构 的建 0余 CENTER N I 筑 .但绝 大多数属 于 中小型 建筑 ,主要 HANGZHOU
8-傅学怡、高颖等-杭州奥体博览城网球中心整体结构设计研究综述

2014 年
杭州奥体博览城网球中心整体结构设计研究综述
傅学怡,高颖、董全利、朱勇军、王涛、席向宇、曹禾
(CCDI 悉地国际设计顾问有限公司,北京 100013)
摘
要: 杭州奥体博览城网球中心的钢结构罩棚采用新颖的八个环状花瓣造型组成的可开启屋盖, 八片花瓣闭合时覆盖整
个场地。下部砼看台和功能用房结构采用框架-支撑-剪力墙结构,外轮廓平面为圆形,上部支承环状花瓣造型的可开启屋 盖钢结构罩棚。固定屋盖罩棚外边缘直径约 133 米,悬挑长度约 26m,罩棚圆形开口直径约达 60 米。罩棚结构最高点标 高 30 米。整个钢罩棚由 24 个单元花瓣旋转复制组成。固定屋盖上方设置 8 片大悬挑移动屋盖,移动屋盖采用平面旋转 45 度开启方式。造型为花瓣形,每榀设置一个固定转轴及三条围绕固定转轴同心旋转的轨道结构,其中两条轨道固定在 移动屋盖上,一条轨道固定在固定屋盖上,单片移动屋盖径向长度 45m,宽 25m,最不利闭合状态时,向圆心悬挑 30m。整 体钢结构罩棚采用悬挑空间管桁架结构受力体系。重点介绍本工程结构体系、结构构成、结构设计的关键技术难点及相应 的专项研究分析处理方法。 关键词: 网球中心;空间钢结构;可开启屋盖;大悬挑
图 10 钢罩棚支座构成 4
第二十三届全国高层建筑结构学术会议论文
2014 年
2.2 上部钢结构移动屋盖 固定屋盖上方设置 8 片花瓣形大悬挑移动屋盖,移动屋盖采用平面旋转 45 度开启方式。每榀设置一 个固定转轴及三条同心旋转轨道结构,其中两条轨道固定在移动屋盖上,一条轨道固定在固定屋盖上。 单 片移动屋盖径向长度 45,宽 25m,闭合状态向圆心悬挑 30m。
ห้องสมุดไป่ตู้
作者介绍:傅学怡(1964-),男,研究员,国家勘查设计大师
以结构之美擎起建筑之美——记建筑结构设计大师傅学怡

物质实体来表达、通过合理的技术手段来实现的。
建筑师要展示结构的力度和美感, 结构工程师则 充分了解建筑的想法,创造性地提出结构方案,把
结构的内在美和建筑的外在美统一起来, 把技术 升华为艺术,共同创造美好的建筑。
傅学怡正是这样一位把
技术升华 CCDI 悉地 国际(原中建国际设计顾问有
勘察设计行业人才交流平台开通
据中设协字 [2012]9 号文,“勘察设计行业人 才交流平台”于 2013 年 1 月 1 日正式开通。 该平 台由中国勘察设计协会主办, 北京建设信源资讯 有限公司提供技术支持。 平台主要面向全国勘察 设计企业和行业从业人员, 为他们提供人才交流
的服务平台, 人才数据将进行有效认证和实时的 数据更新,方便企业找到合适的人才,也为个人快 速找到实现自我价值的企业提供方便, 规范全国 勘察设计行业专业技术人员服务市场, 促进勘察 设计行业和专业技术人才职业的健康发展。 (宗和)
(上接第 2 页)大奖。 该项目荣获了国家科学技术进 步一等奖、国家设计金奖、全国优秀结构设计一等 奖、国际桥梁及结构工程协会杰出结构大奖等 6 项 国内外结构大奖。
多哈卡塔尔外交部大楼, 位于卡塔尔首都多 哈的新城中心,基地呈五边形,建筑主体为圆形塔 楼,44 层,高 231 m,总建筑面积 11 万 m2,顶部为 钢结构穹顶, 其空间螺旋网状交叉斜柱赋予了它 独特的结构魅力。 设计方案由法国著名设计师 John Novel 提出,结构形式为世界首例钢筋混凝土 交叉柱外网筒超高层建筑。 2006 年~2009 年,傅 学怡主持了该项目的设计、科研和施工工作。 接手 该工程后, 他发现原法国工程师标书设计存在重 大隐患。 因结构自重占建筑总重 70%以上,自重作 用下结构南北两侧斜柱轴力相差极大、内力畸形, 将导致两侧压缩变形差异较大, 结构顶点向南侧 移从 5 cm 开始,20 年后将达 30~40 cm, 且不可 逆转,很有可能成为另一个“比萨斜塔”。 在大量分 析研究基础上,他带领设计团队提出了改进措施, 设计采取北侧斜柱空心、 减小南北两侧斜柱压应 力水平差异,提高南侧斜柱配筋 2 项技术措施,减 小结构顶点侧移,满足正常使用,避免新比萨斜塔 出现。 通过试验验证,不仅巧妙地消除了结构安全
9-傅学怡、高颖等-杭州奥体博览城网球中心移动屋盖钢结构设计

杭州奥体博览城网球中心移动屋盖钢结构设计傅学怡,高颖、朱勇军、董全利、王涛、王文标(CCDI悉地国际设计顾问有限公司,北京 100013)摘要:本项目是一个八个花瓣旋转开启的可开启屋盖钢结构,下部为钢筋混凝土结构看台及功能用房,看台区上覆的钢结构罩棚为环状花瓣造型的可开启屋盖,该屋盖闭合时覆盖整个场地。
下部砼结构外轮廓平面为圆形,上部支承环状花瓣造型的可开启屋盖钢结构罩棚,该屋盖闭合时覆盖整个场地。
固定屋盖罩棚外边缘直径约133米,悬挑长度约26m,场地中心罩棚圆形开口直径约达60米,罩棚结构最高点标高30米。
固定屋盖钢罩棚由24个单元花瓣旋转复制组成。
固定屋盖上方设置8片大悬挑花瓣形移动屋盖,移动屋盖采用平面旋转45度开启方式。
每榀设置一个固定转轴及三条同心旋转轨道结构,其中两条轨道固定在移动屋盖上,一条轨道固定在固定屋盖上,单片移动屋盖径向长度45,宽25m,闭合状态向圆心悬挑30m。
钢结构罩棚采用悬挑空间管桁架结构受力体系。
重点介绍本工程移动屋盖钢结构设计的关键技术难点及相应的专项研究分析处理方法。
关键词: 网球中心;空间钢结构;可开启屋盖;大悬挑1 工程概况杭州奥体网球中心采用新颖的八个花瓣旋转开启的可开启屋盖结构,下部为钢筋混凝土结构看台及功能用房,看台区上覆的钢结构罩棚为环状花瓣造型的可开启屋盖,该屋盖闭合时覆盖整个场地。
固定屋盖罩棚外边缘直径约133米,悬挑长度约26m,场地中心罩棚圆形开口直径约达60米,整个钢罩棚由24个单元花瓣组成,每个单元采用了两组倒三角空间立体桁架构成,单元和单元之间公用上弦杆,并通过环桁架下弦系杆连接。
主桁架悬挑端根部高度为4.5m,端部为高度3m。
设置6道屋面环桁架,最端部的屋面环桁架为倒三角立体桁架,其余5道为平面片桁架,垂直于地面。
钢结构罩棚通过24组四管组合V型撑与顶部砼看台型钢柱连接,构成罩棚上支座;径向主桁架上下弦杆向墙面延伸,汇交至下部砼二层混凝土梁顶面,构成罩棚下支座。
奥体中心项目设计报告

奥体中心项目设计报告项目背景奥体中心项目位于城市的中心地带,占地面积约100,000平方米。
它将成为体育比赛、文化活动和娱乐表演的综合性场馆,为城市居民提供一个全方位的休闲娱乐场所。
设计目标本项目的设计目标是打造一个现代化、高效能的奥体中心,满足不同需求的人群。
我们希望通过充分利用场地空间、提供多功能设施和创新的设计理念,为用户提供一个卓越的体验。
设计方案建筑结构奥体中心采用现代化建筑结构,拥有多层楼和大面积玻璃幕墙,营造出轻盈、开放的空间感。
同时,建筑内部采用高强度钢结构和混凝土框架,保证建筑的稳定性和安全性。
多功能设施奥体中心内设有多个功能区域,包括体育比赛场地、文化活动区、娱乐表演场所和商业区域等。
每个区域都有独立的设施和场地,并且可以根据需求进行灵活调整。
体育比赛场地体育比赛场地是奥体中心的核心设施,包括室内篮球场、足球场和游泳馆等。
这些场地采用最先进的设备和技术,为运动员提供最佳的比赛场所。
同时,观众席位于场地周围,可以容纳数千人观赛。
文化活动区文化活动区包括音乐厅、剧院和展览馆等。
这些设施可以用于举办音乐会、话剧表演和艺术展览等各类文化活动。
设计上注重舒适性和音效效果,为观众提供良好的观赏体验。
娱乐表演场所娱乐表演场所是奥体中心的娱乐区域,包括演唱会、时装秀和晚会等节目。
这些场所通过合理的布局和灯光设计,创造出舒适的氛围和观赏效果,吸引更多观众的参与。
商业区域商业区域位于奥体中心的一层和二层,包括餐厅、商店和咖啡馆等。
这些设施为用户提供各类服务,满足他们在活动期间的需求。
设计上注重流线和空间利用效率,提高商业区域的运营效益。
设计理念本项目的设计理念是“融入自然、共融共创”。
我们将以绿色环保和可持续发展为基本原则,在建筑和设施设计中尽量减少对自然资源的消耗。
同时,我们也鼓励人与自然的融合,通过设计优美的室内外景观,为用户提供一个舒适、宜人的空间。
设计效果奥体中心项目的设计效果将达到以下几点:- 独特的外观和标志性建筑,成为城市的地标之一。
杭州奥体中心项目规划方案

杭州奥体中心项目规划方案项目介绍杭州奥体中心项目是浙江省的重点建设项目之一,位于杭州市萧山区金城路和秋涛路的交汇处,总占地面积约250公顷。
项目包括主体场馆、附属设施及配套设施等,并可容纳较多的观众数量。
该项目是为了配合2022年杭州亚运会而建设的。
规划设计总体规划杭州奥体中心项目的总体规划着眼于满足亚运会的需求,同时结合区域景观、交通、环境等特点,对场馆建筑、道路、人车分流、停车等方面进行规划设计。
总体规划分为空间布局和功能布局两部分,其中空间布局以场馆为重心,以道路自然轴线为界,中心为商务区,分为北、中、南三部分。
功能布局分为场馆、旅游配套、商业、休闲配套等四部分。
总体规划中,场馆建筑占比较大,有主体场馆、综合训练馆、游泳馆、田径场馆、网球中心、国际青年体育文化中心等。
建筑设计场馆建筑方面,主要有以下几个设计要点:1.设计风格:建筑设计风格简洁大方,同时融入了中国传统元素,如宫殿式建筑、檐口翘角、顶饰翘角等。
2.建筑功能:主体场馆是场馆建筑中的核心,建筑面积为14万平方米,可容纳8万人。
该场馆主要用于开闭幕式、会议、足球比赛、田径比赛、闭幕式等活动。
3.建筑造型:主体场馆的建筑造型类似于一个巨大的莲花,莲花的“花瓣”则代表着不同的座位区域。
整个建筑外观优美,富有流线感和立体感。
道路设计道路设计主要考虑场馆交通的便捷性,同时也要考虑配套设施和周边商业的发展。
具体设计措施如下:1.交通导向:规划了内环、外环、中轴路、宜环路等主要交通干道,交通导向明晰,方便观众到达各个场馆。
2.人车分流:在主体场馆周边设置非机动车道和步行道,以分流行人和车流量,从而减少拥堵和碰撞事故的发生。
环保设计环保设计主要采取以下措施,保证项目建设过程的环保和可持续发展:1.节约用能:场馆内部采用绿色节能的理念,强调对自然资源的节约使用。
在设计上,采用了高效的能源利用技术,如太阳能光伏技术、地源热泵系统等。
2.水资源的合理利用:场馆水资源采用人工湿地处理和雨水回收技术,将污水处理后用来浇灌植物,同时雨水回收后用于冲洗厕所,从而减少了自来水的使用量,节约了水资源。
2024年广东省深圳市中考二模数学试题(解析版)
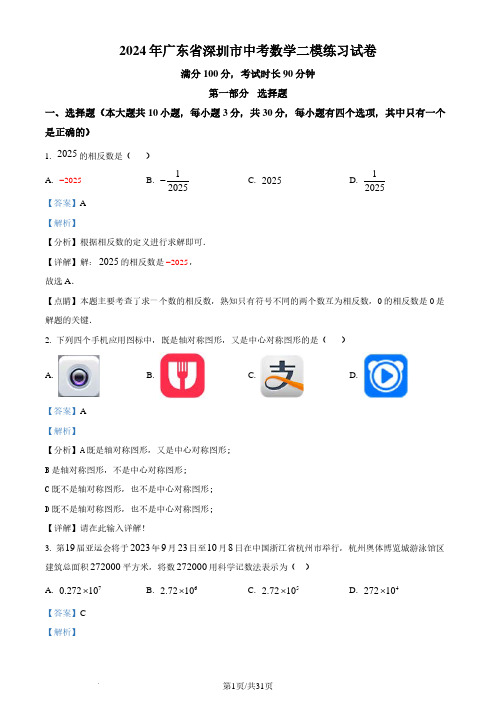
2024年广东省深圳市中考数学二模练习试卷满分100分,考试时长90分钟第一部分 选择题一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的)1. 2025的相反数是( )A. 2025−B. 12025−C. 2025D. 12025【答案】A【解析】【分析】根据相反数的定义进行求解即可.【详解】解:2025的相反数是2025−,故选A .【点睛】本题主要考查了求一个数的相反数,熟知只有符号不同的两个数互为相反数,0的相反数是0是解题的关键.2. 下列四个手机应用图标中,既是轴对称图形,又是中心对称图形的是( )A. B. C. D.【答案】A【解析】【分析】A 既是轴对称图形,又是中心对称图形;B 是轴对称图形,不是中心对称图形;C 既不是轴对称图形,也不是中心对称图形;D 既不是轴对称图形,也不是中心对称图形;【详解】请在此输入详解!3. 第19届亚运会将于2023年9月23日至10月8日在中国浙江省杭州市举行,杭州奥体博览城游泳馆区建筑总面积272000平方米,将数272000用科学记数法表示为( )A. 70.27210×B. 62.7210×C. 52.7210×D. 427210×【答案】C【解析】【分析】用科学记数法表示较大的数时,一般形式为10n a ×,其中110a ≤<,n 为整数,且n 比原来的整数位数少1,据此判断即可.【详解】解:5272000 2.7210=×,故选:C .【点睛】本题考查了科学记数法的表示方法,用科学记数法表示较大的数时,一般形式为10n a ×,其中110a ≤<,n 为整数,且n 比原来的整数位数少1,解题的关键是要正确确定a 和n 的值. 4. 如图.直线//a b ,将一块含有45°角的直角三角板的两个顶点放在直线a ,b 上,如果220∠°.那么1∠度数为( )A. 15°B. 20°C. 25°D. 30°【答案】C【解析】 【分析】根据平行线的性质即可得到结论.【详解】解:如图,过E 作EF ∥直线a ,则EF ∥直线b ,∴∠3=∠1,∠4=∠2=20°,∴∠1=45°-∠2=25°;故选:C .【点睛】本题考查了平行线的性质,熟记两直线平行内错角相等是解题的关键.5. 实数a ,b ,c 在数轴上的对应点的位置如图所示,下列结论正确的是( )A. a c b >>B. c a b a −>−C. 0a b +<D. 22ac bc <【答案】D【解析】【分析】根据a b c ,,对应的点在数轴上的位置,利用不等式的性质逐一判断即可.【详解】解:由数轴得:0a c b <<<,a b <,故选项A 不符合题意;∵c b <,∴c a b a −<−,故选项B 不符合题意; ∵a b <,a b <,∴0a b +>,故选项C 不符合题意;∵a b <,0c ≠,∴22ac bc <,故选项D 符合题意;故选:D .【点睛】本题考查的是实数与数轴,绝对值的概念,不等式的性质,掌握以上知识是解题的关键. 6. 如图,点O 是ABC 的外接圆的圆心,若80A ∠=°,则BOC ∠为( )A. 100°B. 160°C. 150°D. 130°【答案】B【解析】 【分析】根据圆周角定理即可得到BOC ∠的度数.【详解】解:∵点O 是ABC 的外接圆的圆心,∴A ∠、BOC ∠同对着 BC, ∵80A ∠=°,∴2160BOC A ∠°=∠=,故选:B .【点睛】此题考查了圆周角定理,熟练掌握圆周角定理是解答本题的关键,同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.7. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?其译文是 :今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱;现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x 斗,行酒为y 斗,则可列二元一次方程组为( )A. 2501030x y x y += +=B. -2501030x y x y = +=C. 2105030x y x y += +=D. 2103050x y x y += +=【答案】A【解析】 【分析】设醇酒为x 斗,行酒为y 斗,根据两种酒共用30钱,共2斗的等量关系列出方程组即可.【详解】设醇酒为x 斗,行酒为y 斗,由题意,则有2501030x y x y += +=, 故选A .【点睛】本题考查了二元一次方程组的应用,弄清题意,找准等量关系列出相应的方程是解题的关键. 8. 甲、乙两地相距120km ,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了30km /h ,并继续匀速行驶至乙地,汽车行驶的路程()km y 与时间()h x 之间的函数关系如图所示,该车到达乙地的时间是当天上午( )A. 10:35B. 10:40C. 10:45D. 10:50【答案】B【解析】 【分析】根据路程、速度和时间的关系结合函数图像解答即可.【详解】解:∵汽车匀速行驶了一半的路程后将速度提高了30km /h ,甲、乙两地相距120km ,∴汽车1小时行驶了60km ,汽车的速度为60km /h ,∴1小时以后的速度为90km /h , 汽车行驶完后面的路程需要的时间为60604090×=分钟, 故该车到达乙地的时间是当天上午10:40;故选:B .【点睛】本题考查了函数的图像,正确理解题意、灵活应用数形结合思想是解题的关键.9. 如图,在ABC 中,90C ∠=°,30B ∠=°,以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ,再分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ,连接AP 并延长交BC 于点D ,以下结论错误的是( )A. AD 是BAC ∠的平分线B. 60ADC ∠=°C. 点D 在线段AB 的垂直平分线上D. :1:2ABD ABC S S =△△【答案】D【解析】 【分析】本题考查的是角平分线的含义,线段的垂直平分线的判定,含30°的直角三角形的性质,A 根据作图的过程可以判定AD 是BAC ∠的角平分线;B 利用角平分线的定义可以推知30CAD ∠=°,则由直角三角形的性质来求ADC ∠的度数;C 利用等角对等边可以证得AD DB =,由线段垂直平分线的判定可以证明点D 在AB 的垂直平分线上;D 利用30°角所对的直角边是斜边的一半求出1122CD AD DB ==,进而可得:1:2DAC ABD S S =△△,则:2:3ABD ABC S S = . 【详解】解:根据作图方法可得AD 是BAC ∠的平分线,故A 正确,不符合题意;∵9030C B ∠=°∠=°,,∴60CAB ∠=°,∵AD 是BAC ∠的平分线,∴30DAC DAB ∠=∠=°,∴60ADC ∠=°,故B 正确,不符合题意;∵3030B DAB ∠=°∠=°,,∴AD DB =,∴点D 在AB 的垂直平分线上,故C 正确,不符合题意;∵30CAD ∠=°, ∴12CD AD =, ∵AD DB =, ∴12CD DB =, ∴:1:2DAC ABD S S =△△,则:2:3ABD ABC S S = ,故D 错误,符合题意,故选:D .10. 定义:在平面直角坐标系中,对于点()11,P x y ,当点()22,Q x y 满足()12122x x y y +=+时,称点()22,Q x y 是点()11,P x y “倍增点”,已知点()11,0P ,有下列结论:①点()13,8Q ,()22,2Q −−都是点1P 的“倍增点”;②若直线2y x =+上的点A 是点1P 的“倍增点”,则点A 的坐标为()2,4;③抛物线223y x x =−−上存在两个点是点1P 的“倍增点”;④若点B 是点1P 的“倍增点”,则1PB其中,正确结论的个数是( )A. 1B. 2C. 3D. 4 【答案】C【解析】【分析】①根据题目所给“倍增点”定义,分别验证12,Q Q 即可;②点(),2A a a +,根据“倍增点”定义,列出方程,求出a 的值,即可判断;③设抛物线上点()2,23D t t t −−是点1P 的“倍增点”,根据“倍增点”定义列出方程,再根据判别式得出该方程根的情况,即可判断;④设点(),B m n ,根据“倍增点”定义可得()21m n +=,根据两点间距离公式可得()22211PB m n =−+,把()21n m =+代入化简并配方,即可得出21PB 的最小值为165,即可判断. 【详解】解:①∵()11,0P ,()13,8Q ,的∴()()121282288103,x x y y +=+=++×==, ∴()12122x x y y +=+,则()13,8Q 是点1P 的“倍增点”;∵()11,0P ,()22,2Q −−,∴()()121222212202,x x y y +==−×−=−=−+, ∴()12122x x y y +=+,则()22,2Q −−是点1P 的“倍增点”;故①正确,符合题意;②设点(),2A a a +,∵点A 是点1P 的“倍增点”,∴()2102a a ×+=++,解得:0a =,∴()0,2A ,故②不正确,不符合题意;③设抛物线上点()2,23D t t t −−是点1P 的“倍增点”,∴()22123t t t +=−−,整理得:2450t t −−=, ∵()()24415360∆=−−××−=>,∴方程有两个不相等实根,即抛物线223y x x =−−上存在两个点是点1P 的“倍增点”;故③正确,符合题意;④设点(),B m n ,∵点B 是点1P 的“倍增点”,∴()21m n +=, ∵(),B m n ,()11,0P ,∴()22211PB m n =−+ ()()22121m m =−++2565m m =++2316555m =++, ∵50>,∴21PB 的最小值为165,∴1PB = 故④正确,符合题意;综上:正确的有①③④,共3个.故选:C .【点睛】本题主要考查了新定义,解一元一次方程,一元二次方程根的判别式,两点间的距离公式,解题的关键是正确理解题目所给“倍增点”定义,根据定义列出方程求解.第二部分 非选择题二、填空题(本大题共5小题,每小题3分,共15分)11. 若226m n −=−,且m ﹣n =﹣3,则m +n =_____.【答案】2【解析】【详解】解:∵()()226m n m n m n −=+−=−,m ﹣n =﹣3, ∴﹣3(m +n )=﹣6,∴m +n =2,故答案为:2【点睛】本题考查代数式求值,解题的关键是熟练运用平方差公式,本题属于基础题型.12. 一只不透明的袋中装有2个白球和n 个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到白球的概率为14,那么黑球的个数是______. 【答案】6【解析】【分析】根据概率公式建立分式方程求解即可【详解】∵袋子中装有2个白球和n 个黑球,摸出白球的概率为14,∴22n+=14,解得n=6,经检验n=6是原方程的根,故答案为:6【点睛】本题考查了概率公式,根据概率,运用公式建立起分式方程是解题的关键.13. 如图,正六边形ABCDEF的边长为2,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为______.【答案】43π##43π【解析】【分析】延长F A交⊙A于G,如图所示:根据六边形ABCDEF是正六边形,AB=2,利用外角和求得∠GAB=360606°=°,再求出正六边形内角∠F AB=180°-∠GAB=180°-60°=120°,利用扇形面积公式代入数值计算即可.【详解】解:延长F A交⊙A于G,如图所示:∵六边形ABCDEF是正六边形,AB=2,∴∠GAB=360606°=°,∠F AB=180°-∠GAB=180°-60°=120°,∴2120443603603 FABn rSπππ××===扇形,故答案为43π. 【点睛】本题主要考查扇形面积计算及正多边形的性质,熟练掌握扇形面积计算及正多边形的性质是解题的关键.14. 如图,在矩形OABC 和正方形CDEF 中,点A 在y 轴正半轴上,点C ,F 均在x 轴正半轴上,点D 在边BC 上,2BC CD =,3AB =.若点B ,E 在同一个反比例函数的图象上,则这个反比例函数的表达式是__________.【答案】18y x= 【解析】【分析】设正方形CDEF 的边长为m ,根据2BC CD =,3AB =,得到()3,2B m ,根据矩形对边相等得到3OC =,推出()3,E m m +,根据点B ,E 在同一个反比例函数的图象上,得到()323m m m ×=+,得到3m =,推出18y x=. 【详解】解:∵四边形OABC∴3OC AB ==,设正方形CDEF 的边长为m ,∴CD CF EF m ===,∵2BC CD =,∴2BC m =,∴()3,2B m ,()3,E m m +,设反比例函数表达式为k y x=, ∴()323m m m ×=+,解得3m =或0m =(不合题意,舍去), ∴()3,6B ,的∴3618=×=k , ∴这个反比例函数的表达式是18y x =, 故答案为:18y x=.【点睛】本题主要考查了反比例函数,解决问题的关键是熟练掌握矩形性质,正方形性质,反比例函数性质,k 的几何意义.15. 如图,在矩形ABCD 中,E 是AB 的中点,过点E 作ED 的垂线交BC 于点F ,对角线AC 分别交DE ,DF 于点G ,H ,当DH AC ⊥时,则GH EF的值为______.【解析】【分析】设AD a =,AB b =,根据矩形性质和勾股定理可得AC =,再证得ADE BEF ∽,可得AD AE BE BF=,24b BF a =,进而可得24b CF a a =−,再由tan tan CDF CAD ∠=∠,可得CF CD CD AD =,得出2b CF a =,联立得224b b a a a −=,求得a =,再证得DGH DFE △∽△,即可求得答案. 【详解】解: 四边形ABCD 是矩形,设AD a =,AB b =,90BAD B ADC ∴∠=∠=∠=°,AD BC a ==,AB CD b ==,AC ∴==,EF DE ⊥ ,90DEF ∴∠=°,90ADE AED AED BEF ∴∠+∠=∠+∠=°,ADE BEF ∠∠∴=,ADE BEF ∴ ∽, ∴AD AE BE BF=, E 是AB 的中点, 1122AE BE AB b ∴===, 24b BF a∴=, 24b CF BC BF a a∴=−=−, DH AC ⊥ ,90ADH CAD ∴∠+∠=°,90ADH CDF ∠+∠=° ,CDF CAD ∴∠=∠,tan tan CDF CAD ∴∠=∠, ∴CF CD CD AD=,即CF b b a =, 2b CF a∴=, 224b b a a a∴−=,a ∴, 在Rt ADE △中,DE , DH AC AD CD ⋅=⋅ ,AD CD DH AC ⋅∴==, 90DHG DEF ∠=∠=° ,GDH FDE ∠=∠,DGH DFE ∴△∽△,∴GH DH EF DE ==. 【点睛】本题考查了矩形的性质,相似三角形的性质与判定,直角三角形的性质,勾股定理等知识的综合运用,熟练掌握相似三角形的判定与性质是解题的关键.三、解答题(本题共7小题,共55分,解答应写出文字说明、证明过程或演算步骤.) 16. 计算:(1)()2014cos3032π− −+°−−− (2)()()()332a a a a +−−−.【答案】(1)3(2)29a −【解析】【分析】本题考查含特殊角三角函数值的混合运算和整式的乘法.(1)先计算负指数幂,零指数幂,特殊角的三角函数值和二次根式,再进行加减计算;(2)根据平方差公式和单项式乘多项式法则计算,再合并同类项即可.【小问1详解】解: ()2014cos3032π− −+°−−441=+−41=+−−3=【小问2详解】()()()332a a a a +−−−2292a a a −−+29=−a17. 某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A ,B ,C ,D 表示,并将测试结果绘制成如下两幅不完整的统计图.请根据统计图中信息解答以下问题;(1)本次抽取的学生共有_______人,扇形统计图中A 所对应扇形的圆心角是______°,并把条形统计图补充完整;(2)依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,则抽取的这部分学生书写成绩的众数是_______分,中位数是_______分,平均数是_______分;(3)若该校共有学生2800人,请估计一下,书写能力等级达到优秀的学生大约有_____人:(4)A 等级的4名学生中有3名女生和1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.【答案】(1)40;36;见解析(2)70;70;66.5(3)280 (4)12【解析】【分析】(1)由C 等级人数及其所占百分比可得总人数,用360°乘以A 等级人数所占比例即可得; (2)由中位数,众数,平均数的定义结合数据求解即可;(3)利用总人数乘以样本中A 等级人数所占比例即可得;(4)列表或画树状图得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率.【小问1详解】本次抽取的学生人数是1640%40÷=(人), 扇形统计图中A 所对应扇形圆心角的度数是43603640°×=°, 故答案为40人、36°;B 等级人数为()40416146−++=(人),的补全条形图如下:【小问2详解】由条形统计图可知众数为:70由A 、B 、C 的人数相加得:4+6+16=26>20,所以中位数为:70平均数:4906801670145066.540×+×+×+×= 【小问3详解】 等级达到优秀的人数大约有4280028040×=(人); 【小问4详解】画树状图为:∵共有12种等可能情况,1男1女有6种情况,∴被选中的2人恰好是1男1女的概率为12.【点睛】本题考查了扇形统计图,条形统计图,中位数,众数,平均数,树状图等知识点,解题时注意:概率=所求情况数与总情况数之比.18. “母亲节”来临之际,某花店打算使用不超过30000元的进货资金购进百合与康乃馨两种鲜花共1200束进行销售.百合与康乃馨的进货价格分别为每束30元、18元,百合每束的售价是康乃馨每束售价的1.6倍,若消费者用3200元购买百合的数量比用2400元购买康乃馨的数量少10束.(1)求百合与康乃馨两种鲜花的售价分别为每束多少元;(2)花店为了让利给消费者,决定把百合售价每束降低4元,康乃馨的售价每束降低2元.求花店应如何进货才能获得最大利润.(假设购进的两种鲜花全部销售完)为的【答案】(1)康乃馨的售价为每束40元,百合的售价为每束64元;(2)购进百合700束,购进康乃馨500束.【解析】【分析】本题考查了分式方程,一次函数的应用,解题的关键是读懂题意,列出方程和函数关系式. (1)设康乃馨的售价为每束x 元,根据消费者用3200元购买百合的数量比用2400元购买康乃馨的数量少10束得:32002400101.6x x+=,解方程并检验可得答案; (2)设购进百合m 束,根据使用不超过30000元的进货资金购进百合与康乃馨两种鲜花,有()3018120030000m m +−≤,700m ≤,设花店获得利润为w 元,可得:()()()644304021812001024000w m m m =−−+−−−=+,再根据一次函数性质可得答案;【小问1详解】设康乃馨的售价为每束x 元,则百合的售价为每束1.6x 元; 根据题意得:32002400101.6x x+=, 解得:40x =,经检验,40x =是原方程的解,∴1.6 1.64064x =×=,答:康乃馨的售价为每束40元,百合的售价为每束64元;【小问2详解】设购进百合m 束,则购进康乃馨()1200−m 束,∵使用不超过30000元的进货资金购进百合与康乃馨两种鲜花,∴()3018120030000m m +−≤,解得700m ≤,设花店获得利润为w 元,根据题意得:()()()644304021812001024000w m m m =−−+−−−=+,∵100>,∴w 随m 的增大而增大,∴当700m =时,w 取最大值107002400031000×+=(元), 此时12001200700500m −=−=,答:购进百合700束,购进康乃馨500束.19. 如图1为放置在水平桌面l 上的台灯,底座的高AB 为5cm ,长度均为20cm 的连杆BC ,CD 与AB 始终在同一平面上.(1)转动连杆BC ,CD ,使BCD ∠成平角,150ABC ∠=°,如图2,求连杆端点D 离桌面l 的高度DE .(2)将(1)中的连杆CD 再绕点C 逆时针旋转,使165BCD ∠°=,此时连杆端点D 离桌面l 的高度是增加还是减少?增加或减少了多少?(精确到0.1cm 1.41≈ 1.73≈)【答案】(1)39.6cm(2)减少了3.2cm【解析】【分析】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题. (1)如图2中,作BO DE ⊥于O .解直角三角形求出OD 即可解决问题.(2)作DF ⊥l 于F ,CP DF ⊥P ,BG DF ⊥于G ,CH BG ⊥于H .则四边形PCHG 是矩形,求出DF ,再求出DF DE −即可解决问题.【小问1详解】如图2中,作BO DE ⊥于O .∵90OEA BOE BAE ∠=∠=∠=°,∴四边形ABOE 是矩形,∴90OBA ∠=°,∴1509060DBO °−°∠==°,∴)sin 60cm ODBD =⋅°=,∴()539.6cm DE OD OE OD AB =+=+=+≈.【小问2详解】作DF ⊥l 于F ,CP DF ⊥于P ,BG DF ⊥于G ,CH BG ⊥于H .则四边形PCHG 是矩形,∵6090CBH CHB ∠=°∠=°,,∴30BCH ∠=°,∵165BCD ∠=°,∴45DCP ∠=°, )sin 60cm CH BC ∴=⋅°=,)sin 45cm DPCD =⋅°=, ∴DF DP PG GF DP CH AB =++=++()()5cm =++,∴下降高度:55DE DF −=+−−− ()3.2cm =−≈.20. 如图,在ABC 中,90C ∠=°,O 是AB 上一点,以OA 为半径的O 与BC 相切于点D ,与AB 相交于点E .(1)求证:AD 是BAC ∠的平分线;(2)若2BE =,4BD =,求AE 的长.【答案】(1)见解析 (2)6【解析】【分析】(1)根据切线的性质得OD BC ⊥,再由90C ∠=°,得OD AC ∥,由平行线的性质得ODA DAC ∠=∠,又因为等腰三角形得ODA OAD ∠=∠,等量代换即可得证;(2)在Rt BOD 中222BD OD BO +=,由勾股定理即可求半径.【小问1详解】证明:连接OD ;∵O 与BC 相切于点D∴OD BC ⊥∴90ODB ∠=°∵90C ∠=°,∴ODB C ∠=∠∴OD AC ∥∴ODA DAC ∠=∠∵OD OA =∴ODA OAD ∠=∠∴OAD DAC ∠=∠∴AD 是BAC ∠的平分线;【小问2详解】解:∵90C ∠=°∴在Rt BOD 中222BD OD BO +=;∵2BE =,4BD =,设圆的半径为r ,∴()22242r r +=+解得3r =:,∴圆的半径为3∴6AE =.【点睛】本题考查了切线的性质、角平分线的性质、勾股定理,熟悉角平分线的定义与性质是解决本题的关键.21. 如图,BC 是O 的直径,点A 在O 上,OD AC ⊥于点G ,交O 于点D ,过点D 作EF AB ⊥,分别交BA ,BC 的延长线于点E ,F .(1)求证:EF 是O 的切线;(2)若2AE =,4tan 3B =,求O 的半径. 【答案】(1)见解析 (2)5【解析】【分析】(1)由BC 是O 的直径,点A 在O 上,可得90BAC ∠=°,证明EF AC ∥,则OD EF ⊥,进而结论得证;(2)证明四边形AGDE 是矩形,则2DG AE ==,由OD AB ∥,可得tan tan COG B ∠=∠,即43CG OG =,设4CG a =,则3OG a =,勾股定理得,5OC a =,由OG DG OD +=,可得325a a +=,解得1a =,则5OC =,进而可得结果.【小问1详解】证明:∵BC 是O 的直径,点A 在O 上,∴90BAC ∠=°,即AC AB ⊥,∵EF AB ⊥,∴EF AC ∥,∵OD AC ⊥,∴OD EF ⊥,又∵OD 是半径,∴EF 是O 的切线;【小问2详解】解:∵90BAC ∠=°,EF AB ⊥,OD EF ⊥, ∴四边形AGDE 是矩形, ∴2DG AE ==,∵OD AC ⊥,AC AB ⊥, ∴OD AB ∥, ∴COG B ∠=∠, ∴tan tan COG B ∠=∠,即43CG OG =, 设4CG a =,则3OG a =,由勾股定理得,5OC a =,∵OG DG OD +=, ∴325a a +=,解得1a =, ∴5OC =, ∴O 的半径为5.【点睛】本题考查了切线的判定,平行线的判定与性质,直径所对的圆周角为直角,勾股定理,正切,矩形的判定与性质等知识.解题的关键在于对知识的熟练掌握与灵活运用.22. (1)【探究发现】如图①所示,在正方形ABCD 中,E 为AD 边上一点,将AEB △沿BE 翻折到BEF △处,延长EF 交CD 边于G 点.求证:BFG BCG △≌△(2)【类比迁移】如图②,在矩形ABCD 中,E 为AD 边上一点,且8,6,AD AB ==将AEB △沿BE 翻折到BEF △处,延长EF 交BC 边于点,G 延长BF 交CD 边于点,H 且,FH CH =求AE 的长.(3)【拓展应用】如图③,在菱形ABCD 中,6AB =,E 为CD 边上的三等分点,60,D ∠=°将ADE 沿AE 翻折得到AFE △,直线EF 交BC 于点,P 求CP 的长.【答案】(1)见解析;(2)92;()CP 的长为32或65【解析】【分析】(1)根据将AEB ∆沿BE 翻折到∆BEF 处,四边形ABCD 是正方形,得AB BF =,90BFE A ∠=∠=°,即得90BFG C ∠=°=∠,可证()Rt BFG Rt BCG HL ≌;(2)延长BH ,AD 交于Q ,设FH HC x ==,在Rt BCH 中,有2228(6)x x +=+,得73x =,113DH DC HC =−=,由BFG BCH ∆∆∽,得6778633BG FG=+,254BG =,74FG =,而//EQ GB ,//DQ CB ,可得BC CH DQ DH =,即783763DQ =−,887DQ =,设AE EF m ==,则8DE m =−,因EQ EF BG FG =,有144725744m m −=,即解得AE 的长为92;(3)分两种情况:(Ⅰ)当123DE DC ==时,延长FE 交AD 于Q ,过Q 作QH CD ⊥于H ,设DQ x =,QE y =,则6AQ x =−,2CP x =,由AE 是AQF ∆的角平分线,有662x y−=①,在Rt ΔHQE中,2221(1))2x y −+=②,可解得34x =,322CPx ==; (Ⅱ)当123CE DC ==时,延长FE 交AD 延长线于Q ′,过D 作DN AB ⊥交BA 延长线于N ,同理解得125x =,65CP =.【详解】证明:(1) 将AEB ∆沿BE 翻折到∆BEF 处,四边形ABCD 是正方形,AB BF ∴=,90BFE A ∠=∠=°, 90BFG C ∴∠=°=∠,AB BC BF == ,BG BG =,()Rt BFG Rt BCG HL ∴ ≌;(2)解:延长BH ,AD 交于Q ,如图:设FH HC x ==,在Rt BCH 中,222BC CH BH +=,2228(6)x x ∴+=+,解得73x =, 113DH DC HC ∴=−=, 90BFG BCH ∠=∠=° ,HBC FBG ∠=∠,BFG BCH ∴∆∆∽,∴BF BG FG BC BH HC==,即6778633BG FG =+,254BG ∴=,74FG =,//EQ GB ,//DQ CB ,EFQ GFB ∴∆∆∽,DHQ CHB ∆∆∽,∴BC CH DQ DH =,即783763DQ =−, 887DQ ∴=,设AE EF m ==,则8DE m =−, 88144877EQ DE DQ m m ∴=+=−+=−, EFQ GFB ∆∆ ∽,∴EQ EF BG FG=,即144725744m m−=, 解得92m =,AE ∴的长为92;(3)(Ⅰ)当123DE DC ==时,延长FE 交AD 于Q ,过Q 作QH CD ⊥于H ,如图:设DQ x =,QE y =,则6AQ x =−, //CP DQ ,CPE QDE ∴∆∆∽,∴2CP CEDQ DE ==, 2CP x ∴=,ADE ∆ 沿AE 翻折得到AFE ∆,2EF DE ∴==,6AF AD ==,QAE FAE ∠=∠, AE ∴是AQF ∆的角平分线,∴AQ QEAF EF=,即662x y −=①, 60D ∠=° ,1122DH DQ x ∴==,122HE DE DH x =−=−,HQx =, 在Rt HQE △中,222HE HQ EQ +=,2221(1))2x y ∴−+=②, 联立①②可解得34x =, 322CP x ∴==; (Ⅱ)当123CE DC ==时,延长FE 交AD 延长线于Q ′,过D 作DN AB ⊥交BA 延长线于N ,如图:同理Q AE EAF ′∠=∠, ∴AQ Q EAF EF ′′=,即664x y +=,由222HQ HD Q D ′′+=得:2221)(4)2x y ++=, 可解得125x =, 1625CP x ∴==, 综上所述,CP 的长为32或65.【点睛】本题考查四边形的综合应用,涉及全等三角形的判定,相似三角形的判定与性质,三角形角平分线的性质,勾股定理及应用等知识,解题的关键是方程思想的应用.23. 如图,在平面直角坐标系中,经过点()4,0A 的直线AB 与y 轴交于点()0,4B .经过原点O 的抛物线2y x bx c =−++交直线AB 于点A ,C ,抛物线的顶点为D .(1)求抛物线2y x bx c =−++的表达式;(2)M 是线段AB 上一点,N 是抛物线上一点,当MN y ∥轴且2MN =时,求点M 的坐标;(3)P 是抛物线上一动点,Q 是平面直角坐标系内一点.是否存在以点A ,C ,P ,Q 为顶点的四边形是矩形?若存在,直接写出点Q 的坐标;若不存在,请说明理由. 【答案】(1)24y x x =−+(2)或()2,2或()3,1(3)存在,()5,1或()4,2−−或或【解析】【分析】(1)利用待定系数法求出抛物线的解析式;(2)求出直线AB 的表达式为4y x =−+,设(),4M t t −+,()2,4N t t t −+,分当M 在N 点上方时,()2244542MN t t t t t =−+−−+=−+=.和当M 在N 点下方时,()2244542MN t t t t t =−+−−+=−+−=,即可求出M 的坐标;(3)画出图形,分AC 是四边形的边和AC 是四边形的对角线,进行讨论,利用勾股定理、相似三角形的判定与性质、函数图像的交点、平移等知识点进行解答即可得出答案. 【小问1详解】解:∵抛物线2y x bx c =−++过点()4,0A ,()0,0O∴16400.b c c −++= = ,解得40b c = =,∴抛物线的表达式为24y x x =−+. 【小问2详解】设直线AB 的解析式为:y kx b =+′, ∵直线AB 经过()4,0A ,()0,4B ,∴404k b b +′=′= ,∴14k b =− ′=, ∴直线AB 的表达式为4y x =−+.∵MN y ∥轴,可设(),4M t t −+,()2,4N t t t −+,其中04t ≤≤.当M 在N 点上方时,()2244542MN t t t t t =−+−−+=−+=.解得1t =,2t =(舍去).∴1M . 当M 在N 点下方时, ()2244542MN t t t t t =−+−−+=−+−=.解得32t =,43t =. ∴()22,2M ,()33,1M .综上所述,满足条件的点M 的坐标有三个,()2,2,()3,1.【小问3详解】存在.满足条件的点Q 的坐标有4个.()5,1,()4,2−−,,. 理由如下:①如图,若AC 是四边形的边.当2x =时,242y =−+= ∴拋物线的对称轴与直线AB 相交于点()2,2R . 过点C ,A 分别作直线AB 的垂线交抛物线于点1P ,2P , ∵()1,3C ,()2,4D ,∴CD =,CR =2RD =.∵2222+=,∴222CD CR DR +=. ∴90RCD ∠=°. ∴点1P 与点D 重合.当1111CP AQ CP AQ =∥,时,四边形11ACPQ 是矩形. ∵()1,3C 向右平移1个单位,向上平移1个单位得到()12,4P . ∴()4,0A 向右平移1个单位,向上平移1个单位得到()15,1Q . 此时直线1PC 的解析式为2y x =+. ∵直线2P A 与1PC 平行且过点()4,0A , ∴直线2P A 的解析式为4y x =−.∵点2P 是直线4y x =−与拋物线24y x x =−+的交点, ∴244x x x −+=−.解得11x =−,24x =(舍去). ∴()21,5P −−.当2222AC P Q AC P Q ,∥=时,四边形22ACQ P 是矩形. ∵()4,0A 向左平移3个单位,向上平移3个单位得到()1,3C . ∴()21,5P −−向左平移3个单位,向上平移3个单位得到()24,2Q −−. ②如图,若AC 是四边形的对角线,当390APC ∠=°时.过点3P 作3P H x ⊥轴,垂足为H ,过点C 作3CK P H ⊥,垂足为K . 可得3390P KC AHP ∠=∠=°,33PCK AP H ∠=∠. ∴33PCK AP H ∽△△. ∴33P K AHCK P H=.∴2243414t t t t t t −+−−=−−+. ∵点P 不与点A ,C 重合, ∴1t ≠和4t ≠. ∴2310t t −+=.∴3,4t =.∴如图,满足条件的点P 有两个.即3P ,4P .当3333PC AQ PC AQ ∥=,时,四边形33APCQ是矩形.∵3P ()1,3C .∴()4,0A 3Q . 当4444P C AQ P C AQ ∥=,时,四边形44AP CQ 是矩形.∵4P 个单位得到()1,3C .∴()4,0A 个单位得到4Q .综上,满足条件的点Q 的坐标为()5,1或()4,2−−或或. 【点睛】本题主要考查的是二次函数的综合应用,本题主要涉及了待定系数法求函数的解析式、勾股定理,矩形的性质,相似三角形的判定与性质,点的平移等知识,根据题意画出符合条件的图形、进行分类讨论是解题的关键.第31页/共31页。
奥体博览中心主体育场、体育馆和游泳馆配套工程(水源热泵取水工程)项目施工组织设计

十一、投标文件技术部分格式(封面)工程名称:杭州奥体博览中心主体育场、体育馆和游泳馆配套工程(水源热泵取水工程)项目投标文件内容:投标文件技术部分格式投标人:(盖章)法定代表人或委托代理人:(签字或盖章)日期:2015 年6 月30 日目录一、施工组织设计二、项目管理班子配备情况三、项目拟分包情况四、替代方案和报价(如招标人允许提交时由招标人列入此项要求)五、要求其它资料一、施工组织设计杭州奥体博览中心主体育场、体育馆和游泳馆配套工程(水源热泵取水工程)项目招标编号:2015-022(公开招标)施工组织设计编制单位:杭州广正建设工程有限公司编制日期:2015年6月30日目录(一)编制说明(二)施工方法(三)工程投入的施工机械设备情况、主要施工机械进场计划(四)主要劳动力使用计划(五)确保工程质量的技术组织措施(六) 确保安全生产的技术组织措施(七)确保文明施工的技术组织措施(八)确保工期的技术组织措施(九)施工总平面布置设计(十)高温、冬、雨、汛期施工方案附表:表1拟投入的主要施工机械设备表表2劳动力计划表表3计划开、竣工日期和施工进度网络图表4施工总平面布置图及临时用地表(一)编制说明一、工程概况本项目由取水管、进水泵站(含进水泵房、户外型变配电间、阀门井等)、压力给水管、防撞墩及助航标志等工程组成。
取水管起点距新建江堤204米处,终点至取水泵站,长315米,采用一根DN550钢管;途中建设地埋式取水泵站,用地面积为920平方米;泵站出水管分别采用一根DN500PE管和DN400管,其中D500PE管伸至奥体中心南端利民河处对河道进行冲洗,DN400钢管分两路DN250管分别接入主体育场和体育馆,并在先锋河设置DN600PE管、DN550PE管排放口各一座,作为河道配水管在水源热泵不启动时对河道进行冲洗。
项目采用DN600钢管19米,DN400钢管200米,DN250钢管446米,DN250PE管609米,DN400PE管43米,DN500PE管1572米,DN550PE管107米,DN600PE管350米,沿线设砖砌阀门井4座。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图8
主桁架结构构成
图 9 屋面环桁架布置示意图
主桁架悬挑端根部高度为 4.5m。设置 6 道屋面环桁架,最端部的屋面环桁架为倒三角立体桁架,其余 5 道为平面片桁架,垂直于地面。其构成见下图。 将花瓣单元沿场心环向阵列 24 组,形成了钢结构罩棚结构。钢结构罩棚通过 24 组四管组合 V 型撑与 顶部砼看台型钢柱连接,构成罩棚上支座;径向主桁架上下弦杆向墙面延伸,汇交至下部砼二层混凝土梁 顶面,构成罩棚下支座。
注:支座附近受压和压弯杆件从严控制取为 120 5)钢构件应力水平: 钢结构杆件最大组合设计应力≤0.9f(f 为钢材设计强度) , 6)钢结构整体稳定指标:结构线弹性整体稳定屈曲荷载系数 K≥10,非线性整体稳定屈曲荷载系数 K ≥5。 7) 舒适度指标:室外钢梯竖向振动频率≥3.0Hz,看台结构竖向振动频率≥3.5Hz。
2014 年
图 3 混Байду номын сангаас土剪力墙平面布置(红色)
上部钢结构支撑在直径 1200mm 的斜柱上,为提高上部钢结构上支座下方的混凝土的环向抗扭刚度, 在二层和三层斜柱环向设置 8 道交叉钢支撑,该交叉支撑的设置位置与底层环向剪力墙在同一平面位置, 如下图所示。支撑截面圆钢管 680x22(底层) ,圆钢管 570x18(顶层) 。
4 抗震性能设计目标
1)钢结构(包括固定屋盖和移动屋盖) :安评小震弹性,规范中震弹性,规范大震基本不屈服,移动 屋盖轮轨及支座规范大震弹性; 2)混凝土结构:安评小震弹性,竖向构件规范中震弹性,支承上部钢结构的构件规范大震不屈服。
5 关键技术问题
5.1 计算模型说明 考虑到上部钢结构采用可开启屋盖的特殊性,根据开启的不同状态,采用不同的结构模型,并且总装 模型分析的同时,找出各个单体结构与总装结构在主要计算指标上的差别,分析其规律性,其中混凝土单 体模型记入上部钢结构传来的荷载作用,不考虑上部钢结构刚度贡献影响。 总共采用如下 26 个计算模型: 1 单体移动屋盖计算模型 建立 0,3,6,直到 45 度,3 度一个角度,共计 16 个计算模型。
个场地。下部砼看台和功能用房结构采用框架-支撑-剪力墙结构,外轮廓平面为圆形,上部支承环状花瓣造型的可开启屋 盖钢结构罩棚。固定屋盖罩棚外边缘直径约 133 米,悬挑长度约 26m,罩棚圆形开口直径约达 60 米。罩棚结构最高点标 高 30 米。整个钢罩棚由 24 个单元花瓣旋转复制组成。固定屋盖上方设置 8 片大悬挑移动屋盖,移动屋盖采用平面旋转 45 度开启方式。造型为花瓣形,每榀设置一个固定转轴及三条围绕固定转轴同心旋转的轨道结构,其中两条轨道固定在 移动屋盖上,一条轨道固定在固定屋盖上,单片移动屋盖径向长度 45m,宽 25m,最不利闭合状态时,向圆心悬挑 30m。整 体钢结构罩棚采用悬挑空间管桁架结构受力体系。重点介绍本工程结构体系、结构构成、结构设计的关键技术难点及相应 的专项研究分析处理方法。 关键词: 网球中心;空间钢结构;可开启屋盖;大悬挑
2014 年
图 6 固定屋盖钢结构罩棚三维视图
整个钢罩棚由 24 个单元花瓣组成,单元和单元之间公用上弦杆,并通过环桁架下弦系杆连接,如下 图所示:
图7
每组罩棚建筑单元示意图
每组花瓣为两个不同的结构单元构成,由径向悬挑主桁架和环向次桁架组成。其中,径向主桁架悬挑 长度 26m,为罩棚主受力结构。每个单元采用了两组倒三角空间立体桁架构成,二者公用一根上弦杆,并 通过环桁架下弦系杆连接。
闭合状态示意
开启 15 度示意
开启 30 度示意 完全开启状态(45 度)示意
图 13 典型开启状态移动屋盖与轮轨位置示意
移动屋盖下弦为平面,上弦为曲线花瓣状屋面。移动屋盖由沿着径向的花瓣造型的主桁架(主桁架位 置及曲线造型同时结合轨道布置)和沿着环向的次桁架构成,并设置交叉支撑以提高移动屋盖的刚度和整 体性。
2014 年
结论: 1 在重力荷载作用下移动屋盖闭合状态钢结构下支座出现拉力;开启状态钢结构下支座拉力较小。 2 在重力荷载作用下闭合状态每个钢结构上支座具有较大压力和水平外推力,开启状态的水平外推力较 小,比闭合状态水平力约小 50%;闭合状态压力比开启状态的压力略大。 3 从上部钢结构支座反力可知,对于下部混凝土结构而言,闭合状态为主要控制状态。 5.4 看台外倾引起重力荷载作用下混凝土构件受拉解决方案 由上文分析可知,在重力荷载作用下,闭合状态上部钢结构上支座对下部混凝土产生较大压力和水平 外推力,同时由于看台向场外倾斜,看台斜梁和看台板、顶部最外圈环梁,均承受较大的轴向拉力,为充 分考虑其不利影响,设计时对整体结构进行了如下几点针对性专项研究分析。 1) 不同开启状态的研究 建立移动屋盖闭合、开启、开启 15 度、开启 30 度四个状态,计算结果表明,闭合状 态下开台场外倾斜的趋势最明显,相关构件承受的拉力最大。 2) 建立看台折板的分析模型 传统看台建模分析中,看台密肋梁采用 frame 单元,看台板采用斜板 shell 模型,夸大了斜看台的平 面外刚度,看台板径向应力偏大,看台斜梁内力偏小,不利于结构安全。尤其本工程看台向场外倾斜,重 力荷载下上部看台结构沿径向受拉,看台板刚度对结构计算结果影响更为明显,为准确反映实际结构工作 性能,设计时建立了密肋梁、看台踏板均采用 shell 单元,更符合实际的壳元折板模型,并将两种计算模 型分析结果进行了对比,结果表明:采用看台折板模型,混凝土结构变形增大,看台板径向应力大为减小。 可见,采用斜板模拟看台结构误差较大,壳元折板对整体看台进行建模计算,能准确反映实际结构,设计 更为安全合理。
闭合状态示意
开启 15 度示意 图 18
开启 30 度示意 总装整体模型
完全开启状态示意
5.2 结构超长无缝设计 本工程下部混凝土结构周长近 300m,未设永久缝,为超长、超宽大面积混凝土结构。相应的设计措施 如下。 1)设置后浇带将整个工程下部结构切割成双向 30~35m 长的子结构。 2)地下室外墙、边角区域框架柱等竖向构件受力较为不利部位,设计时通过加强构件含钢率措施消 除局部不利影响,地下室外围墙身水平分布筋贯通置于外侧。 3)洞口周边及中部区域等受力不利及应力集中的梁板水平构件,设计时通过适当加强配筋等措施消 除局部不利影响, 截面拉应力由钢筋承担, 钢筋应力水平不超过 200MPa, 控制混凝土裂缝宽度不超过 0.2mm; 采用通长板筋加局部短筋的双层双向式配筋方式,增强楼板的抗裂性能。 4)采取以下针对性施工措施减小温差效应的不利影响:确保混凝土较低温度入模,即保证在月平均 0 气温以下入模;后浇带封闭施工须选择低温月(≤15 C)进行,避免经历较不利的降温状态,钢结构合拢 0 温度取(15±2) C;采用低水化热的普通硅酸盐水泥和级配良好的碎石骨料配制混凝土,并适量掺入粉煤 灰;采用高效减水剂,降低水泥用量,严格控制水灰比,加强混凝土养护等。 5.3 钢结构重力荷载标准值作用下支座反力研究 表 1 重力荷载标准值作用下固定屋盖钢结构支座反力
图 5 结构剖面图
2.2 上部钢结构固定屋盖 本工程砼看台区上覆的钢结构罩棚为环状花瓣造型的的可开启屋盖,该屋盖闭合时覆盖整个场地。固 定屋盖罩棚外边缘直径约 133 米,罩棚最大宽度 37 米,悬挑长度约 26m,场地中心罩棚圆形开口直径约达 60 米。
3
第二十三届全国高层建筑结构学术会议论文
图 10 钢罩棚支座构成 4
第二十三届全国高层建筑结构学术会议论文
2014 年
2.2 上部钢结构移动屋盖 固定屋盖上方设置 8 片花瓣形大悬挑移动屋盖,移动屋盖采用平面旋转 45 度开启方式。每榀设置一 个固定转轴及三条同心旋转轨道结构,其中两条轨道固定在移动屋盖上,一条轨道固定在固定屋盖上。 单 片移动屋盖径向长度 45,宽 25m,闭合状态向圆心悬挑 30m。
图 2 混凝土结构模型三维图
结合建筑平面布局,下部砼结构均匀布置了十道环向剪力墙(其中 2 道位于扩大平台下方) ,与框 架形成框架-剪力墙体系,增加下部砼结构刚度,有利于抗震。墙厚 500mm。 剪力墙布置如下图所示,其中 8 道环向剪力墙均布置在底层 0-6m 标高。
2
第二十三届全国高层建筑结构学术会议论文
作者介绍:傅学怡(1964-),男,研究员,国家勘查设计大师
1
第二十三届全国高层建筑结构学术会议论文
2014 年
图 1 杭州奥体博览城网球中心
2 结构体系及构成
2.1 下部混凝土结构 网球中心决赛场为特级比赛场馆,总建筑面积 24998 ㎡,其中地上 21307 ㎡,地下 3691 ㎡。下部砼 结构为观众看台及各功能用房, 外轮廓平面为圆形, 底层混凝土结构外径为 110m, 内径 55m, 结构宽度 27.5m。 看台顶部外轮廓直径 106 米,看台最高点标高为 20.50 米。下部砼结构为地上三层,首层层高层 6.0m,第 二层为 4.5m,第三层为 10m。
1 工程概况
杭州奥体网球中心位于钱塘江以南萧山区与滨江区的交界、钱塘江与七甲河交汇之处,网球中心在已 建主体育场的东北部,北邻七甲河,东临利民河,首层南临一桥南路,二层南侧通过二层平台和奥林匹克大 道相连,为特级体育建筑。总建筑面积 24998 ㎡,其中地上 21307 ㎡,地下 3691 ㎡。 本项目为新颖的八个花瓣旋转开启的可开启屋盖结构,下部为钢筋混凝土结构看台及功能用房,看台 区上覆的钢结构罩棚为环状花瓣造型的可开启屋盖钢结构,八片花瓣闭合时覆盖整个场地。下部砼结构采 用框架-支撑-剪力墙结构,外轮廓平面为圆形。固定屋盖罩棚外边缘直径约 133 米,悬挑长度约 26m,场 地中心罩棚圆形开口直径约达 60 米。整个固定屋盖钢罩棚由 24 个单元花瓣旋转复制组成。固定屋盖上方 设置 8 片大悬挑花瓣形移动屋盖,移动屋盖采用平面旋转 45 度开启方式。移动屋盖每榀设置一个固定转 轴及三条同心旋转轨道结构,其中两条轨道固定在移动屋盖上,一条轨道固定在固定屋盖上,单片移动屋 盖径向长度 45,宽 25m,最不利闭合状态时,向圆心悬挑 30m。
