梅涅劳斯定理(精选.)
平面几何地几个重要地定理--梅涅劳斯定理
平面几何的几个重要的定理一、梅涅劳斯定理：1=⋅⋅=⋅⋅BAA C CBC B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度，则：到直线、、分别是、、证：设注：此定理常运用求证三角形相似的过程中的线段成比例的条件；。
的交点，证明：与是的中点，是上，在点的平分线，是是斜边上的高，中，：若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠∆11PC BP R Q P AB CA BC ABC ABC l 1=⋅⋅RBARQA CQ ，则、、的延长线分别交于或它们、、的三边的顶点，并且与不经过：若直线定理∆∆CE//BF CKE FKB KE BK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FCKFEK AE DA CD F E D ACK EPCK EP BC EBC CE BH 90HCB ACE HCB HBC ACE HBC ACKEBC BH B EBC ∴≅∴=====⋅⋅=∴⊥︒=∠+∠=∠+∠∠=∠∠=∠∠∆∆∆∆∆＝依分比定理有：＝即：＝于是依梅涅劳斯定理有：、、和三点对于，则：上的高作为等腰三角形即：则：的平分线中，作在证：111111111111D B D A :C B C A BD AD :BC AC D C B A DC B A K 1=，试证：、、、和、、、线分别交这四条直线于引四条直线，另两条直】从点【练习注：此定理常用于证明三点共线的问题，且常需要多次使用 再相乘；共线；、、证明点引的垂线的垂足，、、向是从点、、的外接圆上；位于点例111111C B A AB CA BC P C B A ABC P .2∆三点共线；、、综上可得：也重合与的延长线上时，同在与类似地可证得当矛盾＝这与于是可得即这时设必定重合，不然的话，与线段上，则同在与若的延长线上；线段上，或者同在或者同在与因此，或边上的点的个数也为三点中，位于、、由于在同一直线上的＝，则：又得：，于是由定理交于与直线证：设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RBAR B R AR 1RB AR QA CQ 1BR AR QA CQ 1R AB PQ ''''''''''''''''''><-<->=⋅⋅=⋅⋅∆PC BP PC BP 三点共线；、、求证：，，这时若或边上的点的个数为三点中，位于、、三点，并且上或它们的延长线上的、、的三边分别是、、：设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RBARQA CQ =⋅⋅∆∆ C BA1A 1B 1C 三点共线；、、依梅涅劳斯定理可知，＝可得且将上面三条式子相乘，证：易得：111111111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBA cos PB PABcos AP BC AC PAC cos AP PCAcos CP AB CB ,PCBcos CP PBCcos BP CA BA ⋅⋅︒=∠+∠∠=∠∠=∠∠⋅∠⋅-=∠⋅∠⋅-=∠⋅∠⋅-=直线上；在同一条、、的交点与，与，与，则、、上的切点分别为、、的内切圆在三边】设不等腰【练习Z Y X AB DE CA FD BC EF F E D AB CA BC ABC 2∆三点共线；、、，试证：的交点是与线，直的交点是与，直线的交点为和，直线相交于，，】已知直线【练习222211*********C B A B C A AC A C B BC C B A AB O CC BB AA 311111111111111111111111111111111111111D B D A :C B C A BD AD :BC AC 1C BD B D A C A BD BC AC AD 1LD D B K B BK BD LD 1BKKB C B LC LC BC 1LC C A K A AK AC LC 1AK KA D A LD LD AD BLB AL A L D A AD D A //AD 1==⋅⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅即：得：将上面四条式子相乘可可得：和别用于，则把梅涅劳斯定理分相交与点与若，结论显然成立；证：若的证明练习∆∆共线、、，证明：、、的交点依次为和，和，和，和，记直线、、，在另一条上取点、、】在一条直线上取点【练习N M L N M L BC EF AF CD AF CD ED AB D F B A C E 4三点共线、、可得的边上，由定理都不在、、又得：将上面三条式子相乘可＝＝同理可得：＝代人上式可得：又可得：所截，由定理被直线证：的证明练习Z Y X 2ABC Z Y X 1ZBAZYA CY XC BX BDEAZB AZ AF DC YA CY CEFBXC BX AF AE 1FBAFEA CE XC BX 1XFE ABC 2∆∆ =⋅⋅==⋅⋅共线由梅涅劳斯定理可知可得：将上面的三条式子相乘应用梅涅劳斯定理有：，和，和，和们边上的点：对所得的三角形和在它的交点，和，和，和分别是直线、、证：设的证明练习222222222221111221111221111211211211111111222C ,B ,A 1BA CA CB AB AC BC 1CB AB OC CC AA OA 1BA CA OB BB CC OC 1AC BC BB OB OA AA )B ,C A (OAC ),A ,C B (OBC ),C ,B A (OAB B A AB C A AC C B BC C B A 3=⋅⋅=⋅⋅=⋅⋅=⋅⋅平面几何的几个重要定理――――塞瓦定理 塞瓦定理：1:=⋅⋅∆RBARQA CQ PC BP CR BQ AP AB CA BC ABC R Q P 的充要条件是三线共点、、边上的点，则、、的分别是、、设共线点得：将上面五条式子相乘可，则有点涅劳斯定理于五组三元，应用梅，对、、的交点分别为和，和，和证：记直线的证明练习N ,M ,L ,1VNUNUM WM WL VL 1UFVFWD UD VB WB 1UE VE WC UC VA WA 1WB VBUC WC VN UN 1YM WM VF UF WA VA 1UD WD WL VL VE UE )F ,D ,B (),E ,C ,A (),N ,C ,B (),F ,M ,A (),E ,D ,L (UVW W V U CD AB AB EF CD EF 4∴=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅=⋅⋅∆MQRACPB；相交于一点点、、重合，故必与上，所以都在线段和因为＝于是：，由塞瓦定理有：，于交，且直线相交于与，设再证充分性：若＝以上三式相乘，得：同理：，则：相交于点、、证：先证必要性：设’’‘’‘’‘M CR BQ AP R R AB R R RB ARB R AR BR AR QA CQ PC BP R AB CM M BQ AP RB AR QA CQ PC BP RB ARQA CQ PC BP S S RB AR S S QA CQ S S S S S S PC BP M CR BQ AP BCMACMABMBCMACM ABMCMP BMP ACP ABP 111=⋅⋅=⋅⋅⋅⋅=====∆∆∆∆∆∆∆∆∆∆交于一点；：证明：三角形的中线例1交于一点；成立，即而显然有：我们只须证明，，，的中线证明：记ABC AB CBC A BA B C AC A B CB C A BA B C AC AB CBC A BA B C AC CC BB AA ABC ∆∴=⋅⋅====⋅⋅∆1,,1111111111111111111111分线交于一点；】证明：三角形的角平【练习1 高交于一点；】证明：锐角三角形的【练习2ABCP P BM AN N M BC AC L L AB C ABC ⊥∠∆，证明：的交点是和，设和足分别是的垂线，垂和作边，从于的平分线交于中，角：在锐角例2CB A1A 1B 1C CBA1A 1B 1CABCP P AN BM CK BLBCAC AL BLBCAC AL BLBCNB BK BKC BNL ACALAK AM AKC AML NBBKAK AM CNMC AKBKNB CN MC AM AN BM CK P AN BM CK ABCK ⊥∴∴=⋅=⋅=⇒∆≅∆=⇒∆≅∆=⋅==⋅⋅⊥点三线共点，且为、、理可知：依三角形的角平分线定即要证即要证明：又即要证：三线共点，依塞瓦定理、、要证点，三线共点，且为、、下证证：作1111FDAEDA ANAM BF BD AF CE CD AE FBAFEA CE DC BD P CF BE AD BFBDAF AN CE CD AE AM BF AF BD AN CE AE CD AM BDF ANF CDE AME BC MN BCAD ∠=∠∴=∴⋅=⋅∴=⋅⋅⋅=⋅===∴∆≅∆∆≅∆⊥1,,,//，根据塞瓦定理可得：共点于、、于是，可得，故三线共点；、、，证明：，且、、外有三点】已知【练习CR BN AM BCM ACN ABR CBM CAN BAR R N M ABC γβα=∠=∠=∠=∠=∠=∠∆,,3K LNMCBAFDAEDA F E AB AC CP BP AD P BC D ABC AD ∠∠∆＝，则和交于、分别与、上任一点，是边上，若在的高，且是设例.3ANAM FDA EDA N M DF DE AD A =∠=∠可以转化为证明，。
数学竞赛梅涅劳斯定理
梅涅劳斯定理梅涅劳斯〔Menelaus〕定理〔简称梅氏定理〕最早出现在由古希腊数学家梅涅劳斯的著作?球面学?〔Sphaerica〕。
任何一条直线截三角形的各边，都使得三条不相邻线段之积等于另外三条线段之积，这一定理同样可以轻而易举地用初等几何或通过应用简单的三角关系来证明. 梅涅劳斯把这一定理扩展到了球面三角形。
中文名梅涅劳斯定理外文名Menelaus别称梅氏定理表达式(AF/FB)×(BD/DC)×(CE/EA )=1提出者梅涅劳斯提出时间1678年应用学科数学，物理适用领域范围平面几何学适用领域范围射影几何学定理内容定理证明证明一过点A作AG∥DF交BC的延长线于点G.那么证明二过点C作CP∥DF交AB于P，那么两式相乘得证明三连结CF、AD，根据“两个三角形等高时面积之比等于底边之比〞的性质有。
AF：FB =S △ADF：S△BDF…………〔1〕，BD：DC=S△BDF：S△CDF…………〔2〕，CE：EA=S△CDE：S△ADE=S△FEC：S△FEA=〔S△CDE+S△FEC〕：〔S△ADE+S△FEA〕=S△CDF：S△ADF (3)〔1〕×〔2〕×〔3〕得证明四过三顶点作直线DEF的垂线AA‘，BB'，CC'，如图：充分性证明：△ABC中，BC，CA，AB上的分点分别为D，E，F。
连接DF交CA于E'，那么由充分性可得，(AF/FB)×(BD/DC)×(CE'/E'A)=1又∵∴有CE/EA=CE'/E'A，两点重合。
所以共线推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N 三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
于是AL、BM、CN三线交于一点的充要条件是λμν=-1。
〔注意及塞瓦定理相区分，那里是λμν=1〕此外，用该定理可使其容易理解与记忆：第一角元形式的梅涅劳斯定理如图：假设E，F，D三点共线，那么(sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBE/sin∠ABE)=1即图中的蓝角正弦值之积等于红角正弦值之积。
梅涅劳斯定理
【证法欣赏】
证法1：（平行线分线段成比例）
E
A G
FFA
G
E
BCD
D
BC
证：如图，过A作AG//BC交CF延长线于G，
∵AG//BC，∴
AF
FB
AG
BD
，
CE
EA
CD
AG
，
又
BD
CD
BD
CD
AFCEBDAGCDBD
则1
FBEACDBDAGCD
AFBDCE
∴1
FBDCEA
证法2：（正弦定理）
E
A
F
A
F
梅涅劳斯定理的逆定理也成立，即
如果有三点F、D、E分别在ABC的三边AB、BC、CA或其延长线上，
AFBDCED、E三点共线。
[注]利用梅涅劳斯定理的逆定理可判定三点共线
E
A
F
A
F
中学数学中的著名定理~ 1 ~E
BCD
【定理应用】
梅涅劳斯定理的应用定理1：
若ABC的A的外角平分线交边BC延长线于P，B的平分线交边AC于Q，
C的平分线交边AB于R，则P、Q、R三点共线。
证：由三角形内、外角平分线定理知，
BP
PC
BA
CA
，
CQ
QA
BC
AB
，
AR
RB
CA
CB
，
R
A
F
Q
ARBP，
CQCABABC
则1
RBPCQACBCAAB
BC
P
故P、Q、R三点共线。
【定理应用】
梅涅劳斯定理的应用定理2：
梅涅劳斯(Menelaus)定理
补充讲义梅涅劳斯（Menelaus）定理是由古希腊数学家梅涅劳斯首先证明的。
它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。
AFED证明：塞瓦定理ΔABC的三边BC，CA，AB上有点D，E，F.若AD，BE，CF三线交于一点O.求证：. BD/DC*CE/EA*AF/FB=1∵三角形ABC内一点O，AO，BO，CO交对边于D，E，F。
证（AF/FB）*（BD/DC）*（CE/EA）=1。
1）最简单的证法：用面积证。
2）用梅涅劳斯定理：3）用分角定理：证明：塞瓦定理的应用定理：设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E，又设BE和CD交于S，则AS一定过边BC的中心MAD ESB M C实际运用：2010年上海中考题25．如图9，在Rt△ABC中，∠ACB＝90°.半径为1的圆A与边AB相交于点D，与边AC 相交于点E，连结DE并延长，与线段BC的延长线交于点P.（1）当∠B＝30°时，连结AP，若△AEP与△BDP相似，求CE的长；（2）若CE=2，BD=BC，求∠BPD的正切值；（3）若1tan3BPD∠=，设CE=x，△ABC的周长为y，求y关于x的函数关系式.图9 图10(备用) 图11(备DP武汉2010年中考试题24．(本题满分10分) 已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点。
连结AC，BD交于点P．(1) 如图1，当OA=OB，且D为OA中点时，求APPC的值；(2) 如图2，当OA=OB，且AD1AO4时，求tan∠BPC的值．(3) 如图3，当AD∶AO∶OB=1∶n∶tan∠BPC的值．（图1）（图2）（图3）25．(本题满分12分) 如图．抛物线经过A （－1，0），C （2，）两点， 与x 轴交于另一点B ．(1) 求此地物线的解析式；(2) 若抛物线的顶点为M ，点P 为线段OB 上一动点 (不与点B 重合)，点Q 在线段MB 上 移动，且∠MPQ=45°，设线段OP=x ，MQ=，求y 2与x 的函数关系式，并直接写出 自变量x 的取值范围；(3) 在同一平面直角坐标系中，两条直线x=m ，x=n 分别与抛物线交于点E ，G ，与(2)中的 函数图象交于点F ，H ．问四边形EFHG 能否为平行四边形? 若能，求m ，n 之间的数量关 系；若不能，请说明理由．补充知识点：1、 中线定理：（巴布斯定理）设三角形ABC 的边BC 的中点为P ，则有AB 2+AC 2=2(AP 2+BP 2)AB C212y ax ax b =-+3222yP2、广勾定理：在三角形中，锐角(或钝角)所对的边的平方等于另外两边的平方和，减去(或加上)这两边中的一边与另一边在这边(或其延长线)上的射影的乘积的2倍．A AB CD C （锐角）证明：AC2=AB2+BC2-2BD*BC （钝角）证明：AC2=AB2+BC2+2BD*BC知识补充：（北京市2010年中考题第25题）1、问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA。
平面几何的几个重要的定理--梅涅劳斯定理
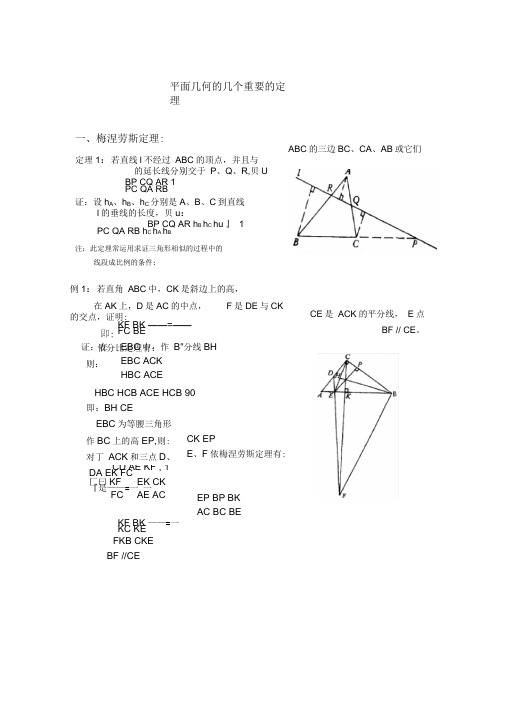
平面几何的几个重要的定理一、梅涅劳斯定理:定理1：若直线l 不经过 ABC 的顶点，并且与的延长线分别交于 P 、Q 、R,贝U BP CQ AR 1 PC QA RB证：设h A 、h B 、h C 分别是A 、B 、C 到直线l 的垂线的长度，贝u ：BP CQ AR h B h C hu 』 1PC QA RB h C h A h B注：此定理常运用求证三角形相似的过程中的线段成比例的条件;例1：若直角 ABC 中，CK 是斜边上的高， 在AK 上，D 是AC 的中点， F 是DE 与CK的交点，证明:KF BK ——=—— FC BE KF BK ——=一 KC KE FKB CKE BF //CECE 是 ACK 的平分线， E 点BF // CE 。
证：在 则：EBC 中，作 B"分线BH EBC ACK HBC ACEHBC HCB ACE HCB 90即：BH CEEBC 为等腰三角形作BC 上的高EP,则:对丁 ACK 和三点D 、 CK EPE 、F 依梅涅劳斯定理有:CD AE KF , 1 DA EK FC匚曰KF EK CK 『是——=一 一FC AE ACEP BP BK AC BC BE依分比定理有: ABC 的三边BC 、CA 、AB 或它们【练习1从点K 引四条直线，另两条直 -一 一 、…AC和 A 1、B 1、C 1、D 1,试证： ------- 1 1 1BC线分别交这四条直线丁 A 、B 、C 、DAD BD定理2：设P 、Q 、R 分别是 ABC 的三边 BC 、CA 、AB 上或它们的延长线上的 P 、Q 、R 三点中，位于 ABC 边上的点的个数为 0或2,这时若 既 PC 三点，并且 CQ AR QA RB 1, 求证：P 、Q 、R 三点共线; 证：设直线PQ 与直线AB 交丁 R ', 丁是由定理 BP CQ AR _ __ ' PC QA R B乂 BP CQ AR PC QA RB 由丁在同一直线上的 _ ' ____ AR AR1,则：^―=—— R B RB P 、Q 、R '三点中，位丁 ABC 边上的点的个数也为 0或2,因此R 与R '或者同在AB 线段上，或者同在 AB 的延长线上； 若R 与R '同在AB 线段上，则R 与R '必定重合，不然的话， 设AR AR ', AR AR BR BR 这时AB AR AB AR ',即BR BR ',丁是可得 _ ____ ' 这与AR =竺 矛盾 BR BR 类似地可证得当 R 与R '同在AB 的延长线上时,综上可得：P 、Q 、R 三点共线； 注：此定理常用于证明三点共线的问题，且常需要多次使用 R 与R '也重合再相乘;例2点P 位丁 ABC 的外接圆上；A 1、B 1、C 1是从点P 向BC 、CA 、AB 引的垂线的垂足, 证明点A 1、B 1、 BA 1BP cos PBC CA 1 CP cos PCB CB 1 CP cos PCA AB 1 AP cos PAC AC 1AP cos PABBC 1 PB cos PBAC i 共线; 证：易得: 将上面三条式子相乘， 且 PAC PBC , PAB PCB , 十曰 BA 1 CB 1 AC 1可得 一111= 1 ,CA 1 AB 1 BC 1依梅涅劳斯定理可知 A 1、B 1、C 1三点共线;PCA PBA 180A 1C 1 A 1D 1B 1C ； :BD【练习2设不等腰 ABC 的内切圆在三边 BC 、CA 、AB 上的切点分别为 D 、E 、F,则EF 与BC , FD 与CA , DE与AB 的交点 X 、Y 、Z 在同一条 直线上；【练习&已知直线 AA i, BB i, CC i 相交于O,直线AB 和A 1B 1的交点为C 2,直线 BC 与B 1C 1的交点是 A 2,直 线AC 与A i C i 的交点是B 2,试证：A 2、B 2、C 2三点共线;【练习M 在一条直线上取点 E 、C 、A,在另一条上取点 B 、F 、D,记直线AB 和ED , CD 和AF ,CD 和AF , EF 和BC 的交点依次为 L 、M 、N,证明：L 、M 、N 共线练习i 的证明练习2的证明乂 AE AF 代人上式可得：BXXC FB =—— CE CY DC AZ EA同理口」彳寸： — —YA AFZB BD将上面三条式子相乘可 得：乳CY J i XC YA ZB 乂 X 、Y 、Z 都不在 ABC 的边上，由定理 2可得X 、Y 、 证： ABC 被直线XFE 所截，由定理 Z 三点共线 证：若AD // A i D^,结论显然成立;若AD 与A i D i 相交与点 AD LD LD BD LD 〔 A i K A i D i AK BK BQ B i K LDi L,则把梅涅劳斯定理分 LC AK A 。
梅涅劳斯(Menelaus)定理(最全)word资料
（Menelaus）定理（简称梅氏定理）是由古希腊数学家梅涅劳斯首先证明的。
它指出：如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点，那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或：设X、Y、Z分别在△ABC的BC、CA、AB所在直线上，则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 证明一：过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得：(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二：过点C作CP∥DF交AB于P，则BD/DC=FB/PF，CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立：若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/E A)=1，则F、D、E三点共线。
利用这个逆定理，可以判断三点共线。
梅涅劳斯(Menelaus)定理证明三：过ABC三点向三边引垂线AA'BB'CC'，所以AD：DB=AA'：BB'，BE：EC=BB'：CC'，CF：FA=CC'：AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四：连接BF。
（AD：DB）·（BE：EC）·（CF:FA)=（S△ADF：S△BDF）·（S△BEF：S△CEF）·（S△BCF：S△BAF）=（S△ADF：S△BDF）·（S△BDF：S△CDF）·（S△CDF：S△ADF）=1此外，用定比分点定义该定理可使其容易理解和记忆：在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
梅涅劳斯定理及例题拓展
梅涅劳斯定理及例题拓展梅涅劳斯介绍：在证明点共线时，有一个非常重要的定理，它就是梅涅劳斯定理，梅涅劳斯（Menelaus ）是公元一世纪时的希腊数学家兼天文学家，著有几何学和三角学方面的许多书籍。
下面的定理就是他首先发现的。
这个定理在几何学上有很重要的应用价值。
定理：设D 、E 、F 依次是三角形ABC 的三边AB 、BC 、CA 或其延长线上的点，且这三点共线，则满足1=⋅⋅FA CF EC BE DB AD 证明：（此定理需要分四种情况讨论，但有两种可以排除） 先来说明两种不可能的情况 情况一：当三点均在三角形边上时，由基本事实可知三点不可能共线（只能组成内接三角形的三角形。
情况二：当一点在三角形一边上，另两点分别在三角形另两边的延长线上时，如图是三角形ABC 直线DE 交AB 于点D ，交AC 于点F ，交BC 于点E ，平移直线DE 即可发现不能可两点同时在延长线上 情况三：当两点分别在三角形两边上，另一点在三角形另一边的延长线上时，如图是三角形ABC 直线DE 交AB 于点D ，交AC 于点F ，交BC 于点E ，∵D 、E 、F 三点共线∴可过C 作CM ∥DE 交AB 于M ，于是FCAF DM BD DM AD EC BE FCAF DM AD DM BD EC BE ⋅=⋅∴==,,所以1=⋅⋅FA CF EC BE DB AD 情况四：三点分别在三角形三边的延长线上时，如图是三角形ABC 直线DE 交AB 于点D ，交AC 于点F ，交BC 于点E ，同情况三∵D 、E 、F 三点共线∴可过C 作CM ∥DE 交AB 于M ，于是FCAF DM BD DM AD EC BE FCAF DM AD DM BD EC BE ⋅=⋅∴==,,所以1=⋅⋅FACF EC BE DB AD∴设D 、E 、F 依次是三角形ABC 的三边AB 、BC 、CA 或其延长线上的点，且这三点共线，则满足1=⋅⋅FACF EC BE DB AD拓展（1题）在任意三角形PQR 中，A2,A4分别是PR,PQ 延长线上的点，做射线A4A2,A6是射线A4A2上的一点，做射线A6Q ，A1是射线A6Q 上的一点，连结A1A2交射线PR 于X ，作射线A4A3交射线PQ 于点A3，交射线A1A6于点Y ，连结A1A3交射线PR 于点A5，连结A6A5交射线PQ 于点Z ，求证X,Y,Z 三点共线（该命题又为一六边形相间各顶点分别在两直线上求证：它的三对对边（所在直线）的交点共线）这个定理为帕波斯定理（2题）给定△ABC内两点O,O',连结AO,AO'交BC于点X,X',BO,BO'交AC于Y,Y',CO,CO'交AB于Z,Z'.设YZ'与Y'Z交于点P,ZX'与Z'X交于点Q,XY'与X'Y 交于点R.求证O,O',P,Q,R五点共线（3题）在任意三角形ABC中，E是直线AC上的一点，D是直线BC上的一点，F 是直线DE上一点，G是直线AC上一点，作直线BG交直线DF于点Q，作直线CF 交直线AB于点P，作直线GF交直线AB于点H作直线DH交直线AC于点R,求证P,Q,R三点共线（4题）一直线截△ABC三边BC,CA,AB或延长线X,Y,Z。
梅涅劳斯定理
当直线交三边所在直线于点时，以及逆定理：在三边所在直线上有三点，且那么三点共线。
注意：以上定理严格来说应该用有向线段形式，且乘积为-1；另外，三点中有偶数个点在线段上时，才有梅氏定理，否则为塞瓦定理. 证明一过点A作AG∥DF交BC的延长线于点G.则证毕证明二过点C作CP∥DF交AB于P，则BD：DC=FB：PF，CE：EA=PF：AF两式相乘得(AF：FB)×(BD：DC)×(CE：EA)=(AF：FB)×(FB：PF)×(PF：AF)=1证明三连结CF、AD，根据“两个三角形等高时面积之比等于底边之比”的性质有。
AF：FB =S△ADF：S△BDF…………（1），BD：DC=S△BDF：S△CDF…………（2），CE：EA=S△CDE：S△ADE=S△FEC：S△FEA=（S△CDE+S△FEC）：（S△ADE+S△FEA）=S△CDF：S△ADF (3)（1）×（2）×（3）得××=××证明四过三顶点作直线DEF的垂线AA‘，BB'，CC'，如图：充分性证明：△ABC中，BC，CA，AB上的分点分别为D，E，F。
连接DF交CA于E'，则由充分性可得，(AF/FB)×(BD/DC)×(CE'/E'A)=1又∵∴有CE/EA=CE'/E'A，两点重合。
所以共线推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点，又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
于是AL、BM、CN三线交于一点的充要条件是λμν=-1。
（注意与塞瓦定理相区分，那里是λμν=1）此外，用该定理可使其容易理解和记忆：第一角元形式的梅涅劳斯定理如图：若E，F，D三点共线，则(sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBA/sin ∠ABE)=1即图中的蓝角正弦值之积等于红角正弦值之积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
梅涅劳斯定理
【定理内容】
如果一条直线与ABC ∆的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点， 那么
1=⋅⋅EA
CE
DC BD FB AF .
[评]等价叙述：ABC ∆的三边AB 、BC 、CA 或其延长线上有三点F 、D 、E ，
则F 、D 、E 三点共线的充要条件是
1=⋅⋅EA
CE
DC BD FB AF 。
三点所在直线称为三角形的梅氏线。
【背景简介】
梅涅劳斯（Menelaus
）定理是由古希腊数学家梅涅劳斯首先证明的。
【证法欣赏】
证法1：（平行线分线段成比例）
证：如图，过A 作BC AG //交CF 延长线于G ，
∵BC AG //，∴BD AG FB AF =，AG
CD
EA CE =， 又
CD
BD CD BD =
B
G
则
1=⋅⋅=⋅⋅CD BD
AG CD BD AG
CD BD EA CE FB AF ∴1=⋅⋅EA CE DC BD FB AF
证法2：（正弦定理）
证：如图，令α=∠AEF ，β=∠AFE ，γ=∠BDE ，
在AEF ∆中，由正弦定理知：
β
αsin sin AE
AF =， 同理
ββγsin )180sin(sin BD BD BF =-︒=，γ
αsin sin CE
CD = ∴βαsin sin =AE AF ，γβsin sin =BF BD ，α
γsin sin =CD CE ， ∴
1=⋅⋅CD CE BF BD AE AF ，即1=⋅⋅EA
CE
DC BD FB AF .
【逆定理】
梅涅劳斯定理的逆定理也成立，即
如果有三点F 、D 、E 分别在ABC ∆的三边AB 、BC 、CA 或其延长线上，且满足
1=⋅⋅EA
CE
DC BD FB AF ，那么F 、D 、E 三点共线。
[注]利用梅涅劳斯定理的逆定理可判定三点共线
B
【定理应用】
梅涅劳斯定理的应用定理1：
若ABC ∆的A ∠的外角平分线交边BC 延长线于P ，B ∠的平分线交边AC 于Q ，
C ∠的平分线交边AB 于R ，则P 、Q 、R 三点共线。
证：由三角形内、外角平分线定理知，
CA BA PC BP =，AB BC QA CQ =，CB CA
RB AR =
， 则
1=⋅⋅=⋅⋅AB
BC
CA BA CB CA QA CQ PC BP RB AR ， 故P 、Q 、R 三点共线。
【定理应用】
梅涅劳斯定理的应用定理2：
过任意ABC ∆的三个顶点A 、B 、C 作它的外接圆的切线，分别和BC 、CA 、AB 的延长线交于点P 、Q 、R ，则P 、Q 、R 三点共线。
证：∵CR 是⊙O 的切线，
∴RAC ∆∽RCB ∆，
∴CB AC
RB RC RC RA ==， 则2)(CB AC RB RC RC RA RB RA =⋅=， 同理：
2)(AC
AB CP BP =，2)(BA BC QA CQ
= ∴
1)()()(2
22=⋅⋅=⋅⋅AB
BC CA BA CB CA QA CQ PC BP RB AR ， 故P 、Q 、R 三点共线。
P
R
【定理应用】
【例1】已知：过ABC ∆顶点C 的直线，与边AB 及中线AD 分别交于点F 和E .
求证：
FB
AF
ED AE 2=
. 证明：直线CEF 截ABD ∆， 由梅涅劳斯定理，
得：1=⋅⋅EA DE CD BC FB AF
又CD BC 2=，
∴21=⋅EA DE FB AF ， 则FB
AF ED AE 2= [注]此例证法甚多，如“平行线”、“面积法”等，详情参看《初中数学一题多解欣赏》．
【定理应用】
【例2】已知：过ABC ∆重心G 的直线分别交边AB 、AC 及CB 延长线于点E 、
F 、D .求证：
1=+FA
CF EA BE . 证：连接AG 并延长交BC 于M ，
则CM BM =，
∵DEG 截ABM ∆，
∴由梅氏定理得，1=⋅⋅DB
MD
GM AG EA BE ；
同理：1=⋅⋅DC MD
GM AG FA CF
∴MD DB AG GM EA BE ⋅=，MD
DC AG GM FA CF ⋅=， ∴11221)(=⨯=+⋅=⋅+=+MD DC DB AG GM MD AG DC DB GM FA CF EA BE 即
1=+FA
CF
EA BE
最新文件 仅供参考 已改成word 文本 。
方便更改
D
B C
C。