运筹学教材编写组《运筹学》课后习题(第10章 动态规划应用举例——第12章 网络计划)【圣才出品】
《运筹学》课后答案

《运筹学》课后答案《运筹学》是一门研究如何在有限资源下做出最佳决策的学科,它涉及到数学、统计学、经济学等多个学科的知识。
掌握运筹学的方法和技巧对于解决实际问题具有重要意义。
下面是《运筹学》课后习题的答案:1. 什么是线性规划问题?线性规划问题是指在一组线性约束条件下,求解一个线性目标函数的最优值的问题。
线性规划问题具有优化的特点,即找到一组满足约束条件的解,使得目标函数取得最大(最小)值。
2. 线性规划问题的标准形式是什么?线性规划问题的标准形式是指将目标函数和约束条件都写成标准形式,即目标函数为最大化(最小化)一个线性函数,约束条件为一组线性不等式和线性等式。
3. 线性规划问题的解的存在性和唯一性是什么?线性规划问题的解的存在性和唯一性是由线性规划问题的特殊结构决定的。
如果线性规划问题有有界解(即目标函数有最大(最小)值),则存在解;如果线性规划问题的目标函数有最大(最小)值,且该最大(最小)值只有一个解,则解是唯一的。
4. 什么是单纯形法?单纯形法是一种解线性规划问题的常用方法,它通过迭代计算来逐步接近最优解。
单纯形法的基本思想是从一个初始可行解出发,通过一系列变换(包括基变换、基可行解的改进等)来逐步接近最优解。
5. 什么是对偶理论?对偶理论是线性规划问题的一个重要理论基础,它通过将原问题转化为对应的对偶问题来研究线性规划问题。
对偶理论可以帮助我们理解线性规划问题的性质和结构,并且可以通过对偶问题的解来得到原问题的解。
6. 什么是整数规划问题?整数规划问题是指在线性规划问题的基础上,将决策变量的取值限制为整数的问题。
整数规划问题具有更为复杂的性质,其解的搜索空间更大,求解难度更大。
7. 什么是分支定界法?分支定界法是解整数规划问题的一种常用方法,它通过将整数规划问题分解为一系列线性规划子问题,通过不断分支和约束来逐步缩小解的搜索空间,最终找到最优解。
8. 什么是动态规划?动态规划是一种解决多阶段决策问题的方法,它通过将问题分解为一系列子问题,并且利用子问题的解来构建整体问题的解。
运筹学教材编写组《运筹学》课后习题-动态规划的基本方法(圣才出品)

(1) A → B2 →C1 → D1 → E ;(2) A → B3 →C1 → D1 → E ; (3) A → B3 →C2 → D2 → E 。
8.3 计算从 A 到 B、C 和 D 的最短路线。已知各段路线的长度如图 8-2 所示。
图 8-2
解:设阶段变量 k = 1, 2,3, 4 ,依次表示 4 个阶段选择路线的过程;状态变量 sk 表示第 k 阶段初所处的位置;决策变量 xk 表示第 k 阶段初可能选择的路线;最优值函数 fk (sk ) 表示 从起点 A 到第 k 阶段状态 sk 的最短距离,则有
xn =sn
n
xn
,或 fn+1(sn+1) = 0
n
(2)设状态变量为 sk = ai xi (k = 1, 2, n) ,状态转移方程为 sk+1 = sk − ak xk ,最 i=k
n
优值函数 fk (sk ) 表示在 sk 状态下从第 k 阶段到第 n 阶段使 z = ci xi2 最小的值,则动态规 i=k
划的基本方程为:
3 / 11
圣才电子书 十万种考研考证电子书、题库视频学习平台
fk (sk )
=
min
0xk sk ak
{ck
xk2
+
f k +1 (sk
− ak xk )}
fn+1(sn − anxn ) = 0(k = n, n −1, 2,1)
8.5 用递推方法求解下列问题。
=
max {2
0x3 10
x32
+
f2 (s2 )} =
max {2
0x3 10
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章:引论1.1 课后习题习题1a)运筹学是一门应用数学的学科,旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域,如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划,优化供应链管理,提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题,优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域,如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中,可以使用运筹学方法优化仓储和运输的布局,提高货物的运输效率。
在生产计划中,可以使用运筹学方法优化产品的生产数量和生产周期,降低生产成本。
在供应链管理中,可以使用运筹学方法优化订单配送和库存管理,提高供应链的效率。
在流程优化中,可以使用运筹学方法优化业务流程,提高整体效率。
习题2在物流管理中,可以使用运筹学方法优化车辆的调度和路线规划,以提高运输效率和降低成本。
在生产计划中,可以使用运筹学方法优化生产线的安排和产品的生产量,以降低生产成本和提高产能利用率。
在供应链管理中,可以使用运筹学方法优化供应链各个环节的协调和调度,以提高整体效率和减少库存成本。
在流程优化中,可以使用运筹学方法优化业务流程的排布和资源的分配,以提高流程效率和客户满意度。
第二章:线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法,用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为:max c^T*xs.t. Ax <= bx >= 0其中,c是目标函数的系数向量,x是决策变量向量,A是约束矩阵,b是约束向量。
习题2使用线性规划方法可以解决许多实际问题,如生产计划、供应链管理、资源分配等。
管理运筹学课后习题答案
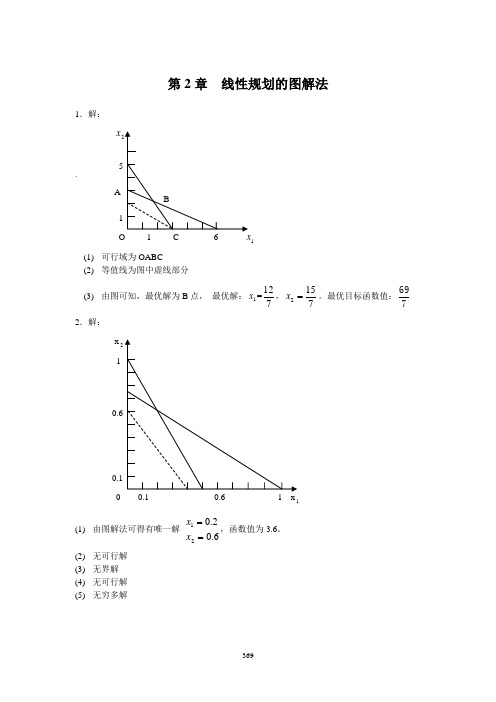
第2章 线性规划的图解法1.解:x`A 1 (1) 可行域为OABC(2) 等值线为图中虚线部分(3) 由图可知,最优解为B 点, 最优解:1x =712,7152=x 。
最优目标函数值:7692.解: x 2 10 1(1) 由图解法可得有唯一解 6.02.021==x x ,函数值为3.6。
(2) 无可行解 (3) 无界解 (4) 无可行解 (5)无穷多解(6) 有唯一解 3832021==x x ,函数值为392。
3.解:(1). 标准形式:3212100023m ax s s s x x f ++++=,,,,9221323302932121321221121≥=++=++=++s s s x x s x x s x x s x x(2). 标准形式:21210064m in s s x x f +++=,,,46710263212121221121≥=-=++=--s s x x x x s x x s x x(3). 标准形式:21''2'2'10022m in s s x x x f +++-=,,,,30223505527055321''2'2'12''2'2'1''2'2'11''2'21≥=--+=+-=+-+-s s x x x s x x x x x x s x x x4.解:标准形式:212100510m ax s s x x z +++=,,,8259432121221121≥=++=++s s x x s x x s x x松弛变量(0,0) 最优解为 1x =1,x 2=3/2.标准形式:32121000811m in s s s x x f ++++=,,,,369418332021032121321221121≥=-+=-+=-+s s s x x s x x s x x s x x剩余变量(0.0.13) 最优解为 x 1=1,x 2=5.6.解:(1) 最优解为 x 1=3,x 2=7. (2) 311<<c (3) 622<<c (4)4621==x x(5) 最优解为 x 1=8,x 2=0. (6) 不变化。
《运筹学》(第二版)课后习题参考答案

生产工序
所需时间(小时)
每道工序可用时间(小时)
1
2
3
4
5
成型
3
4
6
2
3
3600
打磨
4
3
5
6
4
3950
上漆
2
3
3
4
3
2800
利润(百元)
2.7
3
4.5
2.5
3
解:设 表示第i种规格的家具的生产量(i=1,2,…,5),则
s.t.
通过LINGO软件计算得: .
11.某厂生产甲、乙、丙三种产品,分别经过A,B,C三种设备加工。已知生产单位产品所需的设备台时数、设备的现有加工能力及每件产品的利润如表2—10所示。
-10/3
-2/3
0
故最优解为 ,又由于 取整数,故四舍五入可得最优解为 , .
(2)产品丙的利润 变化的单纯形法迭代表如下:
10
6
0
0
0
b
6
200/3
0
1
5/6
5/3
-1/6
0
10
100/3
1
0
1/6
-2/3
1/6
0
0
100
0
0
4
-2
0
1
0
0
-20/3
-10/3
-2/3
0
要使原最优计划保持不变,只要 ,即 .故当产品丙每件的利润增加到大于6.67时,才值得安排生产。
答:(1)唯一最优解:只有一个最优点;
(2)多重最优解:无穷多个最优解;
(3)无界解:可行域无界,目标值无限增大;
运筹学课后习题答案

答: 与一般线性规划的数学模型相比;运输问题的数学 模型具有如下特征:1 运输问题不象一般线性规划问题 那样;线性规划问题有可能有无穷多最优解;运输问题只 有有限个最优 2 运输问题约束条件系数矩阵的元素等于 0或1;且每一列有两个非零元素 3 运输问题的解的个数 不可能大于m+n1个
2022/10/19
22
经过调整和检验;得到最后一表330才是本问题的最优解即 z*=36
经检查;沃格尔法计算所得结果z=35虽然不是最优解;但 是比较接近最优解
2022/10/19
23
5
表329
销地 B1
B2
B3
B4
产量
产地
A1
3
7
6
4
5
A2
2
4
3
2
2
A3
4
3
8
5
6
销量
3
3
3
2
解:1表328用三种方法计算;用闭回路法检验 ①用最小元素法计算如下表所示
2022/10/19
6
① 最小元素法求解如下:
销地 B1
B2
B3
B4
产量
产地
A1
4 5 1 34
68
⑤
A2 A3 销量
51
2
5 30 8
3
7
6
4
5
A2
2
4
3
2
2
A3
4
3
8
5
6
销量
3
3
2
2
解:2表329用三种方法计算;用位势法检验 因为总产量 =13;总销量=10;所以该题的总产量>总销量;所以该题 是产销不平衡的问题;故假设一销地B5 ①用最小元素法计算如下表所示
运筹学答案_第_10_章__动态规划
用,第五年继续使用,总成本=4500 元。
9.最优解为第一年购买的设备到第二、三、四年初各更新一组,用到第 5 年末, 其总收入为 17 万元。
10.最优解为第一批投产 3 台,如果无合格品,第二批再投产 3 台,如果仍全部 不合格,第三批投产 4 台。总研制费用最小为 796 元。
11.
月份
采购量
最优解:X1=4、X2=0、X3=4、X4=3 即第一个月生产 4 台,第一个月生产 0 台,第一个月生产 4 台,第一个月生
产 3 台。
最优值:Z=252000 元 4、最优解:运送第一种产品 5 件
最优值:Z=500 元 5.最大利润 2790 万元。最优安排如下表:
年度
年初完好设备 高负荷工作设备 低负荷工作设备
数
数1Βιβλιοθήκη 1250125
2
100
0
100
3
80
0
80
4
64
64
0
5
32
32
0
6.最优解(0,200,300,100)或(200,100,200,100)或者(100,100, 300,100)或(200,200,0,200)。总利润最大增长额为 134 万。
7.在区 1 建 3 个分店,在区 2 建 2 个分店,不在区 3 建立分店。最大总利润 22。 8.最优解为:第一年继续使用,第二年继续使用,第三年更新,第四年继续使
第 10 章 动态规划
1、最优解:A―B2―C1―D1―E;A―B3―C1―D1―E;A―B3―C2―D2―E 最优值:13
2、最优解:项目 A:300 万元、项目 B:0 万元、项目 C:100 万元、
最优值:Z=71+49+70=190 万元 3、设每个月的产量是 Xi 百台(i=1、2、3、4)
《运筹学》习题与答案

《运筹学》习题与答案(解答仅供参考)一、名词解释1. 线性规划:线性规划是运筹学的一个重要分支,它主要研究在一系列线性约束条件下,如何使某个线性目标函数达到最大值或最小值的问题。
2. 动态规划:动态规划是一种解决多阶段决策问题的优化方法,通过把原问题分解为相互联系的子问题来求解,对每一个子问题只解一次,并将其结果保存起来以备后续使用,避免了重复计算。
3. 整数规划:整数规划是在线性规划的基础上,要求决策变量取值为整数的一种优化模型,用于解决实际问题中决策变量只能取整数值的情形。
4. 马尔可夫决策过程:马尔可夫决策过程是一种随机环境下的决策模型,其中系统的状态转移具有无后效性(即下一状态的概率分布仅与当前状态有关),通过对每个状态采取不同的策略(行动)以最大化期望收益。
5. 最小费用流问题:最小费用流问题是指在网络流模型中,每条边都有一个容量限制和单位流量的成本,寻找满足所有节点流量平衡的同时使得总成本最小的流方案。
二、填空题1. 运筹学的主要研究对象是系统最优化问题,其核心在于寻求在各种(约束条件)下实现(目标函数)最优的方法。
2. 在运输问题中,供需平衡指的是每个(供应地)的供应量之和等于每个(需求地)的需求量之和。
3. 博弈论中的纳什均衡是指在一个博弈过程中,对于各个参与者来说,当其他所有人都不改变策略时,没有人有动机改变自己的策略,此时的策略组合构成了一个(纳什均衡)。
4. 在网络计划技术中,关键路径是指从开始节点到结束节点的所有路径中,具有最长(总工期)的路径。
5. 对于一个非负矩阵A,如果存在一个非负矩阵B,使得AB=BA=A,则称A为(幂等矩阵)。
三、单项选择题1. 下列哪项不是线性规划的标准形式所具备的特点?(D)A. 目标函数是线性的B. 约束条件是线性的C. 决策变量非负D. 变量系数可以为复数2. 当线性规划问题的一个基解满足所有非基变量的检验数都非正时,那么该基解(C)。
A. 不是可行解B. 是唯一最优解C. 是局部最优解D. 不一定是可行解3. 下列哪种情况适合用动态规划法求解?(B)A. 问题无重叠子问题B. 问题具有最优子结构C. 问题不能分解为多个独立子问题D. 子问题之间不存在关联性4. 在运输问题中,如果某条路线的运输量已经达到了其最大运输能力,我们称这条路线处于(A)状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
10.3 某公司打算向承包的三个营业区增设六个销售店,每个营业地区至少增设一个, 从各区赚取的利润与增设的销售店个数有关,其数据如表 10-11 所示。试求各区应分配几 个增设的销售店,才能使总利润最大?其值是多少?
25
28
0
2
47
53
45
53
1
3
67
72
73
57
73
2
4
89
92
92
85
65
92
1,2
5
108 114 112 104
93
70
114
1
6
126 133 134 124 112
98
73
134
2
当 k =1 时
分别取 x1为0,1,…, 6 时。其数值计算如表 10-10 所示:
表 10-10
所以,总的最大增产量为 134,最优分配方案有如下四种:
当 k =2 时, 由题意,可取 x2 1,2,3, 4, s2 2,3, 4,5 ,其数值计算如表 10-13 所示:
表 10-13
当 k =l 时, 由题意,可取 x1 1,2,3, 4 , s1 6 ,其数值计算如表 10-14 所示:
表 10-14 所以,总利润最大值为 710 万元,最优增设方案有三种:
表 10-11
解:按营业区数将此问题划分三个阶段;状态变量 sk 表示第 k 个区至第 3 个区增设的 店数; xk 表示第 k 个区增设的店数, xk 1;状态转移方程为: sk1 sk xk ;阶段指标
pk xk 表示为第 k 区内增设店数为 xk 时所取得的利润;最优值函数 fk sk 表示第 k 个区
至第 3 个区增设 sk 个店的最大利润。于是有递推关系:
其中: f4 s4 0 。
当 k =3 时, 由题意,可取 x3 s3 1,2,3, 4 ,其数值计算如表 10-12 所示:
表 10-12
7 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
解:按零售店数将此问题划分为四个阶段;状态变量 sk 表示分配给第 k 个至第 4 个零 售 店 的 货 物 的 箱 数 ; xk 表 示 分 配 给 第 k 个 零 售 店 的 货 物 箱 数 ; 状 态 转 移 方 程 为 : sk1 sk xk ;
阶段指标 pk xk )表示将 xk 箱货物分配到第 k 个店的盈利;最优值函数 fk sk 表示
表 10-3
当 k =2 时, 分别取 x2 s2 0,1,…, 6 。其数值计算如表 10-4 所示:
表 10-4
2 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
当 k =1 时,将 6 箱货物分配给零售店 l 到零售店 4 时,其最大盈利值为 分别取 x1为0,1,…, 6时,其数值计算如表 10-5 所示:
8 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
10.4 某工厂的 l00 台机器,拟分四个周期使用,在每一周期有两种生产任务。据经验,
把 x1 台机器投入第一种生产任务,则在一个生产周期中将有 x1 /3 台机器报废;余下的机器
全部投入第二种生产任务,则有 l/l0 机器报废,如果于第一种生产任务每台机器可收益 10, 于第二种生产任务每台机器可收益 7,问怎样分配机器,使总收入最大?
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 10 章 动态规划应用举例
10.1 有一部货车每天沿着公路给四个零售店运送 6 箱货物,如果各零售店出售该货物 所得到的利润如表 10-1 所示。试求给各零售店运送几箱货物能使获得总利润最大?其值是 多少?
表 10-1
表 10-8
当 k =2 时, 分别取 x2 s2 0,1,…, 6 。其数值计算如表 10-9 所示:
表 10-9
5 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
x2
p2(x2)+f3(s2-x2)
f2(s2)
x2*
s2
0
1
2
3
4
5
6
0
0
0
0
1
28
sk 箱货物分配给第 k 至第 4 个店的最大盈利值,于是有递推关系:
当 k =4 时,
分别取 x4 s4 0,1,…, 6 。其数值计算如表 10-2 所示:
表 10-2
1 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
当 k =3 时, 分别取 x3 s3 0,1,…, 6 。其数值计算如表 10-3 所示:
解:按周期将该问题划分为四个阶段,第 k 阶段为第 k 周期分配机器;状态变量 sk 表 示第 k 周期初的完好机器数;决策变量 uk 表示第 k 个周期用于第一种任务的机器台数, sk uk 表示第 k 周期用于第二种任务的机器台数;
表 10-5 所以,可以得到总利润最大值为 17,其最优分配方案有如下六种:
10.2 设有某种肥料共 6 个单位重量,准备供给四块粮田用,其每块粮田施肥数量与增 产粮食数如表 10-6 所示,试求对每块粮田施多少单位重量的肥料,Байду номын сангаас使总的增产粮食最多。
表 10-6
3 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
示将 sk 单位的肥料分配给第 k 块粮田至第 4 块粮田的最大增产量。于是有递推关系: 当 k =4 时, 分别取 x4 s4 0,1,…, 6 。其数值计算如表 10-7 所示:
表 10-7
4 / 87
圣才电子书 十万种考研考证电子书、题库视频学习平台
当 k =3 时, 分别取 x3 s3 0,1,…, 6 。其数值计算如表 10-8 所示:
解:按粮田的块数将此问题划分四个阶段;状态变量 sk 表示分配给第 k 块粮田至第 4 块粮田的肥料重量;xk 表示分配给第 k 块粮田的肥料重量;状态转移方程为:sk1 sk xk ;
阶段指标 pk xk 表示将 xk 单位的肥料分配给第 k 块粮田的增产量;最优值函数 fk sk 表
