弹性极限拧紧技术及其应用_王艳忠

合集下载

Kostyrka运动件锁紧装置在机床旋转类功能部件中的应用

加工，因此，这样的加工需求就要求旋转类功能部件应
ＡｐｌａｉｎｏｏｔｒａｃａｐｉｔｆＫｓｙｋｌｍｐｎｌｍｅｔｏｌｅｙｎｒｔｒｃｏｉｇｅｅｎｓｆｒｓｉｗａｓｉｏａｙｄ
ｆｃｉｎａｏｍｐｏｎｔｕｎｔｏｌｃｅｎｓｏｆｍａｃｎｏｏｌｈｉｅｔｓ
ｄｅｉｎｒｔｒｕｎｔｏａｏｐｎｎｓｓｇｏａｆｃｉｎｌｃｍｏｅｔ．ｙＫｅｗｏｄｙｒｓ：ＫｏｔｒａｉｇＥｌｍｅｔｒＳｉｅｙｓｙｋａＣｌｍｐｎｅｎｓｆｌｄｗａｓ；Ｏｎ／ｔｌｎｅＴｙａｏｅｗｏＦａｇｐｅＣｌｍｐｉｌｅｅ；Ｃｌｍｐｎｎｓ；ｎｇＳｅｖｓａｉｇＲｉｇＲｏａｙＦｃｉｎｌＣｏｏｅｔｆＭａｈｎｏｓｔｒｕｎｔｏａｍｐｎｎｓｏｃｉｅＴｏｌ
各项技术最为成熟，国内外各机床企业中得到了广在
泛的应用。
于许多零部件具有多角度平面，要切削刀具除了能需
够摆动进行多角度加工之外，能够实现定向定角度还
１Ｋｏｔｒａ运动件锁紧装置ｓｋｙ
Ｆｃｎｉ能郜件ｕｉｕ功ｎｌ０
Ｋｓｙｋｏｔｒａ运动件锁紧装置在机床旋转类功能部件中的应用
高秀峰① 孙璐②
（沈阳机床（团）计研究院有限公司，宁沈阳１０４； ① 集设辽１１２（沈阳铁路局沈阳通信段，宁沈阳１０２） ② 辽１００

拧紧工艺方法

拧紧工艺方法拧紧工艺方法是指在装配线上对螺栓、螺母或螺钉等零部件进行拧紧的过程。

下面列举了50条关于拧紧工艺方法的详细描述：1. 扭矩控制：通过设置合适的扭矩限制，确保螺栓拧紧到规定的扭矩值。

2. 角度控制：除了扭矩控制外，还可以通过角度控制来确保螺栓拧紧到规定的角度范围内。

3. 扭矩角度联合控制：结合扭矩和角度控制，以确保螺栓的拧紧质量。

4. 拉伸控制：通过拉伸测量来控制螺栓的拧紧力，以确保拧紧质量。

5. 拉力控制：对于需要更高精度的拧紧，可以利用拉力控制技术。

6. 高速拧紧：采用高速拧紧工艺，提高生产效率。

7. 低速拧紧：对于对拧紧精度要求较高的螺栓，可以采用低速拧紧工艺。

8. 自动拧紧：利用自动化设备进行螺栓拧紧，提高生产效率。

9. 半自动拧紧：结合人工和自动化设备进行螺栓拧紧，既保证了拧紧质量又提高了效率。

10. 手动拧紧：对于特殊情况或小批量生产，采用手动拧紧方法。

11. 螺栓松固特性的测定：通过测试螺栓的松固特性，选择合适的拧紧工艺。

12. 螺母端座设置：设计合适的螺母端座，以确保螺栓在拧紧过程中不受损。

13. 拧紧序列设计：合理设计螺栓的拧紧顺序，避免因为拧紧顺序不当而引起的问题。

14. 螺纹润滑：在拧紧过程中保证螺纹的润滑，减小拧紧时的摩擦力。

15. 拧紧设备校准：定期对拧紧设备进行校准，确保其拧紧准确度。

16. 螺纹清洁：在进行拧紧前，清洁螺栓和螺母的螺纹，避免因杂质导致的拧紧不良。

17. 拧紧力矩分析：分析拧紧力矩曲线，判断拧紧质量。

18. 拧紧工艺优化：结合实际情况，优化拧紧工艺，提高生产效率和产品质量。

19. 螺栓拧紧传感器：利用拧紧传感器监测螺栓的实际拧紧情况，实时反馈拧紧力矩。

20. 拧紧过程监控：通过监控拧紧过程，及时发现问题并采取措施。

21. 拧紧参数记录：记录每个螺栓的拧紧参数，建立拧紧数据档案。

22. 拧紧防错措施：采取措施确保错误螺栓拧紧情况的发现和纠正。

23. 自动拧紧机器人：利用机器人进行螺栓的自动拧紧作业，提高生产效率。

拧紧工艺方法

拧紧工艺方法1. 拧紧工艺方法是一种用于紧固螺母、螺栓或螺钉的过程，它通常用于确保机械部件的安全和稳固。

2. 拧紧工艺方法的主要目的是将螺栓或螺母紧密地固定在机械部件上，以防止松动或脱落。

3. 常见的拧紧工艺方法包括手动拧紧、使用扭矩扳手拧紧、气动/电动螺丝刀拧紧以及液压拧紧等。

4. 在手动拧紧中，操作人员使用扳手或扳手将螺栓或螺母旋紧到所需的扭矩值。

5. 使用扭矩扳手进行拧紧时，扭矩扳手会发出声音或者振动来提示操作人员螺栓或螺母已经到达预定的扭矩值。

6. 气动/电动螺丝刀拧紧速度快，适用于大批量的紧固作业，能提高工作效率。

7. 液压拧紧通常用于大型螺栓的拧紧，通过液压力传递来提供高扭矩，适用于工业设备和桥梁结构的拧紧。

8. 在拧紧工艺中，关键是要准确控制扭矩，以确保螺栓或螺母不会过紧或者过松。

9. 另一个重要的因素是操作人员的技能和经验，他们需要准确地判断何时螺栓或螺母已经达到所需的紧固度。

10. 拧紧工艺方法也可以根据需要选择使用预紧力或者角度控制来进行螺栓的紧固。

11. 预紧力是指在正式拧紧之前，根据材料和设计要求施加一定的初始力以使螺栓预压设备部件。

12. 角度控制是指除了扭矩控制外，还根据螺栓的旋转角度来确定螺栓的紧固状态，适用于一些特殊的机械部件。

13. 拧紧工艺方法的选择需要根据具体的应用场景以及机械部件的特点来确定，以确保紧固的准确性和可靠性。

14. 在拧紧工艺中，要根据材料和环境温度等因素，调整扭矩或者预紧力的数值，以适应不同的工作条件。

15. 拧紧工艺也需要考虑到螺栓的强度和材料特性，以确保在不超过其承受范围的情况下完成紧固。

16. 对于需要高精度和高可靠性的拧紧工艺，可以采用联机监控系统来实时监测拧紧力和角度，以确保紧固的准确性。

17. 针对特殊工艺要求，还可以选择激光测量或者超声波测量等高精度的测量方法来进行拧紧工艺的监控和调整。

18. 随着工业自动化程度的不断提高，一些先进的拧紧工艺方法还可以实现自动化控制和远程监控。

拧紧工艺书籍

拧紧工艺书籍拧紧工艺是指通过紧固装置对螺纹连接进行紧固的过程。

它在工业生产中具有重要的应用，涵盖了机械制造、汽车制造、航空航天、船舶制造、电子电气等众多领域。

以下是一些与拧紧工艺相关的参考书籍，可供工程师和技术人员参考使用。

1.《拧紧工艺与设备》（作者：周威飞、高玄民）：本书系统介绍了拧紧工艺及其设备的基本概念、原理、方法和技术要求。

内容包括拧紧工艺的基础知识、拧紧工艺要求与控制、拧紧工艺设备及系统、拧紧工艺的计算与控制等。

对于想要了解和掌握拧紧工艺的读者来说，本书是一本很好的入门参考。

2.《拧紧技术手册》（作者：Milos Krajcar）：本书详细介绍了拧紧工艺中的各种技术和应用。

内容包括套筒扳手和扭矩扳手的使用方法、螺栓预紧力的控制、紧固力矩的计算和控制、拧紧力矩的测量仪器等。

书中配有大量的图示和实例，方便读者理解和应用拧紧技术。

3.《紧固件手册》（作者：蒋建锋）：本书是一本综合性的紧固件参考手册，对于需要选择和应用紧固件的工程师和技术人员非常有用。

书中内容包括不同类型的螺栓、螺母、垫圈、螺柱等紧固件的选用原则和使用方法，以及拧紧力矩的计算和控制等。

此外，还介绍了紧固件的材料、表面处理和质量控制等方面的知识。

4.《机械拧紧工艺与质量控制》（作者：王志红、于建海）：本书主要介绍了机械拧紧工艺及其质量控制的理论和实践。

内容包括螺纹连接和拧紧工艺的基本原理、拧紧力矩控制的方法和技术要求、拧紧质量的检测与评价、机械拧紧工艺的优化和改进等。

书中还提供了拧紧工艺案例和实验的数据分析，有助于读者理解和应用机械拧紧工艺。

5.《紧固技术与拧紧工艺》（作者：杨贞忠、曲存红）：本书主要介绍了紧固技术和拧紧工艺的理论和应用。

内容包括螺纹连接和紧固件的基本知识、拧紧力矩和拧紧角度的控制方法、拧紧工艺参数的选择和调整、拧紧质量的检验和控制等。

本书在理论和实践的结合上进行了深入的探讨，对于需要应用紧固技术和拧紧工艺的工程师和技术人员来说是一本很好的参考手册。

拧紧技术基本知识

21
扭矩 OK, 角度过低
扭矩扭矩 = OK 角度 = 过低
扭矩 = OK
角度 = OK
角度
阿特拉斯科普柯中国香港有限公司 - ACTA
22
扭矩 OK, 角度过高
扭矩
扭矩 = OK 角度 = 过低
扭矩 = OK 角度 = OK
扭矩 = OK 角度 = 过高
角度
阿特拉斯科普柯中国香港有限公司 - ACTA
9
螺栓标识系统
生产商
第一个数 = 1/100 的最大抗张应力 (N/mm2) 100×8 = 800 N/mm2
第二个数 = 抗张应力与屈服之间的关系 0.8 = 80% 公制螺纹
两数相乘得出屈服应力 800* 0.8 = 640 N/mm2
阿特拉斯科普柯中国香港有限公司 - ACTA
10
抗拉强度 / 屈服
应力 N/mm²
抗拉强度
失效 75 % 抗拉应力 100* 8=800 N/mm2
屈服
弹性区
屈服应力 800* 0,8=640 N/mm2
拉伸度
阿特拉斯科普柯中国香港有限公司 - ACTA
11
螺纹类型
套筒对边尺寸12 mm
• M • UNF • UNC
公制英制细螺纹英制粗螺纹
< 30 度 (ISO 5393)
角度
贴合点
扭矩
X Nm > 720 度
软连接
> 720 度 (ISO 5393)
角度
贴合点
阿特拉斯科普柯中国香港有限公司 - ACTA
13
扭矩
硬连接和软连接
过扭
目标
硬软
均值偏差

高压自紧式（R-CON）法兰在化工施工中的应用

-1/2
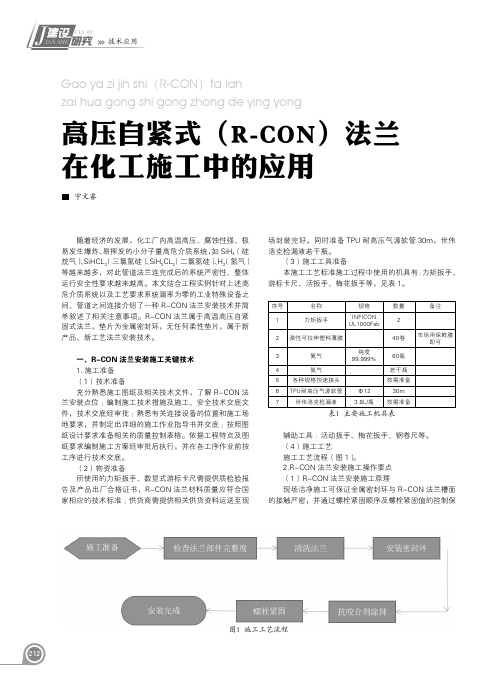
5-1/4,6
2,2-1/2,3
7,6-3/4
4
8-1/2
5
9-3/8
6
10-1/2
8
表2 螺栓扭矩参数表
力矩Torque (N/m)
60 90 110 180 280 405 580
力矩紧固螺杆，每次结束后都要用塞尺检查间距。按照操作规程对螺杆使用 100% 的力矩进行检查，重复检查三次，每次间隔 4 小时。
螺栓型号 Stud Bolt Size
1/2-13 UNC-2 5/8-11 UNC-2 3/4-10 UNC-2 7/8-9 UNC-2
1-8 UNC-2 1-1/8-8 UNC-2 1-1/4-8 UNC-2
螺栓长度（inch） Stud Bolt Length
R-CON夹型号 Clamp Size
（2）R-CON 法兰安装施工适用范围该方法适用于 500℃及以上高温、4.0MPa 以上压力、腐蚀性、有毒介质、易燃易爆等系统。（3）检查法兰部件完整度 ①组织业主、监理、施工方现场检查 R-CON 法兰密封面及密封环的沙眼、气孔以及椭圆度是否符合要求等进行检查确认。 ②利用游标卡尺、角尺调整测量法兰轴向同心度、纵向法兰面平行度。（4）清洗法兰明确清洁施工目的，开展班前交底，强化规范施工意识。现场专人监护，记录洁净施工状态；使用洁净手套和软绸布清洁 HUB 法兰面无颗粒状异物，并用紫光灯检测密封面清洁油污状况每平方厘米内油污小于 4 处（紫光灯照射油污产生荧光反射）。（5）安装密封环将检查完好的垫片置于 R-CON 槽中，必要时可使用木质条板或塑料条板的辅助工具辅助密封环的固定（厚度为 5mm 左右），调节手扳葫芦安装法兰或人孔端盖。注意：为了确保密封性能，不要用手支撑密封环防止密封环污染。（6）抗咬合剂涂抹现场螺栓、螺母、卡套内侧需使用高温抗咬合剂对其进行润滑，防止在二次拆卸检查时不能进行正常拆卸，螺杆与螺母接触面以及两个方向延伸的 2-3 个螺距必须均匀涂有高温抗咬合剂，卡套内侧两面满涂高温抗咬合剂。（7）螺栓紧固 ①采用数显式双头扭力扳手，按照自研规定螺栓扭矩值和紧固顺序紧固螺栓，保证对角螺栓力矩，按照规定次数和扭矩紧固。进行现场班前交底，现场由专人指导并记录明确每一种规格螺栓的扭矩值。明确并严格按照指定螺栓紧固数值紧固螺栓，不得随意变更力矩值紧固。 ②使用数显式扭力扳手，按表 2 扭矩参数表规范扭矩值施工，记录扭矩数值，确保资料同步，终拧后使用同扭矩值复检，确保扭矩达到规定标准。 ③安装螺杆并对角拧紧，使用塞尺测量卡套的距离。根据试验测定的指定力矩拧紧，同时周期性（每次力矩紧固结束后）的对卡套的距离进行测量，如果卡套间距因为操作不当出现了较大的偏差，则会破坏密封环，造成泄露。检查连接处，确保连接处有一定的缝隙，只有在螺杆完全上紧的情况下卡套面才能完全接触。 ④使用螺栓扭矩参数表的 20% 的力矩紧固螺杆，使用塞尺检查 HUB 端面间距，间距差不得大于 0.1mm。依次使用螺栓扭矩参数表的 25%、40%、60% 和 100% 的

一种多自由度拧紧装置

专利名称：一种多自由度拧紧装置
专利类型：实用新型专利
发明人：盛冬平,陈康,何亚峰,门艳忠,吴小锋,尹飞鸿申请号：CN202121134175.3
申请日：20210525
公开号：CN215616299U
公开日：
20220125
专利内容由知识产权出版社提供
摘要：本实用新型公开了一种多自由度拧紧装置，包括基座、拧紧机构、角度调节机构和上钉机构；所述拧紧机构上下活动地设于基座上；所述角度调节机构与基座转动连接；所述上钉机构与角度调节机构固定连接；所述角度调节机构用于调节上钉机构的偏移角度；当所述拧紧机构向下运动时，拧紧机构的拧紧端穿过角度调节机构并伸入上钉机构中。

本实用新型设置了角度调节机构，能够调节上钉机构的偏移角度，并且拧紧机构向下运动时，拧紧机构的拧紧端穿能够过角度调节机构并伸入上钉机构中，从而实现拧紧螺钉，无需像现有技术中需要移动整个拧紧轴的运动的从而提高了工作效率，而且还能调节上钉机构的偏移角度来实现针对一些偏僻位置的螺钉进行拧紧，适用性强。

申请人：常州工学院
地址：213032 江苏省常州市新北区辽河路666号
国籍：CN
代理机构：常州佰业腾飞专利代理事务所(普通合伙)
代理人：王巍巍
更多信息请下载全文后查看。

输毛管中流场状态对纤维丝束开松处理效果的影响

第32卷㊀第3期2024年3月现代纺织技术Advanced Textile TechnologyVol.32,No.3Mar.2024DOI :10.19398∕j.att.202308011输毛管中流场状态对纤维丝束开松处理效果的影响王㊀进1,程贺棚1,李㊀帅1,卢㊀贺2,崔永志2,千翠娥2,于贺春1(1.中原工学院机电学院,郑州㊀450007;2.恒天重工股份有限公司,郑州㊀450000)㊀㊀摘㊀要:纤维输毛管的设计对粘胶纤维或Lyocell 短纤维丝束的开松效果至关重要㊂为了探究纤维丝束在输毛管中的开松机理以及管道内流场状态对纤维运动状态的影响,采用三维建模软件建立输毛管流场模型,在商用软件Cradle CFD 中建立纤维丝束模型结合流场进行耦合计算,研究分析了2000根长度为38mm 纤维丝束在输毛管中的运动过程㊂结果表明:在输毛管中纤维丝束受到流场作用的差异形成了纤维丝束运动的速度差,这是纤维丝束开松的主要原因;输毛管的竖直圆形管道处存在较大的压力梯度,使纤维丝束整体受到压力差异,也为纤维开松创造条件;输毛管的锥型管位置处的速度场较复杂,有利于纤维丝束开松;管径的变化导致产生漩涡,阻碍了纤维的输送㊂研究结果可为化纤与纺织行业输毛管设计提供参考㊂关键词:输毛管;流场模型;Cradle CFD;纤维丝束;开松中图分类号:TS152.8㊀㊀㊀文献标志码:A㊀㊀㊀文章编号:1009-265X(2024)03-0029-09收稿日期:20230808㊀网络出版日期:20231025基金项目:国家自然科学基金项目(51875586); 纺织之光基础研究项目(2017104,2019067)作者简介:王进(1991 ),女,河南新乡人,讲师,主要从事纺织机械设计方面的研究㊂通信作者:于贺春,E-mail:yuhechun1106@㊀㊀在化纤行业中,粘胶或Lyocell 短纤维的开松处理是纤维成品前的一道重要工序,而开松处理设备通常选用输毛管㊂输毛管将经多台切断机切断的束状粘胶或Lyocell 短纤维开松冲散,并输送到给纤槽和精炼机,利于给纤槽均匀铺毛㊁加强精炼机淋洗效果,提高纤维成品品质㊂然而,传统的输毛管主要起输送作用,对开松纤维要求不高[1]㊂探索束状纤维在输毛管中的开松机理及管道内流场状态对纤维运动状态的影响,对促进输毛管管道结构合理化设计,提高纤维开松效果至关重要㊂随着计算流体力学技术的发展,目前含纤维流场的计算流体动力学(Computational fluid dynamics,CFD)模拟在纺织领域受到广泛关注㊂钱成等[2]通过单向耦合方法对集聚纺集聚区内流场分布及纤维运动轨迹进行了模拟,结果发现相比于四罗拉积聚纺,全聚纺内纤维聚集较为均匀,只有少量缠绕㊂邓茜茜等[3]通过比较输棉通道不同位置时转杯纺纱通道内气流分布特征及纤维运动轨迹的差异,分析了不同工况下的气流分布特征和流场对纤维运动的影响㊂林惠婷等[4]采用数值模拟和实验相结合的方法研究转杯纺纱通道内的气流流动特性㊁气流流动与纤维运动形态的关系,进而对纺纱器结构和纺纱工艺参数进行优化设计㊂Chen 等[5]使用转杯中的纤维的粒子模型来探索影响粒子在凝聚槽内运动的因素,给出了纤维粒子运动的数学模型㊂Yang 等[6]利用流体动力使平行于输送它们的主流体的单根纤维对齐,基于在近乎无旋流中使用收敛流线来提供必要的力矩来使纤维旋转,将纤维运动和气流流向进行了耦合计算㊂Hamedi 等[7]研究具有不同取向角度㊁长度和柔韧性的单个纤维在单个圆柱形物体周围的行为,结果表明纤维的初始取向角对纤维与圆柱体接触时的柔韧性和形状有影响㊂杨瑞华等[8]通过Fluent 和EDEM 模拟了纤维在转杯纺纱通道内的运动状况,分析了1mm 和16mm 纤维在转杯内的运动特征㊂韩万里等[9]通过数值模拟和实验验证相结合验证了纤维在熔喷气流场中的运动轨迹,发现纤维成形过程中出现连续的半环形牵伸圈㊁鞭动对纤维细化有重要影响㊂目前国内外有关纤维运动的研究多集中在流场对单纤维运动状态的影响,而关于含大量纤维的纤维丝束在流场中的运动状态的研究尚少,因此开展流场对纤维丝束的开松影响的研究具有愈发重要的意义㊂综上所述,本文通过建立输毛管流场模型和纤维模型,利用流体仿真软件Cradle CFD 对纤维丝束在输毛管流场中的运动过程进行耦合计算,比较输毛管不同位置处流场的分布特征及不同时刻下纤维运动轨迹,探究纤维丝束在输毛管中输送时的开松机理,以及输毛管内流场状态对纤维运动的影响㊂本文研究可以为化纤与纺织行业输毛管设计提供参考㊂1㊀输毛管流场模型构建1.1㊀几何模型利用三维建模软件建立的研究对象模型如图1所示,输毛管模型主要为竖直圆形管道L 1,水平圆形管道L 2㊁L 3,长度分别为l 1㊁l 2㊁l 3;U 型管道U 1;圆锥管C 1;弯管W 1㊁W 2㊂模型参数:竖直圆形管道L 1管径D 1为200mm,长度l 1为1000mm;水平圆形管道L 2㊁L 3管径D 2为300mm,长度l 2为2000mm,l 3为2000mm;圆锥管C 1的小孔径为D 1㊁大孔径为D 2,长度l 4为200mm;U 型管是半径为500mm 的半圆,弯管W 1㊁W 2曲率半径为200mm㊂1.2㊀系统描述输毛管流体输送系统遵循三大守恒定律:质量守恒㊁动量守恒㊁能量守恒㊂本文研究暂不涉及温度变化对输毛管输送纤维的影响,所以输毛管中流场输送满足方程(1)即可:∂ρ∂t+div(ρu )=0(1)㊀㊀输毛管中的液体介质流动为不可压缩流体,因此密度ρ不随时间变化,式(1)可以变化为:div(ρu )=0(2)㊀∂(ρu i )∂t+div(ρuu i )=div(μgrad u i )-∂p ∂x i +S i(3)式中:t 表示时间;u 表示流体速度矢量;u i (i =1,2,3)表示u 在坐标分量x i (i =1,2,3)方向上的分量;μ表示粘度系数;p 表示压力;S i 表示x i 方向上的广义源项㊂流场采用瞬态,压力求解器,RNG k-ε湍流模型及壁面函数法进行计算,对流项采用二阶迎风格式离散,用基于SIMPLEC 的PISO 算法对流场进行求解㊂1.3㊀网格模型和边界条件Cradle CFD 前处理可以对导入的管道三维模型进行网格划分,由于计算的流体区域较为规则,所以对整体区域直接进行网格划分,整体采用六面体结构网格,并且对管道边缘的管壁区域进行网格细化㊂图2(a)所示为Cradle CFD 对模型进行网格划分前的八分木模型,图2(b)所示为管道模型网格划分后的模型㊂图1㊀管道模型Fig.1㊀Pipemodel图2㊀网格划分Fig.2㊀Grid division㊀㊀边界条件设置:对于进口边界,根据实际工程需要,该输毛管入口的流体入流条件设置为速度入流1m∕s;对于出口边界设置为静压出流-自然流出;对于固体边界,管道壁面采用无滑移边界条件㊂㊃03㊃现代纺织技术第32卷2㊀纤维模型的建立2.1㊀动力学方程纤维作为长径比大的柔性体,与普通刚性体相比,其物理特征相对比较复杂,不仅考虑纤维自身的弯曲变形,还要考虑其空间位移变化㊂为了表示纤维在运动过程中所展现出的柔性特征,Cundall等[10]提出离散元法(DEM)对不连续材料的运动进行求解分析㊂在离散元法中,将不连续材料表示为固体粒子的集合体,并根据牛顿第二定律求解每个粒子的运动方程,以此表示不连续材料的流体运动㊂纤维粒子动力学方程表示为:m id 2r id t2=F b +F D (4)式中:m i 表示粒子i 的质量;r i =x i (t )i +y i (t )j +z i (t )k表示粒子i 在流场中的位置;F b 表示粒子i 受到的弯曲恢复力;F D 表示粒子i 在流场中受到的阻力㊂根据粒子在流场中的动力学方程,得到不同时间粒子的流场位置,即纤维在流场中的运动轨迹㊂纤维在输毛管中与流体的耦合运动,可以视为纤维的质量和受力全部集中在球状粒子上,球状粒子在输毛管流场中的空间位置变化即代表着纤维在输毛管流场中的运动㊂如图3所示,本文通过将多个大小相同的粒子通过一维连接成弦状来表示纤维这种长径比和变形比较大的纤维模型,其相邻粒子之间的联结被看作由一个弹簧,阻尼器构成㊂其采用Choi 等[11]的模型,该模型是一个非线性的弹簧模型,它考虑了纤维的屈曲对弯曲运动的影响,相邻粒子之间的连接对拉伸运动具有恢复力F s ㊂F s 可用式(5)表示:图3㊀纤维模型Fig.3㊀Fiber modelF s =0,其他k s (x i -x j -L ),x i -x j >L{(5)弯曲运动是表达纤维运动的重要因素,Choi 模型充分描述了相邻的粒子的运动,相邻粒子间压缩或弯曲运动的恢复力可用公式(6) (8)表示㊂㊀㊀㊀㊀κ=2L sin c -1x i -x j L()(6)㊀㊀f b =k b κ2L 3cos κL 2()-sinc κL 2()éëêêùûúú-1(7)F b =0,x i -x j >L C b (x i -x j -L )ξij ,f b <C b (x i -x j-L )f b ξij ,其他ìîíïïïï(8)式中:F s,b 表示拉伸∕弯曲运动的恢复力;k s,b 表示弹簧抗拉伸∕弯曲运动的刚度;C b 表示屈曲前弹簧抗小变形的刚度,通常与k s 相同㊂x i ,j 表示粒子坐标位置;ξi ,j 表示粒子x i 到x j 的方向向量;κ表示曲率;L 表示弹簧的自然长度,通常是粒子间的初始距离㊂纤维在输毛管中所受到的外力主要是流场施加的,其对纤维的阻力F D [12]可表示为:F D =β1-εu f -v p ()V p(9)式中:β表示动量交换系数;ε表示孔隙率;u f 表示流体速度;v p 表示粒子速度;V p 表示粒子体积㊂2.2㊀接触模型与凝聚模型由于粘胶纤维采用NMMO 甲基吗啉溶剂法生产,在进入到输毛管入口时具有一定的粘性,因此在建立纤维丝束模型时引入了接触模型和凝聚模型㊂纤维和壁面以及纤维和纤维之间的接触采用Hertz-Mindlin 模型[13]㊂其法向弹性力F ns 与法向重叠数δ的函数关系公式表示为:F ns =-43E ∗R ∗δ32(10)当量杨氏模量E ∗和当量半径R ∗定义为:1E ∗=(1-v 2i )E i +(1-v 2j )E j (11)1R ∗=1R i +1R j(12)式中:E i 和E j 表示接触粒子的杨氏模量;v i 和v j 表示接触粒子的泊松比;R i 和R j 分别表示接触粒子的半径㊂凝聚模型为线性模型,线性模型提供相互平行作用的线性和阻尼元件,线性分量提供线性弹性(无张力)摩擦行为,而阻尼分量提供粘滞行为㊂粘聚力F cohesion [14]与法向重叠数δ的函数关系表示为:㊃13㊃第3期王㊀进等:输毛管中流场状态对纤维丝束开松处理效果的影响F cohesion =kA(13)A =2πR ∗δ(14)式中:k 表示内聚力能量密度;取100J∕m 3㊂如图4所示,纤维丝束模型是单纤维模型矩阵排列而成的束状模型,纤维的密度为1540kg∕m 3,摩擦系数为0.7,滚动阻力系数为0.2,泊松比为0.25,弹簧常数为50N∕m㊂图4㊀纤维丝束模型Fig.4㊀Fiber tow model3㊀模拟结果分析3.1㊀输毛管中的压强与速度分布分析图5显示了输毛管Y =0㊁X =3.1m 截面处压力分布㊂图5(a)显示冲毛水在输毛管中流动时管内及对管壁各处的压力自入口处-8770Pa 逐渐增大到U 型管U 1最低处的6101Pa,其原因是冲毛水流速与深度不断增加的双重作用下,冲毛水产生较大的压力梯度㊂而随着液位上升,在U 型管最低处至U型管与锥型管C 1接口处,管内的压力逐渐减小至1405Pa㊂锥型管C 1口径200mm 增大到300mm,由于管径的增大,冲毛水自锥型管C 1流入到水平管L 1,L 3中,冲毛水流动状态转变为不充满状态,从图5可以看出,管内的压力分布为622~1405Pa,在水平管L 2和水平管L 3中冲毛水液面位置处管内压力为622Pa,输毛管底部压力为1405Pa㊂输毛管内的液体压力梯度使纤维在管道中输送时受到不同的压力作用,对纤维丝束的输送开松有一定的作用㊂㊀㊀㊀㊀图5㊀输毛管Y =0,X =3.1m 截面处压力分布图Fig.5㊀Pressure profile of the fiber delivery tube at Y =0,X =3.1m cross section㊀㊀图6显示了输毛管在Y =0㊁X =3.1m 截面处的流体速度分布和矢量分布㊂从图6(a)可以看出,在输毛管的入口边界条件速度为1.0m∕s 时,冲毛水在管壁附近的速度为0.1m∕s,管内部的流体速度为1.0m∕s,管道内存在较大的速度梯度;在竖直管L 1部分,冲毛水在入口速度和重力的作用下流动,其速度均匀维持在1.0m∕s,而在U 型管U 1部分可以看到,由于管路形式发生改变,在㊃23㊃现代纺织技术第32卷竖直管L 1与U 型管U 1连接处,流场速度发生了微变,冲毛水速度从1.0m∕s 左右增加到1.1m∕s,变化的速度区域主要集中在U 型管左半部分,从竖直管L 1与U 型管连接处延伸到了U 型管最低处㊂U 型管右半部分的流场速度依旧稳定在1.0m∕s左右,U 型管与锥型管C 1连接弯管W 1处流场速度产生了较复杂的速度场交混区域,这是因为冲毛水顺着U 型管右半部分运动到弯管W 1位置时,冲毛水撞击弯管管壁,产生能量且运动方向发生急剧变化,从而导致冲毛水的流速度在瞬间产生了升高和降低的不同速度变化,其速度区间主要集中在0.4㊁1.0㊁1.3m∕s,是输毛管管道流场较为复杂的区域㊂冲毛水流入到输毛管的水平管L 2时,由于流体域体积发生变化,流场中速度从弯管W 1处1.3m∕s 逐渐减小至0.6m∕s,此处流场的速度大幅下降有利于纤维丝束的开松,但影响纤维的输送速率㊂从图6(a)和图6(b)可以看出,冲毛水经过弯管W 2处冲毛水速度从0.6m∕s 增长到1.3m∕s,与输毛管U 型管与水平管连接弯管处W 1的流场情况相似,冲毛水运动过程中撞击管壁,运动方向发生变化,流速主要表现为增大㊂图6(b)显示,相比于图6(a)水平管L 2处,水平管L 3内流场速度较大,其不同速度场域分布较多但速度相差不大㊂速度主要集中在0.7~1.1m∕s,速度梯度较小,有利于纤维的均匀输出㊂锥形管C 1的设置减小了冲毛水在输毛管流动时的体积占比,使生产过程中产生的硫化等有害气体与液体分离,便于后续收集㊂图6(c)显示弯管W 1与锥形管C 1连接处,冲毛水水流方向发生改变,又因为锥形管C 1管径从200mm 增大至300mm 导致锥形管下部产生流体漩涡㊂而图6(d)中,水平管道L 3流场矢量方向一致,有利于纤维的持续输送㊂图6㊀输毛管Y =0,X =3.1m 截面处速度及矢量图Fig.6㊀Velocity and vector diagram of the fiber delivery tube at Y =0,X =3.1m cross section3.2㊀纤维在输毛管中的运动分析图7 图11显示了不同时刻下2000根长度为38mm 纤维丝束在输毛管中的运动开松状态㊂图7显示,0.02s 时,纤维丝束由切断机切断初始进入输毛管中,束状纤维丝束聚集紧密,受到冲毛水的作用较小,参考速度标尺,纤维丝束整体各部分速度相同,在冲毛水输送和重力的作用向前运动㊂对比㊃33㊃第3期王㊀进等:输毛管中流场状态对纤维丝束开松处理效果的影响图7(a)和图7(b)可以看出,0.02~1.0s过程中,纤维丝束整体做加速运动,1.0s时纤维丝束由于受到的冲毛水的作用不均匀,纤维丝束局部运动速度在0.8~1.3m∕s区间,纤维丝束整体发生位错,进行开松㊂图8(a)显示,2s时纤维丝束紧贴输毛管管壁运动,在U型管底部纤维丝束整体运动方向发生渐变,贴附管壁的向前运动的过程中纤维速度降低,但部分呈现出疏松状㊂此刻纤维速度为0.75m∕s,小于冲毛水的速度1.0m∕s,纤维向前输送的动力主要是输毛管中冲毛水的作用㊂从图8 (b)可以看出,3s时纤维丝束在经过U型管与锥型管连接弯管W1时,纤维整体开松面积增大,纤维速度差异明显,纤维在经过弯管复杂的流场区域为纤维丝束开松创造了有利条件,这与图6(a)表现出的流场特征相印证㊂图9显示,纤维经过锥型管C1时,进入到水平管L2时,纤维整体被分割为两部分在输毛管中运动,一部分纤维在向前运动时出现回流运动现象,这是由于受到流场中漩涡的影响,与图6(c)流场状态相一致㊂前者在水平管道中运动速度降低,聚集在一起,这是因为在水平管L2处,冲毛水的速度经过弯管W1时先增大后减小所导致的㊂后者在漩涡中做转圈运动,因此管道的设计应避免管道漩涡的出现,这与茅孙良等[15]研究相一致㊂从图9 图11可以看出,5~8s时明显看到纤维被水流漩涡完全分成两部分,前者纤维整体经过水平弯管W2处速度随冲毛水增大,在水平管道L3中整体进一步拉长开松,但没出现整体分割现象,而是连续输送出㊂纤维在经过管道的弯管处时,流场中的速度容易发生骤变,有利于纤维开松,在管道水平处输送时,纤维整体被拉长,聚集密度降低,保证纤维开松的同时也使纤维持续均匀输出㊂㊀㊀㊀㊀㊀图7㊀0.02s㊁1s时纤维运动轨迹及局部放大示意图Fig.7㊀Fiber movement trajectory and local amplification schematic at0.02s and1s㊀㊀㊀㊀㊀图8㊀2s㊁3s时纤维运动轨迹及局部放大示意图Fig.8㊀Fiber movement trajectory and local amplification schematic at2s and3s㊃43㊃现代纺织技术第32卷㊀㊀㊀㊀㊀图9㊀4s㊁5s时纤维运动轨迹及局部放大示意图Fig.9㊀Fiber movement trajectory and local amplification schematic at4s and5s㊀㊀㊀㊀㊀图10㊀6s㊁7s时纤维运动轨迹及局部放大示意图Fig.10㊀Fiber movement trajectory and local amplification schematic at6s and7s图11㊀8s时纤维运动轨迹及局部放大示意图Fig.11㊀Fiber movement trajectory and localamplification schematic at8s4㊀结㊀论利用了流体仿真分析软件对含2000根长度为38mm纤维丝束在输毛管中的运动过程进行了数值模拟研究,分析讨论了纤维丝束在输毛管中的开松机理;比较输毛管不同位置处流场的分布特征及不同时刻下纤维运动轨迹,探究了输毛管流场状态对纤维运动轨迹的影响,得到了以下主要结论:a)当纤维丝束进入竖直管道中,在水流和自身重力作用下呈现加速状态;管道流场中存在压力梯度和速度梯度,纤维在管道中的输送过程受流体作用产生局部速度差,促使纤维位错,达到开松效果㊂b)冲毛水在输毛管弯管处流速变化较大,产生的速度梯度有利于纤维丝束开松;水平管道流场速度梯度较小,速度变化较为平稳,使纤维整体呈现拉长开松,提高纤维在输送过程中的开松效果,并持续均匀输出㊂c)输毛管管径尺寸的突然增大导致输管道产生漩涡,阻碍纤维的向前输送,因此输毛管管道设计应当避免管径尺寸的突然增大,以减少纤维缠绕现象㊂㊃53㊃第3期王㊀进等:输毛管中流场状态对纤维丝束开松处理效果的影响本文研究结果阐述了纤维丝束开松的基本机理,揭示了输毛管内流场状态对纤维输送的影响,研究结果可以为化纤与纺织行业的输毛管设计提供参考㊂参考文献:[1]千翠娥,王朝辉,任晓霞,等.一种适用于粘胶短纤维输毛管的纤维管路开松装置:CN205474156U[P].2016-08-17.QIANCui'e,WANG Chaohui,REN Xiaoxia,et al.A fiber pipeline opening device suitable for viscose staple fiber delivery pipe:CN205474156U[P].2016-08-17. [2]钱成.集聚纺集聚区内流场分布及纤维运动轨迹模拟分析[D].无锡:江南大学,2020.QIAN Cheng.Simulation and Analysis of Flow Field Distribution and Fiber Trajectory in Aggregation Region of Compact Spinning[D].Wuxi:Jiangnan University,2020.[3]邓茜茜,杨瑞华.输棉通道位置对转杯纺纤维运动的影响[J].丝绸,2020,57(8):42-49.DENG Qianqian,YANG Ruihua.Effect of fiber transport channel position on fiber motion in rotor spinning[J]. Journal of Silk,2019,57(8):42-49.[4]林惠婷.转杯纺纺纱器气流场分布及纤维在输纤通道内运动的研究[D].上海:东华大学,2017. LINHuiting.Study on The Airflow Characteristics and Fiber Motion in the Transfer Channel in Rotor Spinning[D]. Shanghai:Donghua University,2017.[5]CHEN R H,SLATER K.Particle motion on the slide wall in rotor spinning[J].Journal of the Textile Institute,1994, 85(2):191-197.[6]DANG H H.Dynamic analysis method for fluid-structure interaction based on ANSYS[J].Ship&Ocean Engineering,2008,37(6):86-89.[7]HAMEDI N,WESTERBERG L G.Simulation of flexiblefibre particle interaction with a single cylinder[J].Processes, 2021,9(2):191.[8]杨瑞华,何闯.纤维在转杯和输纤通道中的运动模拟[J].丝绸,2022,59(7):40-48. YANGRuihua,HE Chuang.Simulation of fiber movement in the rotor and fiber transport channel[J].Journal of Silk, 2022,59(7):40-48.[9]韩万里,谢胜,王新厚,等.熔喷气流场中的纤维运动模拟与分析[J].纺织学报,2023,44(1):93-99. HAN Wanli,XIE Sheng,WANG Xinhou,et al.Simulation and analysis of fiber motion in airflow field of melt blowing [J].Journal of Textile Research,2023,44(1):93-99.[10]CUNDALL P A,STRACK O D L.A discrete numericalmodel for granular assembles[J].Géotechnique,1979, 29(1):47-68.[11]CHOI K J,KO H S.Stable but Responsive cloth[J].ACM Transactions on Graphics,2002,21(3):604-611.[12]SAKAI M,TAKAHASHI H,PAIN C,et al.Study on alarge-scale discrete element model for fine particles in a fluidized bed[J].Advanced Powder Technology,2012, 23(5):673-681.[13]熊海浪.纤维在旋转气流场中的耦合运动机理研究[D].杭州:浙江理工大学,2022.XIONGHailang.Study on the Mechanism of Coupled Motion of Fibers in A Rotating Airflow Field[D].Hangzhou:Zhejiang Sci-Tech University,2022. [14]LUPO M,SOFIA D,BARLETTA D,et al.Calibration ofDEM simulation of cohesive particles[J].Chemical Engineering transactions,2019,74:379-384. [15]茅孙良,贺广明.配有U形输毛管的粘胶短纤维输毛装置:CN210341167U[P].2020-04-17.MAO Sunliang,HE Guangming.Viscose staple fiber wool conveying device with U-shaped wool conveying tube: CN210341167U[P].2020-04-17.㊃63㊃现代纺织技术第32卷Influence of flow field state in fiber delivery tube on the opening and loosening of fiber towsWANG Jin 1,CHENG Hepeng 1,LI Shuai 1,LU He 2,CUI Yongzhi 2,QIAN Cui 'e 2,YU Hechun 1(1.School of Mechatronics Engineering,Zhongyuan University of Technology,Zhengzhou 450007,China;2.Hi-Tech Heavy Industry Co.,Ltd.,Zhengzhou 450000,China)Abstract :In the chemical fiber industry the opening treatment of viscose or Lyocell staple fibers is an importantprocess before the finished fiber.The fiber delivery tube one of the most important units of the post-treatmentequipment connects the cutting machine and the feed tank and is used to transport the staple fiber cut off by thecutting machine and the flushing water.The viscose or Lyocell staple fiber cut by the breaker is fed to the feed tank and the fiber is dispersed during the transportation process so as to achieve uniform fiber laying of the feed tank increase the washing effect of the refining machine and improve the quality of the finished fiber.Howeverthe traditional fiber delivery tube mainly plays the role of transportation and the requirements for open fibers are not high.It is very important to explore the opening mechanism of bundle fibers and the influence of flow field stateon fiber movement state to promote the rational design of fiber delivery tube structure and improve the opening effect of fibers.In this paper based on 3D modeling software and Cradle CFD numerical simulation software the flow fieldmodel and fiber model in thefiber delivery tube were established to simulate the motion state of 2 000fibers towwith length of 38mm in the fiber delivery tube.The fluid inflow condition at the inlet of the fiber delivery tube was set as velocity inflow 1m∕s and the outlet was set as static pressure outflow-natural outflow.The flow field was calculated by using steady state pressure solver RNG k-εturbulence model and wall function method.Theconvection term was discrete by using second-order upwind scheme and was solved by using PISO algorithm based on SIMPLEC.Through the vector analysis of the pressure field velocity field and flow field and the analysis of themotion state of the fiber bundle in the fiber delivery tube the influence of the flow field in the fiber delivery tube on the fiber movement was explored.The results show that when the fiber bundle enters the vertical pipe it accelerates under the water flow and its own gravity.Due to the pressure gradient and velocity gradient in thepipeline flow field the local velocity difference between the conveying process and the conveying fluid in thepipeline results in the opening effect of the fiber dislocation.The velocity of flushing water varies greatly at the bend of the fiber delivery tube and the resulting velocity gradient is conducive to the opening of the fiber bundle.Theflow field velocity gradient of the horizontal pipeline is small and the speed change is relatively stable so that theoverall fiber is elongated and opened which improves the fiber opening effect in the transportation process and guarantees the continuously uniform output.The sudden increase in the diameter of the pipe leads to the vortex of the pipe which hinders the forward transportation of the fiber.Therefore for the design of the fiber delivery tubethe sudden increase in the diameter of the pipe tube should be avoided to reduce the phenomenon of fiber entanglement.In this paper the results of the study describe the basic mechanism of the fiber bundle of openingand reveal the fiber delivery tube flow field state influence on fiber transmission.Such results can provide reference for the design of the fiber delivery tube of chemical fibers and the textile industry.Keywords :fiber delivery tube flow field model Cradle CFD fiber tow opening and loosening㊃73㊃第3期王㊀进等:输毛管中流场状态对纤维丝束开松处理效果的影响。

Espace

车结构带来了一场革命，使单厢车的乘坐更舒适，驶更具乐趣，安全性和质它驾量达到了豪华车的标准雷诺遵循其一贯的设计理念，造了这款充满个性、创动
感十足、并拥有由Ｖｅａｓ开启的特有的雷诺风格的艺术品。ｌｆＳｉ
维普资讯
王艳忠：性极限拧紧技术厦其应用弹
ｃ有限的空间内，．在使用最可靠最经济的联接螺栓，使得材料的强度得到充分的利用。
５２弹性极限拧紧设备简介．
ｂ．程序控制系统计算机，含有故障诊断系统的
Ｅｐｃ概念车的主要革新，即每排座位的车厢顶部和底部均有出气孔。除前车门ｓａｅ上的分立空气调节系统外，车门处也安装了通风流速控制器。后雷诺充分发挥它在安全领域所取得的成功经验，在Ｅｐｃ概念车上采用了ｓａｅ
ａ．对１螺栓按弹性极限法拧紧Ｏ个ｂ．检查凸轮轴旋转力矩。另外，还有一个故障返修区，它当发动机出现故障或由于设备原因导致发动机未完成装配任务时，它都将被自动或人为地送人到返修区。
使得发动机装配成本降低，但制造成本比较高，而且需要经常地维护和保养。

拧紧技术运用中的几个实际问题

拧紧技术运用中的几个实际问题
王成忠
【期刊名称】《凿岩机械气动工具》
【年(卷),期】1998(000)004
【摘要】探讨了装配中经常遇到的几个拧紧技术问题，提出了处理问题的参考意见。

【总页数】1页(P34)
【作者】王成忠
【作者单位】东风汽车公司设备制造厂
【正文语种】中文
【中图分类】TG78
【相关文献】
1.浅谈防汛抗旱工作中几个实际问题 [J], 刘敬玉
2.拧紧技术运用的几个实际问题 [J], 王成忠
3.农作物秸秆处理与利用中的几个实际问题与解决办法 [J], 叶家春
4.对防雷检测工作中几个实际问题的探讨 [J], 潘忠
5.谈谈初中化学用语教学中几个实际问题的解决方法 [J], 黄科
因版权原因，仅展示原文概要，查看原文内容请购买。

塔式起重机高强度螺栓的预紧力与重复使用

塔式起重机高强度螺栓的预紧力与重复使用王保卫谢智全贺习福深圳市特种设备安全检验研究院深圳518029摘要：通过对塔式起重机（以下简称塔吊）塔身连接的高强度螺栓连接副的受力分析，得出预紧力的重要性，然后又介绍两种控制高强度螺栓预紧力的方法，得出高强度螺栓重复使用次数不得超过2次的原由。

关键词：高强度螺栓；预紧力；扭矩法；转角法Abstract: Through the stress analysis of the tower crane high strength bolt connection, obtained that the importance of preload, and then describes two control methods of high strength bolt preload, obtained the reason of re-use high strength bolts no more than 2 times.Keywords：high strength bolt; preload; torque method; corner method高强度螺栓连接方式由于其对于被连接件制作精度要求低，连接方便、成本低廉而广泛应用于中小型塔式起重机的塔身连接上。

但由于施工安装人员缺乏对该种连接方式的认识，往往不按规定控制预紧力，而只将高强度螺栓如普通螺栓一般多次重复使用，高强度螺栓并未起高强度螺栓的真正作用。

本文从分析预紧力对高强度螺栓连接的重要性入手，结合工程实际，得出预紧力的重要性，然后又介绍两种控制高强度螺栓预紧力的方法，得出高强度螺栓重复使用次数不得超过2次的原因。

高强度螺栓的连接方式及受力分析高强度螺栓连接按其受力状况，可分为两种类型，一种是只受预紧力作用的螺栓连接，这种螺栓连接靠螺栓预紧力在被连接件结合面产生的磨擦力传递工作载荷；另一种是承受预紧力和工作载荷的紧螺栓连接，工作时受力情况比较复杂，应从分析螺栓连接的受力和变形关系入手，求出螺栓总拉力的大小。

不同的拧紧策略的优缺点

角度
21
CC China_Documentation Standard v2 20060606
塑性区域角度控制
优势摩擦力影响降到最低最大程度上利用螺拴能力劣势生产条件下检验工具性能很困难设置和校验产品参数的费用较高螺拴一般无法重复使用
22
CC China_Documentation Standard v2 20060606
10
CC China_Documentation Standard v2 20060606
螺拴连接模型－塑性变形阶段
弹性阶段的夹紧力范围主要与材料的屈服点有关。与连接的软硬程序及摩擦系数有些许关系。
对高强度等级的材料，力率会有一个明显的下降，即曲线变平。而对低强度等级的材料，这个趋势并不明显。最终螺拴都会断裂。从屈服点开始到螺拴断裂转过的角度，与夹紧长度关系非常大，一般来说是在几的范围内。dAdF
角度
A
6 CC China_Documentation Standard v2 20060606
螺拴连接模型
夹紧力
角度
扭矩
角度
7 CC China_Documentation Standard v2 20060606
轴向力－扭矩的关系
夹紧力 F通过螺拴头下摩擦、螺距和螺纹副摩擦转化为扭矩，公式如下：
现卓越生产力。
30
CC China_Documentation Standard v2 20060606
31
CC China_Documentation Standard v2 20060606
部分公司自2006年开始即执行该指令。
29
CC China_Documentation Standard v2 20060606

应用韧性断裂准则预测盒形件拉深成形极限

应用韧性断裂准则预测盒形件拉深成形极限
杨玉英;于忠奇;王永志;孙振忠
【期刊名称】《哈尔滨工业大学学报》
【年(卷),期】2004(036)011
【摘要】目前已提出的韧性断裂准则预测板料成形极限,只在简单轴对称件中得到应用.利用作者提出的韧性断裂准则预测了铝合金板LF21,LY21(M)和钢板st17非轴对称的方盒件拉深成形极限,并与成形极限图的预测结果和实验结果进行比较.结果表明,这种方法较好地预测了盒形件拉深成形极限,为预测非轴对称件成形的断裂发生提供了一种有效的方法,也为预测复杂形状零件成形极限奠定了基础.
【总页数】4页(P1507-1510)
【作者】杨玉英;于忠奇;王永志;孙振忠
【作者单位】哈尔滨工业大学,材料科学与工程学院,黑龙江,哈尔滨,150001;哈尔滨工业大学,材料科学与工程学院,黑龙江,哈尔滨,150001;哈尔滨工业大学,材料科学与工程学院,黑龙江,哈尔滨,150001;哈尔滨工业大学,材料科学与工程学院,黑龙江,哈尔滨,150001
【正文语种】中文
【中图分类】TG386
【相关文献】
1.成形极限预测韧性断裂准则及屈服准则的影响 [J], 陈劼实;周贤宾
2.应用专家系统进行盒形件拉深成形极限的分析 [J], 郑晓丹;汪锐;何丹农
3.基于神经网络和遗传算法的板材韧性断裂准则参数优化及成形极限预测 [J], 董国疆;陈志伟;赵长财;李潇逸;杨卓云
4.应用韧性断裂准则预测不同材料的胀形极限 [J], 于忠奇;杨玉英;孙振忠
5.应用韧性断裂准则预测板料的成形极限图 [J], 余心宏;翟妮芝;翟江波
因版权原因，仅展示原文概要，查看原文内容请购买。