数控机床宏程序例题
数控机床编程新手入门教程例题及答案解析
数控机床编程新手入门教程例题及答案解析一、数控机床编程基础在数控机床编程中，了解常用的基本指令是至关重要的。
下面是一个简单的数控机床编程例题：例题：编写一个程序，使数控机床沿着直线路径移动，起点坐标为(0,0)，终点坐标为(50,50)。
答案解析1.首先，我们需要使用G代码中的直线插补指令，通常为G01。
2.设定起点坐标为X0 Y0，终点坐标为X50 Y50，则编程指令如下：N10 G21 ; 设置以毫米为单位N20 G17 ; 设置XY平面N30 G90 ; 设置绝对编程N40 G01 X50 Y50 F100 ; 沿直线从(0,0)到(50,50)移动，进给速度为100mm/min3.上述代码中，N10、N20、N30等为程序行号，用于标识程序的执行顺序。
4.G21用于设置以毫米为单位，G17设置工作平面为XY平面，G90设置为绝对编程模式。
5.G01为直线插补指令，X50 Y50为终点坐标，F100表示进给速度为100mm/min。
二、数控机床编程进阶除了基本的直线插补指令外，数控机床编程还涉及到圆弧插补、刀补、工件坐标系选择等高级操作。
下面是一个进阶的数控机床编程例题：例题：编写一个程序，使数控机床以半径为30mm的圆弧路径进行切削，起点坐标为(0,0)，终点坐标为(50,50)。
答案解析1.类似于直线插补，圆弧插补在数控机床编程中也是常见的。
2.我们使用G02或G03来表示顺时针或逆时针圆弧插补。
3.设定起点坐标为X0 Y0，终点坐标为X50 Y50，半径为30mm，则编程指令如下：N10 G21 ; 设置以毫米为单位N20 G17 ; 设置XY平面N30 G90 ; 设置绝对编程N40 G02 X50 Y50 I0 J50 F100 ; 沿圆弧路径切削，逆时针方向，I、J为圆心偏移，F100为进给速度4.在上述代码中，G02表示逆时针圆弧插补，I、J为圆心相对于起点的偏移量。
总结数控机床编程是一门重要的技能，通过不断练习和实践，可以掌握更多高级的编程技巧。
数控车床编程实例大全
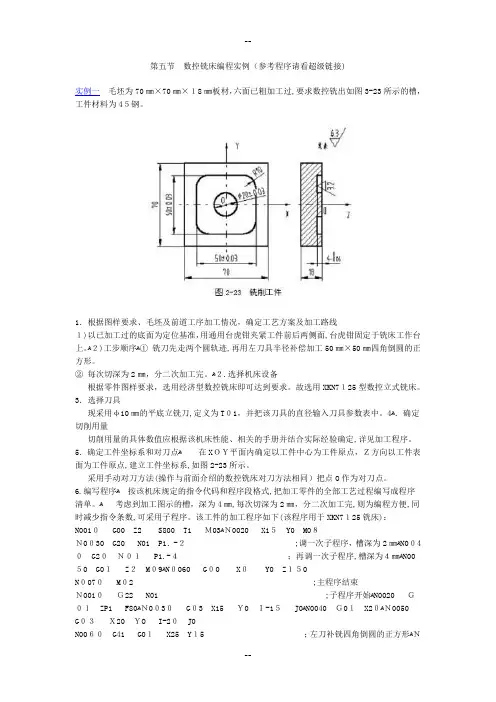
第五节数控铣床编程实例（参考程序请看超级链接)实例一毛坯为70㎜×70㎜×１8㎜板材，六面已粗加工过,要求数控铣出如图3-23所示的槽，工件材料为4５钢。
1．根据图样要求、毛坯及前道工序加工情况，确定工艺方案及加工路线１)以已加工过的底面为定位基准，用通用台虎钳夹紧工件前后两侧面,台虎钳固定于铣床工作台上。
ﻫ２)工步顺序ﻫ①铣刀先走两个圆轨迹,再用左刀具半径补偿加工50㎜×50㎜四角倒圆的正方形。
②每次切深为2㎜，分二次加工完。
ﻫ２.选择机床设备根据零件图样要求，选用经济型数控铣床即可达到要求。
故选用XKN7１25型数控立式铣床。
3．选择刀具现采用φ10㎜的平底立铣刀,定义为T０1，并把该刀具的直径输入刀具参数表中。
ﻫ4．确定切削用量切削用量的具体数值应根据该机床性能、相关的手册并结合实际经验确定,详见加工程序。
5．确定工件坐标系和对刀点ﻫ在XＯＹ平面内确定以工件中心为工件原点，Ｚ方向以工件表面为工件原点,建立工件坐标系,如图2-23所示。
采用手动对刀方法(操作与前面介绍的数控铣床对刀方法相同）把点O作为对刀点。
6.编写程序ﻫ按该机床规定的指令代码和程序段格式,把加工零件的全部工艺过程编写成程序清单。
ﻫ考虑到加工图示的槽，深为4㎜,每次切深为2㎜，分二次加工完,则为编程方便,同时减少指令条数,可采用子程序。
该工件的加工程序如下(该程序用于XKN7１25铣床)：N001０G00 Z2 S800 T1 Ｍ03ﻫＮ0020 X1５ Y0 M0８Ｎ0０30 G20 N01 P1．-２ ;调一次子程序，槽深为2㎜ﻫN0０4０ G2０Ｎ０１P1.-４；再调一次子程序,槽深为４㎜ﻫN00５0 G0１ Z２ M０9ﻫN０060 G０0 X０Y0 Z１５0N０07０ M０2 ;主程序结束Ｎ001０Ｇ22 N01 ;子程序开始ﻫN0020 Ｇ０１ ZP1 F80ﻫＮ0０3０ G０3 X15 Ｙ0 Ｉ-1５ J0ﻫN0040 Ｇ0１ X2０ﻫＮ0050 G０３Ｘ20 ＹO I-2０ J0N00６０ G41 G0１X25 Y１5 ；左刀补铣四角倒圆的正方形ﻫＮ007０ G03 Ｘ１5 Y25 I-10 J0ﻫN0080 G01 X-1５N0０９0 G03 X－２５ Y１5 Ｉ0 J-10N01００ G０1 Y-1５N0１１０ G03 X-１５Y-25 I１０ J0N0120 G0１ X１５N０130 G0３X25 Y-15 I０ J10ﻫＮ0140 G01 Ｙ0N015０Ｇ4０ G0１Ｘ1５ Y0 ；左刀补取消N0160 G24 ；主程序结束实例二毛坯为120㎜×6０㎜×１0㎜板材，5㎜深的外轮廓已粗加工过，周边留2㎜余量,要求加工出如图2-２4所示的外轮廓及φ2０㎜的孔。
数控车床加工椭圆的宏程序
数控车床加工椭圆的宏程序随着数控技术不断进步, 数控车床加工中各种复杂形面也日渐增多, 如椭圆、抛物线、正弦曲线、余弦曲线、双曲线等各种非圆曲面。
对于上述各种复杂成形面, 利用CAM 软件进行自动编程相对简单, 但由于种种原因, 在绝大多数情况下数控车床主要还是依靠手工编程。
椭圆轴线与数控车床Z 轴重合的情形相对比较简单, 其解决方案也多见于各类文献, 但在本例中椭圆轴线与数控车床Z 轴呈一定夹角, 编程和加工难度陡增,主要原因如下: ①机床数控系统本身既不存在加工椭圆等非圆曲线的G 指令, 更没有类似G68 这样的旋转指令, 使编程难度大大增加。
②加工中变量的参数直接影响着加工的效率以及质量, 很容易产生过切报警, 即使程序正确无误, 实际加工时的参数调整也非常困难, 直接影响着加工能否顺利进行, 以及加工精度能否保证。
总而言之, 目前尚未见有表述类似实例的文章。
本实例进行了有益的尝试和探索, 给出了切实可行的解决方案, 为类似问题提供了难得的参考及借鉴。
椭圆宏程序的编制如下。
1. 椭圆方程宏程序主要利用各种数学公式进行运算加工, 因此编制旋转椭圆程序操作者必须要掌握椭圆方程和旋转公式等各种数学公式的计算方法并加以灵活运用。
椭圆方程有两种形式, 分别是椭圆的标准方程和参数方程。
椭圆标准方程:椭圆参数方程:其中a 、b 分别为X、Z 所对应的椭圆半轴。
2. 旋转公式由于数控车床并不像加工中心那样存在着旋转指令, 所以要利用旋转公式来进行椭圆的旋转。
旋转公式的定义:如图1 所示, 平面上绕点O 旋转, 使平面上任意一对对应点P 和P′与一个定点O 连接的线段都相等, 即OP = OP′, 且角∠POP′等于角θ, 点O称为旋转中心, 角θ称为旋转角。
旋转公式: 如图1 所示, 取直角坐标系, 以原点O为旋转中心, 旋转角为θ, 平面上任意一点P ( x, z) 旋转到P′( x′, z′) , 令∠XOP= α, 则∠XOP′= α+ θ, 且OP = OP ′。
数控机床宏程序编程的技巧和实例
数控机床宏程序编程的技巧和实例第一篇：数控机床宏程序编程的技巧和实例论文：数控机床宏程序编程的技巧和实例2011年8月11日前言随着工业技术的飞速发展，产品形状越来越复杂，精度要求越来越高，产品更新换代越来越快，传统的设备已不能适应新要求。
现在我国的制造业中已广泛地应用了数控车床、数控铣床、加工中心机床、数控磨床等数控机床。
这些先进设备的加工过程都需要由程序来控制，需要由拥有高技能的人来操作。
要发挥数控机床的高精度、高效率和高柔性，就要求操作人员具有优秀的编程能力。
常用的编程方法有手工编程和计算机编程。
计算机编程的应用已非常广泛。
与手工编程比较，在复杂曲面和型腔零件编程时效率高、质量好。
因此，许多人认为手工编程已不再重要，特别是比较难的宏程序编程也不再需要。
只须了解一些基本的编程规则就可以了。
这样的想法并不能全面。
因为，计算机编程也有许多不足：1、程序数据量大，传输费时。
2、修改或调整刀具补偿需要重新后置输出。
3、打刀或其他原因造成的断点时，很难及时复位。
手工编程是基础能力，是数控机床操作编程人员必须掌握的一种编程方法。
手工编程能力是计算机编程的基础，是刀具轨迹设计，轨迹修改，以及进行后置处理设计的依据。
实践证明，手工编程能力强的人在计算机编程中才能速度快，程序质量高。
在程序中使用变量，通过对变量进行赋值及处理使程序具有特殊功能，这种有变量的程序叫宏程序。
宏程序是数控系统厂家面向客户提供的的二次开发工具，是数控机床编程的最高级手工方式。
合理有效的利用这个工具将极大地提升机床的加工能力。
作为一名从事数控车床、数控铣床、加工中心机床操作编程二十多年的技师，在平时的工作中，常常用宏程序来解决生产中的难题，因此对宏程序的编程使用积累了一些经验。
在传授指导徒弟和与同事探讨中，总结了许多学习编制宏程序应注意的要点。
有关宏编程的基础知识在许多书籍中讲过，我们在这里主要通过实例从编制技巧、要点上和大家讨论。
一、非圆曲面类的宏程序的编程技巧1、非圆曲面可以分为两类；（1）、方程曲面，是可以用方程描述其零件轮廓的曲面的。
宏程序编程
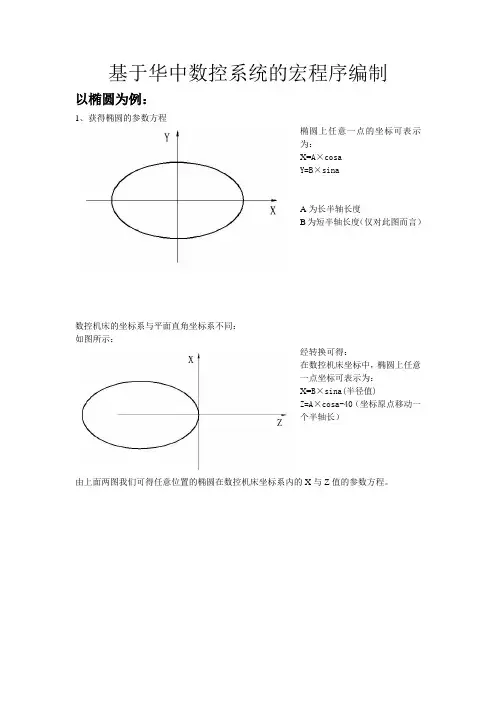
基于华中数控系统的宏程序编制
以椭圆为例：
1、获得椭圆的参数方程
椭圆上任意一点的坐标可表示
为：
X=A×cosa
Y=B×sina
A为长半轴长度
B为短半轴长度（仅对此图而言）
数控机床的坐标系与平面直角坐标系不同：
如图所示：
经转换可得：
在数控机床坐标中，椭圆上任意
一点坐标可表示为：
X=B×sina(半径值)
Z=A×cosa-40（坐标原点移动一
个半轴长）
由上面两图我们可得任意位置的椭圆在数控机床坐标系内的X与Z值的参数方程。
2、编程实例：
分析零件图，得要加工椭圆长半轴长为40mm，短半轴长为25mm，以角度a为变量，设置为#1，椭圆上任意点坐标可表示为：
x=2※25※sin[#1](直径编程)
z=cos[#1]-40
具体程序如下
O1
%1
T0101
S1000M03
G0X80Z2
G71U2R1P1Q2X0.4Z0.2F200
GOX100Z80
T0202
S2000M03
N1GOXOG42
G1Z0F80
G64
#1=0
WHILE#1LE[PI/2]
G1X[2※25※sin[#1]]Z[cos[#1]-40]
#1=#1+PI/180
ENDW
G1X70
Z-60
N2X80
GOX100Z80
M30。
数控车床宏指令
例：G65 H80 P120；
转移到N20程序段
2）条件转移1 #j.EQ.#k (=)
G65 H81 Pn Q#j R#k，n:顺序号
例：G65 H81 P1000 Q#101 R#102；
如果#101=#102，转到N1000；
如果#101≠#102，顺次执行。
3）条件转移2 #j.NE.#k (≠)
G65 H81 Pn Q#j R#k，n:顺序号
例：G65 H81 P1000 Q#101 R#102；
如果#101≥#102，转到N1000；
如果#101＜#102，顺次执行。
7）条件转移6 #j.LE.#k (≤)
G65 H81 Pn Q#j R#k，n:顺序号
例：G65 H81 P1000 Q#101 R#102；
而普通程序中，只能指定常量，常量之间不能运算，程序只能顺序执行，不能跳转，因此功能是固定的，不能变化。
编程人员不必记忆用户宏程序主体的一组命令。只记忆作为代表命令的用户宏程序命令即可，用户宏程序的最大特点是在用户宏程序主体中，可以进行变量间的运算，用宏命令可以给变量设定实际值。
2、宏程序编程的技术特点
课题八数控车床宏指令加工练习
一、概述
用户把实现某种功能的一组指令像子程序一样预先存入存储器中，用一个指令代表这个存储的功能，在程序中只要指定该指令就能实现这个功能。把这一组指令称为用户宏程序本体，简称宏程序。把代表指令称为用户宏程序调用指令，简称宏指令。
1、用户宏程序与普通程序的区别在于：
在用户宏程序本体中，能使用变量，可以给变量赋值，变量间可以运算，程序运行可以挑砖。
H02 G65 P#100 Q#101 R#102；错误
宏程序编程例子入门
宏程序编程例题椭圆解析：椭圆关于中心、坐标轴都是对称的,坐标轴是对称轴,原点是对称中心;对称中心叫做椭圆中心;椭圆和X轴有2两个交点,和Y轴有两个交点,这四个交点叫做椭圆顶点;椭圆标准方程：x2 / a2 + y2 / b2 = 1 a为长半轴,b为短半轴,a > b > 0椭圆参数方程：x=acosMy=bsinM a为长半轴,b为短半轴,a > b > 0 ,M是夹角,是椭圆上任意一点到椭圆中心连线与X正半轴所成的夹角,顺时针为负,逆时针为正;二、数控车床：根据椭圆标准方程：x2 / a2 + y2 / b2 = 1 a为长半轴,b为短半轴,a > b > 0 根据椭圆参数方程：x=acosMy=bsinM a为长半轴,b为短半轴,a > b > 0 ,M是夹角,是椭圆上任意一点到椭圆中心连线与X正半轴所成的夹角,顺时针为负,逆时针为正;可得车床标准方程：z2 / a2 + x2 / b2 = 1 a为长半轴,b为短半轴,a > b > 0 可得椭圆参数方程：z=acosMx=2bsinM a为长半轴,2b为短轴直径,a > b > 0 ,M是夹角,是椭圆上任意一点到椭圆中心连线与Z正半轴所成的夹角,顺时针为负,逆时针为正;通过标准方程推导X的表达式：x =b / a SQRT a a– z z a、b为长、短半轴是常数表示;一车床车削椭圆通常是加工椭圆X正方向部分回转体,用标准方程车削椭圆时,通常设Z为自变量,通过方程把X表达出来,最多就是车削到180度椭圆,然后利用G01插补拟合成椭圆;通过椭圆车床标准方程推导,可以有如下过程：z2 / a2 + x2 / b2 = 1可推导 x2 / b2 =1- z2 / a2 = a2 – z2 / a2可推导 x2 = b2 / a2 a2 – z2 x =b / a SQRT a2 – z2转换为数控格式就为 x =2b / a SQRT a a– z z a为长半轴、2b为短轴直径编程常数表示;设z为自变量1,则x为因变量2,根据上述公式有：2 =b / a SQRT a a- 1 1 例题：长半轴a=5,短半轴b=4的椭圆;有以下几种情况：1、 1为z,为自变量：则1=5 1=5 表示从Z正半轴开始加工;N10 2 = 8 / 5 SQRT 5 5 - 1 1G01 X 2+ D Z 2 + E X正,Z正,表示走逆时针,D、E表示椭圆中心X、Z绝对坐标1=1-1IF 1 GE 0 GOTO10 这是加工第一象限的椭圆,90度椭圆;IF 1 GE -5 GOTO10 这是从第一象限加工到第二象限的椭圆,180度椭圆;2、 1为x,为自变量：则1=-5 1=-5 表示从Z轴负方向开始加工;N10 2 = 8 / 5 SQRT 5 5 - 1 1G01 X 2+ D Z -2 + E X正,Z负,表示走顺时针,D、E表示椭圆中心X、Z 绝对坐标1=1 + 1IF 1 LE 0 GOTO10 这是加工第二象限的椭圆,90度椭圆;通常这是利用反刀加工;IF 1 LE 5 GOTO10 这是从第二象限加工到第一象限的椭圆,180度椭圆;正反刀都可以加工;关于D、E椭圆中心坐标位置的说明,D为直径表达,E的位置有三种：当E＝-a时 2 + E =0,椭圆中心离工件原点相差一个长半轴距离;E=-a+Δ时 2 + E >0,椭圆中心在Z轴上向右偏移,中心离工件原点距离小于一个长半轴;E=-a-Δ时 2 + E <0,椭圆中心在Z轴上向左偏移,中心离工件原点距离大于一个长半轴;二车通过参数方程加工椭圆可以加工0-180度内任意角度,直接通过参数方程加工即可;例题：长半轴a=5,短半轴b=4的椭圆;有以下几种情况：1、设1为M,为角度自变量,x、z为因变量：则1=0 1=0 表示从0度开始加工,即Z正半轴开始加工,若写1=90表示从X正半轴开始加工,其他以此类推N10 Z = 2 = a COS 1X = 3 = 2b SIN 1G01 X 3 +D Z 2 + E X正,Z正,表示走逆时针,D、E表示椭圆中心X、Z绝对1=1+1 + 表示走逆时针方向IF 1 LE 90 GOTO10 这是加工第一象限部分,90度椭圆;IF 1 LE 180 GOTO10 这是从第一象限加工到第二象限的椭圆,180度椭圆; 如果写LE180就是加工0-180度椭圆,其他任意角度以此类推;2、设1为M,为角度自变量,x、z为因变量：则1=180 1=180 表示从180度开始加工,即Z负半轴开始加工,其他任意角度以此类推N10 Z = 2 = a COS 1X = 3 =2 b SIN 1G01 X 3 + D Z -2 + E X正,Z负,表示走顺时针,D、E表示椭圆中心X、Z 绝对坐标1=1-1 - 表示走顺时针方向IF 1 GE 90 GOTO10 这是加工第二象限部分,90度椭圆;通常这是利用反刀加工;IF 1 GE 0 GOTO10 这是从第二象限加工到第一象限的椭圆,180度椭圆;正反刀都可以加工;通过可以通过参数方程和标准加工,通过上述举例可以发现,参数方程编程简单,程序简洁,可以加工任意角度的椭圆;关于椭圆的编程介绍到此为止;椭圆例题图形1O0001N010 G99 G97 G21N020 T0101N030 S600 M03N040 G0 X45 Z5 M08N050 G73 U23 W0 R21N060 G73 P70 Q190 0.1 FN070 G00 X0 S1000N080 G42 G01 0 FN090 101=20N100 WHILE101GE0DO1N110 102=26SQRT1-101101/2020 N120 G01 X102 Z101-20N130 101=N140 END1N150 Z-30N160 G02 X36 Z-35 R5N170 G01 X38N180 X42 Z-37N190 X45N200 G70 P70 Q190N210 G40 G00 X100 Z100 M09N220 T0100 M05N230 M30%方法2O0002N010 G99 G97 G21N020 T0101N030 S600 M03N040 G0 X45 Z5 M08N050 G73 U23 W0 R21N060 G73 P70 Q180 0.1 FN070 G00 X0 S1000N080 G42 G01 0 FN090 101=20N100 102=26SQRT1-101101/2020 N110 G01 X102 Z101-20N120 101=N130 IF101GE0GOTO100N140 Z-30N150 G02 X36 Z-35 R5N160 G01 X38N170 X42 Z-37N180 X45N190 G70 P70 Q180N200 G40 G00 X100 Z100 M09 N210 T0100 M05N220 M30图形2方法1O0001N010 G99 G97 G21N020 T0101N030 S600 M03N040 G0 X53 Z5 M08N050 G73 U25 W0 R23N060 G73 P70 Q210 0.1 FN070 G00 S1000N080 G42 G01 0 FN090 Z-2N100 Z-18N110 X20N120 Z-25N130 101=20N140 WHILE101GE0DO1N150 102=18SQRT1-101101/2020 N160 G01 X102 Z101-45N170 101=N180 END1N190 G01 X38N200 Z-60N210 X50N220 G70 P70 Q210N230 G40 G00 X100 Z100 M09N240 T0100 M05N250 M30%方法2O0001N010 G99 G97 G21N020 T0101N030 S600 M03N040 G0 X53 Z5 M08N050 G73 U25 W0 R23N060 G73 P70 Q200 0.1 FN070 G00 S1000N080 G42 G01 0 FN090 Z-2N100 Z-18N110 X20N120 Z-25N130 101=20N140 102=18SQRT1-101101/2020 N150 G01 X102 Z101-45N160 101=N170 IF101GE0GOTO140N180 G01 X38N190 Z-60N200 X50N210 G70 P70 Q200N230 G40 G00 X100 Z100 M09N240 T0100 M05N250 M30%图形2 切槽与螺纹均不编图形3O0001N010 G99 G97 G21N020 T0101N030 S700 M03N040 G00 X53 Z2 M08N050 G73 U25 W0 R23N060 G73 P70 Q230 0.1 FN070 G00 X0 S1000N080 G42 G01 0 FN090 G03 X16 Z-8 R8N100 G01N110 X20N120N130N140 101=0N150 102=30SQRT1-101101/2020 N160 G01 X52.98-102 ZN170 101=N180 IFGOTO150N190 G01 X32N200 Z-27N210 Z-50N220 X46N230 X48 Z-51N240 G70 P70 Q230N250 G40 G00 X100 Z100 M09 N260 T0100 M05N270 M30N280%图形3 切槽与螺纹均不编图形4O0001N010 G99 G97 G21N020 T0101N030 S700 M03N040 G00 X52 Z2 M08N050 G73 U12 W0 R10N060 G73 P70 Q200 0.1 FN070 G00 X26 S1000N080 G42 G01 0 FN090 G01 X30 Z-2N100 G01 Z-5N110 X36N120 G03 X40 R20N130N140 101=14N150 102=16SQRT1-101101/1414 N160 G01 X44-102 Z101-31N170 101=N180 IF101GE-14GOTO150N190 G01 X44N200 Z-51N210 G70 P70 Q200N220 G40 G00 X100 Z100 M09N230 T0100 M05N240 M30N250%图形4 切槽与螺纹均不编图形5O0001N010 G99 G97 G21N020 T0101N030 S700 M03N040 G00 X62 Z2 M08N050 G73 U13 W0 R10N060 G73 P70 Q190 0.1 FN070 G00 X51 S1000N080 G42 G01 0 FN090 G01 X52N100 G01N110 101=25N120 102=24SQRT1-101101/2525 N130 G01 X58-102 Z101-43N140 101=N150 IF101GE0GOTO120N160 G01 Z-43N170 X51N180 X52 Z-44N190 X60N200 G70 P70 Q190N210 G40 G00 X100 Z100 M09N220 T0100 M05N230 M30N240图形6O0001N010 G97 G99 G21N020 T0101N030 S600 M03N040 G0 X53 Z5 M08N050 G73 U10 W0 R9N060 G73 P70 Q180 0 FN070 G00 X38N080 G42 G01 Z0 1200 FN090 101=0N100 102=38SQRT1-101101/5050 N110 G01 X102 Z101N120 101=N130 IFGOTO100N140 G01 Z-36N150 G02 X38 Z-40 R4N160 G01 X47N170 X48N180 X50N190 G70 P70 Q180N200 G40 G00 X100 Z100 M09N210 T0100 M05N220 M30N230模拟轨迹O0001N010 G97 G99 G21N020 T0101N030 S600 M03N040 G0 X73 Z5 M08N050 G73 U13 W0 R11N060 G73 P70 Q160 0 FN070 G00 X44N080 G42 G01 Z0 1200 FN090 101=20N100 102=24SQRT1-101101/2020N110 G01 X102+44 Z101-20N120 101=N130 IF101GE0GOTO100N140 G01 X68N150 Z-90N160 X70N170 G70 P70 Q160N180 G40 G00 X100 Z100 M09 N190 T0100 M05N200 M30N210。
华中数控铣床宏程序实例
G18G01X[#2]Z[#3]
#5=#2
WHILE#5GE2
G17G01X[#5]
#6=0
WHILE#6LT360
#7=#5*COS[#6*PI/180]
#8=#4*SIN[#6*PI/180]
G01X[#7]Y[#8]
#6=#6+1ENDW
#5=#5+5
ENDW
G54G00X0Y0Z50
M3S1500
Z3
G01Z0F250
#1=90
WHILE#1GE0
#2=30*COS[#1*PI/180]
#3=30*SIN[#1*PI/180]-30
G18G01X[#2]Z[#3]
#4=#2
WHILE#4LT43
G17X[#4]
G02I[-#4]
#4=#4+5
ENDW
G01X[-#2]
Z5
G01Z0F250
#1=180
WHILE#1LT270
#2=30*COS[#1*PI/180]
#3=30*SIN[#1*PI/180]
G18G01X[#2]Z[#3]
#4=#2
WHILE#4GE0
G17G01X[#4]
G02I[-#4]
#4=#4-5
ENDW
G01X[#2]
#1=#1+1
ENDW
G00Z50
M30
(精铣)
G54G00X0Y0Z50
M03S1500
Z5
G01Z0F250
#1=180
WHILE#1LT270
#2=30*COS[#1*PI/180]
#3=30*SIN[#1*PI/180]
宏程序试题及答案
宏程序试题及答案一、单选题（每题2分，共10分）1. 宏程序中，用于定义局部变量的命令是：A. #100B. %100C. #100D. %100答案：A2. 在宏程序中，用于调用子程序的命令是：A. G0B. G1C. M98D. M99答案：C3. 下列哪个符号在宏程序中表示乘法？A. *B. /C. +D. -答案：A4. 宏程序中，用于返回主程序的命令是：A. M98B. M99C. G0D. G1答案：B5. 下列哪个选项不是宏程序的变量类型？A. 局部变量B. 公共变量C. 系统变量D. 常量答案：D二、判断题（每题1分，共5分）1. 宏程序中的变量可以参与运算。
（对）2. 宏程序只能用于数控车床。
（错）3. 宏程序可以提高编程效率。
（对）4. 宏程序中的M98命令用于结束子程序。
（错）5. 宏程序中，#100和%100表示相同的变量。
（错）三、填空题（每题2分，共10分）1. 在宏程序中，_________命令用于定义局部变量。
答案：#2. 宏程序中，_________命令用于定义公共变量。
答案：%3. 在宏程序中，_________命令用于结束子程序。
答案：M994. 宏程序中，_________命令用于调用子程序。
答案：M985. 宏程序中，_________符号用于表示乘法。
答案：*四、简答题（每题5分，共10分）1. 简述宏程序在数控加工中的作用。
答案：宏程序在数控加工中的作用主要是简化编程过程，提高编程效率，减少编程错误，以及实现复杂形状的加工。
2. 列举宏程序中常用的几种变量类型及其用途。
答案：宏程序中常用的变量类型包括局部变量、公共变量和系统变量。
局部变量用于定义子程序中的变量，公共变量用于定义在主程序和子程序中共享的变量，系统变量用于定义数控系统内部使用的变量。
数控宏程序编制两例
数控宏程序编制两例数控宏程序是一种通过编辑代码来控制数控机床进行自动加工的程序。
宏程序可以重复使用，可以提高生产效率和加工精度，且可以自动完成编程过程。
下面将介绍两个数控宏程序编制的例子：1. 零件加工宏程序该宏程序适用于零件的加工，需先测量零件尺寸，并依据测量结果编写数控宏程序。
以轴套为例，宏程序如下：O0001；（宏程序的名称）G10L20P1X10Y20Z30；（设定工具长度、直径及坐标轴位置）T1；（选择工具）M03S1000；（主轴正转并设定转速）G01X0Z0F100；（工件坐标轴归零）G00X-20；（工件坐标轴回原点）G01X-15Z-10；（以100 的进给速率和深度，向工件进给加工）G01X-10；（向工件进给加工）G00X0Z0F100；（以快速进给回到原点位置）M05；（主轴停止）通过以上程序，机床可以自动进行轴套加工，增加了生产效率，又避免了因人为因素引起的误差。
2. 零件检测宏程序该宏程序适用于零件的检测，可以快速高效地检查零件尺寸是否合格。
以零件平面度检测为例，宏程序如下：O0002；（宏程序的名称）G10L20P1X10Y20Z30；（设定工具长度、直径及坐标轴位置）T2；（选择工具）M03S1000；（主轴正转并设定转速）G01X0Z0F100；（工件坐标轴归零）G00X-20；（工件坐标轴回原点）G01X-10Z-3；（以 50 的进给速率和深度，向工件进给检测）G00X0Z0F100；（以快速进给回到原点位置）M05；（主轴停止）IF[#2 LT 0.01]GOTO5；（IF 判断语句，如果测量值小于 0.01 mm，跳转到标记 5）G01X10Z-3；（以 50 的进给速率和深度，向工件进给检测）G00X0Z0F100；（以快速进给回到原点位置）M05；（主轴停止）通过以上程序，机床可以自动进行零件平面度的检测，并根据实际情况跳转到不同的位置进行处理。
总之，数控宏程序可以方便快捷地控制数控机床进行自动加工和检测，极大提高了生产效率和加工精度。
新代数控系统宏程序举例
新代数控系统宏程序举例好嘞，今天咱们聊聊新代数控系统的宏程序，听起来高大上，其实就是个能让咱们的机器更聪明的小玩意儿。
想象一下，咱们平常做个饭，用调料、火候和时间把食材搞定，对吧？宏程序就像调味料，能让咱们的加工过程变得更加丰富多彩。
你说，这是不是特别有意思？什么是宏程序呢？就像做饭时你偶尔会用到的食谱，宏程序是事先设定好的命令集合。
咱们在数控机床上，想要重复做同样的事情，比如说钻孔、铣削等等，那就得靠这些宏程序了。
用它，咱们可以省不少时间，真是一举两得，哈哈！而且啊，宏程序还能让你在不同情况下灵活应对，简直就是个“百变大咖”。
举个简单的例子，想象你有个老朋友，叫小李，他天天都在你家蹭饭。
每次你做饭，他都问：“今天吃什么？”你要是每天都得告诉他，那多麻烦啊！所以，你就给他一个“食谱”，让他自己选。
这就是宏程序的魅力，帮你把复杂的事情变简单，省下来的时间可以去看个电视剧，嘿嘿！宏程序的好处就在于它能处理一些小细节，让你省心。
比方说，有时候你在车间里忙得不可开交，突然需要对一个零件进行精细加工。
这个时候，如果你已经设定好了宏程序，就像有了个小助手，立马帮你搞定。
这时候，你就能从繁琐的操作中解放出来，心里别提有多爽了。
真是“麻烦事儿迎刃而解”，连个“点赞”都不够！说到这里，可能有人会问：这宏程序到底怎么写呢？其实也不复杂，咱们平时用的编程语言，比如说G代码，宏程序就是在这基础上扩展出来的。
就像你把简单的数学题变成了复杂的方程式，其实就是多加了些步骤。
你可以通过输入变量，设置条件，让机器按照你的想法运作。
听起来是不是有点像魔法？嘿嘿，别不信，这可是真实存在的哦。
然后，咱们再来聊聊这些宏程序的实际应用。
比如说，在一些大型工厂里，机器可是天天在忙啊，特别是那些重复的操作。
要是没有宏程序，工人们得在那儿反复输入指令，真是心累。
可一旦用了宏程序，事情就变得轻松多了。
就像你在玩一个游戏，解锁了快捷方式，直接飞过去，省去了一大堆麻烦。
数控机床宏程序编程的技巧和实例
论文：数控机床宏程序编程的技巧和实例西北工业集团有限公司白锋刚2011年8月11日前言随着工业技术的飞速发展，产品形状越来越复杂，精度要求越来越高，产品更新换代越来越快，传统的设备已不能适应新要求。
现在我国的制造业中已广泛地应用了数控车床、数控铣床、加工中心机床、数控磨床等数控机床。
这些先进设备的加工过程都需要由程序来控制，需要由拥有高技能的人来操作。
要发挥数控机床的高精度、高效率和高柔性，就要求操作人员具有优秀的编程能力。
常用的编程方法有手工编程和计算机编程。
计算机编程的应用已非常广泛。
与手工编程比较，在复杂曲面和型腔零件编程时效率高、质量好。
因此，许多人认为手工编程已不再重要，特别是比较难的宏程序编程也不再需要。
只须了解一些基本的编程规则就可以了。
这样的想法并不能全面。
因为，计算机编程也有许多不足：1、程序数据量大，传输费时。
2、修改或调整刀具补偿需要重新后置输出。
3、打刀或其他原因造成的断点时，很难及时复位。
手工编程是基础能力，是数控机床操作编程人员必须掌握的一种编程方法。
手工编程能力是计算机编程的基础，是刀具轨迹设计，轨迹修改，以及进行后置处理设计的依据。
实践证明，手工编程能力强的人在计算机编程中才能速度快，程序质量高。
在程序中使用变量，通过对变量进行赋值及处理使程序具有特殊功能，这种有变量的程序叫宏程序。
宏程序是数控系统厂家面向客户提供的的二次开发工具，是数控机床编程的最高级手工方式。
合理有效的利用这个工具将极大地提升机床的加工能力。
作为一名从事数控车床、数控铣床、加工中心机床操作编程二十多年的技师，在平时的工作中，常常用宏程序来解决生产中的难题，因此对宏程序的编程使用积累了一些经验。
在传授指导徒弟和与同事探讨中，总结了许多学习编制宏程序应注意的要点。
有关宏编程的基础知识在许多书籍中讲过，我们在这里主要通过实例从编制技巧、要点上和大家讨论。
一、非圆曲面类的宏程序的编程技巧1、非圆曲面可以分为两类；（1）、方程曲面，是可以用方程描述其零件轮廓的曲面的。
数控机床宏程序编程实例FANUC
数控机床宏程序编程实例相关知识：用户宏程序是以变量的组合，通过各种算术和逻辑运算，转移和循环等命令，而编制的一种可以灵活运用的程序，只要改变变量的值，即可以完成不同的加工和操作。
用户宏程序可以简化程序的编制，提高工作效率。
宏程序可以像子程序一样用一个简单的指令调用。
宏程序分为A、B两类。
在一些较老的数控系统中采用A类宏程序，而现在常用的一些较为先进的数控系统中则采用B类程序。
本书主要介绍B类宏程序。
（一）变量在常规程序中，总是将一个具体的数值赋给一个地址，为了使程序更具有通用性，更加灵活，在宏程序中设置了变量。
1、变量的表示变量由变量符号#和后面的变量号组成：#i（i=1，2，3，…）。
例如#100，#110，#5等。
变量序号可用表达式，但表达式必须放在[ ]中。
例：#5，#109，#[100+#5 ]。
2、变量的引用将跟随在一个地址后的数值用一个变量来代替，即引入了变量。
例：G01 X#100 Z#101 F#102，当#100=25、#101=-30、#102=0.1时，上式即表示为G01 X25 Z-30 F0.1。
①用表达式指定变量，表达式要放在方括号里：G01 X[#1+#2] F#3。
②引用一个未定义变量时，在遇到地址字之前，该变量被忽略。
③要改变被引用变量的符号，在#前加负号G01 X-#1。
3、变量的类型变量分为局部变量、公共变量和系统变量三种。
①局部变量（#1～#33）局部变量是一个在宏程序中局部使用的变量，可以服务于不同的宏程序，在不同的宏程序中局部变量可以赋不同的值，相互之间不影响。
②公共变量（#100～#199，#500～#999）公共变量也叫通用变量，可在各级宏程序中被共同使用，即这一变量在不同程序级中调用时含义相同。
因此，一个宏程序中经计算得到的一个通用变量的数值，可以被另一个宏程序调用。
③系统变量（#1000～）系统变量用来读取和写入各种数控数据项，如当前位置和刀具偏置值，它的值决定于系统的状态。
数控宏程序编程100例
数控宏程序编程100例I. "English Response:"As a CNC programmer, I have encountered various scenarios where macro programming is essential tostreamline the process and increase efficiency. Let meshare with you 100 examples of CNC macro programming that I have personally used in my career.1. Example 1: Using a macro to automatically set tool offsets for different tools in a tool changer.2. Example 2: Creating a macro to perform a series of complex operations in a single command, saving time and reducing the chance of errors.3. Example 3: Implementing a macro to adjust feed rates based on material hardness, ensuring optimal cutting speeds.4. Example 4: Developing a macro to handle tool wearcompensation, extending tool life and maintaining consistent part quality.5. Example 5: Utilizing a macro to generate custom G-code for specific part geometries, eliminating the need for manual programming.These are just a few examples of how CNC macro programming can revolutionize the way we approach machining tasks. By harnessing the power of macros, we can automate repetitive processes, improve accuracy, and ultimately boost productivity.II. "中文回答:"作为一名数控编程师，我在工作中遇到过许多情况，其中宏程序编程是必不可少的，可以简化流程，提高效率。
数控铣宏程序编程100例
数控铣宏程序编程100例数控铣宏程序编程是数控铣床操作中的重要环节，它可以大大提高生产效率和产品质量。
下面将介绍100个常见的数控铣宏程序编程实例。
1. G90 G54 G0 X0 Y0：将坐标系设置为绝对坐标系，将刀具移动到原点位置。
2. G91 G0 X10 Y10：将坐标系设置为相对坐标系，将刀具移动到当前位置的X轴正方向10mm，Y轴正方向10mm的位置。
3. G92 X0 Y0：将当前位置设置为坐标系原点。
4. G94：将进给速度设置为每分钟进给。
5. G95：将进给速度设置为每转进给。
6. G96 S1000：将主轴转速设置为1000转/分钟。
7. G97：将主轴转速设置为每分钟转速。
8. G98：将主轴转速设置为每转转速。
9. G99：将主轴转速设置为每进给转速。
10. G40：取消刀具半径补偿。
11. G41 D1：启用刀具半径补偿，刀具半径为1mm。
12. G42 D2：启用刀具半径补偿，刀具半径为2mm。
13. G43 H1：启用刀具长度补偿，刀具长度为1mm。
14. G44 H2：启用刀具长度补偿，刀具长度为2mm。
15. G45 H3：启用刀具长度补偿，刀具长度为3mm。
16. G46 H4：启用刀具长度补偿，刀具长度为4mm。
17. G47 H5：启用刀具长度补偿，刀具长度为5mm。
18. G48：取消刀具长度补偿。
19. G49：取消刀具半径和长度补偿。
20. G50 S2000：将主轴转速设置为2000转/分钟。
21. G51：取消坐标系旋转。
22. G52 X10 Y10：将坐标系旋转10度。
23. G53：取消工件坐标系。
24. G54：将工件坐标系设置为1号坐标系。
25. G55：将工件坐标系设置为2号坐标系。
26. G56：将工件坐标系设置为3号坐标系。
27. G57：将工件坐标系设置为4号坐标系。
28. G58：将工件坐标系设置为5号坐标系。
29. G59：将工件坐标系设置为6号坐标系。
数控机床宏程序例题
由浅入深宏程序10-车床旋转正弦函数宏程序正弦函数曲线旋转宏程序坐标点旋转1s = x cos(b) – y sin(b)t = x sin(b) + y cos(b)根据下图，原来的点（#1，#2），旋转后的点（#4，#5），则公式：#4=#1*COS[b]- #2*SIN[b]#5=#1*SIN[b]+ #2*COS[b]公式中角度b，逆时针为正，顺时针为负。
下图中正弦曲线如果以其左边的端点为参考原点，则此条正弦曲线顺时针旋转了16度，即b=-16正弦函数旋转图纸1此正弦曲线周期为24，对应直角坐标系的360对应关系【0,360】 y=sin（x）【0,24】 y=sin(360*x/24)可理解为：360/24是单位数值对应的角度360*x/24是当变量在【0,24】范围取值为x时对应的角度sin(360*x/24)是当角度为360*x/24时的正弦函数值旋转正弦函数曲线粗精加工程序如下：T0101M3S800G0X52Z5#6=26 工件毛坯假设为50mm，#6为每层切削时向+X的偏移量。
N5 G0X[#6+18.539]G1Z0F0.1#1=48N10 #2=sin【360*#1/24】#4=#1*COS[-16]- #2*SIN[-16] 旋转30度之后对应的坐标值#5=#1*SIN[-16]+ #2*COS[-16]#7=#4-【50-3.875】坐标平移后的坐标。
#8=45+2*#5+#6G1X[#8]Z[#7]F0.1 沿小段直线插补加工#1=#1-0.5 递减0.5，此值越小，工件表面越光滑。
IF [#1 GE 0] GOTO 10 条件判断是否到达终点。
Z-50G1X52 直线插补切到工件外圆之外G0Z5#6=#6-2IF [#6 GE 0] GOTO 5G0X150Z150M5M30镂空立方体宏程序范例镂空立方体图纸及宏程序范例此零件六个面加工内容相同，在加工时，调面装夹时要注意考虑夹紧力。
数控宏程序变量赋值试题
数控宏编程变量相关理论知识试卷一、选择题（选择正确的答案，将相应的字母填入题内的括号中。
每题0.5分。
共160题，满分80分）：1．在变量赋值方法Ⅱ中，自变量地址I6对应的变量是()。
A、#40B、#39C、#19D、#262．在运算指令中，形式为#i=ROUND[#j]代表的意义是()。
A、圆周率B、四舍五入整数化C、圆弧度D、加权平均3．下列宏程序的变量表示不正确的是()。
A、#0B、#[200-1]C、#10D、#[#57]4．FOR 当一个带有一个确定值的操作程序被循环重复，()循环就会被运行。
A、FORB、GOTOC、ELSED、WHILE5．在发那克0i系统中，描述算术运算的反正切的正确格式是()。
A、#i=ATAN[#j/#k]B、#i=A TAN[#j]C、#i=ATAN[#j]/[#k]D、#i=TAN[#j]/[#k]6．在变量赋值方法I中，引数（自变量）A对应的变量是()。
A、#22B、#1C、#110D、#257．在运算指令中，形式为#i=TAN{#j}代表的意义是（）A、正切B、合并C、反余切D、立方根8.在运算指令中，形式为#i=SQRT[#j]代表的意义是（）A、矩阵B、平方根C、积数D、权数9．FOR计算循环表达式：FOR变量=初始值TO最后值：NC程序（）.A、ENDLOOPB、ENDIFC、ENDWHILED、ENDFOR10.在运算指令中，形式为#i=#jMOD#K代表的意义是（）A、反三角函数B、平均值C、空D、取余11、在运算指令中，形式为#i=#jXOR#k代表的意义是（）A、立方值B、极限值C、异或D、均值12.在变量赋值方法一中，引数（自变量）M对应的变量是（）A、#13B、#52C、#321D、#9513.计数变量同时会从初始值到最后值增加值必须小于最后值。
变量必须属于（）类型。
A、char（字符）B、float （浮点）C、signed（符号）D、int（整数）14、在变量赋值方法I中，引数（自编量）Ｊ对应的变量是（）。
数控机床宏程序例题
由浅入深宏程序10-车床旋转正弦函数宏程序正弦函数曲线旋转宏程序坐标点旋转1s = x cos(b) – y sin(b)t = x sin(b) + y cos(b)根据下图，原来的点（#1，#2），旋转后的点（#4，#5），则公式：#4=#1*COS[b]- #2*SIN[b]#5=#1*SIN[b]+ #2*COS[b]公式中角度b，逆时针为正，顺时针为负。
下图中正弦曲线如果以其左边的端点为参考原点，则此条正弦曲线顺时针旋转了16度，即b=-16正弦函数旋转图纸1此正弦曲线周期为24，对应直角坐标系的360对应关系【0,360】 y=sin（x）【0,24】 y=sin(360*x/24)可理解为：360/24是单位数值对应的角度360*x/24是当变量在【0,24】范围取值为x时对应的角度sin(360*x/24)是当角度为360*x/24时的正弦函数值旋转正弦函数曲线粗精加工程序如下：T0101M3S800G0X52Z5#6=26 工件毛坯假设为50mm，#6为每层切削时向+X的偏移量。
N5 G0X[#6+18.539]G1Z0F0.1#1=48N10 #2=sin【360*#1/24】#4=#1*COS[-16]- #2*SIN[-16] 旋转30度之后对应的坐标值#5=#1*SIN[-16]+ #2*COS[-16]#7=#4-【50-3.875】坐标平移后的坐标。
#8=45+2*#5+#6G1X[#8]Z[#7]F0.1 沿小段直线插补加工#1=#1-0.5 递减0.5，此值越小，工件表面越光滑。
IF [#1 GE 0] GOTO 10 条件判断是否到达终点。
Z-50G1X52 直线插补切到工件外圆之外G0Z5#6=#6-2IF [#6 GE 0] GOTO 5G0X150Z150M5M30镂空立方体宏程序范例镂空立方体图纸及宏程序范例此零件六个面加工内容相同，在加工时，调面装夹时要注意考虑夹紧力。
宏程序34[试题]
![宏程序34[试题]](https://img.taocdn.com/s3/m/2f27f67a1fb91a37f111f18583d049649b660e2d.png)
单元**********知识目标：1、掌握宏程序的基本知识。
2、掌握椭圆、双曲线等非圆曲线的宏程序的编程方法。
技能目标：1、熟练掌握宏程序的输入域编辑方法2、熟练掌握宏程序零件的加工方法3、掌握零件尺寸误差的调整方法任务1 梯形螺纹的加工一、任务描述使用HNC-21/22M华中世纪星数控系统的数控车床编程并加工如图6-8。
图6-8二、任务分析 梯形螺纹的车削工艺分析加工梯形螺纹的加工有很多种：直进法、斜进法、左右切削法、车直槽法、分层法等等。
由于梯形螺纹较之三角螺纹，其螺距和牙型都大，而且精度高，牙型两侧面表面粗糙度值较小，致使梯形螺纹车削时，吃刀深，走刀快，切削余量大，切削抗力大。
学校的数控车床刚性较差，这就导致了梯形螺纹的车削加工难度较大，在数控车工技能培训中难于掌握，容易产生“扎刀”和“爆刀”现象，进而对此产生紧张和畏惧的心理。
在多年的数车工实习教学中，通过不断的摸索、总结、完善，对于梯形螺纹的车削也有了一定的认知，笔者认为利用宏程序进行分层切削，可以很好地解决出现的问题。
“分层法”车削梯形螺纹实际上是直进法和左右切削法的综合应用。
在车削较大螺距的梯形螺纹时，“分层法”通常不是一次性就把梯形槽切削出来，而是把牙槽分成若干层，每层深度根据实际情况而定。
转化成若干个较浅的梯形槽来进行切削，可以降低车削难度。
每一层的切削都采用左右交替车削的方法，背吃刀量很小，刀具只需沿左右牙型线切削，梯形螺纹车刀始终只有一个侧刃参加切削，从而使排屑比较顺利，刀尖的受力和受热情况有所改善，因此能加工出较高质量的梯形螺纹，且容易掌握，程序简短，容易操作。
三、相关知识梯形螺纹的尺寸计算国家标准规定梯形螺纹的牙型角为30°。
下面就介绍30°牙型角的梯形螺纹。
30°梯形螺纹（以下简称梯形螺纹）的代号用字母“T r ”及公称直径×螺距表示，单位均为mm 。
左旋螺纹需在尺寸规格之后加注“LH ”，右旋则不注出。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由浅入深宏程序10-车床旋转正弦函数宏程序正弦函数曲线旋转宏程序坐标点旋转1s = x cos(b) – y sin(b)t = x sin(b) + y cos(b)根据下图，原来的点（#1，#2），旋转后的点（#4，#5），则公式：#4=#1*COS[b]- #2*SIN[b]#5=#1*SIN[b]+ #2*COS[b]公式中角度b，逆时针为正，顺时针为负。
下图中正弦曲线如果以其左边的端点为参考原点，则此条正弦曲线顺时针旋转了16度，即b=-16正弦函数旋转图纸1此正弦曲线周期为24，对应直角坐标系的360对应关系【0,360】 y=sin（x）【0,24】 y=sin(360*x/24)可理解为：360/24是单位数值对应的角度360*x/24是当变量在【0,24】范围取值为x时对应的角度sin(360*x/24)是当角度为360*x/24时的正弦函数值旋转正弦函数曲线粗精加工程序如下：T0101M3S800G0X52Z5#6=26 工件毛坯假设为50mm，#6为每层切削时向+X的偏移量。
N5 G0X[#6+]0F#1=48N10 #2=sin【360*#1/24】#4=#1*COS[-16]- #2*SIN[-16] 旋转30度之后对应的坐标值#5=#1*SIN[-16]+ #2*COS[-16]#7=#4-【】坐标平移后的坐标。
#8=45+2*#5+#6G1X[#8]Z[#7] 沿小段直线插补加工#1=# 递减，此值越小，工件表面越光滑。
IF [#1 GE 0] GOTO 10 条件判断是否到达终点。
Z-50G1X52 直线插补切到工件外圆之外G0Z5#6=#6-2IF [#6 GE 0] GOTO 5G0X150Z150M5M30镂空立方体宏程序范例镂空立方体图纸及宏程序范例此零件六个面加工内容相同，在加工时，调面装夹时要注意考虑夹紧力。
对于每个面的加工，可以用一个宏程序进行编制。
宏程序编程时，即有深度方向的变化，也有半径的变化，是一种典型的宏程序。
可以先用自己的思路编制一下，图后附有参考程序。
图片1图片2G64G40G90G54G0X0Y0Z100G0Z5#1= (分四层切削，共11mm深)#2=25 （第一层，最大一个沉孔直径为25mm，其次为20、15、10）N10 G1Z[#1]F30G1G41X[#2]D01F200G3 I[-#2]R[#2]G1G40X0#1=##2=#2-5IF [#1 GE -11] GOTO 10G0Z100M5M30点评：程序中有两个变量，但只用一个循环就可以了。
因为两个方向的变化都分别是等值递减的，所以把其中一个直接放到另一个循环里做好递减就可以了。
车削“斜椭圆”的宏程序本文分析了斜椭圆的数控车床加工问题，通过旋转转换方程确定了斜椭圆的参数方程，编制出(包含宏程序的)实际加工程序。
随着数控技术不断进步，数控车床加工中各种复杂型面也日渐增多，如椭圆、抛物线、正弦曲线、余弦曲线和双曲线等各种非圆曲面。
对于上述各种复杂成形面，利用CAM软件进行自动编程相对简单，但由于种种原因，在绝大数情况下数控车床主要还是依靠手工编程。
目前在数控车床上加工正椭圆已不是难事，一些学者进行过这方面的研究并发表了相关论文。
但对斜椭圆零件的加工方面研究较少，主要原因为：①机床数控系统本身既不存在加工椭圆等非圆曲线的G指令，更没有类似数控铣床用G6 8这样的旋转指令，使编程难度大大增加;②加工中变量的参数直接影响着加工的效率以及质量，很容易产生过切报警，即使程序正确无误，实际加工时参数调整也非常困难，直接影响加工能否顺利进行，以及加工精度能否保证。
对于如图1所示的斜椭圆零件，笔者在配置华中世纪星车床数控系统(HNC-21/22T)的数控车床上加工成形，加工出的零件如图2所示。
1.相关数学计算已知：椭圆方程：a2b2(见图1)，椭圆上任一点A 点坐标(Z,X):(acosα ,bsinα )，则：。
若椭圆绕圆心旋转θ (见图3)，则根据旋转公式，求出A 点在工件坐标系(Z0X 坐标系)中的坐标为：A点：Z：acosαcosθ-bsinαsinθ;X ：acosα sinθ +bsinα cosθ。
注意：椭圆顺时针旋转时，公式中的θ 角取负值;逆时针旋转时，θ 角取正值。
2.程序格式(1)如图3和图4所示，编程原点为右端面与轴线的交点。
(2)程序为HNC—21T系统格式。
%1234 (程序名) M3S600T0101G42G00X Z (快速点定位)#12=起始角(α)(椭圆轮廓起始点的参数角)WHILE[#12]LE终点角 (若为凹椭圆轮廓，则应为WHILE[#12]GE负终点角)#13=a*COS[#12*PI/180]*COS[θ]- b*SIN[#12*PI/180]*SIN[θ] (椭圆上任一点 Z坐标值)#14=a*COS[#12*PI/180]*SIN[θ]+b* SIN[#12*PI/180]*COS[θ] (椭圆上任一点 X坐标值)G01 X[2*#14+U]Z[#13+W]F60 (直线插补椭圆，U、W为椭圆圆心在编程坐标系下的坐标，即椭圆平移后需要进行坐标转换，请注意平移方向，以便确定U、W 的正负)。
#12=#12+ (若为凹椭圆轮廓，则应为#12=#G40G00X100Z100M05M303.编程实例实例如图1所示。
(1)计算起始参数角根据公式：可以得到：起始参数角=º。
(2)计算终点参数角根据公式：，得到：终点参数角=97º。
(3)参考程序如下(HNC-21T数控系统)。
使用数控车床切削零件图如图1所示，毛坯材料为45钢，直径50mm，长度为65mm，椭圆的长半轴和短轴分别为25mm和15mm，旋转角度20º(1号刀为粗车35º尖刀，2号刀为精车35º尖刀，3号刀为切断刀)。
%2M3S600T0101G42G00X55Z2G71 U2 P1 Q2F120G0X100Z100M3S1500T0202G0X55Z2N1 G0G01Z0 F60#12=WHILE[#12]LE97#13=25*COS[#12*PI/180]*COS[20]-15*SIN[#12*PI/180]*SIN[20]#14=25*COS[#12*PI/180]*SIN[20]+15*SIN[#12*PI/180]*COS[20] G01 X[2*#14]Z[#13-20]F60#12=#12+ENDWG1X48C1Z-44X44Z-46Z-50N2X50G00X100Z100M5M0M3S700T0303G00X50Z-45G01X1F40G00X50X100Z100M304.程序中变量的确定与注意事项旋转椭圆程序变量的赋值是一个重要环节，因为宏程序是利用许多段微小的直线来逼近轮廓的，取值大，轮廓表面的逼近误差也大。
在加工中，变量的赋值可以按粗车和精车来取值。
粗加工程序变量的取值应根据预留加工余量的大小来确定，在保证加工不过切的前提下，我们可以选择较大的程序变量，但是也不能过大，变量过大会使精加工余量不均匀或形成过切;精加工时我们主要是保证工件的质量，为使工件的几何形状达到要求，需要减少拟合的误差，因此我们应该选择一个较小的程序变量。
5.结语通过实际加工生产，上述措施能很好地解决加工中程序编制，保证工件的形状几何精度，解决加工出现的各种问题，减少加工时间，提高加工效率。
利用宏程序编制数控车床斜椭圆程序编程计算题：请利用宏程序或子程序编制粗、精加工程序答案：提示：如果采用三角函数计算椭圆起点和终点，会造成一定的计算误差。
所以应该采用坐标系的平移和角度变换进行计算。
已知AB=20AOB=30 求出AOB=AB/AO AO=40 所以椭圆长轴为40短轴为30 在xoy 坐标系编程计算题：请利用宏程序或子程序编制粗、精加工程序答案：提示：如果采用三角函数计算椭圆起点和终点，会造成一定的计算误差。
所以应该采用坐标系的平移和角度变换进行计算。
已知AB=20 ∠AOB=30求出∠AOB=AB/AOAO=40所以椭圆长轴为40短轴为30在xoy坐标系中求出起点与终点起点x= y=10在XOY坐标系求椭圆起点：X=xCOS30+ySIN30X=*COS30+10*SIN30X=将x=-10 y=代入公式求出椭圆终点：X=xCOS30+ySIN30X=将计算出的起点和终点值带入公式X=A*COSα求出起点和终点的角度值：起点：=40COSαCOSα=∠α=终点：=40*COSαCOSα=∠α=参考加工程序为：（西门子802D）G40G64T1D1M3S1200G0X100Z2R1=10N1G1X=R1+60 Z0R2=N2 R3=40*COS〈R2〉R4=30*SIN〈R2〉R5=R3*COS〈30〉-R4*SIN〈30〉R6=R3*SIN〈30〉-R4*COS〈30〉G1X=R1+40+2*R6 Z=R5-50R2=R2+1IF R2〈= GOTOB N2G1X=R1+ Z=-60Z-110G0X150Z2R1=R1-2IF R1〉=0 GOTOB N1G0X100Z150M5M2车床椭圆宏程序粗精加工宏程序椭圆宏程序，最经典，最需要掌握的，也是比较基本的一种车床宏程序图片1G99G40G21M03S700G0X42Z5(开始粗加工，从外分层向里切)#2=18 设置分层初始值N10 #1=30*SQRT[1-#2*#2/20*20] 计算椭圆上对应#2=18的#1值#3=2*#2 计算X轴坐标值#4=#1-30+ 计算Z轴坐标值，为给精加工留的余量G0X[#3] 刀具快速移动至切削直径G1Z[#4] 第一层走刀G1U2 利用增量坐标从切削直径向外退离工件1mmG0Z5 快速退刀至Z5，为下次进刀做准备#2=#2-2 变量递减2mm，作为下次切削直径IF #2GE0 GOTO 10 终点判断，是否到达0，等于0时也会切削，之后-2时会跳出循环，执行下一段（精加工，从工件坐标系远点开始切削椭圆，用小直线段模拟椭圆进行加工）15000F#2=0 初始值与粗加工不同N20 #1=30*SQRT[1-#2*#2/20*20]#3=2*#2#4=#1G01X[#3]Z[#4]#2=#2+ 这里决定了划分的小段直线大小，值越小加工出来的椭圆面越光滑IF #2LE20 GOTO 20G0X100Z100M5M30车床任意位置椭圆宏程序的编制不在轴线上的椭圆宏程序编制也没有什么特殊的，只是改下偏置的数值罢了。
椭圆的参数方程为：X=a*COS Y=b*SIN 可改写为： #1=30*cos[#3] #3 为参数方程对应的中角度 #2=20*sin[#3] 图中椭圆长半轴 30mm ，短半轴 20mm ，椭圆中心位置如图所示，不在轴线上，椭圆的参数方程为：X=a*COSθY=b*SINθ可改写为： #1=30*cos[#3] #3为参数方程对应的中角度#2=20*sin[#3]图中椭圆长半轴30mm，短半轴20mm，椭圆中心位置如图所示，不在轴线上，因此在计算编程所用的坐标值时，X方向要再加上40，Z方向要减去30+10=30相应程序如下：T0101M3S800G0X82Z5#6=36N5 G0X[#6+40]-10F#3=0N10 #1=30*COS[#3]#2=20*SIN[#3]#4=2*#2+#6+40 计算出的为半径值，需转化为直径值才能与直径编程对应。