1-3布拉菲空间点阵+原胞+晶胞
合集下载
1.2 布喇菲格子 原胞和晶胞 1.3 密堆积
Cl-的坐标为
1 1 1 , ,， 2 2 2
Cs+的坐标为
(0,0,0)
第三节 密堆积
密堆积、配位数和致密度
1.密堆积(close-packed) 如果晶体由完全相同的一种粒子组成,而粒子被看作小 球,这些全同的小球最紧密的堆积称为密堆积. 2.配位数(coordination number) 在布拉菲格子中，离某一格点最近的格点,称为该格点 的最近邻(nearest neighbour),格点周围最近邻数称为 该格子的配位数.常用符号 z 表示。 它可以描述晶体中粒子排列的紧密程度，粒子排列 越紧密，配位数越大。
Rn n1a1 n2a2 n3a3
则以 a1 , a2 , a3 为棱的平行六面体是晶格体积的最 小重复单元，即原胞 原胞的体积为 a1 (a2 a3 )
2.说明： 1). 对于同一晶格，原胞的取法不唯一，但无论如 何选取，原胞均有相同的体积，每个原胞平均只包 含一个格点。 2). 格点对应基元，如果基元由n个原子组成，则每 个原胞包含n个原子。 3). 原胞反映了晶格的周期性，如：平移对称性。
氯化钠结构属面心立方。 氯化钠的原胞选取方法与面心立方简单格子的选 取方法相同。 每个原胞包含1个格点，每个晶胞包含4个格点 基元由一个Cl-和一个Na+组成。 Cl-的坐标为
1 1 1 , , ， 2 2 2
Na+的坐标为
(0,0,0)
(c)氯化铯结构
Cl
Cs
氯化铯结构是由两个简立方子晶格沿体对角线位 移1/2的长度套构而成。 Cl-和Cs+分别组成简立方格 子，其布拉维晶格为简立方，氯化铯结构属简立方。 每个原胞包含1个格点，每个晶胞包含1个格点。 基元由一个Cl-和一个Cs+组成。
原胞晶胞 ppt课件
(i
j
k)
面心立方
小结
复式格子
氯化钠结构：由两个面心 立方的子晶格彼此沿立方体空间对角线位移二分之 一长度套构而成。 属于复式面心立方结构。
面心立方原胞与晶胞
1) 晶胞基矢 a a i ,b a j,c a k
体积 V a ( b c ) a 3
节点数 4?
晶胞
面心立方原胞与晶胞 1) 晶胞基矢 a a i ,b a j,c a k
体积 V a ( b c ) a 3
节点数：4 2）原胞基矢
晶体的对称性
点阵的对称性
布喇菲空间点阵
晶体的内部结构可以看成有一些相同相的同点的（点结点？）
在空间作规则的周期性的无限分布。
a
晶体结构
a
基元
点阵
晶体结构 = 点阵 + 基元
布喇菲空间点阵
基元：晶体的基本结构单元 (1) 一个基元对应一个节点 (2) 基元（结点）周围的环境相同（等效性） (3) 基元内部有结构，可以由一种或数种原子构成
3. 反映晶格结构周期性与对称性特征的体积重复单元。 原胞只反映晶格的周期性特征， 晶胞则同时反映晶格周期性和对称性。
a
ai ,
b aj,
c
ak
简立方
a1
a 2
(j
k)
a 2
a 2
(k
i)
a3
a 2
(i
j)
体心立方
a1
a 2
(i
j
k)
a2
a 2
(i
j
k)
a3
a 2
1) 晶胞基矢 a a i ,b a j,c a k
1 3布拉菲空间点阵原胞晶胞【精选】
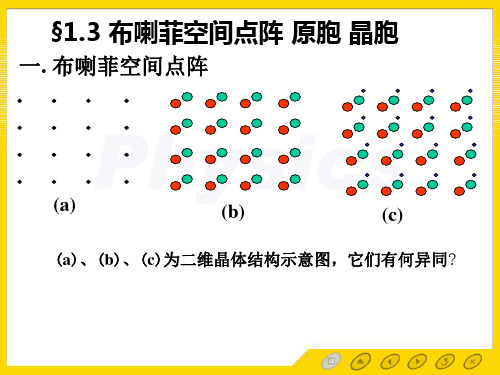
简单晶格必须由同种原子组成；反之，由同种原子组成 的晶格却不一定是简单晶格。如金刚石和hcp晶格都是复 式晶格。
简单晶格
复式晶格
二 原胞
在晶格中取一个格点为顶点，以三个不共面的方向上的周 期为边长形成的平行六面体作为重复单元，这个平行六面体沿
三个不同的方向进行周期性平移，就可以充满整个晶格，形成 晶体，这个平行六面体即为原胞，代表原胞三个边的矢量称为
晶胞（即布喇菲原胞）的体积: V a3
属于立方晶系的晶胞有简立方、体心立方、面心立方
(a)简立方（sc）
a1 ai 每个晶胞包含1个格点。
c b
a2 a j 固体物理学原胞的体积 Ω a3
a3 ak
a
既是晶胞也是原胞
(b)面心立方（fcc）
ak
a1
a2
aj
a3
原胞
ai
平均每个晶胞（布喇菲原胞）包含4个格点。
基元，基元在空间周期性重复排列就形成晶体结构。
晶格+基元=晶体结构
1.1基元、结点（格点）和晶格
(a)
(1)基元
(b)
(c)
在晶体中适当选取某些原子作为一个基本结构单元，这个
基本结构单元称为基元，基元是晶体结构中最小的重复单元，
基元在空间周期性重复排列就形成晶体结构。 特点：任何两个基元中相应原子周围的情况是相同的，
cc
氯化钠结构由两个面心立方子晶格沿体对角线位移1/2的 长度套构而成。
Cl-和Na+分别组成面心立方子晶格。 其布喇菲晶格为面心立方。
氯化钠结构属面心立方。
氯化钠的固体物理学原胞选取方法
与面心立方简单格子的选取方法相同。
每个固体物理学原胞包含1个格点，每个晶胞包含4个格点。 基元由一个Cl-和一个Na+组成。
简单晶格
复式晶格
二 原胞
在晶格中取一个格点为顶点，以三个不共面的方向上的周 期为边长形成的平行六面体作为重复单元，这个平行六面体沿
三个不同的方向进行周期性平移，就可以充满整个晶格，形成 晶体，这个平行六面体即为原胞，代表原胞三个边的矢量称为
晶胞（即布喇菲原胞）的体积: V a3
属于立方晶系的晶胞有简立方、体心立方、面心立方
(a)简立方（sc）
a1 ai 每个晶胞包含1个格点。
c b
a2 a j 固体物理学原胞的体积 Ω a3
a3 ak
a
既是晶胞也是原胞
(b)面心立方（fcc）
ak
a1
a2
aj
a3
原胞
ai
平均每个晶胞（布喇菲原胞）包含4个格点。
基元，基元在空间周期性重复排列就形成晶体结构。
晶格+基元=晶体结构
1.1基元、结点（格点）和晶格
(a)
(1)基元
(b)
(c)
在晶体中适当选取某些原子作为一个基本结构单元，这个
基本结构单元称为基元，基元是晶体结构中最小的重复单元，
基元在空间周期性重复排列就形成晶体结构。 特点：任何两个基元中相应原子周围的情况是相同的，
cc
氯化钠结构由两个面心立方子晶格沿体对角线位移1/2的 长度套构而成。
Cl-和Na+分别组成面心立方子晶格。 其布喇菲晶格为面心立方。
氯化钠结构属面心立方。
氯化钠的固体物理学原胞选取方法
与面心立方简单格子的选取方法相同。
每个固体物理学原胞包含1个格点，每个晶胞包含4个格点。 基元由一个Cl-和一个Na+组成。
晶体学第一章晶胞与点阵
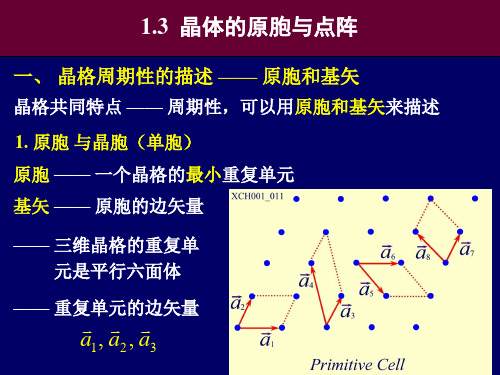
原胞体积
V
a1
(a2
a3)
a3
—— 原胞中只包含一个原子
2) 面心立方晶格
立方体的顶点到三个近邻的面心引三个基矢
基矢
a1
a 2
(
j
k)
a a2 2 (k i )
a3
a 2
(i
j)
原胞体积
V a1 (a2 a3)
1 a3 4
—— 原胞中只包含一个原子
3) 体心立方晶格
钛酸钡原胞可以取 作简单立方体 包含： 3个不等价的O原子 1个Ba原子 1个Ti原子 —— 共五个原子
六角密排晶格的原胞基矢选取
—— 一个原胞中包含A层 和B层原子各一个
—— 共两个原子
二、晶格周期性的描述 —— 布拉菲点阵，点阵平移矢量
1. 点阵（lattice），也叫空间点阵（space lattice）
以点（阵点或结点）代替晶体的基元（晶体的最小组成 单元，由原子、离子或分子构成），得到的描述晶体中质 点排列周期性的数学图形。
阵点（lattice point）—— 环境和性质完全相同； 基元（basis）—— 晶体的最小组成单元。
点阵 + 基元
晶体结构
简单晶格 —— 基元为单原子 复式晶格 —— 基元由多个原子、离子或分子组成
Rl ra l1a1 l2a2 l3a3, 1, 2, 3
原胞中各种等价原子之间的相对位移 例如： 金刚石晶格 —— 碳1位置 —— 碳2位置
对角线位移
B
可以用1，l2，l3的取值可以囊括所有的阵点
由
确定的晶体空间点阵 —— 布拉菲点阵
（布拉菲格子）
2）面网
晶面
， —— 基本平移矢量（基矢），l1， l2 取整数
第一章晶体结构
第一章晶体结构1 布喇菲点阵和初基矢量晶体结构的特点在于原子排列的周期性质。
布喇菲点阵是平移操作112233R n a n a n a =++所联系的诸点的列阵。
布喇菲点阵是晶体结构周期性的数学抽象。
点阵矢量112233R n a n a n a =++，其中，1n ，2n 和3n 均为整数，1a ，2a 和3a 是不在同一平面内的三个矢量，叫做布喇菲点阵的初基矢量，简称基矢。
初基矢量所构成的平行六面体是布喇菲点阵的最小重复单元。
布喇菲点阵是一个无限的分立点的列阵，无论从这个列阵中的哪个点去观察，周围点的分布和排列方位都是完全相同的。
对一个给定的布喇菲点阵，初级矢量可以有多种取法。
2 初基晶胞(原胞)初基晶胞是布喇菲点阵的最小重复单元。
初基晶胞必定正好包含布喇菲点阵的一个阵点。
对于一个给定的布喇菲点阵，初基晶胞的选取方式可以不只一种，但不论初基晶胞的形状如何，初基晶胞的体积是唯一的，()123c V a a a =⋅⨯。
3 惯用晶胞(单饱)惯用晶胞是为了反映点阵的对称性而选用的晶胞。
惯用晶胞可以是初基的或非初基的。
惯用晶胞的体积是初基晶胞体积的整数倍，c V nV =。
其中，n 是惯用晶胞所包含的阵点数。
确定惯用晶胞几何尺寸的数字叫做点阵常数。
4 维格纳—赛兹晶胞(W-S 晶胞)维格纳—赛兹晶胞是另一种能够反映晶体宏观对称性的晶胞，它是某一阵点与相邻阵点连线的中垂面(或中垂线)所围成的最小体积。
维格纳—赛兹晶胞是初基晶胞。
5 晶体结构当我们强调一个实际的晶体与布喇菲点阵的抽象几何图案的区别时，我们用“晶体结构”这个名词[1]。
理想的晶体结构是由相同的物理单元放置在布喇菲点阵的阵点上构成的。
这些物理单元称为基元，它可以是原子、分子或分子团(有时也可以指一组抽象的几何点)。
将基元平移布喇菲点阵的所有点阵矢量，就得到晶体结构，或等价地表示为基元十点阵＝晶体结构[2]当选用非初基的惯用晶胞时,一个布喇菲点阵可以用带有基元的点阵去描写。
1.3 布喇菲空间点阵
基元
晶体微观结构的周期性结构单元
基元：随晶体
简称
不同，基元可以是单个原子，也可以是若干原子之集 团，如:Ca、Cu、Ag、Au、Al、Pb等元素晶体，基元为 单个原子；Mg、Ti、Zn、Cd等元素晶体，基元包括两个 原子 ； 结构较复杂的无机化合物晶体：基元所含原子数目可多 达十几或几十，甚至上百。 结构更复杂的有机化合物晶体：基元所含原子数目多达 一万多，如蛋白质晶体 。
a1 , a2 , a3
简单晶格，任一原子A的位置矢量：
Rl l1a1 l2 a2 l3a3
Rl 2a1 3a2
Rl 3a1 a2 a3
单胞 —— 为了反映晶格的对称性 常取最小重复单元的几倍作为重复单元 单胞的边在晶轴方向，边长等于该方向上的一个周期 单胞的基矢—— 单胞三个边的矢量
每个晶胞共含有4对离子，其原胞的基矢取法与fcc相同。
5 CsCl晶体的结构 CsCl结构 —— 两个简单立方子晶格彼此沿立方体空间 对角线位移1／2 的长度套构而成
6. 金刚石晶格结构
—— 碳原子构成的一个面心立方原胞内还有四个原子 分别位于四个空间对角线的 1／4处 —— 一个碳原子和其它四个碳 原子构成一个正四面体 —— 金刚石结构的半导体晶体 Ge、Si等
1.3 布喇菲空间点阵 原胞 晶胞
19th cent.,Bravais：物质结构研究表明物质内部 有空隙 空间点阵学说：
晶体的内部结构可以概括为由大量相同的点子（格点） 在空间有规则地作周期性的无限分布构成的系统,即布 喇菲点阵。 空间点阵学说+物质微观结构的原子理论 晶体宏观特征起源于晶体独特的微观结构： 组成晶体的原子（或离子，或分子）在空间的规则排 列呈现出一种周期性。X射线衍射技术验证晶体微观结构 的周期性。
2、空间点阵、原胞 晶胞
§1.2 密堆积
配位数情况
如果晶体不是由同一种原子构成，那么相应小球的体积不 等，从而不可能形成密积结构，因此配位数一定小于12。 考虑到周期性和对称性的特点：晶体不可能具有配位数11、 10和9，所以，次一个配位数应该是8、6。
Page 9 第9页
§1.2 密堆积 晶体的配位数也不可能是5，则下一个配位数是4，为四 面体。 配位数是3的为层状结构，而配位数是2的则为链状结构。
显然，WS 原胞也只包含一个格点，因此它与固体物理学原胞的体积 一样，也是最小周期性重复单元。
Page 第 24 24 页
§1.3 布喇菲空间点阵 原胞 晶胞
原胞常取以基矢为棱边的平行六面体，体积为：
上述取法只是原胞的习惯取法，但原则上原胞可以任意多种取法， 只要满足是晶体的最小重复单元这个条件。 无论如何选取，原胞均有相同的体积，每个原胞含有一个格点。对 有限大的晶体（非理想晶体），所含原胞和格点数相等。
但实际上各种晶格结构已有习惯的原胞选取方式。
Page 第 23 23 页
§1.3 布喇菲空间点胞并不能反映晶格的全部宏观对称性，为此，威格纳和
塞兹提出了另一种原胞，称为威格纳—塞兹原胞，简写为WS原胞。 如图所示，若选定某一格点，从 格点出发连接其它邻近的格点并作 这些连线的中垂面，则被这些中垂 面所围成的多面体就是WS原胞。
由于布喇菲格子中格点相互等价，每一格点有相同的最近邻数。
一个粒子周围最近邻的粒子数称为配位数。用以描写晶体中粒子排列 的紧密程度。
最大配位数: 密堆积所对应的配位数。
Page 2 第2页
§1.2 密堆积
Page 3
Page 3 第3页
§1.2 密堆积
Page 4
1.3原胞晶胞
面心立方
原胞 原胞（固体物理学原胞）：以一个结点为顶点，以三个不同
方向的周长为边长的平行六面体。
原胞特点？
原胞
特点: (1) 体积最小的重复单元 (2) 格点只出现在该平行六面体的顶角上。 (3) 每个原胞平均包含一个格点 (4) 原胞的选择方式有多种（形状），但原胞的体积相等。
基矢： 原胞的边长矢量
体心立方的致密度
4 3 r : 原子球半径 r 3 致密度 : n V : 晶胞体积（立方体的体积） V n : 一个晶胞内含有的原子球的个数
4 3 4 3 r r 23 1 3 3 V a
3a (4r ) 3a 2r
2 2
4 3 r 3 3 2 0.68 V 8
立方晶系原胞
简立方
体心立方
面心立方
简立方原胞与晶胞
1) 晶胞基矢 a ai , b aj , c ak 体积 V a (b c ) a3
2）原胞基矢
a1 ai , a2 aj , a3 ak 体积 a1 (a2 a3 ) a3
面心立方 fcc a3 4 a3/4 12
2a 2
体心立方的A层原子球的间隙
体心立方晶格中，A层中原子球的距离
0.31 r
面心立方的致密度？
4 3 r : 原子球半径 r 3 致密度 : n V : 晶胞体积（立方体的体积） V n : 一个晶胞内含有的原子球的个数
1.以刚性原子球堆积模型计算六角密积结构的致密度。 六角密排致密度？
原胞体积 节点数：?
原胞节点只能在顶点
基矢： a1, a2 , a3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
维格纳--塞茨单胞
引入Wigner-Seitz原胞的原因
优点： （1）Wigner-Seitz原胞本身保持了布拉伐格子的
对称性； （2）该取法今后要用到。 缺点： （1）Wigner-Seitz原胞的体积等计算不方便； （2）平移对称性反而不直观。
2.2 几种晶格的实例 (1)一维原子链 一维单原子链
a
a1
固体物理学原胞的体2积
a2 a
jk
Ω a1 a2 a3
ik
1a3 4
2
a 3 a i j 2
(c)体心立方（bcc）
ak
a
a1 i j k 2
a
a2 i j k
a1
a2 aj
ai
2
aka3 a i j k
a3
2
a1 a2
平均每个布拉维原胞包含2个格点。
§1.3 布喇菲空间点阵 原胞 晶胞
一. 布喇菲空间点阵
(a)
(b)
(c)
(a)、(b)、(c)为二维晶体结构示意图，它们有何异同?
(a)
(b)
(c)
一个理想的晶体是由完全相同的结构单元在空间周期性重
复排列而成的。 所有晶体的结构可以用布喇菲格子（又称晶格）来描述，
这种晶格的每个格点上附有一群原子，这样的一个原子群称为
a
j
ai
固体物理学原胞的体积
Ω a1
a3
a2 a3
1 a3
2
立方晶系中几种实际晶体结构
(a)金刚石结构
实际原子排布结 构（包括基元）
cc 金刚石结构是由两个面心立方子晶格沿体对角线位移1/4 的长度套构而成,其晶胞即布拉维晶格为面心立方。
金刚石结构属面心立方，每个晶胞包含4个格点。
每个格点包含2个原子，属于复式晶格。
原胞的基本平移矢量，简称基矢。
2.1 原胞的分类 (1)固体物理学原胞(简称原胞) 构造：取一格点为顶点，由此点向近邻的三个格点作三个不共
面的矢量，以此三个矢量为边作平行六面体即为固体物理学原胞。
特点：格点只在平行六面体的顶角上，面上和内部均无格点， 平均每个固体物理学原胞包含1个格点。是最小的重复单元，它反
氯化钠结构属面心立方。
氯化钠的固体物理学原胞选取方法
与面心立方简单格子的选取方法相同。
每个固体物理学原胞包含1个格点，每个晶胞包含4个格点。 基元由一个Cl-和一个Na+组成。
Cl-的坐标为 1 1 1 ， Na+的坐标为 (000)。
2 2 2
(c)氯化铯结构
Cl
Cs
氯化铯结构是由两个简立方子晶格沿体对角线位移1/2的 长度套构而成。 Cl-和Cs+分别组成简立方格子，其布拉维晶
2
1 (00 )
2
a 2
6
(W) 2
(000)( 1 1 0)
22
(10 2
1) 2
(0
1 2
1) 2
(000)
(11 1) 22 2
2a 12 2
3a 8 2
CsCl
Cs+ 1 Cl- 1
(000)
(11 1) 22 2
3a 8 2
典型的晶体结构
结构型 单晶胞中 原子个数
原子在单晶 胞中的位置
最近邻 距离
配位数
金刚石
8
(000)
1 2
3
1
1
4
41
2
1
32
4
4
1 2
A类碳原子的 共价键方向
B类碳原子的 共价键方向
金刚石结构每个固体物理学原胞
包含1个格点,基元由两个碳原子组成,
位于（000）和
1 1 1 4 4 4
处。
(b)氯化钠结构
cc
氯化钠结构由两个面心立方子晶格沿体对角线位移1/2的 长度套构而成。
Cl-和Na+分别组成面心立方子晶格。 其布喇菲晶格为面心立方。
简单晶格必须由同种原子组成；反之，由同种原子组成 的晶格却不一定是简单晶格。如金刚石和hcp晶格都是复 式晶格。
简单晶格
复式晶格
二 原胞
在晶格中取一个格点为顶点，以三个不共面的方向上的周 期为边长形成的平行六面体作为重复单元，这个平行六面体沿
三个不同的方向进行周期性平移，就可以充满整个晶格，形成 晶体，这个平行六面体即为原胞，代表原胞三个边的矢量称为
晶胞（即布喇菲原胞）的体积: V a3
属于立方晶系的晶胞有简立方、体心立方、面心立方
(a)简立方（sc）
a1 ai 每个晶胞包含1个格点。
c b
a2 a j 固体物理学原胞的体积 Ω a3
a3 ak
a
既是晶胞也是原胞
(b)面心立方（fcc）
ak
a1
a2
aj
a3
原胞
ai
平均每个晶胞（布喇菲原胞）包含4个格点。
格为简立方，氯化铯结构属简立方。
每个固体物理学原胞包含1个格点，每个晶胞包含1个格点 。基元由一个Cl-和一个Cs+组成。
Cl-的坐标为 1 1 1 ， Cs+的坐标为 (000)。
2 2 2
典型的晶体结构
结构型
单晶胞中 原子在单晶 最近邻 原子个数 胞中的位置 距离
配位数
fcc
(Cu) 4
bcc
基元，基元在空间周期性重复排列就形成晶体结构。
晶格+基元=晶体结构
1.1基元、结点（格点）和晶格
(a)
(1)基元
(b)
(c)
在晶体中适当选取某些原子作为一个基本结构单元，这个
基本结构单元称为基元，基元是晶体结构中最小的重复单元，
基元在空间周期性重复排列就形成晶体结构。 特点：任何两个基元中相应原子周围的情况是相同的，
a
一维双原子链
b
a
(2)二维
(a)
(b)
a2 a1
a4 a3
a6
a5
固体物理学原胞
a8 a7
维格纳--塞茨单胞
(3)三维
立方晶系 ab bc ca a b c
取 i , j ,k为坐标轴的单位矢量,
设晶格常量(晶胞棱边的长度)为a,
c b
a
即立方体边长为a, a ai ,b a j,c ak
映了晶体结构的周期性。
基矢：固体物理学原胞基矢通常用 a1 , a2 , a3 表示。
体积为： Ω a1 a2 a3
(2)晶胞、惯用晶胞或布喇菲原胞 构造：使三个基矢的方向尽可能地沿着空间对称轴的方 向，它具有明显的对称性和周期性。 特点：结晶学原胞不仅在平行六面体顶角上有格点，面上 及内部亦可有格点。其体积是固体物理学原胞体积的整数倍。
而每一个基元中不同原子周围情况则不相同。
(2)结点（格点）
一个基元用一个格点（或结点、点子）表示，它可以代
表基元重心的位置，也可以代表基元中任意的位置。
(a)
(b)
(3)晶格
(a)
(
(c)
晶体的内部结构可以概括
b)
为是由一些相同的结点在空间
有规则地做周期性无限分布，
通过这些点做三组不共面的平
行直线族，形成一些网格，称 为晶格(或者说这些点在空间周 期性排列形成的骨架称为晶格, 又称为布喇菲格子)。
基矢：晶胞的基矢一般用 a, b, c 表示。
体积为： v a b c n Ω
(3)维格纳--塞茨原胞 构造：以一个格点为原点，作原点与其它格点连接的中垂面
(或中垂线)，由这些中垂面(或中垂线)所围成的最小体积(或面 积)即为W--S原胞。
特点：它是晶体体积的最小重复单元，每个原胞只包含1个 格点。其体积与固体物理学原胞体积相同。
(
1 2
1 2
0)
(0 1 2
1) 2
(101) 22
3a
(
1 4
1 4
1 4
)(
3 4
3 4
1 4
)(
3 4
1 4
3 4
)(
1 4
3 4
3 4
)
4
4
NaCl
Na+ 4 Cl- 4
(000)
(
1 2
1 2
0)
(0 1 1) 22
(101) 22
( 1 1 1 ) ( 1 00) 222 2
1 (0 0)
晶格是晶体结构周期性的数学 抽象，它忽略了晶体结构的具体内 容，保留了晶体结构的周期性。
1.2 简单晶格和复式晶格
若格点上的基元只包含一个原子，那么晶格为简单晶格。 简单晶格中所有原子在化学、物理和几何环境上都是 完全等同的。
若格点上的基元包含两个或两个以上的原子（或离子）， 那么晶格为复式晶格。
引入Wigner-Seitz原胞的原因
优点： （1）Wigner-Seitz原胞本身保持了布拉伐格子的
对称性； （2）该取法今后要用到。 缺点： （1）Wigner-Seitz原胞的体积等计算不方便； （2）平移对称性反而不直观。
2.2 几种晶格的实例 (1)一维原子链 一维单原子链
a
a1
固体物理学原胞的体2积
a2 a
jk
Ω a1 a2 a3
ik
1a3 4
2
a 3 a i j 2
(c)体心立方（bcc）
ak
a
a1 i j k 2
a
a2 i j k
a1
a2 aj
ai
2
aka3 a i j k
a3
2
a1 a2
平均每个布拉维原胞包含2个格点。
§1.3 布喇菲空间点阵 原胞 晶胞
一. 布喇菲空间点阵
(a)
(b)
(c)
(a)、(b)、(c)为二维晶体结构示意图，它们有何异同?
(a)
(b)
(c)
一个理想的晶体是由完全相同的结构单元在空间周期性重
复排列而成的。 所有晶体的结构可以用布喇菲格子（又称晶格）来描述，
这种晶格的每个格点上附有一群原子，这样的一个原子群称为
a
j
ai
固体物理学原胞的体积
Ω a1
a3
a2 a3
1 a3
2
立方晶系中几种实际晶体结构
(a)金刚石结构
实际原子排布结 构（包括基元）
cc 金刚石结构是由两个面心立方子晶格沿体对角线位移1/4 的长度套构而成,其晶胞即布拉维晶格为面心立方。
金刚石结构属面心立方，每个晶胞包含4个格点。
每个格点包含2个原子，属于复式晶格。
原胞的基本平移矢量，简称基矢。
2.1 原胞的分类 (1)固体物理学原胞(简称原胞) 构造：取一格点为顶点，由此点向近邻的三个格点作三个不共
面的矢量，以此三个矢量为边作平行六面体即为固体物理学原胞。
特点：格点只在平行六面体的顶角上，面上和内部均无格点， 平均每个固体物理学原胞包含1个格点。是最小的重复单元，它反
氯化钠结构属面心立方。
氯化钠的固体物理学原胞选取方法
与面心立方简单格子的选取方法相同。
每个固体物理学原胞包含1个格点，每个晶胞包含4个格点。 基元由一个Cl-和一个Na+组成。
Cl-的坐标为 1 1 1 ， Na+的坐标为 (000)。
2 2 2
(c)氯化铯结构
Cl
Cs
氯化铯结构是由两个简立方子晶格沿体对角线位移1/2的 长度套构而成。 Cl-和Cs+分别组成简立方格子，其布拉维晶
2
1 (00 )
2
a 2
6
(W) 2
(000)( 1 1 0)
22
(10 2
1) 2
(0
1 2
1) 2
(000)
(11 1) 22 2
2a 12 2
3a 8 2
CsCl
Cs+ 1 Cl- 1
(000)
(11 1) 22 2
3a 8 2
典型的晶体结构
结构型 单晶胞中 原子个数
原子在单晶 胞中的位置
最近邻 距离
配位数
金刚石
8
(000)
1 2
3
1
1
4
41
2
1
32
4
4
1 2
A类碳原子的 共价键方向
B类碳原子的 共价键方向
金刚石结构每个固体物理学原胞
包含1个格点,基元由两个碳原子组成,
位于（000）和
1 1 1 4 4 4
处。
(b)氯化钠结构
cc
氯化钠结构由两个面心立方子晶格沿体对角线位移1/2的 长度套构而成。
Cl-和Na+分别组成面心立方子晶格。 其布喇菲晶格为面心立方。
简单晶格必须由同种原子组成；反之，由同种原子组成 的晶格却不一定是简单晶格。如金刚石和hcp晶格都是复 式晶格。
简单晶格
复式晶格
二 原胞
在晶格中取一个格点为顶点，以三个不共面的方向上的周 期为边长形成的平行六面体作为重复单元，这个平行六面体沿
三个不同的方向进行周期性平移，就可以充满整个晶格，形成 晶体，这个平行六面体即为原胞，代表原胞三个边的矢量称为
晶胞（即布喇菲原胞）的体积: V a3
属于立方晶系的晶胞有简立方、体心立方、面心立方
(a)简立方（sc）
a1 ai 每个晶胞包含1个格点。
c b
a2 a j 固体物理学原胞的体积 Ω a3
a3 ak
a
既是晶胞也是原胞
(b)面心立方（fcc）
ak
a1
a2
aj
a3
原胞
ai
平均每个晶胞（布喇菲原胞）包含4个格点。
格为简立方，氯化铯结构属简立方。
每个固体物理学原胞包含1个格点，每个晶胞包含1个格点 。基元由一个Cl-和一个Cs+组成。
Cl-的坐标为 1 1 1 ， Cs+的坐标为 (000)。
2 2 2
典型的晶体结构
结构型
单晶胞中 原子在单晶 最近邻 原子个数 胞中的位置 距离
配位数
fcc
(Cu) 4
bcc
基元，基元在空间周期性重复排列就形成晶体结构。
晶格+基元=晶体结构
1.1基元、结点（格点）和晶格
(a)
(1)基元
(b)
(c)
在晶体中适当选取某些原子作为一个基本结构单元，这个
基本结构单元称为基元，基元是晶体结构中最小的重复单元，
基元在空间周期性重复排列就形成晶体结构。 特点：任何两个基元中相应原子周围的情况是相同的，
a
一维双原子链
b
a
(2)二维
(a)
(b)
a2 a1
a4 a3
a6
a5
固体物理学原胞
a8 a7
维格纳--塞茨单胞
(3)三维
立方晶系 ab bc ca a b c
取 i , j ,k为坐标轴的单位矢量,
设晶格常量(晶胞棱边的长度)为a,
c b
a
即立方体边长为a, a ai ,b a j,c ak
映了晶体结构的周期性。
基矢：固体物理学原胞基矢通常用 a1 , a2 , a3 表示。
体积为： Ω a1 a2 a3
(2)晶胞、惯用晶胞或布喇菲原胞 构造：使三个基矢的方向尽可能地沿着空间对称轴的方 向，它具有明显的对称性和周期性。 特点：结晶学原胞不仅在平行六面体顶角上有格点，面上 及内部亦可有格点。其体积是固体物理学原胞体积的整数倍。
而每一个基元中不同原子周围情况则不相同。
(2)结点（格点）
一个基元用一个格点（或结点、点子）表示，它可以代
表基元重心的位置，也可以代表基元中任意的位置。
(a)
(b)
(3)晶格
(a)
(
(c)
晶体的内部结构可以概括
b)
为是由一些相同的结点在空间
有规则地做周期性无限分布，
通过这些点做三组不共面的平
行直线族，形成一些网格，称 为晶格(或者说这些点在空间周 期性排列形成的骨架称为晶格, 又称为布喇菲格子)。
基矢：晶胞的基矢一般用 a, b, c 表示。
体积为： v a b c n Ω
(3)维格纳--塞茨原胞 构造：以一个格点为原点，作原点与其它格点连接的中垂面
(或中垂线)，由这些中垂面(或中垂线)所围成的最小体积(或面 积)即为W--S原胞。
特点：它是晶体体积的最小重复单元，每个原胞只包含1个 格点。其体积与固体物理学原胞体积相同。
(
1 2
1 2
0)
(0 1 2
1) 2
(101) 22
3a
(
1 4
1 4
1 4
)(
3 4
3 4
1 4
)(
3 4
1 4
3 4
)(
1 4
3 4
3 4
)
4
4
NaCl
Na+ 4 Cl- 4
(000)
(
1 2
1 2
0)
(0 1 1) 22
(101) 22
( 1 1 1 ) ( 1 00) 222 2
1 (0 0)
晶格是晶体结构周期性的数学 抽象，它忽略了晶体结构的具体内 容，保留了晶体结构的周期性。
1.2 简单晶格和复式晶格
若格点上的基元只包含一个原子，那么晶格为简单晶格。 简单晶格中所有原子在化学、物理和几何环境上都是 完全等同的。
若格点上的基元包含两个或两个以上的原子（或离子）， 那么晶格为复式晶格。