平面体系自由度附约束
结构力学第二章-平面体系的几何组成分析

2.4 实铰和虚铰
Ⅰ1
Ⅰ A
Ⅱ(参照刚片) (a) 实铰的相对位置固定
Ⅰ Ⅰ1
虚铰O O1
Ⅱ(参照刚片) (b) 虚铰的相对位置变化
图2.8 实铰和虚铰示例
15
Ⅰ
A Ⅱ
(a) 两刚片用铰结在一起的 两链杆相连
Ⅰ
A Ⅱ
(b) 两刚片用铰直接相连
图2.9实铰的常见情形
16
才从微小运动看,两根链杆所起的作 用相当于在链杆交点处的一个铰所起 的约束作用,此铰可称虚铰。
是一个刚片。一根梁、一根链杆或者支承体系的基础也 可看作是一个刚片。
形状可任意替换
7
2. 2 自由度
体系运动时可以独立改变的几何坐标的数目,称为 该体系的自由度。平面上的一个点的自由度为2(或称 作有2个自由度),平面上一个刚片的自由度为3。
平面内一刚片
平面内一点 n=2 n=3
x
y
8
2.3 约束
3
c.几何瞬变体系:不考虑材料的变形,在任何荷载作用下, 几何形状和位置可能产生微小的改变,随之即变成几何不 变体系的体系。
FP
FP
组成几何不变体系的条件:
• 具有必要的约束数; • 约束布置方式合理
4
d.几何常变体系:体系缺少约束或约束布置不恰当,没有确定的几 何形状与空间位置的体系(可发生持续大量的刚体位移)。
第2章 平面体系的几何组成分析
1
本章导读
学习内容: 1.掌握几何不变体系、几何可变体系、瞬变体系的概念, 2.掌握刚片、自由度、约束、实铰与虚铰的概念; 3.了解平面体系的计算自由度及其计算方法; 4.掌握平面几何不变体系的基本组成规则及其运用; 5.了解体系的几何组成与静力特性之间的关系。
§4-2平面体系的自由度和约束

黄河水利职业技术学院
重庆水利水电职业技术学院
工程力学
/
§4-2 平面体系的自由度和约束
3.多余约束
如果在一个体系中增加一个约束,而体系的自由度并不因此而减少, 则此约束称为多余约束。
工程力学
/
主持单位: 杨凌职业技术学院
黄河水利职业技术学院
参建单位: 杨凌职业技术学院
与别的物体相联的刚性杆。
工程力学
/
§4-2 平面体系的自由度和约束
(2)单铰——联结两个刚片的铰。 (3)复铰——联结三个或三个以上刚片的铰。
工程力学
/
§4-2 平面体系的自由度和约束
(4)刚性连结。
(5)虚铰。
工程力学
平面体系的自由度和约束
主 讲 人:袁 芙 蓉
杨凌职业技术学院
2014.09
工程力学
/
第四章 平面体系的几何组成分析
§4-2Байду номын сангаас平面体系的自由度和约束
工程力学
/
§4-2 平面体系的自由度和约束
1.自由度
平面体系的自由度是指该体系运动时可以独立变化的几何参数
的数目,即确定体系的位置所需的独立坐标的数目。
工程力学
/
§4-2 平面体系的自由度和约束
2.约束
凡是能够减少体系自由度的装置都可称为约束。能减少一个
自由度,就说它相当于一个约束。
(1)链杆——是两端以铰
7-1 平面体系的计算自由度

平面内的刚体的自由度
图3-2
约束
实际结构体系中各构件之间及体系与基础之间,是通过一些装置互相联结在一起的。这些联结装置使ቤተ መጻሕፍቲ ባይዱ系内各构件(刚片)之间相对运动受到限制,使体系减少自由度的装置称为约束(联系)。
凡减少一个自由度的装置称为一个约束或一个联系,如果一个装置能使体系减少N个自由度,则称它为N个约束。
几何可变体系
尚不能确定体系是否几何不变
尚不能确定体系是否几何不变
结构组成分析--判断体系是否几何可变;对于结构,区分静定与超静定的组成
联结两个以上刚片的铰称为复铰。
例如刚片Ⅰ、Ⅱ、Ⅲ共用一个铰A联结(图3-3c),若刚片I的位置已固定,则刚片Ⅱ和Ⅲ都只能绕铰A转,从而各减少了两个自由度,两刚片共减少了四个自由度,故此联结三个刚片的铰实际相当于两个单铰的作用。
联结n个刚片的复铰,其作用相当于(n—l)个单铰。
两刚片之间经刚性联结后使体系自由度减少三个,所以一个刚结相当于三个约束。如图3-4a中刚片Ⅰ和Ⅱ经刚性连接后两刚片之间不能发生任何相对运动,因此可视为一个刚片,其自由度为3。
联结两刚片以上的刚结称为复刚结(图3-4b)。
联结n个刚片的复刚结,相当于(n—1)个单刚结。
图3-3
图3-4
三、平面体系计算自由度
把体系看作由许多刚片受刚结、铰结和链杆的约束而成的。因此,在计算它的自由度时,可按如下步骤进行:
首先按照各刚片都具有自由度的情况计算其自由度的数目,然后计算所加入的约束数,最后将两者相减,便得到该体系的计算自由度W。
W=3m-(3g+2h+r)
式中m—一体系中无多余约束的刚片数(基础不作为刚片数计入);
g—一单刚结数(复刚结换算成等效的单刚结数计入);
第二章第二节平面体系的自由度和约束
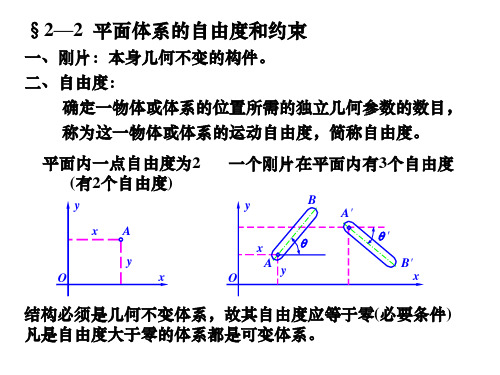
一、刚片:本身几何不变的构件。 二、自由度: 确定一物体或体系的位置所需的独立几何参数的数目, 称为这一物体或体系的运动自由度,简称自由度。
平面内一点自由度为2 (有2个自由度)
y x A x y O x O A y
一个刚片在平面内有3个自由度
y B A'
q
q'
B' x
= 3×11 —3×7 —2×5 —5 =—3
体系具有3个“多余约束”
能否把支杆也看成刚片?
√
例:试计算体系的内部可变度
各杆都 看成1个刚片 M =9 R =2 H =9
V =3M —3R —2H —3
= 3×9 —3×2 —2×9 —3 =0
体系内部可变度=0
把AC、CB分别 看成1个刚片
M =7
链杆数: B=23 体系的内部可变度: V= 2J —B —3 = 2×12 —23 —3 = —2
看成6根杆件 M =6 R =6
H =0
V =3M —3R —2H —3 = 3×6 —3×6 —2×0 —3 = —3 体系具有3个“多余约束”
√
整体看成1个刚片 M =1 R =0 H =0 V =3M —3R —2H —3 = 3×1 —3×0 —2×0 —3 =0 体系没有“多余约束”
×
体系内部 3个“多余约束”没有反映出来
例:试计算图示体系的自由度
结点数: 链杆数:
J=14 B=25
支杆总数: S=3 自由度数: W=2J —B —S = 2×14 —25 —3 =0
例:试计算图示体系的内部可变度
结点数:
J=12
结点数:
J=12
链杆数: B=21 体系的内部可变度: V= 2J —B —3 = 2×12 —21 —3 =0
2.3_平面体系的计算自由度

W (3m 2 j ) (3g 2h b)
m、j、g、h、b意义同前。
6
Tankertanker Design
定性结论
(1) 一个体系若求得W >0,一定是几何可变体 系;
(2) W=0,则S=n,如无多余约束,则为几何不 变。如有多余约束,则为几何可变;
(3) 若W<0,则可能是几何不变体系,也可能 是几何可变体系,取决于具体的几何组成。体 系有多余约束;
m—刚片数; g—简单刚结数;
h—简单铰数;b—简单链杆数
在求解时,地基的自由度为零,不计入刚片数。
5
Tankertanker Design
2. 将体系看作结点以及链杆组成的体系,其中 结点为被约束对象,链杆为约束。则计算自由度 为: W 2 j b
j—结点数;
b—简单链杆数。
3. 混合公式——约束对象为刚片和结点,约束 为铰、刚结和链杆。则计算自由度为:
例2-4
解:
(1)
按式 W=3m-(3g+2h+b)
m=7,h=9,b=3 W=3×m-2×h-b =3×7-2×9-3=0
(2)
按式 W=2j-b j=7,b=14 W=2j-b=2×7-14 =0
例2-5
解: 按式 W=3m-(3g+2h+b) m=1,g=3, b=4,h=0 , 则: W=3m-(3g+2h+b) =3×2-(3×3+2×0+4) = -10
作业:
2-1(a); 2-2(c)
2-4(d); 2-6(d) 2-12(b) 注:必须用铅笔画图,有“解”字。全部统一 用稿纸写,作业只需左上角只写学号后两位, 学习委员排好顺序,在最上面加一张姓名、学 号、成绩表格。 讲第一次作业
平面体系几何组成分析的方法(静定的概念)(建筑力学)
例题分析
例1.分析图示体系的几何构造性。 解析:(1)计算自由度
W 4244 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 进一步判断,依次去掉二元体DFE、BDC、BEC、BCA后,整个体系只剩下 地基了,为几何不变体系。由于去掉二元体并不改变原体系的几何构造性,因此 原体系也是几何不变体系。
二元体规则是非常好用的规则,特别是去二元体,可以大大简化体系 构件数目,使判断简化,其主要有以下几个技巧:
(1)根据需要进行链杆与刚片之间的转化,巧妙使用二元体; (2)当体系比较复杂时,可以先考虑其中的一个它部分之间的连接关系, 判定整个体系的几何构造性。
例题分析
例2.分析图示体系的几何构造性。 解析:(1)计算自由度
W 72 113 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 体系没有二元体,但体系本身是有二元体的,去掉所有二元体,只剩下一个 杆件,所以体系本身几何不变,再考虑其与地基的连接方式,判定体系几何不变。
总结与技巧
示例
例1.分析图示体系的几何构造性。
解析:(1)计算自由度
W 7277 0
体系具有成为几何不变体系的最少约束数目,需进一步判断。 (2)依次去掉二元体FAB、IED、FBJ、IDC如图所示。 (3)三角形GCH看作刚片Ⅰ,地基看作特殊刚片Ⅱ。 (4)刚片Ⅰ、Ⅱ之间通过三根链杆相连,三链杆汇交
第十二章 平面结构体系的几何组成分析

若原体系几何不变(或可变),则新增加一个 二元体后,新体系仍为几何不变(或可变); 同样,在一个已知体系上拿掉二元体,也不
会影响原体系的几何不变性或几何可变性。
因此可将二元体规则叙述如下:在一个体系
上依次增加或减少二元体,原体系的几何可 变性保持不变。
第四节 几何组成分析举例
第四节 几何组成分析举例
=-3
应用此方法解本题时须注意:此时结点B为混合结点, 对于此类结点,计算单刚结点数时,可把铰接杆当作不存 在;而在计算铰结点数时,则把刚接各杆看作一个刚片。
所以,应用式(12-1)计算可得 W=3×m-3×g-2×h-b-r =3×9-3×6 -2×4-9 =-8
表明此体系具有8个多余约束。
三、瞬变体系
在对结构进行分析计算时,必须先分析体系的几 何组成,以确定体系的几何不变性。
几何组成分析的目的是:
(1)判别给定体系是否是几何不变体系,从而确 定它能否作为结构使用;
(2)研究几何不变体系的组成规则,以保证设计 出安全合理的结构;
(3)正确区分静定结构和超静定结构,为结构的 内力计算打下必要的基础
(二)自由度
体系的自由度是指确定体系空间位置所需的独立坐标 数,或者体系运动时可以独立改变的几何参数的数目,通 常记作S。
一个点在平面内自由运动时,它的位置用坐标X,Y完全 可以确定,则平面内一点的自由度等于2,如图12-3(a)所 示。
一个刚片在平面内自由运动时,它的位置
用其上任一点A的坐标x,y和过A点的任一 直线AB的倾角φ完全可以确定,则一个平面 刚片的自由度等于3,如图12-3(b)所示。
解法二:把体系内部看成是由7个刚片AB、BC、CD、DE、 EF、FA、EB,3个单铰F、B、D,3个单刚结点A、B、
平面体系自由度和约束

平面体系自由度和约束自由度:所谓体系的自由度,是指该体系运动时,用来确定其位置所需的独立坐标(或参变量)的个数。
如果一个体系的自由度大于零,则该体系就是几何可变体系。
(1)点的自由度:平面内一动点A,其位置需用两个坐标x和y来确定,所以一个点在平面内有两个自由度。
1.swf(2)刚片的自由度:一个刚片在平面内运动时,其位置将由其上任一点A的坐标x、y 和过点A的任一直线AB的倾角φ来确定,因此,一个刚片在平面内有三个自由度。
2.swf约束:约束是指能够减少自由度的装置(又称联系)。
减少一个自由度的装置,就称为一个约束(或联系)。
约束有两大类:支座约束和刚片间的约束。
1. 支座约束(1)滚轴支座:能限制刚片A点在垂直方向移动,但不能限制其水平方向移动和绕A 点的转动,减少了一个自由度,相当于一个约束。
3.swf(2)铰支座:能限制刚片A点在水平方向和竖直方向移动,但不能限制其绕A点的转动,减少了两个自由度,相当于两个约束。
4.swf(3)固定支座:能限制刚片在水平、竖直方向的移动和转动,使刚片的自由度减少为零,相当于三个约束。
5.swf2. 刚片间的联结约束(1)单铰约束:联结两个刚片的铰称为单铰。
两刚片在平面内独立的自由度个数为六个,用一个铰将刚片Ⅰ、Ⅱ联结起来,对刚片Ⅰ而言,其位置可由A点的坐标x、y和AB 线的倾角φ1来确定,因此其有三个自由度,刚片Ⅱ相对刚片Ⅰ只能绕A点转动,即两刚片间只保留了相对转角φ2,则由刚片Ⅰ、Ⅱ所组成的体系在平面内有四个自由度,则一个单铰约束减少了二个自由度。
一个单铰相当于两个约束。
6.swf(2)复铰约束:用一个铰同时联结三个或三个以上的刚片,则这种铰称为复铰。
设其中一刚片可沿x、y向移动和绕某点转动,则其余两刚片都只能绕其转动,因此各减少两个自由度。
象这种联结三刚片的复铰相当于两个单铰的作用,由此可见,联结n个刚片的复铰,相当于(n-1)个单铰的作用。
7.swf。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
或:6-3×(3-1)=0
板书设计:
平面体系的自由度及约束
教学 课题
教学 目的
教学 重点
主要教学方 法
教 具
平面体系的自由度及约束
(《建筑力学》下册、第16.2平面体系的自由度及约束)
1.了解自由度、约束的概念
2.掌握几种约束的作用
3.通过教学使学生树立起“世上无难事,只要肯登攀”的学习信心
几种约束的作用
举例、演示、推导、总结
粉笔、教鞭、实物、幻灯
=(3-1)(刚片)×0(自由度)
总结:一个复杂的刚性连接相当于(n-1)个简单的刚性连接。
举例
举例、推导
教学过程
时间分配
教 学 内 容
教学方法的运用
总结
(5分钟)
作业
(1分钟)
1、自由度
2、约束
3、几种常见的约束作用
1)链杆
2)铰
3)刚性连接
1、阅读本节课文
2、预习 16.3 几何不变体系的简单组成规则
3-2=1
2).复铰:一个复铰减少2(n-1)个自由度。
一个复铰相当于(n-1)个单铰。
9-6=3 即:9-2×3=3
或:9-2×(4-1)=3
3.刚性连接
简单的刚性连接:一个简单的刚性连接减少三个自由度。
3-3=0
复杂的刚性连接:一个复杂的刚性连接减少3(n-1)个自由度。
一个复杂的刚性连接相当于(n-1)个简单的刚性连接。
教学过程
时间分配
教 学 内 容
教学方法的运用
复习
(5分钟)
新课导入
(34分钟)
1、几何可变体系、几何不变体系的概念
2、平面体系几何组成分析的目的
1、自由度的概念
结论1:平面内的一个点有二种独立的运动方式,确定平面内的一个点的位置需要二个独立的坐标。
结论2:平面内的一个刚片有三种独立的运动方式,确定平面内的一个刚片的位置需要三个独立的坐标。
幻灯、提问
16、2平面体系的自பைடு நூலகம்度和约束
16.2.1自由度
概念: 所谓自由度是指确定体系位置所必须的独立的坐标数。
所谓自由度是指体系独立的运动方式。
16.2.2约束
概念: 能使体系减少自由度的装置称为约束(或称为联系)
几种约束的作用:
1.链杆:一个链杆可以减少一个自由度。
2.铰
1).单铰:一个单铰减少两个自由度。
几种常见的约束作用
1).链杆:一个链杆可减少一个自由度。
2).铰:
单铰:
3(自由度)-2(约束)=1(自由度)
总结:一个单铰可减少两个自由度。
复铰:
9(自由度)-6(约束)=3(自由度)
或:9(自由度)-2(约束)×3(刚片)
=3(自由度)
即:9(自由度)-2(约束)×[4-1](刚片)
=3(自由度)
总结:一个简单的刚性连接可减少三个自由度。
复杂的刚性连接:
6(自由度)-6(约束)=0(自由度)
或:6(自由度)-3(约束)×2(刚片)
=0(自由度)
即:6(自由度)-3(约束)×[3-1](刚片)
=0(自由度)
总结:一个复杂的刚性连接可减少3(n-1)自由度。
(3-1)(刚片)×3(自由度)
-(3-1)(刚片)×3(约束)
总结自由度的概念
1).所谓自由度是指确定体系位置所必须的独立坐标数。
2).所谓自由度是指体系独立的运动方式。
2、约束的概念
能使体系减少自由度的装置称为约束(或称为联系)
幻灯
幻灯
举例:
1、平面内的一个点
(粉笔头作演示)
2、平面内的一个刚片
(黑板擦作演示)
幻灯
举例
教学过程
时间分配
教 学 内 容
教学方法的运用
总结:一个复铰可减少2(n-1)自由度。
(4-1)(刚片)×3(自由度)
-(4-1)(刚片)×2(约束)
=(4-1)(刚片)×1(自由度)
总结:一个复铰相当于(n-1)个单铰。
举例
举例
举例、推导
教学过程
时间分配
教 学 内 容
教学方法的运用
3). 刚性连接:
简单的刚性连接:
3(自由度)-3(约束)=0(自由度)
