浙教版八年级上册特殊三角形常见的题目模型

合集下载

三角形中的5种解题模型-2023年新八年级数学核心知识点与常见题型通关讲解练(浙教版)(解析版)

重难点：三角形中的5种解题模型【知识梳理】一、“8”字模型三角形三个内角的和等于180°对顶角相等二、飞镖模型三角形三个内角的和等于180°三角形的外角等子与它不相邻的两个内角的和.三、“A”字模型三角形三个内角的和等于180°四、“老鹰捉小鸡”模型三角形三个内角的和等于180°三角形的外角等于与它不相邻的两本内角的和.五、（双）角平分线模型1.双内角平分线2.双外角平分线3.内角平分线+外角平分线三角形三个内角的和等于180°三角形的外角等于与它不相邻的两本内角的和.【考点剖析】一、“8”字模型1．（2021秋•宁远县校级期中）如图所示，∠α的度数是（）A．10°B．20°C．30°D．40°【解答】解：∵∠A+∠B+∠AOB＝∠C+∠D+∠COD，∠AOB＝∠COD，∴∠A+∠B＝∠C+∠D∴30°+20°＝40°+α，∴α＝10°故选：A．2．（2022春•叙州区期末）如图，BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，若∠A＝45°，∠P＝40°，则∠C的度数为（）A．30°B．35°C．40°D．45°【解答】解：∵∠A+∠ADG+∠AGD＝180°，∠ABC+∠C+∠BGC＝180°，∴∠A+∠ADG+∠AGD＝∠ABC+∠C+∠BGC．又∵∠AGD＝∠BGC，∴∠A+∠ADG＝∠C+∠GBC．同理可得，∠A+∠ADE＝∠P+∠PBE．∴∠A﹣∠P＝∠PBE﹣∠ADE．∵BP平分∠ABC交CD于点F，DP平分∠ADC交AB于点E，∴∠GBC＝2∠PBE，∠ADG＝2∠ADE．∴∠A﹣∠C＝2（∠A﹣∠P）．∴∠A+∠C＝2∠P．又∵∠A＝45°，∠P＝40°，∴∠C＝35°．故选：B．3．（2022春•靖江市校级月考）已知，如图，线段AD、CB相交于点O，连结AB、CD，∠DAB和∠BCD的平分线AP和CP相交于点P．试问∠P与∠D、∠B之间存在着怎样的数量关系，请说明理由．【解答】解：2∠P＝∠B+∠D，理由如下：如图，在△AOB和△COD中，∵∠AOB＝∠COD，∴∠OAB+∠B＝∠OCD+∠D，在△AEP和△CED中，∵∠AEP＝∠CED，∴∠1+∠P＝∠2+∠D，∵AP、CP分别是∠DAB和∠BCD的角平分线，∴2∠P﹣∠B＝2∠D﹣∠D，整理得，2∠P＝∠B+∠D．4．（2019春•邗江区校级月考）图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：；（2）仔细观察，在图2中“8字形”的个数：个；（3）图2中，当∠D＝50度，∠B＝40度时，求∠P的度数．（4）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结果，不必证明）．【解答】解：（1）∵∠A+∠D+∠AOD＝∠C+∠B+∠BOC＝180°，∠AOD＝∠BOC，∴∠A+∠D＝∠C+∠B，故答案为：∠A+∠D＝∠C+∠B；（2）①线段AB、CD相交于点O8字形”；②线段AN、CM相交于点O，形成“8字形”；③线段AB、CP相交于点N，形成“8字形”；④线段AB、CM相交于点O，形成“8字形”；⑤线段AP、CD相交于点M，形成“8字形”；⑥线段AN、CD相交于点O，形成“8字形”；故“8字形”共有6个，故答案为：6（3）∠DAP+∠D＝∠P+∠DCP，①∠PCB+∠B＝∠PAB+∠P，②∵∠DAB和∠BCD的平分线AP和CP相交于点P，①+②得：∠DAP+∠D+∠PCB+∠B＝∠P+∠DCP+∠PAB+∠P，即2∠P＝∠D+∠B，又∵∠D＝50度，∠B＝40度，∴2∠P＝50°+40°，∴∠P＝45°；（4）关系：2∠P＝∠D+∠B．∠D+∠1＝∠P+∠3①∠B+∠4＝∠P+∠2②①+②得：∠D+∠1+∠4+∠B＝∠P+∠3+∠2+∠P，∵∠DAB和∠DCB的平分线AP和CP相交于点P，∴∠1＝∠2，∠3＝∠4∴2∠P＝∠D+∠B．二、飞镖模型1．（2021春•宝应县月考）如图，求证：∠BDC＝∠A+∠B+∠C．【解答】证明：作射线AD，如图，∵∠3＝∠B+∠1，∠4＝∠C+∠2，∴∠3+∠4＝∠B+∠C+∠1+∠2，2．（2020春•如东县期末）探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；（2）请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，∠A＝54°，则∠ABX+∠ACX＝°；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝α，∠DBE＝β，请直接写出∠DCE的度数（用含α和β的式子表示）；③如图4，∠ABD，∠ACD的12等分线相交于点G1、G2…、G11，若∠BDC＝115°，∠BG1C＝60°，求∠A的度数．【解答】解：（1）∠BDC＝∠A+∠B+∠C．理由：连接AD并延长到点E．∵∠BDE＝∠BAD+∠B，∠CDE＝∠CAD+∠C，∴∠BDE+∠CDE＝∠BAD+∠B+∠CAD+∠C，（2）①∵∠BXC＝∠ABX+∠ACX+∠A＝90°，∠A＝54°，∴∠ABX+∠ACX＝36°．故答案为36．②如图3中，设∠ADC＝∠CDB＝x，∠AEC＝∠CEB＝y，则有∠DCE＝x+y+α，β＝2x+2y+α，∴∠DCE＝．故答案为．③设∠ABD＝x°，∠ACD＝y°．由题意可得，解得∠A＝55°．3．（2020春•锡山区期中）探究与发现：如图1所示的图形，像我们常见的学习用品﹣﹣圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：（1）观察“规形图”，试探究∠BDC与∠A、∠B、∠C之间的关系，并说明理由；（2①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B、C，若∠A＝50°，则∠ABX+∠ACX＝°；②如图3，DC平分∠ADB，EC平分∠AEB，若∠DAE＝50°，∠DBE＝130°，求∠DCE的度数；③如图4，∠ABD，∠ACD的10等分线相交于点G1、G2…、G9，若∠BDC＝140°，∠BG1C＝77°，求∠A的度数．【解答】解：（1）连接AD并延长至点F，且∠BDC＝∠BDF+∠CDF及∠BAC＝∠BAD+∠CAD；相加可得∠BDC＝∠BAC+∠B+∠C；（2）①由（1）的结论易得：∠ABX+∠ACX+∠A＝∠BXC，又因为∠A＝50°，∠BXC＝90°，所以∠ABX+∠ACX＝90°﹣50°＝40°；故答案为：40．②由（1）的结论易得∠DBE＝∠A+∠ADB+∠AEB，易得∠ADB+∠AEB＝80°；而∠DCE＝（∠ADB+∠AEB）+∠A，代入∠DAE＝50°，∠DBE＝130°，易得∠DCE＝90°；③∠BG1C＝（∠ABD+∠ACD）+∠A，∵∠BG1C＝77°，∴设∠A为x°，∵∠ABD+∠ACD＝140°﹣x°∴（140﹣x）+x＝77，14﹣x+x＝77，x＝70∴∠A为70°．题型三：“A”字模型1．（2022春•云龙区校级月考）已知如图，△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）【解答】解：∵∠1、∠2是△CDE的外角，∴∠1＝∠4+∠C，∠2＝∠3+∠C，即∠1+∠2＝2∠C+（∠3+∠4），∵∠3+∠4＝180°﹣∠C＝90°，∴∠1+∠2＝2×90°+90°＝270°．故选：B．2．（2021春•东台市月考）如图，△ABC中，∠C＝75°，若沿图中虚线截去∠C，则∠1+∠2＝°．【解答】解：∵△ABC中，∠C＝75°，∴∠A+∠B＝180°﹣75°＝105°，∵∠1+∠2+∠A+∠B＝360°，∴∠1+∠2＝360°﹣105°＝255°．故答案为：255．3．（2020春•新野县期末）旧知新意：我们容易证明，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？（1）如图1，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系？为什么？初步应用：（2）如图2，在△ABC纸片中剪去△CDE，得到四边形ABDE，∠1＝130°，则∠2﹣∠C＝；（3）小明联想到了曾经解决的一个问题：如图3，在△ABC中，BP、CP分别平分外角∠DBC、∠ECB，∠P与∠A有何数量关系？请利用上面的结论直接写出答案．拓展提升：（4）如图4，在四边形ABCD中，BP、CP分别平分外角∠EBC、∠FCB，∠P与∠A、∠D有何数量关系？为什么？（若需要利用上面的结论说明，可直接使用，不需说明理由．）【解答】解：（1）∠DBC+∠ECB＝180°﹣∠ABC+180°﹣∠ACB＝360°﹣（∠ABC+∠ACB）＝360°﹣（180°﹣∠A）＝180°+∠A；（2）∵∠1+∠2＝∠180°+∠C，∴130°+∠2＝180°+∠C，∴∠2﹣∠C＝50°；（3）∠DBC+∠ECB＝180°+∠A，∵BP、CP分别平分外角∠DBC、∠ECB，∴∠PBC+∠PCB＝（∠DBC+∠ECB）＝（180°+∠A），在△PBC中，∠P＝180°﹣（180°+∠A）＝90°﹣∠A；即∠P＝90°﹣∠A；故答案为：50°，∠P＝90°﹣∠A；（4）延长BA、CD于Q，则∠P＝90°﹣∠Q，∴∠Q＝180°﹣2∠P，∴∠BAD+∠CDA＝180°+∠Q＝180°+180°﹣2∠P＝360°﹣2∠P．题型四：“老鹰捉小鸡”模型1．（2022春•无锡期中）如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（）A．2∠A＝∠1﹣∠2B．3∠A＝2（∠1﹣∠2）C．3∠A＝2∠1﹣∠2D．∠A＝∠1﹣∠2【解答】解：如图，由翻折的性质得，∠3＝∠A′DE，∠AED＝∠A′ED，∴∠3＝（180°﹣∠1），在△ADE中，∠AED＝180°﹣∠3A，∠CED＝∠3+∠A，∴∠A′ED＝∠CED+∠2＝∠3+∠A+∠2，∴180°﹣∠3﹣∠A＝∠3+∠A+∠2，整理得，2∠3+2∠A+∠2＝180°，∴2×（180°﹣∠1）+2∠A+∠2＝180°，∴2∠A＝∠1﹣∠2．故选：A．2．（2022春•洪泽区月考）如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，这个规律是（）A．∠A＝∠1+∠2B．2∠A＝∠1+∠2C．3∠A＝2∠1+∠2D．3∠A＝2（∠1+∠2）【解答】解：∵在△ABC中，∠A+∠B+∠C＝180°①；在△ADE中∠A+∠ADE+∠AED＝180°②；在四边形BCDE中∠B+∠C+∠1+∠2+∠ADE+∠AED＝360°③；∴①+②﹣③得2∠A＝∠1+∠2．故选：B．3．（2021春•江都区校级期末）如图，三角形纸片ABC中∠A＝63°，∠B＝77°，将纸片一角折叠，使点C 落在△ABC的内部，若∠2＝50°，则∠1＝．【解答】解：设折痕为EF，连接CC′．∵∠2＝∠ECC′+∠EC′C，∠1＝∠FCC′+∠FC′C，∠ECF＝∠EC′F，∴∠1+∠2＝2∠ECF，∵∠C＝180°﹣∠A﹣∠B＝180°﹣63°﹣77°＝40°，∴∠1＝80°﹣50°＝30°，故答案为：30°．4．（2021春•南通期末）如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），图中∠1+∠2+∠3+∠4+∠5+∠6＝°．【解答】解：由题意知，∠1+∠2+∠3+∠4+∠5+∠6＝720°﹣（∠B'FG+∠B'GF）﹣（∠C'HI+∠C'IH）﹣（∠A'DE+∠A'ED）＝720°﹣（180°﹣∠B'）﹣（180°﹣C'）＝（180°﹣A'）＝180°+（∠B'+∠C'+∠A'）又∵∠B＝∠B'，∠C＝∠C'，∠A＝∠A'，∠A+∠B+∠C＝180°，∴∠1+∠2+∠3+∠4+∠5+∠6＝360°．故答案为：360．5．（2019春•常熟市月考）将纸片△ABC沿DE折叠使点A落在A′处的位置．（1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．（2）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．【解答】解：（1）2∠A′＝∠1+∠2，理由沿DE折叠使点A落在A′处的位置，∴∠AED＝∠A′ED，∠ADE＝∠A′DE，∵∠AED+∠ADE＝180°﹣∠A，∠1+∠2＝180°+180°﹣2（∠AED+∠ADE），∴∠1+∠2＝360°﹣2（180°﹣∠A′）＝2∠A′；（2）2∠A′＝∠2﹣∠1，理由：∵沿DE折叠使点A落在A′处的位置，∴∠A＝∠A′，∵∠DME＝∠A′+∠1，∠2＝∠A+∠DME，∴∠2＝∠A+∠A′+∠1，即2∠A′＝∠2﹣∠1．【点评】本题考查了折叠的性质，三角形外角性质，三角形内角和定理的应用，主要考查学生运用定理进行推理和计算的能力．题型五：（双）角平分线模型1．（2022春•海州区校级期末）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C 平分∠ACB，若∠BA'C＝122°，则∠1+∠2的度数为（）A．116°B．100°C．128°D．120°【解答】解：∵△ABC纸片沿DE折叠，∴△AED≌△A′ED，∴∠ADE＝∠EDA′，∠AED＝∠DEA′，∴∠1+∠2＝180°﹣2∠ADE+180°﹣2∠AED＝180°﹣（∠ADE+∠AED）+180°﹣（∠ADE+∠AED）＝2∠A，∵A'B平分∠ABC，A'C平分∠ACB，∠BA'C＝122°，∴∠A'BC＝∠ABC，∠A'CB＝∠ACB，∴∠A'BC+∠A'CB＝180°﹣122°＝58°，∴∠ABC+∠ACB＝2（∠A'BC+∠A'CB）＝2×58°＝116°，∴∠A＝180°﹣116°＝64°，∴∠1+∠2＝2∠A＝2×64°＝128°，故选：C．2．（2022春•靖江市校级月考）如图，△ABC中，∠BAC＝50°，∠ABC的角平分线与∠ACB的角平分线交于点O．则∠BOC＝．【解答】解：∵∠BAC＝50°，∴∠ABC+∠ACB＝180°﹣50°＝130°，∵∠ABC的角平分线与∠ACB的角平分线交于点O，∴∠ABO＝∠OBC＝∠ABC，∠ACO＝∠OCB＝∠ACB，∴∠OBC+∠OCB＝∠ABC+∠ACB＝（∠ABC+∠ACB）＝×130°＝65°，∴∠BOC＝180°﹣∠OBC﹣∠OCB＝180°﹣65°＝115°，故答案为：115°．3．（2022春•丹徒区月考）在△ABC中，∠A＝40°：（1）如图（1）BO、CO是△ABC的内角角平分线，且相交于点O，求∠BOC；（2）如图（2）BO、CO是△ABC的外角角平分线，且相交于点O，求∠BOC；（3）如图（3）BO、CO分别是△ABC的一内角和一外角角平分线，且相交于点O，求∠BOC；（4）根据上述三问的结果，当∠A＝n时，分别可以得出∠BOC与∠A有怎样的数量关系（只需写出结论）．【解答】解：（1）∵∠BOC＝180°﹣∠OBC﹣∠OCB，∴2∠BOC＝360°﹣2∠OBC﹣2∠OCB，而BO平分∠ABC，CO平分∠ACB，∴∠ABC＝2∠OBC，∠ACB＝2∠OCB，∴2∠BOC＝360°﹣（∠ABC+∠ACB），∵∠ABC+∠ACB＝180°﹣∠A，∴2∠BOC＝180°+∠A，∴∠BOC＝90°+∠A．当∠A＝40°，∠BOC＝110°；（2）∠OBC＝（∠A+∠ACB），∠OCB＝（∠A+∠ABC），∠BOC＝180°﹣∠0BC﹣∠OCB，＝180°﹣（∠A+∠ACB）﹣（∠A+∠ABC），＝180°﹣∠A﹣（∠A+∠ABC+∠ACB），结论∠BOC＝90°﹣∠A．∠BOC＝90°﹣∠A．当∠A＝40°，∠BOC＝70°．（3）∵∠OCD＝∠BOC+∠OBC，∠ACD＝∠ABC+∠A，而BO平分∠ABC，CO平分∠ACD，∴∠ACD＝2∠OCD，∠ABC＝2∠OBC，∴2∠BOC+2∠OBC＝∠ABC+∠A，∴2∠BOC＝∠A，即∠BOC＝∠A．当∠A＝40°，∠BOC＝20°；（4）∠BOC＝90°+n；∠BOC＝90°﹣n；∠BOC＝n．【点评】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．【过关检测】一、单选题 1．（2022秋·重庆渝北·八年级校考阶段练习）如图,将△ABC 沿着DE 翻折,使B 点与B'点重合,若∠1+∠2=80°,则∠B 的度数为（）A ．20°B ．30°C ．40°D ．50°【答案】C 【分析】由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠,再利用平角的定义可求出BED BDE ∠+∠的度数，进而利用三角形内角和可求∠B 的度数.【详解】由折叠的性质可知','BED B ED BDE B DE ∠=∠∠=∠∵1'180,2'180BED B ED BDE B DE ∠+∠+∠=︒∠+∠+∠=︒∴11(36012)(36080)14022BED BDE ∠+∠=︒−∠−∠=⨯︒−︒=︒ ∴180()18014040B BED BDE ∠=︒−∠+∠=︒−︒=︒故选C【点睛】本题主要考查折叠的性质及三角形内角和定理，掌握折叠的性质及三角形内角和定理是解题的关键.2．（2023·全国·八年级假期作业）如图，AB 和CD 相交于点O ，∠A ＝∠C ，则下列结论中不能完全确定正确的是（）A ．∠B ＝∠DB ．∠1＝∠A ＋∠DC ．∠2＞∠D D ．∠C ＝∠D【答案】D【分析】利用三角形的外角性质，对顶角相等逐一判断即可．【详解】∵∠A ＋∠AOD ＋∠D ＝180°，∠C ＋∠COB ＋∠B ＝180°，∠A ＝∠C ，∠AOD ＝∠BOC ，∴∠B ＝∠D ，∵∠1＝∠2＝∠A ＋∠D ，∴∠2＞∠D ，故选项A ，B ，C 正确，故选D ．【点睛】本题考查了对顶角的性质，三角形外角的性质，熟练掌握并运用两条性质是解题的关键． 3．（2023·全国·八年级假期作业）如图，ABC 中，65A ∠=︒，直线DE 交AB 于点D ，交AC 于点E ，则BDE CED ∠+∠=（）．A ．180︒B ．215︒C ．235︒D ．245︒【答案】D 【分析】根据三角形内角和定理求出ADE AED ∠+∠，根据平角的概念计算即可．【详解】解：65A ∠=︒，18065115ADE AED ∴∠+∠=︒−︒=︒，360115245BDE CED ∴∠+∠=︒−︒=︒，故选：D ．【点睛】本题考查的是三角形内角和定理的应用，掌握三角形内角和等于180︒是解题的关键．4．（2023春·江苏镇江·七年级统考期中）在社会实践手工课上，小茗同学设计了一个形状如图所示的零件，如果52,25A B ︒︒∠=∠=，30,35,72C D E ︒︒︒∠=∠=∠=，那么F ∠的度数是（）．A ．72︒B ．70︒C ．65︒D ．60︒【答案】B【分析】延长BE 交CF 的延长线于O ，连接AO ，根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠，再根据四边形的内角和求出DFO ∠，根据邻补角的性质即可求出DFC ∠的度数．【详解】延长BE 交CF 的延长线于O ，连接AO ，如图，∵180,OAB B AOB ∠+∠+∠=︒∴180,AOB B OAB ∠=︒−∠−∠同理得180,AOC OAC C ∠=︒−∠−∠∵360,AOB AOC BOC ∠+∠+∠=︒∴360BOC AOB AOC ∠=︒−∠−∠360(180)(180)B OAB OAC C =︒−︒−∠−∠−−∠−∠107,B C BAC =∠+∠+∠=︒∵72,BED ∠=︒∴180108,DEO BED ∠=︒−∠=︒∴360DFO D DEO EOF ∠=︒−∠−∠−∠36035108107110,=︒−︒−︒−︒=︒∴180********DFC DFO ∠=︒−∠=︒−︒=︒,故选：B ．【点睛】本题考查三角形内角和定理，多边形内角和，三角形的外角的性质，邻补角的性质，解题关键是会添加辅助线，将已知条件联系起来进行求解．三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角的和；邻补角性质：邻补角互补；多边形内角和：180(2)n ︒−．二、填空题 5．（2023·全国·八年级假期作业）如图是某建筑工地上的人字架，若1120∠=︒，那么32∠−∠的度数为．【答案】60︒【分析】根据平角的定义求出4∠，再利用三角形的外角的性质即可解决问题．【详解】解：如图14180∠+∠=︒，1120∠=︒，460∴∠=︒，324Ð=Ð+ÐQ ，32460∴∠−∠=∠=︒，故答案为：60︒．【点睛】本题考查三角形外角的性质、平角的性质等知识，解题的关键是熟练掌握基本知识，属于中考基础题．6．（2021·河北·统考中考真题）下图是可调躺椅示意图（数据如图），AE 与BD 的交点为C ，且A ∠，B ∠，E ∠保持不变．为了舒适，需调整D ∠的大小，使110EFD ∠=︒，则图中D ∠应（填“增加”或“减少”）度．【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系，进行计算即可判断．【详解】解：∵∠A+∠B=50°+60°=110°，∴∠ACB=180°-110°=70°，∴∠DCE=70°，如图，连接CF 并延长，∴∠DFM=∠D+∠DCF=20°+∠DCF ，∠EFM=∠E+∠ECF=30°+∠ECF ，∴∠EFD=∠DFM+∠EFM=20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°，要使∠EFD=110°，则∠EFD 减少了10°，若只调整∠D 的大小，由∠EFD=∠DFM+∠EFM=∠D+∠DCF+∠E+∠ECF=∠D+∠E+∠ECD=∠D+30°+70°=∠ D+100°，因此应将∠D 减少10度；故答案为：①减少；②10．【点睛】本题考查了三角形外角的性质，同时涉及到了三角形的内角和与对顶角相等的知识；解决本题的关键是理解题意，读懂图形，找出图形中各角之间的关系以及牢记公式建立等式求出所需的角，本题蕴含了数形结合的思想方法． 7．（2022春·七年级单元测试）如图，把ABC 纸片沿DE 折叠，使点A 落在图中的A '处，若29A ∠=︒，90BDA ∠'=︒，则A EC ∠'的大小为．【答案】32︒/32度【分析】利用折叠性质得'45ADE A DE ∠=∠=︒，'AED A ED ∠=∠，再根据三角形外角性质得74CED ∠=︒，利用邻补角得到106AED ∠=︒，则'106A ED ∠=︒，然后利用''A EC A ED CED ∠=∠−∠进行计算即可．【详解】解：∵'90BDA ∠=︒，∴'90ADA ∠=︒，∵ABC 纸片沿DE 折叠，使点A 落在图中的A'处，∴'45ADE A DE ∠=∠=︒，'AED A ED ∠=∠，∵294574CED A ADE ∠=∠+∠=︒+︒=︒，∴106AED ∠=︒，∴'106A ED ∠=︒，∴''1067432A EC A ED CED ∠=∠−∠=︒−︒=︒．故答案为：32︒．【点睛】本题考查了折叠的性质，三角形外角的性质，三角形内角和定理等，理解题意，熟练掌握综合运用各个知识点是解题关键．七年级课时练习）如图，在ABC 中，【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF 的度数，再根据角平分线的定义求得∠EAC+∠ECA 的度数，即可解答．【详解】解：∵∠B+∠BAC+∠BCA=180°，∠B=58°，∴∠BAC+∠BCA=180°﹣∠B=180°﹣58°=122°，∵∠BAC+∠DAC=180°，∠BCA+∠ACF=180°，∴∠DAC+∠ACF=360°﹣（∠BAC+∠BCA ）=360°﹣122°=238°，∵AE 平分∠DAC ，CE 平分∠ACF ，∴∠EAC=12∠DAC ，∠ECA=12∠ACF ，∴∠EAC+∠ECA =12（∠DAC+∠ACF ）=119°，∵∠EAC+∠ECA+∠AEC=180°，∴∠AEC=180°﹣（∠EAC+∠ECA ）=180°﹣119°=61°，故答案为：61°．【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义，熟练掌握三角形的内角和定理和角平分线的定义是解答的关键． 9．（2023春·山东泰安·七年级校考阶段练习）如图，在ABC 中，A α∠=，ABC ∠与ACD ∠的平分线交于点1A ，得1A ∠；1A BC ∠与1ACD ∠的平分线相交于点2A ，得2A ；L ；2019A BC ∠与2019A CD ∠的平分线相交于点2020A ，得2020A ∠，则2020A ∠= ．【答案】20202α【分析】结合题意，根据角平分线、三角形外角、三角形内角和的性质，得112A A ∠=∠，同理得212122A A α∠=∠=；再根据数字规律的性质分析，即可得到答案．【详解】根据题意，A α∠=，ABC ∠与ACD ∠的平分线交于点1A∴11118022A ABC ACB ACD ∠=︒−∠−∠−∠∵ACD A ABC ∠=∠+∠∴111802A ABC ACB A ∠=︒−∠−∠−∠∵180A ABC ACB ∠+∠+∠=︒∴112A A ∠=∠同理，得2121112222A A A α∠=∠=⨯∠=； 323111122222A A A α∠=∠=⨯⨯∠=；43411111222222A A A α∠=∠=⨯⨯⨯∠=；…1122n n n A A α−∠=∠= ∴202020202A α∠= 故答案为：20202α．【点睛】本题考查了三角形和数字规律的知识；解题的关键是熟练掌握三角形内角和、三角形外角、角平分线、数字规律的性质，从而完成求解．三、解答题 10．（2022秋·八年级课时练习）如图，ABC ∆中，(1)若ABC ∠、ACB ∠的三等分线交于点1O 、2O ，请用A ∠表示1BO C ∠、2BO C ∠；(2)若ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅（1O 、21n O O −⋅⋅⋅⋅⋅⋅依次从下到上），请用A ∠表示1BO C ∠，1n BO C −∠．【答案】(1)111203BO C A ∠=︒+∠，22603BO C A ∠=︒+∠，(2)()118011n BO C A n n ︒−∠=+∠，11801n n BO C A n n −︒−∠=+∠【分析】（1）根据三角形的内角和定理可得180ABC ACB A ∠+∠=︒−∠，再由ABC ∠、ACB ∠的三等分线交于点1O 、2O ，可得111(180),3O BC O CB A ∠+∠=︒−∠222(180),3O BC O CB A ∠+∠=︒−∠再根据三角形的内角和定理，即可求解；（2）根据三角形的内角和定理可得180ABC ACB A ∠+∠=︒−∠，再由ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅，可得111(180),O BC O CB A n ∠+∠=︒−∠111(180),n n n O BC O CB A n −−−∠+∠=︒−∠再根据三角形的内角和定理，即可求解．【详解】（1）解：∵180A ABC ACB ∠+∠+∠=︒，∴180ABC ACB A ∠+∠=︒−∠，∵ABC ∠、ACB ∠的三等分线交于点1O 、2O ，∴111(180),3O BC O CB A ∠+∠=︒−∠222(180),3O BC O CB A ∠+∠=︒−∠ ∴11111180()180(180)12033BO C O BC O CB A A ∠=︒−∠+∠=︒−︒−∠=︒+∠，22222180()180(180)6033BO C O BC O CB A A ∠=︒−∠+∠=︒−︒−∠=︒+∠；（2）解：∵180A ABC ACB ∠+∠+∠=︒，∴180ABC ACB A ∠+∠=︒−∠，∵ABC ∠、ACB ∠的n 等分线交于点1O 、21n O O −⋅⋅⋅⋅⋅⋅， ∴111(180),O BC O CB A n ∠+∠=︒−∠111(180),n n n O BC O CB A n −−−∠+∠=︒−∠∴()()111180111180180(180)n BO C O BC O CB A A n n n ︒−∠=︒−∠+∠=︒−︒−∠=+∠，()11111801180180(180)n n n n n BO C O BC O CB A A n n n −−−−︒−∠=︒−∠+∠=︒−︒−∠=+∠．【点睛】本题主要考查了有关角平分线三角形的内角和问题，熟练掌握三角形的内角和定理，并利用类比思想解答是解题的关键．）如图所示，在ABC 中，）如图所示，ABC 的外角平分线）如图所示，ABC 的内角平分线【答案】（1）见解析；（2）见解析；（3）见解析【详解】（1）设,ABO OBC x ACO BCO y ∠=∠=∠=∠=．由ABC 的内角和为180︒，得22180A x y ︒∠++=．①由BOC 的内角和为180︒，得180BOC x y ∠++=︒．②由②得180x y BOC +=−∠︒．③把③代入①，得()2180180A BOC ∠+−∠=︒︒，即2180BOC A ∠=︒+∠，即1902BOC A ∠=+∠︒（2）∵BD 、CD 为△ABC 两外角∠ABC 、∠ACB 的平分线，∴()()1122BCD A ABC DBC A ACB ∠=∠+∠∠=∠+∠、，由三角形内角和定理得，180BDC BCD DBC ∠=︒−∠−∠，=180°-12[∠A+（∠A+∠ABC+∠ACB ）]， =180°-12（∠A+180°）， =90°-12∠A ；（3）如图：∵BD 为△ABC 的角平分线，交AC 与点E ，CD 为△ABC 外角∠ACE 的平分线，两角平分线交于点D∴∠1=∠2，∠5=12（∠A+2∠1），∠3=∠4，在△ABE 中，∠A=180°-∠1-∠3∴∠1+∠3=180°-∠A①在△CDE 中，∠D=180°-∠4-∠5=180°-∠3-12（∠A+2∠1），即2∠D=360°-2∠3-∠A-2∠1=360°-2（∠1+∠3）-∠A②，把①代入②得∠D=12∠A ．【点睛】此题考查的是三角形内角与外角的关系，角平分线的性质，三角形内角和定理，属中学常规题． 12．（2023春·全国·七年级专题练习）如图，在△ABC 中，∠ABC 和∠ACB 的平分线相交于点P ．（1）若∠ABC +∠ACB ＝130°，求∠BPC 的度数．（2）当∠A 为多少度时，∠BPC ＝3∠A ？【答案】（1）115︒；（2）36A ∠=︒【分析】（1）根据角平分线的定义，求得PBC ∠，PCB ∠，再根据三角形内角和定理即可求得BPC ∠；（2）根据（1）的方法求得BPC ∠，再结合条件∠BPC ＝3∠A ，解方程即可求得∠A ．【详解】（1）PB 平分ABC ∠，PC 平分ACB ∠，11,22PBC ABC PCB ACB ∴∠=∠∠=∠，∠ABC+∠ACB ＝130°，1()652PBC PCB ABC ACB ∴∠+∠=∠+∠=︒，180()18065115BPC PBC PCB ∴∠=︒−∠+∠=︒−︒=︒，（2）PB 平分ABC ∠，PC 平分ACB ∠，11,22PBC ABC PCB ACB ∴∠=∠∠=∠，1()2PBC PCB ABC ACB ∴∠+∠=∠+∠，180ABC ACB A ∠+∠=︒−∠，1902PBC PCB A ∴∠+∠=︒−∠，180()BPC PBC PCB Ð=°-Ð+Ð1180(90)2A =︒−︒−∠1902A =+∠︒∠BPC ＝3∠A13902A A ∴∠=︒+∠，36A ∴∠=︒．【点睛】本题考查了与角平分线有关的角度计算，三角形内角和定理，掌握三角形内角和定理是解题的关键． 13．（2023·全国·八年级假期作业）如图所示，已知四边形ABDC ，求证BDC A B C ∠=∠+∠+∠．【答案】见解析【分析】方法1连接BC ，根据三角形内角和定理可得结果；方法2 作射线AD ，根据三角形的外角性质得到31B ∠=∠+∠，42C ∠=∠+∠，两式相加即可得到结论；方法3延长BD ，交AC 于点E ，两次运用三角形外角的性质即可得出结论．【详解】方法1如图所示，连接BC.在ABC 中，180A ABC ACB ∠+∠+∠=，即12180A ABD ACD ∠+∠+∠+∠+∠=.在BCD △中，12180BDC ∠+∠+∠=，++∴∠=∠∠∠；BDC A ABD ACD方法2如图所示，连接AD并延长.∠是ABD△的外角，3∴∠=∠∠.31+ABD∠=∠+∠.同理，42ACD∴∠+∠=∠+∠+∠+∠.3412ABD ACD∠=∠+∠+∠.即BDC A ABD ACD方法3如图所示，延长BD，交AC于点E.∠是ABE的外角，DEC∴∠=∠+∠.DEC A ABDBDC∠是DEC的外角，∴∠=∠+∠.BDC DEC ACDBDC A ABD ACD∴∠=∠+∠+∠.【点睛】本题考查了三角形的外角性质：解题的关键是知道三角形的任一外角等于与之不相邻的两内角的和．也考查了三角形内角和定理．14．（2023春·江苏·七年级专题练习）探究与发现：如图1所示的图形，像我们常见的学习用品——圆规．我们不妨把这样图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？下面就请你发挥你的聪明才智，解决以下问题：(1)观察“规形图”，试探究BDC ∠与A ∠、B ∠、C ∠之间的关系，并说明理由；(2)请你直接利用以上结论，解决以下三个问题：①如图2，把一块三角尺XYZ 放置在ABC 上，使三角尺的两条直角边XY 、XZ 恰好经过点B 、C ，若50A ∠=︒，则ABX ACX ∠+∠=_____°；②如图3，DC 平分ADB ∠，EC 平分AEB ∠，若50DAE ∠=︒，130DBE ∠=︒，则DCE ∠=______°； ③如图4，ABD ∠，ACD ∠的10等分线相交于点1G ，2G ，…，9G ，若140BDC ∠=︒，177BG C ∠=︒，求A ∠的度数．【答案】(1)=++BDC BAC B C ∠∠∠∠(2)①40，②90，③70°【分析】（1）根据题意观察图形连接AD 并延长至点F ，根据一个三角形的外角等于与它不相邻的两个内角的和即可证明；（2）①由（1）的结论可得ABX ACX A BXC ∠+∠+∠=∠，然后把50A ∠=︒，90BXC ∠=︒代入上式即可得到ABX ACX ∠+∠的值；②结合图形可得DBE DAE ADB AEB ∠=∠+∠+∠，代入50DAE ∠=︒，130DBE ∠=︒即可得到ADB AEB ∠+∠的值，再利用上面得出的结论可知()12DCE ADB AEB A ∠=∠+∠+∠，易得答案．③由②方法，进而可得答案．【详解】（1）=++BDC BAC B C ∠∠∠∠，理由如下：连接AD 并延长至点F ，由外角定理可得BDF BAD B ∠=∠+∠，CDF C CAD ∠=∠+∠，∵BDC BDF CDF ∠=∠+∠，∴BDC BAD B C CAD ∠=∠+∠+∠+∠，∵BAC BAD CAD ∠=∠+∠，∴=++BDC BAC B C ∠∠∠∠；（2）①由（1）的结论易得：ABX ACX A BXC ∠+∠+∠=∠，∵50A ∠=︒，90BXC ∠=︒，∴905040ABX ACX ∠+∠=︒−︒=︒，故答案是：40；②由（1）的结论易得=++DBE DAE ADB AEB ∠∠∠∠，DCE ADC AEC A ∠=∠∠∠＋＋，∵50DAE ∠=︒，130DBE ∠=︒，∴80ADB AEB ∠+∠=︒；∵DC 平分ADB ∠，EC 平分AEB ∠， ∴12ADC ADB ∠=∠，12AEC AEB ∠=∠， ∴()14050902DCE ADB AEB A ∠=∠+∠+∠=︒+︒=︒；③由②知，()1110BG C ABD ACD A ∠=∠+∠+∠， ∵177BG C ∠=︒，∴设A ∠为x ︒，∵140ABD ACD x ∠+∠=︒−︒， ∴()11407710x x −=+，∴70x =，∴A ∠为70°．故答案是：70°．【点睛】本题考查三角形外角的性质，三角形的内角和定理的应用，能求出BDC A B C ∠=∠+∠+∠是解答的关键，注意：三角形的内角和等于180°，三角形的一个外角等于和它不相邻的两个内角的和． 15．（2023·全国·八年级假期作业）如图，BP 平分ABC ∠，交CD 于点F ，DP 平分ADC ∠交AB 于点E ，AB 与CD 相交于点G ，42A ∠=︒．（1）若60ADC ∠=︒，求AEP ∠的度数；（2）若38C ∠=︒，求P ∠的度数．【答案】（1）72︒；（2）40︒．【分析】（1）根据角平分线的定义可得∠ADP=12ADC ∠ ，然后利用三角形外角的性质即可得解；（2）根据角平分线的定义可得∠ADP=∠PDF ，∠CBP=∠PBA ，再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP ，∠C+∠CBP=∠P+∠PDF ，所以∠A+∠C=2∠P ，即可得解．【详解】解：（1）∵DP 平分∠ADC ∴∠ADP=∠PDF=12ADC ∠，∵60ADC ∠=︒，∴30ADP ∠=︒，∴304272AEP ADP A ∠=∠+∠=︒+︒=︒；（2）∵BP 平分∠ABC ，DP 平分∠ADC ，∴∠ADP=∠PDF ，∠CBP=∠PBA ，∵∠A+∠ADP=∠P+∠ABP ，∠C+∠CBP=∠P+∠PDF ，∴∠A+∠C=2∠P ，∵∠A=42°，∠C=38°，∴∠P=12（38°+42°）=40°．【点睛】本题考查了三角形的内角和定理及三角形外角的性质，角平分线的定义，熟记定理并理解“8字形”的等式是解题的关键．16．（2023春·河北石家庄·七年级统考期末）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．(1)如果∠A＝70°，求∠BPC的度数；(2)如图②，作△ABC外角∠MBC，∠NCB的角平分线交于点Q，试探索∠Q，∠A之间的数量关系．(3)如图③，延长线段BP，QC交于点E，在△BQE中，存在一个内角等于另一个内角的3倍，求∠A的度数．【答案】(1)125︒(2)1902Q A ∠=︒−∠(3)∠A的度数是45︒或60︒或120︒或135︒【分析】（1）在△ABC中，根据三角形内角和定理求出∠ABC+∠ACB=110°，根据角平分线的定义得出∠PBC＝1 2∠ABC，∠PCB＝12∠ACB，求出∠PBC+∠PCB=55°，再在△BPC中，根据三角形内角和定理求出即可；（2）根据三角形外角性质得出∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，求出∠MBC+∠NCB＝∠ACB+∠A+∠ABC+∠A＝180°+∠A，根据角平分线的定义得出QBC＝12∠MBC，∠QCB＝12∠NCB，求出∠QBC+∠QCB＝90°+12∠A，根据三角形内角和定理求出即可；（3）根据角平分线的定义得出∠ACF＝2∠BCF，∠ABC＝2∠EBC，根据三角形外角性质得出∠ECF＝∠EBC+∠E，求出∠A＝2∠E，求出∠EBQ=90°，分为四种情况：①∠EBQ＝3∠E＝90°，②∠EBQ＝3∠Q，③∠Q＝3∠E，④∠E ＝3∠Q，再求出答案即可【详解】（1）∵∠A＝70°，∴∠ABC+∠ACB＝180°﹣∠A＝110°，∵点P是∠ABC和∠ACB的角平分线的交点，∴∠PBC＝12∠ABC，∠PCB＝12∠ACB，∴∠PBC+∠PCB＝55°，∴∠BPC＝180°﹣（∠PBC+∠PCB）＝125°；（2）∵∠MBC＝∠ACB+∠A，∠NCB＝∠ABC+∠A，∴∠MBC+∠NCB＝∠ACB+∠A+∠ABC+∠A＝180°+∠A，∵点Q是∠MBC和∠NCB的角平分线的交点，∴∠QBC＝12∠MBC，∠QCB＝12∠NCB，∴∠QBC+∠QCB＝12（∠MBC+∠NCB）＝12（180°+∠A）＝90°+12∠A，∴∠Q＝180°﹣（∠QBC+∠QCB）＝180°﹣（90°+12∠A）＝90°﹣12∠A；（3）∵CQ为△ABC的外角∠NCB的角平分线，∴CE是△ABC的外角∠ACF的平分线，∴∠ACF＝2∠BCF，∵BE平分∠ABC，∴∠ABC＝2∠EBC，∵∠ECF＝∠EBC+∠E，∴2∠ECF＝2∠EBC+2∠E，即∠ACF＝∠BC+2∠E，∵∠ACF＝∠ABC+∠A，∴∠A＝2∠E，即∠E＝12∠A，∵∠EBQ＝∠EBC+∠CBQ＝12∠ABC+12∠MBC＝12（∠ABC+∠A+∠ACB）＝90°，如果△BQE中，存在一个内角等于另一个内角的3倍，那么分为四种情况：①∠EBQ＝3∠E＝90°，则∠E＝30°，∠A＝2∠E＝60°；②∠EBQ＝3∠Q，则∠Q＝30°，∠E＝60°，∠A＝2∠E＝120°；③∠Q＝3∠E，则∠E＝22.5°，∠A＝2∠E＝45°；④∠E＝3∠Q，则∠E＝67.5°，∠A＝2∠E＝135°，综合上述，∠A的度数是45°或60°或120°或135°．【点睛】本题考查了三角形的外角性质，三角形内角和定理，角平分线的定义等知识点，熟练掌握知识点及运用分类讨论思想是解题的关键．17．（2022秋·江西赣州·八年级校联考期中）如图，在△ABC中，(1)如果AB=4cm，AC=3cm，BC是能被3整除的的偶数，求这个三角形的周长．(2)如果BP、CP分别是∠ABC和∠ACB的角平分线．a、当∠A=45°时，求∠BPC的度数．b、当∠A=x°时，求∠BPC的度数．【答案】(1)13cm(2)a、112.5°；b、90°＋12x°【分析】（1）利用三角形的三边关系：两边之和大于第三边，两之差小于第三边，得出BC的取值范围为1＜BC＜7，再根据BC是能被3整除的偶数，得到BC=6 cm，再求出周长为13 cm．（2）利用三角形的内角和等于180°，先求出∠ABC+∠ACB，再利用角平分线平分角的知识，求出∠PBC+∠PCB，然后再一次用三角形内角和等于180°，求出∠BPC．【详解】（1）∵AB=4 cm，AC=3 cm∴1＜BC＜7∴BC=6 cm∴三角形的周长为：C△ABC=AB+AC+BC=4+3+6=13cm（2）a、当∠A=45°时，由三角形的内角和可知：∠ABC+∠ACB=180°−∠A=180°−45°=135°∵BP、CP分别是∠ABC和∠ACB的角平分线∴∠PBC=12∠ABC，∠PCB=12∠ACB∴∠PBC+∠PCB=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12×135°=67.5°∴∠BPC=180°− (∠PBC+∠PCB)=180°−67.5°=112.5°b、当∠A=x°时，由三角形的内角和可知：∠ABC+∠ACB=180°−∠A=180°− x°∵BP、CP分别是∠ABC和∠ACB的角平分线∴∠PBC=12∠ABC，∠PCB=12∠ACB∴∠PBC+∠PCB=12∠ABC+12∠ACB=12(∠ABC+∠ACB)=12×(180°− x°)=90°−12x°∴∠BPC=180°− (∠PBC+∠PCB)=180°−(90°−12x°)=90°＋12x°【点睛】本题考查有关三角形的知识．第一小问的解题关键是运用三角形的三边关系：两边之和大于第三边，两之差小于第三边进行解答；第二小问的解题关键是运用三角形的内角和等于180°，以及角平分线平分角的知识结合一起解答，在求角度时，有时不一定需要每个角都求出来，可以利用整体思想．【答案】（1）见解析；（2）26°；（3）()1902P B D ∠=︒+∠+∠；（4）()11802P B D ∠=︒−∠+∠【分析】（1）根据三角形的内角和等于180°和对顶角的性质即可得证；（2）设BAP PAD x ∠=∠=，BCP PCD y ∠=∠=，x ABC y P x P y ADC +∠=+∠⎧⎨+∠=+∠⎩解方程即可得到答案；（3）根据直线AP 平分BAD ∠，CP 平分BCD ∠的外角BCE ∠，得到1=2PAB PAD BAD ∠=∠∠，1=2PCB PCE PCD ∠=∠∠从而可以得到180°()2PAB PCB D B −∠+∠+∠=∠，再根据∠P+∠PAD=∠PCD+∠D ，∠BAD+∠B=∠BCD+∠D 得到=P B PAD PCB PAB PCB ∠−+=∠+∠∠∠∠即可求解；（4）连接PB ，PD 根据APB PBA PAB +∠+∠=∠ 180°，PCB PBC BPC +∠+∠=∠ 180°得到APC ABC PCB PAB ∠+∠+∠+=∠ 360°，同理得到：APC ADC PCD PAD ∠+∠+∠+=∠ 360°，再根据=PCE PCD ∠+∠180°，=PAB PAF +∠∠180°，FAP PAO ∠=∠，PCE PCB ∠=∠，即可求解.【详解】解：（1）A B AOB ∠+∠+∠=180°，C D COD ∠+∠+∠=180°，A B AOB C D COD ∴∠+∠+∠=∠+∠+∠．AOB COD ∠=∠，A B C D ∴∠+∠=∠+∠；（2）AP ，CP 分别平分BAD ∠，BCD ∠，设BAP PAD x ∠=∠=，BCP PCD y ∠=∠=，则有x ABC y P x P y ADC +∠=+∠⎧⎨+∠=+∠⎩，ABC P P ADC ∴∠−∠=∠−∠，()1122P ABC ADC ∴∠=∠+∠=（36°+16°）=26°（3）直线AP 平分BAD ∠，CP 平分BCD ∠的外角BCE ∠，1=2PAB PAD BAD ∴∠=∠∠，1=2PCB PCE BCE ∠=∠∠，∴2PAB B ∠+∠=180°-2PCB D ∠+∠，∴180°()2PAB PCB D B −∠+∠+∠=∠∵∠P+∠PAD=∠PCD+∠D ，∠BAD+∠B=∠BCD+∠D∴=P PAD BAD B PCD BCD ∠+−−−∠∠∠∠∠,P PAB B PCB ∴∠−∠−∠=∠∴P B PAB PCB ∠−=∠+∠∠∴180°()2P B D B−∠−∠+∠=∠，即P ∠=90°()12B D +∠+∠．（4）连接PB ，PD直线AP 平分BAD ∠的外角FAD ∠，CP 平分BCD ∠的外角BCE ∠， FAP PAO ∴∠=∠，PCE PCB ∠=∠，∵APB PBA PAB +∠+∠=∠180°，PCB PBC BPC +∠+∠=∠180° ∴APC ABC PCB PAB ∠+∠+∠+=∠360°同理得到：APC ADC PCD PAD ∠+∠+∠+=∠360°∴2APC ABC ADC PCB PAB PCD PAD ∠+∠+∠+∠++∠+=∠∠720°∴2APC ABC ADC PCE PAB PCD PAF ∠+∠+∠+∠++∠+=∠∠720°∵=PCE PCD ∠+∠180°，=PAB PAF +∠∠180°∴2APC ABC ADC ∠+∠+∠=360°，APC ∴∠=180°-()12ABC ADC ∠+∠【点睛】本题主要考查了角平分线的定义，三角形内角和定理，解题的关键在于能够熟练掌握相关知识进行求解.。

浙教版八年级数学上册全等三角形之手拉手模型、倍长中线-截长补短法

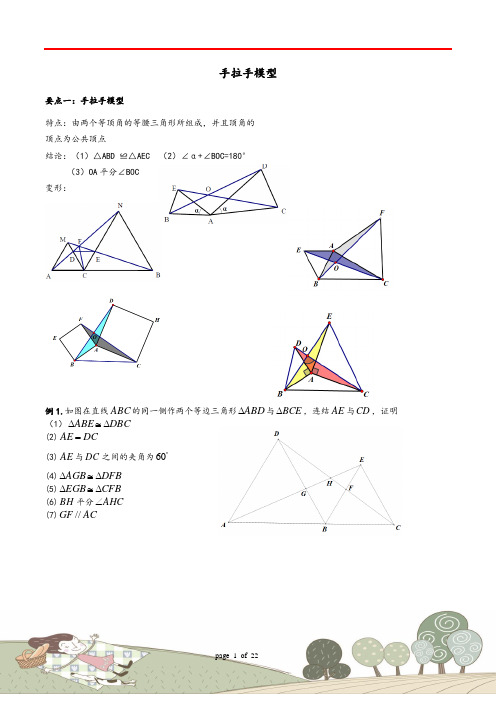
手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形：例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？（2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？（4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？（2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？（4）HB 是否平分AHC ∠？例5：如图，点A. B. C 在同一条直线上，分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ，AE 与DC 所在直线相交于F ，连接FB.判断线段FB 、FE 与FC 之间的数量关系，并证明你的结论。

浙教八年级上册数学特殊三角形经典习题(含答案)

浙教数学八年级上册特殊三角形历年中考典型习题一、等腰三角形1．如图，△ABC中，AB=AC，AM是BC边上的中线，点N在AM上，求证：NB=NC．2．如图，∠AOB的内部有一点P，在射线OA，OB边上各取一点P1，P2 ，使得△PP1P2的周长最小，作出点P1，P2 ，叙述作图过程（作法），保留作图痕迹．3．已知：如图，在△ABC中，∠1＝∠2，DE∥AC，求证：△ADE是等腰三角形．4．如图，△ABC中，AD⊥BC，点E在AC的垂直平分线上，且BD＝DE．(1)如果∠BAE＝40°，那么∠B＝，∠C＝°；(2)如果△ABC的周长为13 cm，AC＝6 cm，那么△ABE的周长＝cm；(3)你发现线段AB与BD的和等于图中哪条线段的长？并证明你的结论．5．如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB．（1）若∠ABC=70°，则∠NMA的度数是度．（2）若AB=8cm，△MBC的周长是14cm．①求BC的长度；②若点P为直线MN上一点，请你直接写出△PBC周长的最小值．6．如图，∠AOB=30̊，OC平分∠AOB，P为OC上一点，PD∥OA交OB于D，PE垂直OA于E，若OD=4cm，求PE的长．7.如图1，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．（1）求证：BE=CE；（2）如图2，若BE的延长线交AC于点F，且BF⊥AC，垂足为F，∠BAC=45°，原题设其它条件不变．求证：EF=CF．8．如图，在四边形ABCD中，AD=4，BC=1，∠A=30°，∠B=90°，∠ADC=120°，求CD的长．9．如图，△ABC 为等边三角形，BD 平分∠ABC 交AC 于点D ，DE ∥BC 交AB 于点E ．（1）求证：△ADE 是等边三角形．（2）求证：AE =21AB ．10．如图所示，D 、E 分别是 △ABC 的边 BC 、AC 上的点，且 AB =AC ，AD =AE ．（1）若 ∠BAD =20̊，则∠EDC = ；（2）若 ∠EDC =20̊，则∠BAD = ；（3）设∠BAD =ɑ ，∠EDC =β，你能由（1）（2）中的结果找到 ɑ、β 所满足的关系吗?请说明理由．11．如图，CN是等边△ABC的外角∠ACM内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．（1）依题意补全图形；（2）若∠ACN=α，求∠BDC的大小（用含的式子表示）；（3）用等式表示线段PB，PC与PE之间的数量关系，并证明．12．如图，点A、B、C在同一直线上，△ABD，△BCE都是等边三角形。

全等三角形的重难点模型(八大题型)(解析版)—八年级数学上册(浙教版)

全等三角形的重难点模型（八大题型）【题型01：平移型】【题型02：翻折型】【题型03：旋转型】【题型04：一线三等角型（三类型）】【题型05：手拉手模型（四大类型）】【题型06：半角模型】【题型07：对角互补模型】【题型08：平行+线段中点构造全等模型】【题型1 平移型】【方法技巧】【典例1】如图，点E，C在线段BF上，AB=DE，BE=CF，AC=DF．(1)求证：△ABC≌△DEF；(2)若∠B=45°，∠F=85°，求∠A的度数．【答案】(1)见解析(2)50°【分析】本题考查全等三角形的判定与性质，三角形内角和定理,解题的关键是熟练运用全等三角形的判定．（1）首先根据BE=CF可得BC=EF，即可判定△ABC≌△DEF；（2）首先根据（1）中两三角形全等，可得∠ACB=∠F=85°，在△ABC中根据三角形内角和定理即可求出∠A．【详解】（1）证明：∵BE=CF，∴BE+EC=CF+EC，即BC=EF，∴在△ABC和△DEF中，AB=DE AC=DF BC=EF，∴△ABC≌△DEF(SSS)．（2）解：∵△ABC≌△DEF，∠B=45°，∠F=85°，∴∠ACB=∠F=85°，∴∠A=180°―∠ACB―∠B=50°．【变式1-1】如图、点B、E、C、F在一条直线上AB=DE，AC=DF，BE=CF．(1)求证：∠A=∠D；(2)求证：AC∥DF．【答案】(1)证明见解析(2)证明见解析【分析】本题考查三角形综合，涉及三角形全等的判定与性质、平行线的判定等知识，熟记相关几何判定与性质是解决问题的关键．（1）由题中条件，利用两个三角形全等的判定定理SSS得到△ABC≌△DEF，再由三角形全等的性质即可得证；（2）由（1）中△ABC≌△DEF得到∠ACB=∠F，再由同位角相等两直线平行即可得证．【详解】（1）证明：∵BE=CF，∴BC=FE，在△ABC 和△DEF 中，AB =DE AC =DF BE =CF∴△ABC≌△DEF (SSS)，∴∠A =∠D ；（2）证明：由（1）知△ABC≌△DEF ，∴ ∠ACB =∠F ，∴ AC∥DF ．【变式1-2】如图，在△ABC 和 △DEF 中，边AC ，DE 交于点H ，AB∥DE ，AB =DE ，BC =EF ．(1)若∠B =55°，∠ACB =100°，求∠CHE 的度数；(2)求证：△ABC≌△DEF ．【答案】(1)∠CHE =25°；(2)证明见解析．【分析】本题考查了三角形的内角和定理，平行线的性质，全等三角形的判定，熟练掌握知识点的应用是解题的关键．（1）根据三角形内角和定理求出∠A ，再根据平行线的性质得出∠CHE =∠A 即可；（2）根据平行线的性质得出∠B =∠DEF ，求出BC =EF ，再根据全等三角形的判定定理推出即可；【详解】（1）解：∵∠B =55°，∠ACB =100°，∴∠A =180°―∠B ―∠ACB =25°，∵AB∥DE ，∴∠CHE =∠A =25°；（2）证明：∵AB∥DE ，∴∠B =∠DEF ，在△ABC 和△DEF 中，AB =DE ∠B =∠DEF BC =EF∴△ABC≌△DEF (SAS)．【变式1-3】如图，点B 、E 、C 、F 在同一直线上，∠A =∠D =90°，BE =CF ，AC =DF ．求证：∠B =∠DEF ．【答案】答案见解析【分析】本题考查了三角形全等的判定与性质，掌握三角形全等的判定定理是解题的关键即可得到答案．根据BE =CF 得到BE +EC =EC +CF 即BC =FE ，之后利用HL 证明Rt △ABC≌Rt △DFE 即可得到答案．【详解】证明：∵BE =CF ，∴BE +EC =EC +CF ，即BC =FE ．∵∠A =∠D =90°，则在Rt △ABC 和Rt △DFE 中，BC =FE AC =DE ，∴Rt △ABC≌Rt △DFE(HL)．∴∠B =∠DEF ．【题型2 翻折型】【方法技巧】【典例2】如图，AB=AD，CB⊥AB，CD⊥AD，垂足分别为B，D．(1)求证：△ABC≌△ADC；(2)若AB=4，CD=3，求四边形ABCD的面积．【变式2-1】如图，已知∠1=∠2，∠C=∠D，求证：AC=BD【答案】证明见解析【分析】本题考查全等三角形的判定与性质，由两个三角形全等的判定定理AAS 得到△ABC≌△BAD (AAS)，再由三角形全等性质即可得证，熟练掌握两个三角形全等判的定定理AAS 及性质是解决问题的关键．【详解】证明：在△ABC 与△BAD 中，∠1=∠2∠C =∠D AB =AB，∴△ABC≌△BAD (AAS)，∴AC =BD ．【变式2-2】如图，已知AD 平分∠BAC ，AB =AC ．求证：△ABD≌△ACD ．【答案】见解析【分析】本题主要考查了全等三角形的判定．根据AD 平分∠BAC ，可得∠BAD =∠CAD ，再根据边角边可证明△ABD≌△ACD ．【详解】证明：∵AD 平分∠BAC，∴∠BAD =∠CAD ，在△ABD 和△ACD 中，∵AB =AC ，∠BAD =∠CAD ，AD =AD ，∴△ABD≌△ACD (SAS)．【变式2-3】如图，AB =AC ，BO =CO ，求证：∠ADC =∠AEB ．【答案】见解析【分析】本题考查了全等三角形的判定与性质、三角形外角的定义及性质，连接OA ，证明△AOB≌△AOC (SSS)得出∠B =∠C ，再由三角形外角的定义及性质即可得出答案，熟练掌握以上知识点并灵活运用是解此题的关键．【详解】证明：如图，连接OA ，在△AOB 和△AOC 中，AB =AC OB =OC OA =OA，∴△AOB≌△AOC (SSS)，∴∠B =∠C ，∵∠DOB =∠EOC ，∴∠B +∠DOB =∠C +∠EOC ，∴∠ADC =∠AEB ．【题型3旋转型】【方法技巧】【典例3】如图，在△ABC 和△AEF 中，点E 在BC 边上，∠C ＝∠F ，AC ＝AF ，∠CAF ＝∠BAE ，EF 与AC 交于点G ．（1）试说明：△ABC ≌△AEF ；（2）若∠B ＝55°，∠C ＝20°，求∠EAC 的度数．【答案】（1）见解答；（2）35°．【解答】（1）证明：∵∠CAF＝∠BAE，∴∠CAF+∠EAC＝∠BAE+∠EAC，即∠BAC＝∠EAF，在△ABC和△AEF中，，∴△ABC≌△AEF（ASA）；（2）解：∵∠B＝55°，∠C＝20°，∴∠BAC＝180°﹣55°﹣20°＝105°，∵△ABC≌△AEF，∴AB＝AE，∴∠B＝∠AEB＝55°，∴∠BAE＝180°﹣∠B﹣∠AEB＝70°，∴∠EAC＝∠BAC﹣∠BAE＝105°﹣70°＝35°．【变式3-1】如图，点E在△ABC外部，点D在BC边上，若∠1＝∠2，∠E＝∠C，AE＝AC，求证：AB＝AD．【答案】证明见解答．【解答】证明：∵∠1＝∠2，∴∠1+∠CAD＝∠2+∠CAD，∴∠BAC＝∠DAE，在△ABC和△ADE中，，∴△ABC≌△ADE（ASA），∴AB＝AD．【变式3-2】如图，点E在△ABC边AC上，AE＝BC，BC∥AD，∠BAC＝∠ADE．（1）求证：△ABC≌△DEA；（2）若∠CAD＝30°，求∠BCD的度数．【答案】（1）见解析；（2）∠BCD＝105°．【解答】（1）证明：∵BC∥AD，∴∠ACB＝∠DAE．在△ABC和△DEA中，∵，∴△ABC≌△DEA（AAS）．（2）解：由（1）知△ABC≌△DEA（AAS），∴AC＝AD，∠ACB＝∠CAD＝30°，∴，∴∠BCD＝∠ACD+∠ACB＝30°+75°＝105°．∴∠BCD＝105°．【变式3-3】如图，在△ABC中，点D是BC的中点，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．求证：△BDE≌△CDF．【答案】证明见解答过程．【解答】证明：∵CF∥AB，∴∠B＝∠FCD，∠BED＝∠F，∵点D是BC的中点，∴BD＝CD，在△BDE与△CDF中，，∴△BDE≌△CDF（AAS）．【变式3-4】如图，∠ABC＝∠ADE，∠BAD＝∠CAE，AC＝AE，求证：△ABC≌△ADE．【答案】见解答．【解答】证明：∵∠BAD＝∠CAE，∴∠BAD+∠CAD＝∠CAE+∠CAD，即∠BAC＝∠DAE．在△ABC和△ADE中，，∴△ABC≌△ADE（AAS）．【题型4 一线三等角型】【方法技巧】模型一一线三垂直如图一，∠D=∠BCA=∠E=90°，BC=AC。

全等三角形中“一线三等角”模型-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)

重难点：全等三角形中“一线三等角”模型【知识梳理】图一如图一，∠D=∠BCA=∠E=90°，BC=AC 。

结论：Rt △BDC ≌Rt △CEA图二如图二，∠D=∠BCA=∠E ，BC=AC 。

结论：△BEC ≌△CDA【考点剖析】例题1．如图，∠A ＝∠B ＝90°，E 是线段AB 上一点，且AE ＝BC ，∠1＝∠2 ．（1）求证：ADE ≌BEC △；（2）若CD ＝10，求DEC 的面积．【详解】（1）∵12∠=∠，C D E BA∴DE CE =，∵∠A ＝∠B ＝90°，在Rt ADE △和Rt BEC △中，DE EC AE BC =⎧⎨=⎩，∴Rt ADE △≌Rt BEC △；（2）∵Rt ADE △≌Rt BEC △，∴ADE BEC ∠=∠，∵90ADE AED ∠+∠=︒，∴90AED BEC ∠+∠=︒，∴90DEC ∠=︒，∵12∠=∠，∴DE CE =，∴DEC 为等腰直角三角形，∴其斜边CD 上的高为5， ∴1105252DEC S =⨯⨯=△．【变式1】．已知，如图，AB ⊥BD 于点B ，CD ⊥BD 于点D ，P 是BD 上一点，且AP=PC ，AP ⊥PC ．（1）求证:△ABP ≌△PDC（2）若AB=3，CD=4，连接AC ，求AC 的长．【详解】（1）证明：,AB BD CD BD ⊥⊥90B D∴∠=∠=︒90BAP APB∴∠+∠=︒AP PC⊥90APB CPD∴∠+∠=︒BAP CPD∴∠=∠AP PC=()ABP PDC AAS∴≅；（2）连接AC，()ABP PDC AAS≅3,4AB BP CD===5 AP∴===在,5 Rt APC AP PC==AC∴==【变式2】如图1，∠ACB＝90°，AC＝BC，AD⊥MN，BE⊥MN，垂足分别为D、E．（1）求证：△ADC≌△CEB；（2）猜想线段AD、BE、DE之间具有怎样的数量关系，并说明理由；（3）题设条件不变，根据图2可得线段AD、BE、DE之间的数量关系是．（1）证明：∵AD⊥MN，BE⊥MN，∴∠CDA ＝∠BEC ＝90°．∴∠ACD ＋∠DAC ＝90°．∵∠ACB ＝90°，∴∠ACD ＋∠BCE ＝90°．∴∠DAC ＝∠ECB ．在△ADC 和△CEB 中，CDA BEC DAC ECBAC CB ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ADC ≌△CEB ．（2）AD ＝BE ＋DE ．理由如下：由（1）知△ADC ≌△CEB ．∴AD ＝CE ，CD ＝BE ．∴AD ＝CE ＝CD ＋DE ＝BE ＋DE ．（3）DE ＝AD ＋BE ．理由：∵AD ⊥MN ，BE ⊥MN ，∴∠ADC=90°，∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACD=90°，∴∠ACD=∠CBE ，又∵∠ADC=∠CEB ，AC=CB ，∴△ADC ≌△CEB ，∴AD=CE ，CD=BE ，∵CD+CE=DE ，∴DE=AD+BE ．【变式3】已知：D ，A ，E 三点都在直线m 上，在直线m 的同一侧作ABC ，使AB AC =，连接BD ，CE ．（1）如图①，若90BAC ∠=︒，BD m ⊥，CE m ⊥，求证ABD ACE ≅；（2）如图②，若BDA AEC BAC ∠=∠=∠，请判断BD ，CE ，DE 三条线段之间的数量关系，并说明理由．【详解】（1）证明：如图①，∵D ，A ，E 三点都在直线m 上，∠BAC ＝90°，∴∠BAD ＋∠CAE ＝90°，∵BD ⊥m ，CE ⊥m ，∴∠ADB ＝∠CEA ＝90°，∴∠BAD ＋∠ABD ＝90°，∴∠ABD ＝∠CAE ，在△ABD 和△CAE 中，ADB AEC ABD CAEAB AC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△CAE （AAS ）；（2）DE ＝BD ＋CE ．理由如下：如图②，∵∠BDA ＝∠AEC ＝∠BAC ，∴由三角形内角和及平角性质，得：∠BAD ＋∠ABD ＝∠BAD ＋∠CAE ＝∠CAE ＋∠ACE ，∴∠ABD ＝∠CAE ，∠BAD ＝∠ACE ，在△ABD 和△CAE 中，＝＝＝⎩∠∠⎪⎨⎪⎧∠∠BAD ACE AB ACABD CAE ，∴△ABD ≌△CAE （ASA ），∴BD ＝AE ，AD ＝CE ，∴DE ＝AD ＋AE ＝BD ＋CE ．【变式4】已知：在△ABC 中，∠BAC=90°，AB=AC ，AE 是多点A 的一条直线，且BD ⊥AE 于D ，CE ⊥AE 于点E.当直线AE 处于如图1的位置时，有BD=DE+CE,请说明理由.当直线AE 处于如图2的位置时，则BD 、DE 、CE 的关系如何？请说明理由.解析：（1）∵BD ⊥AE,CE ⊥AE∴∠BDA=∠AEC=90°∴∠A BD+∠BAD=90°∵∠BAC=90°（2）在△ABD 和△CAE ∴∠BAD+∠EAC=90°∴∠ABD=∠EAC 在△ABD 和△CAE 中∠ADB=∠CEA=90°∠ABD=∠EAC AB=CA ∴△ABD ≌△CAE(AAS)AD=CE,BD=AE ∵AE=AD+DE ∴BD=DE+CE 中解析：∵∠B=40°[来源:学,科,网Z,X,X,K]∴∠BAD+∠BDA=140°∵∠ADE=40°∴∠CDE+∠BDA=140°∴∠BAD=∠CDE在△ABD 和△DCE 中∠B=∠C∠BAD=∠CDEAB=DC∴△ABD ≌△∠ADB=∠CEA=90°AB=CA ∴△ABD ≌△CAE （AAS ）∴AD=CE,BD=AE∵AE=DE-AD ∴BD=DE-CE.例2、如图，在△ABC 中，AB=AC=2，∠B=∠C=40°，点D 在线段BC 上运动（D 不与B,C 重合），连接AD ，作∠ADE=40°，DE 交线段AC 于点E.当DC 等于多少是，△ABD ≌△DCE?请证明你的结论.DCE 【变式1】（2022秋·八年级课时练习）如图，在△ABC 中，AB ＝AC ＝9，点E 在边AC 上，AE的中垂线交BC 于点D ，若∠ADE ＝∠B ，CD ＝3BD ，则CE 等于（）A．3B ．2 【答案】A 【详解】解：∵AB ＝AC ＝9，∴∠B ＝∠C ，∵∠ADE ＝∠B ，∠BAD ＝180°﹣∠B ﹣∠ADB ，∠CDE ＝180°﹣∠ADE ﹣∠ADB ，∴∠BAD ＝∠CDE ，∵AE 的中垂线交BC 于点D ，∴AD ＝ED ，在△ABD 与△DCE 中，BAD CDE B CAD ED ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△DCE （AAS ），∴CD ＝AB ＝9，BD ＝CE ，∵CD ＝3BD ，∴CE ＝BD ＝3故选：A ．【变式2】（2022秋·八年级课时练习）如图，∠B =∠C =∠FDE =80°，DF =DE ，BF =1.5cm ，CE =2cm ，求BC 的长．【答案】3.5【详解】解：∠B=∠C=∠FDE=80°，100,100BDF EDC BDF BFD ∴∠+∠=︒∠+∠=︒EDC BFD ∴∠=∠在BFD △与CDE 中，B C EDC BFDDE DF ∠=∠⎧⎪∠=∠⎨⎪=⎩()BFD CDE AAS ∴≅=1.5,=2BF CD BD CE ∴==2 1.5 3.5BC BD DC ∴=+=+=．【过关检测】一．选择题1．（2021秋•九龙坡区校级期末）如图，∠ACB ＝90°，AC ＝BC ，AD ⊥CE ，BE ⊥CE ，垂足分别是点D 、E ，AD ＝7cm ，BE ＝3cm ，则DE 的长是（）A ．3cmB ．3.5cmC ．4cmD ．4.5cm【分析】根据同角的余角相等，得∠CAD ＝∠BCE ，再利用AAS 证明△ACD ≌△CBE ，得CD ＝BE ＝3cm ，CE ＝AD ＝7cm ，从而得出答案．【解答】解：∵AD ⊥CE ，BE ⊥CE ，∴∠BEC ＝∠CDA ＝90°，∴∠CAD+∠ACD ＝90°，∵∠ACB ＝90°，∴∠ACD+∠BCE ＝90°，∴∠CAD ＝∠BCE ，在△ACD与△CBE中，，∴△ACD≌△CBE（AAS），∴CD＝BE＝3cm，CE＝AD＝7cm，∴DE＝CE﹣CD＝7﹣3＝4cm，故选：C．【点评】本题主要考查了等腰直角三角形的性质，全等三角形的判定与性质，证明△ACD≌△CBE是解题的关键．2．（2021秋•定远县校级期末）如图，E为线段BC上一点，∠ABE＝∠AED＝∠ECD＝90°，AE＝ED，BC ＝20，AB＝8，则BE的长度为（）A．12B．10C．8D．6【分析】根据一线三等角模型证明△ABE≌△ECD，可得AB＝EC，即可解答．【解答】解：∵∠ABE＝∠AED＝90°，∴∠A+∠AEB＝90°，∠AEB+∠DEC＝90°，∴∠A＝∠DEC，∵∠ABE＝∠ECD＝90°，AE＝ED，∴△ABE≌△ECD（AAS），∴AB＝CE＝8∵BC＝20，∴BE＝BC﹣CE＝20﹣8＝12，故选：A．【点评】本题考查了等腰直角三角形，全等三角形的判定与性质，熟练掌握一线三等角模型是解题的关键．3．（2021秋•岑溪市期末）如图，在等腰直角三角形ABC中，AB＝BC，∠ABC＝90°，点B在直线l上，过A作AD⊥l于D，过C作CE⊥l于E．下列给出四个结论：①BD＝CE；②∠BAD与∠BCE互余；③AD+CE＝DE．其中正确结论的序号是（）A．①②B．①③C．②③D．①②③【分析】根据同角的余角相等可得∠ABD＝∠BCE，再根据“AAS”可得△ABD≌△BCE，再逐项分析可得结论．【解答】解：∵AD⊥l，CE⊥l，∴∠ADB＝∠BEC＝90°，∵∠ABC＝90°，∴∠ABD+∠EBC＝∠BCE+∠EBC＝90°，即∠ABD＝∠BCE，在△ABD和△BEC中，，∴△ABD≌△BCE（AAS），∴BD＝CE，故①正确；∵∠BAD+∠ABD＝90°，∠ABD＝∠BCE，∴∠BAD+∠BCE＝90°，即∠BAD与∠BCE互余，故②正确；∵△ABD≌△BCE，∴AD＝EB，DB＝CE，∵BE+D＝DE，∴AD+CE＝DE，故③正确．故选：D．【点评】本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证△ABD≌△CBE 是解题的关键．4．（2021秋•龙湾区期中）如图，OA⊥OB，OB＝4，P是射线OA上一动点，连接BP，以B为直角顶点向上作等腰直角三角形，在OA上取一点D，使∠CDO＝45°，当P在射线OA上自O向A运动时，PD的长度的变化（）A．一直增大B．一直减小C．先增大后减小D．保持不变【分析】过点C作CH⊥OB于H，CG⊥OA于G，利用SAS证明△OBP≌△HCB，得OB＝CH＝4，OP＝HB，即可解决问题．【解答】解：过点C作CH⊥OB于H，CG⊥OA于G，∵△CBP是等腰直角三角形，∴BC＝BP，∠CBP＝90°，∴∠HBC+∠OBP＝90°，∵∠CBH+∠HCB＝90°，∴∠OBP＝∠HCB，在△OBP和△HCB中，，∴△OBP≌△HCB（AAS），∴OB＝CH＝4，OP＝HB，∵∠ODC＝45°，CG⊥OD，∴△GCD是等腰直角三角形，∴CG＝DG，∴PD＝GD﹣PG＝CG﹣（OP﹣4）＝4+OP﹣（OP﹣4）＝8，∴PD的长度保持不变，故选：D．【点评】本题主要考查了等腰直角三角形的判定与性质，全等三角形的判定与性质等知识，构造全等三角形是解题的关键．二．填空题5．（2022秋•拱墅区期中）如图，直线l上有三个边长分别为a，b，c的正方形，则有a2+c2b2（填“＞”或“＜”或“＝”）．【分析】证△EFG≌△GMH，推出FG＝MH＝c，GM＝EF＝a，再由勾股定理即可得出结论．【解答】解：如图，由正方形的性质得：∠EFG＝∠EGH＝∠GMH＝90°，EG＝GH＝b，∵∠FEG+∠EGF＝90°，∠EGF+∠MGH＝90°，∴∠FEG＝∠MGH，在△EFG和△GMH中，，∴△EFG≌△GMH（AAS），∴FG＝MH＝c，GM＝EF＝a，在Rt△EFG中，由勾股定理得：EF2+FG2＝EG2，即a2+c2＝b2，故答案为：＝．【点评】本题考查了全等三角形的判定与性质、正方形的性质，勾股定理等知识，熟练掌握正方形的性质，证明△EFG≌△GMH是解题的关键．6．（2022秋•南陵县期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D，若AD＝8cm，BE＝3cm，则DE＝cm．【分析】由余角的性质可证∠CAD＝∠BCE，即可证明△CDA≌△BEC，可得CD＝BE，CE＝AD，根据DE＝CE ﹣CD，即可解题．【解答】解：∵∠ACB＝90°，BE⊥CE于点E，AD⊥CE于点D，∴∠ACD+∠BCE＝90°，∠ACD+∠CAD＝90°，∴∠CAD＝∠BCE，在△CDA和△BEC中，，∴△CDA≌△BEC（AAS），∴CD＝BE，CE＝AD，∵DE＝CE﹣CD，∴DE＝AD﹣BE，∵AD＝8cm，BE＝3cm，∴DE＝5cm，故答案为：5．【点评】本题主要考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△CDA≌△BEC是解题的关键．7．（2021秋•台江区期末）如图，已知∠CDE＝90°，∠CAD＝90°，BE⊥AD于B，且DC＝DE，若BE＝7，AB＝4，则BD的长为．【分析】利用AAS证明△ACD≌△BDE，得BE＝AD，从而解决问题．【解答】解：∵BE⊥AD，∴∠EBD＝∠CAD＝90°，∴∠BDE+∠ADC＝90°，∠BDE+∠E＝90°，∴∠E＝∠ADC，在△ACD和△BDE中，，∴△ACD≌△BDE（AAS），∴BE＝AD，∴BD＝AD﹣AB＝BE﹣AB＝7﹣4＝3，故答案为：3．ACD≌△BDE是解题的关键．8．（2023春•城阳区期末）如图，在四边形ABCD中，AB＝AD，AB⊥AD，AC⊥DC．过点B作BE⊥CA，垂足为点E．若CD＝2，CE＝6，则四边形ABCD的面积是．【分析】根据垂直定义可得∠ACD＝∠BEA＝∠DAB＝90°，从而可得∠D+∠DAC＝90°，∠DAC+∠EAB＝90°，进而可得∠D＝∠EAB，然后利用AAS证明△ADC≌△BAE，从而可得AC＝BE，DC＝AE＝2，进而可得BE＝AC＝8，最后根据四边形ABCD的面积＝△ADC的面积+△ABC的面积，进行计算即可解答．【解答】解：∵AB⊥AD，AC⊥DC，BE⊥CA，∴∠ACD＝∠BEA＝∠DAB＝90°，∴∠D+∠DAC＝90°，∠DAC+∠EAB＝90°，∴∠D＝∠EAB，∵AD＝AB，∴△ADC≌△BAE（AAS），∴AC＝BE，DC＝AE＝2，∵CE＝6，∴BE＝AC＝AE+CE＝2+6＝8，∴四边形ABCD的面积＝△ADC的面积+△ABC的面积＝DC•AC+AC•BE＝×2×8+×6×6＝8+18＝26，故答案为：26．【点评】本题考查了全等三角形的判定与性质，熟练掌握一线三等角全等模型是解题的关键．9．（2022•铁岭三模）如图，小虎用10块高度都是3cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm．【分析】根据题意可得AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，进而得到∠ADC＝∠CEB＝90°，再根据等角的余角相等可得∠BCE＝∠DAC，再证明△ADC≌△CEB即可，利用全等三角形的性质进行解答．【解答】解：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，∴∠ADC＝∠CEB＝90°，∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，∴∠BCE＝∠DAC，在△ADC和△CEB中，，∴△ADC≌△CEB（AAS）；由题意得：AD＝EC＝9cm，DC＝BE＝21cm，∴DE＝DC+CE＝30（cm），答：两堵木墙之间的距离为30cm．故答案为：30．【点评】此题主要考查了全等三角形的应用，关键是正确找出证明三角形全等的条件．10．（2021秋•北仑区期末）如图，等边三角形ABC中，放置等边三角形DEF，且点D，E分别落在AB，BC上，AD＝5，连结CF，若CF平分∠ACB，则BE的长度为．【分析】如图，在BC上截取EG＝BD，连接FG，根据SAS证明△BED≌△GFE，得FG＝CG＝BE，最后证明AD＝2BE可得结论．【解答】解：如图，在BC上截取EG＝BD，连接FG，∵△ABC和△DEF是等边三角形，∴DE＝EF，AB＝BC，∠DEF＝∠B＝∠ACB＝60°，∵∠DEC＝∠BDE+∠B＝∠DEF+∠FEG，∴∠BDE＝∠FEG，在△BED和△GFE中，，∴△BED≌△GFE（SAS），∴∠B＝∠EGF＝60°，BE＝FG，∵FC平分∠ACB，∴∠ACF＝∠ECF＝30°，∵∠EGF＝∠GFC+∠FCG，∴∠GFC＝∠GCF＝30°，∴FG＝CG＝BE，∵AB＝BC，BD＝EG，∴AD＝BE+CG＝2BE＝5，∴BE＝2.5．故答案为：2.5．【点评】本题考查了等边三角形性质，全等三角形判定和性质，解决问题的关键是作辅助线，构造三角形全等．三．解答题11．（2021秋•嵊州市期末）【问题提出】（1）已知：如图1，AD⊥DE于点D，BE⊥DE于点E，点C在线段DE上，AC＝BC且AC⊥BC，求证：△ADC≌△CEB．【问题解决】（2）如图2，点D，C，E在直线l上．点A，B在l的同侧，AC⊥BC，若AD＝AC＝BC＝BE＝5cm，CD ＝6cm，求CE的长．【分析】（1）根据同角的余角相等可得∠A＝∠BCE，然后利用AAS即可证明结论；（2）作AG⊥CD于G，BH⊥CE于H，根据等腰三角形的性质得CG＝3cm，利用勾股定理得AG＝4cm，由（1）同理得，△ACG≌△CBH（AAS），得CH＝AG＝4cm，从而得出答案．【解答】（1）证明：∵AD⊥DE于点D，BE⊥DE，∴∠D＝∠E＝90°，∴∠ACD+∠BCE＝90°，∠ACD+∠A＝90°，∴∠A＝∠BCE，在△ADC和△CEB中，，∴△ADC≌△CEB（AAS）；（2）解：作AG⊥CD于G，BH⊥CE于H，∵AD＝AC，AG⊥CD，∴CG＝3cm，在Rt△ACG中，由勾股定理得，AG＝4cm，由（1）同理得，△ACG≌△CBH（AAS），∴CH＝AG＝4cm，∵BC＝BE，BH⊥CE，∴CE＝2CH＝8cm．【点评】本题主要考查了全等三角形的判定与性质，等腰三角形的性质，勾股定理等知识，熟练掌握基本几何模型是解题的关键．12．（2022秋•青田县校级月考）如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于点E．AD⊥CE于点D．求证：△BEC≌△CDA．【分析】根据垂直的定义以及等量代换可知∠CBE＝∠ACD，根据已知条件∠BEC＝∠CDA，∠CBE＝∠ACD，BC＝AC，根据全等三角形的判定AAS即可证明△BEC≌△CDA．【解答】证明：∵BE⊥CE于E，AD⊥CE于D，∴∠BEC＝∠CDA＝90°，在Rt△BEC中，∠BCE+∠CBE＝90°，在Rt△BCA中，∠BCE+∠ACD＝90°，∴∠CBE＝∠ACD，在△BEC和△CDA中，∠BEC＝∠CDA，∠CBE＝∠ACD，BC＝AC，∴△BEC≌△CDA．【点评】本题考查了全等三角形的判定定理，本题根据AAS证明两三角形全等，难度适中．13．（2021秋•安陆市校级月考）在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE＝AD+BE；（2）当直线MN绕点C旋转到图2的位置时，求证：DE＝AD﹣BE；（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．【分析】（1）由∠ACB＝90°，得∠ACD+∠BCE＝90°，而AD⊥MN于D，BE⊥MN于E，则∠ADC＝∠CEB ＝90°，根据等角的余角相等得到∠ACD＝∠CBE，易得Rt△ADC≌Rt△CEB，所以AD＝CE，DC＝BE，即可得到DE＝DC+CE＝BE+AD．（2）根据等角的余角相等得到∠ACD＝∠CBE，易得△ADC≌△CEB，得到AD＝CE，DC＝BE，所以DE＝CE﹣CD＝AD﹣BE．（3）DE、AD、BE具有的等量关系为：DE＝BE﹣AD．证明的方法与（2）相同．【解答】（1）证明：∵∠ACB＝90°，∴∠ACD+∠BCE＝90°，而AD⊥MN于D，BE⊥MN于E，∴∠ADC＝∠CEB＝90°，∠BCE+∠CBE＝90°，∴∠ACD＝∠CBE．在△ADC和△CEB中，，∴△ADC≌△CEB，∴AD＝CE，DC＝BE，∴DE＝DC+CE＝BE+AD；（2）证明：在△ADC和△CEB中，，∴△ADC≌△CEB，∴AD＝CE，DC＝BE，∴DE＝CE﹣CD＝AD﹣BE；（3）DE＝BE﹣AD．易证得△ADC≌△CEB，∴AD＝CE，DC＝BE，∴DE＝CD﹣CE＝BE﹣AD．【点评】本题考查了旋转的性质：旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．也考查了直角三角形全等的判定与性质．14．（2021秋•南丹县期末）如图1，∠ABC＝90°，F A⊥AB于点A，D是线段AB上的点，AD＝BC，AF＝BD．（1）判断DF与DC的数量关系为，位置关系为．（2）如图2，若点D在线段AB的延长线上，过点A在AB的另一侧作AF⊥AB，并截取AF＝BD，连接DC，DF，CF，试说明（1）中结论是否成立，并说明理由．【分析】（1）利用SAS证明△ADF≌△BCD，得DF＝CD，∠ADF＝∠BCD，从而得出∠ADF+∠CDB＝90°，即可证明结论；（2）由（1）同理得△ADF≌△BCD，得DF＝CD，∠ADF＝∠BCD，从而得出∠ADF+∠CDB＝90°，即∠CDF ＝90°．【解答】解：（1）∵AF⊥AB，∴∠DAF＝90°，在△ADF与△BCD中，，∴△ADF≌△BCD（SAS），∴DF＝CD，∠ADF＝∠BCD，∵∠BCD+∠CDB＝90°，∴∠ADF+∠CDB＝90°，即∠CDF＝90°，∴CD⊥DF，故答案为：相等，垂直；（2）成立，理由如下：∵AF⊥AB，∴∠DAF＝90°，∵∠ABC＝90°，∴∠CBD＝90°，∴∠DAF＝∠CBD，在△ADF与△BCD中，，∴△ADF≌△BCD（SAS），∴DF＝CD，∠ADF＝∠BCD，∵∠BCD+∠CDB＝90°，∴∠ADF+∠CDB＝90°，即∠CDF＝90°，∴CD⊥DF．【点评】本题主要考查全等三角形的判定与性质，熟悉基本的一线三等角模型是解题的关键．15．（2021秋•东至县期末）如图，在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，若DE＝10，BD＝3，求CE的长．【分析】由∠AEC＝∠BAC＝α，推出∠ECA＝∠BAD，再根据AAS证明△BAD≌△ACE得CE＝AD，AE＝BD＝3，即可得出结果．【解答】解：∵∠AEC＝∠BAC＝α，∴∠ECA+∠CAE＝180°﹣α，∠BAD+∠CAE＝180°﹣α，∴∠ECA＝∠BAD，在△BAD与△ACE中，，∴△BAD≌△ACE（AAS），∴CE＝AD，AE＝BD＝3，∵DE＝AD+AE＝10，∴AD＝DE﹣AE＝DE﹣BD＝10﹣3＝7．∴CE＝7．【点评】本题考查了全等三角形的判定与性质，证明△BAD≌△ACE是解题的关键．16．（2022秋•沭阳县月考）已知：如图，AB⊥BD，ED⊥BD，C是BD上的一点，AC⊥CE，AB＝CD，求证：BC＝DE．【分析】根据直角三角形全等的判定方法，ASA即可判定三角形全等．【解答】证明：∵AB⊥BD，ED⊥BD AC⊥CE（已知）∴∠ACE＝∠B＝∠D＝90°（垂直的意义）∵∠BCA+∠DCE+∠ACE＝180°（平角的意义）∠ACE＝90°（已证）∴∠BCA+∠DCE＝90°（等式性质）∵∠BCA+∠A+∠B＝180°（三角形内角和等于180°）∠B＝90°（已证）∴∠BCA+∠A＝90°（等式性质）∴∠DCE＝∠A （同角的余角相等）在△ABC和△CDE中，，∴△ABC≌△CDE（ASA）∴BC＝DE．（全等三角形对应边相等）【点评】本题考查了全等三角形的判定和性质；熟练掌握三角形全等的判定定理是解题的关键．17．（2022•鹿城区二模）如图，在△ABC中，AB＝AC，点D在BC边上，点E在AC边上，连接AD，DE．已知∠1＝∠2，AD＝DE．（1）求证：△ABD≌△DCE；（2）若BD＝3，CD＝5，求AE的长．【分析】（1）根据AAS可证明△ABD≌△DCE；（2）得出AB＝DC＝5，CE＝BD＝3，求出AC＝5，则AE可求出．【解答】（1）证明：∵AB＝AC，∴∠B＝∠C，在△ABD与△DCE中，，∴△ABD≌△DCE（AAS）；（2）解：∵△ABD≌△DCE，∴AB＝DC＝5，CE＝BD＝3，∵AC＝AB，∴AC＝5，∴AE＝AB﹣EC＝5﹣3＝2．【点评】本题考查了全等三角形的判定与性质，等腰三角形的性质，熟练掌握全等三角形的判定方法是解题的关键．18．（2022秋•浠水县期中）已知，在△ABC中，AB＝AC，D，A，E三点都在直线m上，且DE＝9cm，∠BDA＝∠AEC＝∠BAC（1）如图①，若AB⊥AC，则BD与AE的数量关系为，CE与AD的数量关系为；（2）如图②，判断并说明线段BD，CE与DE的数量关系；（3）如图③，若只保持∠BDA＝∠AEC，BD＝EF＝7cm，点A在线段DE上以2cm/s的速度由点D向点E运动，同时，点C在线段EF上以xcm/s的速度由点E向点F运动，它们运动的时间为t（s）．是否存在x，使得△ABD与△EAC全等？若存在，求出相应的t的值；若不存在，请说明理由．【分析】（1）利用平角的定义和三角形内角和定理得∠CAE＝∠ABD，再利用AAS证明△ABD≌△CAE，得BD ＝AE，CE＝AD；（2）由（1）同理可得△ABD≌△CAE，得BD＝AE，CE＝AD，可得答案；（3）分△DAB≌△ECA或△DAB≌△EAC两种情形，分别根据全等三角形的性质可解决问题．【解答】解：（1）∵∠BDA＝∠AEC＝∠BAC，∴∠BAD+∠CAE＝∠BAD+∠ABD，∴∠CAE＝∠ABD，∵∠BDA＝∠AEC，BA＝CA，∴△ABD≌△CAE（AAS），∴BD＝AE，CE＝AD，故答案为：BD＝AE，CE＝AD；（2）DE＝BD+CE，由（1）同理可得△ABD≌△CAE（AAS），∴BD＝AE，CE＝AD，∴DE＝BD+CE；（3）存在，当△DAB≌△ECA时，∴AD＝CE＝2cm，BD＝AE＝7cm，∴t＝1，此时x＝2；当△DAB≌△EAC时，∴AD＝AE＝4.5cm，DB＝EC＝7cm，∴t＝，x＝7÷＝，综上：t＝1，x＝2或t＝，x＝．【点评】本题是三角形综合题，主要考查了全等三角形的判定与性质，熟练掌握一线三等角基本模型是解题的关键，同时渗透了分类讨论的数学思想．19．（2021秋•岳阳楼区期末）直线l经过点A，△ABC在直线l上方，AB＝AC．（1）如图1，∠BAC＝90°，过点B，C作直线l的垂线，垂足分别为D、E．求证：△ABD≌△CAE；（2）如图2，D，A，E三点在直线l上，若∠BAC＝∠BDA＝∠AEC＝α（α为任意锐角或钝角），猜想线段DE、BD、CE有何数量关系？并给出证明；（3）如图3，∠BAC＝90°过点B作直线l上的垂线，垂足为F，点D是BF延长线上的一个动点，连结AD，作∠DAE＝90°，使得AE＝AD，连结DE，CE．直线l与CE交于点G．求证：G是CE的中点．【分析】（1）由直角三角形的性质证出∠ABD＝∠CAE，可证明△ABD≌△CAE（AAS）；（2）证明△ABD≌△CAE（AAS），由全等三角形的性质得出BD＝AE，DA＝EC，则可得出结论；（3）分别过点C、E作CM⊥l，EN⊥l，由（1）可知△ABF≌△CAM，△ADF≌△EAN，得出AF＝CM，AF＝EN，证明△CMG≌△ENG（AAS），由全等三角形的性质得出CG＝EG，则可得出结论．【解答】（1）证明：∵BD⊥l，CE⊥l，∴∠BDA＝∠AEC＝90°，∴∠ABD+∠DAB＝90°，∵∠BAC＝90°，∴∠CAE+∠DAB＝90°，∴∠ABD＝∠CAE，在△ABD与△CAE中，，∴△ABD≌△CAE（AAS）；（2）解：猜想：DE＝BD+CE，∵∠BDA＝∠BAC＝α，∴∠ABD+∠DAB＝180°﹣∠BDA＝180°﹣α，∠CAE+∠DAB＝180°﹣∠BAC＝180°﹣α，∴∠ABD＝∠CAE，在△ABD与△CAE中，，∴△ABD≌△CAE（AAS），∴BD＝AE，DA＝EC，∴DE＝AE+DA＝BD+CE；（3）证明：分别过点C、E作CM⊥l，EN⊥l，由（1）可知△ABF≌△CAM，△≌△EAN，∴AF＝CM，AF＝EN，∴CM＝EN，∵CM⊥l，EN⊥l，∴∠CMG＝∠ENG＝90°，在△CMG与△ENG中，，∴△CMG≌△ENG（AAS），∴CG＝EG，∴G为CE的中点．【点评】本题是三角形综合题，考查了全等三角形的判定和性质，直角三角形的性质，等腰三角形的性质等知识，添加恰当辅助线构造全等三角形是本题的关键．20．（2021秋•涡阳县期末）如图，把一块直角三角尺ABC的直角顶点C放置在水平直线MN上，在△ABC 中，∠C＝90°，AC＝BC，试回答下列问题：（1）若把三角尺ABC绕着点C按顺时针方向旋转，当AB∥MN时，∠2＝度；（2）在三角尺ABC绕着点C按顺时针方向旋转过程中，分别作AM⊥MN于M，BN⊥MN与N，若AM ＝6，BN＝2，求MN．（3）三角尺ABC绕着点C按顺时针方向继续旋转到图3的位置，其他条件不变，则AM、BN与MN之间有什么关系？请说明理由．【分析】（1）先求出∠B＝45°，再用平行线的性质，即可求出答案；（2）先用同角的余角相等判断出∠2＝∠CAM，同理：∠1＝∠CBN，进而判断出△AMC≌△CNB（ASA），得出AM＝CN，MC＝BN（3）同（2）的方法，即可得出结论．【解答】解：（1）在△ABC中，AB＝AC，∠ACB＝90°，∴∠B＝∠A＝45°，∵AB∥MB，∴∠2＝∠B＝45°，故答案为45；（2）∵AM⊥MN于M，BN⊥MN于N，∴∠AMC＝90°，∠BNC＝90°．∴∠1+∠CAM＝90°，又∵∠1+∠2＝90°，∴∠2＝∠CAM，同理：∠1＝∠CBN，在△AMC和△CNB中，，∴△AMC≌△CNB（ASA），∴AM＝CN，MC＝BN，∴MN＝MC+CN＝AM+BN＝2+6＝8；（3）MN＝BN﹣AM，理由：同（2）的方法得，△AMC≌△CNB（ASA），∴AM＝CN，MC＝BN，∴MN＝MC﹣CN＝BN﹣AM．【点评】此题是几何变换综合题，主要考查了等腰直角三角形的性质，全等三角形的判定和性质，同角的余角相等，判断出△AMC≌△CNB是解本题的关键．21．（2022•信阳模拟）在直线m上依次取互不重合的三个点D，A，E，在直线m上方有AB＝AC，且满足∠BDA＝∠AEC＝∠BAC＝α．（1）如图1，当α＝90°时，猜想线段DE，BD，CE之间的数量关系是；（2）如图2，当0＜α＜180时，问题（1）中结论是否仍然成立？如成立，请你给出证明；若不成立，请说明理由；（3）拓展与应用：如图3，当α＝120°时，点F为∠BAC平分线上的一点，且AB＝AF，分别连接FB，FD，FE，FC，试判断△DEF的形状，并说明理由．【分析】（1）由∠BDA＝∠BAC＝∠AEC＝90°得到∠BAD+∠EAC＝∠BAD+∠DBA＝90°，进而得到∠DBA＝∠EAC，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE；（2）由∠BDA＝∠BAC＝∠AEC＝α得到∠BAD+∠EAC＝∠BAD+∠DBA＝180°﹣α，进而得到∠DBA＝∠EAC，然后结合AB＝AC得证△DBA≌△EAC，最后得到DE＝BD+CE；（3）先由α＝120°和AF平分∠BAC得到∠BAF＝∠CAF＝60°，然后结合AB＝AF＝AC得到△ABF和△ACF 是等边三角形，然后得到FA＝FC、∠FCA＝∠FAB＝60°，然后结合△BDA≌△EAC得到∠BAD＝∠ACE、AD ＝CE，从而得到∠FAD＝∠FCE，故可证△FAD≌△FCE，从而得到DF＝EF、∠DFA＝∠EFC，最后得到∠DFE＝∠DFA+∠AFE＝∠EFC+∠AFE＝60°，即可得证△DEF是等边三角形．【解答】解：（1）DE＝BD+CE，理由如下，∵∠BDA＝∠BAC＝∠AEC＝90°，∴∠BAD+∠EAC＝∠BAD+∠DBA＝90°，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴AD＝CE，BD＝AE，∴DE＝AD+AE＝BD+CE，故答案为：DE＝BD+CE．（2）DE＝BD+CE仍然成立，理由如下，∵∠BDA＝∠BAC＝∠AEC＝α，∴∠BAD+∠EAC＝∠BAD+∠DBA＝°﹣α，∴∠DBA＝∠EAC，∵AB＝AC，∴△DBA≌△EAC（AAS），∴BD＝AE，AD＝CE，∴DE＝AD+AE＝BD+CE；（3）△DEF是等边三角形，理由如下，∵α＝120°，AF平分∠BAC，∴∠BAF＝∠CAF＝60°，∵AB＝AF＝AC，∴△ABF和△ACF是等边三角形，∴FA＝FC，∠FCA＝∠FAB＝∠AFC＝60°，同（2）可得，△BDA≌△AEC，∴∠BAD＝∠ACE，AD＝CE，∴∠FAD＝∠FCE，∴△FAD≌△FCE（SAS），∴DF＝EF，∠DFA＝∠EFC，∴∠DFE＝∠DFA+∠AFE＝∠EFC+∠AFE＝∠AFC＝60°，∴△DEF是等边三角形．【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质，解题的关键是熟练应用一线三等角模型证明三角形全等．22．（2022秋•东台市月考）【一线三等角模型】如图1：点A、B、C在一条直线上，∠A＝∠DBE＝∠C，当BD＝BE时，有△ABD≌△CEB．理由：∵∠A＝∠DBE，∴∠D+∠DBA＝180°﹣∠A，∠DBA+∠CBE＝180°﹣∠DBE，∴∠D＝∠CBE﹣﹣﹣﹣﹣﹣﹣﹣请将全等证明过程补充完整．【模型运用】如图2：∠ABC＝∠CAD＝90°，AB＝4，AC＝AD，求△BAD的面积；【能力提升】如图3：在等边△DEF中，A，C分别为DE、DF边上的动点，AE＝2CD，连接AC，以AC 为边在△DEF内作等边△ABC，连接BF，当点A从点E向点D运动（不与点D重合）时，∠CFB的度数变化吗？如不变请求出它的度数，如变化，请说明它是怎样变化的？【分析】【一线三等角模型】如图1：根据AAS证明三角形全等即可；【模型运用】如图2：过点D作DT⊥BA交BA的延长线于点T．构造全等三角形解决问题即可；【能力提升】∠CFB＝30°不变．如图3中，在CF上取一点N，使得FN＝DC．证明△ADC≌△CNB（SAS），推出BN＝CD，∠D＝∠BNC＝60°，可得结论．【解答】【一线三等角模型】证明：如图1：∵∠A＝∠DBE，∴∠D+∠DBA＝180°﹣∠A，∠DBA+∠CBE＝180°﹣∠DBE，∴∠D＝∠CBE，在△ABD和△CEB中，，∴△ABD≌△CEB（AAS）；【模型运用】解：如图2：过点D作DT⊥BA交BA的延长线于点T．同法可证△ATD≌△CBA（AAS），∴DT＝AB＝4，∴S△ABD＝×AB×DT＝×4×4＝8；【能力提升】解：∠CFB＝30°不变．理由：如图3中，在CF上取一点N，使得FN＝DC．∵△ABC，△DEF都是等边三角形，∴∠D＝∠ACB＝60°，DA＝DF，CA＝CB，∵AE＝2CD，CD＝FN，∴DA＝CN，∵∠ACN＝∠ACB+∠BCN＝∠D+∠CAD，∴∠BCN＝∠DAC，在△ADC和△CNB中，，∴△ADC≌△CNB（SAS），∴BN＝CD，∠D＝∠BNC＝60°，∵NF＝CD，∴NB＝NF，∴∠NBF＝∠NFB，∵∠BNC＝∠NBF+∠NFB＝60°，∴∠NFB＝∠NBF＝30°，∴∠CFB＝30°．【点评】本题属于三角形综合题，考查了等边三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造一线三等角模型，利用全等三角形解决问题．23．（2021秋•江汉区期末）如图，在等边△ABC中，D，E分别为AB，BC边上的点，DE＝EF，∠DEF＝60°．（1）如图1，若点F在AC边上，求证：AD＝CF；（2）如图2，连CF．若∠FCB＝30°，求证：AD＝2BE；（3）如图3，O是BC的中点，点H在△ABC内，∠BHC＝120°，点M，N分别在CH，BH上，MO⊥NO，若∠CAM＝α，直接写出∠BAN的度数（用含有α的式子表示）．【分析】（1）连接DF，根据“有一个角是60°的等腰三角形是等边三角形”可判断△DEF是等边三角形，则DF＝EF，又△ABC是等边三角形，根据三角形内角和可得出，∠AFD＝∠FEC，所以△ADF≌△CFE（AAS），则AD＝CF；（2）过点F作JK∥AC交AB于点J，交BC于点K，过点F作PI∥AB交AC于P，交BC于点I，连接DF，则△BJK和△CPI是等边三角形，△BDE≌△JFD≌KEF，所以DJ＝BE＝FK，因为AB∥PI，FK∥AC，所以四边形AJFP是平行四边形，则AJ＝PF，易得△CPI为等边三角形，由∠FCB＝30°可得CF平分∠PCI，则FI＝FP，所以FP＝AJ，FK＝BE＝DJ，FI＝FK，所以AJ＝DJ＝BE，即AD＝AJ+DJ＝2BE；（3）延长MO到点G，使OG＝OM，连接NG，BG，NM，作∠ACQ＝∠ABN，且使CQ＝BN，连接MQ，AQ，先得到△BOG≌△COM（SAS），再得到△ACQ≌△ABN（SAS）和△BNG≌△CQM（SAS），所以∠NAM＝∠MAQ ＝∠CAM+∠CAQ＝∠CAM+∠BAN，所以∠CAM+∠BAN＝30°，则∠CAM＝α，所以∠BAN＝30°﹣α．【解答】（1）证明：如图，连接DF，∵DE＝EF，∠DEF＝60°，∴△DEF是等边三角形，∴DF＝EF，∵△ABC是等边三角形，∴∠A＝∠C＝60°，∵∠AFE＝∠AFD+∠DFE＝60°+∠AFD，∠AFE＝∠C+∠EFC＝60°+∠FEC，∴∠AFD＝∠FEC，∵∠A＝∠C，DF＝EF，∴△ADF≌△CFE（AAS），∴AD＝CF；（2）证明：如图，过点F作JK∥AC交AB于点J，交BC于点K，过点F作PI∥AB交AC于P，交BC于点I，连接DF，∴∠BJK＝∠BAC＝∠BKJ＝∠ACB＝60°＝∠ABC，∠CPI＝∠BAC＝∠B＝∠CIP＝60°＝∠ACB，∴△BJK和△CPI是等边三角形，∵∠DEF＝60°，DE＝EF，∴△DEF是等边三角形，由（1）中结论可知，△BDE≌△JFD≌KEF，∴DJ＝BE＝FK，∵AB∥PI，FK∥AC，∴四边形AJFP是平行四边形，∴AJ＝PF，∵∠FIK＝∠FKI＝60°，∴FI＝FK，∵△CPI为等边三角形，∠FCB＝30°，∴∠FCI＝∠FCP＝30°，∴CF平分∠PCI，∵△CPI是等边三角形，∴FI＝FP，∵FP＝AJ，FK＝BE＝DJ，FI＝FK，∴AJ＝DJ＝BE，即AD＝AJ+DJ＝（3）解：如图，延长MO到点G，使OG＝OM，连接NG，BG，NM，作∠ACQ＝∠ABN，且使CQ＝BN，连接MQ，AQ，∵MO⊥NO，OM＝OG，∴NG＝MN，∵MO＝OG，BO＝OC，∠MOC＝∠BOG，∴△BOG≌△COM（SAS），∴BG＝CM，∠GBO＝∠OCM，∴BG∥CM，∴∠NBG＝180°﹣∠BHC＝60°，∵BHC＝120°，∴∠HBC+∠HCB＝60°，∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠BAC＝60°，∴∠ABH+∠HBC＝∠ACH+∠HCB＝60°，∴∠ABH＝∠HCB，∠HBC＝∠ACH，∵∠ACQ＝∠ABN，AB＝AC，BN＝CQ，∴△ACQ≌△ABN（SAS），∴AN＝AQ，∠BAN＝∠CAQ，∵∠ACB＝∠ACH+∠BCH＝60°，∠ABN＝∠BCH＝∠ACQ，∴∠MCQ＝∠ACM+∠ACQ＝∠ACH+∠BCH＝60°＝∠NBG，∵BN＝CQ，BG＝CM，∴△BNG≌△CQM（SAS），∴NG＝MQ，∵NG＝NM，∴MQ＝MN，∵AN＝AQ，AM＝AM，∴△NAM≌△QAM（SSS），∴∠NAM＝∠MAQ＝∠CAM+∠CAQ＝∠CAM+∠BAN，又∵∠NAM+∠CAM+∠BAN＝60°，∴∠CAM+∠BAN＝30°，∴∠CAM＝α，∴∠BAN＝30°﹣α．【点评】本题属于三角形的综合题，涉及全等三角形的性质与判定，等边三角形的性质与判定，等腰三角形三线合一等知识，类比思想及构造的思想进行分析，仿造（1）中的结论构造出全等三角形是解题关键．。

浙教版八年级上册数学第2章特殊三角形含答案

浙教版八年级上册数学第2章特殊三角形含答案一、单选题(共15题，共计45分)1、下列图案中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.2、如图，点P在∠MON的角平分线上，过点P作OP的垂线交OM，ON于C、D，PA⊥OM．PB⊥ON，垂足分别为A、B，EP∥BD，则下列结论错误的是（）A. CP＝PDB. PA＝PBC. PE＝OED. OB＝CD3、中，，则一定是（）A.锐角三角形B.等腰三角形C.等边三角形D.等腰直角三角形4、如图，已知A，B两点的坐标分别为(8,0)，(0,8)，点C，F分别是直线和轴上的动点，，点D是线段的中点，连接交轴于点E，当面积取得最小值时，的值是（）A. B. C. D.5、下列各组数是勾股数的是（）A.5，12，13B.4，5，6C.7，12，13D.9，12，136、如图，在平行四边形中，平分，交于点，平分，交于点，，，则长为（）A.8B.9C.10D.127、等腰三角形的两边分别为1和2，则其周长为（）A.5B.4C.4或5D.无法确定8、如图，在△ABC中，AB=AC，D为BC上一点，连接AD，点E在AD上，过点E 作EM⊥AB，EN⊥AC，垂足分别为M，N．下面四个结论：①如果AD⊥BC，那么EM=EN；②如果EM=EN，那么∠BAD=∠CAD；③如果EM=EN，那么AM=AN；④如果EM=EN，那么∠AEM=∠AEN．其中正确有( )A.1个B.2个C.3个D.4个9、如果一个等腰三角形的一个角为30º，则这个三角形的顶角为（）A.120ºB.30ºC.120º或30ºD.90º10、如图，在△中, ，，边上的中线，那么的长是（）A. B. C. D.11、下列图形中，是中心对称图形，但不是轴对称图形的是( )A. B. C. D.12、在Rt△ABC中，D为斜边AB的中点，且BC=3，AC=4，则线段CD的长是（）A.2B.3C.D.513、如图所示，一场暴雨过后，垂直于地面的一棵树在距地面2 m处折断，树尖B恰好碰到地面，经测量AB=4 m，则折断之前树高为（）A. mB. mC. mD.4 m14、如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B 两点，B点的坐标为（3，0），与y轴交于点C（0，﹣3），点P是直线BC下方抛物线上的任意一点，过点P作平行于y轴的直线PM，交线段BC于M，当△PCM是以PM为腰的等腰三角形时，点P的坐标是（）A.（2，-3）或（+1，-2）B.（2，-3）或（，-1-2 ） C.（2，-3）或（，1-2 ） D.（2，-3）或（3- ，2-4 ）15、国旗上每个五角星( ).A.是中心对称图形而不是轴对形；B.是轴对称图形而不是中心对称图形；C.既是中心对称图形又是轴对称图形；D.既不是中心对称图形又不是轴对称图形二、填空题(共10题，共计30分)16、如图所示，在△ABC中，∠B=90°，AB=3，AC=5，线段AC的垂直平分线DE 交AC于D交BC于E，则△ABE的周长为________.17、已知，，，点F在上，作，直线交于E，交延长线于G，连接，，，则的长为________．18、如图，∠MON=90°，长方形ABCD的顶点B、C分别在边OM、ON上，当B 在边OM上运动时，C随之在边ON上运动.若CD=3，BC=8，运动过程中，点D到点O的最大距离为________.19、如图，在△ABC中，AB=AC，点O在△ABC内，且∠OBC=∠OCA，∠BOC=110°，求∠A的度数=________．20、如图是由边长为1m的正方形地砖铺设的地面示意图，小明沿图中所示的折线从A⇒B⇒C所走的路程为________m．21、如图，等腰△ABC中，AB=AC=10，BC=12，AD平分，且AD=8，P，Q分别是AB、AD上的动点，连接BP，PQ，则BP +PQ的最小值为________．22、已知一个等腰三角形的周长为22cm，已知一边长为8cm,求另外两边长为________23、如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12 ，则图中阴影部分的面积是________24、如图，在△ABC中，CD⊥AB交AB于点D，BE⊥AC交AC于点E，F为BC的中点，BC = 10，DE = 8，则△DEF的面积为________．25、如图，等腰△ABC中，AB＝AC＝4，BC＝6，△ABD是等边三角形，点P是∠BAC的角平分线上一动点，连PC、PD，则PD+PC的最小值为________.三、解答题(共5题，共计25分)26、如图，AC⊥BD，垂足点E是BD的中点，且AB=CD，求证：AB//CD.27、如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°.求四边形ABCD的面积.28、如图，在边长为2的正方形ABCD中，点P、Q分别是边AB、BC上的两个动点（与点A、B、C不重合）且始终保持BP=BQ，AQ⊥QE，QE交正方形外角平分线CE于点E，AE交CD于点F，连结PQ．（1）求证：△APQ≌△QCE；（2）求∠QAE的度数；（3）设BQ=x，当x为何值时，QF∥CE，并求出此时△AQF的面积．29、如图，在平行四边形ABCD中，AB＝5，BC＝10，F为AD的中点，CE⊥AB于E，设∠ABC＝α(60°≤α＜90°)．(1)当α＝60°时，求CE的长；(2)当60°＜α＜90°时，①是否存在正整数k，使得∠EFD＝k∠AEF？若存在，求出k的值；若不存在，请说明理由．②连接CF，当CE2－CF2取最大值时，求tan∠DCF的值．30、如图，已知∠B=∠C=90°，AE⊥ED，AB=CE，点F是AD的中点．说明EF与AD垂直的理由．解：因为AE⊥ED（已知），所以∠AED=90°（垂直的意义）．因为∠AEC=∠B+∠BAE（________），即∠AED+∠DEC=∠B+∠BAE．又因为∠B=90°（已知），所以∠BAE=∠CED（等式性质）．在△ABE与△ECD中，∠B=∠C（已知），AB=EC（已知），∠BAE=∠CED，所以△ABE≌△ECD（________），得（全等三角形的对应边相等），所以△AED是等腰三角形．因为（已知），所以EF⊥AD（________）．参考答案一、单选题(共15题，共计45分)1、B2、D3、B4、D5、A6、C7、A8、D9、C10、A11、A12、C13、C14、D15、B二、填空题(共10题，共计30分)16、17、18、19、20、21、23、24、25、三、解答题(共5题，共计25分)26、。

新浙教版八年级上册数学第二章《特殊三角形》第三节等腰三角形的性质

新浙教版八年级上册数学第二章《特殊三角形》第三节等腰三角形的性质【课本相关知识点】1、等腰三角形的性质定理1：等腰三角形的两个底角，这个定理也可以说成，在同一个三角形中，2、推论：等边三角形的每个内角都等于3、等腰三角形的性质定理2：等腰三角形的、底边上的中线和高线互相，简称等腰三角形的【典型例题】【题型一】利用等腰三角形的性质求角度例1、（1）在△ABC 中，AB=AC ，若∠A=50°，则∠B=（2）若等腰三角形的一个角为80°，则顶角为（3）若等腰三角形的一个角为90°，则顶角为（4）若等腰三角形的一个底角为40°，则顶角为温馨提醒：一定要看清题目，是否要分类讨论。

多画图，有助于解题。

例2、如图所示，△ABC 是等腰三角形，AB=AC ，分别以两腰为边向外作等边三角形ABD 与等边三角形ACE ，已知∠DAE=∠DBC ，求△ABC 的三个内角的度数。

【题型二】三线合一中，知“一线”推“二线”（前提一定要在等腰三角形中）例1、如图，已知△ABC（1）若AB=AC ，∠1=∠2，则，（2）若AB=AC ，AD ⊥BC ，则，（3）若AB=AC ，BD=DC ，则，【题型三】运用等腰三角形的性质证明线段相等、垂直、角度相等例1、如图所示，在△ABC 中，AB=AC ，BD 、CE 分别是△ABC 的高，求证：∠BCE=∠CBD例2、如图所示，AB=AE ，∠ABC=∠AED ，BC=ED ，点F 是CD 的中点。

（1）试说明AF ⊥CD（2）在（1）中的结论说明完毕后，还能得出什么新的结论？请你写出三个（不必说明理由）例3、如图所示，在△ABC 中，AB=AC ，E 在CA 的延长线上，∠AEF=∠AFE ，试说明EF ⊥BC 。

巩固练习1、等腰三角形的一个外角是80°，则其底角是2、若等腰三角形的顶角等于50°，则一腰上的高线与底边的夹角等于（）A 25°B 30°C 45°D 65°注意：记住结论：等腰三角形一腰上的高线与底边的夹角等于顶角的一半3、如图所示，已知P 、Q 是△ABC 上的两点，且BP=PQ=QC=AP=AQ ，则∠BAC=4、在△ABC 中，∠ACB=100°，AC=AE ，BC=BD ，求∠DCE 的度数5、如图所示，AB=AC ，D 是BC 边上的一点，AD=AE ，∠BAD=40°，求∠CDE 的度数6、如图所示，∠AOB 是一个钢架，且∠AOB ＝10°，为了使钢架更加牢固，需在内部添加一些钢管EF ，FG ，GH ，…，添加的钢管长度都与OE 相等，则最多能添加这样的钢管________根 7、如图，在△ABC 中，PM 、QN 分别是AB 、AC 的垂直平分线，如果∠BAC=110°，那么∠PAQ=8、已知等边△ABC 和点P ，设点P 到△ABC 三边AB 、AC 、BC 的距离分别为h 1、h 2、h 3，△ABC 的BC 边上的高为h 。

浙教版八年级数学上册第二章知识点+注意点+经典例题

八年级上册第二章《特殊三角形》2.1图形的轴对称[轴对称图形]1.如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.2.有的轴对称图形的对称轴不止一条,如圆就有无数条对称轴.3.折叠后重合的点是对应点,叫做对称点.[轴对称]有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合,•那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点,叫做对称点．两个图形关于直线对称也叫做轴对称.ﻭ［图形轴对称的性质］①关于某直线对称的两个图形是全等形。

②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线.③轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.④如果两个图形的对应点连线被同条直线垂直平分,那么这两个图形关于这条直线对称.[轴对称与轴对称图形的区别][线段的垂直平分线]（1)经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.（2)线段的垂直平分线上的点与这条线段两个端点的距离相等；反过来,与一条线段两个端点距离相等的点在这条线段的垂直平分线上．因此线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合．2。

2等腰三角形+2。

3等腰三角形性质定理＋2。

4等腰三角形判定定理［等腰三角形]★1. 有两条边相等的三角形是等腰三角形。

★2。

在等腰三角形中,相等的两条边叫做腰，另一条边叫做底边.两腰所夹的角叫做顶角,腰与底边的夹角叫做底角.[等腰三角形的性质]★性质1:等腰三角形的两个底角相等（简写成“等边对等角”）★性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合（三线合一）.特别的:(1)等腰三角形是轴对称图形。

(2）等腰三角形两腰上的中线、角平分线、高线对应相等.[等腰三角形的判定定理］★如果一个三角形有两个角相等，那么这两个角所对的边也相等(简写成“等角对等边").特别的:（1）有一边上的角平分线、中线、高线互相重合的三角形是等腰三角形. (2)有两边上的角平分线对应相等的三角形是等腰三角形.（3）有两边上的中线对应相等的三角形是等腰三角形．(4）有两边上的高线对应相等的三角形是等腰三角形.[等边三角形］三条边都相等的三角形叫做等边三角形，也叫做正三角形.[等边三角形的性质]★等边三角形的三个内角都相等，•并且每一个内角都等于60°[等边三角形的判定方法]★(1）三条边都相等的三角形是等边三角形；★(2)三个角都相等的三角形是等边三角形；★(３)有一个角是60°的等腰三角形是等边三角形.２。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级上册第二章特殊三角形
一、将军饮马
例1 如图，在正方形ABCD 中，AB=9，点E 在CD 边上，且DE=2CE ，点P 是对角线AC 上的一个动点，则PE+PD 的最小值是（）
A 、3
B 、10
C 、9
D 、9
【变式训练】
1、如图，在矩形ABCD 中，AD=4，∠DAC=30°，点P 、E 分别在AC 、AD 上，则PE+PD 的最小值是（） A 、2 B 、2 C 、4 D 、
2、如图，∠AOB=30°，P 是∠AOB 内一定点，PO=10，C ，D 分别是OA ，OB 上的动点，则△PCD 周长的最小值为
3、如图，∠AOB=30°，C ，D 分别在OA ，OB 上，且OC=2，OD=6，点C ，D 分别是AO ，BO 上的动点，则CM+MN+DN 最小值为
4、如图，C 为线段BD 上一动点，分别过点B ，D 作AB ⊥BD ，DE ⊥BD ，连结AC ，CE ．（1）已知AB=3，DE=2，BD=12，设CD=x ．用含x 的代数式表示AC+CE 的长；（2）请问点C 满足什么条件时，AC+CE 的值最小？并求出它的最小值；（3）根据（2）中的规律和结论，请构图求出代数式
的最小值
E
B
C
A
D
P
第2题
B
O
A
P
C
D
第1题
B
O
A
C N
第3题
E C
二、等腰三角形中的分类讨论
例2（1）已知等腰三角形的两边长分别为8cm和10cm，则它的周长为
（2）已知等腰三角形的两边长分别为8cm和10cm，则它的腰长为
（3）已知等腰三角形的周长为28cm和8cm，则它的底边为
【变式训练】
1、已知等腰三角形的两边长分别为3cm和7cm，则周长为
2、已知等腰三角形的一个角是另一个角的4倍，则它的各个内角的度数为
3、已知等腰三角形的一个外角等于150°，则它的各个内角的度数为
4、已知等腰三角形一腰上的高与另一边的夹角为25°，则它的各个内角的度数
5、已知等腰三角形底边为5cm，一腰上的中线把其周长分为两部分的差为3cm，则腰长为
6、在三角形ABC中，AB=AC，AB边上的垂直平分线与AC所在的直线相交所得的锐角为40°，则底角∠B的度数为
7、如图，A、B是4×5的网格中的格点，网格中每个小正方形的边长都是单位1，请在图中清晰地标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置
三、两圆一线定等腰
例3在平面直角坐标系xOy中，已知点A（2，3），在坐标轴上找一点P，
使得△AOP是等腰三角形，则这样的点P共有个
B
【变式训练】
1、在平面直角坐标系xOy中，已知点A（1，），在坐标轴上找一点P，使得△AOP是等腰三角形，则符合条件的点P的个数为（）
A．5 B．6 C．7 D．8
2、在平面直角坐标系中，若点A（2，0），点B（0，1），在坐标轴上找一点C，使得△ABC是等腰三角形，这样的点C可以找到个．
3、在坐标平面内有一点A（2，），O为原点，在x轴上找一点B，使O，A，B为顶点的三角形为等腰三角形，写出B点坐标
4、平面直角坐标系中，已知点A（4，2），B（4，-3），试在y轴上找一点P，使△APB为等腰三角形，求点P的坐标
5、如图1，已知一次函数分别与x、y轴交于A、B两点，过点B的直线BC交x轴负半轴与点C，且OC=OB．
（1）求直线BC的函数表达式；
（2）如图2，若△ABC中，∠ACB的平分线CF与∠BAE的平分线AF相交于点F，求证：∠AFC=∠ABC；
（3）在x轴上是否存在点P，使△ABP为等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由
四、折叠问题
例4：如图，在矩形ABCD 中，AB=6，BC=8，将矩形折叠，使得点D 落在线段BC 的点F 处，则线段DE 的长为
【变式训练】
1、如图，在矩形ABCD 中，AB=6，BC=8，将矩形折叠，使得点B 落在对角线AC 的点F 处，则线段BE 的长为
2、如图，在矩形ABCD 中，AB=6，BC=8，沿EF 将矩形折叠，使A 、C 重合，若，则折痕EF 的长为
B
B
B
B
3、如图，在矩形ABCD中，AB=6，BC=8，沿AC将矩形折叠，使得点B落在点E处，则线段EF的长为
4、如图，将边长为4的正方形纸片，置于平面直角坐标系内，顶点A在坐标原点，AB在x轴正方向上，E、F分别是AD、BC的中点，M在DC上，将△ADM沿折痕AM折叠，使点D折叠后恰好
落在EF上的P点处．
（1）求点M、P的坐标；
（2）求折痕AM所在直线的解析式；
（3）设点H为直线AM上的点，是否存在这样的点H，使得以H、A、P为顶点的三
角形为等腰三角形？若存在，请直接写出点H的坐标；若不存在，请说明理由．
例5 如图，在△ABC中，BD、CE分别是边AC、AB上的高线．
（1）如果BD=CE，那么△ABC是等腰三角形，请说明理由；
（2）如果∠A=60°，取BC中点F，连结点D、E、F得到△DEF，请
判断该三角形的形状，并说明理由；
（3）如果点G是ED的中点，求证：FG⊥DE
【变式训练】
1、如图，点M是Rt△ABC斜边BC的中点，点P、Q分别在AB、AC上，且PM⊥QM．
（1）如图1，若P、Q分别是AB、AC的中点，求证：PQ2=PB2+QC2；
（2）如图2，若P、Q分别是线段AB、AC的动点（不与端点重合）（1）中的结论还成立吗？若成立请给与证明，若不成立请说明理由
2、问题发现：如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE．
（1）求证：△ACD≌△BCE；
（2）填空：∠AEB的度数为；
拓展探究：如图2，△ACB和△DCE均为等腰三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，点M 为AB的中点，连接BE、CM、EM，求证：CM=EM．
全等之三垂直（K型图）
例1 如图，已知AC⊥CF，EF⊥CF，AB⊥BE，AB=BE求证：AC=BF,BC=EF
1、如图，已知，AC⊥CF，EF⊥CF，AB⊥CE，AC=CF求证：AB=CE
G
E A
2、已知，AC ⊥CF ，EF ⊥CF ，AG ⊥CE ，AG=CE 求证：AG=CF
3、如图：已知，AE ⊥BD ，CD ⊥BD ，∠ABC=90°，AB=AC ，求证：AE=BD ，BE=CD
4、如图，点A 是直线在第一象限内的一点；连接OA ，以OA 为斜边向上作等腰直角三角形OAB ，若点A 的横坐标为4，则点B 的坐标为
5、已知：如图，点B,C,E 在同一条直线上，∠B=∠E=60°，∠ACF=60°，且AB=CE 证明：△ACB ≌△CFE
E
A
B
D C
G
E
A
60°
60°
60°
F
A
E
全等之手拉手模型
例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC （2） AE=DC
（3） AE 与DC 的夹角为60。

（4） △AGB ≌△DFB （5） △EGB ≌△CFB （6） BH 平分∠AHC （7） GF ∥AC
1、如果两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：（1） △ABE ≌△DBC （2） AE=DC
（3） AE 与DC 的夹角为60。

（4） AE 与DC 的交点设为H,BH 平分∠AHC
2、如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：（1）△ABE≌△DBC
（2）AE=DC
（3）AE与DC的夹角为60。

（4）AE与DC的交点设为H,BH平分∠AHC
3、如图，两个正方形ABCD和DEFG，连接AG与CE，二者相交于H
问：（1）△ADG≌△CDE是否成立？
（2）AG是否与CE相等？
（3）AG与CE之间的夹角为多少度？
（4）HD是否平分∠AHE？
4、如图两个等腰直角三角形ADC与EDG，连接AG,CE,二者相交于H. 问（1）△ADG≌△CDE是否成立？
（2）AG是否与CE相等？
（3）AG与CE之间的夹角为多少度？
（4）HD是否平分∠AHE？
5、两个等腰三角形ABD与BCE，其中AB=BD,CB=EB,∠ABD=∠CBE=a
连接AE与CD.
问（1）△ABE≌△DBC是否成立？
（2）AE是否与CD相等？
（3）AE与CD之间的夹角为多少度？（4）HB是否平分∠AHC？
钢架中的等腰三角形
例 1 如图钢架中，∠A=10°，焊上等长的钢条来加固钢架．若
AB=BC=CD=DE…一直作下去，那么图中这样的钢条至多需要根
1、如图钢架中，焊上等长的钢条P1P2，P2P3，P3P4，P4P5…至多需要8根加固钢架，若P1A=P1P2，则∠A= ．
2、如图钢架BAC中，焊上等长的钢条来加固钢架，若P1A=P1P2，量得
∠BP5P4=100°，则∠A=（）度．
A．10 B．20 C．15 D．25
3、如图钢架BAC中，焊上等长的钢条P1P2，P2P3，P3P4，P4P5来加固钢架，若P1A=P1P2，则∠A的取值范围．
4、如图钢架中，焊上等长的13根钢条来加固钢架，若
AP1=P1P2=P2P3=…=P13P14=P14A，则∠A的度数是。