第5章_对流换热的理论基础
第5章 对流传热理论与计算-5-实验关联式与自然对流

六 计算中需要注意的问题
3 注意的问题
(1)判断问题的性质
这是正确求解对流传热问题的关键。流体有无发生相 变?是自然对流还是强制对流?内部流动还是外部流动? 流态是层流还是湍流?
(2)选择正确的实验关联式
切忌张冠李戴,特别注意公式的适用范围,切不可随
意外推
40
六 计算中需要注意的问题
f w
0.14
2
33
(2) Hausen公式
若 Ref Prf
L /d
10时
Nuf
3.66
1
0.0668
0.04
Ref dL
Prf d L Ref Prf
2
3
可用于热入口段或混合段的层流对流传热
34
四 过渡区强迫对流传热的计算
过渡区:难以找到既简便又精确的计算公式
气体被加热时
气体被冷却时
c t
T T 0.55 fw
ct 1
对液体
m
c t
f w
m 0.11 液体受热时
m 0.25
液体被冷却时
24
引入修正系数ct来考虑不均匀物性场对换热的影响
Nu f
0.023
Ref0.8
Prfn
c t
气体被加热时
气体被冷却时
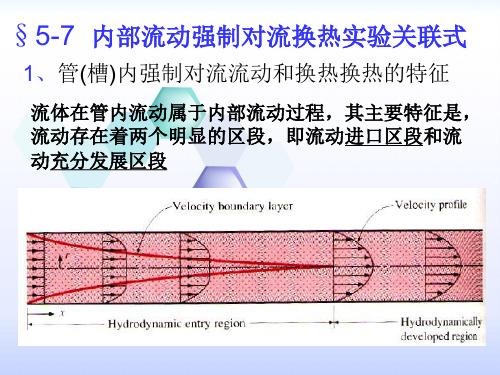
5.5 管内强迫对流传热的实验关联式
说明:
(1)管槽的含义:流动截面是圆形、椭圆形、正 方形、矩形、三角形等
(2)本节内容的重要性: ——指导工程计算的基础、给出的关联式是工程计算 的依据,必须掌握 ——考试的必考内容
传热学第五章_对流换热原理-6
2-2)管内流体平均温度
t f
c p tudf
f
c pudf
2 R 2um
R
turdr
0
f
其中,tf为根据焓值计算的截断面平均温度。
由热平衡方程
dQ hx (tw t f )x * 2R * dx cpumR2dt f
和
dQ q * 2R * dx
可得
dt f 2q 2hx (tw t f ) x
t
( tw t r tw t f
)rR
( r )rR tw t f
const
而同时又有
q
(
t r
)
r
R
h(t w
tf
)
于是,得
(
t r
)
r
R
h
const
tw t f
上式又表明,常物性流体在热充分发展段的一个特点是 换热系数保持不变。
另外,如果边界层在管 中心处汇合时流体流动 仍然保持层流,那么进 入充分发展区后也就继 续保持层流流动状态, 从而构成流体管内层流 流动过程。
若 Pr<1, 则意味着流动进口段长于热进口段; 1-3)管内流动充分发展段的流态判断
Re 2300 2300 Re 10 4 Re 10 4
层流 过渡流 旺盛湍流
2)管内流体平均速度与平均温度
2-1)管内流体运动平均速度
um
f udf 0f
2
R 2
R rudr V
0
f
其中,V-体积流量;f-管的截断面积;u-局部流速
dx c pum R
c pum R
积分上式可得全管长流体的平均温度。
由于热边界存在有均匀壁温和均匀热流两种典型情
传热学第5章

w
•t — 热边界层厚度 •与t 不一定相等
•边界层的传热特性: •在层流边界层内垂直于壁面方向上的热量传递主要依 靠导热。湍流边界层的主要热阻为层流底层的导热热阻 。
1对流换热
•层流:温度呈抛物线分 布•湍流:温度呈幂函数分 布
•湍流边界层贴壁处的温度 梯度明显大于层流
•故:湍流换热比层流换热强!
•边界层内:平均速度梯度很大;
•
y=0处的速度梯度最大
6对流换热
•由牛顿粘性定律:
•速度梯度大,粘滞应力大
•边界层外: u 在 y 方向不变化, u/y=0
•粘滞应力为零 — 主流区
•流场可以划分为两个区: •边界层区:N-S方程
•主流区: u/y=0,=0;无粘性理想流体;
•
欧拉方程
•——边界层概念的基本思想
•强迫对流换热 •自然对流换热
7对流换热
•
(2) 流动的状态 •层流 •:主要靠分子扩散(即导热)。
•湍流 •:湍流比层流对流换热强烈
•
(3) 流体有无相变
•沸腾换热 •凝结换热
8对流换热
• (4) 流体的物理性质
• 1)热导率,W/(mK), 愈大,对流换热愈强烈;
• 2)密度,kg/m3 • 3)比热容c,J/(kgK)。c反映单位体积流体热容
• 与 t 的关系:分别反映流体分子和流体微团的动量
•
和热量扩散的深度
•普朗特数
2对流换热
•综上所述,边界层具有以下特征:
•( • a) (b) 流场划分为边界层区和主流区。
•流动边界层:速度梯度较大,动量扩散主要区域。
•热边界层:温度梯度较大,热量扩散的主要区域
• (c) 流态:边界层分为层流边界层和湍流边界层 。湍流边界层分为层流底层、缓冲层与湍流核心。
传热学(第四版)第五章:对流传热的理论基础

温度边界层和速度边界层数值举例
空气,来流速度0.5 m/s 水,来流速度0.5 m/s
§5-2 对流传热与相似原理
1 问题的提出
能够得到理论解的对流传热问题非常少。试验是不可或缺 的手段,然而,经常遇到如下两个问题: h f (v, , c p , , , l ) (1) 变量太多 A 实验中应测哪些量(是否所有的物理量都测) B 实验数据如何整理(整理成什么样函数关系) (2) 实物试验很困难或太昂贵的情况,如何进行试验?
u
x
v
y
D D x x y y
(5)运动流体的能量守恒方程中引入了流场变量
第五章 对流换热
u和v 。
6
Navier-Stokes方程(1820年~1850年)
无因次化处理
预期解的形式
3 指导实验 • • 同名的已定特征数相等 单值性条件相似:初始条件、边界条件、几何条件、物理条件 实验中只需测量各特征数所包含的物理量,避免了测量的盲 目性——解决了实验中测量哪些物理量的问题 按特征数之间的函数关系整理实验数据,得到实用关联式 ——解决了实验中实验数据如何整理的问题 可以在相似原理的指导下采用模化试验 —— 解决了实物 试验很困难或太昂贵的情况下,如何进行试验的问题
厚度t 范围 — 热边界层 或温度边界层
t — 热边界层厚度
与t 不一定相等
第五章 对流换热 19
根据边界层理论,u v,
u v 0 x y u u u x v x v v u y v y
y x 简化对流传热问题如下:
Nusselt 1910年发表”管内换热理论解” Fourier 1822年发表“热的解析理论”
注册设备工程师辅导-传热学-对流换热部分

注册公用设备工程师执业资格考试基础课辅导传热学讲授:许淑惠教授北京建筑大学1对流换热部分2¾确定h的3 种基本方法1、分析法(理论分析方法)(1) 微分方程分析解(2) 积分方程分析解2、类比法(雷诺类比)(半经验方法)(经验方法)3、试验法(经验方法45一、影响对流换热的一般因素1)流动的起因和流动状态2)流体的热物理性质3)流体的相变4)换热表面几何因素(),,,,,,,,W f p h f u t t c l λραμ=¾流动边界层的几个重要特性:1)边界层很薄,其厚度与壁的定型尺寸相比是极小的;2)在边界层内存在较大的速度梯度;3)边界层流态分为层流与紊流,紊流边界层紧靠壁面处将是层流,称层流底层;4)流场可划分为主流区和边界层区,只有在边界层内才显示流体粘性的影响。
819•速度场相似:对应速度成比例,为速度场相似倍数•稳态温度场相似:空间对应点上过余温度成比例,为温度场相似倍数第六节相似理论基础一、几何相似二、物理现象相似6-1 基本概念1)几何相似:存在为几何相似倍数l C 物理量相似:Cu C θ20(1)为温度场相似倍数;(2)为时间相似倍数。
C θC τ表示物理量相似。
,,,,,l u C C C C C C τθλν•非稳态温度场相似:空间对应点上过余温度成比例:因此当等物理量相似是物理现象相似的前提条件。
•物理相似(物理现象相似)影响物理现象的所有物理量场分别相似的综合,就构成了物理现象相似。
注意三点:(1)必须是同类现象才能谈相似;(2)物理量场的相似倍数间有特定的制约关系,体现这种制约关系,是相似原理的核心;(3)注意物理量的时间性和空间性。
216-2 相似原理•相似原理的三点表述:A.相似性质;B.相似准则间的关系;C.判断相似的条件。
一、相似性质相似性质:彼此相似的现象,它们的同名相似准则必定相等。
=Nu Nu'''=Re'Re''Pr'=Pr'''=''Gr Gr2627二、相似准则间的关系(Re,Pr,)Nu f Gr =(Re,Pr)Nu f =(Re)Nu f =(,Pr)Nu f Gr =4. 自然对流换热,其准则关联式:1、无相变受迫稳态对流换热,且当自然对流不可忽略时,准则关联式:2、无相变受迫稳态对流换热,若自然对流可以忽略不计时,准则关联式:3、对于空气,Pr 可以作为常数,无相变受迫稳态对流换热,准则关联式:Re nNu C =()Pr n Nu C Gr =Re Pr n m Nu C =三、判断相似的条件•判断现象是否相似的条件,满足:A.凡同类现象;B.单值性条件相似;C.同名的相似准则相等。
传热学第五章对流换热

1.流动边界层(Velocity boundary layer )
如果流体为没有粘性流体,流体流过平板时,流速在截 面上一直保持不变。 如果流体为粘性流体,情况会如何呢?我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上, 即y方向上,壁面上速度为零,随着y方向的增加,流速 急剧增加,到达一薄层后,流速接近或等于来流速度, 德国科学家普朗特L.Prandtl研究了这一现象,并且在 1904年第一次提出了边界层的、分类 三、对流换热的机理 四、影响因素 五、研究方法 六、h的物理意义
一.定义
流体流过与其温度不同的固体表面时所发生的热量交换称为 对流换热。 对流换热与热对流不同, 既有热对流,也有导热; 不是基本传热方式。 对流换热遵循牛顿冷却定律:
qw tw
x
y
t∞
u∞
图5-1 对流换热过程示意
圆管内强制对流换热 其它形式截面管道内的对流换热 外掠平板的对流换热 外掠单根圆管的对流换热 外掠圆管管束的对流换热 外掠其它截面形状柱体的对流换热 射流冲击换热
外部流动
对 流 换 热
有相变
自然对流(Free convection) 混合对流 沸腾换热 凝结换热
大空间自然对流 有限空间自然对流
大容器沸腾 管内沸腾 管外凝结 管内凝结
λ ∂t 换热微分方程(描写h的本质,hx = − ∆t ( ∂y ) y =0 dA) 连续性方程(描写流体流动状态,即质量守恒) 动量微分方程(描写流动状态,即动量守恒) 能量微分方程(描写流体中温度场分布)
对流换热微分方程组 先作假设: (1)仅考虑二维问题; (2)流体为不可压缩的牛顿流体,稳定流动; (3)常物性,无内热源; (4)忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象,根据热力学第一定 律,对于这样一个开口系统,有:
传热学 第五章 对流原理.
层流边界层 紊流核心区
过渡区 紊流边界层 层流底层 主流区 速度边界层厚度 临界距离
层流
过渡流
湍流
u
y
x
xc
层流底层 缓冲层
根据流体力学知识,层流边界层厚度 xv 5x 5x 5 vf vf x Re x
在层流边界层内的速度分布线为抛物线型; 在紊流边界层内,层流底层部分的速度 分布较陡,接近于直线,而在底层以外 的区域,由于流体微团的紊流运动,动 量传递被强化了,速度变化趋于平缓。
如果流体的流动是由于流体冷热部分的密度不同 引起的浮升力造成的,则称为自然对流。暖气 片的散热,蒸汽或其他热流体输送管道的热量 损失,都与这类换热有关。 一般来讲:强迫对流 换热优于自然对流。
二、 在分析对流换热时,还应分清流体的流态。 流体力学告诉我们,流体受迫在流道内流 动时可以有两种不同性质的流态。流体分 层地平行于流道的壁面流动,呈现层流状 态。但当流动状态到超过某一临界值时, 流体的流动出现了旋涡,而且在不断地发 展和扩散,引起不规则的脉动,使流动呈 现紊流状态。
α =q/(tf-tw) W
对流换热系数 α表征着对流换热的强弱 。
在数值上,它等于流体和壁面之间的温度 差为 1℃时,通过对流换热交换的热流密 度。单位为W/(m2·℃)。 对流换热量以及相应的换热系数的大小,将 更多地取决于流体的运动性质和情况。
一、速度边界层
流体力学指出,具有粘性且能湿润固 体壁面的流体,流过壁面会产生粘性力。 根据牛顿粘性(内摩擦)定律,流体粘性 力 τ 与垂直于运动方程速度梯度 (dv/dy ) 成正比,即: τ=μ(dv/dy) N/m2 (5-2) 式中,μ 称为流体的动力粘度,单位为Pa· s 或kg/(m· s)。
传热学第五章_对流换热原理-1
Velocity = v Velocity = 0
Velocity Temperature
Boundary Boundary
Layer
Layer
HOT SURFACE, TEMP = TH
3. 热边界层厚度δt和流动边界层厚度δ的区 别与联系
(2) 边界层产生原因:
由于粘性的作用,流体与 壁面之间产生一粘滞力, 粘滞力使得靠近壁面处的 速度逐渐下降,最后使壁 面上的流体速度降为零, 流体质点在壁面上产生一 薄层。随着流体的流动, 粘滞力向内传递,形成的 薄层又阻碍邻近流体层中 微粒运动的作用,依此类 推,形成的薄层又阻碍邻 近流体层微粒运动,到一 定程度,粘滞力不再起作 用。
➢ 如果流体为粘性流体,情况会如何呢?我们用一测速仪来 测量壁面附近的速度分布。测量发现在法向方向上,即y 方向上,壁面上速度为零,随着y方向的增加,流速急剧 增加,到达一薄层后,流速接近或等于来流速度,普朗特 研究了这一现象,并且在1904年第一次提出了边界层的概 念。
普朗特在仔细观察了粘性流体流过固体表面的特性后提出了 突破性的见解。他认为,粘滞性起作用的区域仅仅局限在 靠近壁面的薄层内。在此薄层以外,由于速度梯度很小粘 滞性所造成的切应力可以略而不计,于是该区域中的流动 可以作为理想流体的无旋流动。这种在固体表面附近流体 速度发生剧烈变化的薄层称为流动边界层(又称速度边界 层).图5—5示出了产生流动边界层的两种常见情形。如 图5—5a所示,从y=o处u=0开始,流体的速度随着离开 壁面距离y的增加而急剧增大,经过一个薄层后u增长到接 近主流速度。这个薄层即为流动边界层,其厚度视规定的 接近主流速度程度的不同而不同。通常规定达到主流速度 的99%处的距离y为流动边界层的厚度,记为δ 。
传热学5
分析 解法
采用数学分析求解的方法。
传热学 Heat Transfer
2.如何从获得的温度场来计算h 无论是分析解法还是数值法首先获得都是温度场, 如何由T→h? t q 由傅里叶定律 w y
y 0
牛顿冷却公式
q w qc
qc h t w t
y
主流区
u∞
d 5 .0 离开前缘x处的边界层厚度 x Re x
局部表面传热系数
1/ 2 1/ 3 hx 0.332 Re x Pr x hx x 0.332 Re x1/ 2 Pr 1/ 3 Nu x 努塞尔数
(特征数方程,关联式)
u x 雷诺数: Re x 5 Re Re 5 10 关联式适用范围: c
25/42
传热学 Heat Transfer
1.数量级分析方法的基本思想 分析比较方程中等号两侧各项的数量级大小,在 同一侧内保留数量级大的项而舍去数量级小的项 2.实施方法 ①列出所研究问题中几何变量及物理变量的数量 级的大小,一般以1表示数量级大的物理量的量级。 以Δ表示小的数量级 ②导数中导数的数量级由自变量及因变量的数量 级代入获得
2t t t 2t c p u x v y x 2 y 2
28/42
传热学 Heat Transfer
5.4流体外掠平板传热层流 分析解及比拟理论
29/42
传热学 Heat Transfer
一、外掠等温平板层流流动下对流换热问 题的分析解
u v 0 x y
u u u p 2u 2u ( u v ) Fx ( 2 2 ) x y x x y v v v p 2v 2v ( u v ) Fy ( 2 2 ) x y y x y
第五章对流换热
第五章对流换热思考题1、在对流换热过程中,紧靠壁面处总存在一个不动的流体层,利用该层就可以计算出交换的热量,这完全是一个导热问题,但为什么又说对流换热是导热与对流综合作用的结果。
答:流体流过静止的壁面时,由于流体的粘性作用,在紧贴壁面处流体的流速等于零,壁面与流体之间的热量传递必然穿过这层静止的流体层。
在静止流体中热量的传递只有导热机理,因此对流换热量就等于贴壁流体的导热量,其大小取决于热边界层的厚薄,而它却受到壁面流体流动状态,即流动边界层的强烈影响,故层流底层受流动影响,层流底层越薄,导热热阻越小,对流换热系数h也就增加。
所以说对流换热是导热与对流综合作用的结果。
2、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
3、由对流换热微分方程知,该式中没有出现流速,有人因此得出结论:表面传热系数h与流体速度场无关。
试判断这种说法的正确性?答:这种说法不正确,因为在描述流动的能量微分方程中,对流项含有流体速度,即要获得流体的温度场,必须先获得其速度场,“流动与换热密不可分”。
因此表面传热系数必与流体速度场有关。
4、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
5、对管内强制对流换热,为何采用短管和弯管可以强化流体的换热?答:采用短管,主要是利用流体在管内换热处于入口段温度边界层较薄,因而换热强的特点,即所谓的“入口效应”,从而强化换热。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 影响流态,速度分布,温度分布。
热热面面朝朝上上
d 管内流动
热热面面朝朝下下
外 外部 部绕绕流流
影响对流换热的因素:
h f (u, tw , t f , , , c p , , , l, )
➢ 对强迫对流换热:
h f (u, tw , t f , , , cp , 浮, l,升力) 项包含的因子
✓ 首先确定:u ~ 0(1), t ~ 0(1), l ~ 0(1), ~ 0(1)
✓ 从而: ~ 0( ), t ~ 0( ), x ~ 0(1), y ~ 0( )
✓ 且:u ~ 0(1), t ~ 0(1), v ~ 0(1), v ~ 0( ), t ~ 0( 1 )
x
x
y
y
p ~ 0(1), p ~ 0( ), ~ 0( 2 ), a ~ 0( 2 )
5.2 对流传热问题的数学描述
对流传热问题完整的数学描述:
对流传热微分方程组 + 定解条件
质量守恒方程 动量守恒方程 能量守恒方程
假设: • 二维对流换热;
• 流体为不可压缩,牛顿流体; • 物性参数为常数,无内热源;
• 忽略粘性耗散产生的耗散热。
u
y
5.2.1 对流传热的微分方程组
1. 连续性方程
2. 对流换热: 流体流过另一个物体表面时,
流动方向 u∞
tf
对流和导热联合起作用的热量传递现象。
u
t
tw
Φ
wall
平平壁壁表上面的的对传流热换机理热
3. 牛顿冷却公式
式中:
Ah(t w t f ) q h(tw t f ) ht
✓ h —固体表面的平均表面换热系数。
✓ tw — 固体表面的平均温度。
x
y
连续性方程:
u v 0 x y
数量级分析
11
动量微分方程:
u u v u 1 p ( 2u 2u )
x y
x
x 2 y 2
11 1
11
2(1
1
2)
u v v v 1 p ( 2v 2v )
x y
y
x2 y 2
1 1 1 2 ( 1 )
能量微分方程:
✓ tf — 流体温度。
• 外部绕流(外掠平板,圆 管)tf 为流体的主流温度。
• 内部流动 (各种形状槽道内 的流动)tf 为流体的平均温度。
tf
d
外部外 绕部 流绕流
管内流动
4. 局部表面传热系数与平均表面传热系数 局部对流换热时局部热流密度:
qx hx (tw t f )x 整个换热物体表面的总对流换热量:
Fy
p y
(
2v x 2
2v y 2 )
c
p
(
t
u t x
v t ) ( 2t
y
x 2
2t ) y 2
含有未知量: u , v , p , t ,
适用条件:自然对流,强迫对流换热; 层流,湍流换热。
5.2.1 对流传热的定解条件
1. 几何条件:
对流换热表面的几何形状,尺寸,壁面与 流体的相对位置,壁面粗糙度。
➢ 对自然对流换热:
h f (, , c p , , l,,t)
定性 用来确定物性参数数值的温度。 温度 例如:流体的平均温度;
流体与壁面温度的算术平均值等。
代表几何因素对换热的影响。
特征 长度
例如:管内换热以内径为特征长度;
沿平板流动以流动方向的尺寸为特征长度等。
5.1.3 对流传热的研究方法
➢ 缓冲层 ➢ 湍流核心区
转戾点
外掠平板: Re c 5105
5.3.2 热边界层 (Thermal boundary layer)
1921年,波尔豪森提出。
热边界层厚度δt :
y u∞
t tw 0.99(t tw ) t∞
主流区
u∞
t∞
t
δ
u δt
温度场分区:
热边界层区:
0
热边界层
tw
x
v t ) ( 2t
y
x 2
2t ) y 2
对稳态,忽略重力场,二维强迫对流换热:
u v 0 x y
u
u x
v
u y
1
p x
(
2u x 2
2u y 2 )
u v v v 1 p ( 2v 2v )
x y
y
x2 y 2
u
t x
v
t y
2t a( x2
2t y 2 )
边界层内简化对流换热方程组介绍:
2u x 2
2u y 2 )
➢ y方向:
( v
u
v x
v
v ) y
Fy
p y
(
2v x 2
2v y 2 )
说明:只有重力场作用时
•强迫对流换热:忽略重力项; •自然对流换热:浮升力起重要作用。
3. 能量微分方程
根据微元体的能量守恒导出。
c
p
(
t
u t x
v
t y
)
(
2t x 2
2t y 2
液态金属0.05 气体0.6-0.8
油102-103
对常见流体,Pr范围 0.6—4000 之间。
边界层特点:
边界层厚度:δ<<l, x; δt<<l,x; 流场划分为边界层区和主流区; 边界层有层流边界层和湍流边界层, 湍流边界
层分为层流底层, 缓冲层和湍流核心区三层。 层流边界层和层流底层,热量传递主要靠导热。湍流 边界层的主要热阻在层流底层。
2. 物理条件:
流体的物理性质(ρсλα), 有无内热源。
3. 时间条件: 对流换热过程进行的时间上的特点。
➢ 稳态换热:无初始条件
➢ 非稳态换热:初始时刻的速度场和温度场。
4. 边界条件:
说明对流换热边界上的状态(边界上速度分布,温度分布及与 周围环境之间的相互作用)。
第一类边界条件: 恒壁温边界条件
t w f ( x, y , z , )
t w const
第二类边界条件: 恒热流边界条件
q
w
(
t n
)
w
q w const
5.3 边界层对流传热问题的数学描写
5.3.1 流动边界层 1904年,德国科学家普朗特提出著名的边界层概念。
举例:流体平行外掠平板的强迫对流换热。
y u∞ tf
主流区 u∞
u∞ tf
u∞ uq
导热
0 层层流流边边界界层层
x
u∞
u
导热
q
管管内内层层流流流流动动
湍流 :
➢ 流体内部存在强烈脉动和旋涡运动;
➢ 各部分流体之间迅速混合; ➢ 热量传递:主要靠对流 。
湍流边界层
层流底层:导热 湍流核心区:对流
u∞ tf
主流区 u∞
δ
u
u∞
u 层流底层 q
0 层流边界层 过渡区 湍流边界层
导 热
hx
导热 热阻0 增大
扰动 表面传热系数
热阻 增大
x
普朗特准数Pr
定义: Pr
a
物理意义:
u∞y
u∞
t∞
δ
t∞
δt
u
t
0 层流边界层
tw
x
流体的动量扩散能力与热量扩散能力之比。
对层流边界层,若热边界层和流动边界层 从平板前缘点同时发展:
✓ 当 a, Pr 1 时, t ✓ 当 a, Pr 1 时, t ✓ 当 a, Pr 1 时, t
主流区:
➢ 速度梯度趋于零,粘性力忽略不计; ➢ 流体可近似为理想流体; ➢ 用理想流体的欧拉方程描述。
掠过平板时边界层的形成和发展:
➢层流边界层 ➢过渡区 ➢湍流边界层
y u∞ tf
主流区 u∞
δ
u
u∞
u 层流底层 q
0 层流边界层xc 过渡区 湍流边界层 l x
湍流边界层的三层结构模型:
➢ 层流底层
1. 分析法: 指对描写某一类对流传热问题的偏微分方程及定解
条件进行数学求解,从而获得速度场和温度场的分析解。 可得出精确解或近似解。适用简单问题。 2. 数值法:
对对流换热过程的特征和主要参数变化趋势作出预测。 3. 实验法;
相似原理和量纲分析理论。 4. 比拟法:
利用流体动量传递和热量传递的相似机理,建立 表面传热系数和阻力系数之间的相互关系。
根据微元体的质量守恒导出。
设速度分布:
➢ 二维流动:
V ui v j
u v 0 x y
2. 动量微分方程(Navier-Stokes方程)
根据微元体的动量守恒导出。
DV F grad p 2V D
惯性力 体积力 压力梯度 粘性力
➢ x方向:
( u
u
u x
v
u ) y
Fx
p x
(
u∞ u
δ
u
层流底层 q
0 层流边界层xc 过渡区 湍流边界层 l x
边界层特点 δ<< l
流场分区: 边界层区:
y u∞ tf
主流区 u∞
u∞ u
δ
u
层流底层 q
0 层流边界层xc 过渡区 湍流边界层 l x
➢ 速度梯度大,粘性力不能忽略;
➢ 粘性力与惯性力处同一数量级; ➢ 动量交换的主要区域,用动量微分方程描述。
常温下:水 cp 4186 kJ /(m3 C) 空气 cp 1.21kJ /(m3 C)
