限制玻尔兹曼机学习笔记整理
统计物理第二章
19
现在来比较一下系统的微观状态数目的对数与系统的熵 的表达式，以图得到熵常数S。
S是熵常数 对于定域系统 满足非经典极限条 件的非定域系统 对于定域系统， 取S＝0，有：
S k N ln N N U S
'
lnMB N ln N N U lnFD lnBE N U N
l l
最可几分布 满足的条件
对最可几分布所 对应的系统微观 N ln N 1 l ln l l ln l 1 l l 状态数目取对数， 得到了系统的微 l N ln N l ln l N 观状态数目的对 l l l 数与系统包含的 l N ln N l ln N ln N l l 粒子数、内能等 l l l 的关系式。 N ln N N U 18
U＝＝ e
－－
N＝ e－－
注意： 和 N 均由分布 直接计算 U
6
N e
l
l
e e
l
l
l
e
Z;
-
Z e l
U N lnZ N Y ln Z y
热量是热现象中特有的宏观量，与内能和广义力不同， 没有与热量相对应的微观量；熵本身是一个宏观统计 的结果，也没有与之对应的微观量。因此，不可能根 据分布直接计算得出。一个可行的办法是从热力学第 一、二定律出发，将内能和广义功的统计表达式进行 比较得到。
统计物理
第二章 玻尔兹曼统计
南京工业大学理学院 吴高建
完整版机械原理笔记
第一章平面机构的结构分析1.1研究机构的目的目的：1、探讨机构运动的可能性及具有确定运动的条件2、对机构进行运动分析和动力分析3、正确绘制机构运动简图1.2运动副、运动链和机构1、运动副:两构件直接接触形成的可动联接（参与接触而构成运动副的点、线、面称为运动副元素）低副：面接触的运动副（转动副、移动副），高副：点接触或线接触的运动副注：低副具有两个约束，高副具有一个约束2、自由度：构件具有的独立运动的数目（或确定构件位置的独立参变量的数目）3、运动链：两个以上的构件以运动副联接而成的系统。
其中闭链：每个构件至少包含两个运动副元素，因而够成封闭系统；开链：有的构件只包含一个运动副元素。
4、机构：若运动链中出现机架的构件。
机构包括原动件、从动件、机架。
1.3平面机构运动简图1、机构运动简图：用简单的线条和规定的符号来代表构件和运动副并按一定的比例表示各运动副的相对位置。
机构示意图：不按精确比例绘制。
2、绘图步骤：判断运动副类型，确定位置；合理选择视图，定比例讥绘图（机架、主动件、从动件）1.4平面机构的自由度1、机构的自由度：机构中各活动构件相对于机架的所能有的独立运动的数目。
F=3n - 2p L - p H （n指机构中活动构件的数目，p L指机构中低副的数目，p H指机构中高副的数目）自由度、原动件数目与机构运动特性的关系：1）：F W 0时，机构蜕化成刚性桁架，构件间不可能产生相对运动2）：F > 0时，原动件数等于F时，机构具有确定的运动；原动件数小于机构自由度时，机构运动不确定；原动件数大于机构自由度，机构遭到破坏。
2、计算自由度时注意的情况1 ）复合铰链：m个构件汇成的复合铰链包含m-1个转动副（必须是转动副，不能多个构件汇交在一起就构成复合铰链，注意滑块和盘类构件齿轮容易漏掉，另外机架也是构件。
2）局部自由度：指某些构件（如滚子）所产生的不影响整个机构运动的局部运动的自由度。
解决方法：将该构件焊成一体，再计算。
深度学习笔记 - RBM
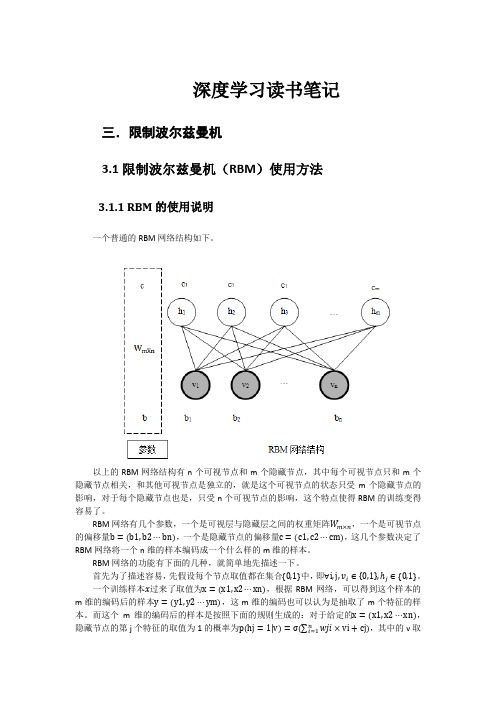
值就是 x，hj 的取值就是 yj，也就是说，编码后的样本 y 的第 j 个位置的取值为 1 的概率是 p(hj = 1|v)。所以，生成 yj 的过程就是：
i）先利用公式p(hj = 1|v) = σ(∑������������=1 ������������������ × vi + cj)，根据 x 的值计算概率p(hj = 1|v)，其 中 vi 的取值就是 xi 的值。
3.3.2 从能量最小到极大似然
上面我们得到了一个样本和其对应编码的联合概率，也就是得到了一个 Gibbs 分布，我 们引人概率的目的是为了方便求解的。但是我们实际求解的目标是能量最小。
下面来看看怎么从能量最小变成用概率表示。内容是来自《神经网络原理》那本书。 在统计力学上的说法也是——能量低的状态比能量高的状态发生的概率高。 定义一个叫做自由能量的东西，是从统计力学来的概念，
变量之间的相关程度决定了能量的高低。把变量的相关关系用图表示出来，并引入概率测度
方式就构成了概率图模型的能量模型，其实实际中也可以不用概率表示，比如立体匹配中直
接用两个像素点的像素差作为能量，所有像素对之间的能量和最小时的配置即为目标解。
RBM 作为一种概率图模型，引入概率就是为了方便采样，因为在 CD（contrastive divergence）算法中采样部分扮演着模拟求解梯度的角色。
RBM 网络有几个参数，一个是可视层与隐藏层之间的权重矩阵������������×������，一个是可视节点 的偏移量b = (b1, b2 ⋯ bn)，一个是隐藏节点的偏移量c = (c1, c2 ⋯ cm)，这几个参数决定了 RBM 网络将一个 n 维的样本编码成一个什么样的 m 维的样本。
其中E������表示系统在状态 i 时的能量，T 为开尔文绝对温度，������B为 Boltzmann 常数，Z 为与 状态无关的常数。
元胞自动机的学习和整理笔记
元胞自动机的学习和整理可以模拟热传导，交通问题等一些东西。
离散抽象成格子。
按照某种规则转划元胞状态。
邻居的定义不一样。
一个元胞的状态随着其他状态改变。
生命游戏是二维的。
等效于通用图灵机。
空气流动的例子。
格子气自动机。
三角形网格（SHP）比正方形好。
用于模拟流体不好在噪声太大。
玻尔兹曼方程可以改进。
（玻尔兹曼方程？？？）环岛和上飞机的问题需要用到。
交通流可以看成流体。
堵车点会移动（用连续方程->各项异形，前面影响后面）。
NS模型。
暂时不考虑倒车的事情。
车以尽量大的速度前进。
N-S模型的假设。
车的速度。
前进，加速，减速和随机变化。
运动的车速度是随机变化。
N-S模型简单。
数据模拟。
N-S模拟数据的模拟。
改进方法。
没听清概率p常数。
另一个问题，烤盘外面热里面凉。
圆利用率不好。
热传导的过程（方程）把空间分成格子（每一个格子都不同）元胞自动机的规范：时间对元胞都是同步的。
变化率和时间呈正比。
有点没听清。
与导热率还有一些关系。
C语言的伪代码分配三维数组释放数组主函数，遍历每一个元胞对数据进行修改。
下一个循环有一些问题画示意图就行了。
边界条件。
灵敏度分析是某种算法，对输入的值有一点点改变，输出有没有改变。
最重要的功能就是仿真。
有些东西就是实验。
交通流随机的。
/f/9420003.html?from=dl&sudaref=www.bai &retcode=0参考书籍。
MKXZ工具与方法基本工作手册
MKXZ工具与方法基本工作手册MKXZ（Multiple Kernelized Extreme Learning Machine）是一种基于多核极限学习机的机器学习方法，它可以用于解决多类别分类和回归问题。
本文将介绍MKXZ工具与方法的基本工作手册，包括算法原理、使用方法和实例分析等内容。
一、算法原理1.1 多核极限学习机（MKELM）简介多核极限学习机是一种基于极限学习机（ELM）的机器学习方法，它主要使用随机生成的隐藏层权重和偏置来建立神经网络模型。
MKELM通过使用多个核函数来提高模型的学习能力和泛化能力。
1.2 多核化的极限学习机（MKXELM）简介多核化的极限学习机是在MKELM的基础上发展而来的方法，它通过将样本数据映射到高维空间中，然后在高维空间中进行学习和分类。
MKXELM通过使用多个核函数和核权重来融合不同的核特征，并构建高性能的分类模型。
1.3 MKXZ（Multiple Kernelized Extreme Learning Machine）简介MKXZ是一种基于MKXELM的机器学习方法，它通过使用多个核函数和核矩阵来构建高性能的分类模型。
MKXZ在MKELM的基础上引入了正则化项和粒子群优化算法，可以进一步提高模型的泛化性能和稳定性。
二、使用方法2.1 数据预处理首先，需要对原始数据进行预处理，包括数据清洗、特征选择、数据缩放等步骤。
可以使用pandas和numpy等库来进行数据处理，确保数据的准确性和一致性。
2.2 模型初始化在使用MKXZ之前，需要初始化模型的参数，包括隐藏层节点数、核函数类型、正则化系数等。
可以使用sklearn库中的ELMRegressor和ELMClassifier来初始化模型，并选择合适的参数。
2.3 数据划分将预处理后的数据划分为训练集和测试集，通常使用交叉验证的方式来划分数据集。
可以使用sklearn库中的train_test_split函数来随机划分数据集，并设置训练集和测试集的比例。
受限玻尔兹曼机详细讲解PPT
– Repeat for all data vectors in the training set. • Negative phase
– Do not clamp any of the units – Let the whole network reach thermal equilibrium at a
temperature of 1 (where do we start?)
– Sample si s j for all pairs of units
– Repeat many times to get good estimates • Weight updates
– Update each weight by an amount proportional to the difference in sis j in the two phases.
– This is a big advantage over directed belief nets
hidden j
i visible
Maximizing the training data log
likelihood
Standard PoE form
•
We want maximizing parameters
• Can observe some of the variables and we would like to solve two problems:
• The inference problem: Infer the states of the unobserved variables.
热力学与统计物理第五章知识总结
§5.1 热力学量的统计表达式我们根据Bolzman分布推导热力学量的统计表达式一、配分函数粒子的总数为令（1）名为配分函数，则系统的总粒子数为（2）二、热力学量1、内能（是系统中粒子无规则运动的总能量的统计平均值）由（1）（2）得（3）此即内能的统计表达式2、广义力，广义功由理论力学知取广义坐标为y时，外界施于处于能级上的一个粒子的力为则外界对整个系统的广义作用力y为（4）此式即广义作用力的统计表达式。
一个特例是（5）在无穷小的准静态过程中，当外参量有dy的改变时，外界对系统所做的功为（6）对内能求全微分，可得（7）（7）式表明，内能的改变分为两项：第一项是粒子的分布不变时，由于能级的改变而引起的内能变化；地二项是粒子能级不变时，由于粒子分布发生变化而引起的内能变化。
在热力学中我们讲过，在无穷小过程中，系统在过程前后内能的变化dU等于在过程中外界对系统所作的功及系统从外界吸收的热量之和：（8）与（6）（7）式相比可知，第一项代表在准静态过程中外界对系统所作的功，第二项代表在准静态过程中系统从外界吸收的热量。
这就是说，在准静态过程中，系统从外界吸收的热量等于粒子在其能级上重新分布所增加的内能。
热量是在热现象中所特有的宏观量，它与内能U和广义力Y不同。
3、熵1）熵的统计表达式由熵的定义和热力学第二定律可知（9）由和可得用乘上式，得由于引进的配分函数是，的函数。
是y的函数，所以Z是，y的函数。
LnZ的全微分为：因此得（10）从上式可看出：也是的积分因子，既然与都是的积分因子，我们可令（11）根据微分方程关于积分因子的理论，当微分式有一个积分因子时，它就有无穷多个积分因子，任意两个积分因子之比是S的函数（dS是用积分因子乘微分式后所得的全微分）比较（9）、（10）式我们有积分后得（12）我们把积分常数选为零，此即熵的统计表达式。
2）熵函数的统计意义由配分函数的定义及得由玻耳兹曼分布得所以（13）此式称为Boltzman关系，表明某宏观状态的熵等于玻耳兹曼k乘以相应的微观状态数的对数。
《第七章 玻耳兹曼统计》小结汇总
《第七章 玻耳兹曼统计》小结一、基本概念： 1、1>>αe 的非定域系及定域系遵守玻耳兹曼统计。
2、经典极限条件的几种表示：1>>αe ；12232>>⎪⎭⎫ ⎝⎛⋅h mkT NVπ;mkTh N V π231>>⋅⎪⎭⎫⎝⎛;()λ>>⋅31n3、热力学第一定律的统计解释：Q d W d dU += l ll l ll da d a dU ∑∑+=εεl ll d a W d ε∑=l ll da Q d ∑=ε即：从统计热力学观点看，做功：通过改变粒子能量引起内能变化；传热：通过改变粒子分布引起内能变化。
二、相关公式1、非定域系及定域系的最概然分布le a l l βεαω--=2、配分函数： 量子体系：∑-=llleβεω1Z∑---==ll l l l ll le e e a βεβεβεωωωNZ N 1半经典体系：()r rr p q r h dp dp dp dq dq dq e h d e l2121,1Z ⎰⎰⎰==-βεβεω 经典体系：()rrr p q r h dp dp dp dq dq dq e h d e l2121,01Z ⎰⎰⎰==-βεβεω 3、热力学公式（热力学函数的统计表达式） 内能：β∂∂=1lnZ -NU物态方程：VlnZ N1∂∂=βp定域系：自由能：1-NkTlnZ F = 熵：B M k .ln S Ω=或⎪⎪⎭⎫⎝⎛∂∂-=ββ11lnZ ln Nk S Z1>>αe 的非定域系（经典极限条件的玻色(费米)系统）： 自由能：!ln -NkTlnZ F 1N kT += 熵：!ln kln S .N k BM Ω=Ω=或!ln lnZ ln Nk S 11N k Z -⎪⎪⎭⎫⎝⎛∂∂-=ββ三、应用： 1、求能量均分定理①求平均的方法要掌握：()dx x xp ⎰=x②能量均分定理的内容---能量均分定理的应用：理想气体、固体、辐射场。
有限元法笔记
【有限元法】《有限元法在电磁场计算中的应用》 电势与磁势表示的电磁场：B A =∇⨯ A tφμε∂∇=-∂ 222AA J t μεμ∂∇-=-∂222t φρφμεε∂∇-=-∂拉普拉斯方程：220A C φ∇=∇= 泊松方程： 22A Jρμφε∇=-∇=【边界条件】 三种边界条件：1、 狄里克莱（Dirichlet ）边界条件 ()11|g φΓ=Γ其中，1Γ为狄里克莱边界，()1g Γ为位置的一般函数。
特殊情况可以为常数或为0； 2、 诺伊曼边界条件()()2222h nφσφΓΓ∂+Γ=Γ∂其中，2Γ表示诺伊曼边界，n 为边界的外向法向矢量，()2σΓ和()2h Γ为一般函数，特殊情况下可以为常数或为0。
【二阶空间微分算子】£22222=a b,,,,c F x y xx yzx y φφφφφφφ⎛⎫∂∂∂∂∂ℜ+++ ⎪∂∂∂∂∂∂⎝⎭其中，F 表示一个一般函数关系，a,b,c 为位置（即x,y ）的一般函数。
根据a,b,c 的关系，又分为如下的方程： 椭圆方程： 24b ac < 双曲方程： 24b ac > 抛物线方程： 24b ac =【加权余数法】加权余数法是在确定近似解函数待定系数的一种方法。
用一组简单函数的组合来逼近微分方程的精确解，会带来一组待定系数，如何确定系数便决定了求解方法。
精确解是一个未知量，很难求得，加权余数法就是要找出近似解所带来的误差，并使之最小化，从而求出近似解。
【加权余数法的余数】定义为近似解和精确解之间在边界上和区域Ω内施加拉普拉斯算子作用之后的误差。
即：22221ni ii R C φφφφΩ==∇-∇=∇=∇∈Ω∑()()()1n i i i R C g φφφΓ=Γ⎡⎤=Γ-Γ=Γ-∈Γ⎢⎥⎣⎦∑其中，φ为近似解，i φ为尝试函数，i C 为待定系数。
g 为边界值。
通常情况下，余数R Ω和R Γ不为0。
但，我们通常可以选取适当的系数i C ，使余数的平均值或积分值为0。
中科院半导体所考研固体物理复习汇总
中科院半导体所考研固体物理复习汇总
（ 2012 考生自我总结版）
欢迎发邮件至 jiazhiwei008@或联系 QQ376588039共同探讨学习
2012 ‐ 2 ‐ 5 间的考研复习，终于结束这段压抑的时光。成绩还没有出来， 总感觉不是那么理想，回想一下这半年，确实也没有付出那么多努力，终给人 生留下一些遗憾。 在复习过程中，自认为最为失败的就是专业课《固体物理》，自己的懒惰 和盲目是主要原因，但没有系统学习过这门课程以及复习资料的混乱也算是比 较重要的原因，遂趁闲暇时间按照自己粗浅的见识将复习资料整理一下，以备 今后更好的学习，也供后来人参考。考试之后最大的感觉就是遗憾，好多本来 并不是不会的题没有能够给出正确的答案，原因就在于没有大量练习而不够熟 练，希望读者能够引以为鉴。 本文档大部分为前人工作成果，在此引用无丝毫盗用之心，只是希望通过 我们共同的努力使学习的过程更为轻松，思路更为清晰。本人水平极为有限， 有何不妥之处， 请发邮件至 jiazhiwei008@或联系 QQ376588039共同探讨 学习，在此表示由衷的感谢。
热膨胀热传导5中子的非弹性散射测声子能谱五能带理论1布洛赫定理2近自由电子模型3紧束缚近似4费密面能态密度和能带的特点六晶体中电子在电场和磁场中的运动考研路上永不言弃1恒定电场作用下电子的运动考研路上永不言弃2用能带论解释金属半导体和绝缘体以及空穴的概念3恒定磁场中电子的运动4回旋共振德哈斯范阿尔芬效应七金属电子论1金属自由电子的模型和基态性质2金属自由电子的热性质3电子在外加电磁场中的运动漂移速度方程霍耳效应二考试要求一晶体结构了解x射线衍射条件基元的几何结构因子及原子形状因子二固体的结合理解离子性结合共价结合金属性结合范德瓦尔斯结合等概念三晶体中的缺陷和扩散大致了解离子晶体中的点缺陷和离子性导电四晶格振动与晶体的热学性质熟练掌握并理解其物理过程要求能灵活应用
Chapter 7 玻耳兹曼统计
y
S Nk (ln Z1 ln Z1 ) k ln N ! (7.1.13) M.B. S k ln (7.1.15) F NkT ln Z1 kT ln N !(7.1.16) N!
因此，只要能确定配分函数Z1就可求出基本热力学函数 内能、物态方程和熵，从而确定系统的全部平衡性质。
二、满足经典极限条件的玻色(费米)系统 Z1 l e l N e Z1 U N ln Z1 Y N ln Z1
满足经典极限条件的玻色（费米）系统的微观状态 数 B.E. F.D. M.B. / N ! 。若要玻耳兹曼关系仍然成 立，须将熵的统计表达式、玻耳兹曼关系和自由能改为
第七章 玻耳兹曼统计 目 录
曲 靖 师 范 学 院 物 理 与 电 子 工 程 学 院
§7.1 §7.2 §7.3 §7.4 §7.5 §7.6 §7.7 §7.8 §7.9
热力学量的统计表达式 理想气体的物态方程 麦克斯韦速度分布律 能量均分定理 理想气体的内能和热容量 理想气体的熵 固体热容量的爱因斯坦理论 顺磁性固体* 负温度状态*
dW / dy
l l 1 l Y al l e e ( ) l e l y l l y l y N 1 N ( ) Z1 = ln Z1 (7.1.6) Z1 y y
4
第七章 玻耳兹曼统计 §7.1 热力学量的统计表达式
所以S 可表示为：
5. 玻耳兹曼关系 a N e Z (7.1.3) ln Z1 ln N U N ln Z1 1
S k N ln N al lnl al lnal (7.1.14) 10 l l
受限玻尔兹曼机RBM
果小磁针方向与外场方向一致，则能量也会降低。我们定义总能量：
Esi J
i , j
s s
i
j
H si
i
N
其中J为一个能量耦合常数，E{si}表示系统处于状态组合{si}下的总 能量。求和下标表示对所有相邻的两个小磁针进行求和。我们看到， 如果si=sj，则总能量就会减少J。H表示外界磁场的强度,它是一个参 数，如果外界磁场向上H为正，否则为负。如果某个小磁针的方向与 外场一致，则总能量减少一个单位。
经元处于断开状态。
玻尔兹曼机
• 结构
能量函数定义为：
根据规则，如果与神经元i相 邻的所有神经元都激活，并且 它们的连接权重为正的话，那 么该神经元就有可能被激活。 这就相当于最小化一个全局的 能量函数。
受限玻尔兹曼机（RBM）
• 简介
Smolensky提出的RBM由一个可见神经元层和一个隐神经 元层组成，由于隐层神经元之间没有相互连接并且隐层神经元独立于 给定的训练样本，这使直接计算依赖数据的期望值变得容易，可见层 神经元之间也没有相互连接，通过从训练样本得到的隐层神经元状态 上执行马尔可夫链抽样过程，来估计独立于数据的期望值，并行交替 更新所有可见层神经元和隐层神经元的值。
以认为是抽取了m个特征的样本。
受限玻尔兹曼机
• 结构（续） 隐藏节点的第j个特征的取值为1的概率为
p(h j 1 v) (i 1 w jivi c j )
n
其中的v取值就是x，hj的取值就是yj。且，
受限玻尔兹曼机
• 结构（续）
生成yj的过程就是： 1.先利用公式
p(h j 1 v) (i 1 w jivi c j )
PHOENICS中文教程
目录 ..................................................................................................................................................... 1 1 简介.............................................................................................................................................. 5 1.1 1.2 1.3 FLAIR 是什么 ? .................................................................................................................. 5 FLAIR 可以做些什么？ ...................................................................................................... 8 FLAIR 组成部分以及 PHOENICS 的关系 ........................................................................ 9 FLAIR 模块 .................................................................................................................. 9 FLAIR 与 PHOENICS 的关系..................................................................................... 9 用户接口功能 (In-Form) ............................................................................................. 9 自动收敛控制 ............................................................................................................. 10 PARSOL 技术............................................................................................................ 10 嵌套网格 .................................................................................................................... 11 LVEL 湍流模型 ......................................................................................................... 12 IMMERSOL 辐射模型 .............................................................................................. 12
(完整版)DeepLearning(深度学习)学习笔记整理系列
Deep Learning（深度学习）学习笔记整理系列目录：一、概述二、背景三、人脑视觉机理四、关于特征4.1、特征表示的粒度4.2、初级（浅层）特征表示4.3、结构性特征表示4.4、需要有多少个特征？五、Deep Learning的基本思想六、浅层学习（Shallow Learning）和深度学习（Deep Learning）七、Deep learning与Neural Network八、Deep learning训练过程8.1、传统神经网络的训练方法8.2、deep learning训练过程九、Deep Learning的常用模型或者方法9.1、AutoEncoder自动编码器9.2、Sparse Coding稀疏编码9.3、Restricted Boltzmann Machine(RBM)限制波尔兹曼机9.4、Deep BeliefNetworks深信度网络9.5、Convolutional Neural Networks卷积神经网络十、总结与展望十一、参考文献和Deep Learning学习资源接上注：下面的两个Deep Learning方法说明需要完善，但为了保证文章的连续性和完整性，先贴一些上来，后面再修改好了。
9.3、Restricted Boltzmann Machine (RBM)限制波尔兹曼机假设有一个二部图，每一层的节点之间没有链接，一层是可视层，即输入数据层（v)，一层是隐藏层(h)，如果假设所有的节点都是随机二值变量节点（只能取0或者1值），同时假设全概率分布p(v,h)满足Boltzmann 分布，我们称这个模型是Restricted BoltzmannMachine (RBM)。
下面我们来看看为什么它是Deep Learning方法。
首先，这个模型因为是二部图，所以在已知v的情况下，所有的隐藏节点之间是条件独立的（因为节点之间不存在连接），即p(h|v)=p(h1|v)…p(h n|v)。
半导体器件物理I复习笔记
半导体器件物理I复习笔记This model paper was revised by the Standardization Office on December 10, 2020半一复习笔记By 潇然平衡PN结的定性分析1. pn结定义：在一块完整的半导体晶片（Si、Ge、GaAs等）上，用适当的掺杂工艺使其一边形成n型半导体，另一边形成p型半导体，则在两种半导体的交界面附近就形成了pn结2. 缓变结：杂质浓度从p区到n区是逐渐变化的，通常称为缓变结3. 内建电场：空间电荷区中的这些电荷产生了从n区指向p区，即从正电荷指向负电荷的电场4. 耗尽层：在无外电场或外激发因素时，pn结处于动态平衡，没有电流通过，内部电场E为恒定值，这时空间电荷区内没有载流子，故称为耗尽层平衡PN结的定量分析1. 平衡PN结载流子浓度分布2. 耗尽区近似：一般室温条件，对于绝大多部分势垒区，载流子浓度比起N区和P区的多数载流子浓度小的多，好像已经耗尽了，此时可忽略势垒区的载流子，空间电荷密度就等于电离杂质浓度，即为耗尽区近似。
所以空间电荷区也称为耗尽区。
在耗尽区两侧，载流子浓度维持原来浓度不变。
理想PN结的伏安特性（直流）1. 理想PN结：符合以下假设条件的pn结称为理想pn结(1) 小注入条件—注入的少数载流子浓度比平衡多数载流子浓度小得多；Δn<n0, Δp<p0,(2) 突变耗尽层条件—外加电压和接触电势差都降落在耗尽层上，耗尽层中的电荷是由电离施主和电离受主的电荷组成，耗尽层外的半导体是电中性的。
(3) 通过耗尽层的电子和空穴电流为常量，不考虑耗尽层中载流子的产生及复合作用；(4)玻耳兹曼边界条件—在耗尽层两端，载流子分布满足玻耳兹曼统计分布。
2. 理想pn结模型的电流电压方程式（肖特来方程式）：产生-复合电流1. 反偏PN结的产生电流2. 正偏PN结的复合电流理想PN结交流小信号特性1. 扩散电阻2. 扩散电容势垒电容在考虑正偏时耗尽层近似不适用的情况下，大致认为正偏时势垒电容为零偏时的四倍，即扩散电容定义：正偏PN结内由于少子存储效应而形成的电容PN结的瞬态PN结击穿1. 雪崩击穿(1) 定义：在反向偏压下，流过pn结的反向电流，主要是由p区扩散到势垒区中的电子电流和由n区扩散到势垒区中的空穴电流所组成。
模拟集成电路设计复习笔记
模集复习笔记By 潇然2018.6.202.2 I/V特性1. I-V特性2. 跨导定义：V GS对I DS的控制能力（I DS对V GS变化的灵敏度）饱和区跨导gm表达式：2. 线性电阻表达式2.3 二级效应1. 体效应γ为体效应系数，典型值0.3-0.4V-1/22. 沟道长度调制效应2.4 MOS器件模型定义：信号相对于偏置工作点而言比较小、不会显著影响偏置工作点时用该模型简化计算由gm、gmb、r O等构成低频小信号模型，高频时还需加上C GS等寄生电容、寄生电阻（接触孔电阻、导电层电阻等）1. MOS小信号模型①沟长调制效应引起的输出电阻②体效应跨导2. 完整的MOSFET小信号模型用于计算各节点时间常数、找出极点2.5 放大器的性能参数AIC设计的八边形法则分别为：速度、功耗、增益、噪声、线性度、电压摆幅、电源电压、输入输出阻抗参数之间互相制约，设计时需要在这些参数间折衷3.2 共源级1. 电阻负载理想情况：考虑沟长调制效应：2. 二极管接法的MOS做负载① NMOS二极管负载存在体效应时的阻抗：忽略η随Vout的变化时，增益只于W/L有关，与偏置电流、电压无关，线性度很好。
② PMOS管负载缺点：a.大增益需要极大的器件尺寸b. 输出摆幅小提高输出摆幅的方法：加电流源3. 电流源做负载4. 深线性区MOS管做负载5. 带源极负反馈①增益与跨导随着RS增大， Gm和增益都变为gm的弱函数,提高了线性度；但以牺牲增益为代价。
另外，可以通过如下方法简便计算：Av=“在漏极节点看到的电阻”/“在源极通路上看到的电阻”②输出电阻3.3 源跟随器（共漏）1. 负载为Rs2. 负载为电流源3. 考虑r O和R L后的增益（注意分析过程）4. 负载为理想电流源时输出电阻Ro3.4 共栅级1. 不考虑沟长调制效应时增益，体效应导致增益增加2. 输入阻抗R D=0时，共栅级输入阻抗相当于源跟随器输出阻抗，故在R D较小时，输入阻抗小3. 输出阻抗计算结果同带源极负反馈的共源级的Rout，故输出阻抗很大3.5 共源共栅级1. 增益（不考虑沟长调制）（注意此处为约等于且结果为负，具体增益参照P71，掌握方法即可）2. 输出阻抗M2管将M1管的输出阻抗提高为原来的（gm2+gmb2）r O2倍；有利于实现高增益3. 其他性质：①作理想电流源，代价：输出摆幅减小②屏蔽特性：Vout端有ΔVout的电压跳变时，表现在X点的电压跳变很小，屏蔽了输出节点对输入管的影响4. 折叠共源共栅5. 总结：4.2 基本差动对1. 大信号差分特性上式假定了M1、M2均工作在饱和区，然鹅2. 大信号共模特性共模输入电平必须满足：3. 小信号差分特性因此，当ΔVin为下值时跨导降为0：，其表征放大器所允许的最大输入差分信号差模增益：用叠加法、半电路法均可求全差分时的差模增益，结论为：①单边输入时差模增益为-gmR D②差分输入时差模增益为-gmR D③单边输入时单端输出增益为-gmR D/24. 小信号共模特性若电路完全对称，则流过M1和M2管的直流电流总为I SS/2，不随Vin,CM的变化而变化，因此，V X和V Y不变；非理想性包括：M1和M2之间有失配（W/L、V TH等），R D1和R D2之间有失配（阻值不完全相等等）；尾电流源ISS的内阻RSS不是无穷大①尾电流内阻非无穷大时若电路完全对称，则V P会随Vin,CM的变化而变化，导致尾电流变化， Vout1和Vout2会随之变化，但Vout1和Vout2总相等，故可短接，将M1、M2并联处理（注意此时跨导为2gm）共模增益为：②输入管失配对共模响应的影响共模到差模转换的增益：5. CMRR-共模抑制比Common-Mode Rejection Ratio，用来综合反映差分放大器的性能5.1 基本电流镜原理：利用输出电流与参考电流的过驱动电压相同)1()()(2121DSTHGSoxnREFVVVLWCIλμ+-=)1()()(2222DSTHGSoxnoutVVVLWCIλμ+-=因此)1()/()1()/(1122DSDSREFoutVLWVLWIIλλ++=复制精度受工艺（宽长比）、沟长调制效应的影响5.3 有源电流镜6.1 密勒效应如果上图1的电路可以转换成图2的电路，则是在所关心的频率下的小信号增益，通常为简化计算，我们一般用低频增益来代替AV，这样足可以使我们深入理解电路的频率特性。
第六部分 自由电子费米气体-总结与习题指导
u
=
∫∞ ε −∞
g
(ε
)
f
(ε
)
dε
(1)
其中 f (ε ) 是费米分布函数， g (ε ) 是状态密度，
( ) f
ε
=
1 e(ε −μ) kBT
+1
(2)
g
(ε
)
=
m π2
2
⎛ ⎜⎝
2mε
2
⎞1 ⎟⎠
2
,
ε >0
(3)
=0
, ε <0
电子气体的化学势 μ 由电子浓度 n 决定，
n
=
∞
∫−∞
g
(ε
CVel
=
⎛ ⎜⎝
∂u ∂T
⎞ ⎟⎠n
V
=
π2 2
⎛ ⎜ ⎝
kBT εF
⎞ ⎟ ⎠
NkB
(6.25)
约为经典值的 0.01 倍. 式中 N 是自由电子数， N = nV .
低温下金属的热容可以写为电子热容和点阵热容之和，
CV = CVel + CVlα = γ T + AT 3
(6.26)
其中 γ 和 A 是两个常量.
数，故
g (ε ) dε = 1 [在能量范围 ε − ε + dε 中的状态数]
(6.8)
V
三维自由电子的状态密度为
⎧
g
(ε
)
=
⎪ ⎨
m 2π 2
2mε 2,
ε >0
(6.9)
⎪⎩ 0
, ε <0
如图 6.1 所示.
2
4 自由电子在基态下的性质 对于由 N 个自由电子组成的系统，基态(绝对零度)下被电子占据的状态可以 用波矢空间中一个球内的点来表示，这个球称为费米球．费密球的半径 kF 称为 费米波矢量，
kelm模型参数
kelm模型参数KELM模型参数及其应用一、什么是KELM模型KELM模型，全称为Kernel Extreme Learning Machine，是一种机器学习算法，通过将输入数据映射到高维空间中进行线性回归或分类任务。
与传统的ELM（Extreme Learning Machine）模型相比，KELM模型在输入数据映射过程中引入了核函数，使得模型具备更强的非线性建模能力。
二、KELM模型的参数1. 核函数选择：KELM模型中的核函数通常有线性核、多项式核、高斯核等多种选择。
不同的核函数适用于不同的数据特征，选择适合的核函数可以提高模型的性能。
2. 隐层神经元个数：KELM模型通过隐层神经元的个数来控制模型的复杂度。
通常情况下，隐层神经元个数越多，模型的拟合能力越强，但也容易导致过拟合问题，需要根据具体的数据集进行调整。
3. 正则化参数：KELM模型中的正则化参数用于控制模型的复杂度和泛化能力。
正则化参数越大，模型的复杂度越低，但可能会导致欠拟合问题；正则化参数越小，模型的复杂度越高，但可能会导致过拟合问题。
选择合适的正则化参数可以平衡模型的拟合能力和泛化能力。
4. 随机数种子：KELM模型中的随机数种子用于控制模型的初始化过程。
通过固定随机数种子，可以保证每次运行模型时得到相同的结果，方便模型的复现和比较。
三、KELM模型的应用KELM模型在机器学习领域有广泛的应用，主要包括以下几个方面：1. 回归问题：KELM模型可以用于解决回归问题，例如房价预测、股票价格预测等。
通过训练模型，可以建立输入变量和输出变量之间的映射关系，实现对未知数据的预测。
2. 分类问题：KELM模型也可以用于解决分类问题，例如垃圾邮件过滤、疾病诊断等。
通过训练模型，可以学习不同类别之间的边界，实现对新样本的分类。
3. 特征提取：KELM模型还可以用于特征提取，例如图像识别、文本分类等。
通过训练模型，可以学习到数据的高维表示，从而提取出更具有判别性的特征。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
return 0; } int MaxMatch() { int i,num; num=0; memset(link,0xff,sizeof(link)); for(i=1;i<=gn;i++) { memset(useif,0,sizeof(useif)); if(can(i)) num++; } return num; } 用尽量少的不相交简单路径覆盖有向无环图(DAG)的所有顶点，这就是 DAG 图的最 小路径覆盖问题。DAG 图的最小路径覆盖数 = 节点数（n）- 最大匹配数（m）
������������ = 其中
1 −������������ ������ ������ ������������
������������
1.2 贝叶斯定理
P(A|B,C)=P(B|A)*P(A)*P(C|A,B)/(P(B)*P(C|B)) P(A)是 A 的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何 B 方面的因素。 P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。 P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。 P(B)是 B 的先验概率或边缘概率，也作标准化常量（normalized constant）。
二分图的最小覆盖分为最小顶点覆盖和最小路径覆盖： ① 最小顶点覆盖是指最少的顶点数使得二分图 G 中的每条边都至少与其中一个点 相关联， ② 二分图的最小顶点覆盖数=二分图的最大匹配数； ②最小路径覆盖也称为最小边覆盖， 是指用尽量少的不相交简单路径覆盖二分图中 的所有顶点。 二分图的最小路径覆盖数=|V|-二分图的最大匹配数；
������������ ∑������ ������=1 ������������
≈ ������(������������ )，
������
那么我们可以通过这些样本来逼近这个均值 1 ∫ ℎ(������)������������ = ������������(������) [������(������)] ≈ ∑ ������(������������ ) ������ ������
������ ������
蒙特卡洛方法的核心是定义好分布之后如何从这个分布上采集样本？ 对于如何在任意分布下采集样本是马尔科夫链蒙特卡洛方法 （MCMC） 解决的问题， 其基本思想就是利用马尔科夫链来产生指定分布下的样本。
1.4.1 马尔科夫链
设������������ 表示随机变量 X 在离散时间 t 时刻的取值。若该变量随时间变化的转移概率仅 仅依赖于它的当前取值，即 P(������������+1 = ������������ |������0 = ������������0 , ������1 = ������������1 , … … , ������������ = ������������ ) = P(������������+1 = ������������ |������������ = ������������ ) 则称这个变量为马尔科夫变量，其中������������0 , ������������1 , … … , ������������ , ������������ ∈ ������ 为随机变量 X 可能的状态。这 个性质成为马尔可夫性质，具有马尔科夫性质的随机过程成为马尔可夫过程。 对于一个马尔科夫随机变量我们只需知道它的当前取值，就足以预测其未来的变化 趋势。而所谓的马尔科夫链就是指一段时间内随机变量 X 的取值序列(������0 , ������1, … … , ������������ )， 它们符合上式。 一般来说，一个马尔科夫链可通过其对应的转移概率来定义。所谓转移概率，是指 随机变量从一个时刻到下一个时刻，从状态������������ 转移到下一个状态������������ 的概率，即 P(������ → ������) ≔ ������������,������ = P(������������+1 = ������������ |������������ = ������������ ) 若记下������������ 表示随机变量 X 在时刻 t 取值������������ 的概率，则 X 在时刻 t+1 取值为������������ 的概率
������ ������
(������)
设状态的数目为 n，则根据上式有
如果存在某个取值， 从它出发转移回自身所需要的转移次数总是整数 d(>1)的倍数， 那么这个马尔可夫过程就是就有周期性。 如果两个取值之间总是能以非零的概率相互转 移， 那么该马尔科夫过程就成为不可约 （不可约指每一个状态都可来自任意的其他状态） 。 如果一个马尔可夫过程既没有周期性又不可约，则称它是各态遍历的。 对于各态遍历的马尔科夫过程，不论������ 0 取何值，随着转移次数的增多，随机变量的 取值分布最终都会收敛于唯一的平稳分布������ ∗ ，即
������
∫ ℎ(������)������������
������
如果我们无法通过数学推导直接求出解析解，那么为了避免对区间(a,b)上的所有 x 值进行枚举(多数情况下这也是不可能的)，我们可以将h(x)分解为某个函数������(������)和一个 定义在(a,b)上的概率密度函数������(������)的乘积。这样整个积分就可以写成
1.4.2 正则分布
假设一个物理系统具备一定的自由度，那么系统所处的状态就具有一定的随机性。 假设系统处于状态 i 的概率为������������ ，则显然有 ������������ ≥ 0, 且 ∑ ������������ = 1
������
根据系统的物理性质，不同的状态可能会使系统具备不同的能量。我们用������������ 表示系 统处于状态 i 时的能量。统计力学的一个基本结论是：当系统与外界达到热平衡时，系 统处于状态 i 的概率������������ 具有以下形式
1.3.5 最大独立集
最大独立集是指寻找一个点集，使得其中任意两点在图中无对应边。对于一般图来 说，最大独立集是一个 NP 完全问题，对于二分图来说 最大独立集=|V|-二分图的最大匹配数。
1.4 MCMC 方法
最早的蒙特卡洛方法旨在通过随机化的方法计算积分，假设给定函数h(x)，我们想 计算如下积分
限制玻尔兹曼机
1. 预备知识
受限玻尔兹曼机 （RBM） 是一种可用随机神经网络来解释的概率图模型。 所谓随机， 是指这种网络中的神经元是随机神经元，其输出只有两种状态（激活、未激活） ，一般 用二进制的 0 和 1 来表示，而状态的具体取值则根据概率统计法则来决定。
1.1 Sigmoid 函数
Sigmoid 函数是神经网络中常用的激活函数 1 S(x) = 1 + ������ −������ 其定义域为(-∞， + ∞),值域为(0,1)。
n→∞
lim ������ 0 ������������ = ������ ∗ ，
且这个平稳分布满足������ ∗ ������ ∗ ������ = ������ ∗ 这就意味着，无论������ 0 取何值，经过足够多转移后，随机变量个取值总会不断接近与该过 程的平稳分布。这就为 MCMC 建立了基础：如果我们想在某个分布下采样，只有模拟 以其为平稳分布的马尔可夫过程， 经过足够多次转移之后， 我们的样本分布就会充分接 近于该平稳分布。这意味着我们近似的采集到了目标分布下的样本。
1.3 二分图 1.3.1 定义
设 G=(V,E)是一个无向图。如顶点集 V 可分割为两个互不相交的子集，并且图中每 条边依附的两个顶点都分属两个不同的子集。则称图 G 为二分图。也就是说在二分图 中，顶点可以分为两个集合 X 和 Y，每一条边的两个顶点都分别位于 X 和 Y 集合中。
1.3.2 最大匹配
(������)
为 �����������
(������+1)
= P(������������+1 = ������������ ) = ∑ P(������������+1 = ������������ |������������ = ������������ ) ∗ P(������������ = ������������ ) = ∑ ������������,������ ∗ ������������
������ ������ ������ ������
∫ ℎ(������)������������ = ∫ ������(������)������(������)������������ = ������������(������) [������(������)] 这样一来原积分就等同于������(������)在������(������)这个分布上的均值。 这时如果我们从分布������(������) 上采集大量的样本点，这些样本点符合分布������(������)，即对∀i，有
在 G 的一个子图 M 中，M 的边集中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。选择这样的边数最大的子集称为图的最大匹配问题,最大匹配的边数称为 最大匹配数.如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为
完全匹配，也称作完备匹配。如果在左右两边加上源汇点后，图 G 等价于一个网络流， 二分图最大匹配问题可以转为最大流的问题。 解决此问的匈牙利算法的本质就是寻找最 大流的增广路径。 基本模式如下： 初始时最大匹配为空 while 找得到增广路径 do 把增广路径加入到最大匹配中去 二分图中的增广路径的性质： (1)有奇数条边。 (2)起点在二分图的左半边，终点在右半边。 (3)路径上的点一定是一个在左半边，一个在右半边，交替出现。 （其实二分图的性 质就决定了这一点，因为二分图同一边的点之间没有边相连，不要忘记哦。 ） (4)整条路径上没有重复的点。 (5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。 (6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。 (7)最后， 也是最重要的一条， 把增广路径上的所有第奇数条边加入到原匹配中去， 并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反） ， 则新的匹配数就比原匹配数增加了 1 个。 初始时最大匹配为空 for 二分图左半边的每个点 i do 从点 i 出发寻找增广路径。 如果找到， 则把它取反 （即增加了总了匹配数） 。 如果二分图的左半边一共有 n 个点， 那么最多找 n 条增广路径。 如果图中共有 m 条边， 那么每找一条增广路径（DFS 或 BFS）时最多把所有边遍历一遍，所花时间也就是 m。 所以总的时间大概就是 O（n * m） 。 #define N 202 int useif[N]; //记录 y 中节点是否使用 0 表示没有访问过，1 为访问过 int link[N]; //记录当前与 y 节点相连的 x 的节点 int mat[N][N]; //记录连接 x 和 y 的边，如果 i 和 j 之间有边则为 1，否则为 0 int gn,gm; //二分图中 x 和 y 中点的数目 int can(int t) { int i; for(i=1;i<=gm;i++) { if(useif[i]==0 && mat[t][i]) { useif[i]=1; if(link[i]==-1 || can(link[i])) { link[i]=t; return 1; } } }