2019-2019创新设计-同步人教A版选修2-1 2-2第一章 1.ppt
2019-2020数学人教A版选修2-2课件:第一章导数及其应用1.5 1.5.1 1.5.2 课后

9.若做变速直线运动的物体 v(t)=t2,在 0≤t≤a 内经过的路程为 9, 则 a 的值为________.
答案 3
解析 将区间[0,a]分为等长的 n 个小区间,第 i 个区间记为i-n 1a,ina (i=1,2,…,n),取每个小区间的右端点的速度近似代替,则 Δt=an,所以 v(ti)=ina2,sn=∑i=n1 ina2·an=an33(1+22+…+n2)
第三页,编辑于星期日:点 二十分。
3.在求由 x=a,x=b(a<b),y=f(x)(f(x)≥0)及 y=0 围成的曲边梯形的 面积 S 时,在区间[a,b]上等间隔地插入 n-1 个分点,分别过这些分点作 x 轴的垂线,把曲边梯形分成 n 个小曲边梯形,下列说法中正确的个数是( )
①n 个小曲边梯形的面积和等于 S; ②n 个小曲边梯形的面积和小于 S; ③n 个小曲边梯形的面积和大于 S; ④n 个小曲边梯形的面积和与 S 之间的大小关系无法确定. A.1 B.2 C.3 D.4
解 将区间[0,2]等分成 n 个小区间,则第 i 个小区间为2i-n 1,2ni(i=
1,2,…,n).
第 i 个小区间的面积 ΔSi=f2i-n 1·2n,
所以 Sn=∑ i=n1f2i-n 1·2n=2n∑ i=n1
4i-12 n2
答案15
第十五页,编辑于星期日:点 二十分。
=n83∑i=n1 (i-1)2
解析 所围成的四边形为直角梯形,x=0 时,y=1,x=2 时,y=3, 所以 S=12×(1+3)×2=4.
答案
解析11
第十一页,编辑于星期日:点 二十分。
8.已知某物体运动的速度 v=2t-1,t∈[0,10],若把区间 10 等分,取 每个小区间右端点处的函数值为近似小矩形的高,则物体运动的路程近似值 为________.
2019-2020学年人教A版选修2-2 函数的最大(小)值与导数 课件(50张)

(2)[a,b]上连续不断的函数 f(x)在(a,b)上满足 f′(x)>0,则 f(a)是函数的最______值,f(b)是函数的最______值.
【答案】 小,大
题型二 闭区间上函数的最值
例 2 求下列函数的最大值和最小值. ππ
y′
+
0
-
0+
y -2
2
-2
2
由上表知 f(x)最大值为 2.
【答案】 C
x-1 (2)求 y= ,x∈[0,4]的最大值和最小值.
x2+1 【解析】 y′=-(xx2+2+21x)+21,
令 y′=0,得 x=1+ 2和 x=1- 2(舍). 又 f(0)=-1,f(4)=137,f(1+ 2)= 22-1, ∴ymax= 22-1,ymin=-1.
x f′(x)
f(x)
π -2
π 2
ππ (- 2 ,- 6 )
π -6
-
0
π-3 3 6
ππ (- 6 , 6 )
+
π x
6
f′(x)
0
3 3-π f(x)
6
ππ (6,2)
-
π 2
π -2
π
π
从上表可知,最大值为 2 ,最小值为- 2 .
(2)f′(x)=3x2-3,令 f′(x)=0,得 x=±1. ∵f(-3)=(-3)3-3×(-3)+3=-15, f(-1)=(-1)3-3×(-1)+3=5, f(1)=13-3×1+3=1, f(32)=(32)3-3×32+3=185, ∴函数的最大值是 5,最小值是-15.
互动 2 函数的最大(小)值可以有多个吗?最大(小)值点 呢?
2019-2020学年新素养同步人教A版数学选修2-1课件:1.1.1命题

2.命题的形式 命题的一般形式为“若 p,则 q”. 其中 p 叫做命题的 条件 ,q 叫做命题的结论.
第四页,编辑于星期日:点 分。
|自我尝试| 1.判断下列各题.(对的打“√”,错的打“×”) (1)“集合{a,b,c}有 3 个子集”是命题( √ ) (2)“x2-3x+2=0”是命题( × )
第二十七页,编辑于星期日:点 分。
解析:可用反证法.假设 l 与 l1,l2 都不相交,因为 l 与 l1 都在平面 α 内,于是 l∥l1,同理 l∥l2,于是 l1∥l2,与已知矛盾, 故 l 至少与 l1,l2 中的一条相交.选 D.
答案:D
第二十八页,编辑于星期日:点 分。
2.给出命题:方程 x2+ax+1=0 没有实数根,则使该命题 为真命题的 a 的一个值可以是( )
第十七页,编辑于星期日:点 分。
跟踪训练 2 下列命题中真命题有( )
①mx2+2x-1=0 是一元二次方程;
②抛物线 y=ax2+2x-1 与 x 轴至少有一个交点;
③互相包含的两个集合相等;
④空集是任何集合的真子集.
A.1 个
B.2 个
C.3 个
D.4 个
第十八页,编辑于星期日:点 分。
解析:①中当 m=0 时,是一元一次方程;②中当 Δ=4+4a<0 时,抛物线与 x 轴无交点;③是正确的;④中空集不是本身的真 子集.
解析:(1)若一个数是奇数,则它不能被 2 整除,是真命题. (2)若(a-1)2+(b-1)2=0,则 a=b=1,是真命题. (3)若两个三角形是相似三角形,则这两个三角形是全等三 角形,是假命题. (4)在空间中,若两条直线平行于同一个平面,则这两条直 线平行,是假命题.
2019-2020学年高二数学人教A版选修2-2教师用书:第1章 1.5.3 定积分的概念 Word版含解析

1.5.3 定积分的概念1.了解定积分的概念.(难点)2.理解定积分的几何意义.(重点、易混点) 3.掌握定积分的几何性质.(重点、难点)[基础·初探]教材整理1 定积分的概念 阅读教材P 45内容,完成下列问题.如果函数f (x )在区间[a ,b ]上连续,用分点a =x 0<x 1<…<x i -1<x i <…<x n =b 将区间[a ,b ]等分成n 个小区间,在每个小区间[x i -1,x i ]上任取一点ξi (i =1,2,…,n ),作和式∑i =1nf(ξi )Δx =________________,当n →∞时,上述和式无限接近某个常数,这个常数叫做函数f (x )在区间[a ,b ]上的定积分,记作⎠⎛a b f (x )d x ,即⎠⎛ab f(x(dx =__________.其中a 与b 分别叫做__________与__________,区间[a ,b ]叫做______,函数f (x )叫做____________,x 叫做__________,f (x )d x 叫做__________.【答案】 ∑i =1n b -a n f (ξi ) lim n→∞∑i =1n b -an f (ξi ) 积分下限 积分上限 积分区间 被积函数积分变量 被积式⎠⎛12(x +1)d x 的值与直线x =1,x =2,y =0,f (x )=x +1围成的梯形的面积有什么关系?【解析】 由定积分的概念知:二者相等. 教材整理2 定积分的几何意义 阅读教材P 46的内容,完成下列问题.从几何上看,如果在区间[a ,b ]上函数f (x )连续且恒有f (x )≥0,那么定积分⎠⎛a b f (x )d x 表示由__________________所围成的曲边梯形的面积.这就是定积分⎠⎛ab f (x )d x 的几何意义.【答案】 直线x =a ,x =b ,y =0和曲线y =f (x)判断(正确的打“√”,错误的打“×”) (1)⎠⎛a b f (x )d x =⎠⎛ab f (t )d t .( ) (2)⎠⎛a b f (x )d x 的值一定是一个正数.( ) (3)⎠⎛012x d x <⎠⎛022x d x ( ) 【答案】 (1)√ (2)× (3)√ 教材整理3 定积分的性质阅读教材P 47的内容,完成下列问题.1.⎠⎛ab kf (x )d x =________________________(k 为常数). 2.⎠⎛a b [f 1(x )±f 2(x )]d x =⎠⎛a b f 1(x )d x ±__________________. 3.⎠⎛ab f (x )d x =______________(其中a <c <b ). 【答案】 1.k ⎠⎛a b f (x )d x 2.⎠⎛a b f 2(x )d x 3.⎠⎛a c f (x )d x +⎠⎛cb f (x )d x填空:(1)由y =0,y =cos x ,x =0,x =π2围成的图形的面积用定积分的形式表示为__________. (2)⎠⎛-11f (x )d x =⎠⎛-10f (x )d x +__________. (3)⎠⎛a b (x 2+2x )d x =⎠⎛ab 2x d x +________. 【答案】 (1) ⎠⎜⎛0π2cos x d x (2)⎠⎛01f (x )d x (3)⎠⎛a b x 2d x[小组合作型]⎠⎛1【精彩点拨】 根据定积分的意义,分四步求解,即分割、近似代替、求和、取极限. 【自主解答】 令f (x )=3x +2. (1)分割在区间[1,2]上等间隔地插入n -1个分点,将区间[1,2]等分成n 个小区间⎣⎢⎡⎦⎥⎤n +i -1n ,n +i n (i =1,2,…,n ),每个小区间的长度为Δx =n +i n -n +i -1n =1n. (2)近似代替、作和取ξi =n +i -1n(i =1,2,…,n ),则S n =∑i =1nf ⎝⎛⎭⎪⎫n +i -1n ·Δx =∑i =1n错误!·错误!=错误!错误!=错误![0+1+2+…+(n -1)]+5=32×n2-n n2+5=132-32n. (3)取极限 ⎠⎛12(3x +2)d x=lim n→∞S n =lim n→∞⎝ ⎛⎭⎪⎫132-32n =132.利用定义求定积分的步骤[再练一题]1.利用定积分的定义计算⎠⎛12(-x 2+2x )d x 的值.【解】 令f (x )=-x 2+2x . (1)分割在区间[1,2]上等间隔地插入n -1个分点,把区间[1,2]等分为n 个小区间⎣⎢⎡⎦⎥⎤1+i -1n ,1+i n (i =1,2,…,n ),每个小区间的长度为Δx =i n -i -1n =1n.(2)近似代替、作和取ξi =1+in (i =1,2,…,n ),则S n =∑i =1nf ⎝ ⎛⎭⎪⎫1+i n ·Δx =∑i =1n ⎣⎢⎡⎦⎥⎤-⎝⎛⎭⎪⎫1+i n 2+2⎝ ⎛⎭⎪⎫1+i n ·1n=-1n3[(n +1)2+(n +2)2+(n +3)2+…+(2n )2]+2n2[(n +1)+(n +2)+(n +3)+…+2n ]=-1n3错误!+错误!·错误!=-13⎝ ⎛⎭⎪⎫2+1n ⎝ ⎛⎭⎪⎫4+1n +16⎝ ⎛⎭⎪⎫1+1n ⎝ ⎛⎭⎪⎫2+1n +3+1n .(3)取极限⎠⎛12(-x 2+2x )d x =lim n→∞S n =lim n→∞ ⎣⎢⎡-13⎝⎛⎭⎪⎫2+1n ⎝ ⎛⎭⎪⎫4+1n +16⎝ ⎛⎭⎪⎫1+1n ⎝ ⎛⎭⎪⎫2+1n + ⎦⎥⎤3+1n=23.(1)⎠⎛-33-39-x2d x ;(2)⎠⎛03(2x +1)d x ; (3)⎠⎛-11-1(x 3+3x )d x . 【导学号:62952046】【精彩点拨】 对于本题(1)、(2)可先确定被积函数、积分区间,画出图形,然后用几何法求出图形面积,从而确定定积分的值;对于(3)可根据被积函数的奇偶性求解.【自主解答】 (1)曲线y =9-x2表示的几何图形为以原点为圆心以3为半径的上半圆如图(1)所示.其面积为S =12·π·32=92π.由定积分的几何意义知⎠⎛-339-x2d x =92π.(2)曲线f (x )=2x +1为一条直线.⎠⎛03(2x +1)d x 表示直线f (x )=2x +1,x =0,x =3围成的直角梯形OABC 的面积,如图(2).其面积为S =12(1+7)×3=12.根据定积分的几何意义知⎠⎛03(2x +1)d x =12.(3)∵y =x 3+3x 在区间[-1,1]上为奇函数,图象关于原点对称,∴曲边梯形在x 轴上方部分面积与x 轴下方部分面积相等.由定积分的几何意义知⎠⎛-11(x 3+3x )d x =0.定积分的几何意义的应用(1)利用定积分的几何意义求⎠⎛ab f (x )d x 的值的关键是确定由曲线y =f (x ),直线x =a ,x =b 及y =0所围成的平面图形的形状.常见的图形有三角形、直角梯形、矩形、圆等可求面积的平面图形.(关键词:平面图形的形状)(2)不规则的图形常利用分割法将图形分割成几个容易求定积分的图形求面积,要注意分割点要确定准确.(关键词:分割)[再练一题]2.上例(1)中变为⎠⎜⎛-32329-x2d x ,如何求解? 【解】 由y =9-x2,知x 2+y 2=9(y ≥0),x ∈⎣⎢⎡⎦⎥⎤-32,32,其图象如图所示:由定积分的几何意义,知⎠⎜⎛-32329-x2d x 等于圆心角为60°的弓形C ED 的面积与矩形ABC D的面积之和.S 弓形=12×π3×32-12×3×332=6π-934,S 矩形=|AB |×|BC |=2×32×9-⎝ ⎛⎭⎪⎫322=932,∴⎠⎜⎛-32329-x2d x =6π-934+932=6π+934.[探究共研型]探究1【提示】 可先把每一段函数的定积分求出后再相加. 探究2 怎样求奇(偶)函数在区间[a ,b ]上的定积分?【提示】 ①若奇函数y =f (x )的图象在[-a ,a ]上连续,则⎠⎛-a a f (x )d x =0;②若偶函数y =g (x )的图象在[-a ,a ]上连续,则⎠⎛-a a g (x )d x =2⎠⎛0a g (x )d x .(1)f (x )=⎩⎨⎧x +1,0≤x<1,2x2,1≤x≤2,则⎠⎛02f (x )d x =( )A.⎠⎛02(x +1)d xB.⎠⎛022x 2d x C.⎠⎛01(x +1)d x +⎠⎛122x 2d x D.⎠⎛122x d x +⎠⎛02(x +1)d x (2)已知⎠⎛02f (x )d x =8,则⎠⎛02[f (x )-2x ]d x =________.【自主解答】 (1)∵f (x )在[0,2]上是连续的,由定积分的性质(3)得⎠⎛02f (x )d x =⎠⎛01f (x )d x +⎠⎛12f (x )d x =⎠⎛01(x +1)d x +⎠⎛122x 2d x .(2)由定积分的性质(2)可得 ⎠⎛02[f (x )-2x ]d x =⎠⎛02f (x )d x -⎠⎛022x d x =⎠⎛02f (x )d x -2⎠⎛02x d x . 又∵⎠⎛02f (x )d x =8,⎠⎛02x d x =12×2×2=2,∴⎠⎛02[f (x )-2x ]d x =⎠⎛02f (x )d x -2⎠⎛02x d x =8-2×2=4.【答案】 (1)C (2)4利用定积分的性质求定积分的技巧灵活应用定积分的性质解题,可以把比较复杂的函数拆成几个简单函数,把积分区间分割成可以求积分的几段,进而把未知的问题转化为已知的问题,在运算方面更加简洁.应用时注意性质的推广:(1)⎠⎛ab [f 1(x )±f 2(x )±…±f n (x )]d x =⎠⎛a b f 1(x )d x ±⎠⎛a b f 2(x )d x ±…±⎠⎛ab f n (x )d x ; (2)⎠⎛a b f (x )d x =⎠⎜⎛a c1f (x )d x +⎠⎜⎛c1c2f (x )d x +…+⎠⎜⎛cnb f (x )d x (其中a <c 1<c 2<…<c n <b ,n ∈N *).[再练一题]3.已知⎠⎛0e x d x =e22,⎠⎛0e x 2d x =e33,求下列定积分的值.(1)⎠⎛0e (2x +x 2)d x ;(2)⎠⎛0e (2x 2-x +1)d x .【解】 (1)⎠⎛0e (2x +x 2)d x=2⎠⎛0e x d x +⎠⎛0e x 2d x =2×e22+e33=e 2+e33.(2)⎠⎛0e (2x 2-x +1)d x =2⎠⎛0e x 2d x -⎠⎛0e x d x +⎠⎛0e 1d x , 因为已知⎠⎛0e x d x =e22,⎠⎛0e x 2d x =e33,又由定积分的几何意义知:⎠⎛0e 1d x 等于直线x =0,x =e ,y =0,y =1所围成的图形的面积,所以⎠⎛0e 1d x =1×e =e ,故⎠⎛0e (2x 2-x +1)d x =2×e33-e22+e =23e 3-12e 2+e.1.下列等式不成立的是( )A.⎠⎛a b [mf (x )+ng (x )]d x =m ⎠⎛a b f (x )d x +n ⎠⎛a b g (x )d xB.⎠⎛a b [f (x )+1]d x =⎠⎛a b f (x )d x +b -aC.⎠⎛a b f (x )g (x )d x =⎠⎛a b f (x )d x ·⎠⎛ab g (x )d x D.⎠⎛-2π2πsin x d x =⎠⎛-2π0sin x d x +⎠⎛02πsin x d x 【解析】 利用定积分的性质可判断A ,B ,D 成立,C 不成立. 例如⎠⎛02x d x =2,⎠⎛022d x =4,⎠⎛022x d x =4, 即⎠⎛022x d x ≠⎠⎛02x d x ·⎠⎛022d x . 【答案】 C2.图1-5-3中阴影部分的面积用定积分表示为()图1-5-3A.⎠⎛012x dxB.⎠⎛01(2x -1)d xC.⎠⎛01(2x +1)d xD.⎠⎛01(1-2x )d x 【解析】 根据定积分的几何意义,阴影部分的面积为⎠⎛012x d x -⎠⎛011d x =⎠⎛01(2x -1)d x .【答案】 B3.由y =sin x ,x =0,x =π2,y =0所围成图形的面积写成定积分的形式是________. 【导学号:62952047】【解析】 ∵0<x <π2,∴sin x >0.∴y =sin x ,x =0,x =π2,y =0所围成图形的面积写成定积分的形式为⎠⎜⎛0π2 sin x d x .【答案】 ⎠⎜⎛0π2 sin x d x4.若⎠⎛a b [f (x )+g (x )]d x =3,⎠⎛a b [f (x )-g (x )]d x =1,则⎠⎛a b [2g (x )]d x =________.【解析】 ⎠⎛ab [2g (x )]d x=⎠⎛a b [(f (x )+g (x ))-(f (x )-g (x ))]d x =⎠⎛a b [f (x )+g (x )]d x -⎠⎛a b [f (x )-g (x )]d x =3-1=2. 【答案】 25.用定积分的几何意义求⎠⎛-114-x2d x .【解】 由y =4-x2可知x 2+y 2=4(y≥0),其图象如图.⎠⎛-114-x2d x 等于圆心角为60°的弓形C E D 的面积与矩形ABCD 的面积之和. S 弓形=12×π3×22-12×2×2sin π3=2π3-3.S 矩形=|AB |·|BC |=23.∴⎠⎛-114-x2d x =23+2π3-3=2π3+3.。
【创新设计】高中数人教A版选修12【配套课件】:2112

课前探究学习
课堂讲练互动
想一想:由合情推理得到的结论可靠吗? 提示 一般来说,由合情推理所获得的结论,仅仅是一种猜想, 未必可靠,例如,费马猜想就被数学家欧拉推翻了.
பைடு நூலகம்
课前探究学习
课堂讲练互动
名师点睛
1.类比推理
(1)类比推理的一般步骤
①找出两类事物之间的相似性或一致性.
②用一类事物的性质去推测另一类事物的性质,得出一个明确
题型二 类比推理在几何中的应用 【例2】 如图所示,在△ABC中,射影定理可
表示为a=b·cos C+c·cos B,其中a,b,c分 别为角A,B,C的对边,类比上述定理,写出 对空间四面体性质的猜想. [思路探索]
课前探究学习
课堂讲练互动
解 如右图所示,在四面体PABC中,设S1,S2, S3,S分别表示△PAB,△PBC,△PCA,△ ABC的面积,α,β,γ依次表示面PAB, 面PBC,面PCA与底面ABC所成二面角的大小. 我们猜想射影定理类比推理到三维空间,其表现形式应为S= S1·cos α+S2·cos β+S3·cos γ.
课前探究学习
课堂讲练互动
解析 由两类对象具有某些类似特征和其中一类对象的某些已知 特征,推出另一类对象也具有这些特征的推理,叫类比推理,上 述三个结论均符合推理结论,故均正确. 答案 C
课前探究学习
课堂讲练互动
方法技巧 数形结合思想在合情推理中的应用 本节关于数形结合思想的考查主要是利用图形归纳、类比一般规 律,从而作出猜想. 【示例】 如图所示是树形图,第一层是一条与水平线垂直的线段,
第2课时 类比推理
课前探究学习
课堂讲练互动
【课标要求】 1.了解合情推理的含义,能利用归纳和类比等进行简单的推理. 2.了解合情推理在数学发现中的作用. 【核心扫描】 1.对合情推理含义的理解.(重点) 2.能利用归纳和类比进行简单的推理.(重点)
最新2019版-创新设计-高考总复习-数学-人教A版-理科-第一章-第1节ppt课件

2.(必修 1P7 练习 2 改编)若集合 A={x∈N|x≤ 2 018},a=2 2,则下列结论正确的
是( )
A.{a}⊆A
B.a⊆A
C.{a}∈A
D.a∉A
解析 因为 a=2 2不是自然数,而集合 A 是不大于 2 018的自然数构成的集合,所 以 a∉A.
答案 D
3.(2017·全国Ⅰ卷)已知集合 A={x|x<2},B={x|3-2x>0},则( )
• 谦称 “家”:用于对别人称自己的辈分高的或同辈 年纪大的亲属。如:家父、家严、家尊(称父亲), 家母、家慈(称母亲)。
• “舍”:用于对别人称自己的辈分低的或同辈年纪 小的亲属。如:舍弟(称弟弟),舍妹(称妹妹)。
• “小”:用于称自己或跟自己有关的人或事物。如: 小弟(男性在朋友或熟人之间谦称自己),小儿 (谦称自己的儿子),小女(谦称自己的女儿), 小店(谦称自己的商店)。
• “奉”:用于自己的举动涉及对方时。如:奉送(赠送),奉还(归 还),奉劝(劝告),奉陪(陪同)。
• 其他:久仰(仰慕已久,初次见面时说),劳驾(用于请别人做事或让 路),赏光(用于请对方接受自己的邀请),赏脸(用于请对方接受自 己的要求或赠品),贵姓(问人姓氏),贵庚(问人年龄),大作(称 人作品的敬辞),大驾(对他人的尊称)。
知识梳
理 1.元素与集合
(1)集合中元素的三个特性:确定性、 互异性 、 无序性 . (2)元素与集合的关系是 属于 或 不属于 ,表示符号分别为∈和∉. (3)集合的三种表示方法:列举法、 描述法 、图示法.
诊断自 测
1.思考辨析(在括号内打“√”或“×”) (1){x|y=x2+1}={y|y=x2+1}={(x,y)|y=x2+1}.( ) (2)若{x2,1}={0,1},则x=0,1.( ) (3)对于任意两个集合A,B,关系(A∩B)⊆(A∪B)恒成立.( ) (4)含有n个元素的集合有2n个真子集.( )
2016-2017《创新设计》同步人教A版选修2-1 2-2第一章 1.7.1

1.7.1 定积分在几何中的应用明目标、知重点会应用定积分求两条或多条曲线围成的图形的面积.1.当x ∈[a ,b ]时,若f (x )>0,由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )所围成的曲边梯形的面积S =ʃba f (x )d x .2.当x ∈[a ,b ]时,若f (x )<0,由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )围成的曲边梯形的面积S =-ʃba f (x )d x .3.当x ∈[a ,b ]时,若f (x )>g (x )>0,由直线x =a ,x =b (a ≠b )和曲线y =f (x ),y =g (x )围成的平面图形的面积S =ʃba [f (x )-g (x )]d x .(如图)探究点一 求不分割型图形的面积思考 怎样利用定积分求不分割型图形的面积?答 求由曲线围成的面积,要根据图形,确定积分上下限,用定积分来表示面积,然后计算定积分即可.例1 计算由曲线y 2=x ,y =x 2所围图形的面积S .解 由⎩⎪⎨⎪⎧y 2=x ,y =x 2得交点的横坐标为x =0及x =1.因此,所求图形的面积为 S =S 曲边梯形OABC —S 曲边梯形OABD =ʃ10x d x -ʃ10x 2d x=23x 32|10-13x 3|10 =23-13=13. 反思与感悟 求由曲线围成图形面积的一般步骤: (1)根据题意画出图形;(2)找出范围,确定积分上、下限; (3)确定被积函数; (4)将面积用定积分表示;(5)用微积分基本定理计算定积分,求出结果.跟踪训练1 求由抛物线y =x 2-4与直线y =-x +2所围成图形的面积.解 由⎩⎪⎨⎪⎧ y =x 2-4y =-x +2得⎩⎪⎨⎪⎧ x =-3y =5或⎩⎪⎨⎪⎧x =2y =0, 所以直线y =-x +2与抛物线y =x 2-4的交点为(-3,5)和(2,0),设所求图形面积为S , 根据图形可得S =ʃ2-3(-x +2)d x -ʃ2-3(x 2-4)d x=(2x -12x 2)|2-3-(13x 3-4x )|2-3 =252-(-253)=1256. 探究点二 分割型图形面积的求解思考 由两条或两条以上的曲线围成的较为复杂的图形,在不同的区间位于上方和下方的曲线不同时,这种图形的面积如何求呢?答 求出曲线的不同的交点横坐标,将积分区间细化,分别求出相应区间曲边梯形的面积再求和,注意在每个区间上被积函数均是由上减下.例2 计算由直线y =x -4,曲线y =2x 以及x 轴所围图形的面积S . 解 方法一 作出直线y =x -4,曲线y =2x 的草图.解方程组⎩⎨⎧y =2x ,y =x -4得直线y =x -4与曲线y =2x 交点的坐标为(8,4). 直线y =x -4与x 轴的交点为(4,0). 因此,所求图形的面积为 S =S 1+S 2 =ʃ42x d x +[]ʃ 842x d x -ʃ 84(x -4)d x=22332x |40+22332x |84-12(x -4)2|84 =403. 方法二 把y 看成积分变量,则 S =ʃ4(y +4-12y 2)d y =(12y 2+4y -16y 3)|40 =403. 反思与感悟 两条或两条以上的曲线围成的图形,一定要确定图形范围,通过解方程组求出交点的坐标,定出积分上、下限,若积分变量选x 运算较繁锁,则积分变量可选y ,同时要更换积分上、下限.跟踪训练2 求由曲线y =x ,y =2-x ,y =-13x 所围成图形的面积.解 画出图形,如图所示.解方程组⎩⎨⎧y =x ,x +y =2,⎩⎪⎨⎪⎧ y =x ,y =-13x ,及⎩⎪⎨⎪⎧x +y =2,y =-13x , 得交点分别为(1,1),(0,0),(3,-1), 所以S =ʃ10[x -(-13x )]d x +ʃ31[(2-x )-(-13x )]d x =ʃ10(x +13x )d x +ʃ31(2-x +13x )d x =(23x 32+16x 2)|10+(2x -12x 2+16x 2)|31 =23+16+(2x -13x 2)|31 =56+6-13×9-2+13 =136. 探究点三 定积分的综合应用例3 在曲线y =x 2(x ≥0)上某一点A 处作一切线使之与曲线以及x 轴所围成的面积为112,试求:切点A 的坐标以及在切点A 处的切线方程. 解 如图,设切点A (x 0,y 0),其中x 0≠0,由y ′=2x ,过点A 的切线方程为 y -y 0=2x 0(x -x 0), 即y =2x 0x -x 20,令y =0,得x =x 02,即C (x 02,0),设由曲线和过点A 的切线与x 轴围成图形的面积为S , 则S =S 曲边△AOB -S △ABC ,∵S 曲边△AOB =ʃx 00x 2d x =13x 3|x 00=13x 30,S △ABC =12|BC |·|AB |=12(x 0-x 02)·x 20=14x 30. ∴S =13x 30-14x 30=112x 30=112.∴x 0=1,从而切点为A (1,1), 切线方程为2x -y -1=0.反思与感悟 本题综合考查了导数的意义以及定积分等知识,运用待定系数法,先设出切点的坐标,利用导数的几何意义,建立了切线方程,然后利用定积分以及平面几何的性质求出所围成的平面图形的面积,根据条件建立方程求解,从而使问题得以解决.跟踪训练3 如图所示,直线y =kx 分抛物线y =x -x 2与x 轴所围图形为面积相等的两部分,求k 的值.解 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1, 所以,抛物线与x 轴所围图形的面积 S =ʃ10(x -x 2)d x =⎝⎛⎭⎫x 22-13x 3|10=16.又⎩⎪⎨⎪⎧y =x -x 2,y =kx , 由此可得,抛物线y =x -x 2与y =kx 两交点的横坐标为x 3=0,x 4=1-k , 所以,S 2=ʃ1-k 0(x -x 2-kx )d x=⎝⎛⎭⎫1-k 2x 2-13x 3|1-k 0=16(1-k )3. 又知S =16,所以(1-k )3=12,于是k =1- 312=1-342.1.在下面所给图形的面积S 及相应表达式中,正确的有( )S =ʃab [f (x )-g (x )]d xS =ʃ80(22x -2x +8)d x① ②S =ʃ41f (x )d x -ʃ74f (x )d xS =ʃ a 0[g (x )-f (x )]d x +ʃ ba [f (x )-g (x )]d x③ ④A .①③B .②③C .①④D .③④ 答案 D 解析 ①应是S =ʃba [f (x )-g (x )]d x ,②应是S =ʃ8022x d x -ʃ84(2x -8)d x ,③和④正确,故选D.2.曲线y =cos x (0≤x ≤32π)与坐标轴所围图形的面积是( )A .2B .3 C.52 D .4答案 B 解析 S =π20⎰cos x d x -3π2π2⎰cos x d x=sin x|π20-sin x|3π2π2=sin π2-sin 0-sin 3π2+sin π2=1-0+1+1=3.3.由曲线y =x 2与直线y =2x 所围成的平面图形的面积为________. 答案 43解析 解方程组⎩⎪⎨⎪⎧ y =2x ,y =x 2,得⎩⎪⎨⎪⎧x =0,y =0,⎩⎪⎨⎪⎧x =2,y =4. ∴曲线y =x 2与直线y =2x 交点为(2,4),(0,0). ∴S =ʃ20(2x -x 2)d x =(x 2-13x 3)|2=(4-83)-0=43.4.由曲线y =x 2+4与直线y =5x ,x =0,x =4所围成平面图形的面积是________. 答案193解析 由图形可得 S =ʃ10(x 2+4-5x )d x +ʃ41(5x -x 2-4)d x =(13x 3+4x -52x 2)|10+(52x 2-13x 3-4x )|41 =13+4-52+52×42-13×43-4×4-52+13+4=193. [呈重点、现规律]对于简单图形的面积求解,我们可直接运用定积分的几何意义,此时 (1)确定积分上、下限,一般为两交点的横坐标. (2)确定被积函数,一般是上曲线与下曲线对应函数的差.这样所求的面积问题就转化为运用微积分基本定理计算定积分了.注意区别定积分与利用定积分计算曲线所围图形的面积:定积分可正、可负或为零;而平面图形的面积总是非负的.一、基础过关1.用S 表示图中阴影部分的面积,则S 的值是( )A .ʃca f (x )d x B .|ʃca f (x )d x | C .ʃba f (x )d x +ʃcb f (x )d x D .ʃcb f (x )d x -ʃba f (x )d x答案 D解析 ∵x ∈[a ,b ]时,f (x )<0,x ∈[b ,c ]时,f (x )>0, ∴阴影部分的面积S =ʃcb f (x )d x -ʃba f (x )d x .2.直线l 过抛物线C :x 2=4y 的焦点且与y 轴垂直,则l 与C 所围成的图形的面积等于( ) A.43 B .2 C.83 D.1623答案 C解析 ∵抛物线方程为x 2=4y ,∴其焦点坐标为F (0,1),故直线l 的方程为y =1.如图所示,可知l 与C 围成的图形的面积等于矩形OABF 的面积与函数y =14x 2的图象和x 轴正半轴及直线x =2围成的图形的面积的差的2倍(图中阴影部分的2倍), 即S =4-2ʃ20x24d x =⎪⎪4-2·x 31220=4-43=83.3.若y =f (x )与y =g (x )是[a ,b ]上的两条光滑曲线的方程,则这两条曲线及直线x =a ,x =b 所围成的平面区域的面积为( ) A .∫b a [f (x )-g (x )]d x B .∫b a [g(x)-f(x)]d x C .∫b a |f (x )-g (x )|d xD.||∫ba [f (x )-g (x )]d x答案 C解析 当f (x )>g (x )时, 所求面积为∫b a [f (x )-g (x )]d x ;当f (x )≤g (x )时,所求面积为∫b a [g (x )-f (x )]d x . 综上,所求面积为∫b a |f (x )-g (x )|d x .4.曲线y =x 2-1与x 轴所围成图形的面积等于( ) A.13 B.23 C .1 D.43答案 D解析 函数y =x 2-1与x 轴的交点为(-1,0),(1,0),且函数图象关于y 轴对称,故所求面积为 S =2ʃ10(1-x 2)d x =2(x -13x 3)|10 =2×23=43.5.由曲线y =x 与y =x 3所围成的图形的面积可用定积分表示为________. 答案 ʃ10(x -x 3)d x解析 画出y =x 和y =x 3的草图,所求面积为如图所示阴影部分的面积,解方程组⎩⎨⎧y =xy =x 3得交点的横坐标为x =0及x =1.因此,所求图形的面积为S =ʃ10(x -x 3)d x .6.由y =x 2,y =14x 2及x =1围成的图形的面积S =______.答案 14解析 图形如图所示:S =ʃ10x 2d x -ʃ1014x 2d x=ʃ1034x 2d x=14x 3|10=14. 二、能力提升7.设f (x )=⎩⎪⎨⎪⎧x 2, x ∈[0,1],2-x , x ∈(1,2],则ʃ20f (x )d x等于( )A.34B.45C.56 D .不存在 答案 C解析 数形结合,如图,ʃ20f (x )d x =ʃ10x 2d x +ʃ21(2-x )d x=13x 3|10+(2x -12x 2)|21=13+(4-2-2+12)=56. 8.若两曲线y =x 2与y =cx 3(c >0)围成图形的面积是23,则c 等于( )A.13B.12 C .1 D.23 答案 B解析 由⎩⎪⎨⎪⎧y =x 2y =cx3得x =0或x =1c . ∵0<x <1c 时,x 2>cx 3,∴S =10c ⎰(x 2-cx 3)d x=(13x 3-14cx 4)|10c =13c 3-14c 3=112c 3=23. ∴c 3=18.∴c =12.9.从如图所示的长方形区域内任取一个点M (x ,y ),则点M 取自阴影部分的概率为________.答案 13解析 根据题意得:S 阴=ʃ103x 2d x =x 3|10=1,则点M 取自阴影部分的概率为S 阴S 矩=13×1=13.10.求曲线y =6-x 和y =8x ,y =0围成图形的面积.解 作出直线y =6-x ,曲线y =8x 的草图,所求面积为图中阴影部分的面积.解方程组⎩⎨⎧ y =6-x y =8x得直线y =6-x 与曲线y =8x 交点的坐标为(2,4),直线y =6-x 与x 轴的交点坐标为(6,0).因此,所求图形的面积S =S 1+S 2=ʃ208x d x +ʃ62(6-x )d x=8×2332x |20+(6x -12x 2)|62 =163+[(6×6-12×62)-(6×2-12×22)] =163+8=403. 11.求由抛物线y =-x 2+4x -3及其在点A (1,0)和点B (3,0)处的切线所围成图形的面积. 解 由y ′=-2x +4得在点A 、B 处切线的斜率分别为2和-2,则两直线方程分别为y =2x -2和y =-2x +6,由⎩⎪⎨⎪⎧y =2x -2,y =-2x +6,得两直线交点坐标为C (2,2), ∴S =S △ABC -ʃ31(-x 2+4x -3)d x =12×2×2-⎝⎛⎭⎫-13x 3+2x 2-3x ⎪⎪⎪31=2-43=23. 12.设点P 在曲线y =x 2上,从原点向A (2,4)移动,如果直线OP ,曲线y =x 2及直线x =2所围成的面积分别记为S 1、S 2.(1)当S 1=S 2时,求点P 的坐标;(2)当S 1+S 2有最小值时,求点P 的坐标和最小值.解 (1)设点P 的横坐标为t (0<t <2),则P 点的坐标为(t ,t 2),直线OP 的方程为y =tx .S 1=ʃt 0(tx -x 2)d x =16t 3, S 2=ʃ2t (x 2-tx )d x =83-2t +16t 3. 因为S 1=S 2,所以t =43,点P 的坐标为(43,169).(2)S =S 1+S 2=16t 3+83-2t +16t 3 =13t 3-2t +83,S ′=t 2-2, 令S ′=0得t 2-2=0.因为0<t <2,所以t =2,因为0<t <2时,S ′<0;2<t <2时,S ′>0.所以,当t =2时,S 1+S 2有最小值83-423, 此时点P 的坐标为(2,2).三、探究与拓展13.已知抛物线y =x 2-2x 及直线x =0,x =a ,y =0围成的平面图形的面积为43,求a 的值.解 作出y =x 2-2x 的图象如图.(1)当a <0时,S =ʃ0a (x 2-2x )d x=(13x 3-x 2)|0a =-a 33+a 2 =43, ∴(a +1)(a -2)2=0.∵a <0,∴a =-1.(2)当a >0时,①若0<a ≤2,则S =-ʃa 0(x 2-2x )d x=-(13x 3-x 2)| a 0 =a 2-13a 3=43, ∴a 3-3a 2+4=0即(a +1)(a -2)2=0.∵a >0,∴a =2.②当a >2时,S =-ʃ20(x 2-2x )d x +ʃa 2(x 2-2x )d x=-(13x 3-x 2)|20+(13x 3-x 2)|a 2=-(83-4)+(13a 3-a 2-83+4) =43+(13a 3-a 2-83+4)=43. ∴13a 3-a 2+43=0 ∴a >2不合题意.综上a =-1,或a =2.。
2019-2020人教A版数学选修2-1 第1章 1.1.2 四种命题 1.1.3 四种命题间的相互关系
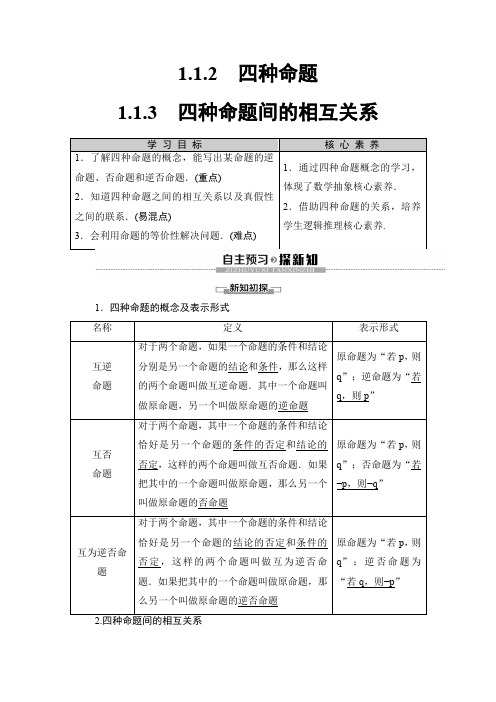
1.1.2四种命题1.1.3四种命题间的相互关系1.四种命题的概念及表示形式(1)四种命题之间的关系(2)四种命题间的真假关系①两个命题互为逆否命题,它们有相同的真假性;②两个命题为互逆命题或互否命题,它们的真假性没有关系.思考:(1)“a=b=c=0”的否定是什么?(2)在原命题,逆命题、否命题和逆否命题四个命题中.真命题的个数会是奇数吗?[提示](1)“a=b=c=0”的否定是“a,b,c至少有一个不等于0”.(2)真命题的个数只能是0,2,4,不会是奇数.1.命题“若一个数是负数,则它的相反数是正数”的逆命题是()A.“若一个数是负数,则它的相反数不是正数”B.“若一个数的相反数是正数,则它是负数”C.“若一个数不是负数,则它的相反数不是正数”D.“若一个数的相反数不是正数,则它不是负数”B[根据逆命题的定义知,选B.]2.命题“若m=10,则m2=100”与其逆命题、否命题、逆否命题这四个命题中,真命题是()A.原命题、否命题B.原命题、逆命题C.原命题、逆否命题D.逆命题、否命题C[原命题正确,则逆否命题正确,逆命题不正确,从而否命题不正确.故选C.]3.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是()A.若f(x)是偶函数,则f(-x)是偶函数B.若f(x)不是奇函数,则f(-x)不是奇函数C.若f(-x)是奇函数,则f(x)是奇函数D.若f(-x)不是奇函数,则f(x)不是奇函数B[原命题的条件是f(x)是奇函数,结论是f(-x)是奇函数,同时否定条件和结论即得否命题,即:若f(x)不是奇函数,则f(-x)不是奇函数.] 4.命题“若ab=0,则a=0”与命题“若a=0,则ab=0”是________命题.(填“互逆”“互否”“互为逆否”)互逆[两个命题的条件和结论交换了,满足互逆命题的概念.]否命题和逆否命题.(1)相似三角形对应的角相等;(2)当x>3时,x2-4x+3>0;(3)正方形的对角线互相平分.[解](1)原命题:若两个三角形相似,则这两个三角形的三个角对应相等;逆命题:若两个三角形的三个角对应相等,则这两个三角形相似;否命题:若两个三角形不相似,则这两个三角形的三个角对应不相等;逆否命题:若两个三角形的三个角对应不相等,则这两个三角形不相似.(2)原命题:若x>3,则x2-4x+3>0;逆命题:若x2-4x+3>0,则x>3;否命题:若x≤3,则x2-4x+3≤0;逆否命题:若x2-4x+3≤0,则x≤3.(3)原命题:若一个四边形是正方形,则它的对角线互相平分;逆命题:若一个四边形对角线互相平分,则它是正方形;否命题:若一个四边形不是正方形,则它的对角线不互相平分;逆否命题:若一个四边形对角线不互相平分,则它不是正方形.1.写出一个命题的逆命题,否命题,逆否命题的方法(1)写命题的四种形式时,首先要找出命题的条件和结论,然后写出命题的条件的否定和结论的否定,再根据四种命题的结构写出所求命题.(2)在写命题时,为了使句子更通顺,可以适当地添加一些词语,但不能改变条件和结论.2.写否命题时应注意一些否定词语,列表如下:1.(1)命题“若y=kx,则x与y成正比例关系”的否命题是()A.若y≠kx,则x与y成正比例关系B.若y≠kx,则x与y成反比例关系C.若x与y不成正比例关系,则y≠kxD.若y≠kx,则x与y不成正比例关系D[条件的否定为y≠kx,结论的否定为x与y不成正比例关系,故选D.](2)命题“若ab≠0,则a,b都不为零”的逆否命题是________.若a,b至少有一个为零,则ab=0[“ab≠0”的否定是“ab=0”,“a,b 都不为零”的否定是“a,b中至少有一个为零”,因此逆否命题为“若a,b至少有一个为零,则ab=0”.]它的逆命题、否命题、逆否命题,在这4个命题中,真命题的个数为() A.0个B.1个C.2个D.4个(2)判断命题“若a≥0,则x2+x-a=0有实根”的逆否命题的真假.思路探究:(1)只需判断原命题和逆命题的真假即可.(1)C[当c=0时,ac2>bc2不成立,故原命题是假命题,从而其逆否命题也是假命题;原命题的逆命题为“若ac2>bc2,则a>b”是真命题,从而其否命题也是真命题,故选C.](2)解:法一:原命题的逆否命题:若x2+x-a=0无实根,则a<0.∵x2+x-a=0无实根,∴Δ=1+4a<0,解得a<-14<0,∴原命题的逆否命题为真命题.法二:∵a≥0,∴4a≥0,∴对于方程x2+x-a=0,根的判别式Δ=1+4a>0,∴方程x2+x-a=0有实根,故原命题为真命题.∵原命题与其逆否命题等价,∴原命题的逆否命题为真命题.判断命题真假的方法(1)解决此类问题的关键是牢记四种命题的概念,正确地写出所涉及的命题,判定为真的命题需要简单的证明,判定为假的命题要举出反例加以验证.(2)原命题与它的逆否命题同真同假,原命题的否命题与它的逆命题同真同假,故二者只判断一个即可.2.判断下列四个命题的真假,并说明理由.(1)“若x+y=0,则x,y互为相反数”的否命题;(2)“若x>y,则x2>y2”的逆否命题;(3)“若x≤3,则x2-x-6>0”的否命题;(4)“对顶角相等”的逆命题.[解](1)命题“若x+y=0,则x,y互为相反数”的逆命题为“若x,y互为相反数,则x+y=0”,则逆命题为真命题,因为原命题的逆命题和否命题具有相同的真假性,所以“若x+y=0,则x,y互为相反数”的否命题是真命题.(2)令x=1,y=-2,满足x>y,但x2<y2,所以“若x>y,则x2>y2”是假命题,因为原命题与其逆否命题具有相同的真假性,所以“若x>y,则x2>y2”的逆否命题也是假命题.(3)该命题的否命题为“若x>3,则x2-x-6≤0”,令x=4,满足x>3,但x2-x-6=6>0,不满足x2-x-6≤0,则该否命题是假命题.(4)该命题的逆命题为“相等的角是对顶角”是假命题,如等边三角形的任意两个内角都相等,但它们不是对顶角.1.当一个命题的条件与结论以否定形式出现时,为了研究方便,我们可以研究哪一个命题?[提示]一个命题与其逆否命题等价,我们可研究其逆否命题.2.在证明“若m2+n2=2,则m+n≤2”时,我们也可以证明哪个命题成立.[提示]根据一个命题与其逆否命题等价,我们也可以证明“若m+n>2,则m2+n2≠2”成立.【例3】(1)命题“对任意x∈R,ax2-2ax-3>0不成立”是真命题,则实数a的取值范围是________.(2)证明:已知函数f(x)是(-∞,+∞)上的增函数,a,b∈R,若f(a)+f(b)≥f(-a)+f(-b),则a+b≥0.思路探究:(1)根据其逆否命题求解.(2)证明其逆否命题成立.(1)[-3,0][∵命题“对任意x∈R,ax2-2ax-3>0不成立”等价于“对任意x ∈R ,ax 2-2ax -3≤0恒成立”,若a =0,则-3≤0恒成立,∴a =0符合题意. 若a ≠0,由题意知⎩⎨⎧a <0,Δ=4a 2+12a ≤0,即⎩⎨⎧a <0,-3≤a ≤0, ∴-3≤a <0,综上知,a 的取值范围是[-3,0].](2)证明:原命题的逆否命题为“已知函数f (x )是(-∞,+∞)上的增函数,a ,b ∈R ,若a +b <0,则f (a )+f (b )<f (-a )+f (-b )”.若a +b <0,则a <-b ,b <-a .又∵f (x )在(-∞,+∞)上是增函数, ∴f (a )<f (-b ),f (b )<f (-a ), ∴f (a )+f (b )<f (-a )+f (-b ). 即原命题的逆否命题为真命题. ∴原命题为真命题.1.若一个命题的条件或结论含有否定词时,直接判断命题的真假较为困难,这时可以转化为判断它的逆否命题.2.当证明一个命题有困难时,可尝试证明其逆否命题成立.3.证明:若a 2-4b 2-2a +1≠0,则a ≠2b +1.[证明] “若a 2-4b 2-2a +1≠0,则a ≠2b +1”的逆否命题为“若a =2b +1,则a 2-4b 2-2a +1=0”.∵a =2b +1,∴a 2-4b 2-2a +1 =(2b +1)2-4b 2-2(2b +1)+1 =4b 2+1+4b -4b 2-4b -2+1=0.∴命题“若a =2b +1,则a 2-4b 2-2a +1=0”为真命题. 由原命题与逆否命题具有相同的真假性可知,原命题得证.1.“命题”的三个关注点(1)我们研究四种命题,一般只研究“若p,则q”形式的命题;有些命题虽然不是这种形式,但可以化为“若p,则q”的形式.(2)对“命题的逆命题、否命题与逆否命题”只要求作一般性的了解,定位在具体、简单的数学命题,重点是四种命题的构成形式及其真假判断.(3)四种命题是相对的,一个命题是什么命题不是固定不变的,但只要我们事先规定好哪个命题是原命题,那么它的其他形式的命题就确定了.2.“互逆命题”“互否命题”“互为逆否命题”与“逆命题”“否命题”“逆否命题”的区别两者具有不同的含义,具体区分如下:前者说的是两个命题的关系,同时涉及两个命题;后者是指与确定的原命题为“互逆”“互否”“互为逆否”关系的那一个命题.1.命题“若a A,则b∈B”的逆命题是()A.若a A,则b B B.若a∈A,则b BC.若b∈B,则a A D.若b B,则a AC[“若p,则q”的逆命题是“若q,则p”,所以本题的逆命题是“若b∈B,则a A”.]2.已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是()A.若a+b+c≠3,则a2+b2+c2<3B.若a+b+c=3,则a2+b2+c2<3C.若a+b+c≠3,则a2+b2+c2≥3D.若a2+b2+c2≥3,则a+b+c=3A[同时否定命题的条件与结论,所得命题就是原命题的否命题,故选A.] 3.命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为()A.1B.2C.3 D.4B[原命题是真命题,从而其逆否命题是真命题,其逆命题是“若a>-6,则a>-3”,是假命题,从而其否命题也是假命题,故真命题的个数是2.] 4.命题“若m>1,则mx2-2x+1=0无实根”的等价命题是________.若mx2-2x+1=0有实根,则m≤1[原命题的等价命题是其逆否命题,由定义可知其逆否命题为:“若mx2-2x+1=0有实根,则m≤1”.]。
