2003年(宇振杯)上海市初中数学竞赛试题(含答案解析)

合集下载

历届最近十年 (新知杯)上海市初中数学竞赛试卷及答案(含模拟试题及解答)

新知杯模拟试题一、填空题（第1-5小题每题8分，第6-10题每题10分，共90分）1. 对于任意实数b a ,，定义b a *=b b a a ++)(，已知5.285.2=*a ，则实数a 的值是_________。

2. 在三角形ABC 中，，其中，，a CA a BC b AB 2122==-=b a ,是大于1的整数，则=-a b 。

3. 一个平行四边形可以被分成92个边长为1的正三角形，它的周长可能是。

4. 已知关于x 的方程02)2()3(2234=++++++k x k x k x x 有实根，并且所有实根的乘积为-2，则所有实根的平方和为。

5. 如图，直角三角形ABC 中1=AC ，2=BC ，P 为斜边AB 上一动点。

BC PE ⊥,CA PF ⊥，则线段EF 长的最小值为。

6. 设b a ,是方程01682=++x x 的两个根，d c ，是方程01862=+-x x 的两个根，则()()()()d b d a c b c a --++的值为。

7. 在平面直角坐标系中有两点()1,1-P ，()2,2Q ,函数1-=kx y 的图像与线段PQ 延长线相交（交点不包括Q ），则实数k 的取值范围是。

8. 方程2009=xyz 的所有整数解有组。

9. 如图，四边形ABCD 中CD BC AB ==,78=∠ABC ,162=∠BCD 。

设BC AD ,延长线交于E ，则=∠AEB _________________.EEC10. 如图，在直角梯形ABCD 中，90=∠=∠BCD ABC ,10==BC AB ,点M 在BC上，使得ADM ∆是正三角形，则ABM ∆与DCM ∆的面积和是________________。

二、（本题15分）如图，ABC ∆中，90=∠ACB ,点D 在CA 上，使得，，31==AD CD 并且，BAC BDC ∠=∠3求BC 的长。

2003年全国初中数学联合竞赛试题及解答

2
为使方程有正整数根要求 4 y 50 4 y 2 y 4 2500 99 y 是完全平方数．
2
经试验得到 y 25 时是完全平方数，解出 x 20 或 30，即 2025 或者 3025 满足题意. 方法二：设这两个两位数分别为 x ， y ，则 x y 100 x y
2
由于 △ABC 是直角三角形，所以抛物线与 x 轴的交点必然在 y 轴两边，所以
c 再由射影定理得到 c 2 ，所以 ac 1 . a
c 0. a
9 3 2．设 m 是整数，且方程 3x2＋mx－2＝0 的两根都大于而小于，则 m＝_________. 5 7
【答】 4. 考虑二次函数 f ( x) 3x2 mx 2 与二次函数的两个交点，由于 3 大于 0，图像开口向上．
所以故：
S△ ADE AD AE 1 AE 3 1 ， S△ ABC AB AC 3 AC 4
AE 3 CE 1 ，所以 AC 4 EA 3
B
C
6．如图，在平行□ABCD 中，过 A，B，C 三点的圆交 AD 于 E，且与 CD 相切．若 AB＝4， BE＝5，则 DE 的长为（ A．3. 【答】D. 连接 CE，由于 ABCE 四点共圆，所以：∠DEC＝∠CBA，在平行四边形 ABCD 中，∠D＝∠ABC，所以有∠DEC＝∠D＝∠ABC，同时，CD 平行于 AB，且 DC 与圆相切，可知：C 为弧 AB 中点，所以∠CEB＝∠CBA，且∠DCE＝∠CBE，故由∠DEC＝∠D 可知△DEC 为等腰三角形，CD＝CE＝AB＝4，由∠DEC＝∠CBE 和∠D＝∠ABC＝∠CEB 可知△CDE∽△BCE，所以：

上海初一初中数学竞赛测试带答案解析

上海初一初中数学竞赛测试班级:___________ 姓名：___________ 分数：___________一、选择题1.六位数由三位数重复构成，如256256，或678678等等，这类数能被何数整除(15届江苏初一2试)六位数六位数A．11;B．101;C．13;D．1001.2.两班学生参加一个测试，20名学生的一班，平均分是80分；30名学生的一班平均分是70分，两班所有学生的平均分是A．75分;B．74分;C．72分;D．77分.3.一个数被10除余9，被9除余8，被8除余7，…，被2除余1，则此数为A．59 ;B．1259;C．2519;D．非以上结论.4.0.000000375与下列数不等的是A．;B．;C．;D．.5.若1+2+3+…+k之和为一完全平方，若n小于100，则k可能的值为A．8;B．1，8 ;C．8，49;D．1,8,49.6.若，则z等于(15届江苏初二1试)若A．;B．;C．;D．.7.一同学在n天假期中观察：（1）下了7次雨，在上午或下午；（2）当下午下雨时，上午是晴天；（3）一共有5个下午是晴天；（4）一共有6个上午是晴天。

则n最小为A．7;B．9;C．10 ;D．11.8.如表所示，则x与y的关系式为（）+x+1C．y=（x2+x+1）（x-1） D．非以上结论9.在下列图形中，各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大（）10.运算※按下表定义，例如3※2=1，那么（2※4）※（1※3）=（）A．1 ;B．2;C．3;D．4.二、填空题1.计算： .2.(17届江苏初一1试)计算等式，式中的应为 .3.三个连续的自然数的最小公倍数是168，那么这三个自然数的和等于 .4.将1,2,3，…，49,50任意分成10组，每组5个数，在每组中取数值居中的那个数为“中位数”，则这10个中位数的最大值是 .5.(15届江苏初一1试)时钟在2点时，分针与时针所夹的角为60°.从0时到3时，会有个时刻，分针与时针也能构成60°的角.6.图中阴影部分占(15届江苏初二1试)图中图形的（填几分之几）.7.如图是由9个等边三角形拼成的六边形，已知中间最小的等边三角形的边长为1，则这个六边形的周长是 (17届江苏初一1试)如图如 .8.已知，点O在三角形内，且，则的度数是(17届江苏初一1试) 度．9.(17届江苏初三)在在在4点钟与5点钟之间，分钟与时钟成一条直线，那么此时时间是 .10.(15届江苏初一1试)一条一条直街上有5栋楼，按从左至右顺序编号为1、2、3、4、5，第k号楼恰好有k （k=1、2、3、4、5）个A厂的职工，相邻两楼之间的距离为50米.A厂打算在直街上建一车站，为使这5栋楼所有A厂职工去车站所走的路程之和最小，车站应建在距1号楼米处.上海初一初中数学竞赛测试答案及解析一、选择题1.六位数由三位数重复构成，如256256，或678678等等，这类数能被何数整除(15届江苏初一2试)六位数六位数A．11;B．101;C．13;D．1001.【答案】D【解析】析：六位数由三位数重复构成，说明这类数一定能被此三位数整除，不妨用构成的六位数除以三位数得到的数即所求的数．解答：解：256256÷256=1001，678678÷678=1001，设三位数abc，则重复构成的六位数为abcabc，abcabc÷abc=1001．故选D．点评：此题考查了学生对数的整除性问题的解答与掌握，此题解答的关键是用构成的六位数除以三位数得出要求的数．2.两班学生参加一个测试，20名学生的一班，平均分是80分；30名学生的一班平均分是70分，两班所有学生的平均分是A．75分;B．74分;C．72分;D．77分.【答案】B【解析】平均数的计算方法是求出所有数据的和，然后除以数据的总个数．解答：解：根据题意得：该组数据的平均数==74．故选B．点评：本题考查的是加权平均数的求法．本题易出现的错误是求80，70这四个数的平均数，对平均数的理解不正确．3.一个数被10除余9，被9除余8，被8除余7，…，被2除余1，则此数为A．59 ;B．1259;C．2519;D．非以上结论.【答案】C【解析】分析：这个最小正整数加上1是2、3、4、5、…10的最小公倍数，求得最小公倍数减1即可求得答案．解答：解：由题意可知所求最小正整数是2，3，4，5，…，10的最小公倍数减去1，2，3，4，5，…，10的最小公倍数是实际就是7，8，9，10的最小公倍数为2520，则所求最小数是2520-1=2519．故选C．点评：此题考查了带余数除法，主要利用求几个数的最小公倍数的方法解决问题．4.0.000000375与下列数不等的是A．;B．;C．;D．.【答案】D【解析】分析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．注意小数和分数相互间的转化．解答：解：0.000 000 375=3.75×10-7=3×10-7=≠.故选D．点评：本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．5.若1+2+3+…+k之和为一完全平方，若n小于100，则k可能的值为A．8;B．1，8 ;C．8，49;D．1,8,49.【答案】D【解析】分析：本题直接求解难度较大，故采用代入法，间接验证．解答：解：∵1+2+3+…+k=k(k+1)∴k(k+1)=n2，当k=1时，则k(k+1)=1，n=1，显然成立．当k=8时，则k(k+1)=36，此时n=6，成立；当k=49时，则k(k+1)=25×49，n=35，成立．故答案为D．点评：本题考查完全平方数．同学们对于做选择题目，采用将选项代入验证的方法，有时候起到事半功倍的效果，本题就是这样，如直接求解，难度非常大，这样求解简单多了．6.若，则z等于(15届江苏初二1试)若A．;B．;C．;D．.【答案】D【解析】略7.一同学在n天假期中观察：（1）下了7次雨，在上午或下午；（2）当下午下雨时，上午是晴天；（3）一共有5个下午是晴天；（4）一共有6个上午是晴天。

近十年(2003-2012年)上海中考数学试题及答案

上海市2003年中考数学试卷一、填空题（本大题共14题，每题2分，满分28分） 1．8的平方根是________． 2．在6，8，21，4中，是最简二次根式的是________． 3．已知函数xx x f 1)(＋＝，那么)12(－f ________． 4．分解因式：1222＋－－a b a ________． 5．函数xxy －＝1的定义域是________． 6．方程x x ＝－＋＋22的根是________．7．上海浦东磁悬浮铁路全长30千米，单程运行时间约8分钟，那么磁悬浮列车的平均速度用科学记数法表示约________米／分钟．8．在平面直角坐标系内，从反比例函数)0(＞＝k xk y 的图象上的一点分别作x 、y 轴的垂线段，与x 、y 轴所围成的矩形面积是12，那么该函数解析式是________．9．某公司今年5月份的纯利润是a 万元，如果每个月份纯利润的增长率都是x ，那么预计7月份的纯利润将达到________万元（用代数式表示）．10．已知圆O 的弦AB ＝8，相应的弦心距OC ＝3，那么圆O 的半径长等于________． 11．在△ABC 中，点D 、E 分别在边AB 、AC 上，CD 平分∠ACB ，DE ∥B C ．如果AC ＝10，AE ＝4，那么BC ＝________．12．如图，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为________．13．正方形ABCD 的边长为1．如果将线段BD 绕着点B 旋转后，点D 落在BC 延长线上的点D ′处，那么tan ∠BAD ′＝________．14．矩形ABCD 中，AB ＝5，BC ＝12．如果分别以A 、C 为圆心的两圆相切，点D 在圆C 内，点B 在圆C 外，那么圆A 的半径r 的取值范围是________．二、多项选择题（本大题共4题，每题3分，满分12分．每题列出的四个答案中，至少有一个是正确的，把所有正确答案的代号填入括号内，错选或不选得0分，否则每漏选一个扣1分，直至扣完为止）15．下列命题中正确的是（）． A ．有限小数是有理数 B ．无限小数是无理数C ．数轴上的点与有理数一一对应D ．数轴上的点与实数一一对应16．已知0＜b ＜a ，那么下列不等式组中无解的是（）． A ．⎩⎨⎧b x a x ＜＞, B ．⎩⎨⎧bx a x ＜－＞－,C ．⎩⎨⎧b x a x ＜－＞,D ．⎩⎨⎧b x a x ＜＞－,17．下列命题中正确的是（）．A ．三点确定一个圆B ．两个等圆不可能内切C ．一个三角形有且只有一个内切圆D ．一个圆有且只有一个外切三角形18．如图，已知AC 平分∠P AQ ，点B 、B ′分别在边AP 、AQ 上．如果添加一个条件，即可推出AB ＝AB ′，那么该条件可以是（）．A ．BB '⊥AC B ．BC ＝B 'CC ．∠ACB ＝∠ACB 'D ．∠ABC ＝∠AB 'C三、（本大题共4题，每题7分，满分28分）19．已知222＝－x x ，将下式先化简，再求值：1)3)((3)3)((1)(2－－＋－＋＋－x x x x x ．20．解方程组21．将两块三角板如图放置，其中∠C ＝∠EDB ＝90°，∠A ＝45°，∠E ＝30°，AB ＝DE ＝6．求重叠部分四边形DBCF 的面积．22．某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示．试结合图示信息回答下列问题：（1）这32名学生培训前考分的中位数所在的等级是________，培训后考分的中位数所在的等级是________；（2）这32名学生经过培训，考分等级“不合格”的百分比由________下降到________；（3）估计该校整个初二年级中，培训后考分等级为“合格”与“优秀”的学生共有________名；（4）你认为上述估计合理吗?理由是什么?答：________，理由：_________________________．四、（本大题共4题，每题10分，满分40分）23．已知：如图，一条直线经过点A（0，4）、点B（2，0），将这条直线向左平移与x 轴负半轴、y轴负半轴分别交于点C、点D，使DB＝DC．求以直线CD为图象的函数解析式．24．已知：如图，△ABC中，AD是高，CE是中线，DC＝BE，DG⊥CE，G是垂足．求证：（1）G是CE的中点；（2）∠B＝2∠BCE．25．卢浦大桥拱形可以近似看作抛物线的一部分．在大桥截面1∶11000的比例图上，跨度AB＝5 cm，拱高OC＝0.9 cm，线段DE表示大桥拱内桥长，DE∥AB，如图（1）．在比例图上，以直线AB为x轴，抛物线的对称轴为y轴，以1 cm作为数轴的单位长度，建立平面直角坐标系，如图（2）．（1）求出图（2）上以这一部分抛物线为图象的函数解析式，写出函数定义域；（2）如果DE 与AB 的距离OM ＝0.45 cm ，求卢浦大桥拱内实际桥长（备用数据：4.12≈，计算结果精确到1米）．26．已知在平面直角坐标系内，O 为坐标原点，A 、B 是x 轴正半轴上的两点，点A 在点B 的左侧，如图．二次函数c bx ax y ＋＋＝2（a ≠0）的图象经过点A 、B ，与y 轴相交于点C ．（1）a 、c 的符号之间有何关系?（2）如果线段OC 的长度是线段OA 、OB 长度的比例中项，试证a 、c 互为倒数；（3）在（2）的条件下，如果b ＝－4，34＝AB ，求a 、c 的值．五、（本大题只有1题，满分12分，（1）、（2）、（3）题满分均为4分） 27．如图（1），在正方形ABCD 中，AB ＝1，是以点B 为圆心，AB 长为半径的圆的一段弧，点E 是边AD 上的任意一点（点E 与点A 、D 不重合），过E 作所在圆的切线，交边DC 于点F ，G 为切点．（1）当∠DEF ＝45°时，求证点G 为线段EF 的中点；（2）设AE ＝x ，FC ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；（3）将DEF 沿直线EF 翻折后得EF D 1∆，如图（2），当65＝EF 时，讨论D AD 1∆与F ED 1∆是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．（1）（2）（3）（备用图）参考答案一、填空题（本大题共14题，每题2分，满分28分）1．22± 2．6 3．22＋ 4．（a －b －1）（a ＋b －1） 5．x ≤1且x ≠0 6．x ＝－2 7．31075.3⨯ 8．xy 12＝9．2)1(x a ＋ 10．5 11．15 12．222- 13．2 14．1＜r ＜8或18＜r ＜25二、多项选择题（本大题共4题，每题3分，满分12分．错选或不选得0分，否则每漏选一个扣1分，直至扣完为止）15．A 、D 16．A 、C 17．B 、C 18．A 、C 、D 三、（本大题共4题，每题7分，满分28分）19．解：原式＝34912222＋－＋＋－x x x x x -+……………………………………3分 5632－－＝x x …………………………………………………………………………………1分解法一：5)2(32--=x x ．………………………………………………………2分 ∵ 222＝－x x ，∴ 原式＝3×2－5＝1．………………………………………1分解法二：从222＝－x x 中解得31±＝x ，1分分别代入，答案正确． (1)20．解：由①，得（2x ＋y ）（2x －y ）＝0, ∴ 2x ＋y ＝0，2x －y ＝0．…………1分，1分它们与方程②分别组成两个方程组：⎩⎨⎧;04,022＝＋－＝＋xy x y x （*）……………………………………………………………………1分⎩⎨⎧-.04,022＝＋－＝xy x y x （**）…………………………………………………………………1分分别解这两个方程组，可知方程组（*）无解；………………………………………1分方程组（**）的解是⎩⎨⎧==;4,211y x ⎩⎨⎧-=-=.4,222y x ………………………………………1分，1分所以原方程组的解是⎩⎨⎧==;4,211y x ⎩⎨⎧-=-=.4,222y x 21．解：在△EDB 中，∵ ∠EDB ＝90°，∠E ＝30°，DE ＝6， ∴ 3233630tan ＝＝⨯=︒⋅DE DB ．……………………………………………1分 ∴ 326－－＝=DB AB AD ．又∵ ∠A ＝45°，∴ ∠AFD ＝45°，得FD ＝AD ．∴ 31224)326(212122－＝－＝⨯=∆AD S ADF ．…………………………………2分在等腰直角三角形ABC 中，斜边AB ＝6，所以9412=∆AB S ABC ＝．…………… 2分∴ )31224(9－－＝＝四边形ADF ABC DBCF S S S ∆∆-＝15312－……………………2分 22．解：（1）不合格，合格；（2）75%，25%；（3）240；（4）合理，该样本是随机样本（或该样本具有代表性）．………………………………………………………每个空格1分四、（本大题共4题，每题10分，满分40分）23．解：设以直线AB 为图象的一次函数解析式为y ＝kx ＋b ．因为直线AB 经过点（0，4）、点（2，0），所以得方程组⎩⎨⎧=.20,4b k b ＋＝……………………………………………………………………………1分解得⎩⎨⎧-=.4,2＝b k …………………………………………………………………………2分所以以直线AB 为图象的一次函数解析式为y ＝－2x ＋4.由于CD ∥AB ，设以直线CD 为图象的一次函数解析式为y ＝－2x ＋b '.………2分解法一：由于DB ＝DC ，DO ⊥CB ，∴ OC OB =．………………………… 2分所以点C 的坐标是（－2，0），得b '＝－4．…………………………………1分，1分所以以直线CD 为图象的一次函数解析式为y ＝－2x －4．………………………1分解法二：由题意，得点D 的坐标是（0，b '），点C 的坐标是（2b '，0）． ∵ DB ＝DC ，∴2222)2()()(2b b b '''＋＝＋．………………………………………………………2分解得4±'＝b ．……………………………………………………………………………1分因为点D '与点A 不重合，所以4＝b '舍去．…………………………………………1分因此以直线CD 为图象的一次函数解析式为y ＝－2x －4．……………………………1分 24．证明：（1）如图，连结DE ．………………………………………………………1分 ∵ ∠ADB ＝90°，E 是AB 的中点，∴ DE ＝AE ＝BE ．………………………………………………………………………2分又∵ DC ＝BE ，∴ DC ＝DE ．………………………………………………………1分又因为DG ⊥CE ，所以G 是CE 中点．…………………………………………………2分（2）∵DE ＝DC ，∴ ∠DCE ＝∠DEC ．……………………………………………1分 ∴ ∠EDB ＝∠DEC ＋∠DCE ＝2∠BCE ．……………………………………………1分又∵ DE ＝BE ，∴ ∠B ＝∠EDB ．………………………………………………… 1分∴ ∠B ＝2∠BCE ．………………………………………………………………………1分25．解：（1）由于顶点C 在y 轴上，所以设以这部分抛物线为图象的函数解析式为1092＋＝ax y ．……………………………………………………………………………1分因为点A （25-，0）（或B （25，0））在抛物线上，所以109)25(02＋＝-⋅a ，得12518＝－a ．……………………………………………1分因此所求函数解析式为)2525(109125182≤≤-x x y ＋＝－．……………………………………………1分，1分（2）因为点D 、E 的纵坐标为209，……………………………………………………1分所以109125182092＋－x =，得245±＝x ……………………………………………2分所以点D 的坐标为（245－，209），点E 的坐标为（245，209）．所以225)245(245＝－＝-DE ．…………………………………………………1分因此卢浦大桥拱内实际桥长为385227501.011000225≈⨯⨯＝（米）．…………………………………………2分 26．（1）解：a 、c 同号．………………………………………………………………2分或当a ＞0时，c ＞0；……………………………………………………………………1分当a ＜0时，c ＜0．……………………………………………………………………1分（2）证明：设点A 的坐标为（1x ，0），点B 的坐标为（2x ，0），则210x x ＜＜． ∴ 1x OA =，2x OB =，c OC =．…………………………………………………1分据题意，1x 、2x 是方程)0(02≠=a c bx ax ＋＋的两个根．…………………………1分∴ acx x =⋅21．…………………………………………………………………………1分由题意，得2OC OB OA ＝⋅，即22c c ac ＝＝．………………………………………1分所以当线段OC 长是线段OA 、OB 长的比例中项时，a 、c 互为倒数．（3）解：当4-=b 时，由（2）知，0421＞＝＝－＋aa b x x ，∴ a ＞0．…………1分解法一：AB ＝OB －OA ＝21221124)(x x x x x x -＋＝－， ∴ aa ac a c a AB 32416)(4)4(22=-==－．……………………………………1分 ∵ 34=AB ，∴3432＝a ．得21=a ．∴ c ＝2. ……………………………………………1分解法二：由求根公式，aa a ac x 322416424164±-±-±＝＝＝，∴ ax 321-＝，a x 322+＝．∴ aa a x x OA OB AB 32323212＝－－＝－＝－＝+．………………………1分 ∵ 34＝AB ，∴ 3432＝a ，得21＝a ．∴ c ＝2…………………………………………………………………………………1分五、（本大题只有1题，满分12分） 27．（1）证明：∵ ∠DEF ＝45°，得∠DFE ＝90°－∠DEF ＝45°，∴ ∠DFE ＝∠DEF ． ∴ DE ＝DF ．又∵ AD ＝DC ，∴ AE ＝FC ．…………1分因为AB 是圆B 的半径，AD ⊥AB ，所以AD 切圆B 于点A ；………………………1分同理，CD 切圆B 于点C ．又因为EF 切圆B 于点G ，所以AE ＝EG ，FC ＝FG ．………………………………1分因此EG ＝FG ，即点G 为线段EF 的中点．……………………………………………1分（2）解：∵ EG ＝AE ＝x ，FG ＝CF ＝y ，∴ ED ＝1－x ，FD ＝1－y ．在R t △DEF 中，由222EF FD ED ＝＋，得222)()1()1(y x y x ＋－＋－= ．…………………………………………………………2分 ∴ )10(11＜＜＋－＝x xxy ．………………………………………………………1分，1分（3）解：当65=EF 时，由（2）得6511＝＋－＋x x x FC AE FG EG EF =+=+=．得311＝x 或212=x ，即31＝AE 或21＝AE ．①当21＝AE 时，D AD 1∆∽F ED 1∆．………………………………………………1分证明如下：设直线EF 交线段1DD 于点H ，如图．据题意，△EDF ≌F ED 1∆；1DD EF ⊥且H D DH 1＝． ∴ 21＝AE ，AD ＝1，得AE ＝ED ，∴ EH ∥1AD ．∴ 11FED FED AD D ∠∠∠＝＝，……………………………………………………1分 ︒∠∠901＝＝EHD D AD ．又∵ ︒=∠=∠901EDF F ED ，∴ D AD F ED 11∠=∠．………………………………………………………………1分 ∴ D AD 1∆∽F ED 1∆．②当31＝AE 时，D AD 1∆与F ED 1∆不相似．…………………………………………1分G图12004年上海市中等学校高中阶段招生文化考试数学试卷(满分120分，考试时间120分钟)一、填空题：（本大题共14题，每题2分，共28分）1．计算：(2)(2)__________a b a b -+=．2．不等式组230320x x -<⎧⎨+>⎩的整数解是______________．3．函数y =的定义域是__________________． 41x =-的根是________________． 5．用换元法解22114x x x x +++=，可设1y x x=+，则原方程可化为关于y 的方程是______________．6．一个射箭运动员连续射靶5次，所得的环数分别是8，6，10，7，9，则这个运动员所得环数的标准差为__________．7．已知0a b <<，则点A (,)a b b -在第________象限．8．正六边形是轴对称图形，它有_______条对称轴．9．在△ABC 中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，AD=1，BD ＝2，则:ADE ABC S S ∆∆=__________．10．在△ABC 中，∠A ＝90°，设∠B ＝θ，AC ＝b ，则AB ＝________(用b 和θ的三角比表示)．11．某山路坡面坡度i =沿此山路向上前进200米,升高了__________米．12．在△ABC 中，点G 是重心，若BC 边上的高为6，则点G 到BC 的距离为______________． 13．直角三角形的两条边长分别为6和8，那么这个三角形的外接圆的半径等于_______________． 14．如图1，边长为3的正方形ABCD 绕点C 按顺时针方向旋转30°后得到的正方形EFCG ，EF 交AD 与点H ，那么DH 的长为___________．二、多项选择题：(本大题共4题，每题3分，共12分)【每题列出的四个答案中，至少有一个是正确的，把所有正确答案的代号填入括号内，错选或不选得0分，否则每漏选一个扣一分，直至扣完为止】C图215．下列运算，计算结果正确的是……………………………………………（）（A ） 437a a a =；（B ） 632a a a ÷=；（C ） 325()a a =；（D ） 333()a b a b =．16．如图2，在△ABC 中，AB=AC ，∠A ＝36°，BD 平分∠ABC ，DE ∥BC 那么在下列三角形中，与相似的三角形是……………………（（A ） △DBE ；（B ） △ADE ；（C ） △ABD ；（D ） △BDC ． 17．下列命题中，正确的是…………………………（）（A ）一个点到圆心的距离大于这个圆的半径，这个点在圆外；（B ）一条直线垂直于圆的半径，这条直线一定是圆的切线；（C ）两个圆的圆心距等于它们的半径之和，这两个圆有三条公切线；（D ）圆心到一条直线的距离小于这个圆的半径，这条直线与圆有两个交点． 18．在函数(0)ky k x=>的图像上有三点111(,)A x y 、222(,)A x y 、333(,)A x y ，已知1230x x x <<<，则下列各式中，正确的是…………………………（）（A ） 130y y <<；（B ） 310y y <<；（C ） 213y y y <<；（D ） 312y y y <<．三、（本大题共4题，每题7分，共28分）19-20．关于x 的一元二次方程2(31)210mx m x m --+-=，其根的判别式的值为1，求m 的值及该方程的根．21．如图3，等腰梯形ABCD 中，AD ∥BC ，∠DBC ＝45°，翻折梯形ABCD ，使点B 重合于点D ，折痕分别交AB 、BC 于点F 、E ．若AD=2，BC ＝8，求：（1）BE 的长；（2）∠CDE 的正切值．22．某区从参加数学质量检测的8000名学生中，随机抽取了部分学生的成绩作为样本，为了节省时间，先将样本分成甲、乙两组，分别进行分析，得表一；随后汇总成样本数据，得到部分结果，如表二．（1）样本中，学生的数学成绩的平均分数约为_________分（结果精确到0.1分）；（2）样本中,数学成绩在[)84,96分数段的频数________，等第为A 的人数占抽样学生总数的百分比为_________，中位数所在的分数段为______________；（3）估计这8000名学生成绩的平均分数约为__________分（结果精确到0.1分）．四、（本大题共4题，每题10分，共40分）23．在平面直角坐标系中，点O 是坐标原点，二次函数)4()5(2+--+=k x k x y 的图像交x 轴于A )0,(1x 、B )0,(2x ，且8)1)(1(21-=++x x ．图4 （1）求二次函数的解析式；（2）将上述二次函数的图像沿x 轴向右平移2个单位，设平移后的图像与y 轴的交点为C ，顶点为P ，求△POC 的面积．24．如图４，在△ABC 中，∠BAC ＝90°，延长BA 到点D ，使AD ＝21AB ，点E 、F 分别为边BC 、AC 的中点．（1）求证：DF=BE ；（2）过点A 作AG ∥BC ，交DF 于点G ，求证：AG=DG25．为加强防汛工作，市工程队准备对苏州河一段长为2240米的河堤进行加固．由于采用新的加固模式，现在计划每天加固的长度比原计划增加了20米，因而完成此段加固工程所需天数将比原计划缩短2天．为进一步缩短该段加固工程的时间，如果要求每天加固224米，那么在现在计划的基础上，每天加固的长度还要再增加多少米？A BCO图5如图6，在平面直角坐标系中，O 为坐标原点，A 点的坐标为(1，0)，点B 在x 轴上，且在点A 的右侧，AB=OA ，过点A 和B 作x 轴的垂线，分别交二次函数2x y =的图像于点C和D ，直线OC 交BD 于点M ，直线CD 交y 轴于点H ，记点C 、D 的的横坐标分别为C x 、D x ，点H 的纵坐标为H y ．26．在△ABC 中，∠BAC ＝90°，AB=AC=22，⊙A 的半径为1，如图5所示．若点O 在BC 上运动（与点B 、C 不重合），设BO ＝x ，△AOC 的面积为y（1）求关于的函数解析式，并写出函数的定义域；（2）以点O 为圆心，BO 长为半径作⊙O ，求当⊙O 与⊙A 相切时，△AOC 的面积．五、（本大题只有1题，满分12分，（1）小题满分6分，（2）（3）小题满分均为3分）27．数学课上，老师出示图6和下面框中的条件．同学发现两个结论：①3:2:ABMC ＝梯形S S CMD ∆ ②数值相等关系：H D C y x x -=∙ （1）请你验证结论①和结论②成立；（2）请你研究：如果上述框中的条件“A 的坐标(1，0)”改为“A 的坐标(t ，0) (t>0)”，其他条件不变，结论①是否仍成立？（请说明理由）（3）进一步研究：如果上述框中的条件“A 的坐标(1，0)”改为“A 的坐标(t ，0) (t>0)”，又将条件“2x y =”改为“)0(2>=a ax y ”，其他条件不变，那么C x 、D x 与H y 有怎样的数值关系？写出结果并说明由）12005年上海市初中毕业生统一学业考试数学试卷一、填空题（本大题共14题，满分42分） 1、计算：()22x＝2、分解因式：22a a -＝ 3、计算：)11＝4、函数y =的定义域是5、如果函数()1f x x =+，那么()1f =6、点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是7、如果将二次函数22y x =的图象沿y 轴向上平移1个单位，那么所得图象的函数解析式是8、已知一元二次方程有一个根为1，那么这个方程可以是（只需写出一个方程） 9、如果关于x 的方程240x x a ++=有两个相等的实数根，那么a ＝ 10、一个梯形的两底长分别为6和8，这个梯形的中位线长为 11、在△ABC 中，点D 、E 分别在边AB 和AC 上，且DE ∥BC ，如果AD ＝2，DB ＝4，AE ＝3，那么EC ＝ 12、如图1，自动扶梯AB 段的长度为20米，倾斜角A 为α，高度BC 为米(结果用含α的三角比表示).13、如果半径分别为2和3的两个圆外切，那么这两个圆的圆心距是 14、在三角形纸片ABC 中，∠C ＝90°，∠A ＝30°，AC ＝3，折叠该纸片，使点A 与点B 重合，折痕与AB 、AC 分别相交于点D 和点E （如图2），折痕DE 的长为二选择题：（本大题共4题，满分12分） 15、在下列实数中，是无理数的为（） A 、0 B 、－3.5 C D 16、六个学生进行投篮比赛，投进的个数分别为2、3、3、5、10、13，这六个数的中位数为（）A 、3B 、4C 、5D 、6图117、已知Rt △ABC 中，∠C ＝90°，AC ＝2，BC ＝3，那么下列各式中，正确的是（）A 、2sin 3B =B 、2cos 3B =C 、23tgB =D 、23ctgB = 18、在下列命题中，真命题是（）A 、两个钝角三角形一定相似B 、两个等腰三角形一定相似C 、两个直角三角形一定相似D 、两个等边三角形一定相似三、（本大题共3题，满分24分） 19、（本题满分8分）解不等式组：()315216x xx x +>-⎧⎨+-<⎩，并把解集在数轴上表示出来.20、（本题满分8分）解方程：228124x x x x x +-=+--21、（本题满分8分，每小题满分各为4分）（1）在图3所示编号为①、②、③、④的四个三角形中，关于y 轴对称的两个三角形的编号为；关于坐标原点O 对称的两个三角形的编号为；（2）在图4中，画出与△ABC 关于x 轴对称的△A 1B 1C 1x-5-4-3-2-15432O1四、（本大题共4题，满分42分） 22、（本题满分10分，每小题满分各为5分）在直角坐标平面中，O 为坐标原点，二次函数2y x bx c =++的图象与x 轴的负半轴相交于点C （如图5），点C 的坐标为（0，－3），且BO ＝CO （1）求这个二次函数的解析式；（2）设这个二次函数的图象的顶点为M ，求AM 的长.23、（本题满分10分）已知：如图6，圆O 是△ABC 的外接圆，圆心O 在这个三角形的高CD 上，E 、F 分别是边AC 和BC 的中点，求证：四边形CEDF 是菱形.24、（本题满分10分，第（1）、（2）、（3）小题满分各为2分，第（4）小题满分4分）小明家使用的是分时电表，按平时段（6：00－22：00）和谷时段（22：00－次日6：00）分别计费，平时段每度电价为0.61元，谷时段每度电价为0.30元，小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示（如图7），同时将前4个月的用电量和相应电费制成表格（如表1）根据上述信息，解答下列问题：（1）计算5月份的用电量和相应电费，将所得结果填入表1中；（2）小明家这5个月的月平均用电量为度；（3）小明家这5个月的月平均用电量呈趋势（选择“上升”或“下降”）；这5个月每月电费呈趋势（选择“上升”或“下降”）；（4）小明预计7月份家中用电量很大，估计7月份用电量可达500度，相应电费将达243元，请你根据小明的估计，计算出7月份小明家平时段用电量和谷时段用电量.25、（本题满分12分，每小题满分各为4分）在△ABC 中，∠ABC ＝90°，AB ＝4，BC ＝3，O 是边AC 上的一个动点，以点O 为圆心作半圆，与边AB 相切于点D ，交线段OC 于点E ，作EP ⊥ED ，交射线AB 于点P ，交射线CB 于点F 。

《圆的基本性质》奥数复习题

《圆的基本性质》复习题姓名学号一、填空题1.如果圆中一条弦长与半径相等，那么此弦所对的圆周角的度数为 .2.在Rt ΔABC 中，AB ＝6，BC ＝8，则这个三角形的外接圆直径是3.在等边三角形ABC 外有一点D ，满足AD=AC ，则∠BDC= 。

4.在四边形ABCD 中，AB=BC=AC=AD ，AH ⊥CD 于H ，CP ⊥BC 交AH 于P ，若AP=l ，则BD=5.如图，点A 、B 、Q 、D 、C 在圆上，BQ 与QD 分别是42°和38°，则∠P+∠Q= . 6．（1998年全国初中数学竞赛试题）已知圆环内直径为a cm ，外直径为b cm ，将50个这样的圆环一个接一个环套地连成一条锁链，那么这条锁链拉直后的长度为 cm 。

7.如图，扇形MON 中,∠MON=90°,过线段MN 的中点A 作AB ∥ON ，交MN 于B ，∠BON= 8.（2008年蚌埠二中自主招生考试数学素质测试题）已知⊙O 的半径1=OA ，弦AB 、AC 的长分别是2、3，则BAC ∠的度数是。

9.（2006年“TRULY 信利杯”全国初中数学竞赛初赛试题）半径为2的⊙O 中，弦AB 与弦CD 垂直相交于点P ，连结OP ，若OP ＝1，则AB ²＋CD ²的值为。

10.如图，在△ABC 中，∠A= 70°，⊙O 截△ABC 的三边所截得的弦长都相等，则∠BOC= .11.如图，△ABC 内接于直径为d 的圆．设BC=a ，AC=b ，那么△ABC 的高 CD= .12.（北京市竞赛题）如图所示，正方形ABCD 的中心为O ，面积为1989 cm ²，P 为正方形内一点，且∠OPB=45°，PA ：PB=5：14，则PB 的长为。

13.如图，在直径为20cm 的半圆0上P 、Q 两点，PC ⊥ AB 于C,QD ⊥AB 于D,QE ⊥ PO 于 E,AC=4cm ，则DE= cm.14.已知P 是正方形ABCD 内的一点，O 为正方形的中心，AP⊥BP ，OP=，PA=6，则正方形ABCD 的边长为。

历年初中数学竞赛真题库含答案

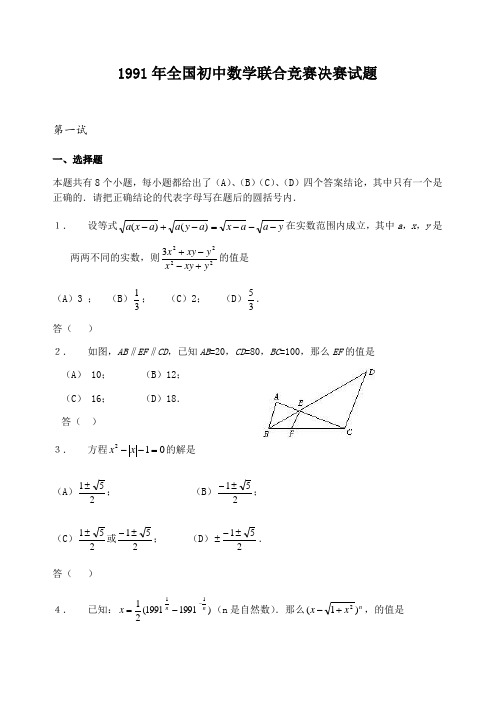
1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题，每小题都给出了（A ）、（B ）（C ）、（D ）四个答案结论，其中只有一个是正确的．请把正确结论的代表字母写在题后的圆括号内．１．设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立，其中a ，x ，y 是两两不同的实数，则22223yxy x y xy x +--+的值是（A ）3 ；（B ）31；（C ）2；（D ）35．答（）２．如图，AB ‖EF ‖CD ，已知AB =20，CD =80，BC =100，那么EF 的值是（A ） 10；（B ）12；（C ） 16；（D ）18．答（）３．方程012=--x x 的解是（A ）251±；（B ）251±-；（C ）251±或251±-；（D ）251±-±．答（）４．已知：)19911991(2111n n x --=（n 是自然数）．那么n x x )1(2+-，的值是（Ａ）11991-；（Ｂ）11991--；（Ｃ）1991)1(n -；（Ｄ）11991)1(--n ．答（）５．若M n 1210099321=⨯⨯⨯⨯⨯ ，其中Ｍ为自然数，n 为使得等式成立的最大的自然数，则Ｍ（Ａ）能被２整除，但不能被３整除；（Ｂ）能被３整除，但不能被２整除；（Ｃ）能被４整除，但不能被３整除；（Ｄ）不能被３整除，也不能被２整除．答（）６．若a ，c ，d 是整数，b 是正整数，且满足c b a =+，d c b =+，a d c =+，那么 d c b a +++的最大值是（Ａ）1-；（Ｂ）5-；（Ｃ）0；（Ｄ）１．答（）７．如图，正方形OPQR 内接于ΔABC ．已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ，32=S 和13=S ，那么，正方形OPQR 的边长是（Ａ）2；（Ｂ）3；（Ｃ）2 ；（Ｄ）3．答（）８．在锐角ΔABC 中，1=AC ，c AB =， 60=∠A ，ΔABC 的外接圆半径R ≤1，则（Ａ）21< c < 2 ；（Ｂ）0< c ≤21；答（）（C ）c > 2；（D ）c = 2．答（）二、填空题１．Ｅ是平行四边形ABCD 中BC 边的中点，AE 交对角线BD 于G ，如果ΔBEG 的面积是１，则平行四边形ABCD 的面积是．２．已知关于x 的一元二次方程02=++c bx ax 没有实数解．甲由于看错了二次项系数，误求得两根为２和４；乙由于看错了某一项系数的符号，误求得两根为－１和４，那么，=+ac b 32 ．3．设m ，n ，p ，q 为非负数，且对一切x >０，qpn m x x x x )1(1)1(+=-+恒成立，则 =++q p n m 22)2( ．４．四边形ABCD 中，∠ ABC 135=，∠BCD 120=，AB 6=，BC 35-=，CD = 6，则AD = ．第二试x + y ， x － y ， x y ， yx 四个数中的三个又相同的数值，求出所有具有这样性质的数对（x , y ）．二、ΔABC中，AB＜AC＜BC，D点在BC上，E点在BA的延长线上，且BD＝BE＝AC，ΔBDE的外接圆与ΔABC的外接圆交于F点（如图）．求证：BF＝AF＋CF三、将正方形ABCD分割为2n个相等的小方格（n是自然数），把相对的顶点A，C染成红色，把B，D染成蓝色，其他交点任意染成红、蓝两色中的一种颜色．证明：恰有三个顶点同色的小方格的数目必是偶数．1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点，又AB PE ⊥于E 点，若3,2==AC BC ，则=⋅EB AE .4.若b a ,都是正实数，且0111=+--b a b a ，则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根，当这样的三角形只有一个时，求a 的取值范围.二、如图，在ABC ∆中，D AC AB ,=是底边BC 上一点，E 是线段AD 上一点，且A CED BED ∠=∠=∠2.求证：CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0，1，2，3，5，6这六个不同数字组成，现有四个编码如下：A ：320651B ：105263C ：612305D ：316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求：M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8：30—9：30)考生注意：本试共两道大题，满分80分.一、选择题（本题满分48分，每小题6分）本题共有8个小题都给出了A，B、C，D，四个结论，其中只有一个是正确的，请把你认为正确结论的代表字母写在题后答案中的圆括号内，每小题选对得6分；不选、选错或选出的代表字母超过一个（不论是否写在圆括号内），一律得0分.〔答〕( )2．设a,b,c是不全相等的任意实数，若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA．都不小于0B．都不大于0C．至少有一个小0于D．至少有一个大于0〔答〕( )3．如图1所示，半圆O的直径在梯形ABCD的底边AB上，且与其余三边BC，CD，DA相切，若BC=2，DA=3，则AB的长A．等于4B．等于5C．等于6D．不能确定〔答〕( )A．1 B．-1 C．22001D．-22001〔答〕( )5．若平行直线EF，MN与相交直线AB，CD相交成如图2所示的图形，则共得同旁内角A．4对B．8对C．12对D．16对〔答〕( )〔答〕( )7．设锐角三角形ABC的三条高AD，BE，CF相交于H。

【数学竞赛】2003年全国初中数学联赛试卷及答案

【数学竞赛】2003年全国初中数学联赛试卷第一试（4月13日上午8:30—9:30）一、选择题（本题满分42分，每小题7分）1.A .5-B .1C .5D .1[答]（）2.在凸10边形的所有内角中，锐角的个数最多是A .0B .1C .3D .5[答]（）3.若函数()0y kx k =>与函数1y x=的图象相交于A ，C 两点，AB 垂直x 轴于B ，则△ABC 的面积为 A .1 B .2 C .k D .2k[答]（）4.满足等式2003的正整数对()x y ，的个数是A .1B .2C .3D .4[答]（）5.设△ABC 的面积为1，D 是边AB 上一点，且13AD AB =．若在边AC 上取一点E ，使四边形DECB 的面积为34，则CE EA的值为 A .12 B .13 C .14 D .15[答]（）6.如图，在□ABCD 中，过A ，B ，C 三点的圆交AD 于E ，且与CD 相切．若AB =4，BE =5，则DE 的长为A .3B .4C .154D .165[答]（） D CA B E二、填空题（本题满分28分，每小题7分）1.抛物线2y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ．若△ABC 是直角三角形，则ac =__________．2.设m 是整数，且方程2320x mx +-=的两根都大于95-而小于37，则m =____________． 3.如图，'AA ，'BB 分别是∠EAB ，∠DBC 的平分线．若''AA BB AB ==，则∠BAC 的度数为_____________．4.已知正整数a ，b 之差为120，它们的最小公倍数是其最大公约数的105倍，那么a ，b 中较大的数是_________．2003年全国初中数学联合竞赛试卷第二试（A ）（4月13日上午10:00—11:30）考生注意：本试三大题，第一题20分，第二、三题各25分，全卷满分70分．一、（本题满分20分）试求出这样的四位数，它的前两位数字与后两位数字分别组成的二位数之和的平方，恰好等于这个四位数．二、（本题满分25分）。

宇振杯上海市数学竞赛题

宇振杯上海市数学竞赛题
姓名：__________
指导：__________
日期：__________
首先这道题包含了全等三角形的判定与性质、图形的旋转以及根的判别式。

接下来老师会带领大家对这部分的知识点进行一下复习。

【全等三角形的判定与性质】
1.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具，在判定三角形全等时，关键是选择恰当的判定条件.
2.在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形.
【根的判别式】
复习完知识点后，我们接着来分析这道题：第(1)问可以作辅助线，构建三角形
全等，根据三角形的周长和正方形的边长得到MN=EM,证明△NAM≌△EAM(SSS),即可求出∠NAM=45°;第(2)问，由（1)知：△NAM≌△EAM,即△AMN中MN边上的高不变等于AB,等于1,所以当MN最小时，△AMN的面积最小，设CM=a,CN=b,MN=2-a-b,根据一元二次方程和二次函数的取值可解答，具体解题思路如下：
今天的试题分享就到这里，也欢迎大家下方留言或评论，来一起说说你们的想法或建议吧!。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2003年（宇振杯）上海市初中数学竞赛试题
（2003年12月7日上午9∶00~11∶00）
一、填空题（本大题10小题，前5题每题6分、后5题每题8分，共70分.）
1、设曲线C 为函数2(0)y ax bx c a =++≠的图象，C 关于y 轴对称的曲线为C 1，C 1关于x 轴对称的曲线为C 2，则曲线C 2是函数y ＝＿＿＿＿＿＿＿＿的图象.
2、甲、乙两商店某种铅笔标价都是1元。

一天学生小王欲购这种铅笔，发现甲、乙两商店都让利优惠：甲痁实行每买5支送1支（不足5支不送），乙店实行买4支或4支以上打8.5折，小王买13支这种铅笔，最少需要化＿＿＿＿＿元。

3、已知实数a 、b 、c 满足0a b c ++=，2220.1a b c ++=，则444a b c ++的值是＿＿＿.
4、已知凸四边形ABCD 的四边长为AB ＝8，BC ＝4，CD ＝DA ＝6，则用不等式表示∠A 大小的范围是＿＿＿＿＿＿。

5、在1，2，3，…，2003中有些正整数n ，使得2x x n +-能分解为两个整系数一次式的乘积，则这样的n 共有＿＿＿＿＿个。

6、设正整数m ，n 满足m < n ，且
()()22211112311m m n n m m +++=+++++，则m n +的值是＿＿＿＿。

7、数1，2，3，…，2k 按下列方式排列：
1 2 …
k 1k + 2k + …
2k ……
()11k k -+ ()12k k -+
… 2k
任取其中一数，并划去该数所在的行与列；这样做了k 次后，所取出的k 个数的和是＿＿＿。

8、如图，边长为1的正三角形ANB 放置在边长为MN ＝3，NP ＝4的正方形MNPQ 内，且NB 在边NP 上。

若正三角形在长方形内沿着边NP 、PQ 、QM 、MN 翻转一圈后回到原来起始位置，则顶点A 在翻转过程中形成轨迹的总长是＿＿＿＿＿（保留π）。

（第8题图）1P Q M （第9题图）
M
N
C B
A
9、如图，△ABC 中，AB ＝BC ＝10，点M 、N 在BC 上，使得MN ＝AM ＝4，∠MAC ＝∠
BAN ，则△ABC 的面积是＿＿＿＿。

10、△ABC 中，∠C ＝3∠A ，AB ＝10，BC ＝8，则AC 的长是＿＿＿＿。

二、（本题16分）
m ，n 均为正整数，若关于x 的方程2420x mx n -+=的两个实数根都大于1，且小于2，求m ，n 的值。

三、（本题16分）
如图，正方形ABCD 的边长为1，点M 、N 分别在BC 、CD
上，使得△CMN 的周长为2。

求
（1）∠MAN 的大小；
（2）△MAN 面积的最小值。

四、（本题18分）
某学生为了描点作出函数2(0)y ax bx c a =++≠的图象，取自变量的7个值：
127x x x <<<，且213276x x x x x x -=-==-，分别算出对应的y 的值，列出下表：
但由于粗心算错了其中一个y 值。

请指出算错的是哪一个值？正确的值是多少？并说明
理由。

M N D C B A。