二次函数图象和性质练习题(1)
初中数学二次函数的图象与性质基础练习题A1(附答案详解)

初中数学二次函数的图象与性质基础练习题1(附答案详解)1.将二次函数2y x 的图像向上平移1个单位,则所得的二次函数表达式为( ) A .2(1)y x =- B .21y x =+ C .2(1)y x =+ D .21y x =-2.如图,二次函数243y x x =-+的图象交x 轴于A ,B 两点,交y 轴于C ,则ABC的面积为( )A .6B .4C .3D .13.在平面直角坐标系中,二次函数y=2(x ﹣1)2+3的顶点坐标是( )A .(1,3)B .(1,﹣3)C .(﹣1,3)D .(﹣1,﹣3) 4.将二次函数y=x 2-4x+2化为顶点式,正确的是( )A .2y (x 2)2=--B .2y (x 2)3=-+C .2y (x 2)2=+-D .2y (x 2)2=-+5.二次函数2y 3x 4=-的图象是一条抛物线,下列关于该抛物线的说法正确的是( ) A .抛物线开口向下B .抛物线经过点()3,4C .抛物线的对称轴是直线x 1=D .抛物线与x 轴有两个交点6.抛物线y =-2x 2经过平移后得到抛物线y =-2x 2-4x -5,平移方法是( )A .向左平移1个单位,再向下平移3个单位B .向左平移1个单位,再向上平移3个单位C .向右平移1个单位,再向下平移3个单位D .向右平移1个单位,再向上平移3个单位7.二次函数y =ax 2+bx +c 的图象如图所示,则一次函数y =ax +b 与反比例函数y =c x的大致图象是( ) A . B . C . D .8.若点()111,P y -,()222,P y -,()331,P y ,都在函数223y x x =-+的图象上,则( )A .213y y y << B .123y y y << C .213y y y >>D .123y y y >>9.已知二次函数y=x 2﹣bx+2(﹣2≤b≤2),当b 从﹣2逐渐增加到2的过程中,它所对应的抛物线的位置也随之变动,下列关于抛物线的移动方向的描述中,正确的是( ) A .先往左上方移动,再往左下方移动B .先往左下方移动,再往左上方移动C .先往右上方移动,再往右下方移动D .先往右下方移动,再往右上方移动10.如图,抛物线与x 轴交于点()1,0-和()3,0,与y 轴交于点()0,3-则此抛物线对此函数的表达式为( )A .223y x x =++B .223y x x =--C .223y x x =-+D .223y x x =+- 11.在平面直角坐标系中,若将抛物线y=2x 2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是__________。
二次函数的图像与性质经典练习题(11套)附带详细答案

练习一1.二次函数的图像开口向____,对称轴是____,顶点坐标是____,图像有最___点,x ___时,y 随x 的增大而增大,x ___时,y 随x 的增大而减小。
2.关于,,的图像,下列说法中不正确的是( )A .顶点相同B .对称轴相同 C .图像形状相同D .最低点相同 2y ax =213y x =2y x =23y x =3.两条抛物线与在同一坐标系内,下列说法中不正确的是( )A .顶点相同B .对称轴相同 C .开口方向相反 D .都有最小值4.在抛物线上,当y <0时,x 的取值范围应为( )A .x >0B .x <0C .x ≠0D .x ≥05.对于抛物线与下列命2y x =2y x =-2y x =-2y x =2y x =-题中错误的是( )A .两条抛物线关于轴对称B .两条抛物线关于原点对称C .两条抛物线各自关于轴对称D .两条抛物线没有公共点6.抛物线y=-b +3的对称轴是___,顶点是___。
7.抛物线y=--4的开口向___,顶点坐标___,对称轴___,x ___时,y 随x y 2x 21(2)2xx 的增大而增大,x ___时,y 随x 的增大而减小。
8.抛物线的顶点坐标是( )A .(1,3)B .(1,3)C .(1,3)D .(1,3) 9.已知抛物线的顶点为(1,2),且通过(1,10),则这条抛物线的表达式为( )A .y=3-2 B .y=3+222(1)3y x =+-------2(1)x -2(1)x +C .y=3-2 D .y=-3-210.二次函数的图像向左平移2个单位,向下平移3个单位,所得新函数表达式为( )A .y=a+3 B .y=a -3C .y=a +3D .y=a-311.抛物线的顶点坐标是( )2(1)x +2(1)x +2y ax =2(2)x -2(2)x -2(2)x +2(2)x +244y x x =--A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)12.对抛物线y=-3与y=-+4的说法不正确的是( )A .抛物线的形状相同B .抛物线的顶点相同C .抛物线对称轴相同D .抛物线的开口方向相反13.函数y=a +c 与y=ax +c(a ≠0)在同一坐标系内的图像22(2)x -22(2)x -2x是图中的( )14.化为y=为a 的形式是____,图像的开口向____,顶点是____,对称轴是____。
人教版九年级上《22.1二次函数的图象和性质》练习题含答案
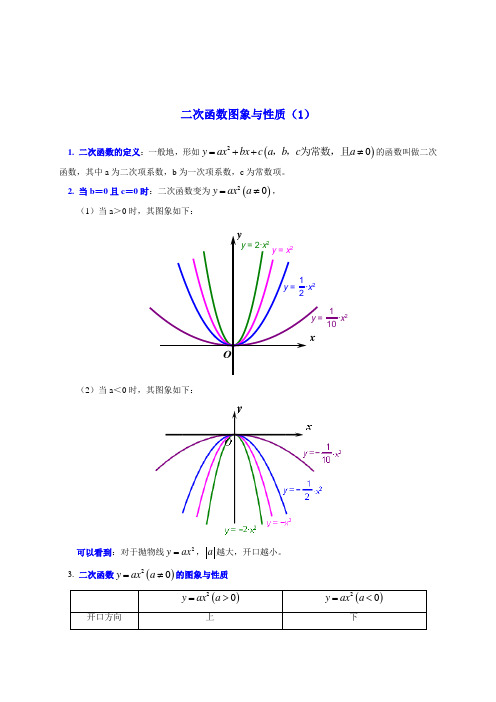
二次函数图象与性质(1)1. 二次函数的定义:一般地,形如()20y ax bx c a b c a =++≠,,为常数,且的函数叫做二次函数,其中a 为二次项系数,b 为一次项系数,c 为常数项。
2. 当b =0且c =0时:二次函数变为()20y ax a =≠, (1)当a >0时,其图象如下:xyy = 2∙x 2y = x 2y = 12∙x 2y =110∙x 2O(2)当a <0时,其图象如下:可以看到:对于抛物线2y ax =,a 越大,开口越小。
3. 二次函数()20y axa =≠的图象与性质()20y ax a =>()20y ax a =<开口方向上下例题1 已知函数42)2(-++=k kx k y 是二次函数,且当0>x 时,y 随x 的增大而增大。
(1)求k 的值;(2)写出抛物线的顶点坐标和对称轴。
思路分析:由二次函数的定义,求出k 的值,然后写出顶点坐标和对称轴。
答案:(1)由二次函数的定义,得242k k +-=,解得13k =-,22k =;当3k =-时,原函数为2y x =-,当0>x 时,y 随x 的增大而减小,故3k =-不合题意,舍去; 当2k =时,原函数为24=y x ,当0>x 时,y 随x 的增大而增大,符合题意; 故2k =。
(2)抛物线24=y x 的顶点坐标为(0,0),对称轴为y 轴。
点评:注意对k 的值进行合理的取舍。
例题2 (1)已知A (1,y 1)、B (-2,y 2)、C (-2,y3)在函数y =241x 的图象上,则y 1、y 2、y 3的大小关系是 。
(2)(潍坊)已知函数y 1=x 2与函数y 2=- 12x +3的图象大致如图,若y 1<y 2,则自变量x的取值范围是 。
思路分析:(1)最直接的思路是将自变量的值代入函数表达式,求出每个点的相应的纵坐标,然后进行比较;当然也可以利用数形结合、以形助数的方法。
二次函数的图象和性质练习题(含参考答案)

新华师大版九年级下册数学第26章 二次函数的图象和性质部分练习题姓名____________ 时间: 90分钟 满分:120分 总分____________一、选择题(每小题10分,共30分)1. 将抛物线2x y =向右平移2个单位,再向上平移1个单位,所得新抛物线对应的函数表达式为 【 】 (A )()122++=x y (B )()122-+=x y(C )()122+-=x y (D )()122--=x y2. 将抛物线()312+-=x y 向左平移1个单位,得到的抛物线与y 轴的交点坐标是 【 】(A )(0 , 2) (B )(0 , 3) (C )(0 , 4) (D )(0 , 7)3. 抛物线321532-⎪⎭⎫⎝⎛+-=x y 的顶点坐标是 【 】(A )⎪⎭⎫ ⎝⎛-3,21 (B )⎪⎭⎫ ⎝⎛--3,21 (C )⎪⎭⎫ ⎝⎛3,21 (D )⎪⎭⎫⎝⎛-3,214. 抛物线322++=x x y 的对称轴是 【 】 (A )直线1=x (B )直线1-=x (C )直线2-=x (D )直线2=x5. 在平面直角坐标系中,将抛物线221x y -=先向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线的解析式为 【 】(A )23212---=x x y (B )21212-+-=x x y (C )23212-+-=x x y (D )21212---=x x y6. 关于抛物线()212--=x y ,下列说法错误的是 【 】(A )顶点坐标为()2,1- (B )对称轴是直线1=x(C )开口向上 (D )当1>x 时,y 随x 的增大而减小7. 如图所示,把抛物线2x y =沿直线x y =向右平移2个单位后,其顶点在直线上的A 处,平移后的抛物线解析式是 【 】(A )()112-+=x y (B )()112++=x y(C )()112+-=x y (D )()112--=x y第 7 题图8. 关于二次函数1422-+=x x y ,下列说法正确的是 【 】 (A )图象与y 轴的交点坐标为(0 , 1) (B )图象的对称轴在y 轴的右侧 (C )当0<x 时,y 的值随x 值的增大而减小 (D )y 的最小值为3-9. 抛物线1822-+-=x x y 的顶点坐标为 【 】 (A )(7,2-) (B )(2 , 7) (C )(2 ,25-) (D )(2 ,9-)10. 已知二次函数()12+-=h x y ,在自变量x 的值满足1≤x ≤3的情况下,与其对应的函数值y 的最小值为5,则h 的值为 【 】 (A )1或5- (B )1-或5 (C )1或3- (D )1或3 二、填空题(每小题3分,共30分)11. 抛物线()5232+-=x y 的顶点坐标为_________.12. 将抛物线2x y =向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为________________.13. 用配方法将二次函数982--=x x y 化为()k h x a y +-=2的形式为________________.14. 抛物线132+-=x x y 的顶点坐标为_________. 15. 抛物线x x y 92+-=的最大值为_________.16. 将抛物线()2432+-=x y 向右平移1个单位,再向下平移3个单位,平移后抛物线的解析式是________________. 17. 已知点()1,4y A ,()2,2y B,()3,2y C -都在二次函数()122--=x y 的图象上,则321,,y y y 的大小关系是__________.18. 抛物线m x x y +-=22与x 轴只有一个交点,则m 的值为_________.19. 已知点()11,y x A ,()22,y x B 为函数()3122+--=x y 图象上的两点,若121>>x x ,则21,y y 的大小关系是__________.20. 如图,把抛物线221x y =平移得到抛物线m ,抛物线m 经过点()0,8-A 和原点O (0 , 0),它的顶点为P ,它的对称轴与抛物线221x y =交于点Q ,则图中阴影部分的面积为_________.三、解答题(共60分) 21.(10分)已知抛物线()31432--=x y . (1)写出抛物线的开口方向、对称轴;(2)函数y 有最大值还是最小值?并求出这个最值;(3)设抛物线与y 轴的交点为P ,与x 轴的交点为Q ,求直线PQ 的函数表达式.22.(10分)已知二次函数的图象以()4,1-A 为顶点,且过点()5,2-B . (1)求该函数的关系式;(2)求该函数的图象与坐标轴的交点坐标.23.(10分)已知抛物线c bx ax y ++=2的顶点坐标为()1,4-,与y 轴交于点(0 , 3),求这条抛物线的函数表达式.24.(10分)如图,在平面直角坐标系中,把抛物线2x y =向左平移1个单位,再向下平移4个单位,得到抛物线()k h x y +-=2.所得抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y轴交于点C ,顶点为D . (1)求k h ,的值; (2)判断△ACD 的形状.yxDC BA O25.(10分)已知抛物线22212-+-=x x y . (1)写出此抛物线的开口方向、对称轴和顶点坐标; (2)求出抛物线与x 轴、y 轴的交点坐标;(3)在(2)中,设抛物线与y 轴交于点A ,与x 轴交于点B ,若以点A 为顶点的抛物线经过点B ,请你求出这条抛物线的解析式,并指出其开口方向和函数的最值.26.(10分)已知二次函数m x x y ++=22的图象1C 与x 轴有且只有一个公共点. (1)求1C 的顶点坐标;(2)将1C 向下平移若干个单位后,得抛物线2C ,如果2C 与x 轴的一个交点为()0,3-A ,求2C 的函数关系式,并求2C 与x 轴的另一个交点坐标;(3)若()1,y n P ,()2,2y Q 是1C 上的两点,且21y y >,求实数n 的取值范围.新华师大版九年级下册数学第26章 二次函数的图象和性质练习题参考答案一、选择题(每小题3分,共30分)二、填空题(每小题3分,共30分)11. (2 , 5) 12. ()522-+=x y 13. ()2542--=x y 14. ⎪⎭⎫⎝⎛-45,2315.481 16. ()1532--=x y 17. 312y y y << 18. 1 19. 21y y < 20. 32三、解答题(共60分) 21.(10分)已知抛物线()31432--=x y . (1)写出抛物线的开口方向、对称轴; (2)函数y 有最大值还是最小值?并求出这个最值;(3)设抛物线与y 轴的交点为P ,与x 轴的交点为Q ,求直线PQ 的函数表达式. 解:(1)开口向上,对称轴为直线1=x ; ……………………………………………2分 (2)函数y 有最小值,最小值为3-=y ; ……………………………………………4分 (3)令0=x ,则()49310432-=--⨯=y ∴⎪⎭⎫ ⎝⎛-49,0P ……………………………5分令0=y ,则()031432=--x 解之得:3,121=-=x x∴()0,1-Q 或Q (3 , 0)……………………………………………6分 设直线PQ 的函数表达式为b kx y +=当⎪⎭⎫ ⎝⎛-49,0P ,()0,1-Q 时⎪⎩⎪⎨⎧=+--=049b k b 解之得:⎪⎪⎩⎪⎪⎨⎧-=-=4949b k∴直线PQ 的函数表达式为4949--=x y ; ……………………………………………8分当⎪⎭⎫ ⎝⎛-49,0P , Q (3 , 0)时⎪⎩⎪⎨⎧=+-=0349b k b 解之得:⎪⎪⎩⎪⎪⎨⎧-==4943b k∴直线PQ 的函数表达式为4943-=x y …………………………………………10分 综上所述,直线PQ 的函数表达式为4949--=x y 或4943-=x y . 22.(10分)已知二次函数的图象以()4,1-A 为顶点,且过点()5,2-B . (1)求该函数的关系式;(2)求该函数的图象与坐标轴的交点坐标. 解:(1)由题意可设该函数的关系式为()k h x a y +-=2∵其顶点为()4,1-A ∴4,1-==k h……………………………………………2分 ∴()412--=x a y把()5,2-B 代入()412--=x a y 得:()54122-=--⨯a解之得:1-=a……………………………………………4分 ∴该函数的关系式为()412---=x y ;(2)令0=x ,则()54102-=---=y∴该函数的图象与y 轴的交点为()5,0-;……………………………………………7分 令0=y ,则()0412=---x∴()412-=-x∴方程无实数解∴该函数的图象与x 轴无交点.…………………………………………10分 23.(10分)已知抛物线c bx ax y ++=2的顶点坐标为()1,4-,与y 轴交于点(0 , 3),求这条抛物线的函数表达式.解:由题意可设该抛物线为()k h x a y +-=2∵其顶点坐标为()1,4- ∴1,4-==k h……………………………………………4分 ∴()142--=x a y把(0 , 3)代入()142--=x a y 得:()31402=--⨯a……………………………………………6分 解之得:41=a …………………………………………10分 ∴这条抛物线的函数表达式为()14412--=x y . 24.(10分)如图,在平面直角坐标系中,把抛物线2x y =向左平移1个单位,再向下平移4个单位,得到抛物线()k h x y +-=2.所得抛物线与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D . (1)求k h ,的值; (2)判断△ACD 的形状.解:(1)平移后,抛物线的解析式为()412-+=x y……………………………………………3分 ∴4,1-=-=k h ;……………………………………………5分 (2)令0=y ,则()0412=-+x解之得:1,321=-=x x ∵点A 在点B 的左边 ∴()0,3-A ,B (1 , 0)……………………………………………6分 ∴3=OA令0=x ,则()34102-=-+=y∴()3,0-C……………………………………………7分 ∴3=OC∴OC OA =∴△AOC 为等腰直角三角形∴︒=∠45ACO∵点D 为抛物线()412-+=x y 的顶点∴()4,1--D……………………………………………8分 过点D 作y DE ⊥轴 ∴4,1==OE DE∴134=-=-=OC OE CE ∴CE DE =∴△DCE 为等腰直角三角形∴︒=∠45DCE∴︒=︒-︒-︒=∠904545180ACD ∴△ACD 为直角三角形.…………………………………………10分 25.(10分)已知抛物线22212-+-=x x y . (1)写出此抛物线的开口方向、对称轴和顶点坐标;(2)求出抛物线与x 轴、y 轴的交点坐标; (3)在(2)中,设抛物线与y 轴交于点A ,与x 轴交于点B ,若以点A 为顶点的抛物线经过点B ,请你求出这条抛物线的解析式,并指出其开口方向和函数的最值. 解:(1)()222212221--=-+-=x x x y ……………………………………………1分 开口向下,对称轴为直线2=x ,顶点坐标为(2 , 0);……………………………………………4分 (2)令0=y ,则()02212=--x 解之得:2=x∴抛物线与x 轴的交点为(2 , 0)……………………………………………5分 令0=x ,则()220212-=-⨯-=y ∴抛物线与y 轴的交点为()2,0-;……………………………………………6分 (3)由题意可设抛物线的解析式为k ax y +=2∵其顶点为A ()2,0- ∴2-=k……………………………………………7分 ∴22-=ax y把B (2 , 0)代入22-=ax y 得:024=-a 解之得:21=a……………………………………………8分∴2212-=x y开口向上,函数的最小值为2-.…………………………………………10分 26.(10分)已知二次函数m x x y ++=22的图象1C 与x 轴有且只有一个公共点. (1)求1C 的顶点坐标;(2)将1C 向下平移若干个单位后,得抛物线2C ,如果2C 与x 轴的一个交点为()0,3-A ,求2C 的函数关系式,并求2C 与x 轴的另一个交点坐标;(3)若()1,y n P ,()2,2y Q 是1C 上的两点,且21y y >,求实数n 的取值范围.解:(1)()11222-++=++=m x m x x y∵其图象1C 与x 轴有且只有一个公共点 ∴01=-m ∴1=m……………………………………………3分∴()21+=x y∴1C 的顶点坐标为()0,1-;……………………………………………4分(2)设2C 的函数关系式为()k x y ++=21把()0,3-A 代入()k x y ++=21得:()0132=++-k解之得:4-=k∴2C 的函数关系式为()412-+=x y……………………………………………7分 令0=y ,则()0412=-+x解之得:1,321=-=x x∴2C 与x 轴的另一个交点坐标为(1 , 0); ……………………………………………8分 (3)2>n 或4-<n .…………………………………………10分。
二次函数的图像与性质-同步练习(含解析)
二次函数的图像与性质同步练习一、单选题1.已知点(3,1y ),(4,2y ), (5,3y )在函数y=2x 2+8x+7的图象上,则y 1,y 2,y 3的大小关系是( )A 、y 1>y 2>y 3B 、y 2> y 1> y 3C 、y 2>y 3> y 1D 、y 3> y 2> y 1 2.已知二次函数y=2x2+8x+7的图象上有有点A ,B ,C ,则y1、y2、y3的大小关系为( )A . y1 > y2> y3B . y2> y1> y3C . y2> y3> y1D . y3> y2> y13.已知二次函数y=x 2+bx+c 的图象上有三个点(﹣1,y 1)、(1,y 2)、(3,y 3),若y 1=y 3,则( )A .y 2>c >y 1B .y 2<c <y 1C .c >y 1>y 2D .c <y 1<y 24.已知抛物线y=-(x+1)2上的两点A (x 1,y 1)和B (x 2,y 2),如果x 1<x 2<-1,那么下列结论一定成立的是( ) A .y 1<y 2<0B .0<y 1<y 2C .0<y 2<y 1D .y 2<y 1<0.5.二次函数y=ax 2+bx+c 的图像如图所示,反比例函数ay x=与正比例函数y=(b+c)x 在同一坐标系中的大致图像可能是( )A .B .C .D .6.在同一坐标系中,二次函数2y ax bx =+与一次函数y bx a =-的图像可能是( )1(2)y -,21(5)3y -,31(1)5y -,A .B .C .D .7.反比例函数ky x=与一次函数()1y k x =-在同一坐标系中的图像可能是( ) A . B .C .D .8.在同一坐标系中,函数x k y =和3+=kx y 的图像可能是( )A .B .C .D . 9.如图,坐标系中抛物线是函数y=ax 2+bx +c 的图象,则下列式子能成立的是( )xxxxyyyyOOOO10.已知抛物线y=ax 2+bx+c (a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线13x =.则下列结论中,正确的是( )A .a <0B .c <﹣1C .a ﹣b+c <0D .2a+3b=011.二次函数2y x bx c =++中(b ,c 是常数)的自变量x 与函数值y 的部分对应值如下表:下列结论正确的是:A .当2x =时,y 有最大值1B .当2x <时,y 随x 的增大而增大C .点(5,9)在该函数的图像上D .若1(,)A m y ,2(1,)B m y +两点都在该函数的图象上,则当32m >时,12y y <. 12.如图,四个二次函数的图象中,分别对应的是:①2y ax =;①2y bx =;①2y cx =;①2y dx =,则a b c d ,,,的大小关系为A .a b c d >>>B .a b d c >>>C .b a c d >>>D .b a d c >>>13.如图,抛物线的对称轴是直线x=1,且经过点P (3,0),则的值为( )A .0B .-1C .1D .214.若二次函数的x 与y 的部分对应值如下表,则当x 1=时,y 的值为( )A .5B .3-C .13-D .27-15.已知二次函数()2y ax bx c a 0=++≠,函数y 与自变量x 的部分对应值如下表所示下列说法错误的是( ) A .图象开口向下 B .抛物线的对称轴是直线x 2= C .2b 4ac 0-> D .当1x 3<<时,y 6<二、填空题16.已知抛物线2y x x =+-65经过点1()4a -,和1()a y -,,则y 1的值是_________. 17.将抛物线()2241y x =--先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为__________.18.将抛物线y =-2x 2向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为_____ 19.将抛物线的解析式y=向上平移3个单位长度,在向右平移1个单位长度后,得到的抛物线的解析式是 .20.如果二次函数y=(-2k+4)x 2-3x+1的图象开口向上,那么常数k 的取值范围是________三、解答题21.已知函数y=(k ﹣2)x k²﹣4k+5+2x 是关于x 的二次函数.求: (1)满足条件的k 的值;(2)当k 为何值时,抛物线有最高点?求出这个最高点,这时,x 为何值时,y 随x 的增大而增大?22.已知函数()242mm y m x +-=+是关于x 的二次函数.()1求m 的值.()2如果这个二次函数的图象经过点()18P -,求m 的值;()3对于()2中二次函数,函数有无最大值?若有,此时的x 为何值.23.求抛物线217322y x x =--+的对称轴、顶点坐标. 24.阅读下面文字:求代数式24x 7x -+的最值,我们可以这样做:()()2224x 74x 4323x x x -+=-++=-+,因为()22x -≥0,所以当x=2时,该代数式有最小值,最小值为3.仿照以上方法,求(1)28a 3a +-的最值.(2)222y y -++的最值.25.把函数y=3x 2+6x+10转化成y=a (x-h )2+k 的形式,然后指出它的图象开口方向,对称轴,顶点坐标和最值.26.如图,已知抛物线y=2x -+mx+3与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0),(1)求m 的值及抛物线的顶点坐标.(2)点P 是抛物线对称轴l 上的一个动点,当PA+PC 的值最小时,求点P 的坐标.参考答案1.D【解析】解:抛物线的对称轴为2482-=-=-=a b x ,又02φ=a ,抛物线开口向上,在对称轴的右边y 随x 的增大而增大,345φφΘ,123y y y φφ∴,故选D 。
二次函数的图象与性质(练) (1)

第13课时二次函数的图象与性质基础过关1. (2017长沙)抛物线y=2(x-3)2+4的顶点坐标是( )A. (3,4)B. (-3,4)C. (3,-4)D. (2,4)2. (2017来宾)设M=-x2+4x-4,则()A. M<0B. M≤0C. M≥0D. M>03. (2017金华)对于二次函数y=-(x-1)2+2的图象与性质,下列说法正确的是( )A. 对称轴是直线x=1,最小值是2B. 对称轴是直线x=1,最大值是2C. 对称轴是直线x=-1,最小值是2D. 对称轴是直线x=-1,最大值是2在同一个平面4. (2017菏泽)一次函数y=ax+b和反比例函数y=cx直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象可能是( )第4题图5. (2017崇左)对于函数y =-2(x -m )2的图象,下列说法不正确的是() A. 开口向下 B. 对称轴是x=m C. 最大值为0 D. 与y 轴不相交6. (2017眉山)若一次函数y =(a +1)x +a 的图象过第一、三、四象限,则二次函数y =ax 2-ax ( ) A. 有最大值4a B. 有最大值-4a C. 有最小值4a D. 有最小值-4a 7. (2017杭州)设直线x =1是函数y =ax 2+bx +c (a,b,c 是实数,且a <0)的图象的对称轴( ) A. 若m >1,则(m -1)a +b >0 B. 若m >1,则(m -1)a +b <0 C. 若m <1,则(m +1)a +b >0 D. 若m <1,则(m +1)a +b <08. (2017攀枝花)二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,则下列命题中正确的是( )第8题图A. a >b >cB. 一次函数y =ax +c 的图象不经过第四象限C. m (am +b )+b <a (m 是任意实数)D. 3b +2c >09. (2017泰安)已知二次函数y =ax 2+bx +c 的y 与x 的部分对应值如下表:下列结论:①抛物线的开口向下;②其图象的对称轴为x =1;③当x <1时,函数值y 随x 的增大而增大;④方程ax 2+bx +c =0有一个根大于4.其中正确的结论有( ) A. 1个 B. 2个 C. 3个 D. 4个10. (2017荆门)在平面直角坐标系xOy 中,二次函数y =ax 2+bx +c (a ≠0)的大致图象如图所示,则下列结论正确的是( ) A. a <0,b <0,c >0 B. -2ba=1 C. a +b +c <0D. 关于x 的方程ax 2+bx +c =-1有两个不相等的实数根第10题图11. (2017湘西州)已知抛物线y =ax 2+bx +c (a ≠0)如图所示,则下列6个代数式:ac ,abc ,2a +b ,a +b +c ,4a -2b +c ,b 2-4ac ,其中值大于0的个数为()第11题图A. 2B. 3C. 4D. 512. (2017天津)已知抛物线y =x 2-4x +3与x 轴相交于点A,B (点A 在点B 左侧),顶点为M .平移该抛物线,使点M 平移后的对应点M ′落在x 轴上,点B 平移后的对应点B ′落在y 轴上,则平移后的抛物线解析式为( )A. y =x 2+2x +1B. y =x 2+2x -1C. y =x 2-2x +1D. y =x 2-2x -113. (2017乐山)已知二次函数y =x 2-2mx (m 为常数),当-1≤x ≤2时,函数值y 的最小值为-2,则m 的值是( )A.32B.C.32 D. -3214. (2017阿坝州)如图,抛物线y =ax 2+bx +c (a ≠0)的对称轴为直线x =1,与x 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: ①4ac <b 2;②方程ax 2+bx +c =0的两个根是x 1=-1,x 2=3;③3a+c>0④当y>0时,x的取值范围是-1≤x≤3⑤当x<0时,y随x增大而增大其中结论正确的个数是()A. 4个B. 3个C. 2个D. 1个第14题图15. (2017上海)已知一个二次函数的图象开口向上,顶点坐标为(0,-1),那么这个二次函数的解析式可以是.(只需写一个)16. (2017盐城盐都区一模)二次函数y=x2+6x+5图象的顶点坐标为.17. (2017衡阳)已知函数y=-(x-1)2图象上两点A(2,y1),B(a,y2),其中a>2,则y1与y2的大小关系是y1y2(填“<”、“>”或“=”).18. (2017广州)当x=时,二次函数y=x2-2x+6有最小值.19. (2017青岛)若抛物线y=x2-6x+m与x轴没有交点,则m的取值范围是.20. (2017兰州)如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为.第20题图21. (2017百色)经过A(4,0),B(-2,0),C(0,3)三点的抛物线的解析式是.22. (2017武汉)已知关于x的二次函数y=ax2+(a2-1)x-a的图象与x 轴的一个交点的坐标为(m,0).若2<m<3,则a的取值范围是.23. (2017南京二模)已知二次函数y1=a(x-2)2+k中,函数y1与自变量x的部分对应值如表:(1)求该二次函数的表达式;(2)将该函数的图象向左平移2个单位长度,得到二次函数y2的图象,分别在y1、y2的图象上取点A(m,n1),B(m+1,n2),试比较n1与n2的大小.24. (2017北京)在平面直角坐标系xOy中,抛物线y=x2-4x+3与x 轴交于点A,B(点A在点B的左侧),与y轴交于点C.(1)求直线BC的表达式;(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC 交于点N(x3,y3).若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.25. (2017南京二模)已知二次函数y=-x2+2mx-2m2-3(m为常数). (1)求证:不论m为何值,该二次函数图象与x轴没有公共点;(2)如果把该函数图象沿y轴向上平移4个单位后,得到的函数图象与x轴只有一个公共点,试求m的值.26. (2017南通一模)已知二次函数y=-2x2+4x+6.(1)求出该函数图象的顶点坐标,图象与x轴的交点坐标;(2)当x在什么范围内时,y随x的增大而增大?(3)当x在什么范围内时,y≤6?27. (2017荆州)已知关于x的一元二次方程x2+(k-5)x+1-k=0,其中k 为常数.(1)求证:无论k为何值,方程总有两个不相等实数根;(2)已知函数y=x2+(k-5)x+1-k的图象不经过第三象限,求k的取值范围;(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.28.(2017杭州)在平面直角坐标系中,设二次函数y1=(x+a)(x-a-1),其中a≠0.(1)若函数y1的图象经过点(1,-2),求函数y1的表达式;(2)若一次函数y2=ax+b的图象与y1的图象经过x轴上同一点,探究实数a,b满足的关系式;(3)已知点P(x0,m)和Q(1,n)在函数y1的图象上,若m<n,求x0的取值范围.满分冲关1. (2017河北)如图,若抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=k(x>0)的图象是()x第1题图2. (2017绍兴)矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( ) A. y=x2+8x+14 B. y=x2-8x+14C. y=x2+4x+3D. y=x2-4x+33. (2017来宾)已知函数y=|x2-4|的大致图象如图所示,如果方程|x2-4|=m(m为实数)有4个不相等的实数根,则m的取值范围是.第3题图4. (2017乌鲁木齐)如图,抛物线y=ax2+bx+c过点(-1,0),且对称轴为直线x=1,有下列结论:第4题图①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(-3,y2),则y1>y2;,0);④无论a,b,c取何值,抛物线都经过同一个点(-ca⑤am2+bm+a≥0.其中所有正确的结论是.(m2+1)=0 5. (2017天门)已知关于x的一元二次方程x2-(m+1)x+12有实数根.(1)求m的值;(m2+1)的图象关于x轴的对称图形,然后将所(2)先作y=x2-(m+1)x+12作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2-4n的最大值和最小值.答案基础过关1. A 【解析】由抛物线顶点式为y =a (x -h )2+k 可知抛物线y =2(x -3)2+4的顶点坐标为(3,4).2. B 【解析】∵M =-(x 2-4x +4)=-(x -2)2,又∵(x -2)2≥0,∴M ≤0.3. B 【解析】由二次函数y =-(x -1)2+2可知,对称轴为直线x =1,排除C 、D ,函数开口向下,有最大值,当x =1时,y 取最大值,为2.4. A 【解析】由图象可知a <0,b >0,c <0,结合选项可知二次函数y =ax 2+bx +c 开口向下,对称轴在y 轴右侧,且交于y 轴的负半轴,故选A.5. D 【解析】逐项分析如下:6. B 【解析】∵一次函数y =(a +1)x +a 的图象过第一、三、四象限,∴⎩⎨⎧==+001a a ,解得-1<a <0,∵二次函数y =ax 2-ax =a (x -12)2-14a ,又∵-1<a <0,∴二次函数y =ax 2-ax 有最大值,且最大值为-14a .7. C 【解析】∵抛物线的对称轴为直线x =1,∴-b 2a =1,b =-2a ;①当m >1时,则m -1>0,∴(m -1)a +b =ma +a +b =ma -a -2a =a (m -3),∵a <0,而m -3的正负性无法确定,∴a (m -3)的正负性无法确定,所以A ,B 错误;②当m <1时,则m -1<0,∴(m +1)a +b =ma +a +b =ma -a -2a =a (m -1),∵a <0,m -1<0,∴a (m -1)>0,所以C 正确,D 错误.8. D 【解析】由题意知,抛物线对称轴为x =-b 2a =-1,即a =21b ,又∵a >0,∴a <b ,故A 错误;∵a >0,c <0,∴一次函数y =ax +c 的图象不经过第二象限,故B 错误;∵m (am +b )+b =am 2+bm +b =am 2+2am +2a =a (m +1)2+a 且a >0,∴a (m +1)2+a 有最小值,最小值为a .∴m (am +b )+b ≥a (m 为任意实数),故C 错误;当x=1时,y =a +b +c >0,∴12b +b +c >0,即3b +2c >0,故D 正确.9. B 【解析】逐序号分析如下:综上所述,正确结论的个数为2.【一题多解】根据题意,将点(0,1),(1,3),(3,1)代入抛物线得:⎪⎩⎪⎨⎧=++=++=13931c b a c b a c ,解得⎪⎩⎪⎨⎧===131-c b a ,则所求抛物线解析式为y =-x 2+3x +1,则a <0,开口向下,①正确;对称轴为x =32≠1,②错误;由抛物线图象可知,当x <32时,y 随x 的增大而增大,则当x <1时,y 随x的增大而增大,③正确;解方程-x 2+3x +1=0得x 1=3-132,x 2=3+132,∵3<13<4,∴3+132<3+42<4,④错误.10. D 【解析】二次函数开口向下,对称轴在y 轴右侧,图象与y 轴交于负半轴,所以a <0,b >0,c <0,故A 错误;对称轴为x =-b 2a >1,故B 错误;当x =1时,y =a +b +c =0,故C 错误;y =ax 2+bx +c 与y =-1有两个交点,故ax 2+bx +c =-1有两个不相等的实数根,故D 正确.11. C 【解析】由抛物线的开口向上,可知a >0,由对称轴在0到1之间得0<-b 2a <1,∴b <0,-b <2a ,即2a +b >0,由抛物线图象知,当x =1时y <0,即a +b +c <0,∵抛物线与y 轴的交点在正半轴上,∴c >0,∴ac >0,abc <0,由图象可知,当x =-2时,y >0,即4a -2b +c >0,由抛物线与x 轴有两个不同的交点,得b 2-4ac >0.故这6个代数式中值大于0的有4个.12. A 【解析】∵抛物线与x 轴交于A 、B 两点,∴令y =0,即x 2-4x +3=0,解得x 1=1,x 2=3,∴A (1,0),B (3,0),∵y =x 2-4x +3=(x -2)2-1,∴M (2,-1).∵要使平移后的抛物线的顶点在x 轴上,需将图象向上平移1个单位,要使B 平移后的对应点B ′落在y 轴上,需向左平移3个单位,∴M ′(-1,0),则平移后二次函数的解析式为y =(x +1)2,即y =x 2+2x +1,故选A.13. D 【解析】因为二次函数的对称轴为x =m ,所以对称轴不确定,因此需要讨论研究的范围落在对称轴哪边,①当m ≥2时,此时-1≤x≤2落在对称轴的左边,当x =2时y 取得最小值-2,即-2=22-2m ×2,解得m =32(舍);②当-1<m <2时,此时在对称轴x =m 处取得最小值-2,即-2=m 2-2m·m ,解得m =-2或m =2,又-1<m <2,故m =2;③当m ≤-1时,此时-1≤x ≤2落在对称轴的右边,当x =-1时y 取得最小值-2,即-2=(-1)2-2m ×(-1),解得m =-32,综上所述,m =-32或 2.14. B 【解析】∵抛物线与x 轴有2个交点,∴b 2-4ac >0,所以①正确;∵抛物线的对称轴为直线x =1,而点(-1,0)关于直线x =1的对称点的坐标为(3,0),∴方程ax 2+bx +c =0的两个根是x 1=-1,x 2=3,所以②正确;∵x =-b 2a =1,即b =-2a ,而x =-1时,y =0,即a -b +c =0,∴a +2a +c =3a +c =0,所以③错误;∵抛物线与x 轴的两点坐标为(-1,0),(3,0),∴当-1<x <3时,y >0,所以④错误;∵抛物线的对称轴为直线x =1,∴当x <1时,y 随x 增大而增大,所以⑤正确.综上所述,结论正确的个数为3.15. y =x 2-1(答案不唯一) 【解析】二次函数的图像开口向上,∴a >0,顶点坐标为(0,-1),可设这个二次函数为y =ax 2-1,解析式可以是y =x 2-1.16. (-3,-4) 【解析】∵y =x 2+6x +5=(x +3)2-4,∴抛物线顶点坐标为(-3,-4).17. > 【解析】∵y =-(x -1)2,∴当x >1时,y 随着x 的增大而减小,∵a >2>1,∴y 1>y 2.18. 1;5 【解析】公式法:当x =-b 2a =--22×1=1时,y =x 2-2x +6有最小值,为4ac -b 24a =4×1×6-(-2)24×1=5. 【一题多解】配方法:∵y =x 2-2x +6=( x 2-2x +1)+5=(x -1)2+5,∴当x =1时,y =x 2-2x +6有最小值,最小值为5.19. m >9 【解析】∵抛物线y =x 2-6x +m 与x 轴没有交点,∴方程x 2-6x +m =0没有实数解,即b 2-4ac =(-6)2-4m <0,解得m >9.【一题多解】抛物线y =x 2-6x +m 化为顶点式得y =(x -3)2+m -9,其开口向上,若抛物线与x 轴没有交点,则顶点在x 轴上方,即m-9>0,解得m >9.20. (-2,0) 【解析】∵抛物线上点P 和点Q 关于x =1对称,P (4,0),可设Q (m ,0),∴24 m =1,解得m =-2,∴Q (-2,0). 21. y =-38(x -4)(x +2) 【解析】根据题意得,设抛物线解析式为y =a (x -4)(x +2),把C (0,3)代入上式得,3=a (0-4)(0+2),解得a=-38,故抛物线解析式是y =-38(x -4)(x +2).22. 13<a <12或-3<a <-2 【解析】令y =0,即ax 2+(a 2-1)x -a =0,(ax -1)(x +a )=0,∴关于x 的二次函数y =ax 2+(a 2-1)x -a 的图象与x 轴的交点为(a 1,0)和(-a ,0),即m =a1或m =-a .又∵2<m <3,则13<a <12或-3<a <-2.23. 解:(1)从表格看,二次函数顶点为(2,1),则k =1, 把(1,2)代入y 1=a (x -2)2+1中得:2=a (1-2)2+1,a =1, ∴二次函数的表达式为y 1=(x -2)2+1;(2)由题意得:y 2=(x -2+2)2+1=x 2+1,把A (m ,n 1)、B(m +1,n 2)分别代入y 1、y 2的表达式中,n 1=(m -2)2+1=m 2-4m +5,n 2=(m +1)2+1=m 2+2m +2,n 1-n 2=(m 2-4m +5)-(m 2+2m +2)=-6m +3,当-6m +3>0时,m <12,当-6m +3<0时,m >12,∴当m <12时,n 1-n 2>0,即n 1>n 2,当m =12时,n 1-n 2=0,即n 1=n 2,当m >12时,n 1-n 2<0,即n 1<n 2.24. 解:(1)∵抛物线y =x 2-4x +3与x 轴交于点A ,B (点A 在点B 左侧),∴令y =0,则有x 2-4x +3=(x -3)·(x -1)=0,解得x 1=1,x 2=3,∴A (1,0),B (3,0).∵抛物线y =x 2-4x +3与y 轴交于点C ,∴令x =0,得y =3,C (0,3).设直线BC 的表达式为y =kx +b (k ≠0),将B (3,0) ,C (0,3)代入y =kx +b ,得⎩⎨⎧==+303b b k , 解得⎩⎨⎧==31-b k , ∴直线BC 的表达式为y =-x +3;(2)∵y =x 2-4x +3=(x -2)2-1,∴抛物线对称轴为x=2,顶点为(2,-1).∵l⊥y轴,l交抛物线于点P、Q,交BC于点N,x1<x2<x3,∴-1<y1=y2=y3<0,点P、Q关于x=2对称,∴-1<-x3+3<0,221xx =2,∴3<x3<4, x1+x2=4,∴7<x1+x2+x3<8.25. (1)证明:令y=0,即-x2+2mx-2m2-3=0,则a=-1,b=2m,c=-2m2-3,∴b2-4ac=(2m)2-4×(-1)×(-2m2-3)=-4m2-12,∵-4m2≤0,∴-4m2-12<0,即b2-4ac<0,∴一元二次方程-x2+2mx-2m2-3=0没有实数根,∴不论m为何值,该二次函数图象与x轴没有公共点;(2)解:将二次函数y=-x2+2mx-2m2-3配方得:y=-(x-m)2-m2-3,∴该二次函数图象的顶点坐标为(m,-m2-3),∵将函数图象沿y轴向上平移4个单位后,得到的函数图象与x轴只有一个公共点,∴-m2-3+4=0,解得m=±1.26. 解:(1)∵y=-2x2+4x+6=-2(x-1)2+8,∴顶点坐标是(1,8),令y=0,则-2x2+4x+6=0,解得x1=-1,x2=3;∴图象与x 轴的交点坐标是(-1,0)、(3,0);(2)∵抛物线的对称轴为x =1,图象开口向下,∴当x ≤1时,y 随x 的增大而增大;(3)令y =-2x 2+4x +6=6,解得x =0或x =2,∵抛物线的图象开口向下,∴当x ≤0或x ≥2时y ≤6.27. (1)证明:∵a =1,b =k -5,c =1-k ,∴b 2-4ac =(k -5)2-4(1-k )=k 2-6k +21,∵k 2-6k +21=(k -3)2+12,其中(k -3)2≥0,∴b 2-4ac =(k -3)2+12>0,∴无论k 为何值,方程总有两个不相等的实数根;(2)解:∵二次函数图象不经过第三象限,∴对称轴x =2-5k >0,且不与y 轴负半轴相交,即1-k ≥0, 联立⎪⎩⎪⎨⎧≥>0-102-5k k ,解得k≤1;(3)依题意得,对于y =x 2+(k -5)x +1-k ,∵该抛物线图象开口向上,∴当x =3时,y <0,∴y =32+3(k -5)+1-k <0,即2k -5<0,k <52,∴k 的最大整数取2.28. 解:(1)∵函数y 1=(x +a )(x -a -1)的图象经过点(1,-2), ∴把x =1,y =-2代入y 1=(x +a )(x -a -1)得,-2=(1+a )(-a ), 化简得,a 2+a -2=0,解得a 1=-2,a 2=1,∴y 1=x 2-x -2;(2)函数y 1=(x +a )(x -a -1)的图象在x 轴的交点为(-a ,0),(a +1,0),①当函数y 2=ax +b 的图象经过点(-a ,0)时,把x =-a ,y =0代入y 2=ax +b 中,得a 2=b ;②当函数y 2=ax +b 的图象经过点(a +1,0)时,把x =a +1,y =0代入y 2=ax +b 中,得a 2+a =-b ;∴实数a ,b 满足的关系式是a 2=b 或a 2+a =-b;(3)∵抛物线y 1=(x +a )(x -a -1)的对称轴是直线x =21-++a a =12,m<n ,∵二次项系数为1,∴抛物线的开口向上,∴抛物线上的点离对称轴的距离越大,它的纵坐标也越大, ∵m<n ,∴点Q 离对称轴x =12的距离比P 离对称轴x =12的距离大,∴|x 0-12|<1-12,∴0<x0<1.满分冲关1. D【解析】在抛物线y=-x2+3中,令y=0,解得x=±3,令x=0,则y=3,∴抛物线与x轴围成封闭区域(边界除外)内的整点有:(-1,1),(1,1),(0,1),(0,2),共4个,∴k=4,∴反比例函数4,其图象经过点(1,4),(2,2),(4,1),∴符合的图解析式为y=x象如选项D.2. A【解析】由于矩形ABCD的两条对称轴为坐标轴,A(2,1),则C(-2,-1),要使A点与C点重合,抛物线移动路径为先向下移动2个单位长度,再向左移动4个单位长度,∵原抛物线为y=x2,∴后来的抛物线解析式为y=(x+4)2-2=x2+8x+14.3. 0<m<4【解析】∵当x=0时,y=|x2-4|=4,得图象与y轴交点坐标为(0,4),∴如解图,直线y=4与y=|x2-4|的图象有三个交点,∴当0<m<4时,有4个交点,即方程有4个不相等的实数根,故m的取值范围为0<m<4.第3题解图4. ②④⑤【解析】∵抛物线开口向上,∴a>0,∵对称轴为直线x =1,∴b<0,∵抛物线图象与y轴交于负半轴,∴c<0,∴abc>0,故①错误;∵抛物线y=ax2+bx+c过点(-1,0),且对称轴为x=1,∴抛物线与x轴的另一个交点坐标为(3,0),∴当x=3时,y=9a+3b+c=0,又∵a>0,∴10a+3b+c>0,故②正确;根据抛物线的对称性可知,x =-2与x =4时y 值相同,∵抛物线开口向上,∴当x 在对称轴左侧时,y 随x 的增大而减小,且-3<-2,∴y 1<y 2,故③错误;抛物线y =ax 2+bx +c 过点(-1,0),∴a -b +c =0,∵抛物线对称轴为x =-b 2a =1,∴b =-2a ,∴a +2a +c =0,即c =-3a ,当x =-c a 时,y =a ·(-c a )2-2a ·(-c a )+c =c 2a +3c =(-3a )2a+3×(-3a )=0,故④正确;∵b =-2a ,∴am 2+bm +a =am 2-2am +a =a (m -1)2,∵a >0,(m -1)2≥0,∴am 2+bm +a ≥0,故⑤正确.故正确的结论是②④⑤.5. 解:(1)∵方程有实数根,∴[-(m +1)]2-4×12(m 2+1)≥0,化简得(m -1)2≤0,∴m -1=0,∴m =1;(2)由(1)可知,y =x 2-2x +1=(x -1)2,关于x 轴对称后的函数解析式为y =-(x -1)2,再向左平移3个单位,向上平移2个单位,得函数解析式为y =-(x -1+3)2+2,化简得y =-x 2-4x -2,∴变化后的函数解析式为y =-x 2-4x -2;(3)∵直线y =2x +n 与y =-x 2-4x -2有交点,令2x +n =-x 2-4x -2,化简后得x 2+6x +n +2=0,∴b2-4ac=62-4×1×(n+2)≥0,解得n≤7,∵n≥m,m=1,∴n≥1,∴1≤n≤7,令t=n2-4n=(n-2)2-4,∴当n=2时,抛物线取得最小值,∴t min=-4;∵抛物线的对称轴为n=2,图象开口向上,∴当n=7时,抛物线取得最大值,∴t max=72-4×7=21,∴n2-4n的最大值为21,最小值为-4.。
中考数学总复习课时训练(专题(13)二次函数的图象与性质(一)附详细解析参考答案

课时训练(十三)二次函数的图象与性质(一)[限时:分钟]夯实基础1.抛物线y=3(x-2)2+5的顶点坐标是()A.(-2,5)B.(-2,-5)C.(2,5)D.(2,-5)2.下列二次函数中,图象以直线x=2为对称轴,且经过点(0,1)的是()A.y=(x-2)2+1B.y=(x+2)2+1C.y=(x-2)2-3D.y=(x+2)2-33.[2018·河西区结课考]已知函数y=(x-1)2,下列结论正确的是()A.当x>0时,y随x的增大而减小B.当x<0时,y随x的增大而增大C.当x<1时,y随x的增大而减小D.当x<-1时,y随x的增大而增大4.[2021·绍兴]关于二次函数y=2(x-4)2+6的最大值或最小值,下列说法正确的是()A.有最大值4B.有最小值4C.有最大值6D.有最小值65.[2021·上海]将函数y=ax2+bx+c(a≠0)的图象向下平移两个单位,以下说法错误的是()A.开口方向不变B.对称轴不变C.y随x的变化情况不变D.与y轴的交点不变6.[2021·泰安]将抛物线y=-x2-2x+3的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过点()A.(-2,2)B.(-1,1)C.(0,6)D.(1,-3)7.[2021·陕西]下表中列出的是一个二次函数的自变量x与函数y的几组对应值:x…-2 0 1 3 …y… 6 -4 -6 -4 …下列各选项中,正确的是()A.这个函数的图象开口向下B.这个函数的图象与x轴无交点C.这个函数的最小值小于-6D.当x>1时,y的值随x值的增大而增大8.对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为.9.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是.10.[2018·河西区一模]请写出一个二次函数的解析式,满足其图象过点(1,0),且与x轴有两个不同的交点:.11.[2021·广东]把抛物线y=2x2+1向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为.12.(1)已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,-5),求a,b的值.(2)已知二次函数y=-x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式.13.[2021·宁波]如图K13-1,二次函数y=(x-1)(x-a )(a 为常数)的图象的对称轴为直线x=2. (1)求a 的值;(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.图K13-1能力提升14.[2019·河西区二模]已知抛物线y=x 2+2mx-3m (m 是常数),且无论m 取何值,该抛物线都经过某定点H ,则点H 的坐标为 ( ) A .-32,1B .-32,-1C .32,94D .-32,9415.[2021·福建]二次函数y=ax 2-2ax+c (a>0)的图象过A (-3,y 1),B (-1,y 2),C (2,y 3),D (4,y 4)四个点,下列说法一定正确的是( ) A .若y 1y 2>0,则y 3y 4>0 B .若y 1y 4>0,则y 2y 3>0 C .若y 2y 4<0,则y 1y 3<0D .若y 3y 4<0,则y 1y 2<016.如图K13-2,抛物线y=ax 2+bx+c 与x 轴相交于点A ,B (m+2,0),与y 轴相交于点C ,点D 在该抛物线上,坐标为(m ,c ),则点A 的坐标是 .图K13-217.[2021·北京]在平面直角坐标系xOy 中,点(1,m )和点(3,n )在抛物线y=ax 2+bx (a>0)上. (1)若m=3,n=15,求该抛物线的对称轴.(2)已知点(-1,y 1),(2,y 2),(4,y 3)在该抛物线上.若mn<0,比较y 1,y 2,y 3的大小,并说明理由.【参考答案】1.C2.C3.C4.D5.D [解析] 将二次函数图象向下平移,不改变开口方向,故A 正确; 将二次函数图象向下平移,不改变对称轴,故B 正确; 将二次函数图象向下平移,不改变函数的增减性,故C 正确;抛物线y=ax 2+bx+c (a ≠0)与y 轴的交点坐标为(0,c ),将二次函数的图象向下平移两个单位,与y 轴的交点坐标为(0,c-2),改变,故D 错误.6.B [解析] y=-x 2-2x+3=-(x 2+2x )+3=-[(x+1)2-1]+3=-(x+1)2+4, ∵将抛物线y=-x 2-2x+3向右平移1个单位,再向下平移2个单位, ∴得到的抛物线的解析式为y=-x 2+2.将选项中的四个坐标代入可知,只有B 选项中的坐标符合题意.7.C [解析] 设二次函数的解析式为y=ax 2+bx+c ,由题知{6=a ×(-2)2+b ×(-2)+c ,-4=c ,-6=a +b +c ,解得{a =1,b =-3,c =-4,∴二次函数的解析式为y=x 2-3x-4=(x-4)(x+1)=x-322-254,∴函数图象开口向上,∴A 错误;∵图象与x 轴的交点为(4,0)和(-1,0),∴B 错误;∵当x=32时,函数有最小值为-254,∴C 正确;∵函数图象的对称轴为直线x=32,根据图象可知当x>32时,y 的值随x 值的增大而增大,∴D 错误. 8.直线x=2 9.(1,4)10.y=x 2-3x+2(答案不唯一) [解析] ∵抛物线过点(1,0),∴设抛物线的解析式为y=a (x-1)(x-m ). ∵抛物线与x 轴有两个不同的交点,∴m ≠1,取a=1,m=2,则抛物线的解析式为y=(x-1)(x-2)=x 2-3x+2. 11.y=2x 2+4x12.解:(1)将(1,3)和(3,-5)分别代入y=ax 2+bx+1, 得:{a +b +1=3,9a +3b +1=-5,解得:{a =-2,b =4.∴a 的值为-2,b 的值为4.(2)由题意得,二次函数的图象经过点(1,0)和(2,0), 将(1,0)和(2,0)分别代入y=-x 2+bx+c , 得{-1+b +c =0,-4+2b +c =0,解得{b =3,c =-2, ∴这个二次函数的表达式为y=-x 2+3x-2.13.解:(1)由二次函数y=(x-1)(x-a )(a 为常数)知,该抛物线与x 轴的交点坐标是(1,0)和(a ,0). ∵对称轴为直线x=2,∴1+a 2=2.解得a=3.(2)由(1)知a=3,则该抛物线解析式是:y=x 2-4x+3,由抛物线向下平移3个单位后经过原点,得平移后图象所对应的二次函数的表达式是y=x 2-4x. 14.C [解析] 由y=x 2+2mx-3m=x 2+m (2x-3)可知当x=32时,无论m 取何值y 都等于94,∴点H 的坐标为32,94.15.C [解析] ∵y=ax 2-2ax+c=a (x-1)2-a+c ,∴抛物线的对称轴为直线x=1,∴四点中距离对称轴远近关系从远到近排列为:A ,D ,B ,C ,当y 2y 4<0时,一定是y 2<0,y 4>0,根据对称性判断y 3<0,y 1>0,∴y 1y 3<0,因此本题选C .16.(-2,0) [解析] 由C (0,c ),D (m ,c ),得函数图象的对称轴是直线x=m2,设A 点坐标为(x ,0),由A ,B 关于对称轴x=m2对称可得x+m+22=m 2,解得x=-2,即A 点坐标为(-2,0).17.解:(1)∵m=3,n=15, ∴点(1,3),(3,15)在抛物线上,将(1,3),(3,15)的坐标代入y=ax 2+bx 得: {3=a +b ,15=9a +3b ,解得{a =1,b =2,∴y=x 2+2x=(x+1)2-1, ∴抛物线对称轴为直线x=-1.(2)由题意得:抛物线y=ax 2+bx (a>0)始终过定点(0,0),则由mn<0可得:①当m>0,n<0时,由抛物线y=ax 2+bx (a>0)始终过定点(0,0)可得此时的抛物线开口向下,即a<0,与a>0矛盾; ②当m<0,n>0时,∵抛物线y=ax 2+bx (a>0)始终过定点(0,0), ∴此时抛物线的对称轴的范围为12<-b2a <32, ∵点(-1,y 1),(2,y 2),(4,y 3)在该抛物线上,∴它们离抛物线对称轴的距离的范围分别为32<-b2a-(-1)<52,12<2--b2a<32,52<4--b2a<72,∵a>0,开口向上,∴由抛物线的性质可知离对称轴越近y 越小, ∴y 2<y 1<y 3.。
二次函数图像和性质习题精选

二次函数图像和性质习题精选一.选择题(共30小题)1.已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是()2.函数y=ax2+1与y=(a≠0)在同一平面直角坐标系中的图象可能是()3.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是()4.已知反比例函数y=的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为()5.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x 与y的部分对应值如下表:下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax 2+(b ﹣1)x+c=0的一个根;(4)当﹣1<x <3时,ax 2+(b ﹣1)x+c >0.其中正确的个数为( )6.二次函数y=ax 2+bx+c (a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) B . 对称轴是直线x=C . 当x <,y 随x 的增大而减小D .7.如图,平面直角坐标系中,点M 是直线y=2与x 轴之间的一个动点,且点M 是抛物线y=x 2+bx+c 的顶点,则方程x 2+bx+c=1的解的个数是( ) 8.已知二次函数y=a (x ﹣h )2+k(a >0),其图象过点A (0,2),B (8,3),则h 的值可以是( )9.二次函数y=ax2+bx+c图象上部分点的坐标满足下表:则该函数图象的顶点坐标为()10.已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,下列说法错误的是()11.如图,二次函数的图象经过(﹣2,﹣1),(1,1)两点,则下列关于此二次函数的说法正确的是()12.设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()13.如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是()14.已知二次函数y=ax2+bx+c (a≠0)的图象如图所示,给出以下结论:①a>0;②该函数的图象关于直线x=1对称;③当x=﹣1或x=3时,函数y的值都等于0.其中正确结论的个数是()15.二次函数y=ax2+bx+c (a≠0)的图象如图所示,下列结论正确的是()16.如图,抛物线y=ax2+bx+c (a>0)的对称轴是直线x=1,且经过点P(3,0),则a﹣b+c 的值为()17.下列图中阴影部分的面积相等的是()18.已知抛物线y=ax2+bx+c(a <0)的部分图象如图所示,当y >0时,x的取值范围是()19.已知:二次函数y=x2﹣4x ﹣a,下列说法错误的是()20.下列表格给出的是二次函数y=ax2+bx+c(a≠0)的几组对应值,那么方程ax2+bx+c=0的一个近似解可以是( A )21.已知二次函数y=ax2+bx+c 的y与x的部分对应值如下表:则下列判断中正确的是()22.已知二次函数y1=ax2+bx+c (a≠0)与一次函数y2=kx+m (k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1<y2成立的x的取值范围是()23.在﹣3≤x≤0范围内,二次函数(a≠0)的图象如图所示.在这个范围内,有结论:①y 1有最大值1、没有最小值; ②y 1有最大值1、最小值﹣3; ③函数值y 1随x 的增大而增大; ④方程ax 2+bx+c=2无解; ⑤若y 2=2x+4,则y 1≤y 2. 其中正确的个数是( )24.抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:根据上表判断下列四种说法:①抛物线的对称轴是x=1;②x>1时,y的值随着x的增大而减小:③抛物线有最高点:④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36.其中正确说法的个数有()25.如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A,B均在抛物线上,且AB 与x轴平行,其中点A的坐标为(0,3),则点B的坐标为()26.如图为二次函数y=ax2+bx+c的图象,给出下列说法:①ab<0;②方程ax2+bx+c=0的根为x1=﹣1,x2=3;③a+b+c>0;④当x<1时,y随x值的增大而增大;⑤当y>0时,x<﹣1或x>3.其中,正确的说法有()27.已知二次函数y=x2+2(a ﹣1)x+2.如果x≤4时,y随x增大而减小,则常数a的取值范围是()28.如图,平行于y轴的直线l 被抛物线y=0.5x2+1,y=0.5x2﹣1所截,当直线l向右平移3个单位时,直线l被两条抛物线所截得的线段扫过的图形面积为)平方单位.(29.已知直线经过点A(0,2),B(2,0),点C在抛物线y=x2的图象上,则使得S△ABC=2的点有()个.30.如图,已知抛物线,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>0时,y1>y2;②使得M 大于3的x值不存在;③当x<0时,x值越大,M值越小;④使得M=1的x值是或.其中正确的是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的图象和性质同步练习
1、对于抛物线22
=-的论断:(1)开口方向不同;(2)形状完全相同;(3)对称轴相同.其中
y x
=+和2
y x
正确的有()
A.0个B.1个C. 2个D.3个
2、下列关于抛物线221
=++的说法中,正确的是()
y x x
A.开口向下B.对称轴是直线x=1
C.与x轴有两个交点D.顶点坐标是(-1,0)
3、二次函数y=ax2+bx+c(a≠0)的图象如图,a,b,c的取值范围()
A.a<0,b<0,c<0 B.a<0,b>0,c<0
C.a>0,b>0,c<0 D.a>0,b<0,c<0
4、与抛物线224
=--关于y轴对称的图象表示的函数关系式是()
y x x
A.224
=++
y x x
y x x
=-++B.224
C.224
=-+
y x x
y x x
=+-D.224
5、若抛物线2
=-++-的图象的最低点的纵坐标为零,则m=_______.
y m x m x m
(1)221
6、对于抛物线2(0)
y ax bx c a
=++≠,当顶点纵坐标等于_________时,顶点在x轴上,此时抛物线与x 轴只有一个公共点,而a≠0,所以,抛物线与x轴只有一个公共点的条件是_________.
7、若抛物线22
y x x m
=++与x轴只有一公共点,则m=_________.
8、函数243
=+-的图象开口向_________,顶点坐标为__________
y x x
9、二次函数22
=+的图象开口_____,对称轴是________,顶点坐标是_______.
y x
10、抛物线2
=+-与x轴交点个数为________.
y x x
23
11、二次函数2
=-的图象向右平移3个单位,在向上平移1个单位,得到的图象的关系式是____.
y x
(3)
12、抛物线2
=-+-的顶点坐标为_________,对称轴为________.
y x x
261
13、已知二次函数2
y ax
=的图象经过点A(-1,1)
①求这个二次函数的关系式;
②求当x=2时的函数y的值.
14、若抛物线2221y x m x m m =-+++的顶点在第二象限,则常数m 的取值范围是( )
A .12m m <->或
B .12m -<<
C .10m -<<
D .1m >
15、 如右图,抛物线顶点坐标是P (1,3),则函数y 随自变量x 的增大而减小的x 的取值范围是( )
A .x >3
B .x <3
C .x >1
D .x <1
16、 二次函数243y x x =-+的图象交x 轴于A 、B 两点,交y 轴于点C ,则△ABC 的面积为( )
A .6
B .4
C .3
D .1 17、抛物线24y x =-与x 轴交于B 、C 两点,顶点为A ,求△ABC 的面积。
18、若抛物线21y a x =,22y a x =的形状相同,那么( )
A .12a a =
B .12a a =-
C .|a 1|=|a 2|
D .a 1与a 2的关系无法确定
19、与抛物线242y x x =--关于x 轴对称的图象表示为( )
A .242y x x =++
B .242y x x =+-
C .242y x x =-+
D .242y ax x =-- 20、抛物线2(0)y ax bx c a =++≠,关于x 轴对称的图象的关系式是_______________.
21、 把抛物线22y x =向右平移一个单位,在向下平移3个单位,得到的抛物线的解析式是_________.
22、若点(2,-1)在抛物线2y ax =上,那么,当x =2时,y =_________
23、若抛物线2y ax bx c =++全部在x 轴的下方,那么a _________0,同时,b 2-4ac _________0.
24、抛物线22y x =和2
3y x =-中开口较大的是__________.
25、已知抛物线213y x =,另一条抛物线y 2的顶点为(2,5),且形状、大小与y 1相同,开口方向相反,则抛物线y 2的关系式为______________.。
