正定中学11届一轮复习学案 圆及直线与圆的位置关系部分答案
高考数学(理)一轮规范练【49】直线与圆、圆与圆的位置关系(含答案)

课时规范练49 直线与圆、圆与圆的位置关系课时规范练第75页一、选择题1.已知p:“a=”,q:“直线x+y=0与圆x2+(y-a)2=1相切”,则p是q的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件答案:A解析:由直线x+y=0与圆x2+(y-a)2=1相切,可得=1,即a=±.∴p⇒q.而q p,∴p是q的充分而不必要条件.2.已知直线l1与圆x2+y2+2y=0相切,且与直线l2:3x+4y-6=0平行,则直线l1的方程是( )A.3x+4y-1=0B.3x+4y+1=0或3x+4y-9=0C.3x+4y+9=0D.3x+4y-1=0或3x+4y+9=0答案:D解析:设直线l1的方程为3x+4y+m=0.∵直线l1与圆x2+y2+2y=0相切,∴=1.[:∴|m-4|=5.∴m=-1或m=9.∴直线l1的方程为3x+4y-1=0或3x+4y+9=0.3.在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于( )A.3B.2C.D.1答案:B解析:如图所示,设AB的中点为D,则OD⊥AB,垂足为D,连接OA.由点到直线的距离得|OD|==1,∴|AD|2=|OA|2-|OD|2=4-1=3,|AD|=,∴|AB|=2|AD|=2.4.若直线x+my=2+m与圆x2+y2-2x-2y+1=0相交,则实数m的取值范围为( )A.(-∞,+∞)B.(-∞,0)C.(0,+∞)D.(-∞,0)∪(0,+∞)答案:D解析:由圆的方程可知圆心坐标为(1,1),半径为1,因为直线与圆相交,所以有<1,解得m2>0,所以实数m的取值范围为(-∞,0)∪(0,+∞).5.过圆x2+y2=1上一点作圆的切线与x轴、y轴的正半轴交于A,B两点,则|AB|的最小值为( )A. B. C.2 D.3答案:C解析:设圆上的点为(x0,y0),其中x0>0,y0>0,则切线方程为x0x+y0y=1.分别令y=0,x=0,得A,B,∴|AB|==2当且仅当x0=y0时,等号成立.6.若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称,过点C(-a,a)的圆P与y轴相切,则圆心P的轨迹方程为( )A.y2-4x+4y+8=0B.y2+2x-2y+2=0C.y2+4x-4y+8=0D.y2-2x-y-1=0答案:C解析:由圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称可知两圆半径相等且两圆圆心连线的中点在直线y=x-1上,故可得a=2,即点C(-2,2),所以过点C(-2,2)且与y轴相切的圆P的圆心的轨迹方程为(x+2)2+(y-2)2=x2,整理得y2+4x-4y+8=0.二、填空题[:7.圆心在原点且与直线x+y-2=0相切的圆的方程为.答案:x2+y2=2解析:圆心(0,0)到直线x+y-2=0的距离d=.∴圆的方程为x2+y2=2.8.已知△ABC的三个顶点分别为A(3,1,2),B(4,-2,-2),C(0,5,1),则BC边上的中线长为.答案:解析:BC中点坐标为D,所以|AD|=.9.设O为坐标原点,C为圆(x-2)2+y2=3的圆心,且圆上有一点M(x,y)满足=0,则= .答案:或-解析:∵·=0,∴OM⊥CM,∴OM是圆的切线.设OM的方程为y=kx,由,得k=±,即=±.三、解答题10.过点(,0)引直线l与曲线y=相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,求直线l的斜率. 解:曲线y=的图象如图所示:若直线l与曲线相交于A,B两点,则直线l的斜率k<0,设l:y=k(x-),则点O到l的距离d=.又S△AOB=|AB|·d=×2·d=,当且仅当1-d2=d2,即d2=时,S△AOB取得最大值.∴,∴k2=,∴k=-.11.已知圆O:x2+y2=4和点M(1,a),(1)若过点M有且只有一条直线与圆O相切,求实数a的值,并求出切线方程;(2)若a=,过点M的圆的两条弦AC,BD互相垂直,求|AC|+|BD|的最大值.解:(1)由条件知点M在圆O上,所以1+a2=4,解得a=±.当a=时,点M为(1,),k OM=,k切线=-,此时切线方程为y-=-(x-1),即x+y-4=0.当a=-时,点M为(1,-),k OM=-,k切线=,此时切线方程为y+(x-1),即x-y-4=0.所以所求的切线方程为x+y-4=0,或x-y-4=0.(2)设O到直线AC,BD的距离分别为d1,d2(d1,d2≥0),则=|OM|2=3.于是|AC|=2,|BD|=2.[:所以|AC|+|BD|=2+2.则(|AC|+|BD|)2=4(4-+4-+2)=4[5+2]=4(5+2).因为2d1d2≤=3,所以,当且仅当d1=d2=时取等号.所以.所以(|AC|+|BD|)2≤4×=40.所以|AC|+|BD|≤2,即|AC|+|BD|的最大值为2.[:12.已知圆x2+y2+2ax-2ay+2a2-4a=0(0<a≤4)的圆心为C,直线l:y=x+m.(1)若m=4,求直线l被圆C所截得弦长的最大值;[:(2)若直线l是圆心C下方的切线,当a在(0,4]上变化时,求m的取值范围.解:(1)∵x2+y2+2ax-2ay+2a2-4a=0,∴(x+a)2+(y-a)2=4a,∴圆心为C(-a,a),半径为r=2.设直线l被圆C所截得的弦长为2t,圆心C到直线l的距离为d,当m=4时,直线l:x-y+4=0,圆心C到直线l的距离为d=|a-2|,t2=(2)2-2(a-2)2=-2a2+12a-8=-2(a-3)2+10,又0<a≤4,∴当a=3时,直线l被圆C所截得弦长的值最大,其最大值为2.(2)圆心C到直线l的距离为d=|m-2a|,∵直线l是圆C的切线,∴d=r,即=2,∴m=2a±2,∵直线l在圆心C的下方,∴m=2a-2=(-1)2-1,∵a∈(0,4],∴m∈[-1,8-4].。
2011年高考数学一轮复习精品学案(人教版A版)§9.4直线、圆的位置关系--学生用

2011年高考数学一轮复习精品学案(人教版A 版)§9.4直线、圆的位置关系★知识梳理★1.判断直线与圆的位置关系有两种方法:①几何法:通过圆心到直线的距离与半径的大小比较来判断,设圆心到直线的距离为d ,圆半径为r ,若直线与圆相离,则 ;若直线与圆相切,则 ;若直线与圆相交,则 。
②代数法:通过直线与圆的方程联立的方程组的解的个数来判断,即通过判别式来判断,若0>∆,则 ;若0=∆,则 ;若0<∆,则 。
2.两圆的位置关系 (1)设两圆半径分别为12,r r ,圆心距为d若两圆相外离,则 ,公切线条数为若两圆相外切,则 ,公切线条数为若两圆相交,则 ,公切线条数为若两圆内切,则 ,公切线条数为若两圆内含,则 ,公切线条数为(2) 设两圆0:111221=++++F y E x D y x C ,0:222222=++++F y E x D y x C ,若两圆相交,则两圆的公共弦所在的直线方程是3. 相切问题的解法:①利用圆心到切线的距离等于半径列方程求解②利用圆心、切点连线的斜率与切线的斜率的乘积为-1③利用直线与圆的方程联立的方程组的解只有一个,即0=∆来求解。
特殊地,已知切点),(00y x P ,圆222r y x =+的切线方程为 ,圆222)()(r b y a x =-+-的切线方程为200))(())((r b y b y a x a x =--+-- 4.圆系方程①以点),(00y x C 为圆心的圆系方程为)0()()(22020>=-+-r r y y x x②过圆0:22=++++F Ey Dx y x C 和直线0:=++c by ax l 的交点的圆系方程为F Ey Dx y x ++++220)(=+++c by ax λ③过两圆0:111221=++++F y E x D y x C ,0:222222=++++F y E x D y x C 的交点的圆系方程为11122F y E x D y x ++++0)(22222=+++++F y E x D y x λ(不表示圆2C )★重难点突破★重点:根据给定的方程判定直线与圆、圆与圆的位置关系;利用直线和圆、圆与圆的位置关系的充要条件解决一些简单的问题;难点:借助数形结合,利用圆的几何性质,将题目所给条件转化为圆心到直线的距离、两圆的连心线或半径的和与差重难点:将方程的理论与圆的几何性质相结合,并加以运用,握直线与圆的位置关系的三种常见题型:①相切——求切线;相交——求距离;③相离——求圆上动点到直线距离的最大(小)值。
正定中学11届一轮复习学案 08高二上学期巩固复习学案八复件

高二(上)数学巩固复习学案八
一、知识目标:
1.线面的位置关系、、
2.线面平行的判定定理
3.线面平行的性质定理
4.直线与平面垂直的定义
5.直线与平面垂直的判定定理
6.判断线面垂直的常用方法
7.直线与平面垂直的性质定理
8.直线和平面所成的角
9.最小角定理
10.(1)点到面的距离
(2)线到面的距离
11.三垂线定理及其逆定理
二、常用方法及数学思想:
1.证明线线平行的常用方法:中位线,平行四边形,比例线段(以上三种都是平面几何中常用的方法)公里4(平行线的传递性),线面平行的性质定理,线面垂直的定理.
2.等价转化思想:立体几何问题平面化
(1)线线平行⇔线面平行;
(2)线线垂直⇔线面垂直;
(3)点到面的距离可以转化为其他点到面的距离,也常用等体积的方法来求;
(4)线到面的距离转化为点到面的距离
三、典题分析:
(一)选择题:
1.下列正确命题的个数是()
(1)垂直于两条异面直线的直线有且只有一条
(2)两线段AB、CD不在同一平面内,如果AC=BD,AD=BC,则AB⊥CD
(3)在正方体中,相邻两侧面的一对异面的对角线所成的角为60º
(4)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直
A.0 B.1 C.2 D.3
2.一条直线若同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是
A异面B相交C平行D不能确定
3.a、b是两条异面直线,A是不在a、b上的点,则下列结论成立的是
A过A有且只有一个平面平行于a、b
B过A至少有一个平面平行于a、b。
高考理科数学(人教版)一轮复习讲义:第九章 第四节 直线与圆、圆与圆的位置关系 Word版含答案

第四节直线与圆、圆与圆的位置关系1.直线与圆的位置关系(半径为r ,圆心到直线的距离为d )2.圆与圆的位置关系设两圆的圆心距为d ,两圆的半径分别为R ,r (R >r ),则判断圆与圆位置关系的注意点对于圆与圆的位置关系,从交点的个数,也就是方程组的解的个数来判断,有时得不到确切的结论.如当Δ<0时,需要再根据图形判断两圆是外离,还是内含;当Δ=0时,还需要判断两圆是外切,还是内切.[熟记常用结论]1.圆的切线方程常用结论(1)过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.(2)过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2.(3)过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2.2.圆系方程(1)同心圆系方程:(x -a )2+(y -b )2=r 2(r >0),其中a ,b 是定值,r 是参数;(2)过直线Ax +By +C =0与圆x 2+y 2+Dx +Ey +F =0交点的圆系方程:x 2+y 2+Dx +Ey+F +λ(Ax +By +C )=0(λ∈R );(3)过圆C 1:x 2+y 2+D 1x +E 1y +F 1=0和圆C 2:x 2+y 2+D 2x +E 2y +F 2=0交点的圆系方程:x 2+y 2+D 1x +E 1y +F 1+λ(x 2+y 2+D 2x +E 2y +F 2)=0(λ≠-1)(该圆系不含圆C 2,解题时,注意检验圆C 2是否满足题意,以防漏解).[小题查验基础]一、判断题(对的打“√”,错的打“×”)(1)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.( ) (2)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )(3)从两圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程.( )(4)如果直线与圆组成的方程组有解,则直线与圆相交或相切.( ) 答案:(1)× (2)× (3)× (4)√ 二、选填题1.直线l :x +3y -4=0与圆C :x 2+y 2=4的位置关系是( ) A .相交过圆心 B .相交不过圆心 C .相切D .相离解析:选C 圆心坐标为(0,0),圆心到直线l 的距离d =|-4|2=2=r ,所以直线l 与圆C相切.故选C.2.圆O 1:x 2+y 2-2x =0和圆O 2:x 2+y 2-4y =0的位置关系是( ) A .外离 B.相交 C .外切D .内切解析:选B 圆O 1:(x -1)2+y 2=1, 圆O 2:x 2+(y -2)2=4,∵|O 1O 2|=(1-0)2+(0-2)2=5,∴|2-1|<|O 1O 2|<2+1,∴两圆相交.故选B.3.若直线x -y +1=0与圆(x -a )2+y 2=2有公共点,则实数a 的取值范围是( ) A .[-3,-1] B.[-1,3]C .[-3,1]D .(-∞,-3]∪[1,+∞) 解析:选C 由题意可得,圆的圆心为(a,0),半径为2, 所以|a -0+1|12+(-1)2≤2,即|a +1|≤2,解得-3≤a ≤1,故选C.4.已知直线l :y =k (x +3)和圆C :x 2+(y -1)2=1,若直线l 与圆C 相切,则k =________.解析:因为直线l 与圆C 相切,所以圆心C 到直线l 的距离d =|-1+3k |1+k 2=1,解得k =0或k = 3.答案:0或 35.直线l :3x -y -6=0与圆x 2+y 2-2x -4y =0相交于A ,B 两点,则|AB |=________. 解析:由x 2+y 2-2x -4y =0,得(x -1)2+(y -2)2=5, 所以该圆的圆心坐标为(1,2),半径r =5, 又圆心(1,2)到直线3x -y -6=0的距离为d =|3-2-6|32+(-1)2=102,由⎝⎛⎭⎫|AB |22=r 2-d 2,得|AB |2=4⎝⎛⎭⎫5-52=10,即|AB |=10. 答案:10考点一 直线与圆的位置关系的判断 [师生共研过关][典例精析](1)直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A .相交 B .相切 C .相离 D .不确定(2)直线y =-33x +m 与圆x 2+y 2=1在第一象限内有两个不同的交点,则m 的取值范围是( )A .(3,2) B.(3,3) C.⎝⎛⎭⎫33,233D.⎝⎛⎭⎫1,233(3)若圆x 2+y 2=r 2(r >0)上恒有4个点到直线x -y -2=0的距离为1,则实数r 的取值范围是( )A .(2+1,+∞) B.(2-1,2+1) C .(0,2-1)D .(0,2+1)[解析] (1)法一:(代数法)由⎩⎪⎨⎪⎧mx -y +1-m =0,x 2+(y -1)2=5, 消去y ,整理得(1+m 2)x 2-2m 2x +m 2-5=0, 因为Δ=16m 2+20>0,所以直线l 与圆相交. 法二:(几何法)由题意知,圆心(0,1)到直线l 的距离 d =|-m |m 2+1<1<5,故直线l 与圆相交.法三:易得直线l 过定点(1,1).把点(1,1)代入圆的方程有1+0<5,∴点(1,1)在圆的内部,故直线l 与圆C 相交.(2)当直线经过点(0,1)时,直线与圆有两个不同的交点,此时m =1;当直线与圆相切时,圆心到直线的距离d =|m |⎝⎛⎭⎫332+1=1,解得m =233(切点在第一象限),所以要使直线与圆在第一象限内有两个不同的交点, 则1<m <233.(3)计算得圆心到直线l 的距离为22=2>1,如图,直线l :x -y -2=0与圆相交,l 1,l 2与l 平行,且与直线l 的距离为1,故可以看出,圆的半径应该大于圆心到直线l 2的距离2+1.[答案] (1)A (2)D (3)A[解题技法]判断直线与圆的位置关系的一般方法1.已知点M (a ,b )在圆O :x 2+y 2=1外,则直线ax +by =1与圆O 的位置关系是( ) A .相切 B.相交 C .相离D .不确定解析:选B 因为M (a ,b )在圆O :x 2+y 2=1外,所以a 2+b 2>1,而圆心O 到直线ax +by =1的距离d =1a 2+b 2<1.所以直线与圆相交. 2.(2019·杭州模拟)若无论实数a 取何值时,直线ax +y +a +1=0与圆x 2+y 2-2x -2y +b =0都相交,则实数b 的取值范围为( )A .(-∞,2) B.(2,+∞) C .(-∞,-6)D .(-6,+∞)解析:选C ∵x 2+y 2-2x -2y +b =0表示圆,∴8-4b >0,即b <2.∵直线ax +y +a +1=0过定点(-1,-1),∴点(-1,-1)在圆x 2+y 2-2x -2y +b =0的内部,∴6+b <0,解得b <-6,∴b 的取值范围是(-∞,-6).故选C.3.圆(x -3)2+(y -3)2=9上到直线3x +4y -11=0的距离等于1的点的个数为( ) A .1 B.2 C .3D .4解析:选C 由圆的方程知圆心坐标为(3,3),半径为3,如图所示,因为圆心到直线的距离为|9+12-11|5=2,又因为圆的半径为3,所以直线与圆相交,故圆上到直线的距离为1的点有3个.考点二 圆与圆的位置关系及应用 [师生共研过关][典例精析]已知圆C 1:(x -a )2+(y +2)2=4与圆C 2:(x +b )2+(y +2)2=1外切,则ab 的最大值为( ) A.62B.32C.94D .2 3[解析] 由圆C 1与圆C 2外切,可得(a +b )2+(-2+2)2=2+1=3,即(a +b )2=9.根据基本不等式可知ab ≤⎝⎛⎭⎫a +b 22=94,当且仅当a =b 时等号成立,ab 的最大值为94.[答案] C[解题技法]圆与圆位置关系问题的解题策略(1)判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x 2,y 2项得到.[过关训练]1.如果圆C :x 2+y 2-2ax -2ay +2a 2-4=0与圆O :x 2+y 2=4总相交,那么实数a 的取值范围是_________________.解析:圆C 的标准方程为(x -a )2+(y -a )2=4, 圆心坐标为(a ,a ),半径为2. 依题意得0<a 2+a 2<4,∴0<|a |<2 2.∴a ∈(-22,0)∪(0,22). 答案:(-22,0)∪(0,22)2.已知两圆x 2+y 2-2x -6y -1=0,x 2+y 2-10x -12y +m =0. (1)m 取何值时两圆外切? (2)m 取何值时两圆内切?(3)当m =45时,求两圆的公共弦所在直线的方程和公共弦的长.解:因为两圆的标准方程分别为(x -1)2+(y -3)2=11, (x -5)2+(y -6)2=61-m ,所以两圆的圆心分别为(1,3),(5,6),半径分别为11,61-m ,(1)当两圆外切时,由(5-1)2+(6-3)2=11+61-m ,得m =25+1011.(2)当两圆内切时,因为定圆半径11小于两圆圆心之间的距离5,所以61-m -11=5,解得m =25-1011.(3)由(x 2+y 2-2x -6y -1)-(x 2+y 2-10x -12y +45)=0,得两圆的公共弦所在直线的方程为4x +3y -23=0.故两圆的公共弦的长为 2(11)2-⎝⎛⎭⎪⎫|4+3×3-23|42+322=27.考点三 圆的弦长问题 [师生共研过关][典例精析](1)(2019·太原模拟)若3a 2+3b 2-4c 2=0,则直线ax +by +c =0被圆O :x 2+y 2=1所截得的弦长为( )A.23 B .1 C.12D.34(2)(2019·成都模拟)已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A ,B 两点,且|AB |=3,则OA ―→·OB ―→的值是( )A .-12B.12 C .-43D .0[解析] (1)因为a 2+b 2=43c 2,所以圆心O (0,0)到直线ax +by +c =0的距离d =|c |a 2+b 2=32,所以直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为212-⎝⎛⎭⎫322=2×12=1,选B.(2)在△OAB 中,|OA |=|OB |=1,|AB |=3,可得∠AOB =120°,所以OA ―→·OB ―→=1×1×cos 120°=-12.[答案] (1)B (2)A[解题技法]有关弦长问题的2种求法[过关训练]1.已知圆C :(x -1)2+(y -2)2=2截y 轴所得线段与截直线y =2x +b 所得线段的长度相等,则b =( )A .- 6 B.±6 C .- 5D .±5解析:选D 记圆C 与y 轴的两个交点分别是A ,B ,由圆心C 到y 轴的距离为1,|CA |=|CB |=2可知,圆心C (1,2)到直线2x -y +b =0的距离也等于1才符合题意,于是|2×1-2+b |5=1,解得b =±5. 2.在直角坐标系xOy 中,曲线y =x 2+mx -2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 解:(1)不能出现AC ⊥BC 的情况,理由如下:设A (x 1,0),B (x 2,0),则x 1,x 2是方程x 2+mx -2=0的两根,所以x 1x 2=-2,又点C 的坐标为(0,1),则AC ―→·BC ―→=(-x 1,1)·(-x 2,1)=x 1x 2+1=-2+1=-1≠0,所以不能出现AC ⊥BC 的情况.(2)证明:设过A ,B ,C 三点的圆与y 轴的另一个交点为D ,由x 1x 2=-2可知原点O 在圆内,则由相交弦定理可得|OC |·|OD |=|OA |·|OB |=|x 1|·|x 2|=2.又|OC |=1,所以|OD |=2,所以过A ,B ,C 三点的圆在y 轴上截得的弦长为|OC |+|OD |=3,为定值.考点四 圆的切线问题 [师生共研过关][典例精析]已知点P (2+1,2-2),点M (3,1),圆C :(x -1)2+(y -2)2=4. (1)求过点P 的圆C 的切线方程;(2)求过点M 的圆C 的切线方程,并求出切线长. [解] 由题意得圆心C (1,2),半径r =2. (1)∵(2+1-1)2+(2-2-2)2=4, ∴点P 在圆C 上. 又k PC =2-2-22+1-1=-1,∴切线的斜率k =-1k PC=1. ∴过点P 的圆C 的切线方程是y -(2-2)=x -(2+1),即x -y +1-22=0. (2)∵(3-1)2+(1-2)2=5>4,∴点M 在圆C 外部. 当过点M 的直线斜率不存在时,直线方程为x =3, 即x -3=0.又点C (1,2)到直线x -3=0的距离d =3-1=2=r , 即此时满足题意,所以直线x =3是圆的切线. 当切线的斜率存在时,设切线方程为y -1=k (x -3), 即kx -y +1-3k =0, 则圆心C 到切线的距离d =|k -2+1-3k |k 2+1=r =2,解得k =34.∴切线方程为y -1=34(x -3),即3x -4y -5=0.综上可得,过点M 的圆C 的切线方程为x -3=0或3x -4y -5=0. ∵|MC |=(3-1)2+(1-2)2= 5,∴过点M 的圆C 的切线长为|MC |2-r 2=5-4=1.[解题技法]1.求过圆上的一点(x 0,y 0)的切线方程的方法先求切点与圆心连线的斜率k ,若k 不存在,则结合图形可直接写出切线方程为y =y 0;若k =0,则结合图形可直接写出切线方程为x =x 0;若k 存在且k ≠0,则由垂直关系知切线的斜率为-1k,由点斜式可写出切线方程.2.求过圆外一点(x 0,y 0)的圆的切线方程的2种方法[提醒] 当点(x 0,y 0)在圆外时,一定要注意斜率不存在的情况.[过关训练]1.(2019·杭州模拟)由直线y =x +1上的一点向圆(x -3)2+y 2=1引切线,则切线长的最小值为( )A .1B .2 C.7D .3解析:选C 切线长的最小值是当直线y =x +1上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为d =|3-0+1|2=22,故切线长的最小值为d 2-r 2=7. 2.(2018·湖北四地七校联考)若圆O 1:x 2+y 2=5与圆O 2:(x +m )2+y 2=20相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是( )A .3 B.4 C .2 3D .8解析:选B 连接O 1A ,O 2A ,由于⊙O 1与⊙O 2在点A 处的切线互相垂直,因此O 1A ⊥O 2A ,所以|O 1O 2|2=|O 1A |2+|O 2A |2,即m 2=5+20=25,设AB 交x 轴于点C .在Rt △O 1AO 2中,sin ∠AO 2O 1=55,∴在Rt △ACO 2中,|AC |=|AO 2|·sin ∠AO 2O 1=25×55=2,∴|AB |=2|AC |=4.故选B. 考点五 直线与圆的综合问题[师生共研过关][典例精析]已知过原点的动直线l 与圆C 1:x 2+y 2-6x +5=0相交于不同的两点A ,B . (1)求圆C 1的圆心坐标;(2)求线段AB 的中点M 的轨迹C 的方程;(3)是否存在实数k ,使得直线L :y =k (x -4)与曲线C 只有一个交点?若存在,求出k 的取值范围;若不存在,说明理由.解:(1)因为圆C 1的方程x 2+y 2-6x +5=0可化为(x -3)2+y 2=4,所以圆心坐标为(3,0). (2)设A (x 1,y 1),B (x 2,y 2)(x 1≠x 2),M (x 0,y 0),则x 0=x 1+x 22,y 0=y 1+y 22. 由题意可知直线l 的斜率必存在, 设直线l 的方程为y =tx . 将上述方程代入圆C 1的方程, 化简得(1+t 2)x 2-6x +5=0. 由题意,可得x 1+x 2=61+t2,Δ=36-20(1+t 2)>0,(*) 所以x 0=31+t 2,代入直线l 的方程,得y 0=3t 1+t 2. 因为x 20+y 20=9(1+t 2)2+9t 2(1+t 2)2=9(1+t 2)(1+t 2)2=91+t 2=3x 0, 所以⎝⎛⎭⎫x 0-322+y 20=94. 由(*)解得t 2<45.又t 2≥0,所以53<x 0≤3.所以线段AB 的中点M 的轨迹C 的方程为⎝⎛⎭⎫x -322+y 2=94⎝⎛⎭⎫53<x ≤3. (3)存在实数k 满足条件.由(2)知,曲线C 是在区间⎝⎛⎦⎤53,3上的一段圆弧. 如图,D ⎝⎛⎭⎫53,253,E ⎝⎛⎭⎫53,-253,F (3,0),直线L 过定点G (4,0).联立直线L 的方程与曲线C 的方程,消去y 整理得 (1+k 2)x 2-(3+8k 2)x +16k 2=0. 由Δ=0,解得k =±34,由求根公式解得交点的横坐标为x =125∈⎝⎛⎦⎤53,3, 由图可知要使直线L 与曲线C 只有一个交点, 则k ∈⎣⎡⎦⎤-257,257∪⎩⎨⎧⎭⎬⎫-34,34. 故所求k 的取值范围为⎣⎡⎦⎤-257,257∪⎩⎨⎧⎭⎬⎫-34,34. [解题技法]直线与圆的综合问题的求解策略(1)利用解析几何的基本思想方法(即几何问题代数化),把它转化为代数问题,通过代数的计算,使问题得到解决.(2)直线与圆和平面几何联系十分紧密,可充分考虑平面几何知识的运用,如在直线与圆相交的有关线段长度计算中,要把圆的半径、圆心到直线的距离、直线被圆截得的线段长度放到一起综合考虑.[过关训练]已知A (2,0),直线4x +3y +1=0被圆C :(x +3)2+(y -m )2=13(m <3)所截得的弦长为43,且P 为圆C 上任意一点.(1)求|PA |的最大值与最小值;(2)圆C 与坐标轴相交于三点,求以这三个点为顶点的三角形的内切圆的半径.解:(1)∵直线4x +3y +1=0被圆C :(x +3)2+(y -m )2=13(m <3)所截得的弦长为43, ∴圆心到直线的距离d =|-12+3m +1|5=(13)2-(23)2=1. ∵m <3,∴m =2,∴|AC |=(-3-2)2+(2-0)2=29,∴|PA |的最大值与最小值分别为29+13,29-13.(2)由(1)可得圆C 的方程为(x +3)2+(y -2)2=13,令x =0,得y =0或4;令y =0,得x =0或-6,∴圆C 与坐标轴相交于三点M (0,4),O (0,0),N (-6,0),∴△MON 为直角三角形,斜边|MN |=213,∴△MON 内切圆的半径为4+6-2132=5-13.。
高三数学人教版a版数学(理)高考一轮复习教案:8.4 直线与圆、圆与圆的位置关系 word版含答案
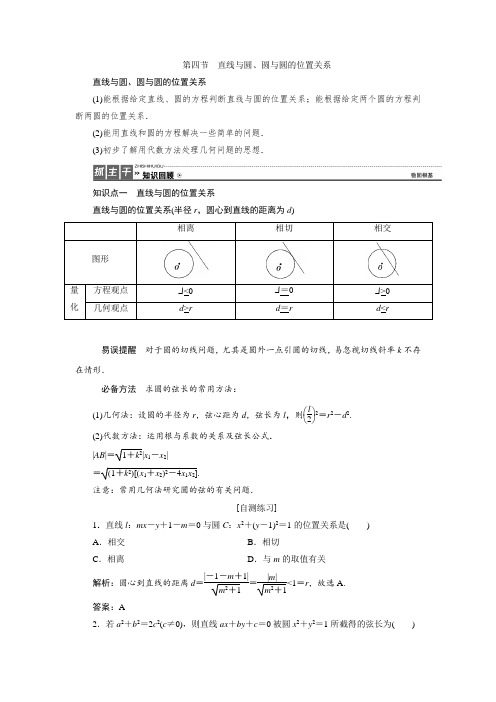
第四节 直线与圆、圆与圆的位置关系直线与圆、圆与圆的位置关系(1)能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系.(2)能用直线和圆的方程解决一些简单的问题. (3)初步了解用代数方法处理几何问题的思想.知识点一 直线与圆的位置关系直线与圆的位置关系(半径r ,圆心到直线的距离为d ) 相离相切相交图形量化方程观点 Δ<0 Δ=0 Δ>0 几何观点 d >rd =rd <r易误提醒 对于圆的切线问题,尤其是圆外一点引圆的切线,易忽视切线斜率k 不存在情形.必备方法 求圆的弦长的常用方法:(1)几何法:设圆的半径为r ,弦心距为d ,弦长为l ,则⎝⎛⎭⎫l 22=r 2-d 2. (2)代数方法:运用根与系数的关系及弦长公式. |AB |=1+k 2|x 1-x 2| =(1+k 2)[(x 1+x 2)2-4x 1x 2].注意:常用几何法研究圆的弦的有关问题.[自测练习]1.直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=1的位置关系是( ) A .相交 B .相切C .相离D .与m 的取值有关解析:圆心到直线的距离d =|-1-m +1|m 2+1=|m |m 2+1<1=r ,故选A.答案:A2.若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为( )A.12 B .1 C.22D. 2解析:因为圆心(0,0)到直线ax +by +c =0的距离d =|c |a 2+b 2=|c |2|c |=22,因此根据直角三角形的关系,弦长的一半就等于1-⎝⎛⎭⎫222=22,所以弦长为 2. 答案:D3.过点(2,3)与圆(x -1)2+y 2=1相切的直线的方程为________.解析:设圆的切线方程为y =k (x -2)+3,由圆心(1,0)到切线的距离为半径1,得k =43,所以切线方程为4x -3y +1=0,又直线x =2也是圆的切线,所以直线方程为4x -3y +1=0或x =2.答案:x =2或4x -3y +1=0 知识点二 圆与圆的位置关系圆与圆的位置关系(两圆半径r 1,r 2,d =|O 1O 2|) 相离外切相交内切内含图形量的关系d >r 1+r 2d =r 1+r 2|r 1-r 2|<d <r 1+r 2d =|r 1-r 2|d <|r 1-r 2|易误提醒 两圆相切问题易忽视分两圆内切与外切两种情形.[自测练习]4.圆O 1:x 2+y 2-2x =0和圆O 2:x 2+y 2-4y =0的位置关系是( ) A .相离 B .相交 C .外切D .内切解析:圆O 1的圆心坐标为(1,0),半径r 1=1,圆O 2的圆心坐标为(0,2),半径r 2=2,故两圆的圆心距d =5,而r 2-r 1=1,r 1+r 2=3,则r 2-r 1<d <r 1+r 2,故两圆相交.答案:B考点一 直线与圆的位置关系|1.对任意的实数k ,直线y =kx -1与圆C :x 2+y 2-2x -2=0的位置关系是( ) A .相离 B .相切C .相交D .以上三个选项均有可能解析:直线y =kx -1恒经过点A (0,-1),圆x 2+y 2-2x -2=0的圆心为C (1,0),半径为3,而|AC |=2<3,故直线y =kx -1与圆x 2+y 2-2x -2=0相交,故选C.答案:C2.(2015·皖南八校联考)若直线y =kx 与圆(x -2)2+y 2=1的两个交点关于直线2x +y +b =0对称,则k ,b 的值分别为( )A.12,-4 B .-12,4C.12,4 D .-12,-4解析:因为直线y =kx 与圆(x -2)2+y 2=1的两个交点关于直线2x +y +b =0对称,所以直线y =kx 与直线2x +y +b =0垂直,且直线2x +y +b =0过圆心,所以⎩⎪⎨⎪⎧k =12,2×2+0+b =0,解得k =12,b =-4.答案:A3.若直线x -my +1=0与圆x 2+y 2-2x =0相切,则m 的值为( ) A .1 B .±1 C .±3D. 3解析:由x 2+y 2-2x =0,得圆心坐标为(1,0),半径为1,因为直线与圆相切,所以圆心到直线的距离等于半径,即|1-0+1|1+m 2=1,解得m =±3. 答案:C判断直线与圆的位置关系常见的两种方法(1)几何法:利用d 与r 的关系. (2)代数法:联立方程之后利用Δ判断.考点二 切线、弦长问题|(1)(2015·高考重庆卷)已知直线l :x +ay -1=0(a ∈R )是圆C :x 2+y 2-4x -2y +1=0的对称轴.过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB |=( )A .2B .4 2C .6D .210(2)(2016·太原一模)已知在圆x 2+y 2-4x +2y =0内,过点E (1,0)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为( )A .3 5B .6 5C .415D .215[解析] (1)由题意得圆C 的标准方程为(x -2)2+(y -1)2=4,所以圆C 的圆心为(2,1),半径为2.因为直线l 为圆C 的对称轴,所以圆心在直线l 上,则2+a -1=0,解得a =-1,所以|AB |2=|AC |2-|BC |2=(-4-2)2+(-1-1)2-4=36,所以|AB |=6,故选C.(2)将圆的方程化为标准方程得(x -2)2+(y +1)2=5,圆心坐标为F (2,-1),半径r =5,如图,显然过点E 的最长弦为过点E 的直径,即|AC |=25,而过点E 的最短弦为垂直于EF 的弦,|EF |=(2-1)2+(-1-0)2=2,|BD |=2r 2-|EF |2=23,∴S 四边形ABCD=12|AC |×|BD |=215. [答案] (1)C (2)D处理切线、弦长问题的策略(1)处理直线与圆的弦长问题时多用几何法,即弦长一半、弦心距、半径构成直角三角形.(2)圆的切线问题的处理要抓住圆心到直线的距离等于半径建立关系解决问题.1.直线l 与圆x 2+y 2+2x -4y +a =0(a <3)相交于A ,B 两点,若弦AB 的中点为(-2,3),则直线l 的方程为( )A .x +y -3=0B .x +y -1=0C .x -y +5=0D .x -y -5=0解析:设直线的斜率为k ,又弦AB 的中点为(-2,3),所以直线l 的方程为kx -y +2k +3=0,由x 2+y 2+2x -4y +a =0得圆的圆心坐标为(-1,2),所以圆心到直线的距离为2,所以|-k -2+2k +3|k 2+1=2,解得k =1,所以直线l 的方程为x -y +5=0,故选C.答案:C2.(2016·云南名校联考)已知圆O :x 2+y 2=1,直线x -2y +5=0上动点P ,过点P 作圆O 的一条切线,切点为A ,则|P A |的最小值为________.解析:过O 作OP 垂直于直线x -2y +5=0,过P 作圆O 的切线P A ,连接OA (图略),易知此时|P A |的值最小.由点到直线的距离公式,得|OP |=|1×0-2×0+5|1+22= 5.又|OA |=1,所以|P A |=|OP |2-|OA |2=2.答案:2考点三 圆与圆的位置关系|1.(2016·惠州调研)圆(x +2)2+y 2=4与圆(x -2)2+(y -1)2=9的位置关系为( ) A .内切 B .相交 C .外切D .相离解析:两圆的圆心距离为17,两圆的半径之差为1、半径之和为5,而1<17<5,所以两圆相交.答案:B2.若点A (1,0)和点B (4,0)到直线l 的距离依次为1和2,则这样的直线有( ) A .1条 B .2条 C .3条D .4条解析:如图,分别以A ,B 为圆心,1,2为半径作圆.依题意得,直线l 是圆A 的切线,A 到l 的距离为1,直线l 也是圆B 的切线,B 到l 的距离为2,所以直线l 是两圆的公切线,共3条(2条外公切线,1条内公切线).答案:C3.若圆x 2+y 2=4与圆x 2+y 2+2ay -6=0(a >0)的公共弦的长为23,则a =________. 解析:两圆的方程相减,得公共弦所在的直线方程为(x 2+y 2+2ay -6)-(x 2+y 2)=0-4⇒y =1a ,又a >0,结合图象(图略),再利用半径、弦长的一半及弦心距所构成的直角三角形,可知1a=22-(3)2=1⇒a =1.答案:1求解两圆位置关系问题的两种方法(1)两圆位置关系的判断常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差得到.19.直线与圆的位置关系中的易错问题【典例】对于任意实数m,直线l:y=m(x-1)+b恒与圆O:x2+y2=a2(a>0)有两个交点,则a,b满足的条件是________.[易错点析]对直线l方程分析不彻底,盲目利用Δ法或几何法无法判断导致失误.[解析]由题意知,①直线l经过定点M(1,b).又直线l恒与圆O:x2+y2=a2(a>0)有两个交点,所以,②点M在圆的内部,所以,12+b2<a2,即a2-b2>1.[答案]a2-b2>1[方法点评]点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.点与圆的位置关系法适用于动直线问题.[跟踪练习](2016·大连双基)圆x2+y2=1与直线y=kx+2没有公共点的充要条件是________.解析:法一:将直线方程代入圆方程,得(k2+1)x2+4kx+3=0,直线与圆没有公共点的充要条件是Δ=16k2-12(k2+1)<0,解得k∈(-3,3).法二:圆心(0,0)到直线y=kx+2的距离d=2k2+1,直线与圆没有公共点的充要条件是d>1,即2k2+1>1,解得k∈(-3,3).答案:(-3,3)A组考点能力演练1.(2016·洛阳二练)已知圆C:x2+y2=4,若点P(x0,y0)在圆C外,则直线l:x0x+y0y =4与圆C的位置关系为()A.相离B.相切C.相交D.不能确定解析:由题意:圆C的圆心到直线l的距离d=4x20+y20,∵点P(x0,y0)在圆x2+y2=4外,∴x20+y20>4,∴d=4x20+y20<2,∴直线l与圆相交.答案:C2.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为()A .(x +2)2+(y -2)2=1B .(x -2)2+(y +2)2=1C .(x +2)2+(y +2)2=1D .(x -2)2+(y -2)2=1解析:C 1:(x +1)2+(y -1)2=1的圆心为(-1,1),所以它关于直线x -y -1=0对称的点为(2,-2),对称后半径不变,所以圆C 2的方程为(x -2)2+(y +2)2=1.答案:B3.(2015·长春二模)设m ,n ∈R ,若直线(m +1)x +(n +1)y -2=0与圆(x -1)2+(y -1)2=1相切,则m +n 的取值范围是( )A .(-∞,2-22]∪[2+22,+∞)B .(-∞,-22]∪[22,+∞)C .[2-22,2+22]D .(-∞,-2]∪[2,+∞) 解析:由直线与圆相切可知 |m +n |=(m +1)2+(n +1)2, 整理得mn =m +n +1,由mn ≤⎝⎛⎭⎫m +n 22可知m +n +1≤14(m +n )2,解得m +n ∈(-∞,2-22]∪[2+22,+∞),故选A. 答案:A4.过点(-2,3)的直线l 与圆x 2+y 2+2x -4y =0相交于A ,B 两点,则|AB |取得最小值时l 的方程为( )A .x -y +5=0B .x +y -1=0C .x -y -5=0D .2x +y +1=0解析:本题考查直线与圆的位置关系.由题意得圆的标准方程为(x +1)2+(y -2)2=5,则圆心C (-1,2),过圆心与点(-2,3)的直线l 1的斜率为k =3-2-2-(-1)=-1.当直线l 与l 1垂直时,|AB |取得最小值,故直线l 的斜率为1,所以直线l 的方程为y -3=x -(-2),即x -y +5=0,故选A.答案:A5.在平面直角坐标系xOy 中,设点P 为圆C :(x -2)2+y 2=5上的任意一点,点Q (2a ,a +2),其中a ∈R ,则线段PQ 长度的最小值为( )A.55B. 5C.355D.655解析:设点Q (x ,y ),则x =2a ,y =a +2,∴x -2y +4=0,∴点Q 在直线x -2y +4=0上.由于圆心(2,0)到直线x -2y +4=0的距离为d =|2-0+4|1+4=655,所以PQ 长度的最小值为d -5=655-5=55,故选A.答案:A6.圆x 2+y 2+x -2y -20=0与圆x 2+y 2=25相交所得的公共弦长为________. 解析:公共弦的方程为(x 2+y 2+x -2y -20)-(x 2+y 2-25)=0,即x -2y +5=0,圆x 2+y 2=25的圆心到公共弦的距离d =|0-2×0+5|5=5,而半径为5,故公共弦长为252-(5)2=4 5.答案:4 57.(2016·泰安调研)已知直线3x -y +2=0及直线3x -y -10=0截圆C 所得的弦长均为8,则圆C 的面积是________.解析:因为已知的两条直线平行且截圆C 所得的弦长均为8,所以圆心到直线的距离d 为两平行直线距离的一半,即d =12×|2+10|3+1=3.又直线截圆C 所得的弦长为8,所以圆的半径r =32+42=5,所以圆C 的面积是25π.答案:25π8.(2016·福州质检)若直线x -y +2=0与圆C :(x -3)2+(y -3)2=4相交于A 、B 两点,则CA →·CB →的值为________.解析:依题意得,点C 的坐标为(3,3).由⎩⎪⎨⎪⎧ y =x +2,(x -3)2+(y -3)2=4,解得⎩⎪⎨⎪⎧ x =3y =5或⎩⎪⎨⎪⎧x =1,y =3, 可令A (3,5),B (1,3),∴CA →=(0,2),CB →=(-2,0), ∴CA →·CB →=0. 答案:09.如图,已知圆C 与y 轴相切于点T (0,2),与x 轴的正半轴交于两点M ,N (点M 在点N 的左侧),且|MN |=3.(1)求圆C 的方程;(2)过点M 任作一直线与圆O :x 2+y 2=4相交于A ,B 两点,连接AN ,BN ,求证:k AN +k BN 为定值.解:(1)因为圆C 与y 轴相切于点T (0,2),可设圆心的坐标为(m,2)(m >0),则圆C 的半径为m ,又|MN |=3,所以m 2=4+⎝⎛⎭⎫322=254,解得m =52,所以圆C 的方程为⎝⎛⎭⎫x -522+(y -2)2=254. (2)由(1)知M (1,0),N (4,0),当直线AB 的斜率为0时,易知k AN =k BN =0,即k AN +k BN=0.当直线AB 的斜率不为0时,设直线AB :x =1+ty ,将x =1+ty 代入x 2+y 2-4=0,并整理得,(t 2+1)y 2+2ty -3=0.设A (x 1,y 1),B (x 2,y 2),所以⎩⎪⎨⎪⎧y 1+y 2=-2tt 2+1,y 1y 2=-3t 2+1,则k AN +k BN =y 1x 1-4+y 2x 2-4=y 1ty 1-3+y 2ty 2-3=2ty 1y 2-3(y 1+y 2)(ty 1-3)(ty 2-3)=-6t t 2+1+6tt 2+1(ty 1-3)(ty 2-3)=0.综上可知,k AN +k BN 为定值.10.已知圆M 的圆心M 在x 轴上,半径为1,直线l :y =43x -12被圆M 截得的弦长为3,且圆心M 在直线l 的下方.(1)求圆M 的方程;(2)设A (0,t ),B (0,t +6)(-5≤t ≤-2),若圆M 是△ABC 的内切圆,求△ABC 的面积S 的最大值和最小值.解:(1)设圆心M (a,0),由已知得点M 到直线l :8x -6y -3=0的距离为12-⎝⎛⎭⎫322=12,∴|8a -3|82+62=12.又点M 在直线l 的下方,∴8a -3>0,∴8a -3=5,a =1,∴圆M 的方程为(x -1)2+y 2=1.(2)设直线AC 的斜率为k 1,直线BC 的斜率为k 2,则直线AC 的方程为y =k 1x +t ,直线BC 的方程为y =k 2x +t +6.由方程组⎩⎪⎨⎪⎧y =k 1x +t ,y =k 2x +t +6,解得C 点的横坐标为6k 1-k 2.∵|AB |=t +6-t =6,∴S =12×⎪⎪⎪⎪6k 1-k 2×6=18|k 1-k 2|.∵圆M 与AC 相切,∴1=|k 1+t |1+k 21,∴k 1=1-t 22t ;同理,k 2=1-(t +6)22(t +6).∴k 1-k 2=3(t 2+6t +1)t 2+6t,∴S =6(t 2+6t )t 2+6t +1=6⎝⎛⎭⎫1-1t 2+6t +1,∵-5≤t ≤-2,∴-8≤t 2+6t +1≤-4, ∴S max =6×⎝⎛⎭⎫1+14=152,S min =6×⎝⎛⎭⎫1+18=274. B 组 高考题型专练1.(2014·高考浙江卷)已知圆x 2+y 2+2x -2y +a =0截直线x +y +2=0所得弦的长度为4,则实数a 的值是( )A .-2B .-4C .-6D .-8解析:由圆的方程x 2+y 2+2x -2y +a =0可得,圆心为(-1,1),半径r =2-a .圆心到直线x +y +2=0的距离为d =|-1+1+2|2= 2.由r 2=d 2+⎝⎛⎭⎫422得2-a =2+4,所以a =-4.答案:B2.(2014·高考重庆卷)已知直线ax +y -2=0与圆心为C 的圆(x -1)2+(y -a )2=4相交于A ,B 两点,且△ABC 为等边三角形,则实数a =________.解析:易知△ABC 是边长为2的等边三角形,故圆心C (1,a )到直线AB 的距离为3,即|a +a -2|a 2+1=3,解得a =4±15.经检验均符合题意,则a =4±15.答案:4±153.(2014·高考山东卷)圆心在直线x -2y =0上的圆C 与y 轴的正半轴相切,圆C 截x 轴所得弦的长为23,则圆C 的标准方程为________.解析:依题意,设圆心的坐标为(2b ,b )(其中b >0),则圆C 的半径为2b ,圆心到x 轴的距离为b ,所以24b 2-b 2=23,b >0,解得b =1,故所求圆C 的标准方程为(x -2)2+(y -1)2=4.答案:(x -2)2+(y -1)2=44.(2015·高考山东卷)过点P (1,3)作圆x 2+y 2=1的两条切线,切点分别为A ,B ,则P A →·PB →=________.解析:在平面直角坐标系xOy 中作出圆x 2+y 2=1及其切线P A ,PB ,如图所示.连接OA ,OP ,由图可得|OA |=|OB |=1,|OP |=2,|P A →|=|PB →|=3,∠APO =∠BPO =π6,则P A →,PB →的夹角为π3,所以P A →·PB →=|P A →|·|PB →|·cos π3=32. 答案:325.(2015·高考重庆卷)若点P (1,2)在以坐标原点为圆心的圆上,则该圆在点P 处的切线方程为________.解析:由题意,得k OP =2-01-0=2,则该圆在点P 处的切线方程的斜率为-12,所以所求切线方程为y -2=-12(x -1),即x +2y -5=0. 答案:x +2y -5=0。
2011年高考一轮课时训练(理)1612直线与圆位置关系(通用)

第二节 直线与圆的位置关系一、填空题1.(2009年广东卷)如下图,点A ,B ,C 是圆O 上的点,且AB =4,∠ACB =45°,则圆O 的面积等于________.第1题图第2题图2.(2009年揭阳模拟)如上图所示,AB 是圆O 的直径,EF 切圆O 于C ,AD ⊥EF 于D ,AD =2,AB =6,则AC 长为________.3.如下图所示,圆O 上的一点C 在直径AB 上的射影为D ,CD =4,BD =8,则圆O 的直径=________.第3题图第4题图4.如上图,PT 是⊙O 的切线,切点为T ,直线P A 与⊙O 交于A 、B 两点,∠TP A 的平分线分别交直线TA 、TB 于D 、E 两点,已知PT =2,PB =3,则P A =______________,TEAD=________.5.如下图所示,圆O 的直径AB =6,C 为圆周上一点,BC =3.过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D ,E ,则∠DAC =________,线段AE 的长为________.第5题图第6题图6.如上图,EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E =46°,∠DCF =32°,则∠A 的度数是________.7.如下图,在Rt △ABC 中,∠C =90°,⊙O 分别与BC 、AC 相切于P 、Q 两点,且圆心O 在AB 上,若AC =m ,BC =n ,则⊙O 的半径等于________.第7题图第8题图8.如上图,P 为圆外一点,P A 切圆于点A ,P A =8,直线PCB 交圆于C 、B 两点,且PC =4,∠ABC =α,∠ACB =β.连结AB 、AC ,则sin αsin β的值等于________.二、解答题9.(2009年银川一中月考)如右图所示,AB 是⊙O 的直径,C 、F 为⊙O 上的点,CA 是∠BAF 的角平分线,过点C 作CD ⊥AF 交AF 的延长线于D 点,CM ⊥AB ,垂足为点M .(1)求证:DC 是⊙O 的切线; (2)求证:AM ·MB =DF ·DA .10如右图所示,四边形ABCD 内接于⊙O ,AB =AD ,过A 点的切线交CB 的延长线于E 点.求证:AB 2=BE ·CD .参考答案1.解读:法一:连结OA 、OB ,则∠AOB =90°,∵AB =4,OA =OB ,∴OA =22,则S 圆=π×(22)2=8π; 法二:2R =4sin 45°=42⇒R =22,则S 圆=π×(22)2=8π.答案:8π 2.2 33.解读:∵BC 2=CD 2+BD 2=BD ·AB , ∴42+82=8AB , ∴AB =10. 答案:10 4.433325.解读:法一:因为直线l 与圆O 相切于点C , ∴∠ABC =∠ACD (弦切角等于同弧对圆周角), ∵AB 为圆O 的直径,且AB =6、BC =3.∴在Rt △ACB 中,∠ABC =60°,∴∠ACD =60°, 又∵AD ⊥CD ,∴∠DAC =30°.法二:连结OC ,∵直线l 切圆O 于点C ,∴OC ⊥l ,又AD ⊥l , ∴AD ∥OC ,∴∠DAB =∠COB =60°, 在Rt △ACB 中,∠CAB =30°,∴∠DAC =30°.连结BE ,易得在Rt △ABE 中,∠EAB =60°,∴AE =12AB =3.答案:π636.解读:法一:∵EB 、EC 是⊙O 的切线, ∴EC =EB . 又∠E =46°,∴∠ECB =180°-46°2=67°.∵∠DCF =32°,∴∠BCD =180°-67°-32°=81°.∵∠A +∠BCD =180°,∴∠A =180°-81°=99°.法二:连结AC ,∵EB 、EC 是⊙O 切线, ∴EB =EC .∴∠ECB =180°-46°2=67°.∵EF 切⊙O 于点C ,∴∠BAC =∠ECB =67°,∠CAD =∠DCF =32°. ∴∠BAD =∠BAC +∠DAC =67°+32°=99°. 答案:99°7.解读:连结OP 、OQ ,则△BOP ∽△OAQ 设半径为R ,则AQ =m -R ,BP =n -R , 由AQ OQ =OP BP ⇒m -R R =R n -R ⇒R =mn m +n . 答案:mn m +n8.解读:∠P AC =∠B =α∠ACP =π-β 在△APC 中,由正弦定理有: APsin (π-β)=PC sin α ⇒8sin β=4sin α,∴sin αsin β=12. 答案:129.证明:(1)连结OC ,∴∠OAC =∠OCA , 又∵CA 是∠BAF 的角平分线,∴∠OAC =∠F AC , ∴∠F AC =∠ACO ,∴OC ∥AD ,∵CD ⊥AF ,∴CD ⊥OC ,即DC 是⊙O 的切线. (2)连结BC ,在Rt △ACB 中,CM ⊥AB ,∴CM2=AM·MB,又∵DC是⊙O的切线,∴DC2=DF·DA,易知△AMC≌△ADC,∴DC=CM,∴AM·MB=DF·DA10.证明:连结AC.因为EA切⊙O于A,所以∠EAB=∠ACB.因为AB=AD,所以∠ACD=∠ACB,于是∠EAB=∠ACD.又四边形ABCD内接于⊙O,所以∠ABE=∠D. 所以△ABE∽△CDA.于是ABCD=BEDA,即AB·DA=BE·CD.所以AB2=BE·CD.。
第1课时 直线与圆的位置关系 学案(含答案)

第1课时直线与圆的位置关系学案(含答案)2.2.2直线与圆的位置关系第1课时直线与圆的位置关系学习目标1.掌握直线与圆的三种位置关系相交.相切.相离.2.会用代数法和几何法来判定直线与圆的三种位置关系.3.会用直线与圆的位置关系解决一些实际问题.知识点直线与圆的三种位置关系及判定位置关系相离相切相交图示几何法比较d与r的大小drdrdr代数法依据方程组解的情况方程组无解方程组只有一组解方程组有两组不同解一.直线与圆的位置关系的判断例1求实数m的取值范围,使直线xmy30与圆x2y26x50分别满足相交;相切;相离.解圆的方程化为标准形式为x32y24,故圆心3,0到直线xmy30的距离为d,圆的半径为r2.若相交,则dr,即2,所以m2或m2;若相切,则dr,即2,所以m2;若相离,则dr,即2,所以2m2.反思感悟直线与圆的位置关系的判断方法1几何法由圆心到直线的距离d与圆的半径r的大小关系判断.2代数法根据直线方程与圆的方程组成的方程组解的个数来判断.3直线系法若直线恒过定点,可通过判断定点与圆的位置关系来判断直线与圆的位置关系.但有一定的局限性,必须是过定点的直线系.跟踪训练1已知直线lx2y50与圆Cx72y1236,判断直线l与圆C的位置关系.解方法一代数法由方程组消去y后整理,得5x250x610.502456112800,该方程组有两组不同的实数解,即直线l 与圆C相交.方法二几何法圆心7,1到直线l的距离为d2.dr6,直线l与圆C相交.二.切线问题例2过点A1,4作圆x22y321的切线l,求切线l 的方程.解122432101,点A在圆外.当直线l的斜率不存在时,l 的方程是x1,不满足题意.设直线l的斜率为k,则切线l的方程为y4kx1,即kxy4k0.圆心2,3到切线l的距离为1,解得k0或k,因此,所求直线l的方程为y4或3x4y130.反思感悟求过某一点的圆的切线方程,首先判定点与圆的位置关系,以确定切线的数目.1求过圆上一点Px0,y0的圆的切线方程如果斜率存在且不为0,先求切点与圆心连线的斜率k,则由垂直关系知,切线斜率为,由点斜式方程可求得切线方程.如果斜率为0或斜率为不存在,则由图形可直接得切线方程为yy0或xx0.2求过圆外一点Px0,y0的圆的切线时,常用几何方法求解设切线方程为yy0kxx0,即kxykx0y00,由圆心到直线的距离等于半径,可求得k,进而求出切线方程.但要注意,若求出的k值只有一个,则另一条切线的斜率一定不存在,可由数形结合求出.跟踪训练2若点P1,2在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为________.答案x2y50解析点P1,2在以坐标原点为圆心的圆上,可得此圆的方程为x2y25,所以该圆在点P处的切线方程为y2x1,即x2y50.三.有关切线的最值问题例3点P是直线2xy100上的动点,PA,PB与圆x2y24分别相切于A,B两点,则四边形PAOB面积的最小值为________.答案8解析如图所示,因为S四边形PAOB2SPOA,又OAAP,所以S四边形PAOB2OAPA22.为使四边形PAOB的面积最小,当且仅当OP达到最小值,即为点O到直线2xy100的距离,故OPmin2.故所求最小值为28.反思感悟与圆有关的最值问题大致分为两类一类运用几何特征及几何手段先确定达到最值的位置,再进行计算;另一类是通过建立目标函数后,转化为函数的最值问题.这类问题具有较强的综合性.跟踪训练3过定点P2,1作动圆Cx2y22aya220的一条切线,切点为T,则线段PT长的最小值为____________.答案解析由题意知圆心C0,a,半径r,则PT,当a1时,PT的长最小为.1.直线与圆位置关系的两种判断方法比较1若直线和圆的方程已知,或圆心到直线的距离易表达,则用几何法较为简单.2若直线或圆的方程中含有参数,且圆心到直线的距离较复杂,则用代数法较简单.2.过一点的圆的切线方程的求法1当点在圆上时,当切线的斜率存在且不为0时,由圆心与该点的连线与切线垂直,从而求得切线的斜率,用直线的点斜式方程可求得圆的切线方程.如果切线斜率不存在或为0,则切线方程可直接写出.2若点在圆外时,过该点的切线将有两条,但在用设斜率来解题时可能求出的切线只有一条,这是因为有一条过该点的切线的斜率不存在.1.直线xy20与圆x12y124的位置关系是A.直线过圆心B.相切C.相离D.相交但直线不过圆心答案D解析圆心坐标为1,1,半径r2,圆心到直线xy20的距离为d2r.又点1,1不在直线xy20上,所以直线与圆相交但不过圆心.2.设直线l过点P2,0,且与圆x2y21相切,则l的斜率是A.1B.C.D.答案C解析设直线l的斜率为k,则l的方程为ykx2,由l 与圆x2y21相切,得1.解得k.3.若直线3x4ym0与圆x2y22x4y40没有公共点,则实数m的取值范围是____________.答案,010,解析将圆x2y22x4y40化为标准方程为x12y221,则圆心坐标为1,2,半径为1.若直线与圆没有公共点,则圆心到直线的距离大于半径,即d1,所以m0或m10.4.平行于直线2xy10且与圆x2y25相切的直线方程为________________.答案2xy50和2xy50解析依题意可设所求切线方程为2xyc0,则圆心0,0到直线2xyc0的距离为,解得c5.故所求切线的直线方程为2xy50和2xy50.5.过点M2,4向圆x12y321引切线,求其切线方程.解由题意可知圆心为1,3,半径r1,因为2124321,所以点在圆外,当斜率存在时,设切线方程为y4kx2,即kxy42k0,由于直线与圆相切,故1,解得k.所以切线方程为24x7y200;当切线斜率不存在时,其切线方程为x2,满足题意.综上,所求切线方程为x2或24x7y200.。
高考数学一轮复习学案:9.4 直线与圆、圆与圆的位置关系(含答案)

高考数学一轮复习学案:9.4 直线与圆、圆与圆的位置关系(含答案)9.4直线与圆直线与圆..圆与圆的位置关系圆与圆的位置关系最新考纲考情考向分析1.能根据给定直线.圆的方程,判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系2.能用直线和圆的方程解决一些简单的问题3.初步了解用代数方法处理几何问题的思想.考查直线与圆的位置关系.圆与圆的位置关系的判断;根据位置关系求参数的范围.最值.几何量的大小等题型主要以选择.填空题为主,要求相对较低,但内容很重要,有时也会在解答题中出现.1判断直线与圆的位置关系常用的两种方法1几何法利用圆心到直线的距离d和圆的半径r的大小关系dr相离2代数法判别式b24ac0相交;0相切;0,圆O2xa22yb22r22r20.方法位置关系几何法圆心距d与r1,r2的关系代数法联立两圆方程组成方程组的解的情况外离dr1r2无解外切dr1r2一组实数解相交|r1r2|1,而圆心O到直线axby1的距离d|a0b01|a2b21a2b21.所以直线与圆相交2圆x2y22x4y0与直线2txy22t0tR的位置关系为A相离B相切C相交D以上都有可能答案C解析直线2txy22t0恒过点1,2,1222214250,点1,2在圆x2y22x4y0内,直线2txy22t0与圆x2y22x4y0相交,故选C.思维升华判断直线与圆的位置关系的常见方法1几何法利用d与r的关系2代数法联立方程之后利用判断3点与圆的位置关系法若直线恒过定点且定点在圆内,可判断直线与圆相交题型二题型二圆与圆的位置关系圆与圆的位置关系典例已知圆C1xa2y224与圆C2xb2y221外切,则ab的最大值为A.62B.32C.94D23答案C解析由圆C1与圆C2外切,可得ab2222213,即ab29,根据基本不等式可知abab2294,当且仅当ab时等号成立,ab的最大值为94.引申探究1若将本典例中的“外切”变为“内切”,求ab 的最大值解由C1与C2内切得ab22221.即ab21,又abab2214,当且仅当ab时等号成立,故ab的最大值为14.2若将本典例条件“外切”变为“相交”,求公共弦所在的直线方程解由题意把圆C1,圆C2的方程都化为一般方程,得圆C1x2y22ax4ya20,圆C2x2y22bx4yb230,由得2a2bx3b2a20,即2a2bx3b2a20为所求公共弦所在直线方程思维升华判断圆与圆的位置关系时,一般用几何法,其步骤是1确定两圆的圆心坐标和半径长;2利用平面内两点间的距离公式求出圆心距d,求r1r2,|r1r2|;3比较d,r1r2,|r1r2|的大小,写出结论跟踪训练xx 重庆调研如果圆Cx2y22ax2ay2a240与圆Ox2y24总相交,那么实数a的取值范围是______________________答案22,00,22解析圆C的标准方程为xa2ya24,圆心坐标为a,a,半径为2.依题意得0a2a222,0|a|22.a22,00,22题型三题型三直线与圆的综合问题直线与圆的综合问题命题点1求弦长问题典例xx全国已知直线lmxy3m30与圆x2y212交于A,B两点,过A,B分别做l的垂线与x轴交于C,D两点,若|AB|23,则|CD|________.答案4解析设AB的中点为M,由题意知,圆的半径R23,|AB|23,所以|OM|3,由|OM||3m3|m213,解得m33,所以直线lx3y60.由x3y60,x2y212,解得A3,3,B0,23,则AC的直线方程为y33x3,BD的直线方程为y233x,令y0,解得C2,0,D2,0,所以|CD|4.命题点2直线与圆相交求参数范围典例已知过点A0,1且斜率为k的直线l与圆Cx22y321交于M,N两点1求k的取值范围;2若OMON12,其中O为坐标原点,求|MN|.解1由题设,可知直线l的方程为ykx1,因为l与C交于两点,所以|2k31|1k21.解得473k473.所以k的取值范围为473,473.2设Mx1,y1,Nx2,y2将ykx1代入方程x22y321,整理得1k2x241kx70.所以x1x241k1k2,x1x271k2.OMONx1x2y1y21k2x1x2kx1x214k1k1k28.由题设可得4k1k1k2812,解得k1,所以l的方程为yx1.故圆心C在l上,所以|MN|2.命题点3直线与圆相切的问题典例已知圆Cx12y2210,求满足下列条件的圆的切线方程1与直线l1xy40平行;2与直线l2x2y40垂直;3过切点A4,1解1设切线方程为xyb0,则|12b|210,b125,切线方程为xy1250.2设切线方程为2xym0,则|22m|510,m52,切线方程为2xy520.3kAC211413,过切点A4,1的切线斜率为3,过切点A4,1的切线方程为y13x4,即3xy110.思维升华直线与圆综合问题的常见类型及解题策略1处理直线与圆的弦长问题时多用几何法,即弦长的一半.弦心距.半径构成直角三角形2圆的切线问题的处理要抓住圆心到直线的距离等于半径,从而建立关系解决问题跟踪训练1过点3,1作圆x22y224的弦,其中最短弦的长为________答案22解析设P3,1,圆心C2,2,则|PC|2,半径r2,由题意知最短的弦过P3,1且与PC 垂直,所以最短弦长为2222222.2过点P2,4引圆x12y121的切线,则切线方程为__________________答案x2或4x3y40解析当直线的斜率不存在时,直线方程为x2,此时,圆心到直线的距离等于半径,直线与圆相切,符合题意;当直线的斜率存在时,设直线方程为y4kx2,即kxy42k0,直线与圆相切,圆心到直线的距离等于半径,即d|k142k|k212|3k|k211,解得k43,所求切线方程为43xy42430,即4x3y40.综上,切线方程为x2或4x3y40.高考中与圆交汇问题的求解考点分析与圆有关的最值问题及直线与圆相结合的题目是近年来高考高频小考点与圆有关的最值问题主要表现在求几何图形的长度.面积的最值,求点到直线的距离的最值,求相关参数的最值等方面解决此类问题的主要思路是利用圆的几何性质将问题转化;直线与圆的综合问题主要包括弦长问题,切线问题及组成图形面积问题,解决方法主要依据圆的几何性质一.与圆有关的最值问题典例11已知点A,B,C在圆x2y21上运动,且ABBC.若点P的坐标为2,0,则|PAPBPC|的最大值为A6B7C8D92过点2,0引直线l与曲线y1x2相交于A,B两点,O为坐标原点,当AOB的面积取最大值时,直线l的斜率等于A.33B33C33D3解析1A,B,C在圆x2y21上,且ABBC,AC为圆的直径,故PAPC2PO4,0,设Bx,y,则x2y21且x1,1,PBx2,y,PAPBPCx6,y故|PAPBPC|12x37,当x1时有最大值497,故选B.2SAOB12|OA||OB|sinAOB12sinAOB12.当AOB2时,AOB的面积最大此时O到AB的距离d22.设AB 的方程为ykx2k0,即kxy2k0.由d|2k|k2122,得k33.也可ktanOPH33.答案1B2B二.直线与圆的综合问题典例21已知直线lxay10aR是圆Cx2y24x2y10的对称轴,过点A4,a作圆C的一条切线,切点为B,则|AB|等于A2B42C6D2102在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2xy40相切,则圆C面积的最小值为A.45B.34C625D.54解析1由于直线xay10是圆Cx2y24x2y10的对称轴,圆心C2,1在直线xay10上,2a10,a1,A4,1|AC|236440.又r2,|AB|240436.|AB|6.2AOB90,点O在圆C上设直线2xy40与圆C相切于点D,则点C与点O间的距离等于它到直线2xy40的距离,点C在以O为焦点,以直线2xy40为准线的抛物线上,当且仅当O,C,D共线时,圆的直径最小为|OD|.又|OD||2004|545圆C的最小半径为25,圆C面积的最小值为25245.答案1C2A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)求k的取值范围
(2)是否存在常数k,使得向量 共线?如果存在,求k值;如果不存在,请说明理由。
注意:
本文件是河北正定中学11届高三全体数学老师编写的教学学案,是正中现用的教学资料。本人将本文件发布于网上,是为了将正中的一些优秀的学习方法和大家共享,可以使大家从本文件有所收获。最后,若有转载,请标明本文件作者:“河北正定中学11届所有数学老师”
(今版教程269页)
12.已知P是直线 上的动点,PA,PB是圆 的两条切线,A,B是切点,求四边形PACB的面积的最小值
13.(今版教程262例4)
已知圆 ,现在构造一系列的圆 ,使圆 同时与圆 和圆 都相切,并都与x轴相切,
(1)求圆 的半径
(2)证明:两个相邻圆 和 在切点间的公切线长为
(3)求 的极限
4.从原点出发向圆 作两条切线,则该圆夹在两条切线间的劣弧长为()
5.若圆 上至少有三个不同点到直线 : 的距离为 ,则直线 的倾斜角的取值范围是( b )
A.[ ] B.[ ] C.[ D.
6、将直线x+y-1=0绕点(1,0)顺时针旋转 后,再向上平移一个单位,此时恰与圆x2+(y-1)2=R2相切,则正数R等于B
A B、 C、1 D、
二、填空题
7.已知直线 和圆 相交于 两点,且 ,则 (-1/2)
(今版教程261页例1)
8.求满足下列条件的圆的方程
(1)经过点(6,5),(0,1)且圆心在直线 上的圆的方程为
(2)经过(-2,4),(3,-1)且在x轴上截得的弦长为6的圆的方程
9.设直线 与圆 相交于 、 两点,且弦 的长为 ,则 ____________.
例3(三年高考两年模拟125页6)如图,已知圆 和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,且满足 ,
(1)求实数a,b间满足的等量关系
(2)求线段PQ长的最小值
(3)若以P为圆心所做的圆P与圆O有公共点,试求半径取最小值时圆P的方程。
例4已知与圆 相切的直线l交x轴,y轴于A,B两点,且 ,
∵
∴ 时,
∴0<r≤
(3)设圆心P(x,y),则
消去m得:y=4(x-3)2-1
又
∴
∴所求轨迹方程为(x-3)2= (y+1)( )
例2:(金版教程262页例5)
(1)若实数x,y满足 ,则 的最大值是
(2)已知圆 ,点A(-1,0),B(1,0),点P为圆上一动点,求 的最大值和最小值及对应的P点坐标
(1)求证:
(2)求线段AB的中点的轨迹方程
(3)求 面积的最小值
四、思想方法总结:
圆及直线与圆的位置关系作业
一、选择题:
1.若直线 与曲线 有两个不同交点,则实数 的取值范围是(B)
2.一束光线从点 出发,经x轴反射到圆C: 上的最短路程是(A)
3.已知圆 ,圆 ,两圆的外公切线交于 点,内公切线交于 点,若 ,则 =(B)
三、命题热点突破:
例1已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆,(1)求实数m取值范围;(2)求圆半径r取值范围;(3)求圆心轨迹方程。
分析:
(1)m满足[-2(m+3)]2+[2(1-4m2)]2-4(16m4+9)>0,即7m2-6m-1<0
∴
(1)半径r=
圆及直线与圆的位置关系
一、考点梳理
1.圆的三种方程
2.圆与直线的位置关系
(1)判断圆与直线的位置关系主要有以下两种方法:
(1)代数法
联立方程消元后得到关于x或y的一元二次方程,其判别式为 ,则
直线与圆相交(有两个公共点)
直线与圆相切(有一个公共点)
直线与圆相离(没有公共点)
(2)几何法:
设圆的半径为 ,圆心到直线的距离为 ,则:
解析:设直线 与圆 相交于 、 两点,且弦 的长为 ,则圆心(1,2)到直线的距离等于1, , 0.
三、解答题
10.求半径是4,与圆 和直线 分别相切的圆的方程
解;
11.已知圆C: 及点
(1)若点 在圆C上,求直线PQ的斜率
(2)若M是圆C上任一点,求 的最大值和最小值
(3)若点 在圆C上,求 的最大值
6.已知圆:(x-1)2+y2=1,作弦OA,则OA中点的轨迹方程是_ ___、 (x≠0)
5、(湖北文8)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为
A.1B.2 C. D.3
答案:选C
解析:切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为d= ,圆的半径为1,故切线长的最小值为 ,选C
A、关于x轴对称B、关于y轴对称
C、关于直线x-y=0对称D、关于直线x+y=0对称
2.从圆 外一点 向这个圆作两条切线,则两切线夹角的余弦值为(b)
A. B. C. D.
3.圆 关于原点 对称的圆的方程为()
4.已知直线 与圆 交于 两点,且 ,其中 为原点,则实数 的值为(C)
5.已知 满足方程 ,则 的最小值是(B)
直线与圆相交(有两个公共点)
直线与圆相切(有一个公共点)
直线与圆相离(没有公共Байду номын сангаас)
3.直线被圆截得的弦长
(1)几何方法
运用弦心距 ,半径 及弦的一半构成的直角三角形,用勾股定理计算弦长
(2)代数方法:
弦长公式
=
4.点与圆,圆与圆的位置关系的判断
同判断直线和圆的位置关系一样
二、考点自测
1.方程x2+y2+2ax-2ay=0所表示的圆()D
