05级《概率论与数理统计》期末试卷
概率论与数理统计期末考试题及答案

模拟试题一一、 填空题(每空3分,共45分)1、已知P(A) = 0.92, P(B) = 0.93, P(B|A ) = 0.85, 则P(A|B ) = 。
P( A ∪B) = 。
2、设事件A 与B 独立,A 与B 都不发生的概率为19,A 发生且B 不发生的概率与B 发生且A 不发生的概率相等,则A 发生的概率为: 2/3 ; ; 3、一间宿舍内住有6个同学,求他们之中恰好有4个人的生日在同一个月份的概率:14212661112C C ⨯ ;没有任何人的生日在同一个月份的概率61266!12C ; 4、已知随机变量X 的密度函数为:,0()1/4,020,2x Ae x x x x ϕ⎧<⎪=≤<⎨⎪≥⎩, 则常数A= , 分布函数F (x )= 1,021,02241,2xe x xx x ⎧≤⎪⎪⎪+<≤⎨⎪>⎪⎪⎩, 概率{0.51}P X -<<=0.53142e -- ; 5、设随机变量X~ B(2,p)、Y~ B(1,p),若{1}5/9P X ≥=,则p = ,若X 与Y 独立,则Z=max(X,Y)的分布律: ; 6、设~(200,0.01),~(4),X B Y P 且X 与Y 相互独立,则D(2X-3Y)= , COV(2X-3Y , X)= ; 7、设125,,,X X X 是总体~(0,1)X N 的简单随机样本,则当k = 时,~(3)Y t =;8、设总体~(0,)0X U θθ>为未知参数,12,,,n X X X 为其样本,11ni i X X n ==∑为样本均值,则θ的矩估计量为: 。
9、设样本129,,,X X X 来自正态总体(,1.44)N a ,计算得样本观察值10x =,求参数a 的置信度为95%的置信区间: ;二、 计算题(35分)1、 (12分)设连续型随机变量X 的密度函数为:1,02()20,x x x ϕ⎧≤≤⎪=⎨⎪⎩其它求:1){|21|2}P X -<;2)2Y X =的密度函数()Y y ϕ;3)(21)E X -;2、(12分)设随机变量(X,Y)的密度函数为1/4,||,02,(,)0,y x x x y ϕ<<<⎧=⎨⎩其他1) 求边缘密度函数(),()X Y x y ϕϕ; 2) 问X 与Y 是否独立?是否相关? 3) 计算Z = X + Y 的密度函数()Z z ϕ;3、(11分)设总体X 的概率密度函数为:1,0(),000xe x x x θϕθθ-⎧≥⎪=>⎨⎪<⎩X 1,X 2,…,X n 是取自总体X 的简单随机样本。
概率论与数理统计期末考试试题及参考答案

概率论与数理统计期末考试试题及参考答案一、选择题(每题2分,共20分)1. 设A、B为两个事件,且P(A) = 0.5,P(B) = 0.6,则P(A∪B)等于()A. 0.1B. 0.3C. 0.5D. 0.7参考答案:D2. 设随机变量X的分布函数为F(x),若F(x)是严格单调增加的,则X的数学期望()A. 存在且大于0B. 存在且小于0C. 存在且等于0D. 不存在参考答案:A3. 设X~N(0,1),以下哪个结论是正确的()A. P(X<0) = 0.5B. P(X>0) = 0.5C. P(X=0) = 0.5D. P(X≠0) = 0.5参考答案:A4. 在伯努利试验中,每次试验成功的概率为p,失败的概率为1-p,则连续n次试验成功的概率为()A. p^nB. (1-p)^nC. npD. n(1-p)参考答案:A5. 设随机变量X~B(n,p),则X的二阶矩E(X^2)等于()A. np(1-p)B. npC. np^2D. n^2p^2参考答案:A二、填空题(每题3分,共15分)1. 设随机变量X~N(μ,σ^2),则X的数学期望E(X) = _______。
参考答案:μ2. 若随机变量X、Y相互独立,且X~N(0,1),Y~N(0,1),则X+Y的概率密度函数f(x) = _______。
参考答案:f(x) = (1/√(2πσ^2))exp(-x^2/(2σ^2))3. 设随机变量X、Y相互独立,且X~B(n,p),Y~B(m,p),则X+Y~_______。
参考答案:B(n+m,p)4. 设随机变量X、Y的协方差Cov(X,Y) = 0,则X、Y的相关系数ρ = _______。
参考答案:ρ = 05. 设随机变量X~χ^2(n),则X的期望E(X) = _______,方差Var(X) = _______。
参考答案:E(X) = n,Var(X) = 2n三、计算题(每题10分,共40分)1. 设随机变量X、Y相互独立,且X~N(0,1),Y~N(0,1),求X+Y的概率密度函数f(x)。
《概率分析与数理统计》期末考试试题及解答(DOC)

《概率分析与数理统计》期末考试试题及
解答(DOC)
概率分析与数理统计期末考试试题及解答
选择题
1. 以下哪个选项不是概率的性质?
- A. 非负性
- B. 有界性
- C. 可加性
- D. 全备性
答案:B. 有界性
2. 离散随机变量的概率分布可以通过哪个方法来表示?
- A. 概率分布函数
- B. 累积分布函数
- C. 概率密度函数
- D. 方差公式
答案:B. 累积分布函数
计算题
3. 一批产品有10% 的不合格品。
从该批产品中随机抽查5个,计算至少有一个不合格品的概率。
解答:
设事件 A 为至少有一个不合格品的概率,事件 A 的对立事件
为没有不合格品的概率。
不合格品的概率为 0.1,合格品的概率为 0.9。
则没有不合格品的概率为 (0.9)^5。
至少有一个不合格品的概率为 1 - (0.9)^5,约为 0.409。
4. 一个骰子投掷两次,计算至少一次出现的点数大于3的概率。
解答:
设事件 A 为至少一次出现的点数大于3的概率,事件 A 的对立事件为两次投掷点数都小于等于3的概率。
一个骰子点数大于3的概率为 3/6 = 1/2。
两次投掷点数都小于等于3的概率为 (1/2)^2 = 1/4。
至少一次出现的点数大于3的概率为 1 - 1/4,约为 0.75。
以上是《概率分析与数理统计》期末考试的部分试题及解答。
希望对你有帮助!。
概率论与数理统计试题(05-0620+B)与答案及评分标准
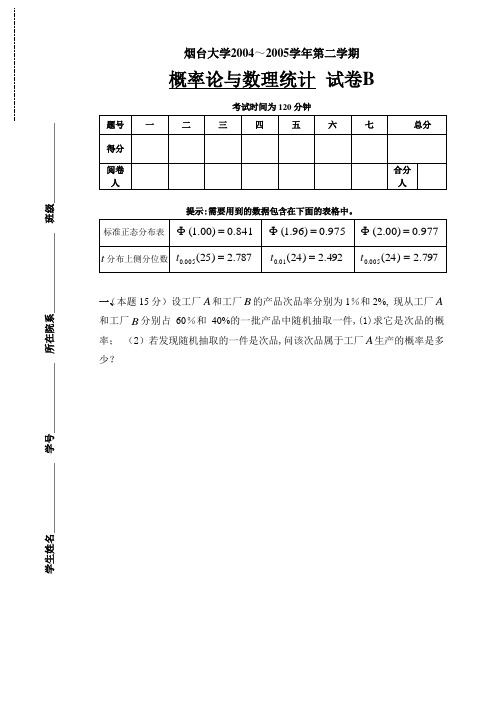
学生姓名______________ 学号______________ 所在院系________________ 班级________________烟台大学2004~2005学年第二学期概率论与数理统计 试卷B考试时间为120分钟提示:需要用到的数据包含在下面的表格中。
一、(本题15分) 设工厂A 和工厂B 的产品次品率分别为1%和2%, 现从工厂A 和工厂B 分别占60%和40%的一批产品中随机抽取一件,(1)求它是次品的概率; (2)若发现随机抽取的一件是次品,问该次品属于工厂A 生产的概率是多少?二、(本题15分) 设随机变量X 的密度函数为 ⎩⎨⎧≤≤=.,0,1,ln )(其它e x x A x f 求: (1)常数A ; (2)X 落在区间),1(e 内的概率; (3)X 的分布函数。
三、(本题15分) 设二维随机变量),(Y X 的联合概率密度为⎩⎨⎧<<<=.,010,,1),(其它,y y x y x f(1)求随机变量X 和Y 的(边缘)概率密度; (2)问X 与Y 是否相互独立?四、(本题15分) 设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤≤-<≤=.,0,21,2,10,)(其它x x x x x f 试求X 的数学期望EX 和方差DX .五、(本题15分) 在每次试验中,事件A 发生的概率为0.5. 问在100次试验中,事件A 发生的次数在45与60之间的概率是多少?六、(本题10分) 设总体X 服从正态分布,均方差(标准差)为0。
9. 从中抽取容量为9的简单随机样本,算得样本均值25=X , 试求总体X 的均值μ的置信度为0。
95的置信区间.七、(本题15分)设总体X 的概率密度函数为⎩⎨⎧<≥=--,,0,,)()(θθθx x e x f x 而n X X X ,,,21 是总体X 的简单随机样本,求θ的极大似然估计量。
大学《概率论与数理统计》期末考试试卷含答案

大学《概率论与数理统计》期末考试试卷含答案一、填空题(每空 3 分,共 30分)在显著性检验中,若要使犯两类错误的概率同时变小,则只有增加 样本容量 .设随机变量具有数学期望与方差,则有切比雪夫不等式 .设为连续型随机变量,为实常数,则概率= 0 . 设的分布律为,,若绝对收敛(为正整数),则=.某学生的书桌上放着7本书,其中有3本概率书,现随机取2本书,则取到的全是概率书的概率为. 设服从参数为的分布,则=. 设,则数学期望= 7 .为二维随机变量, 概率密度为, 与的协方差的积分表达式为 .设为总体中抽取的样本的均值,则= . (计算结果用标准正态分布的分布函数表X ()E X μ=2()D X σ={}2P X μσ-≥≤14X a {}P X a =X ,{}1,2,k k P X x p k ===2Y X =1n k k k x p ∞=∑n()E Y 21k k k x p ∞=∑17X λpoisson (2)E X 2λ(2,3)YN 2()E Y (,)X Y (,)f x y X Y (,)Cov X Y (())(())(,)d d x E x y E y f x y x y +∞+∞-∞-∞--⎰⎰X N (3,4)14,,X X {}15P X ≤≤2(2)1Φ-()x Φ示)10. 随机变量,为总体的一个样本,,则常数=.A 卷第1页共4页 概率论试题(45分) 1、(8分)题略解:用,分别表示三人译出该份密码,所求概率为 (2分)由概率公式 (4分)(2分) 2、(8分) 设随机变量,求数学期望与方差.解:(1) = (3分) (2) (3分) (2分)(8分) 某种电器元件的寿命服从均值为的指数分布,现随机地取16只,它们的寿命相互独立,记,用中心极限定理计算的近似值(计算结果用标准正态分布的分布函数表示).2(0,)XN σn X X X ,,,21 X221()(1)ni i Y k X χ==∑k 21n σA B C 、、P A B C ()P A B C P ABC P A P B P C ()=1-()=1-()()()1-1-1-p q r =1-()()()()1,()2,()3,()4,0.5XY E X D X E Y D Y ρ=====()E X Y +(23)D X Y -()E X Y +E X E Y ()+()=1+3=4(23)4()9()12ov(,)D X Y D X D Y C X Y -=+-8361244XYρ=+-=-100h i T 161ii T T ==∑{1920}P T ≥()x Φ解: (3分) (5分)(4分)(10分)设随机变量具有概率密度,.(1)求的概率密度; (2) 求概率.解: (1) (1分)A 卷第2页共4页(2分)(2分)概率密度函数 (2分)(2) . (3分) (11分) 设随机变量具有概率分布如下,且.i i ET D T E T D T 2()=100,()=100,()=1600,()=160000{1920}0.8}1P T P ≥=≥≈-Φ(0.8)X 11()0x x f x ⎧-≤≤=⎨⎩,,其它21Y X =+Y ()Y f y 312P Y ⎧⎫-<<⎨⎬⎩⎭12Y Y y F y y F y≤>时()=0,时()=1212,{}{1}()d Y y F yP Y y P X y f x x <≤≤=+≤=()=02d 1x y ==-2()=Y Y y f y F y≤⎧'⎨⎩1,1<()=0,其它3102Y YP Y F F ⎧⎫-<<=-=⎨⎬⎩⎭311()-(-1)=222(,)X Y {}110P X Y X +===(1)求常数; (2)求与的协方差,并问与是否独立?解: (1) (2分)由(2分) 可得 (1分)(2), , (3分) (2分) 由可知与不独立 (1分) 三、数理统计试题(25分)1、(8分) 题略. A 卷第3页共4页 证明:,相互独立(4分) ,(4分),p q X Y (,)Cov X Y X Y 1111134123p q p q ++++=+=,即{}{}{}{}{}101011010033P X Y X P Y X p P X Y X P X P X p +====+========+,,1p q ==EX 1()=2E Y 1()=-3E XY 1()=-6,-CovX Y E XY E X E Y ()=()()()=0..ij i j P P P ≠X Y 222(1)(0,1),(1)X n S N n χσ--22(1)X n S σ-2(1)X t n -(1)X t n -(10分) 题略解:似然函数 (4分)由 可得为的最大似然估计 (2分)由可知为的无偏估计量,为的有偏估计量 (4分) 、(7分) 题略 解: (2分)检验统计量,拒绝域 (2分)而 (1分)因而拒绝域,即不认为总体的均值仍为4.55 (2分)A 卷第4页共4页2221()(,)2n i i x L μμσσ=⎧⎫-=-⎨⎬⎩⎭∑2221()ln ln(2)ln() 222ni i x n n L μπσσ=-=---∑2222411()ln ln 0,022n ni i i i x x L L nμμμσσσσ==--∂∂===-+=∂∂∑∑221111ˆˆ,()n n i i i i x x n n μσμ====-∑∑2,μσ221ˆˆ(),()n nE E μμσσ-==11ˆn i i x n μ==∑μ2211ˆ()ni i x n σμ==-∑2σ01: 4.55: 4.55H H μμ=≠x z =0.025 1.96z z ≥=0.185 1.960.036z ==>0H。
概率论与数理统计期末试题与详细解答

《概率论与数理统计》期末试卷一、填空题(每题4分,共20分)1、假设事件A 和B 满足1)(=A B P ,则A 和B 的关系是_______________。
2、设随机变量)(~λπX ,且{}{},21===X P X P 则{}==k X P _____________。
3、设X 服从参数为1的指数分布,则=)(2X E ___________。
4、设),1,0(~),2,0(~N Y N X 且X 与Y 相互独立,则~Y X Z -=___________。
5、),16,1(~),5,1(~N Y N X 且X 与Y 相互独立,令12--=Y X Z ,则=YZ ρ____。
二、选择题(每题4分,共20分)1、将3粒黄豆随机地放入4个杯子,则杯子中盛黄豆最多为一粒的概率为( )A 、323B 、83C 、161D 、812、随机变量X 和Y 的,0=XY ρ则下列结论不正确的是( ) A 、)()()(Y D X D Y X D +=- B 、a X +与b Y -必相互独立 C 、X 与Y 可能服从二维均匀分布 D 、)()()(Y E X E XY E =3、样本nX X X ,,,21 来自总体X ,,)(,)(2σμ==X D X E 则有( )A 、2i X )1(n i ≤≤都是μ的无偏估计 B 、X 是μ的无偏估计C 、)1(2n i X i ≤≤是2σ的无偏估计D 、2X 是2σ的无偏估计 4、设nX X X ,,,21 来自正态总体),(2σμN 的样本,其中μ已知,2σ未知,则下列不是统计量的是( ) A 、ini X ≤≤1min B 、μ-X C 、∑=ni iX 1σ D 、1X X n -5、在假设检验中,检验水平α的意义是( ) A 、原假设0H 成立,经检验被拒绝的概率 B 、原假设0H 不成立,经检验被拒绝的概率 C 、原假设0H 成立,经检验不能拒绝的概率D 、原假设0H 不成立,经检验不能拒绝的概率三、计算题(共28分)1、已知离散型随机变量的分布律为求:X 的分布函数,(2))(X D 。
概率论期末试卷(05年1月)

《概率论与数理统计》期末试卷(2学分用,考试时间120分钟,2003级,2005年1月)注:标准正态分布的分布函数值φ(1.04)=0.8508,φ(1.29)=0.9015,φ(1.65)=0.9505,φ(1.96)=0.9750,φ(2.06)=0.9803一、单项选择题(每小题3分,共15分)1.设事件A 和B 的概率为P (A )=21,P (B )=32,则P (AB )可能为 ( ) A.0 B.1 C. 53 D. 612.从1、2、3、4、5这五个数字中等可能、有放回地接连抽取两个数字,则这两个数字不相同的概率为 ( ) A.21 B. 252 C. 254D.以上都不对3.投掷两个均匀的骰子,已知点数之和是偶数,则点数之和为6的概率为 ( ) A. 185 B. 31 C. 21D.以上都不对4.某一随机变量的分布函数为F (x )=xxe be a ++3,则F (0)的值为 ( )A.0.1B.0.5C.0.25D.以上都不对5.一口袋中有3个红球和2个白球,某人从中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为 ( ) A.2.5 B.3.5 C.3.8 D.以上都不对二、填空题(每小题3分,共15分)1.设A 、B 是相互独立的随机事件,P (A )=0.5,P (B )=0.7,则P (A ∪B )= 。
2.设随机变量ζ~B (n,p ),E (ζ)=3,D (ζ)=1.2,则n= 。
3.随机变量ζ的期望为E (ζ)=5,标准差为σ(ζ)=2,则E (ζ2)= 。
4.甲、乙两射手射击一个目标,他们射中目标的概率分别是0.7和0.8.先由甲射击,若甲未射中再由乙射击。
设两人的射击是相互独立的,则目标被射中的概率为 。
5.设连续型随机变量ζ的概率分布密度为f(x)=222++x x a,a 为常数,则P(ζ≥0)=。
三、(本题10分)将4个球随机地放在5个盒子里,求下列事件的概率:(1)4个球全在一个盒子里; (2)恰有一个盒子有两个球四、(本题10分)设随机变量ζ的分布密度为f(x)={30,130,0≤≤+><x xAx x 当或当(1)求常数A; (2)求P(ζ<1); (3)求ζ的数学期望五、(本题10分)设二维随机变量(ζ,η)的联合分布是(1)ζ与ηη)六、(本题10分)有10盒种子,其中1盒发芽率为90% ,其它9盒为20% 。
《概率论与数理统计》期末考试试题及答案

专业、班级:姓名:学号:
题号
一
二
三
四
五
六
七
八
九
十
十一
十二
总成绩
得分
一、单项选择题(每题3分共18分)
1.D 2.A 3.B 4.A5.A6.B
(1)
(2)设随机变量X其概率分布为 X -1 0 1 2
P 0.2 0.3 0.1 0.4
则 ( )。
(A)0.6(B)1(C)0 (D)
(3)
设事件 与 同时发生必导致事件 发生,则下列结论正确的是()
(A) (B)
(C) (D)
(4)
(5)设 为正态总体 的一个简单随机样本,其中
未知,则()是一个统计量。
(A) (B)
(C) (D)
(6)设样本 来自总体 未知。统计假设
为 则所用统计量为()
(A) (B)
(C) (D)
2、填空题(每空3分共15分)
解:因为 ,所以
(1)根据边缘概率与联合概率之间的关系得出
-1 0 1
0
1
0
0
0
………….4分
(2)因为
所以与 不相互独立
…………8分
七、(8分)设二维随机变量 的联合密度函数为
求:(1) ;(2)求 的边缘密度。
解:(1) …………..2分
=
=[ ] ………….4分
(2) …………..6分
……………..8分
解:用 表示第 户居民的用电量,则
………2分
则1000户居民的用电量为 ,由独立同分布中心极限定理
………3分
= ………4分
……….6分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绍兴文理学院2006学年01学期
经管 专业05级《概率论与数理统计》期末试卷(答题卷)(A)
(考试形式:闭卷)
20分,每小题2分)
设,A B 为随机事件,若()0.4,()0.3,()0.6,P A P B P A B === 则
()P AB = .
2.在三次独立重复射击中,若至少有一次击中目标的概率为3764
,则每次射击击中目标的概率为 .
3.设X 是10次独立重复试验的成功次数,若每次试验成功的概率为0.4,则
2
EX
= .
4.设随机变量X 服从参数为λ的泊松分布,且{2}{4}P X P X ===,则
λ= .
5.设随机变量X 的概率密度为2
301()0
x
x f x ⎧<<=⎨
⎩其它
,且{}0.784P X a >=,
则a = .
6.设25,16,0.4XY D X D Y ρ===,则(2)D X Y += .
7.设随机变量X 服从[0,1]上的均匀分布,则21Y X =+的分布密度
为 .
8.设12,,,n X X X 为取自总体~(0,1)X N 的一个样本, 则22212~n X X X ++ .
9.设12ˆˆ,θθ是参数θ的 ,若12ˆˆD D θθ<,则1ˆθ比2ˆθ有效.
10.设总体22~(,),X N μσσ未知,2,X s 分别为样本均值与样本方差,
则μ的置信度为1α-的置信区间为 .
二、选择题(共10分,每小题2分)
1.同时掷三枚均匀硬币,则恰有两枚正面向上的概率为( ).
(1) 0.5 (2) 0.25 (3) 0.125 (4) 0.375 2.设随机变量X 的概率密度为(),()()f x f x f x =-,()F x 为X 的分布函数,
则对任意的a R ∈,有( ).
(1) 0()1()a
F a f x dx -=-⎰ (2) 0
1()()2
a F a f x dx
-=
-
⎰
(3) ()()F a F a -= (4) ()2()1F a F a -=- 3.设随机变量,X Y 相互独立,且均服从[0.1]上的均匀分布,
则下列服从均匀分布的是( ).
(1) (,)X Y (2) X Y (3) X Y + (4) X Y - 4.设12,,,n X X X 为取自总体X 的一个样本, 则总体方差的一个无偏估计为( ). (1)
2
11
()
n
i
i X X n
=-∑ (2)
1
2
1
1
()
1
n i
i X X n -=--∑
(3)
1
2
1
1
()
n i
i X X n
-=-∑ (4)
2
1
1
()
1
n
i
i X X n =--∑
5.假设检验时,当样本容量一定,若缩小犯第一类错误的概率, 则犯第二类错误的概率( ).
(1) 变小 (2) 变大 (3) 不变 (4) 不确定
三、计算题(共70分,每小题10分)
1.一市场共有10台照相机,其中有3台次品,其余均为正品.某顾客去选购时,已 售出2台,该顾客从剩下的8台中任意选购一台, 求: (1) 该顾客购到正品的概率;
(2) 若已知该顾客购到的是正品,则已售出的两台都是次品的概率.
2.某仪器有3只独立工作的同型号的电子元件,其寿命(单位:小时)都服从同一指数分布,已知其平均寿命为600小时.
求: 该仪器使用200小时后,至少有一只元件损坏的概率.
3.若随机变量,X Y 的分布函数分别为
00
()0221
2
X x x
F x x x <⎧⎪⎪=≤≤⎨
⎪>⎪⎩ ,0
0()11212Y y F y y y y <⎧⎪
=-≤≤⎨⎪>⎩
且X 与Y 相互独立,
(1) 求: (,)X Y 的联合分布函数;
(2) 令 22,X Y ξη==, 求: (,)ξη的联合分布函数(,)G x y ;
(3) 求:3
{1,}2
P X Y <>.
4.游客乘电梯从底层到电视塔顶观光,电梯于每个整点的5分钟,25分钟和55分钟 从底层起行.若一乘客在早上8点的第X 分钟到达底层电梯处,且X 在[0,60]上 服从均匀分布,求:此游客的等候时间Y 及E Y
某车间有200台机床,它们独立地工作,开工率均为0.6,开工时耗电都为1000瓦,问:供电所至少要供给这个车间多少电力才能以99.9%的概率保证这个车间不会因为供电不足而影响生产? ((3.1)0.999,
(17)1Φ=Φ= )
设总体X 的概率密度为(1)01
(;)0x x f x ααα⎧+<<=⎨⎩
其它 ,其中1α>-为未知参
数,n X X X ,,,21 为取自总体X 的样本, 求:α的矩估计量与极大似然估计量.
7.设考生某次考试的成绩服从正态分布,从中随机抽取36位考生的成绩,其平均成绩为66.5分,标准差为15分.问:在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分? (0.025(35) 2.030t = )
绍兴文理学院2006学年01学期
经管 专业 05级《概率论与数理统计》期末试卷(A )
标准答案及评分标准
一、填空题(共20分,每小题2分) 1.0.3 2.
14
3.18.4
4. 6
5.0.6
6. 132
7.1
13()2
0Y y f y ⎧≤≤⎪
=⎨⎪⎩
其它
8.2()n χ 9.无偏估计
10.
2
2
((1),(1))X n X n αα-
-+
-
二、选择题(共10分,每小题2分)
1. (4)
2. (2)
3. (2)
4. (4)
5. (2) 三、计算题(共70分,每小题10分) 1.解:(1)
189360 (5分)
(2) 19
(10分) 2.解: 13
{200}P X e
->= (5分)
所求的概率为: 11e -- (10分)
3.解: (1) 00(1)02,122(,)02,2212,1212,2
x x
y x y F x y x
x y y x y x y <⎧⎪⎪-≤≤≤≤⎪⎪
=⎨≤≤>⎪⎪
->≤≤⎪⎪>>⎩
或1
(3分)
(2) 00
()04214x F x x x ξ<⎧=≤≤⎪>⎪⎩
01()1141
4
y F y y y η<⎧=≤≤>⎩
00104,142
(,)04,4214,1414,4
x y x y G x y x y x y x y <<⎧≤≤≤≤⎪
=⎨
≤≤>⎪⎪⎪>≤≤⎪>>⎩
或 (8分)
(3)
14
(10分)
4.解: 50525525()552555605
5560
X X X
X Y g X X X X X -<≤⎧⎪
-<≤⎪==⎨
-<≤⎪⎪-+<≤⎩ (4分)
11.67E Y = (10分)
5.解: 设1
0i X ⎧=⎨
⎩第i 台机床工作否则
由中心极限定理知200
1i i X =∑近似服从(2000.6,2000.60.4)N ⨯⨯⨯ (3分 )
设供电R kw
,则200
1
{}0.999i i P X R φ=≤=≥∑ (8分)
3.1≥,故至少供电141kw. (10分)
6.解: (1) 矩估计 121ˆ2
1X EX X
αα
α+-=
=+- (5分)
(2) 似然函数为:1
()(1)n
i i L x ααα==+∏ (7分)
1
ln ()ln 1
n
i
i d L n
x d ααα
α==
-+∑ ( 9分)
1
ˆ1ln n
i
i n
x
α
==--∑ (10分)
7.解:首先建立假设
0010:70;
:H H μμμμ==≠
当0H
真时,检验统计量0
~(1),μ-=
-X T t n (3分)
拒绝域为/2(1)
t t n α=
>-. (4分) (5分)
由于0.0251.4(35) 2.030t t =
=<=,
故接受原假设,即认为全体考生的平均成绩为70分. (10分)。
