2012高等数学B(下)期中试卷

合集下载

-2012-2013学年-高等数学(2-1)期中考试试卷---答案

-2012-2013学年-高等数学(2-1)期中考试试卷---答案2012—2013学年第一学期《高等数学(2-1)》期中试卷（工科）专业班级姓名学号开课系室基础数学系考试日期 2012年11月25日页号一二三四五六总分本页满分32 18 10 16 16 8本页得分阅卷人注意事项：1．请在试卷正面答题，反面及附页可作草稿纸；2．答题时请注意书写清楚，保持卷面清洁；3．本试卷共五道大题，满分100分；B ．(0)f 是()f x 的极小值；C ．(0,(0))f 是曲线()y f x =的拐点；D ．(0)f 是()f x 的极大值.3. 当x →∞时，若21ax bx c++与11x +为等价无穷小，则,,a b c 之值为（ B ）． A ．0,1,1a b c ===； B ．0,1a b ==,c 为任意常数；C ．0a =，,b c 为任意常数； D. ,,a b c 均为任意常数.4.设220()(),0x x f x x g x x ⎧>=≤⎩，其中()g x 是有界函数，则()f x 在 0x =处（ D ）. A ．极限不存在；B.极限存在但不连续；C.连续但不可导；D.可导. 5. 设()f x 在0x 可导且01()2f x '=，则0x ∆→时，0|x x dy =是x ∆的（ C ）.A ．等价无穷小；B.高阶无穷小；C.同阶但非等价无穷小；D 低阶无穷小.三、计算题（共4小题，每小题5分，共20分）1.求极限0x →解：（方法一）200sin 12lim lim 11cos 2x x x xx x→→==-；（方法二）001lim 11cos x x x →→==-；（方法三）洛比达法则001sin 11cos cos sin lim 1sin 2cos 21sin x x x x x x x x x x xx x →→→+-+-===+. 2. 设函数()y y x =由方程sin()(0,)xy y xe x x y ππ=>-<<确定，求其在1x =处的切线方程.解：两边取对数得：sin()(1)ln xy y x =-，两边对x 求导，有1cos()()ln y xy y xy y x x-''+=+，又由于1x =时，sin 0y =，y ππ-<<，可得0y =，代入得(1)1y '=-，故在1x =处的切线方程为(1)y x =--，即10x y +-=.3. 设3arctan 6x t t y t t =+⎧⎪⎨=+⎪⎩，求221d y t dx =. 解：222363(1)111dy dy t dt t dx dx dt t +===+++； 22222()66(1)()1211d dy d y d dy t t t dt dx dx dx dx dx t dt t +====+++，故 2241d y t dx ==.本页满分10分本页得分4. 求极限21)(cos lim x x x →. 解：（方法一）2211cos 1cos 100lim(cos )lim(1cos 1)x x x x x x x x --→→=+- 20cos 11lim 2x x x e e →--==；（方法二）22222111sin 1222sin 2200lim(cos )lim (cos )lim(1sin )xx x x xx x x x x x e ---→→∞→==-=；（方法三）洛比达法则sin 2cos 220111ln(cos )lim 200lim(cos )lim x x x x x x x x x x e e e -→-→→===.四、应用题（共3小题，每小题8分，共24分）1. 已知()sin 2ln(1),0()1,0ax a b x x x x f x e x ++-⎧>⎪=⎨⎪-≤⎩在0x =处可导，试求出a 与b .解：由于()f x 在0x =处可导，必连续，故(0)(0)(0)0f f f -+===，又000()sin 2ln(1)()sin 2ln(1)(0)lim lim lim 2x x x a b x x a b x x f a b x x x++++→→→++-+-==+=+-，可得20a b +-=，即2a b +=；又由于()f x 在0x =处可导，则(0)(0)f f -+''=，又 01(0)lim ax x e f a x--→-'==，本页满分16分本页得分2200200()sin 2ln(1)sin ln(1)(0)lim 2lim 1cos 11lim lim [sin ]1(1)x x x x a b x x x x f x x x x x x x +++++→→→→++-+-'==--==--=--，故1,3a b =-=.2. 有一底半径为R cm ，高为h cm 的圆锥容器，今以253cm /s 自顶部向容器内注水，试求当容器内水位等于锥高的一半时水面上升的速率.解：设t 时刻，水的体积，水面半径及水的深度分别为,,V r x ，由于2211()33V R h r h x ππ=--，又从相似三角形可知：r h x R h -=，即h x r R h-=，可得3222332211()1[()]333h x R V R h R h h x hh πππ-=-=--，两边对t 求导，得 222()dV R dx h x dt dt hπ=-，由已知条件25dV dt =，2h x =，代入得2100dx dt R π=，即水面上升的速率为2100cm/s Rπ. 3. 试讨论方程)0(,ln >=a ax x 有几个实根.解：令()ln ,(0,)f x x ax x =-∈+∞，则 1()f x a x '=-，令()0f x '=，解得驻点1x a =，列表如下： x 10,a ⎛⎫ ⎪⎝⎭ 1a 1,a ⎛⎫+∞ ⎪⎝⎭ ()f x ' + 0 — 本页满分16分本页得分()f x 最大值1f a ⎛⎫ ⎪⎝⎭可得，()f x 的最大值为1(ln 1)f a a ⎛⎫=-+ ⎪⎝⎭，讨论如下：（1）当1a e =时，10f a ⎛⎫= ⎪⎝⎭，方程ln x ax =有唯一的实根；（2）当10a e <<时，10f a ⎛⎫> ⎪⎝⎭，又由于 00lim ()lim (ln )x x f x x ax ++→→=-=-∞； ln lim ()lim ()x x x f x x a x→+∞→+∞=-=-∞，故方程ln x ax =有两实根，分别位于10,a ⎛⎫ ⎪⎝⎭与1,a ⎛⎫+∞ ⎪⎝⎭内；当1a e >时，10f a ⎛⎫< ⎪⎝⎭，方程ln x ax =没有实根. 五、证明题（共2小题，每小题8分，共16分）1．设函数()f x 在[0,2]上连续，在(0,2)内可导，且(0)0f =，0)2(=f ，证明：存在(0,2)ξ∈，使得()()f f ξξ'=.证明：令()()x F x e f x -=，则()F x 在[0,2]上连续，在(0,2)内可导，且由于(0)0f =，0)2(=f ，易得(0)(2)0F F ==，根据罗尔定理，至少存在(0,2)ξ∈，使得()0F ξ'=，即()()0e f e f ξξξξ--'-+=，又0e ξ-≠，可得()()f f ξξ'=.本页满分8分本页2．证明：当0>x 时，x x x x <+<+)1ln(1. 证明：（方法一）设t t f ln )(=，则)(t f 在[1,1]x +上连续，在(1,1)x +内可导，由 Lagrange 中值定理，得ln(1)ln11x x ξ+-=，11x ξ<<+，故1111x ξ<<+，即1ln(1)11x x x +<<+，整理得，x x xx <+<+)1ln(1. （方法二）：对()ln(1)f t t =+在[0,]x 上应用Lagrange 中值定理.（方法三）：利用函数的单调性. 得分。

2012学年第二学期11(秋)期中数学试卷

2012学年第二学期11（秋）级期末数学试卷班级：姓名：一．选择题：（每小题3分，共30分）1. 下列四个关系式中正确的是（） A ．∅ ∈{}a B.a ⊂≠ {}a C. {}a ∈{}b a , D. a ∈{}b a , 2．0,0.>>b a 是0>ab 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3．设集合A={(x,y)| x +y=2} ,B = {(x,y)| x -y=4} ,则集合A ∩B = （）A ．x=3，y=-1B ．（3,-1）C ．{(3,-1)}D ．{3,-1}4．若c b a >>，则下列不等式正确的是（） A ．bc ab >B ．bc ac >C ．bc ab >D.c b c a ->-5.若0,0>>b a ，且1=+b a ，则ab 有（） A.最小值41B.最大值41 C. .最小值21 D.最大值21 6．周长为4的长方形中，其面积最大为 ( ) A ．1B ．2C ．3D ．47. 下列不等式中，解集为实数集的是（） A ．012>++x xB ．02>xC ．xx 212<- D ． 0>x 8．下列各组函数中表示同一函数的是（） A ．1)(,)1()(0=-=x g x x f B ．2)(,)(x x g x x f == C ．33)(,)(x x g x x f == D. 22)1()(,)(+==x x g x x f9.函数)5.61,(3≤≤∈=x N x x y 的图像是（） A ．直线B ．射线C ．线段D ．离散的点10.函数2)1(22+--=x a x y 在（4,∞-]上是减函数，则实数a 的取值范围是（） A ．（3,-∞-]B[ -3,)∞+ C . [ 5)∞+ D ．（5,-∞-]二．填空题：（每空3分，共30分）11.集合 { x ∈N | -2<x<3 },用列举法表示。

2012级高数(下)试题及答案解析

南昌大学 2012～2013学年第二学期期末考试试卷一、填空题(每空 3 分，共 15 分) 1. 设:020202x y z Ω≤≤≤≤≤≤，，，则三重积分xyzdV Ω=⎰⎰⎰ _____.2. 交换二次积分的顺序2 22 0(,)yy dy f x y dx ⎰⎰= _________.3. 函数22(,)4()f x y x y x y =---的极大值为_______.4. 将1()6f x x =-展开成x 的幂级数为________.5. 点(2,1,0)到平面3450x y z ++=的距离为__________.二、单项选择题 (每小题3分,共15分)1. 函数xy x yz +=arcsin 的定义域是（）（A ）{}0,|),(≠≤x y x y x ；（B ）{}0,|),(≠≥x y x y x ；（C ）{}(,)|0,0x y x y x ≥≥≠{}0,0|),(≠≤≤x y x y x ；（D ）{}{}0,0|),(0,0|),(<<>>y x y x y x y x .2.设∑为由曲面22y x z +=及平面1=z所围成的立体的表面，则曲面积分22()x y dS ∑+⎰⎰= （）（A ）π22；（B ）π221+；（C ）2π；（D ）0.3.级数∑∞=+111n p n 发散，则（）（A ）0≤p ；（B ）0>p ；（C ）1≤p ；（D ）1<p .4.设函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩,则在点（0，0）处（）（A ）连续且偏导数存在；（B ）连续但偏导数不存在；（C ）不连续但偏导数存在；（D ）不连续且偏导数不存在。

5.设123,,y y y 是常系数线性非齐次方程()y py qy f x '''++=的三个线性无关的解，则0y py qy '''++=的通解为（）（A ）1122C y C y +；（B ）1223C y C y +；（C ）1122C y C y +33C y +；（D ）1122C y C y +123()C C y -+.三、计算题(共24分，每小题8分)1、设arctan x yz x y +=-，求z x ∂∂和2z x y ∂∂∂.2、判断级数1313n n n ∞=-∑的敛散性.3、求微分方程71212y y y x '''-+=的通解四、解答题（一）(共24分，每小题8分) 1、设方程(,)0f xz yz =可确定z 是,x y 的函数，且(,)f u v 具有连续偏导数，求dz .2、计算曲线积分22(sin 2)()L x y dx x y dy --+⎰，其中L 为由点(0,2)A 到(0,0)O 的左半圆周222x y y +=.3、求级数12nn n x n ∞=⋅∑的收敛域与和函数.五、解答题（二）(共16分，每小题8分)1、求椭球面2222349x y z ++=上点（1，1，1 ）处的切平面方程和法线方程.2、利用高斯公式计算曲面积分()()()x y dydz y z dzdx z x dxdy ∑+++++⎰⎰,其中∑为平面0,0,0,1,1,1x y z x y z ====== 所围成的立体的表面的外侧.六、证明题(本题满分6分)设数列{}n a 单调减少，0n a >（1,2,n =）且1(1)nn n a ∞=-∑发散，证明11()1nn n a ∞=+∑收敛.南昌大学 2012～2013学年第二学期期末考试试卷及答案一、填空题(每空 3 分，共 15 分) 1. 设:020202x y z Ω≤≤≤≤≤≤，，，则三重积分xyzdV Ω=⎰⎰⎰8.2. 交换二次积分的顺序2 22 0(,)yy dy f x y dx ⎰⎰=()402,dx f x y dy ⎰⎰.3. 函数22(,)4()f x y x y x y =---的极大值为8.4. 将1()6f x x =-展开成x 的幂级数为()10666n n n x x ∞+=-<<∑.5. 点(2,1,0)到平面3450x y z ++=的距离为.二、单项选择题 (每小题3分,共15分)1. 函数xy x yz +=arcsin 的定义域是（ C ）（A ）{}0,|),(≠≤x y x y x ；（B ）{}0,|),(≠≥x y x y x ；（C ）{}(,)|0,0x y x y x ≥≥≠{}0,0|),(≠≤≤x y x y x ；（D ）{}{}0,0|),(0,0|),(<<>>y x y x y x y x .2.设∑为由曲面22y x z +=及平面1=z所围成的立体的表面，则曲面积分22()x y dS ∑+⎰⎰= （ B ）（A ）π22；（B ）π221+；（C ）2π；（D ）0.3.级数∑∞=+111n p n 发散，则（A ）（A ）0≤p ；（B ）0>p ；（C ）1≤p ；（D ）1<p .4.设函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩,则在点（0，0）处（ C ）（A ）连续且偏导数存在；（B ）连续但偏导数不存在；（C ）不连续但偏导数存在；（D ）不连续且偏导数不存在。

2012高数期中答案

答案一、1、n n )1(1-+2、35.3、1e .4、0.5、1x . 注：答为1||x 不给分6、sin x .7、 arctan x C +.注：答为arctan x 扣1分8、2.9、2-.10、()()f b f a b a--.二、ＡC C B D A 三、 1、解：00x x →→= (2分) 012x →==. (6分)2、解：211212lim lim 111x x x xx x x x x --→∞→∞⎡⎤+⎛⎫⎛⎫⎢⎥=+ ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎣⎦(4分)2e = (6分)3、解：原式=xx x xx x x x cos sin lim 1)sin 1(cot 1lim 020++→→-=-⋅ (3分) 1cos 1lim sin lim 00-=⋅-=++→→xx x x x ．(6分) 4、解：设22212111nn n n x n ++++++=，(1分)则，≤n xn y nnn==+++1111222； (2分) ≥n xn z nnn n nn nn nn =+=+=++++++/1111112222，(3分)因为1lim lim ==∞→∞→n n n n z y ，(4分)由夹逼定理112111lim 222=⎪⎪⎭⎫⎝⎛++++++∞→n n n n n . (6分) 四、1、解：cos(1)(1)sin(1)x dy dx x -=-- (4分)cot(1)x dx =--. (6分)2、解：2[ln(1)][arctan ]dy t dx x '+='(2分) 2221/211t t t t==++ .(6分) 3、解：当0, 1.x y ==(1分) 方程y x y e 1+=两边对x 求导，有xy x x y y y d d e e d d +=，(3分) 得d e d 1e yyy x x =-(4分) 所以,x dy e dx==. (5分)因此,所求的切线方程为1y e x =+. (6分)五、解：要使)(x f 在0x =处可导，必须)(x f 在0x =处连续，(1分)而0(0)lim arcsin()0x f ax ++→==；(0)f b =.(2分)由(0)(0)f f +=，有0b =. (3分) 又 000()(0)arcsin()(0)lim lim lim 0x x x f x f a x a xf a x x x++++→→→-'====-，(4分) 200()(0)2(0)lim lim 20x x f x f x xf x x---→→-+'===-.(5分)由)(x f 在0x =处可导，有(0)(0)f f -+''=(6分), 得2a =.(7分) 故当0,2a b ==时，函数)(x f 在0x =处可导. (8分)六、证明：(1) 令()()1g x f x x =+-, (1分)则()g x 在[0,1]上连续, (2分)又(0)10g =-<，(1)10g =>(3分)，由零点定理知,存在(0,1)ξ∈,使得()()10g f ξξξ=+-=(5分), 即()1f ξξ=-.(6分)(2) 分别在[0,]ξ和[,1]ξ上应用拉格朗日中值定理 (7分),存在(0,)a ξ∈,(,1)b ξ∈使得()(0)1()f f f a ξξξξ--'==, (9分)(1)()1(1)()111f f f b ξξξξξξ---'===---, (11分) 因此()()1f a f b ''=. (12分)附加题、证明：令()[()()][()()]F x f a f x g x g b =--.(2分)因为()F x 在闭区间[]b a ,上连续，在开区间()b a ,内可导，且()()0F a F b ==,(3分) 由罗尔定理, 存在一点(),a b ξ∈,使得()0F ξ'=. (5分)由于()[()()]()[()()]()F x f a f x g x g x g b f x '''=-⋅--⋅, (6分) 所以()[()()]()[()()]()0F f a f g g g b f ξξξξξ'''=-⋅--⋅=,(8分)整理,得()()()()()()f a f fg g b g ξξξξ'-='-.(10分)。

高等数学期中考试试卷

高等数学期中考试试卷一 .填空题（每小题3分，共15分）1.二元函数 ln()z y x =-+的定义域是 .2. 曲线22280y z x ⎧+=⎨=⎩绕z 轴旋转一周所成的旋转曲面方程是。

3.(,)limx y →= 。

4. 已知(,)arctan()yf x y xe =，则全微分df = 。

5. 把二次积分221()xy I dy dx +=⎰转化为极坐标形式 .二.单项选择题（每小题3分，共15分）1. 直线412141x y z -++==--与直线158221x y z --+==-的夹角为（） A. 6π B.4π C.3π D.2π2. 若函数(,)z f x y =在点(,)x y 处连续，则在该点处函数(,)z f x y =( ) A.有极限 B. 偏导数存在 C.可微 D. A,B,C 都不正确。

3. 设点()00，是函数(),f x y 的驻点，则函数(),f x y 在()00，处（）A . 必有极大值B . 可能有极值，也可能无极值C . 必有极小值D . 必无极值4．设2,1(,)0,1x y f x y x y +≤⎧=⎨+>⎩，{(,)|01,01}D x y x y =≤≤≤≤，则(,)Df x y dxdy ⎰⎰的值为（）．A ．1B ．12C ．13D ．165．若(,)f x y 连续，且(,)(,)Df x y xy f u v dudv =+⎰⎰，其中D 是由2y x=，0y =和1x =所围成的闭区域，则(,)f x y =（）A xyB 18xy +C 2xyD 1xy + 三．计算题（每题10分，共50 分）1. 已知平面π过点0(1,0,1)M -和直线211:201x y z L ---==，求平面π的方程。

2. 设z =，求dz3. 设(,)z f x y xy =-，f 具有二阶连续的偏导数，求2zx y∂∂∂4．设(,,)u f x y z =具有连续的偏导数，函数()y y x =与()z z x =分别由方程0xy e y -=和0z e zx -=所确定，求du dx5. 计算二重积分224d d Dx y x y --⎰⎰，其中22{(,)|9}D x y x y =+≤四、设某工厂生产A 和B 两种产品同时在市场销售，售价分别为1p 和2p ，需求函数分别为11221240225q p p q p p =-=+-+，假设企业生产两种产品的成本为221122C q q q q =++，工厂如何确定两种产品的售价时日利润最大？最大日利润为多少？（10分）五、证明题. （共10分）设函数()f x 在[0,1]上连续，证明：211()()()y x dy f x dx e e f x dx =-⎰⎰⎰期中考试题参考答案一、1.()22{,0,0,1}x y y x x x y ->≥+<； 2. 22228x y z ++=； 3. 2；4.22()1y y e dx xdy x e++； 5.21200r d e rdr πθ⋅⎰⎰ 二、1. B ； 2. D ； 3. B ； 4. A ； 5. B.三、1.【解】设平面π的一般方程为0Ax By Cz D +++=，由题意知，π过点0(1,0,1)M -，故有0A C D -+= （1）在已知直线上选取两点12(2,1,1)(4,1,2)M M ，，将其坐标代入平面方程，得 20A B C D +++= （2） 420A B C D +++= （3）由（1）（2）（3）式解得 3,2,3B A C A D A ==-=- 所以平面的方程为3230x y z +--=2．【解】2222222211()2x y dz d d x y dx dy x y x y x y==⋅⋅+=++++ 3．【解】令,u x y v xy =-=，则(,)z f u v =，1u x ∂=∂，vy x∂=∂，1u y ∂=-∂，v x y ∂=∂。

2012学年第二学期期中考试试题卷(文数)

2012年第二学期期中考试试题卷学科：高二数学（文科）满分：100分考试时间：90分钟考试须知：1．本卷共4页；2．本卷答案必须做在答案卷上，做在试题上无效； 3．答题前请在答题卷密封线内填好相关栏目； 4．不得使用计算器。

一、选择题：本大题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 复数等于（▲）A ．B ．C ．D ．2．设,,l m n 表示不同的直线，αβγ，，表示不同的平面，给出下列四个命题，其中正确的命题是（▲）A ．若m l ，且m α，则l αB ．若m l ，且.m α⊥则l α⊥C ．若,,l m n αββγγα===，则l m nD ．若m l m αβ=且,则l α3．已知，函数在上是单调增函数，则a 的最大值是（▲）A ．0B ．1 C. 2 D ．34．已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为1V ，直径为4的球的体积为2V ，则12:V V =（▲） A ．1:2 B ．2:1C ．1:1D ．1:45. “2a =”是“直线214ay ax y x =-+=-与垂直” 的（▲）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．已知双曲线)0,0(12222>>=-b a by a x 的离心率为2，一个焦点与抛物线x y 162=的焦点相同，则双曲线的渐近线方程为（▲）A ．x y 23±=B ．x y 23±=C ．x y 33±=D ．x y 3±=7.曲线在点处的切线方程是（▲） A ． B ．C ．D ． 8．将正整数排成下表：……则在表中数字2013出现在(▲)A ．第44行第78列B ．第45行第78列C ．第44行第77列D ．第45行第77列9.已知函数满足，且的导函数，则的解集为（▲）A. B. C. D.10．如图是函数的大致图象，则等于（▲）A ．B ．C ．D ．二、填空题：本大题有7小题，每小题4分，共28分。

武汉理工2012高数期中试卷及答案

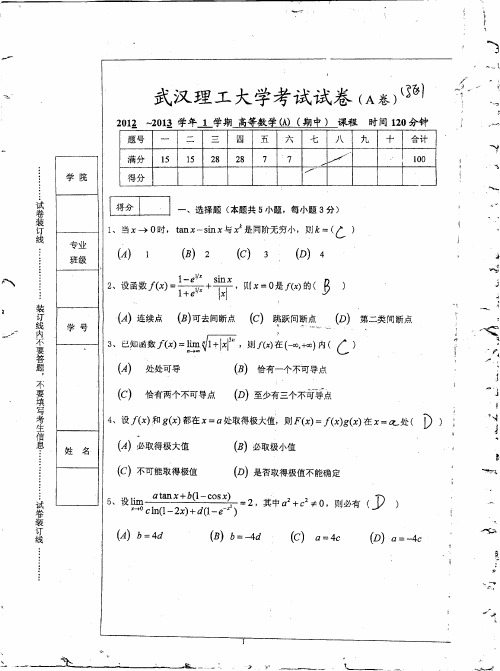
一. 选择题 CBCDD二. 填空题 19210π，9a =12b =，22222()()[2()2()()()]x x fx x f x xe f e e f x f x f e e dx ''+，1y =±三. 计算题1. sin 00sin 1lim .12(1)2x x x x x →→==-⋅- 2.00121ln(sin 2cos )2cos 2sin lim ln(sin cos )lim lim 2sin 2cos 21lim sin cos .x t t t x t t t t x x x x t t t x e e e e x x →∞→→+-++→∞⎛⎫+=== ⎪⎝⎭=令 3. 222000(1cos )(1cos )(0)(1cos )(0)1cos 1lim lim lim (0).tan 1cos 2x x x f x f x f f x f x f x x x x →→→------'==⋅=- 4.设()2()1(1)x f x x e x =--+，()22()211x x f x x e e '=---，()2222()412240,(01)x x x x f x x e e e xe x ''=---=-<<<，故()f x '在[0,1]上单调减少. 01x <<，()(0)0f x f ''<=；则()(0)0.f x f <=即()211.x x e x -<+四．计算题1. 22sec tan sec 1sec tan 11x x x dy dx x x x ⎡⎤+=+⎢++-⎣sec .x dx ⎡⎤=⎢⎣2.方程两端对x 求导，12(1)ln()()(1)y y x y x y y x y'''-=--+--- 上式两端再对x 求导，2(1)[2ln()]y x y y x y'-''+-=-.10,2x y e y -'==-=，，故(0)y e ''=. 3. sin cos tan dy dy dt t t t t dx dx dt t ===--， 22()cos sin tan d dy d y t t t dt dx dx dx dt t -+==- 4. ()()()2111323(1)!2(1)!.2123(1)3(2)n n n n n n n x n n y x x x x x x ++--⎛⎫⎛⎫==+=+ ⎪ ⎪--+-+-⎝⎭⎝⎭ 五．应用题解：过曲线任意点的切线，()4x Y y X x y-=--则距离 2222222414()(,(11,0)41x y L y x y y y x y y =+++=+-≤≤≠-令2422()24(2)0(1)d L y y dy y y -=--=-，得驻点3y =±，由问题的实际意义，距离最小值为驻点处取得，值为3，此时切点坐标为(3±. 六．证明题证明：(1)设()0,()0f a f b ''>> ()()()()lim lim 0x a x a f x f a f x f a x ax a →→-'==>--，由极限的局部保号性，在点a 的右领域内11,()0c a f c ∃>>；()()()()lim lim 0x b x b f x f b f x f b x b x b→→-'==>--，由极限的局部保号性，在点b 的左领域内22,()0c b f c ∃<<；()f x 在区间12[,]c c 上应用零点定理，至少(,)a b ξ∃∈，使()0f ξ=.(2) 因为()()0f a f b ==，()f x 在[],a b 上有二阶导数，()f x 在区间[,]a ξ上应用罗尔定理，至少1(,)a ηξ∃∈，使1()0f η'=； ()f x 在区间[,]b ξ上应用罗尔定理，至少2(,)b ηξ∃∈，使2()0f η'=； ()f x '在区间12[,]ηη上应用罗尔定理，至少(,)a b η∃∈，使()0f η''=.。

2009-2010学年第二学期高等数学B试卷

2 z 求 . x y
解：
z ( x, xy ) yg 2 ( x, xy ) ---4 分 2 f (2 x y ) g1 x
2 z ( x, xy) g 2 ( x, xy) xyg 21 ( x, xy) ----8 分 2 f (2 x y) xg12 xy
2
2 2 3 2
3 2m 时,水箱所用的材料最省. --8 分
1 展开成 x 的幂级数并求其收敛区间。 x x3 1 1 1 1 1 1 1 1 解： f ( x) ------------1 分 ( ) ( x 1)( x 2) 3 x 1 x 2 6 1 x 3 1 x 2
福建师范大学试卷纸
共 6 页，第 5 页
Y C1 cos x C2 sin x, ------2 分
* * 观察可得, y y x 的一个特解为 y1 x, y y e x 的一个特解为 y2 e x . -----6 分 * * 由非齐次线性微分方程的叠加原理知 y* y1 y2 x ex
D D1 D D1

C. xydxdy 4 xydxdy
D D1
D. x dxdy 4 x 2 dxdy
2 D D1
5、若级数 an 收敛，则下列级数不收敛的是（ B ）
n 1

福建师范大学试卷纸
共 6 页，第 1 页
A.
2 an
n 1

B.
(an 1)
五（10 分）求级数
福建师范大学试卷纸
共 6 页，第 4 页
1 1 1 x dt ln -----------------（8 分） 2 1 t 2 1 x 1 1 1 1 1 2 2 ln(1 2) --------（10 分） 2 s ( ) 2 ln 故 n 1 2 1 2 n 0 (2n 1)2 2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

福州大学高等数学B(下)期中试卷
2012年4月22日
一、单项选择(共18分,每小题3分)
1.点(1,1,1)
--到平面21
x
y z
+-=的距离为( )
(D)
2.直线
234
112
x y z
---
==与平面26
x y z
++=的交点为( ).
(A)(2,1,1)(B)(1,2,1)(C)(2,1,2)(D)(1,2,2)
3.
(,)
lim
x y→
=( ).
(A)1(B)2(C) 3(D) 0
4.设)
,
(y
x
f连续且(,)(,)
D
f x y x y f x y dxdy
=++⎰⎰
,其中D由x
y
y
x=
=
=,1
,0围成的区域,则=
)
,
(y
x
f( ).
(A)
1
8
x y
++
(B)
1
4
x y
++(C) 1
x y
++(D) 2
x y
++
5.曲面3
z
e z xy
-+=在点(2,1,0)处的切平面方程是( ).
(A)240
x y
+-=(B)24
x
y z
+-=(C)240
x y
+-=(D)250
x y
+-= 6.
积分122
0010
(,)(,)
x
dx f x y dy dx f x y dy
-
+
⎰⎰⎰交换积分次序后为( ).
(A)1
2
01
(,)
y
dy f x y dx
-
⎰⎰(B)12
01
(,)
y
dy f x y dx
+
⎰⎰
(C)12
01
(,)
y
dy f x y dx
-
⎰⎰(D)12
01
(,)
y
dy f x y dx
+
⎰⎰
学
院
专
业
级
班
姓
名
学
号
1
2
二、填空(共16分,每小题2分)
1.已知点(1,1,1),(2,2,1),(2,1,2)M A B ，则向量MA =
a 与MB = b
的夹角为 .
2.过点(1,1,0)-且平行于直线1
232x y z x y z ++=⎧⎨-+=⎩的直线方程为 .
3.设2(,)(1)arctan x y y
f x y e x x +=+-，则(1,0)x f = .
4.u =(1,0,1)A 处沿A 指向点(3,2,2)B -方向的方向导数为 .
5.已知33z x y axy =+-在点(1,1)取极小值,则常数a = .
6.设()f r
可微且r =则()grad f r = . 7.设22{(,)|1,0}D x y x y y =+≤≥，则2sin()D
x xy dxdy ⎰⎰的值为 .
8.设Ω
为由z =
z =,则三重积分
22(,)I f x y z dxdydz Ω
=+⎰⎰⎰在球面坐标系下的累次积分为=I .
三、计算题(每小题7分,共14分) 1.已知12==||,||a b ，向量a 与b 的夹角为
3
π
，求以 23+a b ，-a b 为边的平行四边形面积.
2. 求过点(0,1,2)且与直线11112
x y z
--==-垂直相交的直线方程.
3
四、计算题(每小题7分,共14分)
1.由0z
e xyz -=所确定的函数为(,)z z x y =，求22z
x
∂∂.
2.设(,)f u v 具有二阶连续的偏导数，2
2
(,)z f xy x y =-，求2,,
z z z
x y x y
∂∂∂∂∂∂∂.
五、计算题(每小题8分,共16分)
1.
计算二次积分10x y
dx dy y
⎰.
2.
计算二重积分D
，其中2222:4,2D x y x y x +≤+≥.
4
六、计算题(每小题8分,共16分)
1.设Ω为由222x y z +=与2z =所围成的区域，计算三重
积分22()x y dxdydz Ω
+⎰⎰⎰.
2.在球面2223x y z ++=的第一卦限上求一点，使该点的切平面与三坐标面围成的四面体的体积最小.
七、证明题(6分)
设()f t 在[]0,1上连续，证明：
1
1
21
1
()(1)()dx f z dz t f t dt π--=-⎰⎰
⎰
⎰.
装订线装订线装订线。