人教版九年级数学上册 二次函数的图像和性质讲义(无答案)
二次函数的图象和性质(第1课时 )九年级数学上册课件(人教版)

然后描点、连线,得到图象如下图.
y
-4 -2 O 2 4
-2 4 6 8
由图象可知,这个函数 具有如下性质: 当x<-1时,函数值y随x
x
的增大而增大; 当x>-1时,函数值y随x 的增大而减小; 当x=-1时,函数取得最 大值,最大值y=3.
练一练 已知二次函数y=x2﹣6x+5. (1)将y=x2﹣6x+5化成y=a(x﹣h)2+k的形式; (2)求该二次函数的图象的对称轴和顶点坐标; (3)当x取何值时,y随x的增大而减小.
( C) A.直线x=2
B.直线x=-2
C.直线x=1
D.直线x=-1
4.【2020·温州】已知(-3,y1),(-2,y2),(1,y3)是抛 物线y=-3x2-12x+m上的点,则( B )
A.y3<y2<y1 B.y3<y1<y2 C.y2<y3<y1 D.y1<y3<y2
5.【2020·河北】如图,现要在抛物线y=x(4-x)上找点 P(a,b),针对b的不同取值,所找点P的个数,三人的 说法如下,
6.【中考·温州】已知二次函数y=x2-4x+2,关于该函 数在-1≤x≤3的取值范围内,下列说法正确的是( D)
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1 C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
7.【中考·成都】在平面直角坐标系xOy中,二次函数y= ax2+bx+c的图象如图所示,下列说法正确的是( B)
(1)求 b、c 的值;
解:把 A(0,3),B-4,-92的坐标分别代入
y=-136x2+bx+c,得 c-=1336,×16-4b+c=-92,解得bc==398.,
(2)二次函数 y=-136x2+bx+c 的图象与 x 轴是否有公共点? 若有,求出公共点的坐标;若没有,请说明理由.
二次函数 微专题复习讲义(二次函数的图像及性质) 人教版九年级上册数学

人教版九年级上册数学《二次函数》微专题复习讲义(二次函数的图像及性质)知识点一:二次函数的定义形如y =ax 2+bx +c (a ,b ,c 是常数,a≠0)的函数,叫做二次函数. 例:如果函数y=(a -1)x 2是二次函数,那么a 的取值范围是 . 知识点二:二次函数解析式(1) 三种解析式:①一般式:y=ax 2+bx+c;②顶点式:y=a(x-h)2+k(a ≠0),其 中二次函数的顶点坐标是(h,k ); ③交点式:y=a(x-x 1)(x-x 2),其中x 1,x 2为抛物线与x 轴交点的横坐标.(2)待定系数法:巧设二次函数的解析式;根据已知条件,得到关于待定系数的方程(组);解方程(组),求出待定系数的值,从而求出函数的解析式. 知识点三:二次函数的图象与性质 1. 图象2. 对称轴x = 2b a-. 3.顶点坐标24,24b ac b a a ⎛⎫-- ⎪⎝⎭.4. 增减性当x>2b a -时,y 随x 的增大而增大;当x <2ba -时,y 随x 的增大而减小. 当x>2b a -时,y 随x 的增大而减小;当x <2ba-时,y 随x 的增大而增大.5. 最值x=2b a -,y 最小=244ac b a-.x=2b a -,y 最大=244ac b a-.6. 系数a 、b 、c 的关系y =ax 2+bx +c (a >0)y =ax +bx +c (a <0)能力过关练习:1.抛物线y=-3x2+6x+2的对称轴是( )A.直线x=2B.直线x=-2C.直线x=1D.直线x=-12.若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-m的图象上的三点,则y 1, y2, y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y23.将抛物线y=-2x2+1向右平移1个单位,再向上平移2个单位后所得到的抛物线为( )A.y=-2(x+1)2-1B.y=-2(x+1)2+3C.y=-2(x-1)2+1D.y=-2(x-1)2+34.抛物线y=x2-2x+m2+2(m是常数)的顶点在( )A.第一象限B.第二象限C.第三象限D.第四象限5.如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①;②;③;④当时,.其中正确结论的个数是( )A.1个B.4个C.3个D.2个6. 已知二次函数y=ax2+bx+c的图象如图所示,则( )A.b>0,c>0B.b>0,c<0C.b<0,c<0D.b<0,c>07.将二次函数y=x2-4x+5化成y=a(x-h)2+k的形式为.8.如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab <0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是.(填上所有正确结论的序号)9.如图,二次函数y=a(x-2)2+k的图象与x轴交于A,B两点,且点A的横坐标为-1,则点B的横坐标为.10.二次函数S=-t2+12t-20(0≤t≤10)的最大值是 ,最小值是.11.如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-x2+6x上一点,且在x轴上方,则△BCD面积的最大值为________.12.若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 ________.13. 已知二次函数y=-x2﹣2x+3.(1)求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标,并画出函数的大致图象;(2)根据图象直接写出函数值y为负数时,自变量x的取值范围.14.如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标.(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.15. 已知如图,抛物线的顶点D的坐标为(1,-4),且与y轴交于点C(0,3).(1)求该函数的关系式;(2)求该抛物线与x轴的交点A,B的坐标.x2+bx+4与x轴相交于A、B两点,与y轴相交于点16. 如图,已知抛物线y=-14C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式.(2)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN 的最大值;。
第一课时二次函数的图像和性质-九年级数学上册课件(人教版)

-14
.
5.把函数y=-x2-4x-5配方得 y=-(x+2)2-1
.它的开口方
向 向下 ,顶点坐标是 (-2,-1)
,对称轴是 直线x=-2
,当x
= -2 时,函数y的最 大 值为 -1 .
课堂练习
6.将下列二次函数的一般式用配方法化成y=a(x-h)2+k的形式,并指 出其图象的开口方向、顶点坐标、对称轴. (1)y=x2-2x+1; (2)y=2x2-4x+6. 解:(1)y=(x-1)2. 开口向上,顶点坐标为(1,0),对称轴为直线x=1. (2)y=2(x-1)2+4. 开口向上,顶点坐标为(1,4),对称轴为直线x=1.
巩固练习
2.利用配方法将抛物线 y=x2-8x+1 化为 y=a(x-h)2+k 的形式,并 写出其开口方向、顶点坐标和对称轴. 解:y=(x-4)2-15. 开口向上,顶点坐标为(4,-15),对称轴为直线x=4.
新知探究
我们已经知道y=a(x-h)2+k的图象和性质,能否
利用这些知识来讨论 y
6
x
21
12(x 6)2 3
先利用对称性列表:
x
… 3 4 5 6 7 8 9…
y 1 (x 6)2 +3 …
2
7.5
5
3.5
3
3.5 5 7.5 …
y
方法二:描点法
8
y
1 2
x2
6x
21
开口方向:向上
6
对称轴:直线x=6
4
顶点:(6,3)
2
-4 -2 O 2 4 6 8 x
新知探究
问题4 结合二次函数 y 1 x2 6x 21 的图象,说出其性质. 2
人教版九年级数学上册 二次函数的图像和性质讲义(无答案)

第10讲 二次函数的图像和性质〔二〕知识要点梳理1. 二次函数2y ax bx c =++通过配方可以变成()2y a x h k =-+的形式,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a-=-=,. 2y ax bx c =++的性质〔1〕. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-. 〔2〕. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a =-时,y 有最大值244ac b a-. 3. 二次函数2y ax bx c =++与一元二次方程02=++c bx ax 的关系(图象与x 轴的交点个数): ① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的间隔 21AB x x =-=② 当0∆=时,图象与x 轴只有一个交点,交点坐标为)0,2(ab - ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.4. 二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,〔假设与x 轴没有交点,那么取两组关于对称轴对称的点〕.画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.经典例题6422++-=x x y 配方成2()y a x h k =-+的形式,并指出它开口方向、对称轴和顶点坐标。
人教版九年级上册22.1二次函数的图象和性质 复习课件(共32张PPT)

o
2
x
5
10
15
D.(4,3)
4
例 3 ( 2 ) ( 山 东 中 考 ) 抛 物 线 y = a x ²+ b x + c 经 过 点 A ( - 2 , 7 ) , B(6,7)C(3,-8),则该抛物线上纵坐标为-8的另一个点D 的坐标是
例 3 ( 3 ) ( 上 海 中 考 ) 抛 物 线 2 ( x + m ) ²+ n ( m , n 是 常 数 )
y
8
6
4
2
10
5
o
5
x
10
15
2
4
例 3 , 如 图 已 知 抛 物 线 y = x ²+ b x + c 的 对 称 轴 为 x = 2 , 点
A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为
(0,3),则点B的坐标为(
)
8y
6 4
x=2
A.(2,3) B.(3,2)
2A
B
C.(3,3)
5
二次函数的解析式(三种形式解析式)
一 般 式 : y = a x ²+ b x + c ( a ≠ ᄋ )
顶 点 式 : y = a ( x - h ) ²+ k ( a8, h , k 为 常 数 , 且 a ≠ ᄋ )
两根式:y=a(x-x1)(x-x2)(a≠ᄋ,x1,x2是抛物线与x轴两交点
解析式为
6
y
4
2
A(-1,0)
B(3,0)
15
10
5
O
x5
10
2
4
∙x 3
2)2 2∙(x +例2) 43:如图,在平面直角坐标系xOy中,抛8 物线C1的顶点为A(-1, -4),且过点B(-3,0)。
人教版数学九年级上册《22.1.2二次函数y=ax2的图象和性质》说课稿1

人教版数学九年级上册《22.1.2二次函数y=ax2 的图象和性质》说课稿1一. 教材分析人教版数学九年级上册《22.1.2二次函数y=ax^2 的图象和性质》这一节,是在学生已经掌握了函数的概念、一次函数的图象和性质的基础上,进一步引导学生学习二次函数的图象和性质。
通过这一节的学习,使学生能够掌握二次函数的一般形式,了解二次函数的图象特征,以及掌握二次函数的性质。
教材通过丰富的例题和练习题,帮助学生巩固所学知识,提高解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的函数知识,对一次函数的图象和性质有了初步的了解。
但是,二次函数相对于一次函数来说,图象和性质更加复杂,需要学生有一定的抽象思维能力。
此外,学生可能对二次函数的图象和性质在实际问题中的应用还不够清晰,需要教师在教学中进行引导和启发。
三. 说教学目标1.知识与技能目标:让学生掌握二次函数的一般形式,了解二次函数的图象特征,掌握二次函数的性质。
2.过程与方法目标:通过观察、分析、归纳等方法,引导学生自主探究二次函数的图象和性质。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的探究精神和合作意识。
四. 说教学重难点1.教学重点:二次函数的一般形式,二次函数的图象特征,二次函数的性质。
2.教学难点:二次函数的图象和性质在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例分析法、小组讨论法等,引导学生主动探究,提高学生的参与度和积极性。
2.教学手段:利用多媒体课件,展示二次函数的图象和性质,使抽象的知识更加直观形象。
同时,利用练习题和案例,帮助学生巩固所学知识。
六. 说教学过程1.导入:通过复习一次函数的图象和性质,引出二次函数的一般形式,激发学生的学习兴趣。
2.探究二次函数的图象特征:让学生观察二次函数的图象,引导学生发现二次函数的顶点、开口方向等特征。
3.探究二次函数的性质:通过小组讨论,让学生归纳出二次函数的增减性、对称性等性质。
人教版九年级上册数学 讲义 二次函数的图像与性质
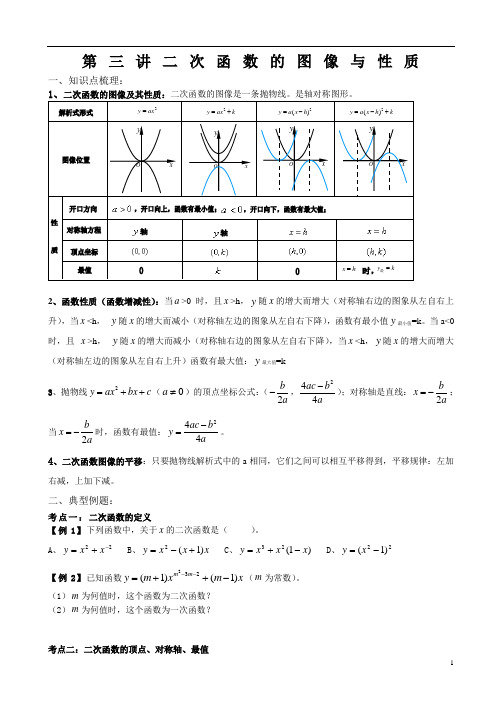
、向左平移 个单位,再向下平移 个单位得到 、向左平移 个单位,再向上平移 个单位得到
、向右平移 个单位,再向下平移 个单位得到 、向右平移 个单位,再向上平移 个单位得到
考点四:二次函数y=ax2+bx+c及图象的认识
【例1】与抛物线 的形状大小开口方向相同,只有位置不同的抛物线是()
A.y1<y2<y3B.y2<y1<y3
C.y3<y1<y2D.y1<y3<y2
【例2】已知二次函数 ,若自变量 分别取 , , ,且 ,则对应的函数值 的大小关系正确的是()
A. B. C. D.
三、强化训练:
【夯实基础】
1、二次函数 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是()
A. =4B. =3C. =-5D. =-1。
2、抛物线 的图象过原点,则 为()
A.0B.1C.-1D.±1
3、直角坐标平面上将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为()
A.(0,0)B.(1,-2)C.(0,-1)D.(-2,1)
4、二次函数 的图象如图所示,则 , , , , 这五个式子中,值为正数的有()
求:(1)函数关系式;(2)此函数图象的顶点和它与 轴的两个交点所构成的三角形面积。
A、4个B、3个C、2个D、1个
考点五:直线与抛物线的位置关系
【例1】在平面直角坐标系中,函数y=-x+1与y=- (x-1)2 的图象大致是( )
【例2】在同一直角坐标系中,函数 与 的图象大致如图()
考点六:二次函数与一元二次不等式
【例1】若A ,B ,C 为二次函数y=x2+4x+5的图象上的三点,则y1,y2,y3的大小关系是( )
人教版九年级上册22.二次函数的图像与性质课件(共129张)

一般地,二次函数 y = ax2 + bx + c(a≠0)的图象叫做抛物线y = ax2 + bx + c
思考:这个二次函数图象有什么特征?
(1)形状是开口向上的抛物线
9
6
(2)图象关于y轴对称
3
(3)有最低点,没有最高点
-3
3
y轴是抛物线y = x 2 的对称轴,抛物线y = x 2 与它的对称 轴的交点(0,0)叫做抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点.
联系(1)等式一边都是ax2+bx+c且 a ≠0 (2)方程ax2+bx+c=0可以看成是 函数y= ax2+bx+c中y=0时得到的. 区分:前者是函数.后者是方程.等式另一 边前者是y,后者是0
知识运用
例1:下列函数中,哪些是二次函数?
(1)y=3x-1 (不是 )
(2)y=3x2 ( 是 )
画形如y=ax2的函数图像: 1、函数y=x2的图像;视察y=x2的表达式,选择适当x值,并计算 相应的y值,完成下表:
x … -3 -2 -1 0 1 2 3 … y=x2 … 9 4 1 0 1 4 9 …
描点,连线 y 10
y=x2
8
6
4
2
?
-4 -3 -2 -1 0 1 2 3 4 x -2
…二次函数的图像和性质…
• y=ax2的函数图像 • y=ax2 +k 的函数图像 • y=a(x-h)2的函数图像 • y=a(x-h)2 +k 的函数图像 • y=ax2+bx+c 的函数图像
…二次函数的图像和性质…
• y=ax2的函数图像 • y=ax2 +k 的函数图像 • y=a(x-h)2的函数图像 • y=a(x-h)2 +k 的函数图像 • y=ax2+bx+c 的函数图像
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第10讲 二次函数的图像和性质(二)
知识要点梳理
1. 二次函数
2y ax bx c =++通过配方可以变成()2y a x h k =-+的形式,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a
-=-=,. 2.二次函数2y ax bx c =++的性质
(1). 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,. 当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2b
x a
=-时,y 有最小值244ac b a -.
(2). 当0a <时,抛物线开口向下,对称轴为2b x a
=-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而增大;当2b x a >-
时,y 随x 的增大而减小;当2b x a
=-时,y 有最大值244ac b a -. 3. 二次函数2y ax bx c =++与一元二次方程02=++c bx ax 的关系(图象与x 轴的交点个数):
① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离
21AB x x =-=.
② 当0∆=时,图象与x 轴只有一个交点,交点坐标为)0,2(a b -
③ 当0∆<时,图象与x 轴没有交点.
1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >;
2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.
4. 二次函数2y ax bx c =++图象的画法
五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).
画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.
经典例题
例1.将二次函数解析式6422++-=x x y 配方成2()y a x h k =-+的形式,并指出它开口方向、对称轴和顶点坐标。
例 2.已知抛物线9)2(2++-=x a x y 的顶点在坐标轴上,求a 的值,并求出顶点坐标
例3.求下列函数的最大值或最小值.
(1)5322--=x x y (2)432+--=x x y . 探索:试一试,当2≤x ≤3时,求二次函数322--=x x y 的最大值和最小值. 例4.(1)已知抛物线324)1(22-+++=k kx x k y ,当k 时,抛物线与x 轴相交于两点.
(2)已知二次函数232)1(2-++-=a ax x a y 的图象的最低点在x 轴上,则a = .
(3)已知抛物线23)1(2----=k x k x y 与x 轴交于两点A (α,0),B (β,0),且1722=+βα,则k 的值是 .
(1)3->k 且1-≠k (2)2=a (3)2=k
例5.已知二次函数1)2(2++-+-=m x m x y , (1)试说明:不论m 取任何实数,这个二次函数的图象必与x 轴有两个交点;
并求两个交点的最小距离
(2)m 为何值时,这个二次函数的图象的对称轴是y 轴?
例6.二次函数c bx ax y ++=2的图象的一部分如右图,已知它的顶点M 在第二象
限,且经过点A (1,0)和点B (0,1)。
(1)请判断实数a 的取值范围,并说明理由;
(2)设此二次函数的图象与x 轴的另一个交点为
C , 值。
当ΔAMC 的面积为ΔABC 面积的45倍时,求a 的
经典练习
1.如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数b bx kx y -+=2的图像大致是( )
2.二次函数2y ax bx c =++的图像如图,则点),(a c b M 在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
3.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,•
则下列结论:①a 、b 同号;②当x=1和x=3时,函数值相
等;
③4a+b=0;④当y=-2时,x 的值只能取0.其中正确的个数
是( )
A .1个
B .2个
C .3个
D .4个
4.在同一直角坐标系中,一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )
5、二次函数2(0)y ax bx c a =++≠的图象如图,
当0y <时,x 的取值范围是( )
A .13x -<<
B .3x >
C .1x <-
D .3x >或1x <-
A B C D x y O
A x y O
B x y O
C x y O D
6、二次函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是( )
A .3<k
B .03≠<k k 且
C .3≤k
D .03≠≤k k 且
7.已知抛物线2y ax bx c =++(a >0)的对称轴为直线1x =,且经过点
()()212y y -1,,,,试比较1y 和2y 的大小:1y _2y (填“>”,“<”或“=”) 8.已知二次函数11)(2k 2--+=x kx y 与x 轴交点的横坐标为1x 、2x (21x x <),则对
于下列结论:①当x =-2时,y =1;②当2x x >时,y >0;③方程0
11)(22=-+-x k kx 有两个不相等的实数根1x 、2x ;④22114k x x k
+-,其中所有正确的结论是 (只需填写序号).
9.如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A (-1,0)、点B (3,0)和点C (0,-3),一次函数的图象与抛物线交于B 、C 两点。
⑴二次函数的解析式为 .一次函数的解析式为 ⑵当自变量x 时,两函数的函数值都随x 增大而增大.
⑶当自变量 时,一次函数值大于二次函数值. ⑷当自变量x 时,两函数的函数值的积小于0. 10. (十堰市)如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C . (1) 求抛物线的解析式;
(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的
点P 的坐标;若不存在,请说明理由.
(3) 如图②,若点E 为第二象限抛物线上一动点,连
接BE 、CE ,求四边形BOCE 面积的最大值,并求此
1 -1 -3 3 x
y
O A B
C
时E 点的坐标.
能力拓展题
1.若点(2,5),(4,5)是抛物线c bx ax y ++=2上的两个点,那么抛物线的对称轴是( )
A .直线1=x
B .直线2=x
C .直线3=x
D .直线4=x
2.二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列4个结论:①0abc >;
②b a c <+;③420a b c ++>;④240b ac ->;其中正确的结论有( )
A .1个
B .2个
C .3个
D .4个
3.若二次函数224y ax x =+-的值总是负值,则a 的取值范围为
4.已知关于x 的二次函数43)12(22+++--=m m x m x y
(1)探究m 满足什么条件时,二次函数y 的图象与x 轴的交点的个数.
(2)设二次函数的图象与x 轴的交点为A ,B 且522=+OB OA ,与y 轴的交点为C ,它的顶点为M ,求直线CM 的解析式.
课后作业
1.已知二次函数c bx ax y ++=2的y 与x 的部分对应值如下表:
x …
1- 0 1 3 … y … 3-
1 3 1 … 则下列判断中正确的是( )
A .抛物线开口向上
B .抛物线与y 轴交于负半轴
C .当x =4时,y >0
D .方程02=++c bx ax 的正根在3与4之间
2.二次函数y =ax 2+4x +a 的最大值是3,则a 的值为 。
3.当0<a 时,求抛物线22212a ax x y +++=的顶点在第 象限
4.已知函数2y ax bx c =-+的部分图象如图所示,当x______时,y 随x 的 增大而减小.
第4题
5. 已知抛物线h x x y +-=42的顶点A 在直线14--=x y 上,则抛物线的顶点坐标为 .。
