基本平面图形复习及习题
北师大版初一(上)数学配套习题第四章:基本平面图形

第四章:基本平面图形◆4.1 线段、射线、直线■课后作业 家长签字:1、数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画一条长15厘米的线段AB ,则AB 盖住的整数点的个数共有( )个A .13或14个 B.14或15个 C.15或16个 D.16或17个2、如下图是某风景区的旅游路线示意图,其中,,B C D 为风景点,E 为两条路的交叉点,图中数据为相应两点的路程(单位:千米).一学生从A 处出发,以2千米/时的速度步行观览景色,每个景点的逗留时间约为0.5小时.(1)当他沿着路线A B C E A ----游览回到A 处时,共用了3小时,求CE 的长;(2)若此学生打算从A 处出发,步行速度与在景点的逗留时间保持不变,且在最短时间内游览完三个景点返回A 处,请你为他设计一条步行路线,并说明这样设计的理由.(不考虑其他因素)3、如图,从A 到B 最短的路线是( )A. A —G —E —BB. A —C —E —BC. A —D —G —E —BD. A —F —E —B4、已知线段AB=10cm ,直线AB 上有点C ,且BC=4cm ,M 是线段AC 的中点,则AM = cm 。
5、平面内有三个点,过任意两点画一条直线,则可以画直线的条数是( )A.2条B.3条C.4条D.1条或3条6、在直线l 上顺次取A 、B 、C 三点,使得AB=5㎝,BC=3㎝,如果O 是线段AC 的中点,那么线段OB的长度是( )A 、0.5㎝ B 、1㎝ C 、1.5㎝ D 、2㎝7、点P 是直线l 外一点,,,A B C 为直线l 上三点,4,5,2PA cm PB cm PC cm ===,则点P 到直线l 的距离是( )A 、2cm B 、小于2cm C 、不大于2cm D 、4cm8、如图所示, 把一根绳子对折成线段AB , 从P 处把绳子剪断, 已知12AP PB =, 若剪断后的各段绳子中最长的一段为40cm, 则绳子的原长为( )A. 30 cmB. 60 cmC. 120 cmD. 60 cm 或120 cm9、下列说法不正确的是( )A.若点C 在线段BA 的延长线上,则BA AC BC =-B.若点C 在线段AB 上,则AB AC BC =+C.若AC BC AB +>,则点C 一定在线段AB 外D.若,,A B C 三点不在一直线上,则AB AC BC <+二、填空题10、若线段AB=10㎝,在直线AB 上有一点C ,且BC=4㎝,M 是线段AC 的中点,则AM= ㎝.11、在边长都是1的正方形方格纸上画有如图所示的折线,它们的各段依次标着①,②,③,④,…的序号.那么序号为24的线段长度是 .12、在直线上取A 、B 、C 三点,使得AB = 9 厘米,BC = 4 厘米,如果O 是线段AC 的中点,则线段OA的长为 厘米.13、往返于甲、乙两地的火车中途要停靠三个站,则有 种不同的票价(来回票价一样),需准备 种车票.14、如图,从学校A 到书店B 最近的路线是①号路线,其道理用几何知识解释应是________________。
中考数学专题复习题:基本平面图形

中考数学专题复习题:基本平面图形一、单项选择题(共10小题)1.下列各直线、线段、射线的表示中,正确的是()A.直线abB.射线bC.线段aD.线段Ab2.下列说法,正确的是()A.经过一点有且只有一条直线B.两条射线组成的图形叫做角C.两条直线相交至少有两个交点D.两点确定一条直线3.如图中的线段,直线或射线,能相交的是()A.B.C.D.4.如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为()A.4cmB.2cmC.4cm或2cmD.小于或等于4cm,且大于或等于2cm5.如图,已知线段AB=10cm,点N在AB上,NB=2cm,M是AB中点,那么线段MN的长为()A.6cmB.5cmC.4cmD.3cm6.如图所示,能用,,三种方法表示同一个角的图形是()A.B.C.D.7.下列说法正确的是()A.两边成一直线的角是平角B.一条射线是一个周角C.两条射线组成的图形叫做角D.平角是一条直线8.甲看乙的方向是北偏东40°,则乙看甲的方向是()A.南偏东50°B.南偏西40°C.南偏东40°D.南偏西50°9.用一副三角板不能画出()A.75°角B.135°角C.160°角D.105°角10.一个多边形从一个顶点可引出7条对角线,那么这个多边形的边数是()A.10B.11C.12D.13二、填空题(共5小题)11.如图,共有________条射线.12.如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别AC、AB的中点,若线段DE=2cm,则AB=________cm.13. 67°42’+32°45’ =________.14.如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=________.15.若某一个顶点与和它不相邻的其他各顶点连接,可将多边形分成七个三角形,则这个多边形是________边形.三、解答题(共1小题)16.如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.。
(精心整理)基本平面图形——练习题

CDB EAOCA DBC N M BA 21EOD CBA图(6)D 'B 'AOCGDB第五章基本平面图形一、1. 1.46°= ° ′ ″. 28°7′12″= °.2. 如图,已知OE 平分∠AOB ,OD 平分∠BOC ,∠AOB 为直角, ∠EOD=70°,则∠BOC 的度数为 .3. 如图,直线上四点A 、B 、C 、D,看图填空:①AC=______+BC;②CD=AD —_______;③AC+BD —BC=_______.4、如图,由泰山到青岛的某一次列车,运行途中停靠的车站依次是:泰山—济南—淄博—潍坊—青岛,那么要为这次列车制作的火车票有______.5.用一个钉子把一根细木条钉在墙上,木条就可能绕着钉子 ,原因是 ;当用两个钉子把木条钉在墙上时,木条就被固定住,其依据是 . 6.如图,AB 的长为m ,BC 的长为n ,M 、N 分别是AB 、BC 的中点,则MN=7、如图(6),把一张长方形的纸按图那样折叠后,B 、D 两点落在B ′、D ′点处, 若得∠AOB ′=700, 则∠B ′OG 的度数为 。
8、如上右图,是一副三角板重叠而成的图形,则∠AOD+∠BOC=_____________. 9.如图,直线AB 、CD 相交于O ,∠COE 是直角,∠1=57°,则∠2=10. 一个人从A 点出发向北偏东65°的方向走到B 点,再从B 点出发向南偏西15°方向走到C 点,那么∠ABC 的度数是 二、10、下列说法中,正确的是( )A .直线a 、b 经过点M B. 直线A 、B 相交于点C C. 直线A 、B 相交于点m D. 直线AB,CD 相交于点m11. 一轮船航行到B 处测得的小岛A 的方向为北偏东30°,那么从A 处观测此时B 处的方向为( )A.北偏东30°B.北偏东60°C.南偏西30°D.南偏西60°12、在时刻8:32时,时钟上的时针与分针之间的所成的夹角是()A.70°B.64°C.76°D.80°13.如图,圆的半径为4,阴影部分扇形的面积是()A. πB. 2πC. 3πD. 4π14. 同一平面内有四点,每过两点画一条直线,则直线的条数是()A.1条 B.4条 C.6条 D.1条或4条或6条15、已知A、B两点之间的距离是10 cm,C是线段AB上的任意一点,则AC中点与BC中点间的距离是()A.3 cmB.4 cmC.5 cmD.不能计算16、平面上有四点,经过其中的两点画直线最多可画出( ).A.三条B.四条C.五条D.六条17、如图,O为直线AB上一点,∠COB=26°30′,则∠1=( ).A.153°30′B.163°30′C.173°30′D.183°30′18、如图6,∠AOB为平角,且∠AOC=21∠BOC ,则∠BOC的度数是()19、如图7,军舰从港口沿OB方向航行,它的方向是()A.东偏南30°B.南偏东60°C.南偏西30°D.北偏东30°20、下列说法中正确的是( )A、8时45分,时针与分针的夹角是30°B、6时30分,时针与分针重合C、3时30分,时针与分针的夹角是90°D、3时整,时针与分针的夹角是90°21、如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是()A. 9cmB.1cmC.1cm或9cmD.以上答案都不对22、如图,下列表示角的方法,错误的是( )A.∠1与∠AOB表示同一个角;B.∠AOC也可用∠O来表示C.图中共有三个角:∠AOB、∠AOC、∠BOC;D.∠β表示的是∠BOC23、已知OA⊥OC,∠AOB:∠AOC=2:3,则∠BOC的度数为()A.30B.150C.30或150D.以上都不对24、如图,四条表示方向的射线中,表示北偏东60°的是( )(1)ba(3)a(2)BBDCBA25.下列各角中,不能用一副三角板拼出的角度为()A. 60°B.75°C. 135°D. 140°26.关于中点的说法正确的是()A.若AB=BC,则点B是线段AC的中点B.若AB=21AC,则点B是线段AC的中点C. 若BC=21AC,则点B是线段AC的中点D. 若AB=BC =21AC,则点B是线段AC的中点27.在下列时刻,钟面上时针与分针成直角的情况()A.12时15分B.9时C.3时30分D.6时45分28.直线l上顺次三点A、B、C,M是AB中点,N是AC若AB=12cm,BC=8cm,则MN=()A.2 cmB.4 cmC.8 cmD.10 cm29.如图,下列说法错误的是()A. A点在O点的北偏东60°方向B. B点在O点的西偏北30°方向C.C点在O点的正南方向D. D点在O点的东南方向30.下面四个选项中,能用∠1,∠AOB,∠O三种方法表示同一个角的是()A B C D31. 一根绳子弯曲成如图(1)所示的形状,当剪刀像图(2)那样沿虚线a把绳子剪断时,绳子被剪为5段;当剪刀像图(3)那样沿虚线b(b∥a)把绳子再剪一次时,绳子被剪为9段.若剪刀在虚线a,b之间再剪(n-1)次(剪刀的方向与a平行),这样一共剪n次时(不含沿虚线a剪的一次)绳子的段数为()A.4n+1B.4n+2C.4n+3D.4n+533、如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?34.你能在图中找出一点P,使点P到点A、B、C、D四个点的距离之和最小吗?东四、35如图,A 、B 、C 、D 在同一条直线上,已知AC=BD=18cm ,且AB:AD=2:11,求AB,BC 的长度。
基本平面图形 专题练习题

北师大版七年级数学上册第四章基本平面图形专题练习题专题(一) 线段的计算1、如图,点C在线段AB上,点M,N分别是AC,BC的中点.(1)若AC=9 cm,CB=6 cm,则MN=_____cm;(2)若AC=a cm,CB=b cm,则MN=_____cm;(3)若AB=m cm,求线段MN的长;(4)若C为线段AB上任意一点,且AB=n cm,其他条件不变,你能猜想MN的长吗?并用一句简洁的话描述你发现的结论.2、若MN=k cm,求线段AB的长.3、若C在线段AB的延长线上,且满足AB=p cm,M,N分别为AC,BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.4、如图,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.(1)若AB=24,CD=10,求MN的长;(2)若AB=a,CD=b,请用含有a,b的式子表示出MN的长.5、如图,N 为线段AC 中点,点M ,B 分别为线段AN ,NC 上的点,且满足AM ∶MB ∶BC =1∶4∶3.(1)若AN =6,求AM 的长; (2)若NB =2,求AC 的长.6、如图,点B ,D 在线段AC 上,BD =13AB ,AB =34CD ,线段AB ,CD 的中点E ,F 之间的距离是20,求线段AC 的长.7、已知线段AB =60 cm ,在直线AB 上画线段BC ,使BC =20 cm ,点D 是AC 的中点,求CD 的长.8、如图,数轴上A ,B 两点对应的有理数分别为10和15,点P 从点A 出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q 同时从原点O 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t 秒.(1)当0<t <5时,用含t 的式子填空:BP =____,AQ =____; (2)当t =2时,求PQ 的值; (3)当PQ =12AB 时,求t 的值.专题(二) 角度的计算1、如图,已知∠AOB 内部有三条射线OE ,OC ,OF ,且OE 平分∠BOC ,OF 平分∠AOC. (1)若∠AOC =30°,∠BOC =60°,则∠EOF =____; (2)若∠AOC =α,∠BOC =β,则∠EOF =____;(3)若∠AOB =θ,你能猜想出∠EOF 与∠AOB 之间的数量关系吗?请说明理由.2、若∠EOF =γ,求∠AOB.3、如图,若射线OC 在∠AOB 的外部,且∠AOB =θ,OE 平分∠BOC ,OF 平分∠AOC ,则上述(3)中的结论还成立吗?请说明理由.4、如图,已知∠AOB内部有顺次的四条射线:OE,OC,OD,OF,且OE平分∠AOC,OF平分∠BOD.(1)若∠AOB=160°,∠COD=40°,则∠EOF的度数为____;(2)若∠AOB=α,∠COD=β,求∠EOF的度数;(3)从(1)(2)的结果中,你能看出什么规律吗?5、如图,OC平分∠AOB,∠AOD∶∠BOD=3∶5,已知∠COD=15°,求∠AOB的度数.6、如图,OC是∠AOB的平分线.(1)当∠AOB=60°时,求∠AOC的度数;(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;(3)当∠AOB=α,∠EOC=90°时,直接写出∠AOE的度数.(用含α的式子表示)7、如图1,点O 为直线AB 上一点,过点O 作射线OC ,使∠BOC =60°,将一直角三角板的直角顶点放在点O 处,一边ON 在射线OB 上,另一边OM 在直线AB 的上方.(1)在图1中,∠COM =30度;(2)将图1中的三角板绕点O 按逆时针方向旋转,使得ON 在∠BOC 的内部,如图2,若∠NOC =16∠MOA ,求∠BON 的度数; (3)将图1中的三角板绕点O 以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON 恰好平分锐角∠BOC 时,旋转的时间是____秒;(直接写出结果) (4)在旋转过程中,∠MOC 与∠NOB 始终保持的数量关系是____,并请说明理由. 参考答案专题(一) 线段的计算1、如图,点C 在线段AB 上,点M ,N 分别是AC ,BC 的中点.(1)若AC =9 cm ,CB =6 cm ,则MN =7.5cm ; (2)若AC =a cm ,CB =b cm ,则MN =12(a +b)cm ;(3)若AB =m cm ,求线段MN 的长;(4)若C 为线段AB 上任意一点,且AB =n cm ,其他条件不变,你能猜想MN 的长吗?并用一句简洁的话描述你发现的结论.解:(3)因为点M 是AC 的中点,所以CM =12AC.因为点N 是BC 的中点,所以CN =12BC.所以MN =CM +CN =12AC +12BC =12AB =12m cm.(4)猜想:MN =12AB =12n cm.结论:当C 为线段AB 上一点,且M ,N 分别是AC ,BC 的中点,则MN =12AB 一定成立.2、若MN =k cm ,求线段AB 的长. 解:因为点M 是AC 的中点,所以CM =12AC.因为点N 是BC 的中点,所以CN =12BC.所以MN =CM +CN =12AC +12BC =12AB.所以AB =2MN =2k cm.3、若C 在线段AB 的延长线上,且满足AB =p cm ,M ,N 分别为AC ,BC 的中点,你能猜想MN 的长度吗?请画出图形,并说明理由.解:猜想:MN =12AB =12p cm.理由如下:当点C 在线段AB 的延长线上时,如图.因为点M 是AC 的中点,所以CM =12AC.因为点N 是BC 的中点,所以CN =12BC.所以MN =CM -CN =12(AC -BC)=12AB =12p cm.4、如图,已知点C ,D 为线段AB 上顺次两点,M ,N 分别是AC ,BD 的中点. (1)若AB =24,CD =10,求MN 的长;(2)若AB =a ,CD =b ,请用含有a ,b 的式子表示出MN 的长.解:(1)因为AB =24,CD =10, 所以AC +DB =AB -CD =14. 因为M ,N 分别是AC ,BD 的中点, 所以MC +DN =12(AC +DB)=7.所以MN =MC +DN +CD =17. (2)因为AB =a ,CD =b , 所以AC +DB =AB -CD =a -b. 因为M ,N 分别是AC ,BD 的中点, 所以MC +DN =12(AC +DB)=12(a -b).所以MN =MC +DN +CD =12(a -b)+b =12(a +b).5、如图,N 为线段AC 中点,点M ,B 分别为线段AN ,NC 上的点,且满足AM ∶MB ∶BC =1∶4∶3.(1)若AN =6,求AM 的长; (2)若NB =2,求AC 的长.解:设AM =x ,则MB =4x ,BC =3x , 所以AC =AM +MB +BC =8x. 因为N 为线段AC 中点, 所以AN =NC =12AC =4x.(1)因为AN =6, 所以4x =6.解得x =32.所以AM =32.(2)NB =NC -BC =4x -3x =2,解得x =2. 所以AC =8x =16.6、如图,点B ,D 在线段AC 上,BD =13AB ,AB =34CD ,线段AB ,CD 的中点E ,F 之间的距离是20,求线段AC 的长.解:设BD =x ,则AB =3x ,CD =4x , 因为线段AB ,CD 的中点分别是E ,F , 所以BE =12AB =1.5x ,DF =12CD =2x.因为EF =BE +DF -BD =20, 所以1.5x +2x -x =20.解得x =8.所以AC =AE +EF +CF =1.5x +20+2x =12+20+16=48.7、已知线段AB =60 cm ,在直线AB 上画线段BC ,使BC =20 cm ,点D 是AC 的中点,求CD 的长.解:当点C 在线段AB 上时,如图1.图1CD =12AC =12(AB -BC)=12×(60-20)=12×40=20(cm).当点C 在线段AB 的延长线上时,如图2.图2CD =12AC =12(AB +BC)=12×(60+20)=12×80=40(cm).所以CD 的长为20 cm 或40 cm.8、如图,数轴上A ,B 两点对应的有理数分别为10和15,点P 从点A 出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q 同时从原点O 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t 秒.(1)当0<t <5时,用含t 的式子填空: BP =5-t ,AQ =10-2t ; (2)当t =2时,求PQ 的值; (3)当PQ =12AB 时,求t 的值.解:(2)当t =2时,AP <5,点P 在线段AB 上,OQ <10,点Q 在线段OA 上,如图1.图1此时PQ =OP -OQ =(OA +AP)-OQ =(10+t)-2t =10-t =8. (3)①当点P 在点Q 右边时,如图2.图2此时,AP =t ,OQ =2t ,OA =10,AB =5. 所以PQ =OA +AP -OQ =10+t -2t =10-t. 当PQ =12AB 时,即10-t =2.5,解得t =7.5.②当点P 在点Q 左边时,如图3.图3此时,OQ =2t ,AP =t ,OA =10,AB =5. 所以PQ =OQ -OA -AP =2t -10-t =t -10.当PQ =12AB 时,即t -10=2.5,解得t =12.5. 综上所述,当PQ =12AB 时,t =7.5或12.5.专题(二) 角度的计算1、如图,已知∠AOB 内部有三条射线OE ,OC ,OF ,且OE 平分∠BOC ,OF 平分∠AOC.(1)若∠AOC =30°,∠BOC =60°,则∠EOF =45°;(2)若∠AOC =α,∠BOC =β,则∠EOF =α+β2; (3)若∠AOB =θ,你能猜想出∠EOF 与∠AOB 之间的数量关系吗?请说明理由.解:∠EOF 与∠AOB 之间的数量关系是∠EOF =12∠AOB =12θ. 理由:因为OE 平分∠BOC ,OF 平分∠AOC ,所以∠EOC =12∠BOC ,∠COF =12∠AOC. 所以∠EOF =∠EOC +∠COF =12∠BOC +12∠AOC =12(∠BOC +∠AOC)=12∠AOB =12θ.2、若∠EOF =γ,求∠AOB.解:因为OE 平分∠BOC ,OF 平分∠AOC ,所以∠EOC =12∠BOC ,∠COF =12∠AOC. 所以∠EOF =∠EOC +∠COF =12∠BOC +12∠AOC =12(∠BOC +∠AOC)=12∠AOB. 因为∠EOF =γ,所以∠AOB =2γ.3、如图,若射线OC 在∠AOB 的外部,且∠AOB =θ,OE 平分∠BOC ,OF 平分∠AOC ,则上述(3)中的结论还成立吗?请说明理由.解:∠EOF =12θ成立, 理由:因为OE 平分∠BOC ,OF 平分∠AOC ,所以∠EOC =12∠BOC ,∠COF =12∠AOC. 所以∠EOF =∠COF -∠EOC =12∠AOC -12∠BOC =12(∠AOC -∠BOC)=12∠AOB =12θ. 4、如图,已知∠AOB 内部有顺次的四条射线:OE ,OC ,OD ,OF ,且OE 平分∠AOC ,OF 平分∠BOD.(1)若∠AOB =160°,∠COD =40°,则∠EOF 的度数为100°;(2)若∠AOB =α,∠COD =β,求∠EOF 的度数;(3)从(1)(2)的结果中,你能看出什么规律吗?解:(2)因为∠EOF =∠COE +∠COD +∠FOD =12∠AOC +∠COD +12∠BOD =12(∠AOC +∠BOD)+∠COD =12(∠AOB -∠COD)+∠COD =12∠AOB +12∠COD ,∠AOB =α,∠COD =β, 所以∠EOF =12α+12β=12(α+β). (3)若∠AOB 内部有顺次的四条射线:OE ,OC ,OD ,OF ,且OE 平分∠AOC ,OF 平分∠BOD ,则∠EOF =12(∠AOB +∠COD). 5、如图,OC 平分∠AOB ,∠AOD ∶∠BOD =3∶5,已知∠COD =15°,求∠AOB 的度数.解:设∠AOD =3x ,则∠BOD =5x.所以∠AOB =∠AOD +∠BOD =3x +5x =8x.因为OC 平分∠AOB ,所以∠AOC =12∠AOB =12×8x =4x. 所以∠COD =∠AOC -∠AOD =4x -3x =x.因为∠COD =15°,所以x =15°.所以∠AOB =8x =8×15°=120°.6、如图,OC 是∠AOB 的平分线.(1)当∠AOB =60°时,求∠AOC 的度数;(2)在(1)的条件下,∠EOC =90°,请在图中补全图形,并求∠AOE 的度数;(3)当∠AOB =α,∠EOC =90°时,直接写出∠AOE 的度数.(用含α的式子表示)解:(1)因为OC 是∠AOB 的平分线,所以∠AOC =12∠AOB. 因为∠AOB =60°,所以∠AOC =30°.(2)如图1,∠AOE =∠EOC +∠AOC =90°+30°=120°.如图2,∠AOE =∠EOC -∠AOC =90°-30°=60°.所以∠AOE 的度数为120°或60°.(3)90°+α2或90°-α2. 7、如图1,点O 为直线AB 上一点,过点O 作射线OC ,使∠BOC =60°,将一直角三角板的直角顶点放在点O 处,一边ON 在射线OB 上,另一边OM 在直线AB 的上方.(1)在图1中,∠COM =30度;(2)将图1中的三角板绕点O 按逆时针方向旋转,使得ON 在∠BOC 的内部,如图2,若∠NOC =16∠MOA ,求∠BON 的度数; (3)将图1中的三角板绕点O 以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON 恰好平分锐角∠BOC 时,旋转的时间是3或21秒;(直接写出结果)(4)在旋转过程中,∠MOC与∠NOB始终保持的数量关系是∠MOC-∠NOB=30°,并请说明理由.解:(2)设∠NOC=x°,则∠MOA=6x°,∠BON=60°-x°.由题意,得6x°+90°+60°-x°=180°,解得x=6.所以∠BON=60°-x°=60°-6°=54°.图3(4)∠MOC-∠NOB=30°,①当ON在∠BOC的内部时,如图3,因为∠MOC+∠CON=∠NOM=90°,所以∠MOC+(∠BOC-∠NOB)=90°.所以∠MOC+60°-∠NOB=90°.所以∠MOC-∠NOB=30°.图4②当ON在∠BOC的外部时,如图4,因为∠MOC-∠CON=∠NOM=90°,所以∠MOC-(∠NOB-∠BOC)=90°.所以∠MOC-∠NOB+60°=90°.所以∠MOC-∠NOB=30°.综上所述,∠MOC-∠NOB=30°.。
小学平面几何知识及习题
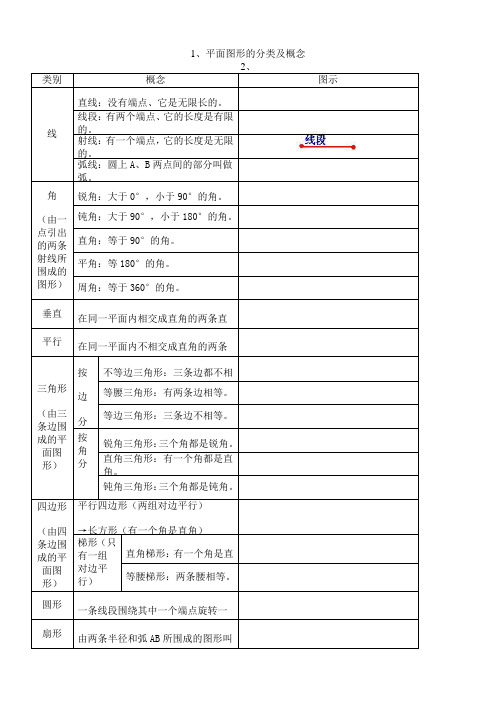
1、平面图形的分类及概念2、立体图形的分类及概念1、距离:从直线外一点到这条直线所垂直线段的长度叫做距离。
2、三角形的内角和等于180°。
3、周长:围成一个图形的所有边长的总和叫做这个图形的周长。
4、面积:物体的表面或围成的平面图形的大小,叫做它们的面积。
5、表面积:一个立体图形所有的面的面积总和,叫做它的表面积。
6、体积:一个立体图形所占空间的大小,叫做它的体积。
7、容积:一个容器所能容纳物体体积的多少叫做该容器的容积。
8、角的计量单位是"度",用符号"°"表示。
9、角的大小要看两条边叉开的大小,叉开的越大,角越大。
角的大小与角的两边画出的长短没有关系。
10、平行线间的距离都相等。
11、轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合。
这个图形叫做轴对称图形。
12、对称轴:这条直线叫做对称轴。
13、两条直线相交成直角时,这两条直线叫做互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
5、关于几何的一些操作知识1、画一个角的步骤如下:⑴画一条射线,使量角器的中心和射线的端点重合,零刻度线和射线重合;⑵在量角器所取刻度线的地方点一个点;⑶以画出的射线的端点为端点,通过刚画的点,再画一条射线。
2、垂线的画法: 1)过直线上一点画这条直线的垂线。
2)过直线外一点画这条直线的垂线。
3、画平行线的步骤是:⑴固定三角板,沿一条直角边先画一条直线;⑵用直尺紧靠三角板的另一条直线边,固定直尺然后平移三角板;⑶再沿一条直角边画出另一条直线4、例:画一个长是2.5厘米,宽是2厘米的长方形。
画的步骤如下:⑴画一条2.5厘米长的线段;⑵从画出的线段两端,在同侧画两条与这条线段垂直的线段,使它们分别长2厘米。
⑶把这两条线段另外的端点连接起来。
5、圆的画法:⑴分开圆规的两脚,在直线上确定半径:⑵固定圆规有针尖的脚,确定圆心;⑶旋转有铅笔尖的一只脚画出一个圆。
天津市七年级数学试卷平面图形的认识(二)压轴解答题复习题(附答案)

天津市七年级数学试卷平面图形的认识(二)压轴解答题复习题(附答案)一、平面图形的认识(二)压轴解答题1.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.(1)如(图1),当AE⊥BC时,求证:DE∥AC(2)若∠C=2∠B,∠BAD=x°(0<x<60)①如(图2),当DE⊥BC时,求x的值.②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.2.如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN.(1)求∠ABN的度数(2)当点P运动时,∠CBD的度数是否随之发生变化?若不变化,请求出它的度数。
若变化,请写出变化规律.(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数。
3.小明同学在完成七年级下册数学第1章的线上学习后,遇到了一些问题,请你帮他解决一下.(1)如图1,已知,则成立吗?请说明理由.(2)如图2,已知,平分,平分 . 、所在直线交于点,若,,求的度数.(3)将图2中的线段沿所在的直线平移,使得点B在点A的右侧,若,,其他条件不变,得到图3,请你求出的度数(用含m,n的式子表示).4.如图,现有一块含有30°的直角三角板ABC,且l1∥l2,其中∠ABC=30°。
(1)如图(1),当直线l1 和l2分别过三角板ABC的两个顶点时,且∠1=35°,则∠2=________°(2)如图(2),当∠ADE=80°时,求∠GFB的度数。
(3)如图(3),点Q是线段CD上的一点,当∠QFC=2∠CFN时,请判断∠ADE和∠QFG的数量关系,并说出理由。
5.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型一“猪蹄模型”.即已知:如图1,,为、之间一点,连接,得到 .求证:小明笔记上写出的证明过程如下:证明:过点作,∴∵,∴∴ .∵∴请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.(1)如图,若,,则 ________.(2)如图,,平分,平分,,则________.6.如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.(1)正方形ABCD的面积为________,边长为________,对角线BD=________;(2)求证:;(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为________,若点E所表示的数为整数,则点E所表示的数为________7.如图1,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.(1)求证:∠BAG=∠BGA;(2)如图2,若∠ABG=50°,∠BCD的平分线交AD于点E、交射线GA于点F.求∠AFC 的度数;(3)如图3,线段AG上有一点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,请直接写出的值.8.如图,直线CB和射线OA,CB//OA,点B在点C的右侧.且满足∠OCB=∠OAB=100°,连接线段OB,点E、F在直线CB上,且满足∠FOB=∠AOB,OE平分∠COF.(1)求∠BOE(2)当点E、F在线段CB上时(如图1),∠OEC与∠OBA的和是否是定值?若是,求出这个值;若不是,说明理由。
六年级下册第五章《基本平面图形》单元习题归类一
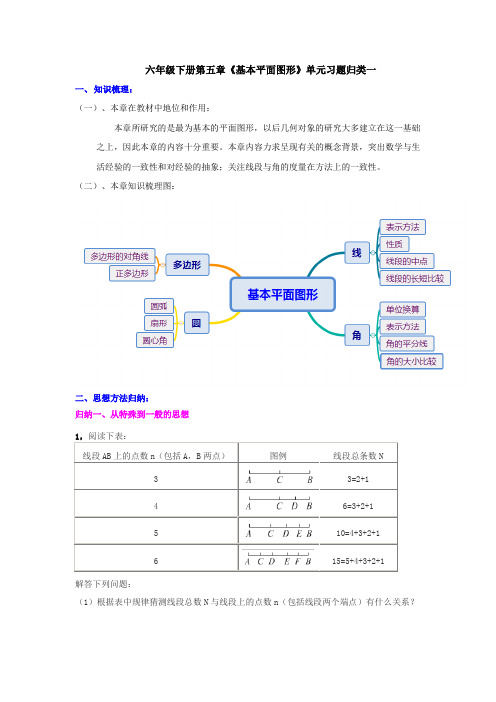
六年级下册第五章《基本平面图形》单元习题归类一一、知识梳理:(一)、本章在教材中地位和作用:本章所研究的是最为基本的平面图形,以后几何对象的研究大多建立在这一基础之上,因此本章的内容十分重要。
本章内容力求呈现有关的概念背景,突出数学与生活经验的一致性和对经验的抽象;关注线段与角的度量在方法上的一致性。
(二)、本章知识梳理图:二、思想方法归纳:归纳一、从特殊到一般的思想分析:解答本题的关键是在数角的个数时,能按一定的顺序计算,从OA至OE的边分别按照顺时针或逆时针的顺序数,做到不重复不遗漏.)(2)如图所示,在∠AOE的内部从点O引出三条射线OB,OC,OD,图中共有多少个角?(3)如图所示,有公共端点的六条射线,能组成多少个角?(4)有公共端点的n条射线,能组成多少个角?3,观察下列各图,并阅读图形下面的文字,像这样,10条直线相交,交点的个数最多是( )分析:要使的交点最多,必须交点不重合;由此可以知道:设原有n条直线,最多有m个交点,此时增加一条直线,交点个数最多增加n个。
4,为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手,如图所示.列表如下:5,一个多边形从一个顶点最多能引出三条对角线,这个多边形是()。
分析:从多边形对角线的定义知,从一个顶点最多能引对角线的条数,要去掉与“它本身、与它相邻的两个点”所引的3条对角线。
n边形从一个顶点最多能引(n-3)条对角线,所以可列方程为n-3=3,解得n=6。
跟踪练习1,如图所示,P 为直线L 外一点,A,B 为直线L 上两点,把点P 和点A ,B 连接起来,一共可以得到多少个三角形?若在直线上增加一个点C 错误!未找到引用源。
,一共可以得到多少个三角形?若直线L 上有n 个点,一共可以得到多少个三角形?归纳二、分类讨论思想分析:当OC 在∠AOB 内部时,∠AOC=∠AOB-∠BOC;当OC 在∠AOB 外部时,8,过同一平面内三个点中的任意两个点画直线.可以画几条呢?分析:我们可以把它分成两类.如图①.当三点在同一直线上时.可以画1条直线;如图②,当三点不在同一直线上时,可以画3条直线.9,过同一平面内四个点中的任意两个点,可以画几条直线?请画出图形.分析:已知点中,是否有3个点,或者4个点在同一直线上,因此要分三种情况加以讨论:4点在一条直线上;3点在一条直线上;任意3点不在一条直线上.② ①跟踪练习1在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD错误!未找到引用源。
1基本平面图形练习题

CA DBCM A DB 基本平面图形练习题第一部分:直线、射线、线段1、填表:图形 表示方法向几个方向延伸端点数可否度量线 段 射 线 直 线2、经过两点有__________条直线。
两点之间的所有连线中,______最短。
两点之间______的长度叫做两点之间的距离。
3、在 上且把线段分成 两条线段的点叫做线段的中点。
线段的中点只有 个。
4、(1)经过一个已知点A 可以画____条直线;(2)经过两个已知点A 、B 可以画_____条直线; (3)将一根细木条固定在墙上,至少需要____枚钉子5、(1)小明从某地乘车到成都,发现这条火车路线上共有7个站,且任意两站之间的票价都不相同,有____种不同的票价;要准备______种不同的车票.(2)某足球比赛中有20个球队进行单循环比赛(每两队之间必须比赛一场),那么一共要进行多少场比赛? 6、如果直线l 上一次有3个点A,B,C,那么(1)以A 、B 、C 为端点的射线各有 条,因而共有射线_____条,线段共有_____条。
(2)增加一个点增加_____条射线,增加_____条线段。
(3)若在直线l 上有n 个点, 共有_____条射线,线段的总条数是_____。
7、两条直线相交,有____个交点,三条直线相交,最多有____个交点,四条直线相交,有____个交点,10条直线相交,交点的个数最多是___个,n 条直线相交,交点的个数最多是____个 8、如图,直线上四点A 、B 、C 、D,看图填空:①=AC _____BC +;②-=AD CD _____;③=-+BC BD AC _____ 9、在直线AB 上,有cm AB 5=,cm BC 3=,求AC 的长.⑴当C 在线段AB 上时,=AC _______.(2)当C 在线段AB 的延长线上时,=AC _______. 10、如图所示:点C 是线段AB 上的一点,M 、N 分别是线段AC 、CB 的中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本平面图形
概念题:
1、在实际生产和生活中,下列四个现象: ①用两个钉子把木条固定在墙上; ②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线; ③从A 地到B 地架设天线,总是尽可能沿着线段AB 架设; ④把弯曲的公路改直,就能缩短路程.
其中可用“两点之间,线段最短”来解释的现象有( ). 2、平面上有三点A ,B ,C ,如果AB =8,AC =5,BC =3,那么( ).
A .点C 在线段A
B 上 B .点
C 在线段AB 的延长线上 C .点C 在直线AB 外
D .点C 可能在直线AB 上,也可能在直线AB 外
3、已知α、β都是钝角,甲、乙、丙、丁四人计算6
1
(α+β)的结果
依次是28°、48°、60°、88°,其中只有一人计算正确,他是( ) A.甲
B.乙
C.丙
D.丁
4、已知线段AB =10 cm ,BC =5 cm ,A 、B 、C 三点在同一条直线上,
则AC =_ _.
5、如图所示,云泰酒厂有三个住宅区,A ,B ,C 各区分别住有职工
30人,15人,10人,且这三点在金斗大道上(A ,B ,C 三点共线),已知AB =100米,BC =200米.为了方便职工上下班,该厂的接送车打算在这个路段上只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( ). A .点A B .点B C .AB 之间 D .BC 之间
6、如图所示,由泰山到青岛的某一次列车,运行途中停靠的车站依
次是:泰山——济南——淄博——潍坊——青岛,那么要为这次列车制作的火车票有__________种.
钟表问题:
1、在下列说法中,正确的个数是( ).
①钟表上九点一刻时,时针和分针形成的角是平角; ②钟表上六点整时,时针和分针形成的角是平角; ③钟表上十二点整时,时针和分针形成的角是周角; ④钟表上差一刻六点时,时针和分针形成的角是直角; ⑤钟表上九点整时,时针和分针形成的角是直角. A .1 B .2 C .3 D .4 2、现在是9点20分,此时钟面上的时针与分针的夹角是__________. 3、上午九点时分针与时针互相垂直,再经过 分钟后分针与时针第一次成一条直线.
角度单位换算:
1、(1)将24.29°化为度、分、秒;
(2)将36°40′30″化为度. 2、(1)15°30′5″=_______″;
(2)7 200″=_______´=________°; (3)0.75°=_______′=________″; (4)30.26°=_______°_______´______〞.
线段和差:
1、如图,C 是AB 的中点,D 是BC 的中点,下面等式不正确的是( ).
A .CD =AC -D
B B .CD =AD -BC
C .C
D =1
2
AB -BD D .CD =13AB
2、如图,C ,D 是线段AB 上两点,若CB =4 cm ,DB =7 cm ,且D 是AC 的中点,则AC 的长等于( ).
A .3 cm
B .6 cm
C .11 cm
D .14 cm 3、如图,点C 是线段AB 上的点,点D 是线段BC 的中点,若AB =10,AC =6,则CD =__________.
4、如图,线段AB =BC =CD =DE =1 cm ,那么图中所有线段的长度之和等于________cm.
5、如图,已知AB 和CD 的公共部分BD =13AB =1
4
CD .线段AB ,
CD 的中点E ,F 之间的距离是10 cm ,求AB ,CD 的长.
6、如图已知点C 为AB 上一点,AC =12cm, CB =3
2
AC ,D 、E 分别为
AC 、AB 的中点。
求DE 的长。
(8分) 角度计算:
1、如图,OM 平分∠AOB ,ON 平分∠COD .若∠MON =42°,∠BOC =5°,则∠AOD = __________.
1题图 2题图
2、如图,点O 是直线AD 上一点,射线OC 、OE 分别是∠AOB 、∠BOD 的平分线,若∠AOC =25°,则∠COD =_________, ∠BOE =__________.
3、已知在平面内,∠AOB =70°,∠BOC =40°,求∠AOC 的度数.
A B
C
E
D
4、如图,直线AB 、CD 相交于点O ,OE 平分∠AOD ,∠FOC =97°,∠1=40°,求∠2和∠3的度数.
4题图 5题图
5、已知:如图,∠AOB 是直角,∠AOC =30°,ON 是∠AOC 的平分线,OM 是∠BOC 的平分线.求∠MON 的大小.
6、把∠AOB 绕点O 逆时针旋转一个角度,得∠B O A ''。
(1)若∠AOB 绕点O 逆时针旋转任意一个角度,问∠A AO '与∠B BO '有什么关系? 试说明理由。
(2)若∠AOB =90°,且∠AOB 绕点O 逆时针旋转60°,则∠B AO '的度数是多少?
(3)若∠0160='B AO ,且AOA '∠︰A OB '∠=3︰2。
则∠OB A '的度数是多少?
A
B
O
A '
B '。
