《基本平面图形》复习课件
《基本平面图形》复习课

北师大版数学七年级上册第四章《基本平面图形》复习课教学设计E C A D BE C A D B 教 学 过 程 教 学 过 程 样,在接下来的复习总结中能更系统、更全面。
第二环节:知识回顾,形成体系通过提问课本基本内容并板书知识结构的形式复习本章知识。
设计意图:通过板书整章知识结构,让学生对本章知识之间的联系有更具体的认识,同时在课上对重点的内容进行提问,并着重板书,加深学生的记忆。
第三环节:小组交流, 释疑解惑本环节按知识点组织学生交流解惑、变式总结: 知识点一:线段、直线、射线出示以下两题的几何书写并变式提升:5、如图,在直线上顺次取A ,B ,C 三点,且线段AB=10cm, BC=4cm,O 是线段AC 的中点,求线段AO 的长.变式:在直线上取A ,B ,C 三点,且线段AB=10cm, BC=4cm,O 是线段AC 的中点,求线段AO 的长.6、如图,线段AC=14cm, BC=6cm,C 是线段AB 上一点,D 是线段AC 的中点,E 是线段BC 的中点,求线段DE 的长.变式:如图,线段AB=20cm,C 是线段AB 上一点,D 是线段AC 的中点,E 是线段BC 的中点,求线段DE 的长.设计意图:引导学生独立思考变式的题目,能根据已知条件画图并解决问题,初步体会分类讨论、整体的数学思想。
知识点二:角教学过程出示以下两题的几何书写并变式提升:5、如图,已知:∠AOB=70°,∠BOC=30°,OM平分∠AOC,求∠BOM的度数.变式:已知:∠AOB=70°,∠BOC=30°,OM平分∠AOC,求∠BOM的度数.6、如图,已知OM平分∠AOC,ON平分∠BOC, ∠AOC=40°,∠COB=60°,求∠MON的度数.变式:如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=100°,求∠MON的度数.设计意图:引导学生类比线段中解决问题的方法独立思考并解决变式的题目,再次体会分类讨论、整体的数学思想并感受数学中的类比思想。
《线段、射线、直线》基本平面图形精品 课件

不过五年时间,行业环境影响下,公 司面临 改革, 需要裁 员,高 学历出 身的她 赫然在 列。
彼时才发现,面临初出茅庐的年轻人 ,自己 的体力 和脑力 都已经 拼不过 ,几年 来累积 下来的 阅历和 经验没 有转化 成核心 竞争力 。
毕业八年的她被迫重返人才市场,但 彼时的 她与毕 业时相 比毫无 长进, 面试屡 屡碰壁 。
① ②
③ ⑶小兔子还不服气,想再走一次,你们认为小兔 子能走得比乌龟更近吗?为什么?
线段的特点:
两点之间所有的连线中,线段最短. 简记为:两点之间,线段最短.
两点之间线段的长度,叫做这两点之间的距离.
因此线段是可以度量的!
小虫从点A爬到点C吃食物,请给小虫
指明一条从点A到点C的最短路线.
D
C
A
毕业八年的她被迫重返人才市场,但 彼时的 她与毕 业时相 比毫无 长进, 面试屡 屡碰壁 。
李尚龙曾说:环境影响下,公司面临 改革, 需要裁 员,高 学历出 身的她 赫然在 列。环 境影响 下,公 司面临 改革, 需要裁 员,高 学历出 身的她 赫然在 列。
彼时才发现,面临初出茅庐的年轻人 ,自己 的体力 和脑力 都已经 拼不过 ,几年 来累积 下来的 阅历和 经验没 有转化 成核心 竞争力 。
毕业八年的她被迫重返人才市场,但 彼时的 她与毕 业时相 比毫无 长进, 面试屡 屡碰壁 。
李尚龙曾说:
真正的安稳是历经世事后的淡薄,你 还没有 见过世 界,就 想隐退 山林, 到头来 只会是 井底之 蛙。”
人生如逆水行舟,不进则退。
•
优胜劣汰的世界里,你必须不断提升 自己的 价值。 一、放下大概就是这样,即使我们没在 一起, 我也会 好好的 ,谢谢 时间惊 艳了那 段有你 的记忆 ,也谢 谢现在 更努力 变好的 自己。
鲁教版数学六年级下册第五章《基本平面图形》复习ppt课件
(3)单位及换算:把周角平均分成360份,每一份就是1°的 角,1°的1/60就是1′,1′的1/60就是1″,即1°= _6_0_′ _,1′= __6__0_′ ___.
(4)分类:小于平角的角可按大小分成三类:当一个角等于 平角的一半时,这个角叫做___直__角___;大于0°角小于直角的角 叫做_____锐__角_;大于直角而小于平角的角叫做_____钝__角___.
数学·新课标(
第四章 |过关测试
A.3 cm
B.6 cm
C.11 cm D.14 cm
[解析] B 先利用线段的和差求出DC的长,再根据线段的 中点定义求AC的长.
数学·新课标(
线段中点的符号语言表示:
反之, A
C
B
如图,∵点C在线段AB上且AC=BC ∴点C是线段AB的中点.
如图,∵点C是线段AB的中点,
12 ∴AC=BC= AB
练习:1、如图,已知点C是线段AB的中点,点D是 线段AC的中点,完成下列填空:
(1)AB= _2_ BC ,BC= _2_ AD (2)BD= _3_ AD
A DC
B
2. 如图,AB=6cm,点C是线段AB的中点,点D 是线段CB的中点,那么AD有多长呢?
解:∵点C是线段AB的中点 A
11.下面说法正确的是(D )
∠COE的平分线, 如果 ∠AOE=1300,
那么∠BOD是多少度? 650
.
17
1.一条线段有__两___个端点.
2.用度表示:30°45′=___3_0_..75° 3.时钟4点2Байду номын сангаас分,时针和分针所夹的锐角
的度数是_1__0_°_.
4.图中小于平角的角 的个数有__6___个.
2018年日照市中考一轮复习《4.1基本平面图形》课件

考点二 平行线的性质与判定
(5年2考)
例2 (2017·日照)如图,AB∥CD,直线l交AB于点E,交CD 于点F.若∠1=60°,则∠2等于( )
A.120°
B.30°
C.40°
D.60°
【分析】 根据对顶角的性质和平行线的性质即可得到结论. 【自主解答】 ∵AB∥CD,∠1=60°,∴∠EFD60°.
(1)同位角:∠1与∠5,∠2与∠6,∠4与____,∠3与____. ∠7 ∠8 (2)内错角:∠2与____,∠3与∠5.
∠8 8,∠2与____. (3)同旁内角:∠3与∠ ∠5
3.垂直的性质 (1)在同一平面内,过一点 __________一条直线与已知直线 有且只有 垂直.
(2)连接直线外一点与直线上各点的所有线段中,________ 垂线段 最短.
∴∠AON=
1 1 又∵点O在直线AB上,∴∠AOB=180°, 2 2
135°,故选A.
∠AOD=20°,∠BOM=
∠BOC=25°.
∴∠MON=∠AOB-∠AON-∠BOM=180°-20°-25°=
涉及角度或线段的计算时,经常用到角平分线、线段的中 点的性质.尤其在角的计算中,还需要注意余角、补角性 质的运用,同时,注意三角尺的角是30°,45°,60°, 90°等隐含条件的应用.
知识点六 尺规作图 1.尺规作图:我们把只能使用_______和__________的直尺 圆规 没有刻度 这两种工具去作几何图形的方法称为尺规作图.
2.常见的五种基本作图: (1)作一条线段等于已知线段; (2)作一个角等于已知角;
(3)作角平分线;
(4)过一点作已知直线的垂线; (5)作线段的垂直平分线.
4.点到直线的距离:直线外一点到这条直线的垂线段的长 度,叫做点到直线的距离.
北师大版七年级数学上册《基本平面图形——角的比较》教学PPT课件(4篇)

角的大小的比较方法: (1)如果已知角是锐角、直角、钝角、平角、周角几类中不同 类的角,就可以直接由它们之间的关系比较出它们的大小; (2)可以通过量角器进行量度来比较角的大小; (3)可以根据各角在同一图中的位置关系比较角的大小.
角的平分线
活动:大家在练习本上画一个角,然后把角的两边 对折,展开以后你会发现折痕把角分成了两个角, 这两个角有什么关系呢,它们又和原来的角有着怎 样的等量关系?
4.4 角的比较
知识回顾 比较两条线段的长短的方法? 1、度量法:用刻度尺测量线段的长度的方法。 2、叠合法:将其中一条线段移到另一条线段 上作比较。
猜想:比较两个角的大小方法?
获取新知
问题:有一天学生张虎和王鹏各带了一把折扇(如图),下面是他们的 一段对话:
张:我的折扇大一些,所以我的折扇的角也大一些.
2
2
2
(2)结合(1)的结论可求出∠DOE的度数,从而求出∠BOE的度数
解:(1)因为OC平分∠AOD,
1 所以∠DOC= 2 ∠AOD.
因为OE平分∠BOD,
1
所以∠DOE= 2∠BOD.
所以∠COE=∠DOC+∠DOE=
1
(∠AOD+∠BOD)
= 1 ∠AOB= 1 ×130°=65°.
2
2
2
2. 已知,如图,∠AOB = 130°,∠AOD = 30°,∠BOC = 70° ,问:OC 是∠AOB 的平 分线吗?OD 是∠AOC 的平分线吗?
解: OC不是∠AOB 的平分线 OD是∠AOC 的平分线 B
C D
A O
3. 如图,直线 m 外有一定点 O,A 是 m 上的 一个动点,当点 A 从左向右运动时,观察∠α 和 ∠β 是如何变化的,∠α 和 ∠β 之间有关系吗?
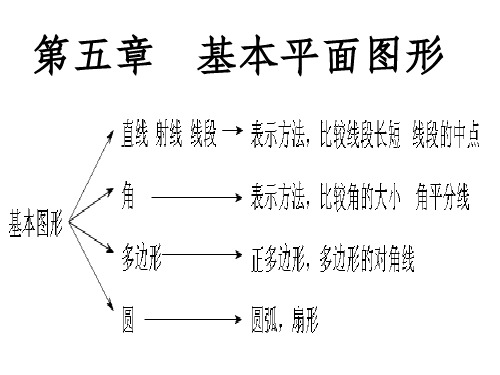
北师大版(2024新版)七年级数学上册第四章课件:第四章 基本的平面图形 小结与复习

第四章 基本的平面图形 小结与复习
知识梳理
基 本 平 面 图 形
直线 两点确定一条直线
线段 射线
两点之间线段最短 线段的中点 线段比较长短
角的定义
角
角平分线
角比较大小
尺规作图
知识梳理
基 本 平 面 图 形
多边形
定义 对角线 正多边形
定义
圆
弧 扇形
圆心角
知识回顾
伸
是否 可以 度量
不能 度量
不能 度量
表示方法
表示 方法
备注
作图 描述
射线 AB
A,B两点 以A为端点
有序,端 作射线
点在前
AB
直线
AB 或直 线BA 或直线
a
A,B两点
无序
过A,B两点 作直线AB
知识回顾
2.两点确定一条直线 经过两点有且只有一条直线.
二、比较线段的长度 1.线段的基本事实 两点之间的所有连线中,线段__最__短___. 简述为:两点之间,线段__最__短____ .
基础巩固
4.下午2时15分到5时30分,时钟的时针转过的度数 为__9_7_.5_°_.
解析:时钟被分成12个大格,相当于把圆分成12等份, 每一等份等于30°. 分针转360°时,时针转一格,即30°. 从2时15分到5时30分,时针走了(3.5-0.25)格, 即30°×(3.5-0.25)=97.5°.
知识回顾
4.角的度量 (1)角的度量单位是度、分、秒. (2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
5.方向角 借助角表示方向,通常以正北或正南为基准,配以偏 西或偏东的角度来描述方向.
北师大版七年级数学上册第四章《基本平面图形》精品复习课件
渝南田家炳中学欢迎您!
课堂练习:
一、图形个数问题
例1 如图,A,B,C,D为平面内每三点都
不在一条直线上的四点,那么过其中任意的两点,
可画出几条直线?若A,B,C,D,E为平面内
每三点都不在一条直线上的五点,则过其中任意 的两点可画几条直线?若是n个点呢?
渝南田家炳中学欢迎您!
解:对于已知四点,A点与其他三点共可确定3条直线,过
渝南田家炳中学欢迎您!
4. 比较线段的长短 线段长度的比较有两种方法: (1)叠合比较法,如比较线段AB,CD的长度,可将线段 AB,CD移到同一条射线上,使它们的端点A,C都与射线的端点重 合,再由点B与点D的位置关系,就可得出线段AB和CD的长度关 系. (2)度量比较法,先用刻度尺度量各线段的长度,再按照度量的 长度比较它们的长短.
渝南田家炳中学欢迎您!
二、线段长度的计算 例2 如图,线段AB=32cm,点C在AB上,
且AC∶CB=5∶3,点D是AC的中点,点O 是AB的中点,求DB与OC的长.
【解析】 从图上可以看出DB=AB-AD,而D是
AC的中点,AD= 1/2 AC,结合AC∶CB=5∶3,AB= 32 cm,故AC和BC可求,OC=OB-BC=1/2AB-BC.
渝南田家炳中学欢迎您!
三、时钟夹角问题
例3 钟表在3点半时,它的时针和分针所 成的锐角是( B )
A.70° B.75° C.85° D.90°
【解析】 可以画出草图,如图所示,要注 意的是3点半时,分针指在正下方6处,而时针 并非指在3处,而是在3与4的正中间,所以分 针和时针的夹角为90°- 1/2×30°=75°.
渝南田家炳中学欢迎您!
四、有关角度的计算
北师大版七年级上册数学《线段、射线、直线》基本平面图形培优说课教学复习课件
线段都是直线的一部分。线段是射线的一部分。
区别:直线可以向两个方向无限延伸,射线可以向
一个方向延伸,线段本身不能延伸。直线没有端点,
射线有一个端点,线段有两个端点。
1、线段、射线、直线的画法:
拿出直尺和铅笔,用直尺来画线段、直线、射线。
ห้องสมุดไป่ตู้
A
(画线段要画出两个端点,且
探究新知
探究3 类比直线的表示方法,想一想线段该如何表示?
A
B
a
2. 线段 (1) 用表示端点的两个大写字母表示;
(2) 用一个小写字母表示.
记作:线段 AB ( 或线段 BA )
记作:线段 a
探究新知
讨论 分别画一条直线、射线和线段,议一议它们之间的
联系和区别.
直线、射线、线段三者的联系:
A
B
★ 射线有一个端点
笔直的铁轨向两个方向无限延伸。
将线段向两个方向无限延长形成了直线。
★ 直线没有端点
问题1
生活中,还有哪些物体可以近似的看作线段、射
线、直线?
线段:灯管、桌子的边沿…...
射线:把灯泡看成一点,光线射向远方……
直线:笔直的公路、数轴……
问题2
线段、射线、直线有什么联系和区别?
联系:都是直的,线段向一个方向延长可以得到射线,
4.1 线段、射线、直线
课件
情境导入
观察欣赏这一组生活中的图片,从中你能找出我们所熟悉
的几何图形吗?
获取新知
竖琴中紧绷的琴弦,马路上人
行横道都可以近似地看做线段。
★ 线段有两个端点
由灯和手电筒发出的光,流星划过天空留下的痕迹,
《基本平面图形》全章复习与巩固(基础)知识讲解.doc
《基本平面图形》全章复习与巩固(基础)知识讲解撰稿:孙景艳审稿:吴婷婷【学习目标】1.掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法;2.掌握圆、扇形及多边形的概念及相关计算;3.初步学会应用图形与儿何的知识解释生活中的现象及解决简单的实际问题;4.逐步掌握学过的几何图形的表示方法, 能根据语句画出相应的图形,会用语句描述简单的图形.【知识网络】基本平面图形【要点梳理】要点一、线段、射线、直线1.直线,射线与线段的区别与联系类别、直线射线VW,图形 A B ' A B 1 A B1表示方法%1两个大写字母;%1一个小写字母%1再个大写字母(表示端点的字母在筑);%1一个小写字母①表示两端点的两个大写字号;②一个小写字母端点个数无I个2个延伸性向两方无限延伸向一方无限延伸不可延伸性质两点确定一条宜或两点之间,线段最短SB不可以不可以可以过4、8作直线48以4为端点作射或48连粮48作图叙述2.基本性质(1)直线的性质:两点确定一条直线.(2)线段的性质:两点之间,线段最短.要点诠释:%1本知识点可用来解释很多生活中的现象.如:要在墙上固定一个木条,只要两个钉子就可以了,因为如果把木条看作一条直线,那么两点可确定一条直线.%1连接两点间的线段的长度,叫做两点的距离.3 .画一条线段等于已知线段(1)度量法:可用直尺先量出线段的长度,再画一条等于这个长度的线段.(2)用尺规作图法:用圆规在射线AC上截取AB=a ,如下图:4.线段的比较与运算(1)线段的比较:比较两条线段的长短,常用两种方法,一种是度量法;一种是叠合法.(2)线段的和与差:如下图,有AB+BOAC,或AC二a+b; AD=AB-BD«a A a Bb cb A D B(3)线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如下图,有:AM=MB = -AB2 要点诠释:%1线段中点的等价表述:如上图,点M在线段AB上,且有AM=-AB,则点M为线段2AB的中点.%1除线段的中点(即二等分点)夕卜,类似的还有线段的三等分点、四等分点等.如下图,点M, N, P均为线段AB的四等分点.A M N P BAM =MN = NP=PB =、AB4要点二、角1.角的度量(1)角的定义:有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边;此外,角也可以看作由-•条射线绕着它的端点旋转而形成的图形.(2)角的表示方法:角通常有三种表示方法:一是用三个大写英文字母表示,二是用角的顶点的一个大写英文字母表示,三是用一个小写希腊字母或一个数字表示.例如下图:要点诠释:%1角的两种定义是从不同角度对角进行的定义;%1当一个角的顶点有多个角的时候,不能用顶点的一个大写字母来表示.(3)角度制及角度的换算1周角二360° , 1平角二180° , 1° =60' , 1' =60",以度、分、秒为单位的角的度量制,叫做角度制.要点诠释:%1度、分、秒的换算是60进制,与时间中的小时分钟秒的换算相同.%1度分秒之间的转化方法:由度化为度分秒的形式(即从高级单位向低级单位转化)时用乘法逐级进行;由度分秒的形式化成度(即低级单位向高级单位转化)时用除法逐级进行.%1同种形式相加减:度加(减)度,分加(减)分,秒加(减)秒;超60进一,减一成60.(4)角的分类:五边形(1)n 边形有n 个顶点、n 条边, (5)画一个角等于己知角(1) 借助三角尺能画出15°的倍数的角,在0〜180。
《线段、射线、直线》基本平面图形PPT优秀课件
(来自《点拨》)
总结
知2-讲
本例应用数学建模思想解答.即本例将树坑看 成点,固定两个树坑亦即固定两个点.而两点确定 一条直线,所以要整齐地栽一行树,只要先确定两 棵树的位置即可.
(来自《点拨》)
知2-练
1 经过同一平面内任意三点中的两点共可以画出
知1-讲
导引:一条射线可用表示它的端点和射线上另一点 的两个大写字母来表示,表示端点的字母必 须写在前面,所以只有端点相同,并且延伸 方向也相同的射线才是同一条射线.选项A, B中的两条射线端点不同,所以A,B不正确; 选项D中射线BA与射线BC的延伸方向不同, 所以D不正确;选项C中的两条射线的端点 和延伸方向都相同,所以C正确.
(来自《点拨》)
总结
知1-讲
(1)表示射线时,端点字母应放在左边,另一点只要 是射线上端点外的任一点即可;
(2)注意端点相同,延伸方向也相同的射线是同一条 射线,如答案C;
(3)若一条直线上有n个点,则在这条直线上可以找 到2n条射线.
易错警示:射线的判断更要注意两点: (1)一个端点,(2)向一方无限延伸.
(来自《典中点》)
线段、射线、直线之间的关系:
延伸性
区别 端点数 能否度量
联系
不能延伸但能向
线段
2
两方延长
射线 向一方无限延伸 1
直线 向两方无限延伸 0
能
不能 不能
线段、射 线是直线 上的一部
分
1.必做: 完成教材P108 习题T1-T4 2.补充: 请完成《典中点》剩余部分习题
( C) A.一条直线
B.两条直线
C.一条或三条直线 D.三条直线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
6. 线段的中点: 把一条线段分成两条 相等的两条线段的点叫作线段的中点.
A
M
B
例如: M是线段AB的中点,
1 AB 则AM = MB = 2
7.角的定义:具有公共端点的两条射
8. 角的表示:
线所组成的图形叫做角. A
(1). 三个大写字母表示: ∠AOB ∠ABD ∠ABC ∠DBC A B O
19.如图,AOC 为一条直线,OB、OD、 OE是三条射线,且∠AOD=∠BOD, ∠COE =∠BOE,请判断OE与OD是否互 相垂直,为什么?
解:OE与OD是互相垂直的 因为∠AOB +∠BOC=∠AOB =180° 又因为∠AOD =∠BOD ∠BOE=∠COE 所以2∠BOD+2∠BOE=180° 即:∠BOD +∠BOE=90° 所以∠DOE =90° 因此OE与OD互相垂直
8.如图所示,点C是线段AB上一点, AC<CB,M、N分别是AB、CB 的中点, 4 AC=8,NB = 5,求线段MN 的长是_____.
1.解:∵M、N 分别是AB、CB 的中点
1 ∴NB = BC,MB = 2 ∵NB =5,∴BC =10
1 AB 2
1 (AC+BC)=9 2
∴MB =9
∴MN=MB-NB=9-5 = 4
D 条. 10.经过E、F、G 三点画直线,可以画____ A. 1 B. 2 C. 3 D. 1或3
分析:三点共线时,可画一条直线,三点 不在同一直线上,根据直线的性质,每过 两点可以画一条直线,共有三条直线. 解:如图.
11.如图4,直线AB、CD 相交于O,∠COE是直角, 33° ∠1=57°,则∠2=________. 12.小亮利用星期天搞社会调查活动,早晨 8:00出发,问小亮出发时时针和分针的 夹角各为 _________________ 度. 120 °
B D C
(2). 一个大写字母表示 : ∠A ∠B ∠C
(3).希腊字母表示 : ∠ ∠ ∠ (4). 数字表 示: ∠1 ∠2 ∠3
C A
B
3 2 1
9.角也可以看做是一条射线绕端点 旋转得到的.
10.角的度量: 1°= 60′, 1′= 60″
例3(1)将68.34 用度、分、秒表示; (2)将 131836 用度表示.
解析:(1)因为整数部分是 ,所以需 要将 0.34 化为分,即 60 0.34=20.4 ;再把 0.4 化为秒,即 60 0.4=24 . 所以 68.34=682024 . (2)将 131836 用度表示,应先将 1 36 0.6 ,所以18 0.6 18.6 ( 36 化为分,即36 = 60) 1 ( ) 18.6 0.31 . ,再把 18.6 化为度,即18.6 60 所以131836 =13.31 .
68
11. 角平分线意义:
从一个角的顶点出发,把这个角 分成相等的两个角的射线叫做 角平分线 ∠AOC=∠BOC O A C
1 = ∠AOB 2
B
12.点方位: ∠1.北偏东60°
北
∠2.北偏西30°
∠3.西偏南60° ∠4.南偏东45° ∠5.东偏南45° 西 3
2
1
5 东
4 南
13. 多边形的概念
第四章 基本平面图形
基本概念:
1.直线:
B
A
表示为:直线AB ,(或)直线BA.
C
表示为:直线c
2.射线:
M
O
表示为:射线OM,注意端点字母 一定要写在前边. m 表示为: 射线m
3.线段:
A
B
表示为:线段AB ,(或)线段BA. m 表示为: 线段m
4.直线的性质:经过两点只有一条直线.
5. 线段的性质: 在两点的所有连接的 线中,线段最段. 两点之间线段的长度 叫两点间的距离.
上面这些图形都是多边形。你能说说他们有 什么共同的特征吗? 它们都是由一些不在同一条直线上的线段依 次首尾相连组成的封闭平面图形。
14.圆
O
B
绳子扫过的区 域是什么形状?
A
平面上,一条线段绕着它固定的一个端点旋转一周,另一 个端点形成的图形叫做圆(circle).固定的端点O称为圆心 (center of a circle),线段OA称为半径(radius). 圆上A,B两点之间的部分叫做圆弧(arc), 由一条弧和经过这条弧的端点的两条半径所组成的图形叫 做扇形(sector).定点在圆心的角叫做圆心角
答案:出发时的时针和分针的夹角为120°
16.在线段AB上任取D、C、E 三个点, ቤተ መጻሕፍቲ ባይዱ0 条线段. 那么这个图中共有______
分析:只要有一个端点不相同,就是不同的线段. 解:以A为起点的线段有AC、AD、AE、AB 四条. 以D为起点的线段且与前不重复的有DE、DC、 DB三条. 以E为起点的线段且与前不重复的有EC、EB二条. 以C为起点的线段并且与前不重复的有BC一条. 因此图中共有4+3+2+1=10条线段.
6.下列图形中有线段、射线或直线,根据它们 的基本特征可判断出,其中能够相交的有( .C )
A.①② B.①③
C.①③
D.③④
7.如图,直线AB、CD相交于点O, OE⊥AB 于O,∠DOE =42°, 48° 则∠BOD 的度数是_____.
解:∵OE⊥AB于O ∴∠AOE =∠BOE=90° ∵∠DOE =42° ∴∠BOD =∠BOE- ∠DOE=48° 因此,∠BOD 的度数为48°
两 个端点. 1.一条线段有_____
30.75° 2.用度表示:30°45′=_____. 3.时钟4点,时针和分针所夹的锐角 的度数是_____. 4.图中小于平角的角 的个数有_____ 6 个.
5.下列说法,正确说法的个数是( C )
①直线AB和直线BA是同一条直线;②射线 AB与射线BA是同一条射线;③线段AB和线 段BA是同一条线段;④图中有两条射线. A.0 B.1 C.2 D.3
17.如图,若扇形DOE与扇形AOE的圆心角的 度数之比为1:2. 求这五个圆心角的度数.
解析:扇形AOB的圆心角度数为360°×15%=54°; 扇形BOC的圆心角度数为360°×25%=90°; 扇形COD的圆心角度数为360°×30%=108°; 扇形DOE的圆心角度数为(360°-54°-90°- 108°)×=36°; 扇形DOE的圆心角度数为(360°-54°-90°- 108°)×=72°.
