2011全国大学生数模竞赛A题三维立体绘图MATLAB代码
2011高教社杯全国大学生数学建模竞赛A题

2011高教社杯全国大学生数学建模竞赛
承诺书
我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):A
我们的参赛报名号为(如果赛区设置报名号的话):
所属学校(请填写完整的全名):_______________
参赛队员(打印并签名) :1.
2.
3.
指导教师或指导教师组负责人(打印并签名):
日期:2011年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):
2011高教社杯全国大学生数学建模竞赛
编号专用页
赛区评阅编号(由赛区组委会评阅前进行编号):
全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):。
matlab三维绘图命令和演示

三维绘图1 三维绘图指令2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,plot则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。
下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图,MATLAB提供了一个peaks函数,可产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点,其方程式为:要画出此函数的最快方法即是直接键入peaks:peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2) ●我们亦可对peaks函数取点,再以各种不同方法进行绘图。
meshz可将曲面加上围裙:[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果:[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果:[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线:[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线:[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线:contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影:contour(peaks, 20);●plot3可画出三度空间中的曲线:t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线:t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);3 三维绘图的主要功能绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色(一)三维线图plot3 ——基本的三维图形指令调用格式:plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。
MATLAB绘图函数代码及图形

第一题定积分极限微分function y=f1F=1while F~=0syms x y zF=input('请输入表达式:(变量为x,y,z) 退出-0 ')if F~=0Sel=input('请选择要进行的计算:1-微分 2-极限 3-定积分其他-返回 ') switch Selcase 1Var=input('请输入进行微分的变量: ')N=input('请输入阶数: ')disp('结果为: ')diff(F,Var,N)case 2Var=input('请输入进行极限的变量: ')Val=input('请输入极限要趋近的值: ')disp('结果为: ')limit(F,Var,Val)case 3Var=input('请输入积分变量: ')Val_1=input('请输入积分下限: ')Val_2=input('请输入积分上限: ')disp('结果为: ')int(F,Var,Val_1,Val_2)endendF=input('0-退出,其他-继续')end第二题矩阵的运算function y=f2%syms result;while(1)disp('--------------------------------------');disp('1 -Add');disp('2 -Sub');disp('3 -Multi');disp('4 -Divide');disp('0 -Exit');ch = input('Choose an item to continue:');if( ch == 0)return;endM1 = input('Enter the first Matrix:');M2 = input('Enter the second Matrix:');switch(ch)case 1,result = M1+M2;case 2,result = M1-M2;case 3,result = M1*M2;case 4,result = M1/M2;enddisp('The result is :');disp(result);end%End function第三题矩阵的操作function y=f3while(1)disp('--------------------------------------');disp('1 -转置');disp('2 -求秩');disp('3 -求逆');disp('4 -行列式');disp('0 -Exit');ch = input('Choose an item to continue:');if( ch == 0)return;endM = input('Enter the Matrix:');switch(ch)case 1,result = M';case 2,result = rank(M);case 3,result = inv(M);case 4,result = det(M);enddisp('The transform result is :');disp(result);end%End functionendendend第四题向量的判定function y=f4(vec_1,vec_2,dem_1)vec_1=input('第一个向量:')vec_2=input('第二个向量:')Sel_2=input('选择: 1-判断两向量是否共线 2-判断三向量是否共面') if Sel_2==1A=[vec_1;vec_2]if rank(A)==1disp('两向量共线!')elsedisp('两向量不共线!')endelse if Sel_2==2vec_3=input('请输入第三个向量:')dem_3=length(vec_3)if dem_3==dem_1if cro(vec_1,vec_2)*vec_3'==0disp('三向量共面!')elsedisp('三向量不共面!')endelsedisp('输入向量维数不一致!')endendend第五题向量的长度,方向角的计算点积叉积混合积及投影的计算function y=f5n=1while n~=0vec_1=input('请输入第一个向量:')dem_1=length(vec_1)Sel=input('请选择:1-计算向量的方向角,长度 2-计算向量其他运算其他-返回')if Sel==2vec_2=input('请输入第二个向量:')dem_2=length(vec_2)if dem_1==dem_2Sel_1=input('请选择运算:1-点积 2-向量积(三维) 3-投影(三维) 4-混合积(三维) 5-判断共线,共面')switch Sel_1case 5JUDGE(vec_1,vec_2,dem_1)case 1vec_1*vec_2'case 2PAN(vec_1,vec_2)case 3vec_1*vec_2'./sqrt(vec_2*vec_2')case 4vec_3=input('请输入第三个向量(三维):')dem_3=length(vec_3)if dem_3==dem_1A=PAN(vec_1,vec_2)*vec_3'else disp('维数不一致!')endendelsedisp('输入错误!')endelseif Sel==1disp('模为:')Mol=sqrt(vec_1*vec_1')A=eye(dem_1)m=1while m~=dem_1+1acos(A(m,:)*vec_1'./(sqrt(A(m,:)*A(m,:)')*Mol))*180/pim=m+1endelsen=0endendSel=input('继续计算向量的长度、方向角的计算','向量的点积、叉积、混合积及投影-1,退出-2: ')if Sel==2n=0endend第六题点到直线,平面的距离的计算function y=f6n=1while n~=0Point=input('请输入一个三维点坐标向量:')Sel=input('请选择: 1-点到直线的距离 2-点到面的距离 ')switch Selcase 1LinVec=input('请输入直线方程的方向向量:(三维)')LinPot=input('请输入直线方程所经过的点:(三维)')if length(LinVec)==length(LinPot) & length(LinVec)==length(Point)A=p(LinVec,LinPot-Point)disp('点到直线的距离为:')A*A'./(LinVec*LinVec')else disp('输入数值是非法数值!确认后请重新输入!')endPoint=input('1-继续 2-退出')if Point==2n=0endcase 2PlantVec=input('请输入平面法向量:')PlantPot=input('请输入平面上任意一点:')if length(PlantVec)==length(PlantPot) & length(PlantVec)==length(Point)disp('点到平面的距离为:')[PlantPot-Point]*PlantVec'./(PlantVec*PlantVec')disp('输入数值是非法数值!确认后请重新输入!') end endend第七题 椭圆球 function y=pic1 a = 10; b = 20; c = 10;[x,y] = meshgrid(-2:0.1:2,-2:0.1:2);xa = x.^2/a^2; yb = y.^2/b^2;xyz = (ones(size(x))-xa-yb)*c^2; z = xyz.^0.5; mesh(x,y,z);第八题 双曲抛物面 function []=pic2 a = 5; b = 5;[x,y] = meshgrid(-2:0.1:2,-2:0.1:2);xa = x.^2/a^2; yb = y.^2/b^2; z = yb-xa; mesh(x,y,z);第九题 椭圆抛物面 function y=pic3 a = 2; b = 2;[x,y] = meshgrid(-2:0.1:2,-2:0.1:2);xa = x.^2/a^2; yb = y.^2/b^2; z = xa+yb; mesh(x,y,z);第十题 单页双曲面 function y=pic4 theta=0:pi/20:2*pi rho=1:0.05:3[theta,rho]=meshgrid(theta,rho) r=sqrt(rho.^2-1)[x,y,z]=pol2cart(theta,rho,r)figure(1)hold on z=-zsurf(x,y,z) axis off第十一题 双叶双曲面 function k=pic5t1=[-2*pi:0.05:2*pi]; t2=[-1*pi:0.05:1*pi];[t1,t2]=meshgrid(-2*pi:0.05:2*pi,-1*pi:0.05:1*pi); z=0.2*sqrt(sin(t2).*sin(t2)+1);h1=mesh(2*cos(t1).*sin(t2),sin(t1).*sin(t2),z);hold onh2=mesh(2*cos(t1).*sin(t2),sin(t1).*sin(t2),-z);第十二题椭圆锥面function k=tupian4(x,y)x=[-3:0.01:3];y=[-2:0.01:2];[x,y]=meshgrid(-3:0.01:3,-2:0.01:2); z=sqrt((x/3).^2+(y/2).^2); mesh(x,y,z); hold onmesh(x,y,-z);第十三题 常见二维图形theta=0:0.1:2*pi figure(1) rho=2*thetapolar(theta,rho) title('r=at')t=-2*pi:0.1:2*pi figure(1)x=2*(t-sin(t)) y=2*(1-cos(t)) plot(x,y,'g') xlabel('x') ylabel('y') title('摆线')theta=0:0.1:10*pi figure(1)rho=sqrt(4*sin(2*theta)) polar(theta,rho,'g') hold on rho=-rhopolar(theta,rho,'g')legend('r^2=a^2sin2t',2) hold onrho=sqrt(4*cos(2*theta)) polar(theta,rho,'r') hold on rho=-rhopolar(theta,rho,'r')legend('r^2=a^2cos2t',2)theta=0:0.1:4*pi figure(1)rho=exp(0.2*theta) polar(theta,rho) title('r=exp(at)')x=-5:0.1:5y=(1/sqrt((2*pi)))*exp(-x.^2./2) figure(1)plot(x,y,'g') xlabel('x') ylabel('y')title('概率曲线 ')t=0:0.1:2*pi figure(1)x=2*(cos(t)).^3 y=2*(sin(t)).^3 plot(x,y,'g') xlabel('x') ylabel('y')title('x^2/3+y^2/3=a^2/3')theta=0:0.1:2*pi figure(1)rho=2*cos(3*theta) polar(theta,rho,'g')legend('r=asin3t',4)hold onrho=2*sin(3*theta) polar(theta,rho,'r')legend('r=acos3t')theta=0:0.1:2*pi figure(1)rho=2*cos(2*theta) polar(theta,rho,'g') legend('r=acos2t',4)t=0:0.1:2*pi figure(1) x=2*cos(t) y=2*sin(t) plot(x,y,'g') xlabel('x') ylabel('y')title('x^2/a^2+y^2/b^2=1')theta=0:0.1:2*pi figure(1)rho=2*(1-cos(theta)) polar(theta,rho)title('r=a(1-cos(t))')x=-1:(1/20):1 figure(1)subplot(2,2,1) y=asin(x)plot(x,y,'g') title('asin(x)') axis([-1 1 -2 2])subplot(2,2,2) y=acos(x)plot(x,y,'g') title('acos(x)') axis([-1 1 0 4])subplot(2,2,3)y=atan(x)plot(x,y,'g') title('atan(x)') hold on y=y+piplot(x,y,'--') hold on y=y-2*piplot(x,y,'--')axis([-1.5 1.5 -4 4])subplot(2,2,4) y=atan(x)plot(x,y,'g') title('acot(x)') x=-xy=y+pi/2plot(x,y,'--') hold on y=y+piplot(x,y,'--') hold on y=y-2*piplot(x,y,'--')axis([-1.5 1.5 -pi 2*pi])x=-5:0.1:5y=8*2.^3./(x.^2+4*2.^2) figure(1)plot(x,y,'g') hold on x=-2:0.1:2y=sqrt(4-x.^2)+2 plot(x,y,'r') hold ony=-sqrt(4-x.^2)+2 plot(x,y,'r')xlabel('x') ylabel('y')title('y=8a^3/(x^2+4a^2)')y=-5:0.1:5 figure(1)x=(2*(1+y.^2)).^(0.5)plot(x,y,'g')hold onx=-xplot(x,y,'g') xlabel('x') ylabel('y')title('x^2/a^2-y^2/b^2=1')x=-2:0.1:2 figure(1)subplot(2,4,1) y=x.^2plot(x,y,'g') title('x^2')subplot(2,4,2) y=x.^3plot(x,y,'g') title('x^3')subplot(2,4,3) y=x.^(-1)plot(x,y,'g') title('1/x')subplot(2,4,4) x=0:0.1:2 y=x.^0.5plot(x,y,'g')title('x^(1/2)') subplot(2,4,5) x=-2:0.1:2y=(x.^2).^(1/3) plot(x,y,'g') title('x^(2/3)')subplot(2,4,6) x=0:0.1:2 y=x.^(1/3) plot(x,y,'g') hold on x=-x y=-yplot(x,y,'g') title('x^(1/3)')subplot(2,4,7)x=0:0.1:2plot(x,y,'g')hold ony=-yplot(x,y,'g')title('x^(1/3)')x=-4*pi:(pi/20):4*pifigure(1)subplot(2,2,1)y=sin(x)plot(x,y,'g')title('sin(x)')subplot(2,2,2)y=cos(x)plot(x,y,'g')title('cos(x)')subplot(2,2,3)x=-(pi/2-0.0001):pi/20:(pi/2-0.0001)y=tan(x)plot(x,y,'g')title('tan(x)')hold onx=x+piplot(x,y,'g')hold onx=x-2*piplot(x,y,'g')axis([-(1.5*pi-0.0001) (1.5*pi-0.0001) -10 10])subplot(2,2,4)x=0:pi/20:(pi-0.0001)y=cot(x)plot(x,y,'g')title('cot(x)')hold onx=x-piplot(x,y,'g')axis([-(pi-0.0001) (pi-0.0001) -10 10])theta=0:0.1:4*pifigure(1)polar(theta,rho) title('rt=a')。
2011年数学建模A题matlab作图程序

A=xlsread('地址');x=A(:,1);y=A(:,2);z=A(:,3);scatter(x,y,5,z)%散点图figure[X,Y,Z]=griddata(x,y,z,linspace(min(x),max(x),200)',linspace(min(y),max(y),200),'v4');%插值pcolor(X,Y,Z);shading interp%伪彩色图figure,contourf(X,Y,Z) %等高线图figure,surf(X,Y,Z)%三维曲面和那个其实一样的,表格你们自己处理一下xls文件就行clcclearclose allD=load('ZuoBiao.dat');M=load('JinShu.dat');x=D(:,2);y=D(:,3);z=D(:,4);c=D(:,5);xi=linspace(min(x),max(x),100);yi=linspace(min(y),max(y),100);[xi,yi]=meshgrid(xi,yi);zi=griddata(x,y,z,xi,yi);ci=griddata(x,y,c,xi,yi);marker={'*','o','s','^','p'};color={'k','r','y','c','b'};mat={'As','Cd','Cr','Cu','Hg','Ni','Pb','Zn'};str={'等高线','生活区','工业区','山林区','交通区','绿地区'};for j=1:8% 等高线图形figurecontourf(xi,yi,zi,0:10:500);% set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)% clabel(C,h,[0:10:50,50:50:300,300:100:500]);title(['金属',mat{j}, ' 二维等高线分布图'])xlabel('X')ylabel('Y')colormap summercolorbargrid onhold onfor i=1:5loc=c==i;plot(x(loc),y(loc),marker{i},'markerfacecolor',color{i},'MarkerEdgeColor',color{i});endlegend(str,'location','best')for k=1:length(x)text(x(k)-200,y(k)+200,num2str(M(k,j+1)),'fontsize',8);endend% 三维体图figureh=surf(xi,yi,zi);set(h,'cdata',ci);colormap hsvtitle('三维图立体(颜色条表示分类)')xlabel('X')ylabel('Y')colorbarhidden offhold onfor i=1:5loc=c==i;plot3(x(loc),y(loc),z(loc),marker{i},'markerfacecolor',color{i});endstr{1}='三维图';legend(str,'location','best')。
2011数学建模A题神经网络优秀论文,带代码

图 1 该城区的地形分布图
首先,我们根据样本点的位置和海拔绘制出该城区的地貌,见图 1。我们运 用 matlab 软件,根据各个网格区域中的重金属含量,用三角形线性插值的方法 得到各种重金属含量在空间上分布的等值线图。
1 图 2-1
2
1 图 2-2
2
图 2-1 给出了 As 在该区域的空间分布:图中可以观察到 As 有两个明显的高 值中心,我们标记为区域 1 和 2。这两个区域都处于工业区分布范围内,并以该 两个区域作为中心向外延伸, 浓度逐渐减少,同时我们注意到在山区的很多区域
Ni
(3211,5686) (24001,12366)
Pb
(1991,3329) (4508,5412)
Zn
(1699,2867) (3725,5487) (9583,4512) (13653,9655)
综合分析所得污染源所在位置,发现不同金属的污染源有同源现象,依据 同源性汇聚污染源,绘制了八种重金属的污染源汇总图。 问题四:神经网络模型的优点是具有较强的自组织、自学习能力、泛化能 力和充分利用了海拔高度的信息;缺点是训练要求样本点容量较大。可以通过搜 集前几年该城区八种重金属浓度的采样数据和近几年工厂分布多少位置的变化、 交通路段车流量的变化、 人口及生活区分布变化与植被分布多少位置的变化等数 据,进一步拓展神经网络模型,得到该城市地质环境的演变模式。
符号
意义
k i j
x ij
xi
表示不同功能区 表示金属的种类 表示不同的样本 表示样本 j 中金属 i 的浓度 表示金属 i 背景值的平均值 表示金属 i 背景值的标准差
表示 x i j 标准化后的值
i
Y ij
i
Ik
Matlab三维立体画图
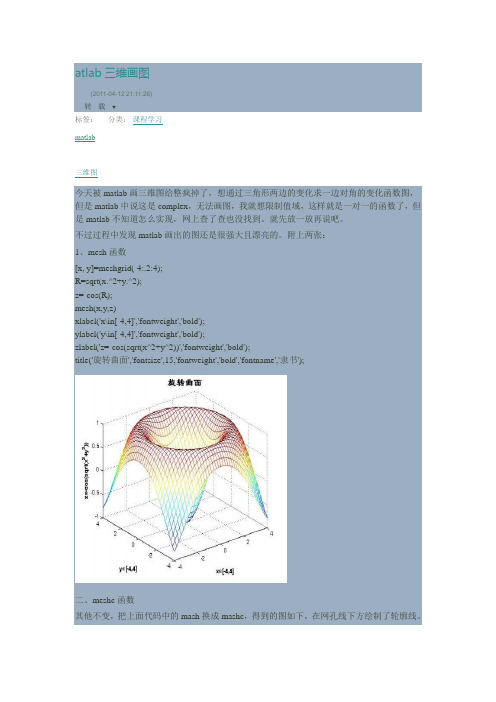
atlab 三维画图(2011-04-12 21:11:26) 转载▼标签: matlab 三维图分类: 课程学习今天被matlab 画三维图给整疯掉了,想通过三角形两边的变化求一边对角的变化函数图,但是matlab 中说这是complex ,无法画图,我就想限制值域,这样就是一对一的函数了,但是matlab 不知道怎么实现,网上查了查也没找到。
就先放一放再说吧。
不过过程中发现matlab 画出的图还是很强大且漂亮的。
附上两张: 1、mesh 函数[x, y]=meshgrid(-4:.2:4); R=sqrt(x.^2+y.^2); z=-cos(R); mesh(x,y,z)xlabel('x\in[-4,4]','fontweight','bold'); ylabel('y\in[-4,4]','fontweight','bold');zlabel('z=-cos(sqrt(x^2+y^2))','fontweight','bold');title('旋转曲面','fontsize',15,'fontweight','bold','fontname','隶书');二、meshc 函数其他不变,把上面代码中的mash 换成mashc ,得到的图如下,在网孔线下方绘制了轮廓线。
三、mashz函数Matlab 三维作图1 画一个可透视的椭球figurea = 15;b = 10;c = 5;k = 5;n = 2^k-1;theta = pi*(-n:2:n)/n;phi = (pi/2)*(-n:2:n)'/n;X = a*cos(phi)*cos(theta);Y = b*cos(phi)*sin(theta);Z = c*sin(phi)*ones(size(theta));surf(X,Y,Z,'FaceColor','interp',...'EdgeColor','none',...'FaceLighting','phong')axis tightcamlight leftalpha(.33) % 产生透视效果这是在7.1.上画的图:....................建立空间等高线[X,Y] = meshgrid([-2:.25:2]); Z = X.*exp(-X.^2-Y.^2);contour3(X,Y,Z,30)h = findobj('Type','patch');set(h,'LineWidth',2)title(' 空间等高线')..................§4.2 三维作图§4.2.1 mesh(Z)语句mesh(Z)语句可以给出矩阵Z元素的三维消隐图,网络表面由Z坐标点定义,与前面叙述的x-y平面的线格相同,图形由邻近的点连接而成.它可用来显示用其它方式难以输出的包含大量数据的大型矩阵,也可用来绘制Z变量函数.显示两变量的函数Z=f(x,y),第一步需产生特定的行和列的x-y矩阵.然后计算函数在各网格点上的值.最后用mesh函数输出.下面我们绘制sin(r)/r函数的图形.建立图形用以下方法:x=-8:.5:8;y=x';x=ones(size(y))*x;y=y*ones(size(y))';R=sqrt(x.^2+y.^2)+eps;z=sin(R)./R;mesh(z) %% 试运行mesh(x,y,z),看看与mesh(z)有什么不同之处?各语句的意义是:首先建立行向量x,列向量y;然后按向量的长度建立1-矩阵;用向量乘以产生的1-矩阵,生成网格矩阵,它们的值对应于x-y坐标平面;接下来计算各网格点的半径;最后计算函数值矩阵Z.用mesh函数即可以得到图形.图4.2.1三维消隐图第一条语句x的赋值为定义域,在其上估计函数;第三条语句建立一个重复行的x矩阵,第四条语句产生y的响应,第五条语句产生矩阵R(其元素为各网格点到原点的距离).用mesh方法结果如上.另外,上述命令系列中的前4行可用以下一条命令替代:[x, y]=meshgrid(-8:0.5:8)§4.2.2与mesh相关的几个函数(1) meshc与函数mesh的调用方式相同,只是该函数在mesh的基础上又增加了绘制相应等高线的功能.下面来看一个meshc的例子:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshc(z) %% 试运行meshc(x,y,z),看看与meshc(z)有什么不同之处?我们可以得到图形:图4.2.2.1 meshc图地面上的圆圈就是上面图形的等高线.(2)函数meshz与mesh的调用方式也相同,不同的是该函数在mesh函数的作用之上增加了屏蔽作用,即增加了边界面屏蔽.例如:[x,y]=meshgrid([-4:.5:4]);z=sqrt(x.^2+y.^2);meshz(z) %% 试运行meshz(x,y,z),看看与meshz(z)有什么不同之处?我们得到图形:图4.2.2.2 meshz图§4.2.3其它的几个三维绘图函数(1)在Matlab中有一个专门绘制圆球体的函数sphere,其调用格式如下:[x,y,z]=sphere(n)此函数生成三个(n+1)×(n+1)阶的矩阵,再利用函数surf(x,y,z)可生成单位球面.[x,y,z]=sphere 此形式使用了默认值n=20sphere(n) 只绘制球面图,不返回值.运行下面程序:sphere(30);axis square;我们得到球体图形:图4.2.3.1 球面图若只输入sphere画图,则是默认了n=20的情况.(2) surf函数也是Matlab中常用的三维绘图函数.其调用格式如下:surf(x,y,z,c)输入参数的设置与mesh相同,不同的是mesh函数绘制的是一网格图,而surf绘制的是着色的三维表面.Matlab语言对表面进行着色的方法是,在得到相应网格后,对每一网格依据该网格所代表的节点的色值(由变量c控制),来定义这一网格的颜色.若不输入c,则默认为c=z.我们看下面的例子:%绘制地球表面的气温分布示意图.[a,b,c]=sphere(40);t=abs(c); %求绝对值surf(a,b,c,t);axis equalcolormap('hot')我们可以得到图形如下:图4.2.3.2 等温线示意图§4.2.4图形的控制与修饰(1)坐标轴的控制函数axis,调用格式如下:axis([xmin,xmax,ymin,ymax,zmin,zmax])用此命令可以控制坐标轴的范围.与axis相关的几条常用命令还有:axis auto 自动模式,使得图形的坐标范围满足图中一切图元素axis equal 严格控制各坐标的分度使其相等axis square 使绘图区为正方形axis on 恢复对坐标轴的一切设置axis off 取消对坐标轴的一切设置axis manual 以当前的坐标限制图形的绘制(2)grid on 在图形中绘制坐标网格.grid off 取消坐标网格.(3)xlabel, ylabel, zlabel分别为x轴, y轴, z轴添加标注.title为图形添加标题.以上函数的调用格式大同小异,我们以xlabel为例进行介绍:xlabel('标注文本','属性1','属性值1','属性2','属性值2',…)这里的属性是标注文本的属性,包括字体大小、字体名、字体粗细等.例如:[x, y]=meshgrid(-4:.2:4);R=sqrt(x.^2+y.^2);z=-cos(R);mesh(x,y,z)xlabel('x\in[-4,4]','fontweight','bold');ylabel('y\in[-4,4]','fontweight','bold');zlabel('z=-cos(sqrt(x^2+y^2))','fontweight','bold');title('旋转曲面','fontsize',15,'fontweight','bold','fontname','隶书');图4.2.4.1添加标注。
数学建模算法的matlab代码
二,hamiton回路算法提供一种求解最优哈密尔顿的算法---三边交换调整法,要求在运行jiaohuan3(三交换法)之前,给定邻接矩阵C和节点个数N,结果路径存放于R中。
bianquan.m文件给出了一个参数实例,可在命令窗口中输入bianquan,得到邻接矩阵C和节点个数N以及一个任意给出的路径R,,回车后再输入jiaohuan3,得到了最优解。
由于没有经过大量的实验,又是近似算法,对于网络比较复杂的情况,可以尝试多运行几次jiaohuan3,看是否能到进一步的优化结果。
%%%%%%bianquan.m%%%%%%%N=13;for i=1:Nfor j=1:NC(i,j)=inf;endendfor i=1:NC(i,i)=0;endC(1,2)=6.0;C(1,13)=12.9;C(2,3)=5.9;C(2,4)=10.3;C(3,4)=12.2;C(3,5)=17.6;C(4,13)=8.8;C(4,7)=7.4;C(4,5)=11.5;C(5,2)=17.6;C(5,6)=8.2;C(6,9)=14.9;C(6,7)=20.3;C(7,9)=19.0;C(7,8)=7.3;C(8,9)=8.1;C(8,13)=9.2;C(9,10)=10.3;C(10,11)=7.7;C(11,12)=7.2;C(12,13)=7.9;for i=1:Nfor j=1:Nif C(i,j) < infC(j,i)=C(i,j);endendendfor i=1:NC(i,i)=0;endR=[4 7 6 5 3 2 1 13 12 11 10 9 8];<pre name="code" class="plain">%%%%%%%%jiaohuan3.m%%%%%%%%%%n=0;for I=1:(N-2)for J=(I+1):(N-1)for K=(J+1):Nn=n+1;Z(n,:)=[I J K];endendendR=1:Nfor m=1:(N*(N-1)*(N-2)/6)I=Z(m,1);J=Z(m,2);K=Z(m,3); r=R;if J-I~=1&K-J~=1&K-I~=N-1 for q=1:(J-I)r(I+q)=R(J+1-q);endfor q=1:(K-J)r(J+q)=R(K+1-q);endendif J-I==1&K-J==1r(K)=R(J);r(J)=R(K);endif J-I==1&K-J~=1&K-I~=N-1 for q=1:(K-J)r(I+q)=R(I+1+q); endr(K)=R(J);endif K-J==1&J-I~=1&K~=Nfor q=1:(J-I)r(I+1+q)=R(I+q); endr(I+1)=R(K);endif I==1&J==2&K==Nfor q=1:(N-2)r(1+q)=R(2+q);endr(N)=R(2);endif I==1&J==(N-1)&K==Nfor q=1:(N-2)r(q)=R(1+q);endr(N-1)=R(1);endif J-I~=1&K-I==N-1for q=1:(J-1)r(q)=R(1+q);endr(J)=R(1);endif J==(N-1)&K==N&J-I~=1r(J+1)=R(N);for q=1:(N-J-1)r(J+1+q)=R(J+q);endendif cost_sum(r,C,N)<cost_sum(R,C,N)R=rendendfprintf('总长为%f\n',cost_sum(R,C,N))%%%%%%cost_sum.m%%%%%%%%functiony=cost_sum(x,C,N)y=0;for i=1:(N-1)y=y+C(x(i),x(i+1));endy=y+C(x(N),x(1));三,灰色预测代码<pre name="code" class="plain">clearclcX=[136 143 165 152 165 181 204 272 319 491 571 605 665 640 628];x1(1)=X(1);X1=[];for i=1:1:14x1(i+1)=x1(i)+X(i+1);X1=[X1,x1(i)];endX1=[X1,X1(14)+X(15)]for k=3:1:15p(k)=X(k)/X1(k-1);p1(k)=X1(k)/X1(k-1);endp,p1clear kZ=[];for k=2:1:15z(k)=0.5*X1(k)+0.5*X1(k-1);Z=[Z,z(k)];endZB=[-Z',ones(14,1)]Y=[];clear ifor i=2:1:15Y=[Y;X(i)];endYA=inv(B'*B)*B'*Yclear ky1=[];for k=1:1:15y(k)=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1); y1=[y1;y(k)];endy1clear kX2=[];for k=2:1:15x2(k)=y1(k)-y1(k-1);X2=[X2;x2(k)];endX2=[y1(1);X2]e=X'-X2m=abs(e)./X's=e'*en=sum(m)/13clear ksyms ky=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1)Y1=[];for j=16:1:21y11=subs(y,k,j)-subs(y,k,j-1);Y1=[Y1;y11];endY1%程序中的变量定义:alpha是包含α、μ值的矩阵;%ago是预测后累加值矩阵;var是预测值矩阵;%error是残差矩阵; c是后验差比值function basicgrey(x,m) %定义函数basicgray(x)if nargin==1 %m为想预测数据的个数,默认为1 m=1;endclc; %清屏,以使计算结果独立显示if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x';endn=length(x); %取输入数据的样本量x1(:,1)=cumsum(x); %计算累加值,并将值赋及矩阵be for i=2:n %对原始数列平行移位 Y(i-1,:)=x(i,:);endfor i=2:n %计算数据矩阵B的第一列数据z(i,1)=0.5*x1(i-1,:)+0.5*x1(i,:);endB=ones(n-1,2); %构造数据矩阵BB(:,1)=-z(2:n,1);alpha=inv(B'*B)*B'*Y; %计算参数α、μ矩阵for i=1:n+m %计算数据估计值的累加数列,如改n+1为n+m可预测后m个值ago(i,:)=(x1(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1, :)*(i-1))+alpha(2,:)/alpha(1,:);endvar(1,:)=ago(1,:);f or i=1:n+m-1 %可预测后m个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下m个预测值end[P,c,error]=lcheck(x,var); %进行后验差检验[rela]=relations([x';var(1:n)']); %关联度检验ago %显示输出预测值的累加数列alpha %显示输出参数α、μ数列var %显示输出预测值error %显示输出误差P %显示计算小残差概率 c %显示后验差的比值crela %显示关联度judge(P,c,rela) %评价函数显示这个模型是否合格<pre name="code" class="plain">function judge(P,c,rela) %评价指标并显示比较结果if rela>0.6'根据经验关联度检验结果为满意(关联度只是参考主要看后验差的结果)'else'根据经验关联度检验结果为不满意(关联度只是参考主要看后验差的结果)'endif P>0.95&c<0.5'后验差结果显示这个模型评价为“优”'else if P>0.8&c<0.5'后验差结果显示这个模型评价为“合格”'else if P>0.7&c<0.65'后验差结果显示这个模型评价为“勉强合格”' else'后验差结果显示这个模型评价为“不合格”' endendendfunction [P,c,error]=lcheck(x,var)%进行后验差检验n=length(x);for i=1:nerror(i,:)=abs(var(i,:)-x(i,:)); %计算绝对残差c=std(abs(error))/std(x); %调用统计工具箱的标准差函数计算后验差的比值cs0=0.6745*std(x);ek=abs(error-mean(error));pk=0;for i=1:nif ek(i,:)<s0pk=pk+1;endendP=pk/n; %计算小残差概率%附带的质料里有一部分讲了关联度function [rela]=relations(x)%以x(1,:)的参考序列求关联度[m,n]=size(x);for i=1:mfor j=n:-1:2x(i,j)=x(i,j)/x(i,1);endfor i=2:mx(i,:)=abs(x(i,:)-x(1,:)); %求序列差endc=x(2:m,:);Max=max(max(c)); %求两极差Min=min(min(c));p=0.5; %p称为分辨率,0<p<1,一般取p=0.5for i=1:m-1for j=1:nr(i,j)=(Min+p*Max)/(c(i,j)+p*Max); %计算关联系数endendfor i=1:m-1rela(i)=sum(r(i,:))/n; %求关联度end四,非线性拟合function f=example1(c,tdata)f=c(1)*(exp(-c(2)*tdata)-exp(-c(3)*tdata));<pre name="code" class="plain">function f=zhengtai(c,x) f=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c( 2)^2));x=1:1:12;y=[01310128212]';c0=[2 8];for i=1:1000c=lsqcurvefit(@zhengtai,c0,x,y);c0=c;endy1=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c (2)^2));plot(x,y,'r-',x,y1);legend('实验数据','拟合曲线')x=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16]';y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4]';f=@(c,x)c(1)*(exp(-c(2)*x)-exp(-c(3)*x));c0=[114 0.1 2]';for i=1:50opt=optimset('TolFun',1e-3);[c R]=nlinfit(x,y,f,c0,opt)c0=c;hold onplot(x,c(1)*(exp(-c(2)*x)-exp(-c(3)*x)),'g')endt=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];c0=[1 1 1];for i=1:50 c=lsqcurvefit(@example1,c0,t,y);c0=c;endy1=c(1)*(exp(-c(2)*t)-exp(-c(3)*t));plot(t,y,' +',t,y1);legend('实验数据','拟合曲线')五,插值拟合相关知识在生产和科学实验中,自变量及因变量间的函数关系有时不能写出解析表达式,而只能得到函数在若干点的函数值或导数值,或者表达式过于复杂而需要较大的计算量。
2011年数学建模A题 城市表格模板层土壤重金属污染分析(附所有图件的Matlab源代码)
A题城市表层土壤重金属污染分析摘要通过建立地区三维地形图与各种元素丰度分布等值线图,结合地形、元素传播特征、风向,利用数学方法综合确定污染源的位置,并对各类污染作简要的分析。
对于问题一,利用Matlab,做出地形图与各元素等值线图,确定各分布。
在通过几何平局法,确定总体重金属污染情况。
对于问题二,基于问题一,可知汽车尾气、工业“三废”、生活垃圾共同造成重金属污染。
对于问题三,由于各元素传播特征不同,传播能力弱的,其元素丰度高处就为污染源。
例如CrCd。
传播能力强者,由有相似分布者,可联合分析,认为其为同一污染源排出。
如As、Hg、Zn。
关键词:污染物分布Matlab等值线一. 问题重述通过GPS记录了某城市城区的空间坐标,给出了不同功能区土壤表层0—10cm的8种主要重金属的含量,并给出了此城区的不同重金属的背景值,均值,标准偏差。
现通过数学建模来完成以下任务:(1)给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2)通过数据分析,说明重金属污染的主要原因。
(3)分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4)分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?二.问题分析(1)问题一属于统计归纳的数学问题。
通过数学方法进行图像拟合,从中发现规律,找到图中污染集中分布区域。
之后,再把八种元素综合考虑,试图确定不同地(2)对于问题二,可在第一问的基础上,结合各种重金属污染的传播特点,综合确定污染原因。
(3)问题三,对于不易传播的元素,可认为其元素丰度最高值处为污染源,对于其他元素,应通过其污染物散落范围综合求解得出。
(4)问题四,可在获知风向、水流方向的因素的情况下,综合利用微分方程求解污染源。
三、模型假设(1)假设As、Hg、Zn由同一污染源排放。
(2)对于第一问,忽略高程的影响。
2011年数学建模国赛_三维曲面插值与拟合-30页
得用拟合或插值。
常用的拟合有多项式拟合POLYFIT插值有INTERP1,SPLINE,LAGR1等。
在Matlab中,用于曲线和曲面平滑的方法与函数很多,曲线平滑可用smooth和smoothts 等,三维数据可用smooth3,另外样条工具箱中也有不少可用于平滑数据的函数,如三次样条csaps和B样条spaps等。
matlab中三维作图功能总结2007-12-09 11:29plot3 画三维坐标中的点,连线,但只能顺序连接。
surf(X,Y,Z) 用X和Y定义x-y坐标网格,Z定义网格上每一点的高度,来生成三维曲面。
如:[X,Y,Z] = peaks(30);surf(X,Y,Z)mesh,和surf一样,只不过生成的是网格。
surface 用法也一样。
fill3 只能生成平面。
重点在色彩。
[X,Y,Z]=meshgrid(1:3,1:3,1:5) 生成3*3*5的三维网格,X,Y,Z都是3*3*5三维矩阵。
这只是生成坐标网格,还需要一个V(X,Y,Z)定义图形。
ndgrid 生成三维以上网格时用。
smooth3 作用于体数据,使光滑isosurfaceX,Y,Z如meshgrid的定义。
V中元素为1则表示存在,即要显示。
但要连成片的1才会显示。
V中元素如a>1时,表示要显示的这个点离上方的网格距离是单位距离的1/a圆滑程度由isovalue决定,0.9999是最硬,越接近0越圆滑。
可同时配合isocaps. isocaps 生成并显示图形与坐标系交界处的平面。
patch 接收isosuface返回的参数,生成图形。
Matlab 曲面插值和拟合附录:Matlab 样条工具箱(Spline ToolBox)【信息来源教师博客】Matlab样条工具箱中的函数提供了样条的建立,操作,绘制等功能;一. 样条函数的建立第一步是建立一个样条函数,曲线或者曲面。
这里的样条函数,根据前缀,分为4类: cs* 三次样条pp* 分段多项式样条,系数为t^n的系数sp* B样条, 系数为基函数B_n^i(t)的系数rp* 有理B样条二. 样条操作样条操作包括:函数操作:求值,算术运算,求导求积分等等节点操作:主要是节点重数的调节,设定,修改等等附:样条工具箱函数1. 三次样条函数csapi 插值生成三次样条函数csape 生成给定约束条件下的三次样条函数csaps 平滑生成三次样条函数cscvn 生成一条内插参数的三次样条曲线getcurve 动态生成三次样条曲线2. 分段多项式样条函数ppmak 生成分段多项式样条函数ppual 计算在给定点处的分段多项式样条函数值3. B样条函数spmak 生成B样条函数spcrv 生成均匀划分的B样条函数spapi 插值生成B样条函数spap2 用最小二乘法拟合生成B样条函数spaps 对生成的B样条曲线进行光滑处理spcol 生成B样条函数的配置矩阵4. 有理样条函数rpmak 生成有理样条函数rsmak 生成有理样条函数5. 样条操作函数fnval 计算在给定点处的样条函数值fmbrk 返回样条函数的某一部分(如断点或系数等) fncmb 对样条函数进行算术运算fn2fm 把一种形式的样条函数转化成另一种形式的样条函数 fnder 求样条函数的微分(即求导数)fndir 求样条函数的方向导数fnint 求样条函数的积分fnjmp 在间断点处求函数值fnplt 画样条曲线图fnrfn 在样条曲线中插入断点。
2011全国数学建模大赛A题相关matlab程序
2011全国数学建模大赛A题相关matlab程序(2011-09-16 16:42:56)这是我在今年全国大学生数学建模大赛中解答A题的相关MATLAB程序(供大家参考),同时晒两张相关图片:%绘单个元素空间分布图程序clear all;load shuju.txta=shuju(1:end,8);%b=a/69;%load data.txtx=data(1:end,1);y=data(1:end,2);z=data(1:end,3);scatter3(x,y,z,50,b,'filled')xlabel('X')ylabel('Y')zlabel('海拔')%算各区污染平均指数程序clear all;load shuju.txtfor i=1:8a=shuju(1:end,i); %i随数据文本列数决定p=[3.6 130 31 13.2 35 12.3 31 69]b(:,i)=a/p(i); %i随数据文本列数决定endload data.txtx=data(1:end,4);m=1;sum=0;for i=1:319if x(i)==5cb(m)=b(i,8);sum=sum+cb(m);m=m+1;endendav=sum/(m-1)%层次分析法一致性检验程序clearclose allclcticdisp('please input Matrix A')A=input('A=\n');%A矩阵为需要分析的n阶方阵![n,n]=size(A);x=ones(n,100);y=ones(n,100);m=zeros(1,100);m(1)=max(x(:,1));y(:,1)=x(:,1);x(:,2)=A*y(:,1);m(2)=max(x(:,2));y(:,2)=x(:,2)/m(1);p=0.0001;i=2;k=abs(m(2)-m(1));while k>p;i=i+1;x(:,i)=A*y(:,i-1);m(i)=max(x(:,i));y(:,i)=x(:,i)/m(i);k=abs(m(i)-m(i-1));enda=sum(y(:,i));w=y(:,i)/a;t=m(i);disp('权重向量w=')disp(w)%fprintf('权重向量w=%f\n',w);fprintf('最大特征根t=\n %f\n',t);%以下为该方阵的一致性检验!CI=(t-n)/(n-1);RI=[0 0 .58 .90 1.12 1.24 1.32 1.41 1.45 1.49 1.51]; CR=CI/RI(n);if CR<0.1;disp('CI=')disp(CI)disp('RI=')disp(RI(n))disp('CR=')disp(CR)fprintf('所以\n CR<0.1\n\n');disp('因此该方阵可以通过一致性检验!!!')else disp('因此该方阵不可以通过一致性检验!!!') end%总权重计算程序clear all;clcload chu.txta=chu(1,:);%b=chu(2,:);%c=chu(3,:);%d=chu(4,:);%e=chu(5,:);%k=chu(5,:);sum=0;for i=1:4 %根据总矩阵列数决定4所在位置的数据l(i)=a(i)*b(i);sum=sum+l(i);endsum1=0;for i=1:4l(i)=a(i)*c(i);sum1=sum1+l(i);endsum2=0;for i=1:4l(i)=a(i)*d(i);sum2=sum+l(i);endsum3=0;for i=1:4l(i)=a(i)*e(i);sum3=sum+l(i);endsum4=0;for i=1:4%3这一位的数由阵列列数决定l(i)=a(i)*k(i);sum4=sum+l(i);endsumsum1sum2sum3sum4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011全国大学生数模竞赛A题
三维立体绘图MATLAB代码及图像
下载两个数据文件保存到MATLAB工作目录中,同时将下面的程序拷贝到一个M文件里面运行即可。
MATLAB代码和数据文件请到这里下载:/thread-19793-1-1.html
A题城市表层土壤重金属污染分析
随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:
(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?
程序代码:
clc
clear
close all
D=load('ZuoBiao.dat');
M=load('JinShu.dat');
x=D(:,2);
y=D(:,3);
z=D(:,4);
c=D(:,5);
xi=linspace(min(x),max(x),100);
yi=linspace(min(y),max(y),100);
[xi,yi]=meshgrid(xi,yi);
zi=griddata(x,y,z,xi,yi);
ci=griddata(x,y,c,xi,yi);
marker={'*','o','s','^','p'};
color={'k','r','y','c','b'};
mat={'As','Cd','Cr','Cu','Hg','Ni','Pb','Zn'};
str={'等高线','生活区','工业区','山林区','交通区','绿地区'};
for j=1:8
% 等高线图形
figure
contourf(xi,yi,zi,0:10:500);
% set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
% clabel(C,h,[0:10:50,50:50:300,300:100:500]);
title(['金属 ',mat{j}, ' 二维等高线分布图'])
xlabel('X')
ylabel('Y')
colormap summer
colorbar
grid on
hold on
for i=1:5
loc=c==i;
plot(x(loc),y(loc),marker{i},'markerfacecolor',color{i },'MarkerEdgeColor',color{i});
end
legend(str,'location','best')
for k=1:length(x)
text(x(k)-200,y(k)+200,num2str(M(k,j+1)),'fontsize',8);
end
end
% 三维体图
figure
h=surf(xi,yi,zi);
set(h,'cdata',ci);
colormap hsv
title('三维图立体(颜色条表示分类)')
xlabel('X')
ylabel('Y')
colorbar
hidden off
hold on
for i=1:5
loc=c==i;
plot3(x(loc),y(loc),z(loc),marker{i},'markerfacecolor',color{i });
end
str{1}='三维图';
legend(str,'location','best')
图像如下:。
