2014届湖北重点中学高三联考数学模拟试题
湖北省部分重点中学2014届高三第二次联考_(文)数学试题

湖北省部分重点中学2014届高三第二次联考高三数学试卷(文史类)命题学校:武汉六中 命题教师:袁泉润 审题教师:张霞考试时间:2014年元月20日下午14:00—16:00 试卷满分:150分一、选择题:(本大题共10小题,每小题5分,共50分;在每小题给出的四个选项中,只有一个选项是符合题目要求的.) 1、已知全集U= {}1,2,3,4,5,集合A= {}3,4,B= {}1,2,3,则()U C A B I 等于( ) A .{}3 B .{}1,3 C .{}1,2 D .{}1,2,3 2、已知a 是实数,iia -+1是纯虚数,则a 等于( )A .1-B .1C .2D .3、已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是( )A .13cmB .23cmC .33cmD .63cm4、已知{}n a 是各项为正数的等比数列,12341,4,a a a a +=+=则5678a a a a +++=( )A .80B .20C .32D .25535、若a= 3(,sin )2α,b= 1(cos ,)3α,且a // b ,则锐角α=( )A .015B .030C .045D .0606、已知 1.224log log ,0.7x y z π-===,则( )A .x y z <<B .z y x <<C .y z x <<D . y x z << 7、设函数()sin()(0,)2f x x πωϕωϕ=+><的图象关于直线23x π=对称,且它的最小正周期为π,则 ( )A. ()f x 在区间53,124ππ⎡⎤⎢⎥⎣⎦上是减函数 B. ()f x 的图象经过点⎛ ⎝⎭C.()f x 的图象沿着x 轴向右平移6π个单位后所得图象关于y 轴对称 D. ()f x 在30,4π⎡⎤⎢⎥⎣⎦上的最小值为1-8、已知直二面角l αβ--,点A ∈α,B ∈β,A 、B 到棱l 的距离相等,直线AB 与平面β所成的角为030,则AB 与棱l 所成的角的余弦是( )A .B .2C .12D .49、已知点(,0)(0)F c c >是双曲线12222=-by a x 的右焦点,F 关于直线y x =的对称点A 恰在该双曲线的右支上,则该双曲线的离心率是( )A 1B .12 C 1 D .251+ 10、已知()ln 2f x x x =+-,()ln 2g x x x x =+-在()1,+∞上都有且只有一个零点,()f x 的零点为1x ,()g x 的零点为2x ,则( )A .2112x x <<<B .1212x x <<<C .1212x x <<<D .212x x << 二、填空题:(本大题共7小题,每小题5分,共35分) 11.若4cos()5πα+=,则sin(2)2πα-=__________.12.不等式lg(1)0x +≤的解集是__________. 13.已知a 、b 为实数,0a >,则ba b b a++的最小值为__________. 14.ABC ∆中,过点A 作AH BC ⊥,垂足为H ,3,2BH HC ==,则()32AB AC BC +uu u r uuu ruu ur g =__________. 15.由直线2y x =+上的点向圆22(4)(2)1x y -++=引切线,则切线长的最小值为__________.16.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台、且冰箱至少生产20台。
湖北省部分重点中学2014届高三数学二月联考试题 理 新人教A版

湖北省局部重点中学2014届高三二月联考高三数学试卷〔理科〕考试时间:2014年2月6日下午15:00—17:00 试卷总分为:150分一、选择题:本大题共10小题,每一小题5分,共50分. 在每一小题给出的四个选项中, 只有一项为哪一项符合题目要求的.1.,x y R ∈,i 为虚数单位,且(2)1x i y i --=-+,如此(1)x yi ++的值为 ( 〕A .4B .4+4iC .4-D .2i2.设集合A ={4,5,7,9},B ={3,4,7,8,9},全集U = A ⋃B ,如此集合)(B A C U ⋂ 的真子集共有 A .3个B .6个C .7个D .8个3.要得到函数)42sin(π+=x y 的图象,只要将函数x y 2cos =的图象〔 〕A .向左平移4π单位B .向右平移4π单位C .向右平移8π单位D .向左平移8π单位4.半径为R 的球的内接正三棱柱的三个侧面积之和的最大值为〔 〕A 、233RB 、23RC 、222RD 、22R5.数据123 n x x x x ,,,,是武汉市n *(3 )n n N ≥∈,个普通职工的2013年的年收入,设这n 个数据的中位数为x ,平均数为y ,方差为z ,如果再加上比尔.盖茨的2013年的年收入1n x +〔约900亿元〕,如此这1n +个数据中,如下说法正确的答案是〔 〕 A .年收入平均数大大增大,中位数一定变大,方差可能不变 B .年收入平均数大大增大,中位数可能不变,方差变大 C .年收入平均数大大增大,中位数可能不变,方差也不变 D .年收入平均数可能不变,中位数可能不变,方差可能不变。
6.在各项均为正数的等比数列}{n a 中,2475314))((a a a a a =++,如此如下结论中正确的答案是〔 〕A .数列}{n a 是递增数列;B .数列}{n a 是递减数列;C .数列}{n a 既不是递增数列也不是递减数列;D .数列}{n a 有可能是递增数列也有可能是递减数列.7.实数0,0a b >>,对于定义在R 上的函数)(x f ,有下述命题:①“)(x f 是奇函数〞的充要条件是“函数()f x a -的图像关于点(,0)A a 对称〞; ②“)(x f 是偶函数〞的充要条件是“函数()f x a -的图像关于直线x a =对称〞; ③“2a 是()f x 的一个周期〞的充要条件是“对任意的R x ∈,都有()()f x a f x -=-〞; ④ “函数()y f x a =-与()y f b x =-的图像关于y 轴对称〞的充要条件是“a b =〞 其中正确命题的序号是( ) A .①②B .②③C .①④D .③④8.在边长为1的正三角形ABC 中,BD →=xBA →,CE →=yCA →,x >0,y >0,且x +y =1, 如此CD →·BE →的最大值为( )A .-58B .-34C .-32D .-389.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P 是C 上一点,假设126PF PF a +=,且12PF F ∆的最小内角为30,如此C 的渐近线方程为〔 〕 A .x y ±=B .x y 2±=C .x y 22±= D .2y x =±10.函数)1,0(1log )(≠>-=a a x x f a ,假设1234x x x x <<<,且12()()f x f x =34()()f x f x ==,如此12341111x x x x +++=〔 〕 A. 2 B. 4 C.8 D. 随a 值变化二.填空题:本大题共6小题,考生共需作答5小题,每一小题5分,共25分,请将答案填在答题卡....的.对应题号的位置上,答错位置,书写不清,模棱两可均不得分. (一) 必考题〔11—14题〕11.执行如下列图的程序框图,输出的S =.12.假设不等式组02(1)1y y x y a x ≥⎧⎪≤⎨⎪≤-+⎩表示的平面区域是一个三角形,如此a 的取值范围是.?10<nnn S S 2⋅+=13.椭圆12222=+by a x 的面积计算公式是ab S π=,如此22114x --=⎰________; 14. 设数列.,1,,12,1,,13,22,31,12,21,11 kk k -这个数列第2010项的值是________; 这个数列中,第2010个值为1的项的序号是.〔二〕选考题〔请考生在第15、16两题中任选一题作答,如果全选,如此按第15题作答结果计分.〕 15.〔选修4-1:几何证明选讲〕如图,AB 为半径为2的圆O 的直径,CD 为垂直于AB 的一条弦, 垂足为E ,弦BM 与CD 交于点F .如此2AC +BF·BM=16.〔选修4-4:坐标系与参数方程〕在极坐标系中,直线ρ(cos θ-sin θ)+2=0被曲线C :ρ=2所截得弦的中点的极坐标为________. 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17.〔本小题总分为12分〕锐角ABC ∆的三个内角C B A ,,所对的边分别为c b a ,,。
湖北省七市州2014年4月高三数学联考(Word解析版)
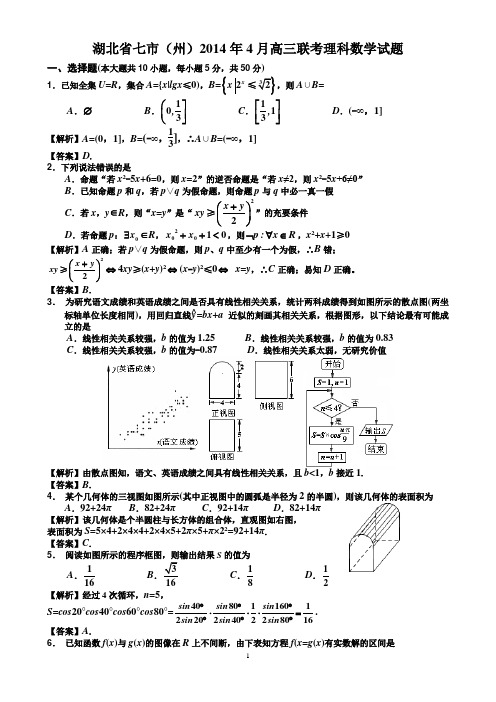
Hale Waihona Puke -1 x 0 1 2 3 f(x) -0.677 3.011 5.432 5.980 7.651
g(x) -0.530 3.451 4.890 5.241 6.892 A.(-1,0) B.(0,1) C.(1,2) D.(2,3) 【解析】设 h(x)=f(x)-g(x),则 h(-1)=-0.147,h(0)=-0.44,h(1)=0.542, ∴h(0)· h(1)<0,h(x)的零点在(0,1)内,即 f(x=g(x)的解属于(0,1). 【答案】B.
湖北省七市(州)2014 年 4 月高三联考理科数学试题
一、选择题(本大题共 10 小题,每小题 5 分,共 50 分)
1.已知全集 U=R,集合 A={x|lgx≤0),B= x 2 x ≤ 3 2 ,则 A∪B=
1 1 B. 0 , C . , 1 3 3 1 【解析】A=(0,1],B=(-∞, ],∴A∪B=(-∞,1] 3 【答案】D.
2
2
【解析】由散点图知,语文、英语成绩之间具有线性相关关系,且 b<1,b 接近 1. 【答案】B. 4. 某个几何体的三视图如图所示(其中正视图中的圆弧是半径为 2 的半圆),则该几何体的表面积为 A.92+24π B.82+24π C.92+14π D.82+14π 【解析】该几何体是个半圆柱与长方体的组合体,直观图如右图, 表面积为 S=5× 4+2× 4× 4+2× 4× 5+2π× 5+π× 22=92+14π. 【答案】C. 5. 阅读如图所示的程序框图,则输出结果 S 的值为
2
1 , 8
A.
湖北省部分重点中学2014届高三第二次联考数学理图片版含答案

湖北省部分重点中学2014届高三第二次联考高三数学试卷(理科)参考答案CDDDBCACBB②和③ 3或13 2(0,]3 216.解:(Ⅰ)∵()2π3πcos 2cos 22cos 22323f x x x x x x ⎛⎫⎛⎫=--=-=- ⎪ ⎪⎝⎭⎝⎭, ∴.故函数()f x 的最小正周期为π;递增区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦(k ∈Z )(Ⅱ)解法一:π23B f B ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,∴π1sin 32B ⎛⎫-=- ⎪⎝⎭. ∵0πB <<,∴ππ2π333B -<-<,∴ππ36B -=-,即π6B =. 由余弦定理得:2222cos b a c ac B =+-,∴2132a a =+-⨯,即2320a a -+=,故1a =(不合题意,舍)或2a =. 因为222134b c a +=+==,所以∆ABC 为直角三角形.解法二:π23B f B ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,∴π1sin 32B ⎛⎫-=- ⎪⎝⎭. ∵0πB <<,∴ππ2π333B -<-<,∴ππ36B -=-,即π6B =.由正弦定理得:1πsin sin 6a A ==,∴sin C =,∵0πC <<,∴π3C =或2π3. 当π3C =时,π2A =;当2π3C =时,π6A =.(不合题意,舍) 所以∆ABC 为直角三角形. 17.(Ⅰ) 延长AD ,FE 交于Q .因为ABCD 是矩形,所以BC ∥AD ,所以∠AQF 是异面直线EF 与B C 所成的角.在梯形ADEF 中,因为DE ∥AF ,AF ⊥FE ,AF=2,DE =1得∠AQF =30°.(Ⅱ) 方法一:设AB =x .取AF 的中点G .由题意得DG ⊥AF .因为平面ABCD ⊥平面ADEF ,A B ⊥AD ,所以AB ⊥平面ADEF ,(第17题图)所以AB ⊥DG .所以DG ⊥平面ABF .过G 作GH ⊥BF ,垂足为H ,连结DH ,则DH ⊥BF ,所以∠DHG 为二面角A -BF -D 的平面角.在直角△AGD 中,AD =2,AG =1,得DG.在直角△BAF 中,由AB BF =sin ∠AFB =GH FG ,得GH x, 所以GH.在直角△DGH 中,DG,GH,得DH=. 因为cos ∠DHG =GH DH =13,得x所以AB方法二:设AB =x .以F 为原点,AF ,FQ 所在的直线分别为x 轴,y 轴建立空间直角坐标系Fxyz .则 F (0,0,0),A (-2,0,0),E0,0),D (-10),B (-2,0,x ), 所以DF =(1,0),BF =(2,0,-x ).因为EF ⊥平面ABF ,所以平面ABF 的法向量可取1n =(0,1,0).设2n =(x 1,y 1,z 1)为平面BFD 的法向量,则111120,0,x z x x -=⎧⎪⎨-=⎪⎩ 所以,可取2n =,1. 因为cos<1n ,2n >=1212||||n n n n ⋅⋅=13,得 x所以AB18.解:(1)当1n =时,由111211a S a -=⇒=.又1121n n a S ++-=与21n n a S -=相减得:12n n a a +=,故数列{}n a 是首项为1,公比为2的等比数列,所以12n n a -=(2)设n a 和1n a +两项之间插入n 个数后,这2n +个数构成的等差数列的公差为(第17题图)n d , 则11211n n n n a a d n n -+-==++, 又(12361)611952,2014195262+++++=-=, 故61616220146262262(621)2612.6363b a d =+-⋅=+⨯=⨯ 19 0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==.(Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.………9分(Ⅲ)由(Ⅱ)可得:()222 4.12(1)11.76(1)20.40(1)E X p p p p p p ⎡⎤=-++-+-⎣⎦ 211.76p p =-++. ………………11分因为E(X 1)< E(X 2), 所以21211.76p p <-++.所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.620.解:(1)依题意,得2a =,c e a == 1,322=-==∴c a b c ;故椭圆C 的方程为2214x y += . (2)方法一:点M 与点N 关于x 轴对称,设),(11y x M ,),(11y x N -, 不妨设01>y .由于点M 在椭圆C 上,所以412121x y -=. (*) 由已知(2,0)T -,则),2(11y x TM +=,),2(11y x TN -+=,21211111)2(),2(),2(y x y x y x TN TM -+=-+⋅+=⋅∴3445)41()2(1212121++=--+=x x x x 51)58(4521-+=x . 由于221<<-x ,故当581-=x 时,TM TN ⋅取得最小值为15-. 方法二:点M 与点N 关于x 轴对称,故设(2cos ,sin ),(2cos ,sin )M N θθθθ-, 不妨设sin 0θ>,由已知(2,0)T -,则)sin ,2cos 2()sin ,2cos 2(θθθθ-+⋅+=⋅TN TM3cos 8cos 5sin )2cos 2(222++=-+=θθθθ51)54(cos 52-+=θ. 故当4cos 5θ=-时,TM TN ⋅取得最小值为15-,此时83(,)55M -, (3) 方法一:设),(00y x P ,则直线MP 的方程为:)(010100x x x x y y y y ---=-, 令0y =,得101001y y y x y x x R --=, 同理:101001y y y x y x x S ++=, 故212021202021y y y x y x x x S R --=⋅ (**)又点M 与点P 在椭圆上,故)1(42020y x -=,)1(42121y x -=,代入(**)式,得: 4)(4)1(4)1(421202*********202021=--=----=⋅y y y y y y y y y y x x S R . 所以4=⋅=⋅=⋅S R S R x x x x OS OR ,OR OS +的最小值为4 方法二:设(2cos ,sin ),(2cos ,sin )M N θθθθ-,不妨设sin 0θ>,)sin ,cos 2(ααP ,其中θαsin sin ±≠.则直线MP 的方程为:)cos 2(cos 2cos 2sin sin sin αθαθαα---=-x y ,令0y =,得θαθαθαsin sin )sin cos cos (sin 2--=R x , 同理:θαθαθαsin sin )sin cos cos (sin 2++=S x , 故4sin sin )sin (sin 4sin sin )sin cos cos (sin 42222222222=--=--=⋅θαθαθαθαθαS R x x . 所以4=⋅=⋅=⋅S R S R x x x x OS OR ,OR OS +的最小值为421、解:(I )'121()(1)2(1)(1)[(1)2]n n n n f x nx x x x x x n x x --=---=---, 当1[,1]2x ∈时,由'()0n f x =知1x =或者2n x n =+, 当1n =时,11[,1]232n n =∉+,又111()28f =,(1)0n f =,故118a =; 当2n =时,11[,1]222n n =∈+,又211()216f =,(1)0n f =,故2116a =; (II )当3n ≥时,1[,1]22n n ∈+, ∵1[,)22n x n ∈+时,'()0n f x >;(,1)2n x n ∈+时,'()0n f x <; ∴()n f x 在2n x n =+处取得最大值,即2224()()22(2)n n n n n n a n n n +==+++ 综上所述,21,(1)84,(2)(2)n n n n a n n n +⎧=⎪⎪=⎨⎪≥⎪+⎩. 当2n ≥时,欲证 2241(2)(2)n n n n n +≤++,只需证明2(1)4n n+≥ ∵011222222(1)()()()n n n n n n n C C C C n n n n+=+⋅+⋅++⋅ 2(1)41212142n n n-≥++⋅≥++=,所以,当2n ≥时,都有21(2)n a n ≤+成立. (III )当1,2n =时,结论显然成立;当3n ≥时,由(II )知3411816n n S a a a =+++++2221111181656(2)n <++++++ 11111111()()()816455612n n <++-+-++-++ 1117816416<++=. 所以,对任意正整数n ,都有716n S <成立.。
数学理卷·2014届湖北省部分重点中学高三11月联考(2013.11)word版

全品高考网 湖北省部分重点中学2014届高三第一次联考数学(理)试题命题学校:武汉市第六中学 命题老师:欧阳彪 审题老师:张荣花考试时间:2013年11月7日上午9:00-11:30 试卷满分:150第一部分 选择题一、选择题:本大题共有10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
请把它选出后在答题卡上规定的位置上用铅笔涂黑。
1.已知两个集合{})2ln(|2++-==x x y x A ,⎭⎬⎫⎩⎨⎧≤-+=012|x e x x B ,则=B A ( ). A. ⎪⎭⎫⎢⎣⎡221-, B. ⎥⎦⎤ ⎝⎛21-1-, C. ()e ,1- D. ()e ,22.若i z ⎪⎭⎫ ⎝⎛-+-=54cos 53sin θθ是纯虚数,则⎪⎭⎫ ⎝⎛-4tan πθ=( ) A. 71-B. 7-C. 37- D. 1- 3.已知命题p :所有素数都是偶数,则p ⌝是 ( ) A.所有的素数都不是偶数 B.有些素数是偶数 C.存在一个素数不是偶数 D. 存在一个素数是偶数4. 设R a ∈,函数x x ae e x f --=)(的导函数为)(x f ',且)(x f '是奇函数,则=a ( )A. 0B. 1C. 2D. 1-5.三个实数成等差数列,首项是9.若将第二项加2、第三项加20可使得这三个数依次构成等比数列{}n a ,则3a 的所有取值中的最小值是 ( )A. 1B. 4C. 36D. 496. 已知函数)(x f y =的定义域为{}5,83|≠≤≤-x x x 且,值域为{}0,21|≠≤≤-y y y 且.下列关于函数)(x f y =的说法:①当3-=x 时,1-=y ;全品高考网②将)(x f y =的图像补上点()0,5,得到的图像必定是一条连续的曲线;③)(x f y =是[)5,3-上的单调函数;④)(x f y =的图象与坐标轴只有一个交点.其中正确命题的个数为( )A. 1B. 2C. 3D. 47. 等比数列{}n a 的前n 项和为n S ,若1+n S ,n S ,2+n S 成等差数列,则其公比q 为 ( )A. 2-=qB. 1=qC. 12=-=q q 或D. 12-=-=q q 或 8. 已知函数)(x f 是定义在()()+∞∞-,00, 上的偶函数,当0>x 时,()⎪⎩⎪⎨⎧>-≤<-=-2,22120,12)(|1|x x f x x f x ,则函数1)(4)(-=x f x g 的零点个数为( ) A. 4 B. 6 C. 8 D. 109. 设△ABC 的内角A ,B ,C 所对的边分别为c b a ,,,若三边的长为连续的三个正整数,且C B A >>,C A 2=,则C B A sin :sin :sin 为 ( )A .4:3:2B .5:4:3C .6:5:4D .7:6:5 10. 在ABC △所在的平面内,点P P 、0满足=P 041AB ,λ=,且对于任意实数λ,恒有≥⋅P P 00⋅, 则 ( )A.︒=∠90ABCB. ︒=∠90A C BC.BC AC =D. AC AB =第二部分 非选择题二、填空题:本大题共5小题,每小题5分,满分25分。
湖北省八校2014届高三12月第一次联考理科数学试卷-含答案

鄂南高中 华师一附中 黄冈中学 黄石二中荆州中学 襄阳四中 襄阳五中 孝感高中湖北省 八校 2014届高三第一次联考数学试题(理科)考试时间:2013年12月13日下午 15︰00—17︰00 试卷满分150分 考试用时120分钟本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分150分,考试时间120分钟.★ 祝考试顺利 ★注意事项:1.考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3.填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内. 答在试题卷上无效.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 方程2250x x -+=的一个根是( ) A .12i +B .12i -+C .2i +D .2i -2. 集合2{3,log }P a =,{,}Q a b =,若{0}P Q =,则PQ =( )A .{3,0}B .{3,0,2}C .{3,0,1}D .{3,0,1,2}3. 下列命题,正确的是( )A .命题:x ∃∈R ,使得210x -<的否定是:x ∀∈R ,均有210x -<.B .命题:若3x =,则2230x x --=的否命题是:若3x ≠,则2230x x --≠.C .命题:存在四边相等的四边形不是正方形,该命题是假命题.D .命题:cos cos x y =,则x y =的逆否命题是真命题.5. 函数32()(0,)f x ax bx cx d a x =+++≠∈R 有极值点,则( ) A . 23b ac ≤ B. 23bac ≥ C . 23b ac < D . 23b ac >6. 一个几何体的三视图如图,则该几何体的体积为( )A .13B.23C .2D .1 7. △ABC 中,角,,A B C 成等差数列是sin sin )cos C A A B =+成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8. 在弹性限度内,弹簧所受的压缩力F 与缩短的距离l 按 胡克定律F kl =计算.今有一弹簧原长80cm ,每压缩1cm 需0.049N 的压缩力,若把这根弹簧从70cm 压缩至50cm (在弹性限度内),外力克服弹簧的弹力做了( )功(单位:J ) A .0.196B .0.294C .0.686D .0.989.在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,F 是侧面11BCC B内的动点,且1A F ∥平面1D AE ,记1A F 与平面11BCC B 所成的角为θ, 下列说法错误的是( )A .点F 的轨迹是一条线段B .1A F 与1D E 不可能平行C . 1A F 与BE 是异面直线D .tan θ≤正(主)视图 侧(左)视图俯 视 图第6题图1F(一)必考题(11—14题)11. 平面向量,a b 满足||1,||2==a b ,且()(2)7+⋅-=-a b a b ,则向量,a b 的夹角为______.12. 已知正三角形内切圆的半径r 与它的高h 的关系是:13r h =,把这个结论推广到空间正四面体,则正四面体内切球的半径r 与正四面体高h 的关系是_________. 13. 将函数sin(2)y x ϕ=+的图象向左平移4π个单位后得到的函数图象关于点4(,0)3π成中心对称,那么||ϕ的最小值为________. 14. 无穷数列{}n a 中,12,,,m a a a 是首项为10,公差为2-的等差数列;122,,,m m m a a a ++是首项为12,公比为12的等比数列(其中*3,m m ∈N ≥),并且对于任意的*n ∈N ,都有2n m n a a +=成立.若51164a =,则m 的取值集合为____________.记数列{}n a 的前n 项和为n S ,则使得12852013m S +≥ *3,)m m ∈(N ≥的m 的取值集合为____________.(二)选考题(请考生在15、16两题中任选一题作答.如果全选,则按第15题作答结果计分)在极坐标系中,曲线1:4C ρ=上有3个不同的点到曲线2:sin()4C m ρθ+=的距离等于2,则______m =.(Ⅰ)求的值;(Ⅱ)求函数()f x 在[0,2]π上的单调递增区间.18.(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,满足:2418,a a +=791S =.递增的等比数列{}n b 前n 项和为n T ,满足:12166,128,126k k k b b b b T -+===. (Ⅰ)求数列{}n a ,{}n b 的通项公式;(Ⅱ)设数列{}n c 对*n ∀∈N ,均有12112nn nc c c a b b b ++++=成立,求122013c c c +++.19.(本小题满分12分)如图,在直三棱柱111ABC A B C -中,底面△ABC 为等腰直角三角形,90ABC ∠=,D 为棱1BB 上一点,且平面1DAC ⊥平面11AA C C . (Ⅰ)求证:D 为棱1BB 的中点;(Ⅱ)ABAA 1为何值时,二面角1A A D C --的平面角为60.20.(本小题满分12分)如图,山顶有一座石塔BC ,已知石塔的高度为a .(Ⅰ)若以,B C 为观测点,在塔顶B 处测得地面上一点A 的俯角为α,在塔底C 处测得A 处的俯角为β,用,,a αβ表示山的高度h ;(Ⅱ)若将观测点选在地面的直线AD 上,其中D 是塔顶B 在地面上的射影. 已知石塔高度20a =,当观测点E 在AD 上满足DE =BC 的视角(即BEC ∠)最大,求山的高度h .21.(本小题满分13分)已知n a 是关于x 的方程1210n n n x x x x --++++-=(0,2)x n n >∈N 且≥的根, 证明:(Ⅰ)1112n n a a +<<<; (Ⅱ)11()22n n a <+.22.(本小题满分14分)已知函数()e 1x f x ax =--(e 为自然对数的底数). (Ⅰ)求函数()f x 的单调区间;ABCA 1B 1C 1D 第19题图第20题(Ⅱ)当0a >时,若()0f x ≥对任意的x ∈R 恒成立,求实数a 的值; (Ⅲ)求证:22222232323ln 1ln 1ln 12(31)(31)(31)n n ⎡⎤⎡⎤⎡⎤⨯⨯⨯++++++<⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦.湖北省八校2014届高三第一次联考 理科数学参考答案及评分细则一、选择题(每小题5分,共10小题) 1—5 A C B B D 6—10 B A A B A 二.填空题(每小题5分,共5小题)11. 2π 12. 14r h = 13. 6π14.{}45,15,9; {}6 第一个空2分,第二个空3分15.216. 2m =±三、解答题(共5小题,共75分) 17. (Ⅰ)2()4sin()cos 3f x x x πωω=+1分14sin ()cos cos 22x x x ωωω⎡=⋅-+⋅⎢⎣⎦22sin cos x x x ωωω=-cos 2)sin 2x x ωω=+- 2cos(2)6x πω=+5分 由题意,T π=,2,12ππωω∴== 6分(Ⅱ)()2cos(2)6f x x π=+[]0,2x π∈时,2,4666x ππππ⎡⎤+∈+⎢⎥⎣⎦故[]2,26x πππ+∈或[]23,46x πππ+∈时,()f x 单调递增9分即()f x 的单调增区间为511,1212ππ⎡⎤⎢⎥⎣⎦和1723,1212ππ⎡⎤⎢⎥⎣⎦12分18. (Ⅰ)由题意24317742187()7912a a a a a S a +==⎧⎪⎨+===⎪⎩得349,13a a ==,则43n a n =- 2分211k k b b b b -=,1,k b b ∴方程2661280x x -+=的两根,得12,64k b b ==4分111(1)12611k k k b b qb q S q q ---===--,12,64k b b ==代入求得2q =,2n n b ∴=6分(Ⅱ)由12112nn nc c c a b b b ++++= 112121(2)n n n c c c a n b b b --+++=≥ 相减有1nn n nc a a b +=-4=22,42n n n n c b +∴≥==, 9分又121c a b =,得110c = 210(1)2(2)n n n c n +=⎧=⎨≥⎩122013c c c ∴+++=45201520161022226++++=-12分19.解:(Ⅰ)过点D 作DE ⊥ A 1 C 于E 点,取AC 的中点F ,连BF ﹑EF∵面DA 1 C ⊥面AA 1C 1C 且相交于A 1 C ,面DA 1 C 内的直线DE ⊥ A 1 C 故直线DE⊥面11ACC A3分又∵面BA C ⊥面AA 1C 1C 且相交于AC ,易知BF ⊥AC ,∴BF ⊥面AA 1C 1C 由此知:DE∥BF ,从而有D ,E ,F ,B 共面,又易知BB 1∥面AA 1C 1C ,故有DB∥EF ,从而有EF∥AA 1,又点F 是AC 的中点,所以DB = EF = 21 AA 1 = 21BB 1,即D 为1BB 的中点 6分A 1C 1B 1ACBD HEFG(Ⅱ)解法1:建立如图所示的直角坐标系, 设AA 1 = 2b ,AB =BC =a ,则D (0,0,b ), A 1 (a ,0,2b ), C (0,a ,0) 所以,),,0(),,0,(1b a b a DA -==设面DA 1C 的法向量为),,(z y x =则 00,00=-+⋅=+⋅+bz ay x bz y ax可取),,(a b b --= 8分又可取平面AA 1DB 的法向量)0,,0(a ==cos ,m n u r r222222200ab b aa b a ba b +-=⋅+⋅--⋅==据题意有:21222=+a b b 解得:AB AA 1=22=ab12分 (Ⅱ)解法2:延长A 1 D 与直线AB 相交于G ,易知CB ⊥面AA 1B 1B ,过B 作BH ⊥A 1 G 于点H ,连CH ,由三垂线定理知:A 1 G ⊥CH ,由此知∠CHB 为二面角A -A 1D - C 的平面角; 9分设AA 1 = 2b ,AB =BC =a ; 在直角三角形A 1A G 中,易知AB = BG . 在∆Rt DBG 中,BH =DGBGBD ⋅ =22ba ab +⋅,在∆Rt CHB 中,tan ∠CHB = BH BC = bb a 22+,据题意有:bb a 22+ = tan 600=3 ,解得:22=a b 所以 ABAA1 12分20. 解:(1)在△ABC 中,BAC αβ∠=-,90BCA β∠=+,由正弦定理得:sin sin BC ABBAC BCA=∠∠ sin(90)cos sin()sin()a a AB ββαβαβ+∴==--则cos sin sin sin()a h AB a a βαααβ=⋅-=--=cos sin sin()a αβαβ⋅- 4分(2)设DEx =,20tan h BED x +∠=,tan hCED x∠= tan tan tan 1tan tan BED CEDBEC BED CED∠-∠∴∠=+∠⋅∠ 6分 22020(20)(20)1x h h h h x x x ==++++≤当且仅当(20)h hx x+=即x =tan BEC ∠最大,从而BEC ∠最大=180h = 12分21. (Ⅰ)设12()1n n n f x x x x x --=++++-,则'12()(1)21n n f x nx n x x --=+-+++显然'()0f x >,()f x ∴在R +上是增函数(1)10(2)f n n =->≥11(1())122()11212n f -=--1()02n =-< ()f x ∴在1(,1)2上有唯一实根,即112n a << 4分假设1n n a a +≥,*1()k k n n a a k N +∴≥∈则1()n f a +=111111111n n n n n n n n n n n n a a a a a a a ++-+++++++-≥++++-11n n n n n a a a ->+++-()n f a =1()()0n n f a f a +==,矛盾,故1n n a a +<8分(Ⅱ)111111()()1()()()12222n n n n n n n n f a f a a a --⎡⎤-=+++--+++-⎢⎥⎣⎦11111(())(())()222n n n n n n n a a a ---+-++-12n a >- (12n a >)()0n f a =,11()()22n f =-11()22n n a ∴<+13分方法二:121n n n n n n a a a a --=+++由(Ⅰ)1na -=12n n n n n a a a -+++12111()()()222n n ->+++=11()22n -11()22n n a ∴<+22 (Ⅰ)'()x f x e a =-1分 0a ∴≤时,'()0f x >,()f x 在R 上单调递增。
湖北省部分重点中学2014届高三数学上学期期中联考试题 文 新人教A版

2013年秋季湖北省部分重点中学期中联考高三数学试卷(文科)考试时间:2013年11月7日下午2:30~4:30 试卷满分:150分一.选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若全集{}{}0,1,2,32U U C A ==且,则集合A 的真子集共有 A .3个B .5个C .7个D .8个 2. sin42sin72cos42cos72+=A .32B .12C .sin114D .cos114 3.下列各组命题中的假命题是A .1,20x x R -∀∈>B .2,(1)0x N x +∀∈->C .,lg 1x R x ∃∈<D .,tan 2x R x ∃∈= 4.右图是函数sin()(0,0,)2y A x A πωφωφ=+>><在区间5[,]66ππ-上的图象,为了得到这个函数的图象,只要将sin ()y x x R =∈的图象上所有的点 A .向左平移3π个单位长度,再把所得各点的横坐标缩短 到原来的12倍,纵坐标不变B .向左平移3π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D .向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变5.已知等比数列{}n a 中,公比1q >,且168a a +=,3412a a =,则116a a = A .2 B .3 C .6 D .3或66.若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间A. (),a b 和(),b c 内B. (),a -∞和(),a b 内C. (),b c 和(),c +∞内D. (),a -∞和(),c +∞内6π-56π7.设a ,b ,c 均为正数,且122log aa =, 121log 2b b ⎛⎫= ⎪⎝⎭, 21log 2cc ⎛⎫= ⎪⎝⎭则A .a <b <cB .c <b <aC .c <a <bD .b <a <c8.P 是ABC ∆所在平面上的一点,满足20PA PB PC ++=,若ABC ∆的面积为1,则ABP ∆的面积为 A. 1 B. 2 C. 21 D. 319.从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为 A .2097 B .2264 C .2111 D .201210.函数x x f x2log )31()(-=,正实数c b a ,,满足c b a <<且0)()()(<⋅⋅c f b f a f .若实数d 是方程0)(=x f 的一个解,那么下列四个判断:①a d < ②a d > ③c d > ④c d < 中有可能成立的个数为A .1B .2C .3D .4二.填空题:本大题共5小题,每小题5分,满分25分.把答案填在答题卡的横线上. 11.函数164x y =-的值域是 ▲ . 12.已知3tan()35πα-=-,则22sin cos 3cos 2sin αααα-= ▲ . 13.如右图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ,测得15BCD ︒∠=,30BDC ︒∠=,30CD =米,并在点C 测得塔顶A 的仰角为60︒,则塔高AB =▲ 米.14. 已知向量=(1,3)OA ,=(2,1)OB - ,(1,2)OC m m =+-,若点A 、B 、C 能构成三角形,则实数m 满足的条件是 ▲ . 15.已知函数f (x )=|x +11x-|,则关于x 的方程2()6()0f x f x c -+= (c ∈R )有6个不同实数解的充要条件是 ▲ .三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.1 23 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 19 20 21 22 23 24 2526 27 28 29 30 31 32 33 343536 37 383940…16.(本小题满分12分)已知集合231{|1,[,2]},{|||1}22A y y x x xB x x m ==-+∈-=-≥;命题:p x A ∈,命题:q x B ∈,并且命题p 是命题q 的充分条件,求实数m 的取值范围.17.(本小题满分12分) 已知sin 2()23sin .sin x f x x x=+(1)求()f x 的最大值及取得最大值时x 的取值的集合; (2)在△ABC 中,a b c 、、分别是角A ,B ,C 所对的边,若3a =,且对()f x 的定义域内的每一个x ,都有()()f x f A ≤恒成立,求AB AC ⋅的最大值.18.(本小题满分12分)叙述两角差的余弦公式,并用向量的数量积证明.19.(本小题满分12分)已知数列{}n a 满足:121,(0).a a a a ==>数列{}n b 满足1(*)n n n b a a n N +=∈. (1)若{}n a 是等差数列,且312b =,求a 的值及{}n a 的通项公式; (2)若{}n a 是等比数列,求{}n b 的前项和n S ;(3)当{}n b 是公比为1a -的等比数列时,{}n a 能否为等比数列?若能,求出a 的值;若不能,请说明理由.20.(本小题满分13分)。
湖北省八校2014届高三12月第一次联考理科数学试卷

鄂南高中 华师一附中 黄冈中学 黄石二中荆州中学 襄阳四中 襄阳五中 孝感高中湖北省 八校 2014届高三第一次联考数学试题(理科)考试时间:2013年12月13日下午 15︰00—17︰00 试卷满分150分 考试用时120分钟本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
全卷满分150分,考试时间120分钟.★ 祝考试顺利 ★注意事项:1.考生在答题前,请务必将自己的姓名、准考证号等信息填在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,答在试卷上无效.3.填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内. 答在试题卷上无效.第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 方程2250x x -+=的一个根是( ) A .12i +B .12i -+C .2i +D .2i -2. 集合2{3,log }P a =,{,}Q a b =,若{0}PQ =,则PQ =( )A .{3,0}B .{3,0,2}C .{3,0,1}D .{3,0,1,2}3. 下列命题,正确的是( )A .命题:x ∃∈R ,使得210x -<的否定是:x ∀∈R ,均有210x -<.B .命题:若3x =,则2230x x --=的否命题是:若3x ≠,则2230x x --≠.C .命题:存在四边相等的四边形不是正方形,该命题是假命题.D .命题:cos cos x y =,则x y =的逆否命题是真命题.4. 已知,x y 满足220240330x y x y x y +-⎧⎪-+⎨⎪--⎩≥≥≤,则关于22x y +的说法,正确的是( )5. 函数32()(0,)f x ax bx cx d a x =+++≠∈R 有极值点,则( ) A . 23b ac ≤B. 23b ac ≥ C . 23b ac <D . 23b ac >6. 一个几何体的三视图如图,则该几何体的体积为( )A .13B.23C .2D .17. △ABC 中,角,,A B C 成等差数列是sin sin )cos C A A B =+成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件8. 在弹性限度内,弹簧所受的压缩力F 与缩短的距离l 按 胡克定律F kl =计算.今有一弹簧原长80cm ,每压缩1cm 需0.049N 的压缩力,若把这根弹簧从70cm 压缩至50cm (在弹性限度内),外力克服弹簧的弹力做了( )功(单位:J ) A .0.196B .0.294C .0.686D .0.989.在正方体1111ABCD A B C D -中,E 是棱1CC 的中点,F 是侧面11BCC B内的动点,且1A F ∥平面1D AE ,记1A F 与平面11BCC B 所成的角为θ,下列说法错误的是( )A .点F 的轨迹是一条线段 B.1A F 与1D E 不可能平行 C . 1A F 与BE 是异面直线 D .tan θ≤12. 已知正三角形内切圆的半径r 与它的高h 的关系是:13r h =,把这个结论推广到空间正四面体,则正四面体内切球的半径r 与正四面体高h 的关系是_________. 13. 将函数sin(2)y x ϕ=+的图象向左平移4π个单位后得到的函数图象关于点4(,0)3π成中心对称,那正(主)视图 侧(左)视俯 视 图第6题1F么||ϕ的最小值为________. 14. 无穷数列{}n a 中,12,,,m a a a 是首项为10,公差为2-的等差数列;122,,,m m m a a a ++是首项为12,公比为12的等比数列(其中*3,m m ∈N ≥),并且对于任意的*n ∈N ,都有2n m n a a +=成立.若51164a =,则m 的取值集合为____________.记数列{}n a 的前n 项和为n S ,则使得12852013m S +≥ *3,)m m ∈(N ≥的m 的取值集合为____________.(二)选考题(请考生在15、16两题中任选一题作答.如果全选,则按第15题作答结果计分)在极坐标系中,曲线1:4C ρ=上有3个不同的点到曲线2:sin()4C m ρθ+=的距离等于2,则______m =.(Ⅱ)求函数()f x 在[0,2]π上的单调递增区间.18.(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,满足:2418,a a +=791S =.递增的等比数列{}n b 前n 项和为n T ,满足:12166,128,126k k k b b b b T -+===. (Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)设数列{}n c 对*n ∀∈N ,均有12112nn nc c c a b b b ++++=成立,求122013c c c +++.19.(本小题满分12分)如图,在直三棱柱111ABC A B C -中,底面△ABC 为等腰直角三角形,90ABC ∠=,D 为棱1BB 上一点,且平面1DA C ⊥平面11AA C C .(Ⅰ)求证:D 为棱1BB 的中点;(Ⅱ)ABAA 1为何值时,二面角1A A D C --的平面角为60. BA 1B 1C 1D20.(本小题满分12分)如图,山顶有一座石塔BC ,已知石塔的高度为a .(Ⅰ)若以,B C 为观测点,在塔顶B 处测得地面上一点A 的俯角为α,在塔底C 处测得A 处的俯角为β,用,,a αβ表示山的高度h ;(Ⅱ)若将观测点选在地面的直线AD 上,其中D 是塔顶B 在地面上的射影. 已知石塔高度20a =,当观测点E 在AD 上满足DE =BC 的视角(即BEC ∠)最大,求山的高度h .21.(本小题满分13分)已知n a 是关于x 的方程1210n n n x x x x --++++-=(0,2)x n n >∈N 且≥的根,证明:(Ⅰ)1112n n a a +<<<; (Ⅱ)11()22n n a <+. 22.(本小题满分14分)已知函数()e 1x f x ax =--(e 为自然对数的底数). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当0a >时,若()0f x ≥对任意的x ∈R 恒成立,求实数a 的值; (Ⅲ)求证:22222232323ln 1ln 1ln 12(31)(31)(31)n n ⎡⎤⎡⎤⎡⎤⨯⨯⨯++++++<⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦.湖北省八校2014届高三第一次联考 理科数学参考答案及评分细则一、选择题(每小题5分,共10小题) 1—5 A C B B D 6—10 B A A B A 二.填空题(每小题5分,共5小题)11. 2π 12. 14r h = 13.6π14.{}45,15,9; {}6 第一个空2分,第二个空3分2m=±三、解答题(共5小题,共75分) 17. (Ⅰ)2()4sin()cos 3f x x x πωω=+1分14sin ()cos cos 22x x x ωωω⎡=⋅-+⋅⎢⎣⎦22sin cos x x x ωωω=-cos2)sin 2x x ωω+-2cos(2)6x πω=++5分 由题意,T π=,2,12ππωω∴== 6分(Ⅱ)()2cos(2)6f x x π=++[]0,2x π∈时,2,4666x ππππ⎡⎤+∈+⎢⎥⎣⎦故[]2,26x πππ+∈或[]23,46x πππ+∈时,()f x 单调递增9分即()f x 的单调增区间为511,1212ππ⎡⎤⎢⎥⎣⎦和1723,1212ππ⎡⎤⎢⎥⎣⎦ 12分18. (Ⅰ)由题意24317742187()7912a a a a a S a +==⎧⎪⎨+===⎪⎩得349,13a a ==,则43n a n =- 2分211k k b b bb -=,1,k b b ∴方程2661280x x -+=的两根,得12,64k b b ==4分111(1)12611k k k b b q b q S q q---===--,12,64k b b ==代入求得2q =,2n n b ∴=6分(Ⅱ)由12112nn nc c c a b b b ++++= 112121(2)n n n c c c a n b b b --+++=≥ 相减有1nn n nc a a b +=-4=22,42n n n n c b +∴≥==, 9分又121c a b =,得110c = 210(1)2(2)n n n c n +=⎧=⎨≥⎩ 122013c c c ∴+++=45201520161022226++++=-12分19.解:(Ⅰ)过点D 作DE ⊥ A 1 C 于E 点,取AC 的中点F ,连BF ﹑EF∵面DA 1 C ⊥面AA 1C 1C 且相交于A 1 C ,面DA 1 C 内的直线DE ⊥ A 1 C故直线DE ⊥面11ACC A3分又∵面BA C ⊥面AA 1C 1C 且相交于AC ,易知BF ⊥AC ,∴BF ⊥面AA 1C 1C 由此知:DE∥BF ,从而有D ,E ,F ,B 共面,又易知BB 1∥面AA 1C 1C ,故有DB∥EF ,从而有EF∥AA 1,又点F 是AC 的中点,所以DB = EF = 21 AA 1 = 21 BB 1, 即D 为1BB 的中点(Ⅱ)解法1:建立如图所示的直角坐标系,设AA 1 = 2b ,AB =BC =a ,则D (0,0,b ), A 1 (a ,0,2b ), C (0,a ,0)所以,),,0(),,0,(1b a b a -==设面DA 1C 的法向量为),,(z y x = 则0,00=-+⋅=+⋅+bz ay x bz y ax可取),,(a b b --= 8分 又可取平面AA 1DB 的法向量)0,,0(a == cos ,m n u r r 222222200ab b aa b a ba b +-=⋅+⋅--⋅==据题意有:21222=+a b b解得: ABAA 1=22=ab12分 (Ⅱ)解法2:延长A 1 D 与直线AB 相交于G ,易知CB ⊥面AA 1B 1B ,过B 作BH ⊥A 1 G 于点H ,连CH ,由三垂线定理知:A 1 G ⊥CH ,由此知∠CHB 为二面角A -A 1D - C 的平面角; 9分设AA 1 = 2b ,AB =BC =a ;在直角三角形A 1A G 中,易知AB = BG . 在∆Rt DBG 中,BH =DGBGBD ⋅ = 22ba ab +⋅,在∆Rt CHB 中,tan ∠CHB = BHBC = b b a 22+,据题意有:bb a 22+ = tan 600= 3 ,解得:22=a b 所以 ABAA112分20. 解:(1)在△ABC 中,BAC αβ∠=-,90BCA β∠=+,由正弦定理得:sin sin BC ABBAC BCA=∠∠sin(90)cos sin()sin()a a AB ββαβαβ+∴==-- 则cos sin sin sin()a h AB a a βαααβ=⋅-=--=cos sin sin()a αβαβ⋅- 4分(2)设DEx =,20tan h BED x +∠=,tan hCED x∠= tan tan tan 1tan tan BED CEDBEC BED CED∠-∠∴∠=+∠⋅∠ 6分22020(20)(20)1x h h h h x x x ==++++≤当且仅当(20)h hx x+=即x tan BEC ∠最大,从而BEC ∠最大=180h = 12分 21. (Ⅰ)设12()1n n n f x x x x x --=++++-,则'12()(1)21n n f x nx n x x --=+-+++显然'()0f x >,()f x ∴在R +上是增函数(1)10(2)f n n =->≥11(1())122()11212n f -=--1()02n =-< ()f x ∴在1(,1)2上有唯一实根,即112n a << 4分假设1n n a a +≥,*1()k k n n a a k N +∴≥∈则1()n f a +=111111111n n n n n n n n n n n n a a a a a a a ++-+++++++-≥++++-11n n n n n a a a ->+++-()n f a =1()()0n n f a f a +==,矛盾,故1n n a a +<8分(Ⅱ)111111()()1()()()12222n n n n n n n n f a f a a a --⎡⎤-=+++--+++-⎢⎥⎣⎦11111(())(())()222n n n n n n n a a a ---+-++-12n a >- (12n a >)()0n f a =,11()()22n f =-11()22n n a ∴<+13分方法二:121n n n n n n a a a a --=+++由(Ⅰ)1na -=12n n n n n a a a -+++12111()()()222n n ->+++=11()22n -11()22n n a ∴<+22 (Ⅰ)'()x f x e a =-1分 0a ∴≤时,'()0f x >,()f x 在R 上单调递增。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014届湖北百所重点中学高三联考数学模拟试题考察范围 :集合与逻辑、函数与导数60%;三角函数40%★ 祝考试顺利 ★一、选择题:本大题共10小题,每题5分,共50分.在每小题给出的四个选项中,只有一个符合一目要求的.1.集合A={}1610-2-+=x x y x ,集合B={}A x x y y ∈=,log 2,则=⋂BC A R ( ) A.[]32, B.(]21, C.[]83, D.(]83,2.若命题p:[]012,3,3-0200≤++∈∃x x x ,则对命题p 的否定是( )A []012,3,3-0200>++∈∀x x xB ()()012,,33-,-0200>+++∞∞∈∀x x x C. ()()012,,33-,-0200≤+++∞∞∈∃x x x D. []012,3,3-0200<++∈∃x x x3.曲线sin ,cos 2y x y x π==和直线x=0,x=所围成的平面区域的面积为( )()20.sin cos A x x dx π-⎰()40.2sin cos B x x dx π-⎰()20.cos sin C x x dx π-⎰ ()40.2cos sin D x x dx π-⎰4.函数3()33x f x =-的值域为( )A .(,1)-∞-B .(1,0)(0,)-+∞C .(1,)-+∞D .(,1)(0,)-∞-+∞5.在ABC ∆中,,3,23sin )(sin AC BC C B A ==+-则=∠B ( ) A.3π B.6π C.36ππ或 D.2π6.已知R c b a ∈,,,则1632222=++c b a 是[]1,1-∈++c b a 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.定义行列式运算1234a a a a =1423a a a a -. 将函数3sin ()1cos x f x x=的图象向左平移n (0n >)个单位,所得图象对应的函数为偶函数,则n 的最小值为( )A .6pB .3pC .56pD .23p 8.定义在R 上的函数()f x 的图象关于点3(,0)4-成中心对称,对任意的实数x 都有3()()2f x f x =-+,且(1)1,f -=(0)2f =-,则f(1)+f(2)+f(3)+.....+f(2014)的值为( ) A .2-B .1-C .0D .19.已知函数()()()()222222,228.f x x a x a g x x a x a =-++=-+--+设()()(){}()()(){}{}()12max ,,min ,,max ,H x f x g x H x f x g x p q ==表示,p q 中的较大值,{}min ,p q 表示,p q 中的较小值,记()1H x 得最小值为,A ()2H x 得最大值为B ,则A B -=( )A .2216a a -- B .2216a a +- C .16- D .1610.已知函数⎩⎨⎧<≥=)0()-(log )0(3)(3x x x x f x ,函数)()()()(2R t t x f x f x g ∈++=.关于)(x g 的零点,下列判断不正确...的是( ) A.若)(,41x g t =有一个零点 B.若)(,412-x g t <<有两个零点 C.若)(,2-x g t =有三个零点 D.若)(,2-x g t <有四个零点二、填空题:本大题共5小题,每小题5分,共25分. 11.函数)13lg(13)(2++-=x xx x f 的定义域是 ___________ ;12.若E ,F 是等腰直角△ABC 斜边AB 上的三等分点,则ECF an ∠t =________. 13..2sin 120⎰-πdx x 求___________ ;14.若函数)(log )(3ax x x f a -=)1,0(≠>a a 在区间21(-,0)内单调递增,则a 取值范围是______15.如题(15)图,图中的实线是由三段圆弧连接而成的一条封闭曲线C ,各段弧所在的圆经过同一点P (点P 不在C 上)且半径相等. 设第i 段弧所对的圆心角为(1,2,3)i i α=,则232311coscossinsin3333αααααα++-=____________ .三、解答题:16.(本小题满分12分)设命题p :函数f (x )=x 3-ax -1在区间[-1,1]上单调递减;命题q :函数y =ln(x 2+ax +1)的值域是R.如果命题p 或q 为真命题,p 且q 为假命题,求a 的取值范围. 17(本小题满分12分)已知向量2(cos ,1),(3sin ,cos )222x x xm n =-=,设函数()f x m n =∙+1 (1).若[0,]2x π∈, 11()10f x =,求cos x 的值;(2).在△ABC 中,角A ,B ,C 的对边分别是,,a b c ,且满足2cos 23b A c a ≤-,求()f x 的取值范围.18.(本小题满分12分)已知函数2()25(1)f x x ax a =-+>.(1 ).若函数()f x 的定义域和值域均为[1,]a ,求实数a 的值;(2).若()f x 在区间(],2-∞上是减函数,且对任意的[]12,1,1x x a ∈+,总有12()()4f x f x -≤,求实数a 的取值范围;19.(本小题满分12分)定义在R 上的奇函数()f x 有最小正周期4,且()0,2x ∈时,3()91xx f x =+。
(1).求()f x 在[]2,2-上的解析式;(2).判断()f x 在()0,2上的单调性,并给予证明;(3).当λ为何值时,关于方程()f x λ=在[]2,2-上有实数解?20.(本小题满分13分) 如图:某污水处理厂要在一个矩形污水处理池()ABCD 的池底水平铺设污水净化管道FHE Rt ∆(,H 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H 是AB 的中点,,E F 分别落在线段,BC AD 上.已知20AB =米,103AD =米,记BHE θ∠=.(1).试将污水净化管道的长度L 表示为θ的函数,并写出定义域; (2).若sin cos 2θθ+=,求此时管道的长度L ;(3).问:当θ取何值时,污水净化效果最好?并求出此时管道的长度.21.(本小题满分14分)已知函数1)1()(-+=tx x f 的定义域为()+∞,1-,其中实数t 满足10≠≠t t 且.直线:l )(x g y =是)(x f 的图像在0=x 处的切线.(1).求l 的方程:)(x g y =;(2).若)()(x g x f ≥恒成立,试确定t 的取值范围; (3).若()1,0,21∈a a ,求证:12212121aaaaa a a a +≥+.注:当α为实数时,有求导公式1-='αααx x )(.2014届湖北百所重点中学高三联考数学模拟试题参考答案一、选择题:题号 12345678910答案D A D D B A C D C D二、填空题:11、)(1 1/3-, 12、43 13、2-22 14、)[1,4/3 15、21三、解答题: 16.解:p 为真命题⇔f ′(x )=3x 2-a ≤0在[-1,1]上恒成立⇔a ≥3x 2在[-1,1]上恒成立⇔a ≥3.q 为真命题⇔Δ=a 2-4≥0恒成立⇔a ≤-2或a ≥2. 由题意p 和q 有且只有一个是真命题.p 真q 假⇔⎩⎪⎨⎪⎧a ≥3,-2<a <2⇔a ∈∅,p 假q 真⇔⎩⎪⎨⎪⎧a <3,a ≤-2或a ≥2⇔a ≤-2或2≤a <3.综上可知:a ∈(-∞,-2]∪[2,3).231cos 161()3sin cos cos 1sin 1222223111sin cos sin()22262x x x xf x x x x x π+=-+=-+=-+=-+、解:()∵11()10f x =,∴3sin()65x π-=;又∵[0,]2x π∈,∴[,]663x πππ-∈-,即4cos()65x π-=433cos cos[()]cos()cos sin()sin 6666661010x x x x ππππππ∴=-+=---=-22bcosA 2c 2sin cos 2sin 3sin 2sin cos 2sin()3sin 2sin cos 2[sin cos cos sin ]3sin 32sin cos 3sin cos (0,]26B A c A B A A B AB A A B A B A A B A B B π≤≤-⇒≤+-⇒≤+-⇒≥⇒≥⇒∈()由-得: ∴1sin()(,0]62B π-∈-,即11()sin()()(0,]622f B B f B π=-+⇒∈18.(1)52)(2+-=ax x x f 在],(a -∞上的减函数, ∴52)(2+-=ax x x f 在[1,]a 上单调递减 a f x f ==∴)1()(max 且1)()(min ==a f x f2=∴a(2) ()f x 在区间(],2-∞上是减函数,2≥∴a )(x f ∴在],1[a 上单调递减,在]1,[+a a 上单调递增2min 5)()(a a f x f -==∴,{})1(),1(max )(max +=a f f x f 0)2(2)6(26)1()1(22≥-=-=---=+-a a a a a a a f f a f x f 26)1()(max -==∴对任意的[]12,1,1x x a ∈+,总有12()()4f x f x -≤4)()(min max ≤-∴x f x f , 即31≤≤-a 又 2≥a ,32≤≤∴a19. 解:(1)(0)0,(2)(24)(2),(2)= -(2)f f f f f f =-=-+=-又(2)(2)=0f f ∴-= (1)分当20x -<<时,0-2x <<,故()(-)f x f x =-=193193+-=+---x xx x ………………3分⎪⎪⎩⎪⎪⎨⎧∈+-=-∈+-=∴).2,0(,193.2,2,0,0)0,2(,193)(x x x x f xxxx (4)(2)任取1212,(0,2)x x x x ∈<且,12121212121233(33)(13)()()1919(19)(19)x x x x x x x x x x f x f x +---=-=++++……………………6分因为1212,(0,2)x x x x ∈<且故12330x x -<,12130x x +-<,12(19)(19)x x ++>012()()0f x f x ∴-> 故f(x)在(0,2)上单调递减。
