第五届中国东南地区高中数学奥林匹克竞赛试题(缺答案)
中国数学奥林匹克第五届试题

第五届中国数学奥林匹克(1990年)1.如下图,在凸四边形ABCD中,AB与CD不平行,圆O1过A、B且与边CD相切于P,圆O2过C,D且与边AB相切于Q,圆O1与O2相交于E、F。
求证:EF平分线段PQ的充要条件是BC//AD。
2.设x是一个自然数,若一串自然数x0=1,x2, ... , x n=x满足x i-1<i=1,2, ...,l,则称{ x0 , x1 , ... , x n}为x的一条因子链。
l称为该因子链的长度。
L(x)与R(x)分别表示x的最长因子链的长度和最长因子链的条数。
对于x=5k×31m×1990n,k、m、n都是自然数,试求L(x)与R(x)。
3.设函数f(x)对x>0有定义,且满足条件:i.对任何x、y≧0,f(x)f(y)≦x2 f(x/2) +y2 f(y/x);ii.存在常数M>0,当0≦x≦1时,| f(x) | ≦M。
求证:f(x)≦x2。
4.设a是给定的正整数,A和B是两个实数,试确定方程组:x2 +y2 +z2 =(13a)2,x2(Ax2+By2)+y2(Ay2+Bz2)+z2(Az2+Bx2)=(2A+B)(13a)4/3 有整数解的充份必要条件(用A、B的关系式表示,并予以证明)。
5.设X是一个有限集合,法则f使的X的每一个偶子集E(偶数个元素组成的子集)都对应一个实数f(E),满足条件:a.存在一个偶子集D,使得f(D)>1990;b.对于X的任意两个示相交的偶子集A、B,有f(A∪B)=f(A)+f(B)-1990。
求证:存在X的子集P、Q,满足iii.P∩Q是空集,P∪Q=X;iv.对P的任何非空偶子集S,有f(S)>1990v.对Q的任何偶子集T,有f(T)≦1990。
6.凸n边形及n-3条在n边形内不相交的对角线组成的图形称为一个剖分图。
求证:当且仅当3|n时,存在一个剖分图是可以一笔划的圈(即可以从一个顶点出发,经过图中各线段恰一次,最后回到出发点)。
第五届中国东南地区数学奥林匹克竞赛试题(缺答案)
第五届中国东南地区数学奥林匹克
福建龙岩
1.已知集合是正整数,T是S的子集,满足:对任意的(其中可以相同)都有,求所有这种集合T的元素个数的最大值。
2.设数列的表达式。
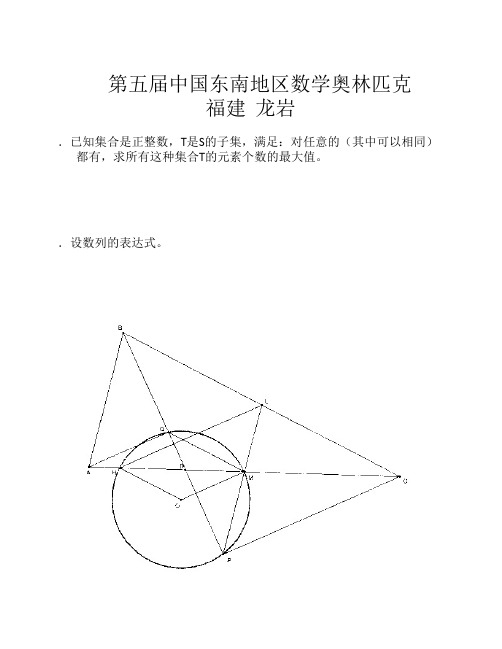
3.在△ABC中,BC>AB,BD平分∠ABC交AC于D,如图,CP垂直BD,垂足为P,AQ垂直BP,Q为垂足。
M是AC中点,E是BC中点。
若△PQM的
外接圆O与AC的另一个交点为H。
求证:O、H、E、M四点共圆。
4.设正整数,取每一对不同的数、个差按从小到大顺序排成一个数列,称为集合A的“衍生数列”,记为。
衍生数列中能被m整除的数的个数
记为(m).
证明:对于任一正整数所对应的“衍生数列” 及
5.求出最大的正实数成立不等式;
6.如下左图,△ABC的内切圆I分别切BC,AC于点M,N,点E,F分别为边AB,AC的中点,D是直线EF与BI的交点。
证明:M,N,D三点共
线。
7.杰克(Jack)船长与他的海盗们掠夺到6个珍宝箱A1,A2,A3,A4,A5,A6,其中A i内有金币a i枚,互不相等。
海盗们设计了一种箱子的布局图(如上右图),并推派一人和船长轮流拿珍宝箱。
每次可任意拿走不和两个或两个以上的箱子相连的整个箱子。
如果船长最后所取得的金币不少于海盗们所取得的金币,那么船长获胜。
问:若船长先拿,他是否有适当的取法保证获胜?
8.设n为正整数,个数;
(i)每一位数码;
(ii)当
(1)求的值;
(2)确定被13除得的余数。
2019年中国东南地区数学奥林匹克竞赛_PDF压缩

a
单独考虑左边, 左边可以看成是一个 a 的函数, b 为参数, 那么关于 a 取最
小值的时候有
Å
ã
Ç…
å
ab + (1 + b2) + b (b + 1) ≥ 2 ab · b + (1 + b2) (b + 1) = (b + 1)3
a
a
于是我们只需要取 k ≤ (b + 1)3b−2 即可.
设
值得一说的是, 在这个题目中, 对于任何整数 n, 我们可以定义一个新的 函数 fn(a) = f (an), 那么 fn(ab) = f (abn) 要整除 max{ f (an), b} = max{ fn(a), b}. 也就是说 fn 也是一个满足相同性质的函数, 那么实际上, 我们可以证明对任 意一个 k 满足 f (k) = 1, 那么 {mk}∞m=1 中有无限多个 m 满足 f (mk) = 1. 更复 杂的话, 有兴趣的同学可以自行尝试推导一下这个 f (k) = 1 的解的密度.
评析 3. 欧几里德证明素数无限的方法是数论里面很典范的一种证明方式, 在证明某一类数字有无限多个的时候, 通过反证假设这一类数字只有有限 个, 不妨设为 k1 < k2 < . . . < kn, 套路上我们可以考虑 kn, kn + 1, k1k2 . . . kn, k1k2 . . . kn + 1, [k1, k2, . . . , kn] 等数字来找到矛盾, 本题也是如此.
22 2 2
22
Å
b b ã1/3
Å ab ab
ã1/3
Å bb
ã1/3
≥3 a· ·
2023东南数学奥林匹克试题

2023东南数学奥林匹克试题
2023东南数学奥林匹克试题主要包括以下几个部分:
1. 整式与恒等式:涉及多项式的计算和恒等式的问题。
例如,求多项式的值,或者根据多项式的性质求解未知数。
2. 代数与不等式:考察代数方程的解法,以及不等式的性质和证明。
3. 几何:考察平面几何和立体几何的知识点,例如勾股定理、相似三角形、圆的性质等。
4. 组合数学:考察组合数学中的计数、排列、组合等知识点,例如排列组合的公式和性质,以及一些常见的组合数学问题。
5. 概率与统计:考察概率和统计的基本概念和计算方法,例如概率的基本性质、期望和方差等。
具体题目可能包括:
1. 已知函数 f(x) = x^2 - 2x + 3,求 f(3) 的值。
2. 已知二次方程 x^2 - 2x - 3 = 0,求该方程的解。
3. 已知三角形 ABC 的三边长分别为 a、b、c,且 a + b = 7,ab = 10,求三角形 ABC 的面积。
4. 已知有 5 个不同的红球和 3 个不同的白球,从中任取 3 个球,求取出红球个数 x 的分布律。
5. 已知随机变量 X 的分布列为 P(X=1) = ,P(X=2) = ,P(X=3) = ,求 X 的期望和方差。
以上是2023东南数学奥林匹克试题的部分内容,如果您需要完整的试题及答案解析,建议前往相关网站查询。
第五届高一试题(初赛)-“枫叶新希望杯”全国数学大赛真题(高中版)

第五届高一试题(初赛)-“枫叶新希望杯”全国数学大赛真题一、单选题1.满足{},,,M a b c d ⊆且{}{},,,M a b c a b ⋂=的集合M 的个数是( )个.A .1B .2C .3D .42.已知()f x 是R 上的奇函数,()g x 是R 上的偶函数.若()()223f x g x x x -=++,则()()f x g x +=.A .223x x -+-B .223x x +-C .223x x --+D .223x x -+ 3.已知3(N )211n a n n *=∈-,记数列{}n a 的前n 项和为n S ,则使0n S >的n 的最小值为 A .13 B .12 C .11 D .104.设,αβ是锐角三角形的两个互不相等的内角,若()sin cos cos x y αβαβ=+=+,,sin sin z αβ=+,则( ).A .x y z <<B .x y z >>C .x z y <<D .y x z <<5.已知集合(){}2lg 32M x y x x ==-+-,()(){}2244m aN m x x x x =-+<-+,若M 是N 的真子集,则a 的取值范围是( ).A .()2,+∞B .(),2-∞C .[)2,+∞D .(],2-∞6.已知()()()lg 2,21,2x x f x x ⎧-≠⎪=⎨=⎪⎩若关于x 的方程()()20f x bf x c ++=恰有3个不同的实数解123,,x x x ,则()123f x x x ++等于( ).A .0B .lg2C .lg4D .1二、填空题7.设[]x 为不大于x 的最大整数,集合[]{}2|10A x x x =--=,1|242x B x ⎧⎫=<<⎨⎬⎩⎭,则A B ⋂等于. 8.数列{}n a 中113125n n a a a -==-,,则2009a =. 9.cot 20cos10tan 702cos 40-=o o o o o .10.已知实数,x y 满足()()33(1)200912,(1)200912x x y y -+-=--+-=,则x y +=.11.已知()()01log 1log 1x y x y a x b y <<<=+=+,,,则a b ,的大小关系是.12.在不考虑空气阻力的条件下,火箭的最大速度()km /s y 和燃料的质量()kg x 、火箭(除燃料外)的质量()kg m 的函数关系是())4ln ln 2ln2y m x ⎡⎤=+-+⎣⎦,要使火箭的最大速度可达12km /s ,则燃料质量与火箭质量的比值是.三、解答题13.若函数()()2sin cos sin cos f x a x x x x a b =+++的定义域为π0,2⎡⎤⎢⎥⎣⎦,值域为[]5,1-,求,a b . 14.已知函数()f x 满足()()()f x y f x f y +=⋅且1(1)2f =. (1)当*n N ∈时,求()f n 的表达式; (2)设*()n a n f n n N =⋅∈,,求证:1232n a a a a +++⋯+<; 15.设函数()f x 为R 上的增函数,令()()()2F x f x f x =--.(1)判断并证明()F x 在R 上的单调性;(2)若()()120F x F x +>,判断12x x +与2的大小关系并证明;(3)若数列{}n a 的通项公式为1011.5n n a n -=-,试问是否存在正整数n ,使()n F a 取得最值?若存在,求出n 的值;若不存在,请说明理由.16.已知等差数列{}n a 满足()*1212n a a n n -+=∈N ,设n S 是数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和,记()()*2n n f n S S n =-∈N . (1)求n a ;(2)比较()1f n +与()()*f n n ∈N 的大小;(3)如果函数()()[]()2log 12,g x x f n x a b =-∈对一切大于1的正整数n ,其函数值都小于零,那么,a b 应满足什么条件?。
2023东南数学奥林匹克试题

2023东南数学奥林匹克试题摘要:一、前言二、2023 东南数学奥林匹克试题概述1.试题类型及分值2.试题难度及特点三、试题解答1.选择题2.填空题3.解答题四、试题解析1.试题涉及知识点2.解题思路及方法五、总结正文:一、前言2023 年东南数学奥林匹克吸引了众多数学爱好者的关注。
本次竞赛的试题具有较高的难度和挑战性,考验了选手们的数学素养和应变能力。
本文将详细介绍2023 年东南数学奥林匹克的试题内容,并给出试题解析,帮助大家更好地理解和掌握相关知识点。
二、2023 东南数学奥林匹克试题概述1.试题类型及分值2023 年东南数学奥林匹克试题共分为选择题、填空题和解答题三种类型,总分为120 分。
选择题共10 题,每题10 分;填空题共5 题,每题20 分;解答题共3 题,每题40 分。
2.试题难度及特点本届东南数学奥林匹克试题难度较高,知识点覆盖面广,考察了选手们在代数、几何、组合、数论等方面的基本功。
试题具有一定的创新性和灵活性,要求选手具备较强的逻辑思维能力和解决问题的技巧。
三、试题解答1.选择题(1)题目一...(2)题目二...(3)题目三...(4)题目四...(5)题目五...2.填空题(1)题目一...(2)题目二...(3)题目三...(4)题目四...(5)题目五...3.解答题(1)题目一...(2)题目二...(3)题目三...四、试题解析1.试题涉及知识点本届东南数学奥林匹克试题涉及的知识点主要包括:代数、几何、组合、数论等。
要求选手具备扎实的数学基本功和良好的知识体系。
2.解题思路及方法针对不同类型的试题,选手们需要灵活运用各种解题方法,如代数法、几何法、归纳法、组合计数等。
在解题过程中,要注意分析题目条件,挖掘题目中的隐含信息,善于将复杂问题分解为简单问题,逐步求解。
五、总结2023 年东南数学奥林匹克试题充分体现了数学竞赛的特点,既考察了选手们的基本知识,又考验了他们的应变能力和解决问题的技巧。
36第五届陈省身杯全国高中数学奥林匹克

= B A C一2 ( 9 0 。 一 A C B)
2 0 1 4年 第 9期
= A凹 一 A BC.
+
—
3 7
1
+ +
; 2 k+l
则 A H O+ O A H= 9 0 。 . 从而, A O H= 9 0 。 .
A B> A C , 0、 H 分 别 为 △A B C的外 心 、 垂心, 直 线B H与 A C交于 点 B , 直线 C H与 A 交 于 点
C
c 若 O H/ / B C 。 , 证 明:
C O S 2 B +C O S 2 C+l
=
图 1
Q
当且仅 当
0或 +X k 一
l
X k+ x k+
= 0。 且
七十
A= 0时 , 等号成立 , 即 , = =… = .
3 . 先证 明一个引理.
2 . 令{ = —  ̄ 1 — ; 2 2 + ; 2 — 2 — X 3 +… +
3 4
n一 1 n n 1
切线 c . 若 D、 E为 f 上 的两个点 , 且A D= A E, 过 D、
E分 别作 o 0的割 线 D C B、 E G F, 直线 F B、 G C与 2
1 ) .
类似定义 A ( i = 1 , 2 , …, 凡 ; = 1 , 2 , …, n 一 1 ) 记 A A A ( + 1 )= , 其 中, i=1 , 2, …, n ;
= 一 =
—
—
+ 一 十
—
—
+ … 十
+ 十
X2
3
4
东南数学竞赛试题及答案

东南数学竞赛试题及答案1. 代数问题:求解方程 \( ax^2 + bx + c = 0 \) 的根,其中 \( a = 2 \),\( b = 5 \),\( c = 3 \)。
2. 几何问题:在一个圆中,弦AB的长度为10,弦AB上的圆心角为30°。
求圆的半径。
3. 数列问题:给定数列 \( a_n = 2n - 1 \),求前10项的和。
4. 概率问题:一个袋子里有5个红球和3个蓝球。
随机抽取3个球,求至少有2个红球的概率。
5. 组合问题:从10个人中选出5个人组成一个委员会,其中必须包括至少1名女性和至少1名男性。
如果这10个人中有4名女性和6名男性,求所有可能的委员会组合数。
6. 函数问题:给定函数 \( f(x) = x^3 - 3x^2 + 2x \),求 \( f(x) \) 的导数 \( f'(x) \) 并找出其极值点。
7. 极限问题:求极限 \( \lim_{x \to 0} \frac{\sin(x)}{x} \)。
8. 积分问题:计算定积分 \( \int_0^1 (2x + 1)^2 dx \)。
答案1. 代数问题:使用求根公式,\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \),得到 \( x = \frac{-5 \pm \sqrt{25 - 4 \times 2 \times 3}}{4}= \frac{-5 \pm \sqrt{1}}{4} \),解得 \( x_1 = 1 \) 和 \( x_2= -2 \)。
2. 几何问题:根据圆心角和弦的关系,半径 \( r = \frac{AB}{2\sin(\frac{\angle AOB}{2})} = \frac{10}{2 \sin(15^\circ)} \)。
3. 数列问题:数列前10项的和为 \( S_{10} = 1 + 3 + 5 + \ldots + 19 =100 \)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五届中国东南地区数学奥林匹克
1.已知集合n n S },3,,3,2,1{ =是正整数,T 是S 的子集,满足:对任意的T z y x ∈,,(其
中z y x ,,可以相同)都有T z y x ∉++,求所有这种集合T 的元素个数的最大值。
2.设数列n n n n n a n n a a a a 试求通项满足.,3,2,1),21(2,1:}{11 =+⋅+==+的表达式。
3.在△ABC 中,BC>AB ,BD 平分∠ABC 交AC 于D ,如图,CP 垂直BD ,垂足为P ,AQ 垂直
BP ,Q 为垂足。
M 是AC 中点,E 是BC 中点。
若△PQM 的外接圆O 与AC 的另一个交点为H 。
求证:O 、H 、E 、M 四点共圆。
4.设正整数},,,{,2,21n a a a A n n m =≥元整数集对于任一个,取每一对不同的数i a 、2,),(n
i j j C a a i j a 由这作差->个差按从小到大顺序排成一个数列,称为集合A 的“衍生数列”,记为A 。
衍生数列A 中能被m 整除的数的个数记为A (m ).
证明:对于任一正整数},,2,1{},,,{,221n B a a a A n m n ==≥及集合元整数集所对
应的“衍生数列” A 及).()(,m B m A B >满足不等式
5.求出最大的正实数z y x z y x ,,1,222的任何数使得对于满足=++λ成立不等式; .2
5||≤
+yz xy λ
6.如下左图,△ABC 的内切圆I 分别切BC ,AC 于点M ,N ,点E ,F 分别为边AB ,AC 的中点,
D 是直线EF 与BI 的交点。
证明:M ,N ,D 三点共线。
7.杰克(Jack )船长与他的海盗们掠夺到6个珍宝箱A 1,A 2,A 3,A 4,A 5,A 6,其中A i 内有
金币a i 枚,i a i 诸,6,5,4,3,2,1=互不相等。
海盗们设计了一种箱子的布局图(如上右图),并推派一人和船长轮流拿珍宝箱。
每次可任意拿走不和两个或两个以上的箱子相连的整个箱子。
如果船长最后所取得的金币不少于海盗们所取得的金币,那么船长获胜。
问:若船长先拿,他是否有适当的取法保证获胜?
8.设n 为正整数,n a a a n n f 21)()(称为波形数位数表示满足以下条件的个数; (i )每一位数码 ,2,1,},4,3,2,1{1=≠∈+i a a a i i i 且;
(ii )当.,2,1,,3211 =--≥+++i a a a a n i i i i 的符号相反与时
(1)求)10(f 的值;
(2)确定)2008
(f 被13除得的余数。
