2016年高考(326)安徽合肥一中2016届上期高三段三考试
安徽省合肥市第一中学2016届高三上学期段三考试数学(理)试题
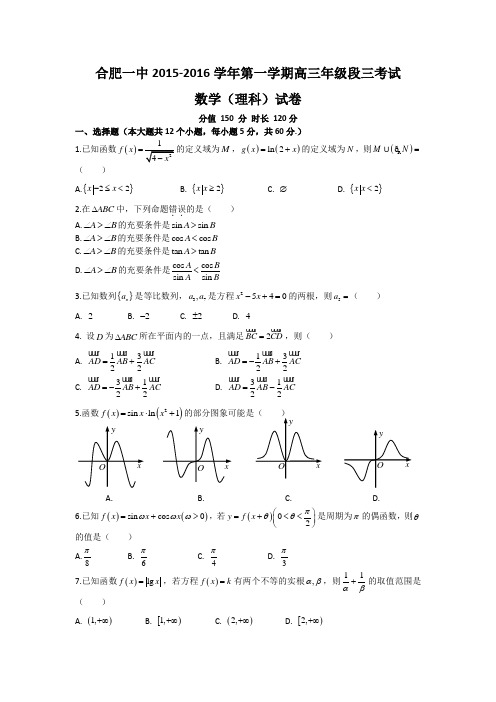
合肥一中2015-2016学年第一学期高三年级段三考试数学(理科)试卷分值 150 分 时长 120分一、选择题(本大题共12个小题,每小题5分,共60分.)1.已知函数()f x =M ,()()ln 2g x x =+的定义域为N ,则()R M N =ð( ) A.{}22x x -≤<B. {}2x x ≥C. ∅D. {}2x x <2.在ABC ∆中,下列命题错误..的是( ) A.A B ∠>∠的充要条件是sin sin A B > B.A B ∠>∠的充要条件是cos cos A B < C.A B ∠>∠的充要条件是tan tan A B > D.A B ∠>∠的充要条件是cos cos sin sin A BA B<3.已知数列{}n a 是等比数列,37,a a 是方程2540x x -+=的两根,则5a =( ) A. 2B. 2-C. 2±D. 44. 设D 为ABC ∆所在平面内的一点,且满足2BC CD =,则( ) A. 1322AD AB AC =+B. 1322AD AB AC =-+C. 3122AD AB AC =-+D. 3122AD AB AC =-5.函数()()2sin ln 1f x x x =⋅+B. C.D.6.已知()()sin cos 0f x x x ωωω=+>,若()02y f x πθθ⎛⎫=+<< ⎪⎝⎭是周期为π的偶函数,则θ的值是( )A.8π B.6π C.4π D.3π 7.已知函数()lg f x x =,若方程()f x k =有两个不等的实根,αβ,则11αβ+的取值范围是( ) A. ()1,+∞B. [)1,+∞C. ()2,+∞D. [)2,+∞8.若变量,x y 满足约束条件32122120,0x y x y x y x y -≥-⎧⎪+≤⎪⎨+≤⎪⎪≥≥⎩,则34z x y =+的最大值是( )A.12B.26C.28D.33 9. 已知sin 23sin 2αβ=,则()()tan tan αβαβ-=+( )A.2B.34C.32D.1210.设()()312f x x x =-++,{}n a 是公差为12的等差数列,且()()()()1234f a f a f a f a +++()5f a +()618f a +=,则1a =( )A.14-B. 74-C. 54-D. 34-11.已知数列{}n a 满足()*123N n n a a n ++=∈,且14a =,其前n 项和为n S ,则满足不等式1230n S n --<的最小整数n 是( ) A.5 B.6 C.7D.812. 设()()()ln 01f x ax a =<<,过点(),0P a 且平行于y 轴的直线与曲线():C y f x =的交点为Q ,曲线C 在点Q 处的切线交x 轴于点R ,则PQR ∆的面积的最大值是( ) A.1B.24e C.12D.28e 二、填空题(本大题共4个小题,每小题5分,共20分.) 13.若函数()()x x f x x e ae -=+是偶函数,则a =________.14.已知向量,a b 的夹角为56π,且2a =,b = 23c a b =+ ,则c = ________.15.设数列{}n a 满足1412n n n a a a +-=+,则首项1a =________时,此数列只有10项.16.定义函数()f x x x =<⋅<>>,其中x <>表示不小于x 的最小整数,如 1.32<>=,2.12<->=-,当(]()*0,N x n n ∈∈时,函数()f x 的值域为n A ,记集合n A 中的元素的个数为n a ,则122015111a a a +++= ________.三、解答题(解答应写出必要的文字说明、证明及演算步骤.) 17.(本小题满分12分)数列{}n a 满足:122a a ==,2122n n n a a a ++=-+. (Ⅰ)设1n n n b a a +=-,证明{}n b 是等差数列; (Ⅱ)求数列{}n a 的通项公式.18.(本小题满分12分)已知ABC ∆三个角,,A B C 所对的边分别为,,a b c ,且,,a b c 成等比数列. (Ⅰ)求角B 的取值范围;(Ⅱ)设()3sin 4cos f x x x =+,求()f B 的最大值及()f B 取得最大值时tan B 的值.19.(本小题满分12分)已知()ln f x x x =,()32g x x ax =+. (Ⅰ)讨论函数()g x 的极值点的个数;(Ⅱ)若不等式()()2f x g x '≤在()0,x ∈+∞上恒成立,求实数a 的取值范围.20.(本小题满分12分)设n S 是数列{}n a 的前n 项和,且11a =,0n a ≠,()222*12,Nn n n S n a S n n -=+≥∈. (Ⅰ)证明()*22N n n a a n +-=∈;(Ⅱ)若3log n n a b =,求数列{}n n a b ⋅的前n 项和n T .21.(本小题满分12分) 设()()1x f x a x e =--.(Ⅰ)当0x >时,()0f x <,求实数a 的最大值;(Ⅱ)设()1x e g x x-=,11x =,()()1*N n x n e g x n +=∈,证明()*11N 2n n n x x n +>>∈.请考生在22-24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目的题号涂黑.把答案填在答题卡上. 22.(本小题满分10分)选修4-1:几何证明选讲如图,AB 是O 的直径,弦,BD CA 的延长线相交于点E ,EF 垂直BA 的延长线于点F ,求证: (Ⅰ)DEA DFA ∠=∠;(Ⅱ)2AB BE BD AE AC =⋅-⋅.23.(本小题满分10分)选修4-4:坐标系与参数方程 在直角坐标系xOy 中,直线1C 的参数方程为12x t y t =+⎧⎨=+⎩(t 为参数),以该直角坐标系的原点O 为极点,x 轴的非负半轴为极轴的极坐标系下,圆2C的方程为2cos ρθθ=-+.(Ⅰ)求直线1C 的普通方程和圆2C 的圆心的极坐标; (Ⅱ)设直线1C 和圆2C 的交点为,A B ,求弦AB 的长. 24.(本小题满分10分)选修4-5:不等式选讲已知函数()()2R f x m x m =--∈,且()20f x +≥的解集为[]1,1-. (Ⅰ)求实数m 的值; (Ⅱ)若,,a b c 为正实数,且11123m a b c++=,求证239a b c ++≥.A B O ∙DCE F合肥一中2015-2016学年第一学期高三年级段三考试数学(理科)试卷参考答案一、选择题二、填空题13.1-;15.710;16.20151008. 三、解答题17.(1)11212,0n n b b b a a +-==-=,所以数列{}n b 是以为0首项,2为公差的等差数列. (2)由(1)可知2(1)n b n =-,累加可得234n a n n =-+18.(1)由条件可知2b ac =所以222221cos 222a cb ac ac B ac ac +-+-==≥,所以03B π<≤.(2)()5sin()f x x ϕ=+,其中43sin ,cos 55ϕϕ== 所以()5sin()f B B ϕ=+,32ππϕ<<,50336B B ππϕπ<≤∴<+≤ 可知当2B πϕ+=时,max ()5f B =.此时cos 3tan sin 4B ϕϕ== 19.(1)2()3210g x x ax '=++=的判别式2412a ∆=-.①当a ≤≤24120a ∆=-≤,()0g x '≥, 所以()y g x =在R 单调递增,无极值,无极值点.②当a <a >0∆>所以2()3210g x xax '=++=有两个不等的实根12,x x ,则12x x =<=列表:根据表格可知此时函数()x g 有两个极值点,极大值点1x ,极小值点2x .(2)即:123ln 22++≤ax x x x 对()+∞∈,0x 上恒成立可得x x x a 2123ln --≥对()+∞∈,0x 上恒成立 设()xx x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=令()0'=x h ,得31,1-==x x (舍)当10<<x 时,()0'>x h ;当1>x 时, ()0'<x h∴当1=x 时,()x h 取得最大值, ()x h max =-2,2-≥∴a .a ∴的取值范围是[)+∞-,2.20.(1).当2n ≥时,由已知得2221nn n S S n a --= 因为10n n n a S S -=-≠,所以21n n S S n -+=. …………………………①于是21(1)n n S S n ++=+. …………………………………………………②由②-①得:121n n a a n ++=+.……………………………………………③于是2123n n a a n +++=+.……………………………………………………④由④-③得:22(2)n n a a n +-=≥.………………………………………⑤由①有214S S +=,所以22a =.由③有235a a +=,所以33a =,311a a ∴-=所以:*22()n n a a n N +-=∈(2)由(1)可知:数列21{}k a -和2{}k a 分别是以1,2为首项,2为公差的等差数列. 所以22(1)22ka k k =+-⨯=,211(1)221k a k k -=+-⨯=-*()n a n n N ∴=∈,3,3n n n n n b a b n ∴=⋅=⋅由错位相减法可得到:1(21)334n n n T +-⋅+=21.(1)()(1)e x f x a x '=--,令()0f x '=得:1x a =- 当10a -≤时,'()0f x ≤在0>x 时恒成立,所以()y f x =在上(0,)+∞单调递减;()(0)10f x f a ∴<=-≤ 即当0>x 时,0<)(x f 成立当10a ->时,()y f x =在(0,1)a -上单调递减增,在(1,)a -+∞单调递减;0010,()(0)10x a f x f a ∴∃=->>=->与0>x 时,0<)(x f 矛盾,以实数a 的最大值为1.23.(Ⅰ)由1C 的参数方程消去参数t 得普通方程为10x y -+=圆2C 的直角坐标方程22(1)(4x y ++-=,所以圆心的直角坐标为(-,因此圆心的一个极坐标为2(2,)3π.(答案不唯一,只要符合要求就给分)(Ⅱ)由(Ⅰ)知圆心(-到直线10x y -+=的距离d所以AB ==. 24.解:(1) ∵ f(x +2)=m -|x|≥0,∴ |x|≤m , ∴ m≥0,-m≤x≤m ,∴ f(x +2)≥0的解集是[-1,1],故m =1.(2)由(1)知1a +12b +13c=1,a 、b 、c ∈R+,由柯西不等式得a +2b +3c =(a +2b +3c)⎝⎛⎭⎫1a +12b +13c ≥(a·1a +2b·12b +3c·13c)2=9. 另解:1112332()(23)3()()()9232323a b a c c b a b c a b c b a c a b c ++++=++++++≥当且仅当"23"a b c ==时,取等号.。
安徽省合肥市2016年高三第三次教学质量检测语文试题Word版含解析

合肥市2016年高三第三次教学质量检测语文试题第I卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1--3题。
人和其他动物所不同的。
是具有学习的能力。
人的行为方式并不固执地受着不学而能的生理反应所支配。
所谓“学”就是在出生之后以一套人为的行为方式作模型,把本能的那一套方式加以改造的过程。
学的方法是“习”。
“习’’是指反复地做,靠时间中的磨练,使一个人惯于一种新的做法。
因之,学习必须打破个人今昔之隔。
这是靠了我们人类的一种特别发达的能力。
时间中的桥梁——记忆。
在动物的学习过程中,我们也可以说它们有记忆,但是它们的“记忆”是在简单的生理水准上。
一个小白老鼠在迷宫里学得了捷径,它所学得的是一套新的生理反应。
和人的学习不相同的是,它们并不靠一套象征体系的。
人固然有很多习惯,在本质上是和小白老鼠走迷宫一般的,但是他却时常多一个象征体系帮他的忙。
所谓象征体系中最重要的是“词”。
我们不断地在学习时说着话,把具体的情境抽象成一套能普遍应用的概念,概念必然是用词来表现的,于是我们靠着词,使我们从特殊走上普遍,在个别情境中搭下了桥梁;又使我们从当前走到今后,在片刻情境中搭下了桥梁。
从这方面看去,一个动物和时间的接触,可以说是一条直线的,而人和时间的接触,却比一条直线来得复杂。
他有能力闭了眼睛置身于“昔日”的情境中,人的“当前”中包含着从“过去”拔萃出来的投影,即时间的选择累积。
一个依本能而活动的动物不会发生时间上阻隔的问题,它的寿命是一联串的“当前”。
但是人却不然,人的“当前’’是整个靠记忆所保留下来的“过去”的累积。
如果记忆消失了,我们的“时间”就可以说是阻隔了。
人有此能力是事实,人利用此能力,发展此能力,还是因为他“当前”的生活必须有着“过去,,所传下来的办法。
人的学习是向一套已有方式的学习,唯有学会了这套方式才能在人群中生活下去。
这套方式并不是每个人个别的创制,而是社会的遗业。
小白老鼠并不向别的老鼠学习,每只老鼠都得自己在具体情境里,从“试验错误”的过程中,得到个别的经验,它们并不能互相传递经验,互相学习。
封常清阅读答案

封常清阅读答案【篇一:2016届安徽省合肥市高三第三次教学质量检测语文试题(word)】ass=txt>语文试题第i卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1--3题。
人和其他动物所不同的。
是具有学习的能力。
人的行为方式并不固执地受着不学而能的生理反应所支配。
所谓?学?就是在出生之后以一套人为的行为方式作模型,把本能的那一套方式加以改造的过程。
学的方法是?习?。
?习’’是指反复地做,靠时间中的磨练,使一个人惯于一种新的做法。
因之,学习必须打破个人今昔之隔。
这是靠了我们人类的一种特别发达的能力。
时间中的桥梁——记忆。
在动物的学习过程中,我们也可以说它们有记忆,但是它们的?记忆?是在简单的生理水准上。
一个小白老鼠在迷宫里学得了捷径,它所学得的是一套新的生理反应。
和人的学习不相同的是,它们并不靠一套象征体系的。
人固然有很多习惯,在本质上是和小白老鼠走迷宫一般的,但是他却时常多一个象征体系帮他的忙。
所谓象征体系中最重要的是?词?。
我们不断地在学习时说着话,把具体的情境抽象成一套能普遍应用的概念,概念必然是用词来表现的,于是我们靠着词,使我们从特殊走上普遍,在个别情境中搭下了桥梁;又使我们从当前走到今后,在片刻情境中搭下了桥梁。
从这方面看去,一个动物和时间的接触,可以说是一条直线的,而人和时间的接触,却比一条直线来得复杂。
他有能力闭了眼睛置身于?昔日?的情境中,人的?当前?中包含着从?过去?拔萃出来的投影,即时间的选择累积。
一个依本能而活动的动物不会发生时间上阻隔的问题,它的寿命是一联串的?当前?。
但是人却不然,人的?当前’’是整个靠记忆所保留下来的?过去?的累积。
如果记忆消失了,我们的?时间?就可以说是阻隔了。
人有此能力是事实,人利用此能力,发展此能力,还是因为他?当前?的生活必须有着?过去,,所传下来的办法。
人的学习是向一套已有方式的学习,唯有学会了这套方式才能在人群中生活下去。
2016-2017学年安徽省合肥一中高三(上)第三次段考数学试卷(文科)

2016-2017学年安徽省合肥一中高三(上)第三次段考数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A=,B={x|x2<2x},则“x∈A∩B”是“x∈(0,1)”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件2.(5分)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了()A.24里B.48里C.96里D.192里3.(5分)将函数f(x)=sinx﹣cosx的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是()A.B. C.D.4.(5分)已知一个几何体的三视图如图所示,则该几何体的体积为()A.27﹣B.18﹣C.27﹣3πD.18﹣3π5.(5分)已知向量与的夹角为60°,|=2,|=6,则2在方向上的投影为()A.1 B.3 C.5 D.76.(5分)如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后x分钟,瓶内液面与进气管的距离为h厘米,已知当x=0时,h=13.如果瓶内的药液恰好156分钟滴完.则函数h=f(x)的图象为()A.B.C.D.7.(5分)已知数列{a n}是公比为2的等比数列,数列{b n}是公差为3且各项均为正整数的等差数列,则数列{a}是()A.公差为5的等差数列B.公差为6的等差数列C.公比为6的等比数列D.公比为8的等比数列8.(5分)若α∈(,π),3cos2α=sin(﹣α),则sin2α的值为()A.B.﹣C.D.﹣9.(5分)已知f(x)是定义在R上周期为4的奇函数,当x∈[﹣2,0)时,f (x)=2x+log2(﹣x),则f(2017)=()A.B.C.﹣2 D.210.(5分)已知不等式|y+4|﹣|y|≤2x+对任意实数x,y都成立,则常数a 的最小值为()A.1 B.2 C.3 D.411.(5分)已知函数f(x)的定义域为R,对任意x1<x2,有>﹣1,且f(1)=1,则不等式f(log2|3x﹣1|)<2﹣log2|3x﹣1|的解集为()A.(﹣∞,0)B.(﹣∞,1)C.(﹣1,0)∪(0,3)D.(﹣∞,0)∪(0,1)12.(5分)已知函数f(x)=x(lnx﹣ax)有两个极值点,则实数a的取值范围是()A.(﹣∞,0)B.(0,)C.(0,1) D.(0,+∞)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若变量x,y满足约束条件,则z=3x+y的取值范围是.14.(5分)已知△ABC是边长为2的等边三角形,点D、E分别是边AB、BC的中点,点F为DE中点,则=.15.(5分)数列{a n}满足a n+1=,a1=,S n为{a n}的前n项和,则S2016=.16.(5分)在△ABC中,边AB的垂直平分线交边AC于D,若C=,BC=8,BD=7,则△ABC的面积为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)已知数列{a n}的前n项和为S n,且2S n=1﹣a n(n∈N*).(1)求数列{a n}的通项公式;(2)设,记数列{a n b n}的前n项和为T n,求证:T n<.18.(12分)已知向量,,函数f(x)=cos2x.(1)求函数f(x)的解析式及其单调递增区间;(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若c=且f(C)=0,求△ABC周长的取值范围.19.(12分)在如图所示的几何体中,D是AC的中点,EF∥DB.(Ⅰ)已知AB=BC,AE=EC,求证:AC⊥FB;(Ⅱ)已知G,H分别是EC和FB的中点,求证:GH∥平面ABC.20.(12分)某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似地表示为:y=,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.(Ⅰ)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?(Ⅱ)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?21.(12分)已知函数f(x)=x2﹣(a+2)x+alnx,其中a∈R.(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线的斜率为1,求a的值;(Ⅱ)求函数f(x)的单调区间.22.(12分)已知函数f(x)=(ax2+x+2)e x(a>0),其中e是自然对数的底数.(1)当a=2时,求f(x)的极值;(2)若f(x)在[﹣2,2]上是单调增函数,求a的取值范围;(3)当a=1时,求整数t的所有值,使方程f(x)=x+4在[t,t+1]上有解.2016-2017学年安徽省合肥一中高三(上)第三次段考数学试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)(2016秋•包河区校级月考)若集合A=,B={x|x2<2x},则“x∈A∩B”是“x∈(0,1)”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件【解答】解:A=={x|0≤x<1},B={x|x2<2x}={x|0<x<2},故A∩B=(0,1),则“x∈A∩B”是“x∈(0,1)”充要条件,故选:C.2.(5分)(2017•宣城二模)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了()A.24里B.48里C.96里D.192里【解答】解:由题意可知此人每天走的步数构成为公比的等比数列,由题意和等比数列的求和公式可得=378,解得a1=192,∴第此人二天走192×=96步故选:C3.(5分)(2016秋•包河区校级月考)将函数f(x)=sinx﹣cosx的图象向右平移m个单位(m>0),若所得图象对应的函数为偶函数,则m的最小值是()A.B. C.D.【解答】解:将函数f(x)=sinx﹣cosx=2sin(x﹣)的图象向右平移m个单位(m>0),可得y=2sin(x﹣m﹣)的图象,若所得图象对应的函数为偶函数,则﹣m﹣=kπ+,k∈Z,即m=﹣kπ﹣,又m>0,故当,k=﹣1时,m的最小值为,故选:A.4.(5分)(2016•武汉校级模拟)已知一个几何体的三视图如图所示,则该几何体的体积为()A.27﹣B.18﹣C.27﹣3πD.18﹣3π【解答】解:由三视图可知,该几何体为放到的直四棱柱,且中间挖去半个圆柱,由三视图中的数据可得:四棱柱的高为3,底面为等腰梯形,梯形的上、下底边分别为2、4,高为2,圆柱的高为3,圆柱底面的半径都是1,∴几何体的体积V==,故选:B.5.(5分)(2016秋•包河区校级月考)已知向量与的夹角为60°,|=2,|=6,则2在方向上的投影为()A.1 B.3 C.5 D.7【解答】解:向量与的夹角为60°,|=2,|=6,可得•=2×6×cos60°=6,•(2)=22+•=2×4+6=14,则2在方向上的投影为==7.故选:D.6.(5分)(2014•抚州一模)如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后x分钟,瓶内液面与进气管的距离为h厘米,已知当x=0时,h=13.如果瓶内的药液恰好156分钟滴完.则函数h=f(x)的图象为()A.B.C.D.【解答】解:由题意知,每分钟滴下πcm3药液,当4≤h≤13时,xπ=π•42•(13﹣h),即h=13﹣,此时0≤x≤144;当1≤h<4时,xπ=π•42•9+π•22•(4﹣h),即,此时144<x≤156.∴函数单调递减,且144<x≤156时,递减速度变快.故选:A.7.(5分)(2016•湛江一模)已知数列{a n}是公比为2的等比数列,数列{b n}是公差为3且各项均为正整数的等差数列,则数列{a}是()A.公差为5的等差数列B.公差为6的等差数列C.公比为6的等比数列D.公比为8的等比数列【解答】解:由数列{a n}是公比为2的等比数列,可得.由数列{b n}是公差为3且各项均为正整数的等差数列,∴b n﹣b n=3,+1则===23=8.∴数列{a}是公比为8的等比数列.故选:D.8.(5分)(2016•湖南模拟)若α∈(,π),3cos2α=sin(﹣α),则sin2α的值为()A.B.﹣C.D.﹣【解答】解:3cos2α=sin(﹣α),可得3cos2α=(cosα﹣sinα),3(cos2α﹣sin2α)=(cosα﹣sinα),∵α∈(,π),∴sinα﹣cosα≠0,上式化为:sinα+cosα=,两边平方可得1+sin2α=.∴sin2α=.故选:D.9.(5分)(2016秋•包河区校级月考)已知f(x)是定义在R上周期为4的奇函数,当x∈[﹣2,0)时,f(x)=2x+log2(﹣x),则f(2017)=()A.B.C.﹣2 D.2【解答】解:∵f(x)是定义在R上周期为4的奇函数,∴f(2017)=f(1)=﹣f(﹣1),由当x∈[﹣2,0)时,f(x)=2x+log2(﹣x),∴f(﹣1)=,故f(2017)=﹣,故选:A.10.(5分)(2014•河西区三模)已知不等式|y+4|﹣|y|≤2x+对任意实数x,y 都成立,则常数a的最小值为()A.1 B.2 C.3 D.4【解答】解:令f(y)=|y+4|﹣|y|,则f(y)≤|y+4﹣y|=4,即f(y)max=4.∵不等式|y+4|﹣|y|≤2x+对任意实数x,y都成立,∴2x+≥f(y)max=4,∴a≥﹣(2x)2+4×2x=﹣(2x﹣2)2+4恒成立;令g(x)=﹣(2x)2+4×2x,则a≥g(x)max=4,∴常数a的最小值为4,故选:D.11.(5分)(2016•邯郸二模)已知函数f(x)的定义域为R,对任意x1<x2,有>﹣1,且f(1)=1,则不等式f(log2|3x﹣1|)<2﹣log2|3x﹣1|的解集为()A.(﹣∞,0)B.(﹣∞,1)C.(﹣1,0)∪(0,3)D.(﹣∞,0)∪(0,1)【解答】解:∵函数f(x)的定义域为R,对任意x1<x2,有>﹣1,即>0,故函数R(x)=f(x)+x是R上的增函数,由不等式f(log2|3x﹣1|)<2﹣log2|3x﹣1|,可得f(log2|3x﹣1|)+log2|3x﹣1|<2=f(1)+1,∴log2|3x﹣1|<1,故﹣2<3x﹣1<2,且3x﹣1≠0,求得3x<3,且x≠0,解得x<1,且x≠0,故选:D.12.(5分)(2013•湖北)已知函数f(x)=x(lnx﹣ax)有两个极值点,则实数a 的取值范围是()A.(﹣∞,0)B.(0,)C.(0,1) D.(0,+∞)【解答】解:函数f(x)=x(lnx﹣ax),则f′(x)=lnx﹣ax+x(﹣a)=lnx﹣2ax+1,令f′(x)=lnx﹣2ax+1=0得lnx=2ax﹣1,函数f(x)=x(lnx﹣ax)有两个极值点,等价于f′(x)=lnx﹣2ax+1有两个零点,等价于函数y=lnx与y=2ax﹣1的图象有两个交点,在同一个坐标系中作出它们的图象(如图)当a=时,直线y=2ax﹣1与y=lnx的图象相切,由图可知,当0<a<时,y=lnx与y=2ax﹣1的图象有两个交点.则实数a的取值范围是(0,).故选B.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)(2016秋•包河区校级月考)若变量x,y满足约束条件,则z=3x+y的取值范围是[1,9] .【解答】解:作出不等式对应的平面区域如图,由z=3x+y,得y=﹣3x+z,平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z,经过点A(0,1)时,直线y=﹣3x+z的截距最小,此时z最小.此时z的最小值为z=0×3+1=1,平移直线y=﹣3x+z,由图象可知当直线y=﹣3x+z,经过点B时,直线y=﹣3x+z 的截距最大,此时z最大.由,解得B(2,3)此时z的最大值为z=2×3+3=9,故答案为:[1,9].14.(5分)(2016秋•包河区校级月考)已知△ABC是边长为2的等边三角形,点D、E分别是边AB、BC的中点,点F为DE中点,则=.【解答】解:如图,据条件:====;∴===.故答案为:.15.(5分)(2016秋•包河区校级月考)数列{a n}满足a n+1=,a1=,S n为{a n}的前n项和,则S2016=1008.【解答】解:a1=,a2=2a1﹣1=,a3=2a2=,a4=2a3=,a5=2a4﹣1=,∴{a n}为周期为4的摆动数列,∴S2016=(a1+a2+a3+a4)×=2×504=1008.故答案为:1008.16.(5分)(2016秋•荆州期中)在△ABC中,边AB的垂直平分线交边AC于D,若C=,BC=8,BD=7,则△ABC的面积为20,或24.【解答】解:如图所示,△BCD中,设CD=x,由余弦定理可得:,化为:x2﹣8x+15=0,解得x=3,或5.∴AC=10,或12.=sinC=20,或24.∴S△ABC故答案为:20,或24.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)(2016秋•包河区校级月考)已知数列{a n}的前n项和为S n,且2S n=1﹣a n(n∈N*).(1)求数列{a n}的通项公式;(2)设,记数列{a n b n}的前n项和为T n,求证:T n<.【解答】(本小题满分10分)解:(1)当n=1时,由2S1=1﹣a1得:.2S n=1﹣a n(n∈N*).=1﹣a n﹣1(n∈N*).可得2S n﹣1两式相减可得:a n=a n﹣1 n≥2,∴数列{a n}是等比数列,首项为,公比为,∴a n=;(2)证明:∵(n∈N*),∴.∴∴;∴∴∴.18.(12分)(2016秋•包河区校级月考)已知向量,,函数f(x)=cos2x.(1)求函数f(x)的解析式及其单调递增区间;(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若c=且f(C)=0,求△ABC周长的取值范围.【解答】解:(1)向量,,函数f(x)=cos2x=cos(2x+)+sin2x﹣cos2x=cos2xcos﹣sin2xsin+﹣cos2x=﹣sin2x﹣cos2x+=sin(2x+)+;由,k∈Z,得,k∈Z;所以函数f(x)的单调递增区间为,k∈Z;(2)由(1),又C为△ABC的内角,所以,解得;又c=2,由正弦定理可得,所以a=2sinA,b=2sinB,所以;由,且,所以,所以,所以,所以△ABC的周长的取值范围是.19.(12分)(2016•山东)在如图所示的几何体中,D是AC的中点,EF∥DB.(Ⅰ)已知AB=BC,AE=EC,求证:AC⊥FB;(Ⅱ)已知G,H分别是EC和FB的中点,求证:GH∥平面ABC.【解答】(Ⅰ)证明:如图所示,∵D是AC的中点,AB=BC,AE=EC,∴△BAC、△EAC都是等腰三角形,∴BD⊥AC,ED⊥AC.∵EF∥DB,∴E、F、B、D四点共面,这样,AC垂直于平面EFBD内的两条相交直线ED、BD,∴AC⊥平面EFBD.显然,FB⊂平面EFBD,∴AC⊥FB.(Ⅱ)已知G,H分别是EC和FB的中点,再取CF的中点O,则OG∥EF,∵OG∥BD,∴OG∥BD,而BD⊂平面ABC,∴OG∥平面ABC.同理,OH∥BC,而BC⊂平面ABC,∴OH∥平面ABC.∵OG∩OH=O,∴平面OGH∥平面ABC,∴GH∥平面ABC.20.(12分)(2014•东港区校级模拟)某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似地表示为:y=,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.(Ⅰ)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?(Ⅱ)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?【解答】解:(Ⅰ)当x∈[200,300)时,该项目获利为S,则S=200x﹣(x2﹣200x+80000)=﹣(x﹣400)2,∴当x∈[200,300)时,S<0,因此,该项目不会获利当x=300时,S取得最大值﹣5000,所以政府每月至少需要补贴5000元才能使该项目不亏损;(Ⅱ)由题意可知,生活垃圾每吨的平均处理成本为:=.当x∈[120,144)时,=(x﹣120)2+240所以当x=120时,取得最小值240;当x∈[144,500)时,=x+﹣200≥2﹣200=300当且仅当x=,即x=400时,取得最小值300因为240<300,所以当每月处理量为120吨时,才能使每吨的平均处理成本最低.21.(12分)(2013•朝阳区一模)已知函数f(x)=x2﹣(a+2)x+alnx,其中a ∈R.(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线的斜率为1,求a的值;(Ⅱ)求函数f(x)的单调区间.【解答】解:(Ⅰ)由f(x)=x2﹣(a+2)x+alnx,可知,函数定义域为{x|x>0},且f′(x)=2x﹣(a+2)+.由题意,f′(2)=4﹣(a+2)+=1,解得a=2.(Ⅱ)f′(x)=2x﹣(a+2)+=(x>0).令f′(x)=0,得x1=1,x2=.(1)当a≤0时,≤0,令f′(x)>0,得x>1;令f′(x)<0,得0<x<1.则函数f(x)的单调递减区间为(0,1),单调递增区间为(1,+∞).(2)当0<<1,即0<a<2时,令f′(x)>0,得0<x<或x>1.则函数f(x)的单调递增区间为(0,),(1,+∞).令f′(x)<0,得<x<1.则函数f(x)的单调递减区间为(,1).(3)当=1,即a=2时,f′(x)≥0恒成立,则函数f(x)的单调递增区间为(0,+∞).(4)当>1,即a>2时,令f′(x)>0,得0<x<1或x>,则函数f(x)的单调递增区间为(0,1),(,+∞).令f′(x)<0,得1<x<.则函数f(x)的单调递减区间为(1,).22.(12分)(2016•扬州一模)已知函数f(x)=(ax2+x+2)e x(a>0),其中e 是自然对数的底数.(1)当a=2时,求f(x)的极值;(2)若f(x)在[﹣2,2]上是单调增函数,求a的取值范围;(3)当a=1时,求整数t的所有值,使方程f(x)=x+4在[t,t+1]上有解.【解答】解:(1)f(x)=(2x2+x+2)e x,则f′(x)=(2x2+5x+3)e x=(x+1)(2x+3)e x…(2分)令f′(x)=0,∴,…(4分)(2)问题转化为f′(x)=[ax2+(2a+1)x+3]e x≥0在x∈[﹣2,2]上恒成立;又e x>0即ax2+(2a+1)x+3≥0在x∈[﹣2,2]上恒成立;…(6分),令g(x)=ax2+(2a+1)x+3,∵a>0,对称轴①当﹣1﹣≤﹣2,即时,g(x)在[﹣2,2]上单调增,∴g(x)的最小值g(x)=g(﹣2)=1>0,∴0<a≤…(8分)②当﹣2<﹣1﹣<0,即时,g(x)在[﹣2,﹣1﹣]上单调减,在[﹣1﹣,2]上单调增,∴△=(2a+1)2﹣12a≤0,解得:,∴<a≤1+,综上,a 的取值范围是.…(10分)(3)∵a=1,设h(x)=(x2+x+2)e x﹣x﹣4,h′(x)=(x2+3x+3)e x﹣1令φ(x)=(x2+3x+3)e x﹣1,φ′(x)=(x2+5x+6)e x令φ′(x)=(x2+5x+6)e x=0,得x=﹣2,﹣3∴,…(13分)∵,∴存在x0∈(﹣1,0),x∈(﹣∞,x0)时,φ(x)<0,x∈(x0,+∞)时,φ(x)>0∴h(x)在(﹣∞,x1)上单调减,在(x1,+∞)上单调增又∵由零点的存在性定理可知:h(x)=0的根x1∈(﹣4,﹣3),x2∈(0,1)即t=﹣4,0.…(16分)参与本试卷答题和审题的老师有:刘老师;lincy;w3239003;gongjy;双曲线;刘长柏;沂蒙松;qiss;豫汝王世崇;wfy814;caoqz;minqi5;wkl197822;zhczcb;742048;maths(排名不分先后)菁优网2017年5月7日。
安徽省示范高中2016届高三上学期第三次联考语文试题.doc

安徽省示范高中2016届高三上学期第三次联考语文试题阅读下面的文字,完成1—3题。
教育公共服务的方式:民主协商对话受传统公共行政的影响,第二次世界大战后建立起来的公共教育体制,都是由政府举办并向社会提供教育服务的,因而具有强烈的国家垄断色彩。
公民在向国家纳税之后,只能无条件地接受由政府设立的公立学校提供的教育服务,他们对于公立学校提供的教育没有任何发言权,只能被动地接受。
此外,由于政府的垄断,公立学校的办学完全根据政府的计划进行,而不必直接面对学习者的选择和同行的竞争,对于家长和学生的教育需求可以置之不理。
针对政府垄断学校教育供给的局面和政府漠视家长和学生教育需求的状况,新公共管理理论提出“社会公众是政府顾客”的理念,坚持“顾客至上”。
认为政府的职责就是根据“顾客”的需要提供口应性的教育服务,要尊重并赋予顾客应有的权利,坚持“顾客导向”,以“顾客满意”为宗旨。
然而,新公共服务理论也认为,与政府互动的并不简单地是顾客,同时还是公民。
与政府直接交易的人的确可以被视为顾客,但从政府那里接受一种职业服务-例如教育——的人则可以恰当地被称之为当事人、公民。
公民不只是顾客,他们是“所有者或主人”。
正因为接受政府服务的人是“所有者或主人”,而不单纯是“顾客”,因此,有权参与决定政府提供哪些公共服务。
提供什么样的公共服务,以及以什么方式提供公共服务等等,而不单单是处于服从、被动接受的地位。
换言之,政府提供公共服务应该坚持民主协商对话的方式。
这就要求公共管理者积极回应公民的要求,倾听公民呼声,方便公民选择,鼓励公民参与,部门绩效评价以公民为主体等。
教育领域的民主协商对话要求公民成为教育政策制定和实施的主体,让公民来参与教育决策的制定,让公民和政府共享政策制定的权由;关注教育政策的回应性,建立公民表达教育利益和诉求的畅通渠道,培养公民的教育责任意识。
实践还证明,只有注重教育政策的制定与实施中的公众参与,政策制定才具有合法性和合理性,政策的实施才具有效力。
2016届安徽省合肥市第一中学高三段三考试数学(理)试题

合肥一中2015-2016学年第一学期高三年级段三考试数学(理科)试卷分值 150 分 时长 120分一、选择题(本大题共12个小题,每小题5分,共60分.)1.已知函数()214f x x =-的定义域为M ,()()ln 2g x x =+的定义域为N ,则()RMN =ð( )A.{}22x x -≤<B. {}2x x ≥C. ∅D. {}2x x <2.在ABC ∆中,下列命题错误..的是( ) A.A B ∠>∠的充要条件是sin sin A B > B.A B ∠>∠的充要条件是cos cos A B < C.A B ∠>∠的充要条件是tan tan A B >D.A B ∠>∠的充要条件是cos cos sin sin A BA B<3.已知数列{}n a 是等比数列,37,a a 是方程2540x x -+=的两根,则5a =( ) A. 2B. 2-C. 2±D. 44. 设D 为ABC ∆所在平面内的一点,且满足2BC CD =,则( ) A. 1322AD AB AC =+ B. 1322AD AB AC =-+C. 3122AD AB AC =-+D. 3122AD AB AC =- 5.函数()()2sin ln 1f x x x =⋅+的部分图象可能是( )A. B. C. D.6.已知()()sin cos 0f x x x ωωω=+>,若()02y f x πθθ⎛⎫=+<< ⎪⎝⎭是周期为π的偶函数,则θ的值是( )A.8π B.6π C.4π D.3π 7.已知函数()lg f x x =,若方程()f x k =有两个不等的实根,αβ,则11αβ+的取值范围是( )A. ()1,+∞B. [)1,+∞C. ()2,+∞D. [)2,+∞x y O O x y yx O O x y8.若变量,x y 满足约束条件32122120,0x y x y x y x y -≥-⎧⎪+≤⎪⎨+≤⎪⎪≥≥⎩,则34z x y =+的最大值是( )A.12B.26C.28D.33 9. 已知sin 23sin 2αβ=,则()()tan tan αβαβ-=+( )A.2B.34C.32D.1210.设()()312f x x x =-++,{}n a 是公差为12的等差数列,且()()()()1234f a f a f a f a +++()5f a +()618f a +=,则1a =( )A.14-B. 74-C. 54-D. 34-11.已知数列{}n a 满足()*123N n n a a n ++=∈,且14a =,其前n 项和为n S ,则满足不等式1230n S n --<的最小整数n 是( ) A.5 B.6 C.7 D.812. 设()()()ln 01f x ax a =<<,过点(),0P a 且平行于y 轴的直线与曲线():C y f x =的交点为Q ,曲线C 在点Q 处的切线交x 轴于点R ,则PQR ∆的面积的最大值是( ) A.1B.24e C.12D.28e 二、填空题(本大题共4个小题,每小题5分,共20分.) 13.若函数()()x x f x x e ae -=+是偶函数,则a =________. 14.已知向量,a b 的夹角为56π,且2a =,3b =,23c a b =+,则c =________. 15.设数列{}n a 满足1412n n n a a a +-=+,则首项1a =________时,此数列只有10项. 16.定义函数()f x x x =<⋅<>>,其中x <>表示不小于x 的最小整数,如 1.32<>=, 2.12<->=-,当(]()*0,N x n n ∈∈时,函数()f x 的值域为n A ,记集合n A 中的元素的个数为n a ,则122015111a a a +++=________.三、解答题(解答应写出必要的文字说明、证明及演算步骤.) 17.(本小题满分12分)数列{}n a 满足:122a a ==,2122n n n a a a ++=-+. (Ⅰ)设1n n n b a a +=-,证明{}n b 是等差数列; (Ⅱ)求数列{}n a 的通项公式.18.(本小题满分12分)已知ABC ∆三个角,,A B C 所对的边分别为,,a b c ,且,,a b c 成等比数列. (Ⅰ)求角B 的取值范围;(Ⅱ)设()3sin 4cos f x x x =+,求()f B 的最大值及()f B 取得最大值时tan B 的值.19.(本小题满分12分)已知()ln f x x x =,()32g x x ax =+. (Ⅰ)讨论函数()g x 的极值点的个数;(Ⅱ)若不等式()()2f x g x '≤在()0,x ∈+∞上恒成立,求实数a 的取值范围.20.(本小题满分12分)设n S 是数列{}n a 的前n 项和,且11a =,0n a ≠,()222*12,Nn n n S n a S n n -=+≥∈. (Ⅰ)证明()*22N n n a a n +-=∈;(Ⅱ)若3log n n a b =,求数列{}n n a b ⋅的前n 项和n T .21.(本小题满分12分) 设()()1x f x a x e =--.(Ⅰ)当0x >时,()0f x <,求实数a 的最大值;(Ⅱ)设()1x e g x x-=,11x =,()()1*N n x n e g x n +=∈,证明()*11N 2n n n x x n +>>∈.请考生在22-24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目的题号涂黑.把答案填在答题卡上. 22.(本小题满分10分)选修4-1:几何证明选讲如图,AB 是O 的直径,弦,BD CA 的延长线相交于点E ,EF 垂直BA 的延长线于点F ,求证: (Ⅰ)DEA DFA ∠=∠;(Ⅱ)2AB BE BD AE AC =⋅-⋅.23.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线1C 的参数方程为12x ty t =+⎧⎨=+⎩(t 为参数),以该直角坐标系的原点O 为极点,x 轴的非负半轴为极轴的极坐标系下,圆2C 的方程为2cos 23sin ρθθ=-+. (Ⅰ)求直线1C 的普通方程和圆2C 的圆心的极坐标; (Ⅱ)设直线1C 和圆2C 的交点为,A B ,求弦AB 的长. 24.(本小题满分10分)选修4-5:不等式选讲已知函数()()2R f x m x m =--∈,且()20f x +≥的解集为[]1,1-. (Ⅰ)求实数m 的值; (Ⅱ)若,,a b c 为正实数,且11123m a b c++=,求证239a b c ++≥.ABO∙DCEF合肥一中2015-2016学年第一学期高三年级段三考试数学(理科)试卷参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 DCABBACCDABD二、填空题 13.1-;14.7;15.710;16.20151008. 三、解答题17.(1)11212,0n n b b b a a +-==-=,所以数列{}n b 是以为0首项,2为公差的等差数列. (2)由(1)可知2(1)n b n =-,累加可得234n a n n =-+18.(1)由条件可知2b ac =所以222221cos 222a cb ac ac B ac ac +-+-==≥,所以03B π<≤.(2)()5sin()f x x ϕ=+,其中43sin ,cos 55ϕϕ== 所以()5sin()f B B ϕ=+,32ππϕ<<,50336B B ππϕπ<≤∴<+≤ 可知当2B πϕ+=时,max ()5f B =.此时cos 3tan sin 4B ϕϕ== 19.(1)2()3210g x x ax '=++=的判别式2412a ∆=-.①当33a -≤≤时,24120a ∆=-≤,()0g x '≥, 所以()y g x =在R 单调递增,无极值,无极值点.②当3a <-或3a >时,0∆>所以2()3210g x xax '=++=有两个不等的实根12,x x ,则22123333a a a a x x ----+-=<=列表:根据表格可知此时函数()x g 有两个极值点,极大值点1x ,极小值点2x .(2)即:123ln 22++≤ax x x x 对()+∞∈,0x 上恒成立可得x x x a 2123ln --≥对()+∞∈,0x 上恒成立 设()xx x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=令()0'=x h ,得31,1-==x x (舍)当10<<x 时,()0'>x h ;当1>x 时, ()0'<x h∴当1=x 时,()x h 取得最大值, ()x h max =-2,2-≥∴a .a ∴的取值范围是[)+∞-,2.20.(1).当2n ≥时,由已知得2221nn n S S n a --= 因为10n n n a S S -=-≠,所以21n n S S n -+=. …………………………①于是21(1)n n S S n ++=+. …………………………………………………②由②-①得:121n n a a n ++=+.……………………………………………③于是2123n n a a n +++=+.……………………………………………………④由④-③得:22(2)n n a a n +-=≥.………………………………………⑤由①有214S S +=,所以22a =.由③有235a a +=,所以33a =,311a a ∴-=所以:*22()n n a a n N +-=∈(2)由(1)可知:数列21{}k a -和2{}k a 分别是以1,2为首项,2为公差的等差数列. 所以22(1)22ka k k =+-⨯=,211(1)221k a k k -=+-⨯=-*()n a n n N ∴=∈,3,3n n n n n b a b n ∴=⋅=⋅由错位相减法可得到:1(21)334n n n T +-⋅+=21.(1)()(1)e x f x a x '=--,令()0f x '=得:1x a =- 当10a -≤时,'()0f x ≤在0>x 时恒成立,所以()y f x =在上(0,)+∞单调递减;()(0)10f x f a ∴<=-≤ 即当0>x 时,0<)(x f 成立当10a ->时,()y f x =在(0,1)a -上单调递减增,在(1,)a -+∞单调递减;0010,()(0)10x a f x f a ∴∃=->>=->与0>x 时,0<)(x f 矛盾,以实数a 的最大值为1.23.(Ⅰ)由1C 的参数方程消去参数t 得普通方程为10x y -+=圆2C 的直角坐标方程22(1)(3)4x y ++-=,所以圆心的直角坐标为(1,3)-,因此圆心的一个极坐标为2(2,)3π.(答案不唯一,只要符合要求就给分) (Ⅱ)由(Ⅰ)知圆心(1,3)-到直线10x y -+=的距离131622d --+==,所以624104AB =-=. 24.解:(1) ∵ f(x +2)=m -|x|≥0,∴ |x|≤m , ∴ m≥0,-m≤x≤m ,∴ f(x +2)≥0的解集是[-1,1],故m =1.(2)由(1)知1a +12b +13c=1,a 、b 、c ∈R+,由柯西不等式得a +2b +3c =(a +2b +3c)⎝⎛⎭⎫1a +12b +13c ≥(a·1a +2b·12b +3c·13c )2=9. 另解:1112332()(23)3()()()9232323a b a c c ba b c a b c b a c a b c ++++=++++++≥当且仅当"23"a b c ==时,取等号.。
合肥一中2015-2016上学期高三年级段三考试语文课件

合肥一中2015~2016学年第一学期高三年级段三考试语文试题注意事项:1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
满分150分,考试时间150分钟。
答卷前,考生务必将自己的姓名、考生号填写在答题卡上。
2.作答时,将答案巧在答题卡上,写在试卷上无效。
第Ⅰ卷(阅读题)甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题知其白而守其黑:国画之美生根于中国文化天籁、神韵、简朴是中国文化的源头,国画产生于中国文化之中。
中国文化很注重天人合一,这种特质造就了中国文化的开放性、包容性和启智性。
对中国绘画而言,中国文化的启智性是非常重要的。
中国绘画不需要像西方文化那样严格的逻辑分析,而需要的是感悟力。
一方面,要遵循自然之道,体会天地大美。
天地山川、草木虫鱼都有其自身之美、有它运行的目的,中国绘画就是要你去体会这种美、这种内在目的性,然后将其运用到笔墨中,表现出来,而不需要你问“这树长在这儿对不对”“这老鼠怎么比南瓜还大啊”……另一方面,天地大美只有通过感悟才能转化为人类的美感。
明代“心学”流派的重要代表人物王阳明在《传习录》中写道:一朵花在深山开放,你不知道它存在,可是当你看到这朵花的时候,这朵花的颜色、形态就渐渐显现出来,它果然是个美艳的存在。
中国文人讲“气韵生动”,其中的“韵”并不是单纯的作诗时押韵的“韵”,意义更为丰富饱满,注重的是创作主体(无论是艺术家还是诗人)对于宇宙惯有的一个诗性的判断。
天地大美自然而生,可是也需要画家对其有诗性的判断、有所感悟才会于人有意义。
所以,当中国人的智慧和感悟在哲学上的体现用到绘画上来的时候,绘画就受益无穷了。
老子哲学里有“知其白,守其黑”,说的是深知本性洁白,却守持混沌昏黑的态势,这就是中国人的思维,也正是国画美之所在。
笔墨加上宣纸就是黑和白,只有维持黑白间比例的平衡和谐才能守住国画的这种美。
中国禅宗讲,“妙悟者不在多言”。
王维在《山水诀》中将此视为对山水画的要求,其实,这是对整个中国绘画的要求——以少许胜多许,以最简练的语言表现最丰富的内容。
安徽省合肥市2016年高三第三次教学质量检测语文试题

安徽省合肥市2016年高三第三次教学质量检测语文试题第I卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1--3题。
人和其他动物所不同的。
是具有学习的能力。
人的行为方式并不固执地受着不学而能的生理反应所支配。
所谓“学”就是在出生之后以一套人为的行为方式作模型,把本能的那一套方式加以改造的过程。
学的方法是“习”。
“习’’是指反复地做,靠时间中的磨练,使一个人惯于一种新的做法。
因之,学习必须打破个人今昔之隔。
这是靠了我们人类的一种特别发达的能力。
时间中的桥梁——记忆。
在动物的学习过程中,我们也可以说它们有记忆,但是它们的“记忆”是在简单的生理水准上。
一个小白老鼠在迷宫里学得了捷径,它所学得的是一套新的生理反应。
和人的学习不相同的是,它们并不靠一套象征体系的。
人固然有很多习惯,在本质上是和小白老鼠走迷宫一般的,但是他却时常多一个象征体系帮他的忙。
所谓象征体系中最重要的是“词”。
我们不断地在学习时说着话,把具体的情境抽象成一套能普遍应用的概念,概念必然是用词来表现的,于是我们靠着词,使我们从特殊走上普遍,在个别情境中搭下了桥梁;又使我们从当前走到今后,在片刻情境中搭下了桥梁。
从这方面看去,一个动物和时间的接触,可以说是一条直线的,而人和时间的接触,却比一条直线来得复杂。
他有能力闭了眼睛置身于“昔日”的情境中,人的“当前”中包含着从“过去”拔萃出来的投影,即时间的选择累积。
一个依本能而活动的动物不会发生时间上阻隔的问题,它的寿命是一联串的“当前”。
但是人却不然,人的“当前’’是整个靠记忆所保留下来的“过去”的累积。
如果记忆消失了,我们的“时间”就可以说是阻隔了。
人有此能力是事实,人利用此能力,发展此能力,还是因为他“当前”的生活必须有着“过去,,所传下来的办法。
人的学习是向一套已有方式的学习,唯有学会了这套方式才能在人群中生活下去。
这套方式并不是每个人个别的创制,而是社会的遗业。
小白老鼠并不向别的老鼠学习,每只老鼠都得自己在具体情境里,从“试验错误”的过程中,得到个别的经验,它们并不能互相传递经验,互相学习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年高考(326)安徽合肥一中2016届上期高三段三考试合肥一中2015~2016学年第一学期高三年级段三考试语文试题注意事项:1.本试卷分第卷(阅读题)和第卷(表达题)两部分。
满分150分,考试时间150分钟。
答卷前,考生务必将自己的姓名、考生号填写在答题卡上。
2.作答时,将答案巧在答题卡上,写在试卷上无效。
第卷(阅读题)甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题知其白而守其黑:国画之美生根于中国文化天籁、神韵、简朴是中国文化的源头,国画产生于中国文化之中。
中国文化很注重天人合一,这种特质造就了中国文化的开放性、包容性和启智性。
对中国绘画而言,中国文化的启智性是非常重要的。
中国绘画不需要像西方文化那样严格的逻辑分析,而需要的是感悟力。
一方面,要遵循自然之道,体会天地大美。
天地山川、草木虫鱼都有其自身之美、有它运行的目的,中国绘画就是要你去体会这种美、这种内在目的性,然后将其运用到笔墨中,表现出来,而不需要你问这树长在这儿对不对这老鼠怎么比南瓜还大啊……另一方面,天地大美只有通过感悟才能化为人类的美感。
明代心学流派的重要代表人物王阳明在《传习录》中写道:一朵花在深山开放,你不知道它存在,可是当你看到这朵花的时候,这朵花的颜色、形态就渐渐显现出来,它果然是个美艳的存在。
中国文人讲气韵生动,其中的韵并不是单纯的作诗时押韵的韵,意义更为丰富饱满,注重的是创作主体(无论是艺术家还是诗人)对于宇宙惯有的一个诗性的判断。
天地大美自然而生,可是也需要画家对其有诗性的判断、有所感悟才会于人有意义。
所以,当中国人的智慧和感悟在哲学上的体现用到绘画上来的时候,绘画就受益无穷了。
老子哲学里有知其白,守其黑,说的是深知本性洁白,却守持混沌昏黑的态势,这就是中国人的思维,也正是国画美之所在。
笔墨加上宣纸就是黑和白,只有维持黑白间比例的平衡和谐才能守住国画的这种美。
中国禅宗讲,妙悟者不在多言。
王维在《山水诀》中将此视为对山水画的要求,其实,这是对整个中国绘画的要求——以少许胜多许,以最简练的语言表现最丰富的内容。
中国绘画就是有无相生之道的形象体现,笔墨的有和画面空白的无相互辉映才造就了国画之美。
元代山水画家倪瓒的画就非常注重黑白间的比例,比如他的《容膝斋图》,几棵小树,一个茅亭,朦胧的远山,没有人物,没有动态。
然而,你一看就能感受到一种淡淡的哀愁,一种天荒地老式的沉默和寂寞。
八大山人画的鸟,蜷曲着身子,寥寥几笔,把鸟的全部内在生命表达得淋漓尽致。
他的画已经撇除了一切的繁文缛节、一切的矫揉造作和一切的事功媚俗,剩下的只有士气的符号,简捷清纯、精微广大、高明中庸。
中国画的这种简结丰润源远流长,早在远古时期陶瓷上的绘画就有体现。
猪纹陶钵属于河姆渡文化时期,但刻画在陶罐上的猪极富神韵。
大量的留白、相当简单的细条,却将猪那种神情、动态刻画得栩栩如生,能引发你无尽的联想。
人面彩陶瓶属于五千年前的仰韶文化时期。
这个作品反映的是远古先民的一种思考状态,你可以看出他在思考,你看他的眼睛里若有疑惑,可是这个疑惑又混混沌沌,让人感到没有答案而有所茫然。
这个茫然体现出一个童稚的天真。
还有,嘴边那个酒窝在那儿,像一个很憨厚的人,混沌、茫然、天真、憨厚、简朴。
从这个简单的作品中,我们看到了天籁、神韵、简朴。
这就是我们文化的源头,这种对于艺术的感悟、对于微言大义的追求流传了几千年,深深地扎根手中国的国画之中。
1.关于中国绘画的特点,下列表述不正确的一项是()(3分)A.中国绘画遵循自然之道,通过笔墨来真实再现天地山川、草木虫鱼自身的美及其运行的目的。
B.中国绘画是有无相生之道的形象体现,注重以少许胜多许,用笔简洁却使画面丰润而富有神韵。
C.画家通过感悟天地大美,对其作出诗性判断,创作出的作品才有可能具备气韵生动的特点。
D.中国绘画是中国文化的一部分,天籁、神韵、简朴是中国文化的源头,当然也是中国绘画的源头。
2.下列关于知其白而守其黑的解说,有错误的一项是A.知其白而守其黑作为中国绘画的一个重要美学原则,是老子哲学思想在中国绘画中的一种集中体现。
B.知其白而守其黑是中国人思维的一种表现,也影响着画家的国画创作,使国画呈现出不同于西方绘画的美。
C.知其白而守其黑与中国禅宗所说的妙悟者不在多言的道理相似,强调以最简练的笔墨或语言表现最丰富的内容。
D.在中国绘画中,黑和白分别对应笔墨的有和画面的无,国画的美就在这有无之间。
3.根据原文内容,下列理解和分析正确的一项是A.八大山人寥寥几笔便将鸟的内在生命表达得淋漓尽致,他的创作就是国画中表现出符号化趋势的代表。
B.国画家将自己的感悟融入绘画中,启发读者去感受、体会美,这一过程无须像西方文化那样严格的逻辑分析。
C.仰韶文化时期人面彩陶瓶上的先民神情若有疑惑和茫然,形象地将五千年前远古时期先民的无知与天真展现出来。
D.王维在《山水诀》中把禅宗的妙悟者不在多言视为对山水画的要求,首倡了中国画以少许胜多许的绘画准则。
二、古代诗文阅读(36分)(一)文言文阅读(19分)阅读下面的文言文,完成4~7题。
邓训,字平叔,南阳新野人,大司徒禹第六子也。
少有大志,不好文学,禹常非之。
显宗即位,初以为郎中。
训乐施下士,士大夫多归之。
永平中,理摩沱、石臼河,从都虑至羊肠仓,欲令通漕。
太原吏人苦役,连年无成,运所经三百八十九隘,前后没溺死者不可胜算。
建初三年,拜训谒者,使监领其事。
训考量隐括,知大功难立,具以上言。
肃宗从之,遂罢其役,更用驴辇,岁省费亿万计,全活徒士数千人。
章和二年,护羌校尉张纡诱诛烧当种羌迷吾等,由是诸羌大怒,谋欲报怨,朝廷忧之。
公卿举训代纡为校尉。
先是小月氏胡分居塞内,胜兵者二三千骑,皆勇健富强,每与羌战,常以少制多。
时迷吾子迷唐,来至塞下,未敢攻训,先欲胁月氏胡。
训拥卫稽故,令不得战。
议者戚以羌胡相攻,县官之利,以夷伐夷,不宜禁护。
训日:不然。
今张纡失信,众羌大动。
原诸胡所以难得意者,皆恩信不厚耳。
今因其迫急:以德怀之,庶能有用。
遂令开城及所居园门,悉驱胡妻子内之,严兵守卫。
羌掠无所得,又不敢逼诸胡,因即解去。
由是湟中诸胡皆言汉家常欲斗我曹今邓使君待我以恩信开门内我妻子乃得父母咸欢喜叩头日唯使君所命训遂抚养其中少年勇者数百人,以为义从。
羌胡俗耻病死,每病临困,辄以刃自刺。
训闻有困疾者,辄拘持缚束,不与兵刃,使医药疗之,愈者非一,小大莫不感悦。
迷唐伯父号吾乃将其母及种人八百户,自塞外来降。
永元二年,大将军窦宪将兵镇武威,宪以训晓羌胡方略,上求俱行。
训初厚于马氏,不为诸窦所亲,及宪诛,故不离其祸。
四年冬,病卒官,时年五十三。
吏人羌胡爱惜,旦夕临者日数千人。
羌俗父母死,耻悲泣,皆骑马歌呼。
至闻训卒,莫不吼号,或以刀自割,又刺杀其犬马牛羊,日:邓使君已死,我曹亦俱死耳。
遂家家为训立祠,每有疾病,辄此请祷求福。
(节选自《后汉书·邓训传》)注:烧当种羌迷吾:烧当种羌,当时的羌族部落名称。
迷吾,部族首领。
4.下列对文中画波浪线部分的断句,正确的一项是()(3分)A.由是湟中诸胡皆言/汉家常欲斗我曹/今邓使君待我以恩信/开门内我妻子/乃得父母/咸欢喜叩头曰/唯使君所命/B.由是湟中诸胡/皆言汉家常欲斗我曹/今邓使君待我以恩信/开门内我/妻子乃得/父母咸欢喜/叩头曰/唯使君所命/C.由是湟中诸胡/皆言汉家常欲斗/我曹今邓使君/待我以恩信开门内我妻子/乃得父母/咸欢喜叩头曰/唯使君所命/D.由是湟中诸胡皆言/汉家常欲斗/我曹今邓使君/待我以恩信/开门内我/妻子乃得/父母咸欢喜/叩头曰/唯使君所命/5.下列对文中加点词语的相关解说不正确的一项是()(3分)A.大司徒是官职名。
周礼地方官有大司徒,为六卿之一,掌管教化。
B.年号是皇帝纪年的名号,始于汉武帝。
显宗即为年号,显宗即位亦可称为显宗元年。
C.通漕即开通水运河道。
D.羌胡指我国古代的羌族和匈奴,亦用于泛称西北部的少数民族。
6.下列对原文有关内容的理解和分析,不正确的一项是()(3分)A.邓训少有远志,礼贤下士。
邓训是东汉官员邓禹的六儿子,他年轻时有远大志向,但他不喜欢文学,因此常常被父亲责怪;邓训喜欢施恩于人,士大夫大多归依他的门下。
B.邓训心系百姓,治理有方。
肃宗任命邓训为谒者,派他监理漕运,邓训知道这件事难以成功,上报皇上,肃宗听从他的意见停止了漕运,因此保全和救活了服役的几千人。
C.邓训深明大义,以德立信。
羌人迷吾的儿子迷唐为父报仇心切,欲胁迫小月氏胡人一起攻打邓训,在这关键时刻,邓训力排众议,下令打开城门并敞开家门,放胡人进城,派重兵保护。
D.邓训恩施异族,深受爱戴。
羌胡人生病时,邓训找来医生为其治病,羌胡之人非常感动,前来归顺;邓训死后羌人以悼念父母的方式祭奠他并为之立祠。
7.把文中划横线的句子翻译成现代汉语(10分)(1)今因其迫急,以德怀之,庶能有用。
(5分)(2)训初厚于马氏,不为诸窦所亲,及宪诛,故不离其祸。
(5分)(二)古代诗歌阅读(11分)阅读下列这首宋词,完成8~9题虞美人·用李后主韵二首(其一)刘辰翁梅梢腊尽春归了。
毕竟春寒少。
乱山残烛雪和风。
犹胜阴山北海窖中。
年光老去才情在。
唯有华风改。
醉中幸自不曾愁。
准唱春花秋叶泪偷流。
(注)刘辰翁:南米末年词人,入元不仕。
8.犹胜阴山北海窖中引用了哪个著名典故?请简要说明其作用。
(5分)9.下阕不曾愁与泪偷流矛盾吗?为什么?试作简要分析。
(6分)(三)名篇名句默写(6分)10.补写出下列句子中的空缺部分。
(6分)(1)《氓》中初露男子的粗暴性格,同时也写出女子的性格温柔体贴的句子是:,。
(2)白居易《钱塘湖春行》中,一联,从植物的变化写出了早春欣欣向荣的景象。
(3)《阿房宫赋》中杜牧告诫后人,如果不能吸收历史的教训终将重蹈覆辙的语句是,。
乙选考题请考生在第二、四两火题中选定其中一题作答。
只能做选定大题内的小题,不得选做另一大题内的小题。
如果多做,则按所做的第一大题计分。
三、文学类文本阅读(25分)11.阅读下面的文字,完成(1)~(4)题。
(25分)主刀奚同发因为刘晓波的孩子明天要手术,黄大夫主刀,这次约见,刘妻颇费周折。
黄大夫虽身居省会,却名闻全国,外省患者来就医,仅挂他的号,便成为一种增值品。
在晓波夫妇对面一落座,黄大夫便声明,自己只喝茶,其他什么他们看着点,反正他不会动一下。
稍顷,黄大夫毫无寒暄进入主题,简明扼要讲解了这种病的来龙去脉及手术方略,还一再表示,手术风险有,但与城市交通事故相比还算低的。
晓波夫妇静静地倾听,时不时点头,嗯声连连。
今年4岁的儿子,前些天突发疾病,若不手术,一旦神经系统受到影响将终生不治。
不到半小时,黄大夫便要结束谈话:就这样吧,我还要接孙子。
你们也准备一下,明夭早起孩子不能吃饭,不能喝水……晓波顺口道:瞧您老,工作这么忙,还要带孙子,真辛苦!儿子没在本地工作,还是也忙啊?黄大夫没吱声,对视刘晓波的目光躲闪了一下。
