模糊聚类分析
模糊聚类分析实验报告
实验报告（一）一、实验内容模糊聚类在土地利用分区中的应用二、实验目的本次上机实习主要以指导学生掌握“如何应用模糊聚类方法进行土地利用规划分区”为目标。
三、实验方法本次试验是在Excel中实现。
利用《土地利用规划学》P114页数据，使用“欧氏距离法”、建模糊相似矩阵，并进行模糊聚类分析实现土地利用分区。
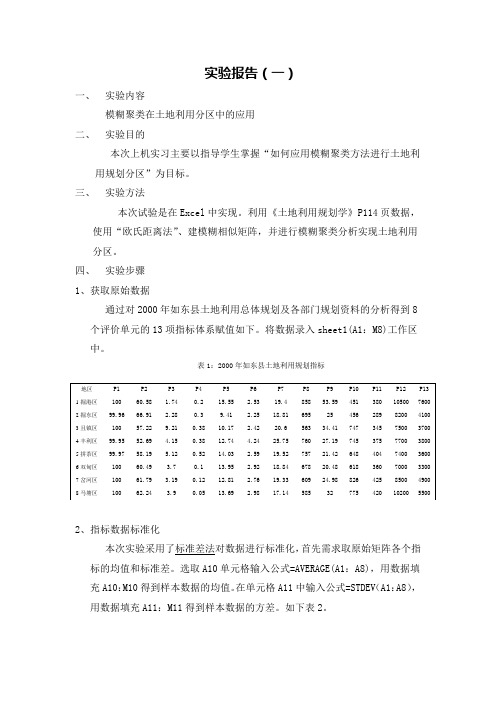
四、实验步骤1、获取原始数据通过对2000年如东县土地利用总体规划及各部门规划资料的分析得到8个评价单元的13项指标体系赋值如下。
将数据录入sheet1(A1：M8)工作区中。
表1：2000年如东县土地利用规划指标2、指标数据标准化本次实验采用了标准差法对数据进行标准化，首先需求取原始矩阵各个指标的均值和标准差。
选取A10单元格输入公式=AVERAGE(A1：A8)，用数据填充A10：M10得到样本数据的均值。
在单元格A11中输入公式=STDEV（A1：A8），用数据填充A11：M11得到样本数据的方差。
如下表2。
表2：13个指标值得均值和标准差选取A13单元格输入公式=(A1-A$10)/A$11，并用数据填充A13：M20区域得到标准化矩阵如下表3。
表3：标准化数据矩阵3、求取模糊相似矩阵本次试验是通过欧氏距离法求取模糊相似矩阵。
其数学模型为：mr ij=1−c√∑(x ik−x jk)2k=1选取A23单元格输入公式=SQRT((A$13-A13)^2+(B$13-B13)^2+(C$13-C13)^2+(D$13-D13)^2+(E$13-E13)^2+(F$13-F13)^2+(G$13-G13)^2+(H$13-H13)^2+(I$13-I13)^2+(J$13-J13)^2+(K$13-K13)^2+(L$13-L13)^2+(M$13-M13)^2)求的d11，B23中输入公式=SQRT((A$14-A13)^2+(B$14-B13)^2+(C$14-C13)^2+(D$14-D13)^2+(E$14-E13)^2+(F$14-F13)^2+(G$14-G13)^2+(H$14-H13)^2+(I$14-I13)^2+(J$14-J13)^2+(K$14-K13)^2+(L$14-L13)^2+(M$14-M13)^2)q 求的d12。
模糊聚类分析方法
第二节 模糊聚类分析方法在科学技术、经济管理中常常要按一定的标准（相似程度或亲疏关系）进行分类。
例如，根据生物的某些性状可对生物分类，根据土壤的性质可对土壤分类等。
对所研究的事物按一定标准进行分类的数学方法称为聚类分析，它是多元统计“物以类聚”的一种分类方法。
由于科学技术、经济管理中的分类界限往往不分明，因此采用模糊聚类方法通常比较符合实际。
一、模糊聚类分析的一般步骤1、第一步：数据标准化[9]（1） 数据矩阵设论域12{,,,}n U x x x =为被分类对象，每个对象又有m 个指标表示其性状，即12{,,,}i i i im x x x x = (1,2,,)i n =，于是，得到原始数据矩阵为111212122212m m n n nm x x x x x x x x x ⎛⎫⎪ ⎪ ⎪⎪⎝⎭。
其中nm x 表示第n 个分类对象的第m 个指标的原始数据。
（2） 数据标准化在实际问题中，不同的数据一般有不同的量纲，为了使不同的量纲也能进行比较，通常需要对数据做适当的变换。
但是，即使这样，得到的数据也不一定在区间[0,1]上。
因此，这里说的数据标准化，就是要根据模糊矩阵的要求，将数据压缩到区间[0,1]上。
通常有以下几种变换： ① 平移·标准差变换i k kikkx x x s -'= (1,2,,;1,2,i n k m ==其中 11n k i k i x x n ==∑，k s = 经过变换后，每个变量的均值为0，标准差为1，且消除了量纲的影响。
但是，再用得到的ikx '还不一定在区间[0,1]上。
② 平移·极差变换111m i n {}m a x {}m i n {}i k i k i nikik iki ni nx x x x x ≤≤≤≤≤≤''-''=''-，(1,2,,)k m =显然有01ikx ''≤≤，而且也消除了量纲的影响。
模糊聚类分析法
关于模糊聚类法的研究及在空间信息技术中的应用模糊聚类分析 (3)一、简介 (3)1. 简要介绍 (3)2. 分类方法 (3)1. 综述 (3)2. 系统聚类法 (2)逐步聚类法 (3)2.最优分类 (3)模糊聚类分析1. 简要介绍涉及事物之间的模糊界限时按一定要求对事物进行分类的数学方法。
聚类分析是数理统计中的一种多元分析方法，它是用数学方法定量地确定样本的亲疏关系，从而客观地划分类型。
事物之间的界限，有些是确切的，有些则是模糊的。
例如人群中的面貌相像程度之间的界限是模糊的，天气阴、晴之间的界限也是模糊的。
当聚类涉及事物之间的模糊界限时，需运用模糊聚类分析方法。
模糊聚类分析广泛应用在气象预报、地质、农业、林业等方面。
通常把被聚类的事物称为样本，将被聚类的一组事物称为样本集。
模糊聚类分析有两种基本方法：系统聚类法和逐步聚类法。
2. 分类方法1综述数据分类中，常用的分类方法有多元统计中的系统聚类法、模糊聚类分析等.在模糊聚类分析中，首先要计算模糊相似矩阵，而不同的模糊相似矩阵会产生不同的分类结果；即使采用相同的模糊相似矩阵，不同的阑值也会产生不同的分类结果•“如何确定这些分类的有效性”便成为模糊聚类和模糊。
识别研究中的一个重要问题.文献,把有效性不满意的原因归结于数据集几何结构的不理想•但笔者认为，不同的几何结构是对实际需要的反映，我们不能排除实际需要而追求所谓的“理想几何结构”，不理想的分类不应归因于数据集的几何结构.针对同一模糊相似矩阵，文献建立了确定模糊聚类有效性的方法•用固定的显著性水平，在不同分类的F—统计量和F检验临界值的差中选最大者，即为有效分类•但是，当显著性水平变化时，此方法的结果也会变化.文献引进了一种模糊划分嫡来评价模糊聚类的有效性，并人为规定当两类的嫡大于一数时，此两类可合并，通过逐次合并，最终得到有效分类•此方法人为干预较多，当这个规定数不同时，也会得到不同的结果•另外这两种方法也未比较不同模糊相似矩阵的分类结果2•系统聚类法系统聚类法是基于模糊等价关系的模糊聚类分析法。
4模糊聚类分析
四 模糊聚类分析方法模糊聚类分析，是从模糊集的观点来探讨事物的数量分类的一类方法。
这里将主要介绍基于模糊等价关系与基于最大模糊支撑树的模糊聚类分析方法。
一、基于模糊等价关系的模糊聚类分析方法基于模糊等价关系的模糊聚类分析方法的基本思想是：由于模糊等价关系~R是论域集U 与自己的直积U U ⨯上的一个模糊子集，因此可以对~R 进行分解，当用λ-水平对~R 作截集时，截得的U U ⨯的普通子集~R λ就是U 上的一个普通等价关系，也就得到了关于U 中被分类对象元素的一种分类。
当λ由1下降到0时，所得的分类由细变粗，逐渐归并，从而形成一个动态聚类谱系图。
由此可见，分类对象集U 上的模糊等价关系~R 的建立是这种聚类分析方法中的一个关键性的环节。
(一)建立模糊等价关系为了建立分类对象集合U 上的模糊等价关系R *，通常需要首先计算各个分类对象之间的相似性统计量，建立分类对象集合U 上的模糊相似关系~R 。
1.模糊相似关系的建立关于各分类对象之间相似性统计量r ij 的计算，除了采用夹角余弦公式和相似系数计算公式以外，还可以采用如下几个计算公式。
(1)数量积法：在(1)式中，M 是一个适当选择之正数，一般而言，它应满足：(2)绝对值差数法：在(2)式中，c为适当选择之正数，使0≤r ij＜1(i≠j)。
(3)最大最小值法：(4)算术平均最小法：(5)绝对值指数法：(6)指数相似系数法：在(6)式中，s k是第k个指标的方差，即2 将模糊相似关系~R 改造为迷糊等价关系~R *。
由于模糊相似关系~R 满足自反性和对称性，但一般而言，它并不满足传递性，也就是说它并不是模糊等价关系。
因此，为了聚类，我们必须采用传递闭合的性质将这种模糊相似关系~R 改造为模糊等价关系~R *。
改造的办法是将~R 自乘，即这样下去，就必然会存在一个自然数K ，使得：这时，~~k R R *=便是一个模糊等价关系了。
(二)在不同的截集水平下进行聚类用上述模糊等价关系~R *，在不同的截集水平下聚类，可以得到不同的聚类结果：二、基于最大模糊支撑树的模糊聚类分析方法除了依据模糊等价关系进行聚类分析外，还可以应用最大模糊支撑树进行聚类分析。
模糊聚类分析法
模糊聚类分析方法
分类伴随着模糊性，将模糊数学中的有关概念与方法引进聚类分析，通过建立模糊相似关系，进而对客观事物进行分类。
（1）原始数据标准化
要构造模糊关系矩阵，必须对样本进行数据进行预处理，使样本数据压缩到[0，1]闭区间内，首先求出n个样本的第j个指标的平均值和标准差。
原始数据标准化值为
运用极值标准化公式，将标准化数据压缩到[0，1]闭区间内
其中与分别表示中最小值和最大值。
（2）相似系数法——标定
为了建立模糊相似矩阵，引入相似系数
这里表示两个样本与之间相似程度的变量，当接近于1，表明这两个样本越接近。
的确定方法：
相关系数法：
归一化互信息
表示样本的表达数据在个不同表达水平的发生率（概率）
距离法：欧氏距离
C选取适当的正数，使在[0，1]区间内
（3）模糊相似矩阵——聚类
通过上述标定，得到模糊相似矩阵，反映了样本间的相似关系，但它只具有自反性和对
称性，不具有传递性，此时，可以通过平方法得到的传递闭包，而就是论域上
的一个模糊等价矩阵，选择不同的值，得到不同的水平截集，得到动态聚类结果，生成动态聚类树。
模糊聚类分析方式
第二节 模糊聚类分析方式在科学技术、经济治理中常常要按必然的标准（相似程度或亲疏关系）进行分类。
例如，依照生物的某些性状可对生物分类，依照土壤的性质可对土壤分类等。
对所研究的事物按必然标准进行分类的数学方式称为聚类分析，它是多元统计“物以类聚”的一种分类方式。
由于科学技术、经济治理中的分类界限往往不分明，因此采纳模糊聚类方式通常比较符合实际。
一、模糊聚类分析的一样步骤一、第一步：数据标准化[9]（1） 数据矩阵设论域12{,,,}n U x x x =为被分类对象，每一个对象又有m 个指标表示其性状，即12{,,,}i i i im x x x x = (1,2,,)i n =，于是，取得原始数据矩阵为111212122212m m n n nm x x x x x x x x x ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭。
其中nm x 表示第n 个分类对象的第m 个指标的原始数据。
（2） 数据标准化在实际问题中，不同的数据一样有不同的量纲，为了使不同的量纲也能进行比较，通常需要对数据做适当的变换。
可是，即便如此，取得的数据也不必然在区间[0,1]上。
因此，那个地址说的数据标准化，确实是要依照模糊矩阵的要求，将数据紧缩到区间[0,1]上。
通常有以下几种变换： ① 平移·标准差变换ik kikkx x x s -'= (1,2,,;1,2,,)i n k m ==其中 11n k ik i x x n ==∑，k s =。
通过变换后，每一个变量的均值为0，标准差为1，且排除量纲的阻碍。
可是，再用取得的ik x '还不必然在区间[0,1]上。
② 平移·极差变换111min{}max{}min{}ikik i nikikik i ni nx x x x x ≤≤≤≤≤≤''-''=''-，(1,2,,)k m =显然有01ik x ''≤≤，而且也排除量纲的阻碍。
模糊聚类分析 ppt课件
rij
xi • x j xi x j
1
xi
m
xi2k
2
,i
1,2,
,n
k1
• (3) 相关系数法
rij
m
xik xi
k1
m
(xik xi)2
k1
xjk xj
m
(xjk xj )2
k1
x i
1 m
m
x ik
k 1
x j
1 m
m
x jk
k 1
• (4) 贴近度法
• 当对象xi的特性指标向量xi=(xi1, xi2, , xim)为模 糊向量, 即xik[0, 1] (i=1,2, ,n ; k=1,2, ,m) 时, xi与xj的相似程度rij可看作模糊子集xi与xj的 贴近度。在应用中, 常见的确定方法有：最大最
X的一个分类的系列。这样, 在实际应用问题中 可以选择“某个水平”上的分类结果, 这就是模 糊聚类分析的理论基础。
• 实际问题中建立的模糊关系常常不是等价关系 而是相似关系, 这就需要将模糊相似关系改造为 模糊等价关系, 传递闭包正是这样一种工具。
• 定义 设RF(XX). 若R1F(XX)是传递的且满足： 1) RR1, 2) 若S是X上的模糊传递关系且RS, 必有R1S. 则称R1为R的传递闭包, 记为t(R). 模糊关系R的传递闭包是包含R的最小传递关系。
• 如上所述, 模糊相似矩阵R的传递闭包t(R)就是 一个模糊等价矩阵。以t(R)为基础而进行分类 的聚类方法称为模糊传递闭包法。
• 具体步骤如下: (1) 利用平方自合成方法求出模 糊相似矩阵R的传递闭包t(R); (2) 适当选取置信
水平值[0, 1], 求出t(R)的截矩阵t(R), 它是X
模糊聚类分析
模糊聚类分析系统聚类法是基于模糊等价关系的模糊聚类分析法。
在经典的聚类分析方法中可用经典等价关系对样本集X进行聚类。
设R是X上的经典等价关系。
对X中的两个元素x和y，若xRy或(x，y)∈R，则将x和y并为一类，否则x和y不属于同一类。
相应地，可用X上的模糊等价关系对样本集X进行模糊聚类。
设慒是X上的模糊等价关系，是慒的隶属函数。
对于任何α∈【0，1】，定义慒的α截关系Sα是X上的经典等价关系。
根据Sα得到X 的一种聚类,称为在α水平上的聚类。
应用这种方法,分类的结果与α的取值大小有关。
α取值越大,分的类数越多。
α小到某一值时,X中的所有样本归并为一类。
这种方法的优点在于可按实际需要选取α的值，以便得到恰当的分类。
系统聚类法的步骤如下:①用数字描述样本的特征。
设被聚类的样本集为X={x1，…,xn}。
每个样本均有p种特征,记作xi=(xi1，…，xip);i=1，2，…,n;xip表示描述样本xi的第p个特征的数。
②规定样本之间的相似系数rij(0≤rij≤1;i，j=1，…，n)。
rij描述样本xi与xj之间的差异或相似的程度。
rij 越接近于1,表明样本xi与xj之间的差异越小;rij 越接近于0，表明xi与xj之间的差异越大。
rij可用主观评定或集体评分的方法规定，也可用公式计算，如采用夹角余弦法、最小最大法、算术平均最小法等。
因为rii=1(xi与自身没有差异),rij=rji(xi与xj之间的差异等同于xj与xi之间的差异),所以由rij(i，j=1，…，n)可得X上的模糊相似关系。
一般，R不具备可传递性，因而R不一定是X上的模糊等价关系。
③运用合成运算R=R⋅R(或R=R⋅R等)求出最接近相似关系R的模糊等价关系S=R(或R等)。
若R已是模糊等价关系，则取S=R。
④选取适当水平α(0≤α≤1),得到X 的一种聚类。
模糊聚类分析方法
模糊聚类分析方法对所研究的事物按一定标准进行分类的数学方法称为聚类分析，它是多元统计“物以类聚”的一种分类方法。
载科学技术、经济管理中常常要按一定的标准（相似程度或亲疏关系）进行分类。
例如，根据生物的某些性状可对生物分类，根据土壤的性质可对土壤分类等。
由于科学技术、经济管理中的分类界限往往不分明，因此采用模糊聚类方法通常比较符合实际。
一、模糊聚类分析的一般步骤1、第一步：数据标准化[9]（1 ）数据矩阵设论域U { x1,x2,L ,x n} 为被分类对象，每个对象又有m 个指标表示其性状，即x i {x i1,x i2,L ,x im} （i 1,2,L ,n），于是，得到原始数据矩阵为L x1mx11x12L x2mx21x22M M ML x nmx n1x n2其中X nm表示第n个分类对象的第m个指标的原始数据。
（2 ）数据标准化在实际问题中，不同的数据一般有不同的量纲，为了使不同的量纲也能进行比较，通常需要对数据做适当的变换。
但是，即使这样，得到的数据也不一定在区间［0,1］上。
因此，这里说的数据标准化，就是要根据模糊矩阵的要求，将数据 压缩到区间［0,1］上。
通常有以下几种变换: ① 平移•标准差变换经过变换后，每个变量的均值为 0,标准差为1，且消除了量纲的影响。
但 是，再用得到的x ik 还不一定在区间［0,1］上 ② 平移•极差变换X k min{ X k } X ik亠 ，(k 1,2,L ,m)m.ax{X ik } min{ $}1 i n1 i n显然有0 X ik 1，而且也消除了量纲的影响。
③ 对数变换X ik lg X k(i 1,2,L ,n;k 1,2,L ,m)取对数以缩小变量间的数量级。
2、第二步：标定(建立模糊相似矩阵)设论域U {X !,X 2,L ,X n }， X i {X i1,X i2,L ,X im }，依照传统聚类方法确定相似 系数，建立模糊相似矩阵，X i 与X j 的相似程度r ij R(X i ,X j )。
模糊聚类分析
1.有联属关系的：～数，世～。 2.高等学校中教学单位：中文[department ] 。 3.关联：干～。关～[relate to ]。 4.联结，栓：名誉所～。 5.牵挂：～恋。～念。 6.是：确～实情。 7.从井下把土～上来。 8.约束;羁绊 [restrain] 愚士系俗兮,窘若囚拘。—汉· 贾谊《鹏鸟赋》 9.（jì ）结，扣 。[tie; fasten ]
模糊聚类分析
Fuzzy Clustering Analysis
零、关系与经典等价关系
方以類聚，物以群分，吉凶生矣。 《易· 繫辭上》
• 聚类是一个古老的问题，它伴随着人类社 会的产生和发展而不断深化。人类要认识 世界就必须区别不同的事物并认识事物间 的相似性。 • 按确定的标准对客观事物进行分类的数学 方法称为聚类分析。
2012年1月31日，福建宁德市古田县水口镇湾口村段
食人鱼（又名食人鲳）栖息在主流、较大支流，河宽甚 广、水流较湍急处。在巴西的亚马逊河流域，食人鱼被列 入当地最危险的四种水族生物之首。
2012年7月7日 广西柳州的张先生在柳江河遭遇3条食人鱼袭击
经典分类←→等价关系
Mona Lisa or La Gioconda (1503~1505/1507) — Louvre, Paris, France
吾未见好德如好色者也。 天下皆知美之为美，斯恶已；皆知上之为善，斯不善已。 给我一个支点和一根足够长的杠杆，我就能撬动整个地球。 勤劳一日，可得一夜安眠，勤劳一生，可得幸福长眠。 欲安其家，先安其国。 弱者坐待时机；强者制造时机。 追求科学需要特殊的勇敢。 我不知道世人怎样看我，但我自己以为我不过像一个在海 边玩耍的孩子，不时为发现比寻常更为美丽的一块卵石或 一片贝壳而沾沾自喜，至于展现在我面前的浩翰的真理海 洋，却全然没有发现 • 我没有什么特别的才能，不过喜欢寻根刨底地追究问题罢 了。
模糊聚类分析
模糊聚类分析
FCM(Fuzzy C-Means)算法是模糊聚类算法，其属于软聚类，即一个样本点可以属于多个类。
不同于层次、均值和密度聚类，一个样本只能属于或者不属于一个类。
模糊聚类的话，就是引入了隶属值的概念，即每一个样本都是使用[0,1]的隶属值（类似概率或几率值）来确定其属于各簇的程度，当你的隶属值设置成仅有0或者1的时候，它其实就是一个K-mean聚类了，同时模糊聚类存在一个限制条件就是一个样本隶属于各个簇的隶属值之和等于1。
聚类思想是使簇内的样本点之间的越小差异，而簇间的差异越大。
模糊聚类中的C与K均值中的K是相同意思，都是指聚类的个数，而在模糊聚类中除了这个C以外还有一个参数m。
其中C用于控制聚类的数目，参数m用于控制算法的柔性的，可以影响聚类的准确度，m取值太小，样本点会分布会比较分散，导致噪声（异常值）的影响很大，而取值太大，样本点会分布集中，对偏度主流的样本点的控制度又比较弱。
一般m取值为2即可，（R里面默认也是2）。
模糊聚类算法是通过迭代计算目标函数的最小值来判断算法的运转；具体的公式推导过程可以参考（https:///zjsghww/article/details/50922168）：其算法大致步骤如下：1：随机产生C个簇中心（或随机产生一些隶属值）；2：
计算隶属矩阵（或计算簇中心）；3：有了隶属矩阵（或簇中心）再重新计算簇中心（或隶属矩阵）；4：计算目标函数；5：判断目标函数达到最小值或趋于不再存在较大的波动，则停止运算，确定聚类最终结果，否则重新计算隶属矩阵（或簇中心）。
模糊聚类的实现和应用
模糊聚类的实现和应用随着数据量的不断增加和数据种类的不断增多，如何从数据中获取有用信息变得越来越重要。
在这个背景下，聚类是一种非常有用的数据挖掘技术。
特别地，模糊聚类（fuzzy clustering）可以用来处理一些复杂且不确定的数据集，如音频信号、文本和图像。
本文将讨论模糊聚类的实现和应用。
一、什么是模糊聚类？在传统聚类方法中，每个数据点只能属于一个簇。
然而，在实际情况中，有些数据点可能存在于多个簇中。
为了解决这个问题，模糊聚类被提出来。
模糊聚类允许每个数据点有一定的隶属度（membership degree），即属于每个簇的可能性是多少。
模糊聚类最初由福田洋教授于1973年提出，可以看作是K-means算法（一种典型的聚类算法）的一个改进。
二、模糊聚类的实现模糊聚类的实现很简单，只需要给定聚类的数量和数据集即可。
具体的方法如下：1. 初始化聚类中心。
2. 计算每个数据点和每个聚类中心之间的距离。
3. 计算每个数据点属于不同聚类的隶属度。
4. 根据每个数据点的隶属度更新聚类中心。
5. 重复2-4直到聚类中心没有改变或达到预设的迭代次数。
这是一个基础的模糊聚类算法，也是比较高效的。
除了这个算法，还有一些其它的模糊聚类算法，例如模糊C均值（FCM）、模糊自组织映射（FOSOM）和模糊最佳联合聚类（FOBIC）。
三、模糊聚类的应用模糊聚类已经被广泛地应用于各个领域，以下是一些例子：1. 图像分割模糊聚类可以用于对图像进行分割。
图像分割是将图像分为若干部分的过程，是图像处理中的重要技术。
模糊聚类可以根据像素的灰度值以及周围像素的值，将像素聚成几个簇。
这个方法能够用于识别图像中的不同物体。
2. 音频处理在音频处理领域，模糊聚类可以用于音乐分类和语音信号分析。
比如说，一些研究人员使用模糊聚类对音频文件进行分类。
他们首先提取音频文件的一些特征，然后使用模糊聚类算法将这些特征聚类。
这样做可以非常有效地将音乐文件分类到不同的流派和风格。
基于模糊聚类的人群行为分析
基于模糊聚类的人群行为分析随着人们生活水平的提高和科技的发展，越来越多的数据被收集和分析，数据分析在各个领域得到广泛应用。
在市场营销领域，人群行为分析是一项重要的工作，可以帮助企业更精准地定位客户和制定营销策略。
本文将介绍基于模糊聚类的人群行为分析方法，探讨其原理和应用场景。
一、模糊聚类的原理模糊聚类是一种聚类分析方法，与传统的硬聚类不同，它通过计算样本与各个聚类中心之间的相似性来确定样本所属类别的概率，因此可以将样本分类到多个不同的类别中。
模糊聚类的核心是模糊集合论，它可以将元素归属到不同的隶属度中。
在进行聚类时，首先需要设置聚类数量，然后随机选取几个样本作为聚类中心。
接着计算每个样本到各个聚类中心的距离，根据距离计算样本与各个聚类中心的隶属度。
最后根据隶属度将样本分类到不同的类别中，同时更新聚类中心的位置。
这个过程会循环迭代多次，直到聚类中心的位置稳定不变为止。
二、基于模糊聚类的人群行为分析在市场营销中，人群行为分析是非常重要的一环。
它可以通过收集和分析用户数据，了解用户的行为和喜好，然后根据此制定个性化的营销策略，提高销售和用户满意度。
基于模糊聚类的人群行为分析适用于以下场景：1、用户分类分析通过分析用户的浏览、搜索、购买等行为数据，可以将用户分为不同的类别。
这可以帮助企业精确了解不同用户群体的需求和偏好，制定不同的营销计划。
2、商品分类分析通过分析用户对不同商品的点击、浏览、收藏等行为，可以将商品分为不同的类别。
这可以帮助企业了解哪些商品是热门商品，哪些商品是长尾商品，然后根据情况调整进货和促销策略。
3、内容分类分析通过分析用户对不同类型的内容的浏览和收藏行为，可以将内容分为不同的类别。
这可以帮助企业制定更具针对性的内容营销策略，在各个媒体上发布不同的内容，以提高用户的关注度和转化率。
三、结语基于模糊聚类的人群行为分析是一种非常有效的分析方法，可以帮助企业更精准地了解用户和市场的需求，制定个性化的营销策略。
Matlab笔记-模糊聚类分析原理及实现
23. 模糊聚类分析原理及实现聚类分析，就是用数学方法研究和处理所给定对象，按照事物间的相似性进行区分和分类的过程。
传统的聚类分析是一种硬划分，它把每个待识别的对象严格地划分到某个类中，具有非此即彼的性质，这种分类的类别界限是分明的。
随着模糊理论的建立，人们开始用模糊的方法来处理聚类问题，称为模糊聚类分析。
由于模糊聚类得到了样本数与各个类别的不确定性程度，表达了样本类属的中介性，即建立起了样本对于类别的不确定性的描述，能更客观地反映现实世界。
本篇先介绍传统的两种（适合数据量较小情形，及理解模糊聚类原理）：基于择近原则、模糊等价关系的模糊聚类方法。
（一）预备知识一、模糊等价矩阵定义1设R=(r ij )n ×n 为模糊矩阵，I 为n 阶单位矩阵，若R 满足 i) 自反性：I ≤R （等价于r ii =1）； ii) 对称性：R T =R;则称R 为模糊相似矩阵，若再满足iii) 传递性：R 2≤R （等价于1()nik kj ij k r r r =∨∧≤）则称R 为模糊等价矩阵。
定理1设R 为n 阶模糊相似矩阵，则存在一个最小的自然数k（k <n ）, 使得R k 为模糊等价矩阵，且对一切大于k 的自然数l ，恒有R l =R k . R k 称为R 的传递闭包矩阵，记为t(R). 二、模糊矩阵的λ-截矩阵定义2设A =(a ij )n ×m 为模糊矩阵，对任意的λ∈[0,1], 作矩阵()()ij n mA a λλ⨯=其中，()1, 0, ij ijij a aa λλλ≥⎧=⎨<⎩称为模糊矩阵A 的λ-截矩阵。
显然，A λ为布尔矩阵，且其等价性与与A 一致。
意义：将模糊等价矩阵转化为等价的布尔矩阵，可以得到有限论域上的普通等价关系，而等价关系是可以分类的。
因此，当λ在[0,1]上变动时，由A λ得到不同的分类。
若λ1＜λ2, 则A λ1≥A λ2, 从而由A λ2确定的分类是由A λ1确定的分类的加细。
模糊聚类分析
模糊聚类分析----96845308-7160-11ec-a68e-7cb59b590d7d聚类分析就是将一个没有类别标记的样本集按照某种准则划分成若干个子集（类），使相似的样本尽可能归为一类，而不相似的样本尽可能划分到不同的类中。
由于在对样本集进行聚类的过程中，没有任何关于类别的先验知识，所以聚类分析属于无监督分类的范畴。
传统的聚类分析是一种硬划分，它严格地将每个待识别对象划分为一个类。
阶级划分的界限是明确的，具有非此即彼的性质。
在现实世界中，无论是一组对象根据其亲和力和相似性形成一个组，还是一个对象是否属于一个类别，其边界往往是不明确的，并且具有“这个和那个”的性质。
对于这种具有不确定性的聚类问题，模糊聚类分析提供了一种强有力的分析工具。
模糊聚类分析能够建立样本对于类别的不确定性描述，表达样本类属的中介性，已经成为聚类分析研究的主流。
粗略来讲，模糊聚类分析方法可分为两类：基于模糊等价关系的聚类方法和基于目标函数的聚类方法。
有时，这两类方法也结合起来使用。
一、数据预处理在模糊聚类分析中，我们称待分类的对象为样本。
要对样本进行合理的分类，首先应考虑样本的各种特性指标（观测数据）。
设有n个被分类对象，即样本集为x={x1，x2，…，xn}每一个xi有m个特性指标，即xi可表示为特性指标向量xi={xi1，xi2，…，xim}其中xij表示第i个样本的第j个特性指标。
于是，n个样本的特性指标矩阵为⎜⎜x21⎜M⎜⎜十、⎜n1x12lx1m⎜x22lx2m⎜xn2lxnm⎜⎜通常，我们也将样本集记为特性指标矩阵的形式，即x=(xij)n×m。
如果M个特征指标的维度和数量级不同，在运行过程中可能会突出一些大数量级特征指标的作用，而一些小数量级特征指标的作用可能会减少甚至被排除，导致每个特征指标的分类缺乏统一的尺度。
因此，为了消除不同特征指标单位和数量级的影响，当特征指标的维度和数量级不同时，通常会提前对各种指标值进行数据标准化（归一化），使每个指标值统一在一个共同的数值特征范围内。
模糊聚类分析方法
第二节 模糊聚类分析方法在科学技术、经济管理中常常要按一定的标准（相似程度或亲疏关系）进行分类。
例如，根据生物的某些性状可对生物分类，根据土壤的性质可对土壤分类等。
对所研究的事物按一定标准进行分类的数学方法称为聚类分析，它是多元统计“物以类聚”的一种分类方法。
由于科学技术、经济管理中的分类界限往往不分明，因此采用模糊聚类方法通常比较符合实际。
一、模糊聚类分析的一般步骤1、第一步：数据标准化[9]（1） 数据矩阵设论域12{,,,}n U x x x =为被分类对象，每个对象又有m 个指标表示其性状，即12{,,,}i i i im x x x x = (1,2,,)i n =，于是，得到原始数据矩阵为111212122212m m n n nm x x x x x x x x x ⎛⎫ ⎪ ⎪⎪ ⎪⎝⎭。
其中nm x 表示第n 个分类对象的第m 个指标的原始数据。
（2） 数据标准化在实际问题中，不同的数据一般有不同的量纲，为了使不同的量纲也能进行比较，通常需要对数据做适当的变换。
但是，即使这样，得到的数据也不一定在区间[0,1]上。
因此，这里说的数据标准化，就是要根据模糊矩阵的要求，将数据压缩到区间[0,1]上。
通常有以下几种变换： ① 平移·标准差变换ik kikkx x x s -'= (1,2,,;1,2,,)i n k m ==其中 11n k ik i x x n ==∑，k s = 经过变换后，每个变量的均值为0，标准差为1，且消除了量纲的影响。
但是，再用得到的ikx '还不一定在区间[0,1]上。
② 平移·极差变换111min{}max{}min{}ikik i nikikik i ni nx x x x x ≤≤≤≤≤≤''-''=''-，(1,2,,)k m =显然有01ikx ''≤≤，而且也消除了量纲的影响。
模糊聚类的分析
模糊聚类的分析模糊聚类是一种新兴的数据挖掘技术，它既可以结合经典聚类方法，又可以采用模糊逻辑理论。
模糊聚类把数据聚类的过程分解为两个阶段：测量和模糊聚类。
它的优点在于可以处理不确定的数据，并且对大量的数据有明显的优势。
模糊聚类是以模糊逻辑理论为基础的一种聚类方法。
与常规的聚类方法不同，模糊聚类的目的是把数据点归类到具有不同程度相似度的聚类中。
模糊聚类可以使用模糊逻辑，捕捉数据点之间不显著的相关性，而绕开实际相关矩阵中的障碍。
模糊聚类的核心过程主要有两种：测量和模糊聚类。
测量过程是模糊聚类中最重要的步骤，其目的是识别数据点之间的相似度。
模糊聚类过程的核心是构建模糊关联矩阵，它可以把数据点归类到不同的相似度类别中。
通常，模糊聚类的测量过程主要采用距离度量和角度度量来完成。
距离度量主要是指以欧氏距离、曼哈顿距离和切比雪夫距离为代表，能够直接测量数据点之间的距离；角度度量则是以余弦相似度为代表，能够衡量数据点之间的角度大小。
模糊聚类的聚类过程是把数据点归类到不同的聚类中。
这一步骤是根据距离或角度度量值来实现的，它把数据点归类到按照相似度排列的聚类中。
通常，模糊聚类的聚类过程主要由两个步骤组成：构建模糊关联矩阵（FCM）和求解模糊关联矩阵（FCM）。
模糊聚类有着很多优点：首先，它可以处理不确定性数据，它可以综合考虑模糊逻辑中不确定性的因素；其次，它对大数据有明显的优势，它可以对大规模的数据进行有效的聚类处理。
在聚类分析的实际应用中，模糊聚类的作用也正在发挥出来，它可以用于汽车维修、航空航行反演分析、银行信用风险分析、智能多媒体表达等多个领域中。
同时，模糊聚类也把聚类自身的边界变得更加模糊，让聚类结果更加灵活，同时也提高了聚类结果的可解释性。
综上所述，模糊聚类是一种新型的数据挖掘方法，它在聚类分析领域有着重要的意义，它的应用可以帮助我们把数据点归类到不同的相似度类别中，使得分析过程更加针对性和高效。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 目录 1引言: ................................................................................................................... 3 2 理论准备： ......................................................................................................... 3 2.1 模糊集合理论 .............................................................................................. 3 2.2模糊C均值聚类(FCM) ................................................................................... 4 2.3 加权模糊C均值聚类(WFCM) ......................................................................... 4 3 聚类分析实例 ..................................................................................................... 5 3.1数据准备 ...................................................................................................... 5 3.1.1数据表示 ............................................................................................... 5 3.1.2数据预处理 ........................................................................................... 5 3.1.3 确定聚类个数 ....................................................................................... 6 3.2 借助clementine软件进行K-means聚类 ...................................................... 7 3.2.1 样本在各类中集中程度 ........................................................................ 8 3.2.2 原始数据的分类结果 ............................................................................ 8 3.2.3结果分析 ............................................................................................... 9 3.3模糊C均值聚类 .......................................................................................... 10 3.3.1 数据集的模糊C划分 .......................................................................... 10 3.3.2 模糊C均值聚类的目标函数求解方法 ................................................ 10 3.3.3 MATLAB软件辅助求解参数设置 .......................................................... 11 3.3.4符号表示 ............................................................................................. 11 2
3.3.5代码实现过程 ..................................................................................... 11 3.3.6 FCM聚类分析 ..................................................................................... 11 3．4 WFCM算法 ................................................................................................. 14 3.4.1 WFCM聚类结果展示 ............................................................................ 14 3.4.2样本归类 ............................................................................................. 16 3.4.3归类代码实现 ..................................................................................... 16 4．结论 ................................................................................................................ 17 5 参考文献........................................................................................................... 18 6 附录 .................................................................................................................. 18 3
模糊聚类与非模糊聚类比较分析 摘要： 聚类分析是根据样本间的相似度实现对样本的划分，属于无监督分类。传统的聚类分析是研究“非此即彼”的分类问题，分类结果样本属于哪一类很明确，而很多实际的分类问题常伴有模糊性，即它不仅仅是属于一个特定的类，而是“既此又彼”。因此为了探究模糊聚类与非模糊聚类之间聚类结果的差别，本文首先采用系统聚类方法对上市公司132支股票数据进行聚类，确定比较合理的聚类数目为11类，然后分别采用K-means聚类与模糊聚类方法对股票数据进行聚类分析，最终得出模糊聚类在本案例中比K-means聚类更符合实际。 关键字：模糊集合，K-means聚类，FCM聚类，WFCM聚类
1引言: 聚类分析是多元统计分析的方法之一，属于无监督分类，是根据样本集的内在结构，按照样本之间相似度进行划分，使得同类样本之间相似性尽可能大，不同类样本之间差异性尽可能大。传统的聚类分析属于硬化分，研究对象的性质是非此即彼的，然而，现实生活中大多数事物具有亦此亦彼的性质。因此传统的聚类分析方法往往不能很好的解决具有模糊性的聚类问题。为此，模糊集合理论开始被应用到分类领域，并取得不错成果。 本文的研究目的是通过对比传统聚类和模糊聚类的聚类结果，找出二者之间的不同之处，并说明两种聚类分析方法在实例中应用的优缺点。
2理论准备： 2.1 模糊集合理论 模糊集合定义：设Ｕ 为论域，则称由如下实值函数μA：Ｕ [ 0，1 ]， u μA( u )所确定的集合 A 为Ｕ上的模糊集合，而称μA为模糊集合A 的隶
属函数，μA ( u )称为元素 u 对于A 的隶属度。若A(u) =１，则认为u完全属于A； 若A(u) =０，则认为u完全不属于A，模糊集合是经典集合的推广。 4
2.2模糊C均值聚类(FCM) 预先给定类别数c，把含有n个样本的数据集分成c个模糊类，用每个类的类别中心 𝑉𝑗 代表该类，通过反复迭代运算，逐步降低目标函数的误差值，当目标函数收敛时，聚类完成。 目标函数:
211min,cnmFCMijJUPijijd(1)
约束条件：
i11cij (2)
𝜇𝑖𝑗∈ 0,1 ，∀i,j 2.3 加权模糊C均值聚类(WFCM) 算法过程与FCM类似，只是目标函数不同，WFCM算法考虑了各样本点对分类的重要性，在FCM算法中加入了权值𝑝𝑖，𝑝𝑖称为样本点的密度，本文中𝑝𝑖采用径向基函数方法来确定，当样本点x远离类中心𝑥𝑐时函数取值很小，此时该样本点对分类的重要性比较小。最常用的径向基函数是高斯核函数 ,形式为 exp^2/2*^2cckxxxx (3)
目标函数： 211min,cnmFCMijJUPijiijpd (4)
约束条件： 𝜇𝑖𝑗∈ 0,1 ,∀ 𝑖,𝑗,11ciji (5)