SSP第3章倒格子布里渊110827-P
《异度装甲》完全攻略

《异度装甲》完全攻略DISK1CHAPTER 1 はじまりは、山奥の村ラハン“恩,终于画完了,”飞(フェイ)伸了个懒腰,“好吧,是时候休息一下了。
”(现在就可以控制飞了,先熟悉一下各键的功能吧)上楼和村长面前的迪莫西谈话(一个小技巧,如果谈话时可以走动,说明此次交谈无关紧要;反之,则是剧情对话或重要对话)。
刚要出门,阿露露的弟弟丹闯了进来,发了一通牢骚后,要飞来外面和他谈谈。
出村长家找到丹,他竟要求你带着姐姐私奔(汗……),此处两个选项,分别是答应和拒绝,选哪个都不要紧。
接下来去见阿露露,她家门口站着一个女的,很好找。
到2楼和阿露露谈话,答应帮她去向希坦(シタン)先生借照相机和灯(不得不PS一下,阿露露家的BGM很好听)。
在离开村子前,先把村子里的宝物搜刮一空吧,到了先生家后就再也回不来了。
一切准备就绪后,出发!(阿露露的家)CHAPTER 2 谷をこえ、ひとり山道をゆけば没什么要特别注意的,记得去拿宝箱和蜘蛛。
有一处地方要用大跳(加速+跳)。
这里的敌人是狼和小猪(汗……),狼会用连续攻击,小猪会用HP吸收,都很容易对付,找找战斗的感觉吧。
过了吊桥,朝右上方走就到了先生家。
CHAPTER 3 つかの間の平穏山頂の家にて先去厨房见见唯阿姨和先生的女儿米多莉(ミドリ)吧,听唯阿姨说先生在机械屋那边,过去看看,果然在屋顶看到了希坦。
他让飞先等等,于是飞走进屋里,发现一个奇怪的盒子,调查一下,居然是一个会演奏音乐的天使像。
这时先生也进来了,一番寒喧后,大家准备去吃晚餐了。
然而,当飞一出门,天使像突然碎掉--这,难道是什么预兆吗?希坦若有所思。
CHAPTER 4 夜道で見た!闇にふるもの晚饭后告辞先生一家,朝村子走去。
刚走到吊桥,听到巨大的轰鸣声,还有东西从头上飞过。
这时先生匆匆赶到,据他说这是邻国基斯雷夫的机甲群。
正说着,从ラハン村方向传来了爆炸声!两人急忙赶去……村里要打一场机甲战,对手是2架ムシャ百式,HP只有150左右,想输都难。
布里渊区图示
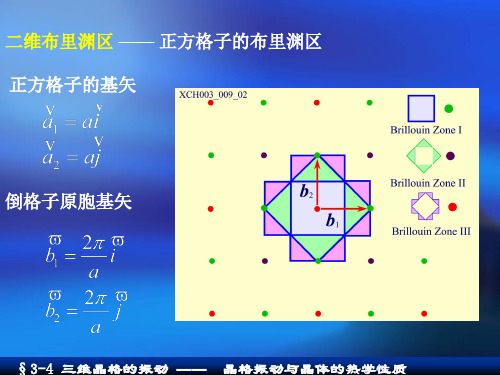
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
SSP第3章倒格子布里渊110827-P

FCC (正基矢) a (j + k) 2 a a 2 = (k + i ) 2 a a 3 = (i + j) 2
可见 BCC 倒格子是一个边长为4π/a 的FCC格子。 倒格子原点最近邻有十二个格点。 所以BCC晶格第一布里渊区是一个 正十二面体。
17
3.5 晶体的X射线衍射
所以有 eiK h ⋅R l = 1
h
h
h
Q R l 是正格矢, ∴ K h应是 R l 的倒格矢
F (Kh)是物理量 Γ (r) 在傅氏 空间的表示形式
即:物理量在正格子中表示和在倒格子中表示满足傅氏变换关系; 正空间周期性物理量的傅氏空间就是其倒空间; 正格子和倒格子互为傅氏变换。
10
3Байду номын сангаас3 倒格子的性质
13
3.4 布里渊区
3.4.2 布里渊区界面方程
令,Kh为倒格矢,如下图, A为Kh的垂直平分面 k为倒空间的矢量 则,A上所有点都应满足
1 K h2 2 证明:由图可见, k ⋅Kh = Q K 1 k ⋅ h = Kh Kh 2 1 Kh 2
A
1 Kh 2
0 k
k’
Kh
∴
k ⋅Kh =
1 2 Kh 2
可以验证,当波矢Kh取为
K h = h1b1 + h2b 2 + h3b 3, h1h2 h3为整数
其中 b1,b2,b3 由 验证:
a i ⋅b j = 2πδ ij
确定,则以上条件成立。
K h ⋅ R l = (h1b1 + h2b 2 + h3b 3 ) ⋅ (l1a1 + l2a 2 + l3a3 )
孙会元固体物理基础第三章能带论课件3.10 金属的费米面和能带论的局限性

因此,费米面完全在第一布里渊区内,在周期势的作用下, 费米面都是稍稍变形的球。
对于立方晶系的二价碱土金属(Ca(fcc),Sr(fcc), Ba(bcc)),每个原胞有两个 s 价电子。 由于费米球和第一布里渊区等体积,因而和区界面 相交,导致电子并没有全部在第一布里渊区,而是有一 部分填到了第二区,因此费米面在第一区形成空穴球面 ,第二区形成电子球面. 对于六角密堆积结构的二价金属Be、Mg,由于在第 一布里渊区六角面上几何结构因子为零,弱周期势场在 此不产生带隙,仅当考虑二级效应,如自旋轨道耦合时 才能解除简并。 这些金属的费米面可看作由自由电子球被布里渊区 边界切割,并将高布里渊区部分移到第一布里渊区得到 .因此,费米面的形状很复杂,会出现空穴型宝冠状、电 子型雪茄状等.
以第一布里渊区中心为原点,以费米波矢为半径画 自由电子的费米圆. (费米面的广延区图)
3) 将落在各个布里渊区的费米球片断平移适当 的倒格矢进入简约布里渊区中等价部位(费米面 的简约区图)。
第一区
=1
第一区
第二区
=2,3
第三区圆,即费米面 同布里渊区边界垂直相交,尖角处要钝化,就 可以得到近自由电子的费米面。
三价金属铝,具有面心立方结构,每个原胞含有 3个价电子,自由电子的费米球将延伸至第一布 里渊区以外.由于周期势的作用,使得第二、第三 布里渊区的费米面变得支离破碎.
一价贵金属包括Cu,Ag,Au等均为面心立方结构,它 们s 轨道附近还有d轨道,形成固体时, s 轨道交叠积分 大, 演变成宽的s带, d轨道因交叠积分小, 变成一窄的d 带. 11个电子将d带填满, s带填了一半. 费米面在s带中, 但d带离费米面很近, 导致球形费米面发生畸变, 因而 出现复杂的输运行为, 但是仍属于单带金属. 比如对于金属铜,假设晶格常数为a,其费米半径
§5.5 布里渊区

§5.5 布里渊区本节我们举例说明二维和三维晶格的布里渊区。
一、二维正方格子正格子原胞基矢 a a a a == 2,1; 倒格子原胞基矢 ab a b π=π=22,21 。
如图5.10所示,倒格子空间离原点最近的倒格点有四个,相应的倒格矢为b b b b 2,2,1,1--, 它们的垂直平分线的坐标是 ak x π±= 及 a k y π±= 这些垂直平分线围成的区域就是简约布里渊区。
它也是一个正方形,其中一些特殊点和线有惯用的符号表示,中心:Γ; 边界线中心:X ; 角顶点:M; ΓX 线:∆; ΓM 线:∑。
离Γ点次近邻的四个倒格点相应的倒格矢是b b b b b b b b 21,21),2(1,21+--+-+它们的垂直平分线,同第一布里渊区边界围成的区域合起来成为第二布里渊区,这个区的各部分别平移一个倒格矢,可以同第一个区重合。
同理可得第三,第四,……,一系列布里渊区。
二、体心立方格子正基矢 )(21k j i a a ++-=, )(22a a +-= , )(23a a -+= 。
可证倒基矢 )(21k j ab +π= , )(22k i ab +π= , )(23i j ab +π= 。
(习题:证明bcc 的倒格子是fcc 。
)倒格矢:图5.10])21()31()32[(2332211k n n j n n i n n ab n b n b n G n +++++π=++= 离原点最近的有12个倒格点,其坐标可一般地写为)21,31,32(2n n n n n n a +++π. 具体写出是)0,1,1(2a π, )0,1,1(2aπ )0,1,1(2a π, )0,1,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,1,0(2a π, )1,1,0(2aπ )1,1,0(2a π, )1,1,0(2aπ 相应的倒格矢长度为 π=22),,(321an n n G 这12个倒格矢的中垂线围成菱形正面体,称为简约布里渊区,如图5.11所示,其体积正好是倒格子原胞的大小。
布里渊区

布里渊区
主讲人: 主讲人:许本超 答疑人: 答疑人:李海龙 封福明
固体物理 固体物理
内容
• • • • • • • • • 1.倒易空间 2. 布里渊区基本概念 3. 典型格子的第一布里渊区 4.布里渊区的几何性质 5. 衍射条件在布里渊区诠释 6.布里渊区中的K点 7.布里渊区和能带的关系 8.布里渊区和费米面 9.MS计算能带实例图
14
固体物理 固体物理
7.2布里渊区和能带的关系
能带论的基本出发点: 能带论的基本出发点 固体中的电子可以在整个固体中运动 电子在运动过程中要受晶格原子势场的作用 由于周期场的微扰, 由于周期场的微扰,
E
E6
E(k)函数在布里渊区 函数在布里渊区
允许带
E5
边界k=± 边界 ±nπ/a处出现 处出现
3.2体心立方晶格的F.B.Z 体心立方晶格的F.B.Z 体心立方晶格的 体心立方晶格的倒格子为面心立方晶格
可以看出, 可以看出,面心立方倒 格子(即体心立方晶格) 格子(即体心立方晶格) 的F.B.Z为正菱形十二 为正菱形十二 面体(非正十二面体) 面体(非正十二面体)
8
固体物理 固体物理
3.3面心立方晶格的F.B.Z 面心立方晶格的 面心立方晶格的F.B.Z 面心立方晶格的倒格子为体心立方晶格
如右图所示, 如右图所示,黑框为体心立方 倒格子,取其体心(黄点) 倒格子,取其体心(黄点)作 为原点,红点(8个 为原点,红点(8个)为此原 点最相邻的倒格点,蓝点(6 点最相邻的倒格点,蓝点( 个)为此原点次相邻倒格点 可以看出, 可以看出,体心立方倒 格子(即面心立方晶格) 格子(即面心立方晶格) 的F.B.Z为截角的八面体 为截角的八面体 十四面体) (十四面体)
黄昆版固体物理学课后答案解析答案 (2)

《固体物理学》习题解答黄昆 原着 韩汝琦改编 (陈志远解答,仅供参考)第一章 晶体结构、解:实验表明,很多元素的原子或离子都具有或接近于球形对称结构。
因此,可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。
这样,一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。
它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比,即:晶体原胞的空间利用率, VcnVx = (1)对于简立方结构:(见教材P2图1-1) a=2r , V=3r 34π,Vc=a 3,n=1∴52.06r8r34a r 34x 3333=π=π=π=(2)对于体心立方:晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= (3)对于面心立方:晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4,Vc=a 3(4)对于六角密排:a=2r 晶胞面积:S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积:V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个(5)对于金刚石结构,晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 3、试证:六方密排堆积结构中633.1)38(ac 2/1≈=证明:在六角密堆积结构中,第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形,第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切,于是:NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。
…、证明:面心立方的倒格子是体心立方;体心立方的倒格子是面心立方。
证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩r r r r r rr r r由倒格子基矢的定义:1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r同理可得:232()2()b i j k ab i j k aππ=-+=+-r rr r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
《方根书简》图文攻略全章节图文流程攻略

什么鬼,跟鬼魂通信? 应老板娘的要求,将亚弥制服照递给老板娘,虽然老板娘并没有实际 见过本人。但也告知了这身制服来自松江大庭高中,并热情地表示会问询 同一辈于该高中毕业的表妹。 这么些惊悚的信息累积起来,自然疲劳至极,去大澡堂放松时被一个 奇怪的老人搭讪。老人家自称泉小云,年轻时为了追捕犯人前往各地城 市。
获得猫护符??任务达成移动松江市公所继续在后门外找到逗弄猫的眼镜??对当然不给好脸但是接下来玩家将开始体验本作最为刺激的追问模式了所谓追问模式就是按照定顺序使中的线索技巧性地击溃对的防线从获得重要的情报
《方根书简》图文攻略 全章节图文流程攻略
《方根书简》这款悬疑类冒险解谜游戏很多玩家没有体验过,下面小 编就为大家带来《方根书简》全章节图文流程攻略,希望对各位玩家有所 帮助。 游戏介绍 《方根书简》是一款悬疑类冒险解谜游戏,也是“角川游戏悬疑系 列”的第一弹,在这里将会以地方文化和历史作为故事基础,上演一段精彩 且跌宕起伏的人生故事。该作目前已经正式上架了,今天着迷小编为大家 带来的是方根书简中文版图文攻略,包括游戏剧情,结局等相关内容。
第二封信完全是在说眼镜仔 照样是回信环节: P. S . Max想利用高中生活的最后一年做些什么呢? 我想去废墟探险 我想研究历史 √我想参加学校的活动 岛根有什么不可思议的故事吗? 岛根有什么著名武将吗? √岛根盛行哪种活动呢? 移动至空地,与路过的阿姨交谈,将亚弥制服照交给她看,对方居然 说洋房失火之前就在窗边看到应该已经去世的亚弥,而且是坐在书桌前写 信的样子。 闹鬼的说法还真是多,先去信上说的八重垣神社的镜池吧。究竟往哪 走呢,查看观光导览获知地点后,移动至八重垣神社。 到了神社,调查旁边的树木,便能找到通往镜池的道路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 倒格子的定义
3.2.1 倒格子定义之一
设,布拉菲格子基矢为 a1,a2,a3, 将由矢量
R l = l1a1 + l2a 2 + l3a3, li 为整数, = 1,2,3 i
决定的格子,称为正格子, 将满足下述关系:
2π ai ⋅ b j = 2πδ ij = 0 i= j i≠ j i, j = 1,2,3
16
3.4 布里渊区
3.4.5 体心立方(BCC)的第一布里渊区
BCC (正基矢) a a1 = (-i + j + k ) 2 a a 2 = (i − j + k ) 2 a a 3 = (i + j − k ) 2
b1 = 2π a 2 × a3 a1 ⋅ (a 2 × a3 )
BCC (倒基矢) 2π b1 = (j + k) a 2π b2 = (k + i ) a 2π b3 = (i + j) a
3.3.2 倒格子的倒格子是原布拉菲格子
按倒格子基矢定义构造基矢 c1, c2, c3,可以证明 ci = ai,i = 1,2,3。
2π (b 2 × b 3 ) 2π = * b 2 × b 3 利用 a × b × c = b(a ⋅ c) − c(a ⋅ b) b1 ⋅ b 2 × b 3 Ω (a3 × a1 ) × (a1 × a 2 ) (2π ) 2 = a1[(a3 × a1 ) ⋅ a 2 ] Q b 2 × b3 = (a3 × a1 ) × (a1 × a 2 ) Ω2 − a 2 [(a3 × a1 ) ⋅ a1 ] 2 2 (2π ) (2π ) = a1[(a3 × a1 ) ⋅ a 2 ] = a1Ω = a1 2 Ω Ω = a1Ω 2π (2π ) 2 2π (b 2 × b 3 ) Rl,Kh所代表点的集合都 a1 = * ∴ c1 = Ω b1 ⋅ b 2 × b 3 Ω 是布拉菲格子,且互为 正倒格子。事实上在 * 3 又 Ω Ω = (2π ) eiK h ⋅R l = 1 ∴ c1 = a1 同理:c 2 = a 2, c3 = a 3 中 Rl,Kh地位全同。 即令:c1 =
b3 =
2π a1 × a 2 a1 ⋅ (a 2 × a3 )
5
3.2 倒格子的定义
3.2.3 倒格子定义之三
采用波函数定义倒格子 设有以 a1,a2,a3为基矢的布拉菲格子
R l = l1a1 + l2a 2 + l3a3, li 为整数, = 1,2,3 i
并有平面波 eik⋅r 。 定义,具有给定布拉菲格子周期性的那些平面波,其波矢 Kh 所 代表点的集合称为 Rl 的倒格子。 其数学表达为 ,如有
∴ d h1h2h3 = OA⋅ G h1h2h3 / Gh1h2h3
→
a3 a3/h3 0 a1/h1 A C Gh1h2h3 B a2 a2/h2 a1
a1 = ⋅ (h1b1 + h2b 2 + h3b 3 ) / Gh1h2h3 h1 = 2π / Gh1h2h3 即:Gh1h2h3 = 2π / d h1h2h3,
= 2π (h1l1 + h2l2 + h3l3 ) = 2πµ Q li , hi 都是整数, µ 也应是整数, ∴ eiK h ⋅R l = ei 2πµ = 1
7
3.3 倒格子的性质
3.3.1 倒格子原胞体积 Ω*与正格子原胞体积 Ω 的关系
可以证明,
Ω* = (2π )3 /Ω, 即,Ω*Ω = (2π )3 (a 2 × a3 ) (a3 × a1 ) (a1 × a 2 ) ⋅[ × ] a1 ⋅ (a 2 × a3 ) a1 ⋅ (a 2 × a 3 ) a1 ⋅ (a 2 × a3 )
13
3.4 布里渊区
3.4.2 布里渊区界面方程
令,Kh为倒格矢,如下图, A为Kh的垂直平分面 k为倒空间的矢量 则,A上所有点都应满足
1 K h2 2 证明:由图可见, k ⋅Kh = Q K 1 k ⋅ h = Kh Kh 2 1 Kh 2
A
1 Kh 2
0 k
k’
Kh
∴
k ⋅Kh =
1 2 Kh 2
15
3.4 布里渊区
3.4.4 面心立方(FCC)的第一布里渊区
FCC (正基矢) a a1 = ( j + k ) 2 a a 2 = (k + i ) 2 a a3 = (i + j) 2
FCC (倒基矢) 2π (-i + j + k ) a 2π b2 = (i − j + k ) a 2π b3 = (i + j − k ) a b1 =
b1 = 2π a 2 × a3 a1 ⋅ (a 2 × a3 )
BCC (正基矢) a a1 = (-i + j + k ) 2 a a 2 = (i − j + k ) 2 a a 3 = (i + j − k ) 2
可见 FCC倒格子是一个边长为 4π/a的BCC格子。 倒格子原点最近邻有八个格点。 所以FCC晶格第一布里渊区是一个 截顶十四面体。
3.3.4 倒格矢 G h1h2h3 = h1b1 + h2b 2 + h3b 3 与正格子中晶面系 (h1h2h3) 正交
因为已知,晶面系 (h1h2h3) 中最靠近原点的晶面 ABC 在基矢a1, a2, a3上的截距分别为 a1/h1, a2/h2, a3/h3,如下图,Gh1h2h3 为 晶面 ABC 的法线, → → → → → → a a a3 a1 有, CA = OA− OC = − , CB = OB − OC = 2 h − 3 h h1 h3 2 3
14
3.4 布里渊区
3.4.3 布里渊区性质
1、各布里渊区的形状都关于原点对 称。 2、各布里渊区都可通过平移倒格矢 到达第一布里渊区,且与之完全重合。 3、每个布里渊区的体积都相等,且 等于倒格子原胞体积。
G
4、布里渊区的形状完全由晶体布拉菲格子决定(倒格矢由正格 矢定义),所以不管晶体的基元代表什么,只要布拉菲格子相同, 布里渊区形状就相同。 5、简约布里渊区----第一布里渊区
9
3.3 倒格子的性质
3.3.3 晶体中物理量的傅里叶变换关系
设,晶体任一 r 处有物理量Γ (r), 由晶格的周期性,应有Γ (r) = Γ (r+Rl),Rl为任意正格矢, 周期性函数可作傅里叶级数展开如下:
Γ (r ) = ∑ F (K h )eiK h ⋅r Γ (r + R l ) = ∑ F (K h )eiK h ⋅(r + R l ) = ∑ F (K h )eiK h ⋅r ) ⋅ eiK h ⋅R l
= (a 2 × a3 ) ⋅ {a1[(a3 × a1 ) ⋅ a 2 ] − a 2 [(a3 × a1 ) ⋅ a1 ]} = (a 2 × a3 ) ⋅ a1[(a3 × a1 ) ⋅ a 2 ] = ΩΩ = Ω2
∴ Ω* = (2π )3 /Ω, 即,Ω*Ω = (2π )3
8
3.3 倒格子的性质
eiK h ⋅( R l + r ) = eiK h ⋅r
对于任何 r 和 Rl 成立,那么 Kh 决定的格子就是布拉菲格子 Rl 的 倒格子。
6
3.2 倒格子的定义
倒格子定义之三验证
由以上定义,要求 Kh满足,
eiK h ⋅R l = 1
这是因为,
eiK h ⋅( R l + r ) = eiK h ⋅r , 即:eiK h ⋅R l ⋅ eiK h ⋅r = eiK h ⋅r,即:eiK h ⋅R l = 1
∴ c = 2π
(= a1 ⋅ b1 )
显然,倒格子基矢,也即倒格 a1 ⋅ (a 2 × a3 ) 矢的量纲是 [长度]-1,与 波矢的量纲一致。 由此,可以直接定义倒格子基矢为:
b1 = 2π a 2 × a3 a1 ⋅ (a 2 × a3 )
b2 =
2π a3 × a1 a1 ⋅ (a 2 × a3 )
a1 =
FCC (正基矢) a (j + k) 2 a a 2 = (k + i ) 2 a a 3 = (i + j) 2
可见 BCC 倒格子是一个边长为4π/a 的FCC格子。 倒格子原点最近邻有十二个格点。 所以BCC晶格第一布里渊区是一个 正十二面体。
17
3.5 晶体的X射线衍射
可以验证,当波矢Kh取为
K h = h1b1 + h2b 2 + h3b 3, h1h2 h3为整数
其中 b1,b2,b3 由 验证:
a i ⋅b j = 2πδ ij
确定,则以上条件成立。
K h ⋅ R l = (h1b1 + h2b 2 + h3b 3 ) ⋅ (l1a1 + l2a 2 + l3a3 )
Q Ω* = b1 ⋅ (b 2 × b 3 ) = (2π )3 = (2π )3
3
Ω 利用 a × b × c = b(a ⋅ c) − c(a ⋅ b)
(a 2 × a3 ) ⋅ [(a3 × a1 ) × (a1 × a 2 )]
分解, (a 2 × a3 ) ⋅ [(a3 × a1 ) × (a1 × a 2 )]
由此得证,倒格矢 G h1h2h3 的长度 Gh1h2h3 是
晶面系 (h1h2 h3 ) 面间距 d h1h2h3 倒数的 2π 倍。
倒格矢取向及长度与晶面的关系,使得倒格矢与晶面一一对应。
12
3.4 布里渊区
3.4.1 布里渊区定义
定义:在倒格子中,以某一格点为坐标原点,作所有倒格矢的垂 直平分面,倒格子空间被这些平面分成许多包围原点的多面 体区域,这些区域称为布里渊区。 第一布里渊区:最靠近原点的平 面所围的区域。 第二布里渊区:第一布里渊区界 面与次远垂直平分面所围的 区域。 第三布里渊区示意。 第 n 个布里渊区是从原点出发, 跨过 (n-1) 个垂直平分面达 到的所有点的集合。
