高一数学必修三模块测试题 (人教A版)
人教A版高中数学必修三试卷综合测试题

人教A版高中数学必修三试卷综合测试题高中数学研究材料(XXX精心整理制作)必修三综合测试题考试时间:90分钟,试卷满分:100分一、选择题:本大题共14小题,每小题4分,共56分。
在每小题给出的四个选项中,只有一项是符合要求的。
1.如果输入n=3,那么执行右图中算法的结果是()。
A。
输出3B。
输出4C。
输出5D。
程序出错,输出不了任何结果解析:输入3,第二步n=n+1,n变成4,第三步n=n+1,n变成5,最后输出5.所以答案是C。
2.一个容量为1000的样本分成若干组,已知某组的频率为0.4,则该组的频数是()。
A。
400B。
40C。
4D。
600解析:样本容量为1000,某组的频率为0.4,那么该组的频数就是0.4*1000=400.所以答案是A。
3.从1、2、3、4这4个数中,不放回地任意取两个数,两个数都是奇数的概率是()。
A。
1/6B。
1/4C。
3/8D。
1/2解析:两个数都是奇数的组合是(1,3)和(3,1),(1,3)和(3,1)的概率是1/4,所以答案是B。
4.用样本估计总体,下列说法正确的是()。
A。
样本的结果就是总体的结果B。
样本容量越大,估计就越精确C。
样本的标准差可以近似地反映总体的平均状态D。
数据的方差越大,说明数据越稳定解析:样本是总体的一部分,样本的结果只能代表总体的一部分,所以A错误;样本容量越大,估计就越精确,所以B正确;样本的标准差不能反映总体的平均状态,所以C错误;方差越大,数据越不稳定,所以D错误。
所以答案是B。
5.把11化为二进制数为()。
A。
1011(2)B。
(2)C。
(2)D。
0110(2)解析:11除以2商为5余1,5除以2商为2余1,2除以2商为1余0,1除以2商为0余1,所以11的二进制表示为1011.所以答案是A。
6.已知x可以在区间[-t,4t](t>0)上任意取值,则x∈[-t/2,t/2]的概率是()。
A。
1/6B。
1/4C。
3/10D。
2020版数学人教A版必修3练习:模块综合试卷(二) Word版含解析

模块综合试卷(二)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.(2018·长春质检)已知某班级部分同学一次测验的成绩统计如图所示,则其中位数和众数分别为( )A .95,94B .92,86C .99,86D .95,91答案 B解析 由题中茎叶图可知,此组数据由小到大排列依次为76,79,81,83,86,86,87,91,92,94,95,96,98,99,101,103,114,共17个,故中位数为92,出现次数最多的为众数,故众数为86,故选B.2.已知a =,b =,执行如图所示的程序框图,则输出的值为( )23A.B. C.D.2222-122+12答案 D解析 由a =,b ===2,知a >b 不成立,故输出=.23lg 3lg 3a +1b 2+123.用辗转相除法求得459和357的最大公约数是( )A .3 B .9 C .17 D .51答案 D解析 459=357×1+102,357=102×3+51,102=51×2,则51是459和357的最大公约数.4.某校有40个班,每班50人,要求每班随机选派3人参加“学生代表大会”,在这个问题中样本容量是( )A .40B .50C .120D .150答案 C解析 选派人数是40×3=120,即为样本容量.5.已知函数y =a -x ,当a 在集合中任意取值时,函数为增函数的概率为( ){13,15,12,4,7}A. B. C. D.25121335答案 D解析 y =a -x =x 为增函数时,有>1,即0<a <1.(1a )1a由于a ∈,所以函数为增函数包含3个基本事件,基本事件总数为5,则函数{13,15,12,4,7}为增函数的概率为.356.如图所示,四个可以自由转动的转盘被平均分成若干个圆心角相同的扇形,转动转盘,当转盘停止转动后,有两个转盘的指针指向白色区域的概率相同,则这两个转盘是( )A .转盘1和转盘2B .转盘2和转盘3C .转盘2和转盘4D .转盘3和转盘4答案 C解析 四个转盘指针指向白色区域的概率分别为P 1=,P 2==,P 3==,P 4=,故P 2=3826132121613P 4,即转盘2和转盘4指针指向白色区域的概率相同.7.某实验室有4个饲养房,分别养有18,54,24,48只白鼠供实验用,某项实验需抽取24只白鼠,你认为最合适的抽样方法是( )A .在每个饲养房各抽取6只B .把所有白鼠都加上编号不同的颈圈,用简单随机抽样法确定24只C .从4个饲养房分别抽取3,9,4,8只D .先确定这4个饲养房应分别抽取3,9,4,8只,再在各饲养房自己加号码颈圈,用简单随机抽样的方法确定答案 D解析 因为这24只白鼠要从4个饲养房中抽取,所以要先用分层抽样法决定各个饲养房应抽取的只数,再用简单随机抽样法从各个饲养房选出所需的白鼠.选项C 用了分层抽样法,但在每层中没有考虑到个体的差异,也就是说在各个饲养房中抽取样本时,没有说明是否具有随机性.8.羊村村长慢羊羊决定从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊去割草,则喜羊羊和美羊羊恰好只有一只被选中的概率为( )A.B. C. D.310673545答案 C解析 从喜羊羊、美羊羊、懒羊羊、暖羊羊、沸羊羊中选派两只羊的方法有10种,其中喜羊羊和美羊羊恰好只有一只的有6种,由古典概型概率计算公式可得,所求概率为.359.现有1位女教师和2位男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出1道题进行说题,其中恰有1男1女抽到相同题目的概率为( )A. B. C. D.13231234答案 C解析 设2道题分别为A ,B ,所以抽取情况有AAA ,AAB ,ABA ,ABB ,BAA ,BAB ,BBA ,BBB ,共8种,其中第1个,第2个字母分别表示2位男教师抽取的题目,第3个字母表示女教师抽取的题目,则满足恰有1男1女抽到相同题目的事件为ABA ,ABB ,BAA ,BAB ,共4种.故所求事件的概率为.1210.执行下面的程序,则输出的s 的值是( )i =1WHILE i<6 i =i +2 s =2*i +1WEND PRINT s ENDA .11B .15C .17D .19答案 B解析 当i =3时,s =7,当i =5时,s =11,此时仍满足条件“i <6”,因此再循环一次,即i =7时,s =15,此时不满足“i <6”,所以s =15.11.为参加CCTV 举办的中国汉字听写大赛,某中学举行了一次大型选拔活动,随机统计了甲、乙两班各6名学生的汉字听写的成绩如图所示,设甲、乙两班数据平均数依次为1,2,x x 标准差依次为s 1,s 2,则( )A.1>2,s 1>s 2B.1>2,s 1<s 2x x x xC.1=2,s 1>s 2D.1=2,s 1<s 2x x x x 答案 C解析 1=(3×8+6+2×5+120×2+130×3+140)=135,x 162=×(2×9+7+8+5+2+120×2+130×3+140)=135,x 16s =×[(-7)2+(-9)2+02+32+32+102]=,21161243s =[(-8)2+(-6)2+32+02+42+72]=29,所以1=2,s 1>s 2,故选C.216x x 12.一批热水器共98台,其中甲厂生产的有56台,乙厂生产的有42台,用分层抽样的方法从中抽出一个容量为14的样本,那么抽得甲、乙两厂生产的热水器的台数分别是( )A .9,5 B .8,6 C .10,4 D .7,7答案 B解析 抽得甲厂生产的热水器的台数是×14=8,抽得乙厂生产的热水器的台数是×14=569842986.二、填空题(本大题共4小题,每小题5分,共20分)13.若六进制数13m 502(6)化为十进制数为12 710,则m =________.答案 4解析 根据将k 进制数转化为十进制数的方法有13m 502(6)=1×65+3×64+m ×63+5×62+0×61+2=12 710,解得m =4.14.一组样本数据按从小到大的顺序排列为13,14,19,x,23,27,28,31,中位数为22,则x =________.答案 21解析 中位数为=22,所以x =21.x +23215.设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.答案 495解析 取a 1=815,则b 1=851-158=693≠815,则a 2=693;由a 2=693知b 2=963-369=594≠693,则a 3=594;由a 3=594知b 3=954-459=495≠594,则a 4=495;由a 4=495知b 4=954-459=495=a 4,则输出b =495.16.如图所示,正方形ABCD 内接于圆O ,且AE =BE =CG =DG ,AH =CF =AD ,则往圆O14内投掷一点,该点落在四边形EFGH 内的概率为________.答案 1π解析 设AB =4a ,则圆O 的面积为8πa 2,四边形EFGH 的面积为16a 2-2××a ×2a -2×12×3a ×2a =8a 2,则所求概率为=.128a 28πa 21π三、解答题(本大题共6小题,共70分)17.(10分)将一枚骰子连续抛掷两次,观察向上的点数.(1)求点数之和是5的概率;(2)设a ,b 分别是将一枚骰子连续抛掷两次后得到的向上的点数,求等式2a -b =1成立的概率.解 该试验所有可能的结果有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),基本事件总数为36.记事件A ={点数之和是5},则事件A 所含的基本事件有(1,4),(2,3),(3,2),(4,1),共4个,所以P (A )==.43619(2)若等式2a -b =1成立,则a -b =0,即连续抛掷两次骰子所得的点数相等.记事件B ={向上的点数相等},则事件B 所包含的基本事件为(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6个,所以P (B )==.6361618.(12分)某公路设计院有工程师6人,技术员12人,技工18人,要从这些人中抽取n 个人参加市里召开的科学技术大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体,如果参会人数减少1人,则在采用系统抽样时,需要在总体中先剔除2个个体,求n .解 总体容量为6+12+18=36.当样本容量为n 时,由题意知,系统抽样的间隔为,分层抽样的比例是,抽取的工程师36n n36人数为×6=,技术员人数为×12=,技工人数为×18=,n 36n 6n 36n 3n 36n2所以n 应是6的倍数,36的约数,即n =6,12,18.当样本容量为(n -1)时,总体容量剔除以后是34人,系统抽样的间隔为,因为必须34n -134n -1是整数,所以n 只能取18,即样本容量n =18.19.(12分)某中学举行电脑知识竞赛,现将高一参赛学生的成绩进行整理后分成五组绘制成如图所示的频率分布直方图,已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.求(1)高一参赛学生的成绩的众数、中位数;(2)高一参赛学生的平均成绩.解 (1)用频率分布直方图中最高矩形所在的区间的中点值作为众数的近似值,得众数为65,又因为第一个小矩形的面积为0.3,前两个小矩形的面积和为0.3+0.4=0.7>0.5,所以设第二个小矩形底边的一部分长为x ,则x ×0.04=0.2,得x =5,所以中位数为60+5=65.(2)依题意,平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,所以平均成绩约为67分.20.(12分)下表数据是水的温度x (℃)对黄酮延长性y (%)效应的试验结果,y 是以延长度计算的.x /℃300400500600700800y /%405055606770(1)画出散点图;(2)指出x ,y 是否线性相关,若线性相关,求y 关于x 的回归方程;(3)估计水的温度是1 000 ℃时,黄酮延长性的情况.解 (1)散点图如下:(2)由散点图可以看出样本点分布在一条直线的附近,可见y 与x 线性相关.计算得=550,=x y 57,≈0.058 86,=-≈57-0.058 86×550=24.627.b ^a ^y b ^x 因此所求的回归方程为=0.058 86x +24.627.y ^(3)将x =1 000代入回归方程得=0.058 86×1 000+24.627=83.487,即水的温度是1 000 ℃y ^时,黄酮延长性大约是83.487%.21.(2018·漳平模拟)某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a ,b ),(a ,),(a ,b ),(,b ),(,),(a ,b ),(a ,b ),(a ,b a a b ),(,b ),(a ,),(,),(a ,b ),(a ,),(,b ),(a ,b ),其中a ,分别表示甲组研发b a b a b b a a 成功和失败;b ,分别表示乙组研发成功和失败.b (1)若某组成功研发一种新产品,则给该组记1分,否则记0分.试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;(2)若该企业安排甲、乙两组各自研发一种新产品,试估计恰有一组研发成功的概率.解 (1)甲组研发新产品的成绩为1,1,1,0,0,1,1,1,0,1,0,1,1,0,1,其平均数甲==;x 101523方差为s ==.2甲115[(1-23)2×10+(0-23)2×5]29乙组研发新产品的成绩为1,0,1,1,0,1,1,0,1,0,0,1,0,1,1,其平均数乙==;x 91535方差为s ==.2乙115[(1-35)2×9+(0-35)2×6]625因为甲>乙,s <s ,所以甲组的研发水平优于乙组.x x 2甲2乙(2)记恰有一组研发成功为事件E ,在所抽得的15个结果中,恰有一组研发成功的结果是(a ,),(,b ),(a ,),(,b ),(a ,),(a ,),(,b ),共7个.因此事件E 发生的频率为.b a b a b b a 715用频率估计概率,即得所求概率为P (E )=.71522.(12分)某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩(假设考试成绩均在[65,90]内)分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90].得到频率分布直方图如图所示.(1)求测试成绩在[80,85)内的频率;(2)从第三、四、五组学生中用分层抽样的方法抽取6名学生组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名学生中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有1名学生被抽中的概率.解 (1)测试成绩在[80,85)内的频率为1-(0.01+0.07+0.06+0.02)×5=0.2.(2)第三组的人数为0.06×5×100=30,第四组的人数为0.2×100=20,第五组的人数为0.02×5×100=10,所以第三组抽取3人,第四组抽取2人,第五组抽取1人.设第三组抽到的3人为A 1`,A 2,A 3,第四组抽到的2人为B 1,B 2,第五组抽到的1人为C .从6名学生中随机选取2名的可能情况有15种:(A 1,A 2),(A 1,A 3),(A 1,B 1),(A 1,B 2),(A 1,C ),(A 2,A 3),(A 2,B 1),(A 2,B 2),(A 2,C ),(A 3,B 1),(A 3,B 2),(A 3,C ),(B 1,B 2),(B 1,C ),(B 2,C ).设“第四组2名学生中至少有1名学生被抽中”为事件M ,则事件M 包含的基本事件为(A 1,B 1),(A 1,B 2),(A 2,B 1),(A 2,B 2),(A 3,B 1),(A 3,B 2),(B 1,B 2),(B 1,C ),(B 2,C ),共9个.所以,第四组至少有1名学生被抽中的概率P (M )==. 91535。
人教A版高中数学选择性必修第三册习题课(三) 成对数据的统计分析含答案

习题课(三) 成对数据的统计分析一、选择题1.在建立两个变量y 与x 的回归模型时,分别选择了4个不同的模型,它们的R 2如下,其中拟合得最好的模型为( )A .模型1的R 2为0.75B .模型2的R 2为0.90C .模型3的R 2为0.25D .模型4的R 2为0.55解析:选B R 2的值越大,意味着残差平方和越小,也就是说拟合效果越好. 2.对两个变量y 和x 进行回归分析,得到一组样本数据:(x 1,y 1),(x 2,y 2),…,(x n ,y n ),则下列说法中不正确的是( )A.由样本数据得到的经验回归方程y ^=b ^x +a ^必过样本点的中心(x -,y -) B.残差平方和越小的模型,拟合的效果越好C.用决定系数R 2来刻画回归效果,R 2的值越小,说明模型的拟合效果越好D.若变量y 和x 之间的样本相关系数r =-0.936 2,则变量y 与x 之间具有线性相关关系 解析:选C R 2的值越大,说明残差平方和越小,也就是说模型的拟合效果越好. 3.对两个变量y 与x 进行回归分析,分别选择不同的模型,它们的样本相关系数r 如下,其中拟合效果最好的模型是( )A .模型Ⅰ:样本相关系数r 为0.96B .模型Ⅱ:样本相关系数r 为-0.81C .模型Ⅲ:样本相关系数r 为-0.53D .模型Ⅳ:样本相关系数r 为0.35 解析:选A |r |越大,拟合效果越好.4.关于残差和残差图,下列说法正确的是( ) A .残差就是随机误差 B .残差图的横坐标是残差C .残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越高D .残差点均匀分布的带状区域的宽度越窄,说明模型拟合精度越低解析:选C 根据残差分析的概念可知,C 选项正确.残差是真实值减去估计值. 5.某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(x i ,y i )(i =1,2,…,20)得到下面的散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是A .y =a +bxB .y =a +bx 2C .y =a +b e xD .y =a +b ln x解析:选D 用光滑的曲线把图中各点连接起来,由图象的大致走向判断,此函数应该是对数函数类型的,故应该选用的函数模型为y =a +b ln x .6.根据如下所示的列联表得到如下四个判断:①根据小概率值α=0.001的独立性检验,认为患肝病与嗜酒有关;②根据小概率值α=0.01的独立性检验,认为患肝病与嗜酒有关;③没有证据显示患肝病与嗜酒有关.患病状况 饮酒习惯合计嗜酒(Y =0)不嗜酒(Y =1)患肝病(X =0) 7 775 42 7 817 未患肝病(X =1)2 099 49 2 148 合计9 874919 965其中正确命题的个数为( ) A .1 B .2 C .3D .0 解析:选B 根据列联表中的数据,经计算得到 χ2=9 965×(7 775×49-42×2 099)27 817×2 148×9 874×91≈56.632,由56.632>10.828>6.635.且P (χ2≥10.828)≈0.001,P (χ2≥6.635)≈0.01. 所以①②均正确. 二、填空题7.调查某地若干户家庭的年收入x (单位:万元)和年饮食支出y (单位:万元)显示,年收入x 与年饮食支出y 具有线性相关关系,并由调查数据得到y 对x 的经验回归方程y ^=0.254x +0.321.由经验回归方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.解析:由经验回归方程y ^=0.254x +0.321,知x 每增加1,y 增加0.254. 答案:0.2548.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归方程为y ^=0.67x +54.9.零件数x /个 10 2030 40 50 加工时间y /min62758189现发现表中有一个数据模糊看不清,请你推断出该数据的值为________. 解析:由表知x =30,设模糊不清的数据为m , 则y =15(62+m +75+81+89)=307+m 5,因为y =0.67x +54.9,即307+m5=0.67×30+54.9,解得m =68.答案:689.假设关于某设备的使用年限x (单位:年)和所支出的维修费用y (单位:万元)有如下的统计资料:x /年 2 3 4 5 6 y /万元2.23.85.56.57.0若由资料可知y 对x 呈线性相关关系,且经验回归方程为y ^=a ^+b ^x ,其中已知b ^=1.23,请估计使用年限为20年时,维修费用约为________万元.解析:由表中数据可知, x -=2+3+4+5+65=4,y -=2.2+3.8+5.5+6.5+7.05=5.∵经验回归直线一定经过点(x -,y -), ∴5=a ^+1.23×4,∴a ^=0.08,∴经验回归方程为y ^=1.23x +0.08.故估计使用年限为20年时,维修费用约为y =1.23×20+0.08=24.68(万元). 答案:24.68 三、解答题10.2023年某市开展了“寻找身边的好老师”活动,市六中积极行动,认真落实,通过网络关注评选“身边的好老师”,并对选出的五位“好老师”的班主任的工作年限和被关注数量进行了统计,得到如下数据:(1)若“好老师”的被关注数量y 与其班主任的工作年限x 满足经验回归方程,试求经验回归方程y ^=b ^x +a ^,并就此分析:“好老师”的班主任工作年限为15年时被关注的数量;(2)若用y ix i(i =1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.解:(1)因为x -=8,y -=36,所以b ^=40+120+320+600+600-5×8×3616+36+64+100+144-5×82=6,a ^=36-6×8=-12, 所以y ^=6x -12.当x =15时,y ^=6×15-12=78(百人).(2)这5次统计数据,被关注数量的“即时均值”分别为3,3,5,6,4.从5组“即时均值”任选2组,共有C 25=10种情况,其中2组数据之和小于8为(3,3),(3,4),(3,4)共3种情况,所以这2组数据之和小于8的概率为310.11.“双11”已经成为网民们的网购狂欢节,某电子商务平台对某市的网民在今年“双11”的网购情况进行摸底调查,用随机抽样的方法抽取了100人,其消费金额t (百元)的频率分布直方图如图所示:(1)求网民消费金额t 的平均值t -和中位数t 0.(2)把下表中空格里的数填上,并判断能否根据小概率值α=0.001的独立性检验,认为网购消费与性别有关?单位:人消费金额 性别合计 男(Y =0)女(Y =1)t ≥t 0(X =0) t <t 0(X =1) 30 合计45解:(1)以每组的中间值代表本组的消费金额,则网民消费金额t 的平均值 t -=2.5×0.2+7.5×0.3+12.5×0.2+17.5×0.15+22.5×0.1+27.5×0.05=11.5. 直方图中第一组,第二组的频率之和为0.04×5+0.06×5=0.5. 所以t 的中位数t 0=10. (2)补充列联表如下:消费金额 性别合计男(Y =0) 女(Y =1) t ≥t 0(X =0) 25 25 50 t <t 0(X =1) 20 30 50 合计4555100零假设为H 0:网购消费与性别独立,即网购消费与性别无关. 根据列联表中的数据,经计算得到χ2=100×(25×30-25×20)250×50×45×55=10099≈1.01<10.828=x 0.001.根据小概率值α=0.001的独立性检验,没有充分证据推断H 0不成立,因此可以认为H 0成立,即认为网购消费与性别无关.12.流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春季该园患流感小朋友按照年龄与人数统计,得到如下数据:(1)求y 关于x 的回归直线方程;(2)计算变量x ,y 的样本相关系数r (计算结果精确到0.01),并回答是否可以认为该幼儿园去年春季患流感人数与年龄负相关很强.(若|r |∈[0.75,1],则x ,y 相关性很强;若|r |∈[0.3,0.75),则x ,y 相关性一般;若|r |∈[0,0.3),则x ,y 相关性较弱)参考数据:30≈5.477.参考公式:b ^=∑i =1n (x i -x )(y i -y )∑i =1n(x i -x )2=∑i =1nx i y i -n x y∑i =1nx 2i -n x2,样本相关系数r =∑i =1n(x i -x )(y i -y )∑i =1n(x i -x )2·∑i =1n(y i -y )2.解:(1)由题意得,x =2+3+4+5+65=4,y =22+22+17+14+105=17,b ^=∑i =15(x i -x )(y i -y )∑i =15(x i -x )2=(-2)×5+(-1)×5+0×0+1×(-3)+2×(-7)(-2)2+(-1)2+02+12+22=-3.2,a ^=y -b ^x =17+3.2×4=29.8, 故y 关于x 的线性回归方程为y ^=-3.2x +29.8.(2)∵r =∑i =15(x i -x )(y i -y )∑i =15(x i -x )2·∑i =15(y i -y )2=-3210×108=-16330≈-0.97,∴r <0,说明x ,y 负相关.又|r |∈[0.75,1],说明x ,y 相关性很强.因此,可以认为该幼儿园去年春季流感人数与年龄负相关很强.。
高中数学人教A版必修3综合测试题及答案 9
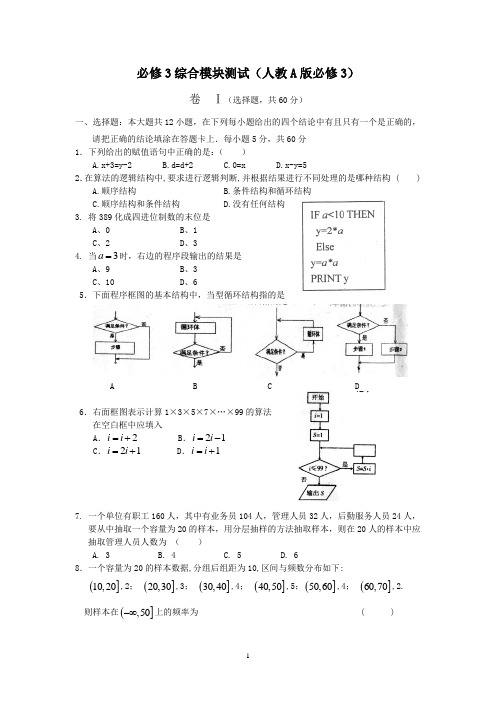
必修3综合模块测试(人教A 版必修3)卷 Ⅰ(选择题,共60分)一、选择题:本大题共12小题,在下列每小题给出的四个结论中有且只有一个是正确的,请把正确的结论填涂在答题卡上.每小题5分,共60分 1.下列给出的赋值语句中正确的是:( )A.x+3=y-2B.d=d+2C.0=xD.x-y=5 2.在算法的逻辑结构中,要求进行逻辑判断,并根据结果进行不同处理的是哪种结构 ( ) A.顺序结构 B.条件结构和循环结构 C.顺序结构和条件结构 D.没有任何结构 3. 将389化成四进位制数的末位是 A 、0 B 、1 C 、2 D 、34. 当3a =时,右边的程序段输出的结果是 A 、9 B 、3 C 、10 D 、65.下面程序框图的基本结构中,当型循环结构指的是A B C D6.右面框图表示计算1×3×5×7×…×99的算法 在空白框中应填入A .2i i =+B .21i i =-C .21i i =+D .1i i =+7. 一个单位有职工160人,其中有业务员104人,管理人员32人,后勤服务人员24人,要从中抽取一个容量为20的样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员人数为 ( )A. 3B. 4C. 5D. 68.一个容量为20的样本数据,分组后组距为10,区间与频数分布如下:(]10,20,2; (]20,30,3; (]30,40,4; (]40,50,5;(]50,60,4; (]60,70,2. 则样本在(],50-∞上的频率为 ( )A.120 B. 14 C.12 D.7109.把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( ) A. 对立事件B. 互斥但不对立事件C. 不可能事件D. 以上都不对10. 从区间()0,1内任取两个数,则这两个数的和小于56的概率是A 、35B 、45C 、1625D 、257211.如图,在正方形中撒一粒豆子,则豆子落在正方形内切圆内部的概率为A .4πB .44π-C .41π-D .4π12.同时上抛三枚硬币,落地后,三枚硬币图案两正一反的概率是A .34 B .14 C .38 D .12二、填空题(每小题4分,共16分)13. 某初级中学领导采用系统抽样方法,从该校预备年级全体800名学生中抽50名学生做 牙齿健康检查。
人教A版高中数学必修三测试题及答案全套

人教A版高中数学必修三测试题及答案全套阶段质量检测(一)(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知函数输入自变量x的值,输出对应的函数值.设计程序框图时,需用到的基本逻辑结构是()A.顺序结构B.条件结构C.顺序结构、条件结构D.顺序结构、循环结构2.下列赋值语句正确的是()A.M=a+1 B.a+1=MC.M-1=a D.M-a=13.若十进制数26等于k进制数32,则k等于()A.4 B.5 C.6 D.84.用“辗转相除法”求得360和504的最大公约数是()A.72 B.36 C.24 D.2 5205.程序框图(如图所示)能判断任意输入的数x的奇偶性,其中判断框内的条件是()A.m=0? B.x=0?C.x=1? D.m=1?6.如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为()A .S =S *(n +1)B .S =S*x n +1C .S =S * nD .S =S*x n7.已知一个k 进制的数132与十进制的数30相等,那么k 等于( ) A .7或4 B .-7 C .4 D .以上都不对8.用秦九韶算法求多项式:f (x )=12+35 x -8 x 2+79 x 3+6 x 4+5 x 5+3 x 6在x =-4的值时,v 4的值为( )A .-57B .220C .-845D .3 392 9.对于下列算法:如果在运行时,输入2,那么输出的结果是( ) A .2,5 B .2,4 C .2,3 D .2,9 10.下列程序的功能是( ) S =1i =1WHILE S <=10 000 i =i +2S =S*i WEND PRINT i ENDA .求1×2×3×4×…×10 000的值B .求2×4×6×8×…×10 000的值C .求3×5×7×9×…×10 001的值D .求满足1×3×5×…×n >10 000的最小正整数n11.(2015·新课标全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )A .0B .2C .4D .1412.如果执行如图所示的程序框图,输入正整数N (N ≥2)和实数a 1,a 2,…,a N ,输出A ,B ,则( )A .A +B 为a 1,a 2,…,a N 的和 B.A +B 2为a 1,a 2,…,a N 的算术平均数C .A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数D .A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数 二、填空题(本大题共4小题,每小题5分,共20分)13.用更相减损术求三个数168,54,264的最大公约数为________. 14.将258化成四进制数是________.15.阅读如图所示的程序框图,运用相应的程序,若输入m 的值为2,则输出的结果i =________.16.下面程序执行后输出的结果是________,若要求画出对应的程序框图,则选择的程序框有________________.T=1S=0WHILE S<=50S=S+1T=T+1WENDPRINT TEND三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(10分)画出函数的程序框图.18.(12分)用“更相减损术”求(1)中两数的最大公约数;用“辗转相除法”求(2)中两数的最大公约数.(1)72,168;(2)98,280.19.(12分)利用秦九韶算法判断函数f(x)=x 5+x 3+x 2-1在[0,2]上是否存在零点.20.(12分)已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(x n,y n),…(1)若程序运行中输出的一个数组是(9,t),求t的值.(2)程序结束时,共输出(x,y)的组数为多少?(3)写出程序框图的程序语句.21.(12分)设计算法求11×2+12×3+13×4+…+199×100的值.要求画出程序框图,并用基本语句编写程序.22.(12分)如图甲所示在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图乙所示的程序框图给出.图甲图乙(1)写出程序框图中①,②,③处应填充的式子;(2)若输出的面积y值为6,则路程x的值为多少?并指出此时点P在正方形的什么位置上.答案1. 答案:C2. 解析:选A根据赋值语句的功能知,A正确.3. 解析:选D由题意知,26=3×k1+2,解得k=8.4. 解析:选A504=360×1+144,360=144×2+72,144=72×2,故最大公约数是72.5. 解析:选D阅读程序易知,判断框内应填m=1?,应选D.6. 解析:选D由题意知,由于求乘积,故空白框中应填入S=S*x n.7. 解析:选C132(k)=1×k2+3×k+2=k 2+3 k+2=30,即k=-7或k=4.∵k>0,∴k=4.8. 解析:选B f(x)=(((((3 x+5) x+6) x+79) x-8) x+35) x+12,当x=-4时,v0=3;∴v 1=3×(-4)+5=-7;v 2=-7×(-4)+6=34,v 3=34×(-4)+79=-57;v 4=-57×(-4)-8=220.9. 解析:选A输入a的值2,首先判断是否大于5,显然2不大于5,然后判断2与3的大小,显然2小于3,所以结果是b=5,因此结果应当输出2,5.10. 解析:选D法一:S是累乘变量,i是计数变量,每循环一次,S乘以i一次且i增加2. 当S>10 000时停止循环,输出的i值是使1×3×5×…×n>10 000成立的最小正整数n.法二:最后输出的是计数变量i,而不是累乘变量S.11. 解析:选B a=14,b=18.第一次循环:14≠18且14<18,b=18-14=4;第二次循环:14≠4且14>4,a=14-4=10;第三次循环:10≠4且10>4,a=10-4=6;第四次循环:6≠4且6>4,a=6-4=2;第五次循环:2≠4且2<4,b=4-2=2;第六次循环:a=b=2,跳出循环,输出a=2,故选B.12. 解析:选C由于x=a k,且a>A时,将x值赋给A,因此最后输出的A值是a1,a2,…,a N 中最大的数;由于x=a k,且x<B时,将x值赋给B,因此最后输出的B值是a1,a2,…,a N中最小的数,故选C.13. 解析:为简化运算,先将3个数用2约简为84,27,132.由更相减损术,先求84与27的最大公约数.84-27=57,57-27=30,30-27=3,27-3=24,24-3=21,21-3=18,18-3=15,15-3=12,12-3=9,9-3=6,6-3=3.故84与27的最大公约数为3.再求3与132的最大公约数,易知132=3×44,所以3与132的最大公约数就是3.故84,27,132的最大公约数为3;168,54,264的最大公约数为6.答案:614. 解析:利用除4取余法.则258=10 002(4).答案:10 002(4)15. 解析:由程序框图,i=1后:A=1×2,B=1×1,A<B?否;i=2后:A=2×2,B=1×2,A <B?否;i=3后:A=4×2,B=2×3,A<B?否;i=4后:A=8×2,B=6×4,A<B?是,输出i=4.答案:416. 解析:本题为当型循环语句,可以先用特例循环几次,观察规律可得:S=1,T=2;S=2,T=3;S=3,T=4;…;依此循环下去,S=49,T=50;S=50,T=51;S=51,T=52.终止循环,输出的结果为52.本题使用了输出语句、赋值语句和循环语句,故用如下的程序框:起止框、处理框、判断框、输出框.答案:52起止框、处理框、判断框、输出框17. 解:程序框图如图所示.18. 解:(1)用“更相减损术”168-72=96,96-72=24,72-24=48,48-24=24.∴72与168的最大公约数是24.(2)用“辗转相除法”280=98×2+84,98=84×1+14,84=14×6.∴98与280的最大公约数是14.19. 解:f (0)=-1<0,下面用秦九韶算法求x=2时,多项式f(x)=x 5+x 3+x 2-1的值.多项式变形为f (x)=((((x+0) x+1) x+1) x+0) x-1,v0=1,v 1=1×2+0=2,v 2=2×2+1=5,v 3=5×2+1=11,v 4=11×2+0=22,v 5=22×2-1=43,所以f(2)=43>0,即f (0)·f (2)<0,又函数f (x)在[0,2]上连续,所以函数f(x)=x 5+x 3+x 2-1在[0,2]上存在零点.20. 解:(1)由程序框图知:当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 015时,输出最后一对,共输出(x,y)的组数为1 008.(3)程序框图的程序语句如下:21. 解:程序框图如图.程序如下. S =0k =1DOS =S +1/(k*(k +1)) k =k +1LOOP UNTIL k >99PRINT S END22. 解:(1)由题意,得y =⎩⎪⎨⎪⎧2x ,0≤x ≤4,8,4<x ≤8,24-2x ,8<x ≤12,故程序框图中①,②,③处应填充的式子分别为:y =2x ,y =8,y =24-2x .(2)若输出的y 值为6,则2x =6或24-2x =6,解得x =3或x =9.当x =3时,此时点P 在正方形的边BC 上,距C 点的距离为1;当x =9时,此时点P 在正方形的边DA 上,距D 点的距离为1.阶段质量检测(二)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列各选项中的两个变量具有相关关系的是( ) A .长方体的体积与边长 B .大气压强与水的沸点 C .人们着装越鲜艳,经济越景气 D .球的半径与表面积 2.下列说法错误的是( )A .在统计里,最常用的简单随机抽样方法有抽签法和随机数法B .一组数据的平均数一定大于这组数据中的每个数据C .平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D .一组数据的方差越大,说明这组数据的波动越大3.(2016·开封高一检测)某学校有老师200人,男学生1 200人,女学生1 000人,现用分层抽样的方法从全体师生中抽取一个容量为n 的样本,已知女学生一共抽取了80人,则n 的值是( )A .193B .192C .191D .1904.某班学生父母年龄的茎叶图如图,左边是父亲年龄,右边是母亲年龄,则该班同学父亲的平均年龄比母亲的平均年龄大( )A .2.7岁B .3.1岁C .3.2岁D .4岁5.如果在一次实验中,测得(x ,y )的四组数值分别是A (1,3),B (2,3.8),C (3,5.2),D (4,6),则y 与x 之间的回归直线方程是( )A.y ^=x +1.9B.y ^=1.04x +1.9 C.y ^=0.95x +1.04 D.y ^=1.05x -0.96.观察新生婴儿的体重,其频率分布直方图如图,则新生婴儿体重在(2 700,3 000)的频率为( )A .0.001B .0.1C .0.2D .0.37.某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93,下列说法正确的是( )A .这种抽样方法是一种分层抽样B .这种抽样方法是一种系统抽样C .这五名男生成绩的方差大于这五名女生成绩的方差D .该班男生成绩的平均数大于该班女生成绩的平均数8.小波一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为( )图1图2A .1%B .2%C .3%D .5%9.某校高一、高二年级各有7个班参加歌咏比赛,他们的得分的茎叶图如图所示,对这组数据分析正确的是( )A .高一的中位数大,高二的平均数大B .高一的平均数大,高二的中位数大C .高一的平均数、中位数都大D .高二的平均数、中位数都大10.在样本频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的14,且样本容量为160,则中间一组的频数为( )A .32B .0.2C .40D .0.2511.为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别分段为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )A .6B .8C .12D .1812.设矩形的长为a ,宽为b ,若其比满足ba =5-12≈0.618,则这种矩形称为黄金矩形.黄金矩形给人以美感,常应用于工艺品设计中.下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:甲批次:0.598 0.625 0.628 0.595 0.639 乙批次:0.618 0.613 0.592 0.622 0.620根据上述两个样本来估计两个批次的总体平均数与标准值0.618比较,正确结论是( ) A .甲批次的总体平均数与标准值更接近 B .乙批次的总体平均数与标准值更接近 C .两个批次总体平均数与标准值接近程度相同 D .两个批次总体平均数与标准值接近程度不能确定 二、填空题(本大题共4小题,每小题5分,共20分)13.甲、乙、丙、丁四名射击手在选拔赛中的平均环数x 及其标准差s 如下表所示,则选送决赛的最佳人选应是________.14.在某次测量中得到的A 若B 样本数据恰好是A 样本数据每个都加2后所得数据,则A ,B 两样本的数字特征(众数、中位数、平均数、方差)对应相同的是________.15.某校开展“爱我母校,爱我家乡”摄影比赛,9位评委为参赛作品A 给出的分数茎叶图如图,记分员去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是________.16.某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的部分频率分布直方图.在统计方法中,同一组数据常用该组区间的中点值作为代表,观察图形的信息,据此估计本次考试的平均分为________.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(10分)已知一组数据从小到大的顺序排列,得到-1,0,4,x,7,14,中位数为5,求这组数据的平均数与方差.18.(12分)2015年春节前,有超过20万名来自广西、四川的外来务工人员选择驾乘摩托车沿321国道返乡过年,为防止摩托车驾驶人员因长途疲劳驾驶而引发交通事故,肇庆市公安交警部门在321国道沿线设立了多个休息站,让过往的摩托车驾驶人员有一个停车休息的场所.交警小李在某休息站连续5天对进站休息的摩托车驾驶人员每隔50人询问一次省籍,询问结果如图所示:(1)交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?19.(12分)某制造商为运动会生产一批直径为40 mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:40.0240.0039.9840.0039.9940.0039.9840.0139.9839.9940.0039.9939.9540.0140.0239.9840.0039.9940.0039.96(1)完成下面的频率分布表,并画出频率分布直方图;(2)假定乒乓球的直径误差不超过0.02 mm 为合格品,若这批乒乓球的总数为10 000只,试根据抽样检查结果估计这批产品的合格只数.20.(12分)某零售店近5个月的销售额和利润额资料如下表:(1)(2)用最小二乘法计算利润额y 关于销售额x 的回归直线方程;(3)当销售额为4千万元时,利用(2)的结论估计该零售店的利润额(百万元).⎣⎢⎢⎡⎦⎥⎥⎤参考公式:b ^=∑i =1n(x i-x )(y i-y )∑i =1n(x i-x )2,a ^=y -b ^x 21.(12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:甲:82 81 79 78 95 88 93 84 乙:92 95 80 75 83 80 90 85 (1)用茎叶图表示这两组数据;(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.22.(12分)已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出这两种鱼各1 000条,给每条鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机地捕出1 000条鱼,记录下其中有记号的鱼的数目,立即放回池塘中.这样的记录做了10次,并将记录获取的数据制作成如图甲所示的茎叶图.(1)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量; (2)为了估计池塘中鱼的总重量,现按照(1)中的比例对100条鱼进行称重,根据称重鱼的重量介于[0,4.5](单位:千克)之间,将测量结果按如下方式分成九组:第一组[0,0.5),第二组[0.5,1),…,第九组[4,4.5].如图乙是按上述分组方法得到的频率分布直方图的一部分.①估汁池塘中鱼的重量在3千克以上(含3千克)的条数;②若第三组鱼的条数比第二组多7条、第四组鱼的条数也比第三组多7条,请将频率分布直方图补充完整;③在②的条件下估计池塘中鱼的重量的众数及池塘中鱼的总重量.图甲 图乙答 案1. 解析:选C A 、B 、D 均为函数关系,C 是相关关系.2. 解析:选B 平均数不大于最大值,不小于最小值.3. 解析:选B1 000×n200+1 200+1 000=80,解得n =192.4. 解析:选C 分别求出父亲年龄和母亲年龄的平均值,可得父亲的平均年龄比母亲的平均年龄大3.2岁,故选C.5. 解析:选Bx =14(1+2+3+4)=2.5,y =14(3+3.8+5.2+6)=4.5.因为回归直线方程过样本点中心(x ,y ),代入验证知,应选B.6. 解析:选D 由直方图可知,所求频率为0.001×300=0.3.7. 解析:选C A 不是分层抽样,因为抽样比不同.B 不是系统抽样,因为是随机询问,抽样间隔未知.C 中五名男生成绩的平均数是x =86+94+88+92+905=90,五名女生成绩的平均数是y =88+93+93+88+935=91,五名男生成绩的方差为s 21=15(16+16+4+4+0)=8,五名女生成绩的方差为s 22=15(9+4+4+9+4)=6,显然,五名男生成绩的方差大于五名女生成绩的方差.D 中由于五名男生和五名女生的成绩无代表性,不能确定该班男生和女生的平均成绩.8. 解析:选C 由图2知,小波一星期的食品开支为300元,其中鸡蛋开支为30元,占食品开支的10%,而食品开支占总开支的30%,所以小波一星期的鸡蛋开支占总开支的百分比为3%,故选C.9. 解析:选A 由茎叶图可以看出,高一的中位数为93,高二的中位数为89,所以高一的中位数大.由计算得,高一的平均数为91,高二的平均数为6477,所以高二的平均数大.故选A.10. 解析:选A 由频率分布直方图的性质,可设中间一组的频率为x ,则x +4x =1,∴x =0.2,故中间一组的频数为160×0.2=32,选A.11. 解析:选C 志愿者的总人数为20(0.16+0.24)×1=50,所以第三组人数为50×0.36=18,有疗效的人数为18-6=12.12. 解析:选A 甲批次的样本平均数为15×(0.598+0.625+0.628+0.595+0.639)=0.617;乙批次的样本平均数为15×(0.618+0.613+0.592+0.622+0.620)=0.613.所以可估计:甲批次的总体平均数与标准值更接近.13. 解析:平均数反映平均水平大小,标准差表明稳定性.标准差越小,稳定性越好. 答案:乙14. 解析:由s 2=1n [(x 1-x )2+(x 2-x )2+…+(x n -x )2],可知B 样本数据每个变量增加2,平均数也增加了,但s 2 不变,故方差不变.答案:方差15. 解析:由于需要去掉一个最高分和一个最低分,故需要讨论:①若x ≤4,∵平均分为91,∴总分应为637分.即89+89+92+93+92+91+90+x =637,∴x =1. ②若x >4,则89+89+92+93+92+91+94=640≠637,不符合题意,故填1. 答案:116. 解析:在频率分布直方图中,所有小长方形的面积和为1,设[70,80)的小长方形面积为x ,则(0.01+0.015×2+0.025+0.005)×10+x =1,解得x =0.3,即该组频率为0.3,所以本次考试的平均分为45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.答案:7117. 解:由于数据-1,0,4,x,7,14的中位数为5, 所以4+x 2=5,x =6.设这组数据的平均数为x ,方差为s 2,由题意得 x =16×(-1+0+4+6+7+14)=5,s 2=16×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=743.18. 解:(1)根据题意,因为有相同的间隔,符合系统抽样的特点,所以交警小李对进站休息的驾驶人员的省籍询问采用的是系统抽样方法.(2)从图中可知,被询问了省籍的驾驶人员中 广西籍的有5+20+25+20+30=100(人), 四川籍的有15+10+5+5+5=40(人),设四川籍的驾驶人员应抽取x 名,依题意得5100=x40,解得x =2,即四川籍的应抽取2名. 19. 解:(1)(2)∵抽样的20只产品中在[39.98,40.02]范围内有18只,∴合格率为1820×100%=90%,∴10 000×90%=9 000(只).即根据抽样检查结果,可以估计这批产品的合格只数为9 000. 20. 解:(1)散点图如图所示,两个变量有线性相关关系.(2)设回归直线方程是y ^=b ^x +a ^. 由题中的数据可知y =3.4,x =6.所以b ^=∑i =1n(x i -x )(y i -y )∑i =1n(x i -x )2=(-3)×(-1.4)+(-1)×(-0.4)+1×0.6+3×1.69+1+1+9=1020=0.5. a ^=y -b ^x =3.4-0.5×6=0.4.所以利润额y 关于销售额x 的回归直线方程为 y ^=0.5x +0.4.(3)由(2)知,当x =4时,y =0.5×4+0.4=2.4,所以当销售额为4千万元时,可以估计该商场的利润额为2.4百万元.21. 解:(1)作出茎叶图:(2)x 甲=18(78+79+81+82+84+88+93+95)=85, x乙=18(75+80+80+83+85+90+92+95)=85. s 2甲=18[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,s 2乙=18[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.∵x甲=x 乙,s 2甲<s 2乙,∴甲的成绩较稳定,派甲参赛比较合适.22. 解:(1)根据茎叶图可知,鲤鱼与鲫鱼的平均数目分别为80,20. 由题意知,池塘中鱼的总数目为1 000÷80+202 000=20 000(条),则估计鲤鱼数目为20 000×80100=16 000(条),鲫鱼数目为20 000-16 000=4 000(条).(2)①根据题意,结合直方图可知,池塘中鱼的重量在3千克以上(含3千克)的条数约为20 000×(0.12+0.08+0.04)×0.5=2 400(条).②设第二组鱼的条数为x ,则第三、四组鱼的条数分别为x +7、x +14,则有x +x +7+x +14=100×(1-0.55),解得x =8,故第二、三、四组的频率分别为0.08、0.15、0.22,它们在频率分布直方图中的小矩形的高度分别为0.16,0.30,0.44,据此可将频率分布直方图补充完整(如图).③众数为2.25千克,平均数为0.25×0.04+0.75×0.08+1.25×0.15+…+4.25×0.02=2.02(千克), 所以鱼的总重量为2.02×20 000=40 400(千克).阶段质量检测(三)(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列说法正确的是( ) A .随机事件的概率总在[0,1]内 B .不可能事件的概率不一定为0 C .必然事件的概率一定为1 D .以上均不对2.下列事件中,随机事件的个数为( )①在某学校校庆的田径运动会上,学生张涛获得100米短跑冠军;②在明天下午体育课上,体育老师随机抽取一名学生去拿体育器材,抽到李凯; ③从标有1,2,3,4的4张号签中任取一张,恰为1号签; ④在标准大气压下,水在4 ℃时结冰. A .1 B .2 C .3 D .43.甲、乙、丙三人随意坐一排座位,乙正好坐中间的概率为( ) A.12 B.13 C.14 D.164.从一批产品中取出三件产品,设A =“三件产品全不是次品”,B =“三件产品全是次品”,C =“三件产品不全是次品”,则下列结论正确的是( )A .A 与C 互斥B .B 与C 互斥C .任何两个均互斥D .任何两个均不互斥5.(2016·郑州高一检测)函数f (x )=x 2-x -2,x ∈[-5,5],那么任取一点x 0,使得f (x 0)≤0的概率是( ) A.310 B.15 C.25 D.456.如图,在矩形ABCD 中,点E 为边CD 的中点.若在矩形ABCD 内部随机取一个点Q ,则点Q 取自△ABE 内部的概率等于( )A.14B.13C.12D.237.给甲、乙、丙三人打电话,若打电话的顺序是任意的,则第一个打电话给甲的概率是( ) A.16 B.13 C.12 D.238.如图,EFGH 是以O 为圆心、半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,则P (A )=( )A.4πB.1π C .2 D.2π9.在区间[-π,π]内随机取两个数分别记为a ,b ,则使得函数f (x )=x 2+2ax -b 2+π2 有零点的概率为( )A.π4 B .1-π4 C.4π D.4π-1 10.如图所示,茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中有一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率是( )A.25B.710C.45D.91011.掷一枚均匀的正六面体骰子,设A 表示事件“出现2点”,B 表示“出现奇数点”,则P (A ∪B )等于( )A.12B.23C.13D.2512.节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( )A.14B.12C.34D.78二、填空题(本大题共4小题,每小题5分,共20分)13.(2016·青岛高一检测)一个口袋内装有大小相同的10个白球,5个黑球,5个红球,从中任取一球是白球或黑球的概率为________.14.如图所示,在正方形内有一扇形(见阴影部分),点P 随意等可能落在正方形内,则这点落在扇形外且在正方形内的概率为________.15.已知集合A ={(x ,y )|x 2+y 2=1},集合B ={(x ,y )|x +y +a =0},若A ∩B ≠∅的概率为1,则a 的取值范围是________.16.从1,2,3,4这四个数字中,任取两个,这两个数字都是奇数的概率是________,这两个数字之和是偶数的概率是________.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(10分)从甲、乙、丙、丁四个人中选两名代表.求:(1)甲被选中的概率;(2)丁没被选中的概率.18.(12分)袋子中装有大小和形状相同的小球,其中红球与黑球各1个,白球n 个.从袋子中随机取出1个小球,取到白球的概率是12. (1)求n 的值;(2)记从袋中随机取出的一个小球为白球得2分,为黑球得1分,为红球不得分.现从袋子中取出2个小球,求总得分为2分的概率.19.(12分)一个袋中装有四个形状、大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率.(2)先从袋中随机取一个球,该球的编号为m ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n ,求n <m +2的概率.20.(12分)已知集合Z ={(x ,y )|x ∈[0,2],y ∈[-1,1]}.(1)若x ,y ∈Z ,求x +y ≥0的概率;(2)若x ,y ∈R ,求x +y ≥0的概率.21.(12分)(2015·福建高考)全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.(1)现从融合指数在[4,5)和[7,8]2家进行调研,求至少有1家的融合指数在[7,8]内的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.22.(12分)袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;(2)向袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两种卡片颜色不同且标号之和小于4的概率.答案1. 解析:选C随机事件的概率总在(0,1)内,不可能事件的概率为0,必然事件的概率为1.2. 解析:选C①在某学校校庆的田径运动会上,学生张涛有可能获得100米短跑冠军,也有可能未获得冠军,是随机事件;②在明天下午体育课上,体育老师随机抽取一名学生去拿体育器材,李凯不一定被抽到,是随机事件;③从标有1,2,3,4的4张号签中任取一张,不一定恰为1号签,是随机事件;④在标准大气压下,水在4 ℃时结冰是不可能事件.故选C.3. 解析:选B甲、乙、丙三人随意坐有6个基本事件,乙正好坐中间,甲、丙坐左右两侧有2个基本事件,故乙正好坐中间的概率为26=1 3.4. 解析:选B因为事件B是表示“三件产品全是次品”,事件C是表示“三件产品不全是次品”,显然这两个事件不可能同时发生,故它们是互斥的,所以选B.5. 解析:选A由f(x0)≤0,即x20-x0-2≤0,得-1≤x0≤2,其区间长度为3,由x∈[-5,5],区间长度为10,所以所求概率为P=310.6. 解析:选C不妨设矩形的长、宽分别为a、b,于是S矩形=ab,S△ABE=12ab,由几何概型的概率公式可知P =S △ABE S 矩形=12. 7. 解析:选B 给三人打电话的不同顺序有6种可能,其中第一个给甲打电话的可能有2种,故所求概率为P =26=13.故选B. 8. 解析:选D 豆子落在正方形EFGH 内是随机的,故可以认为豆子落在正方形EFGH 内任一点是等可能的,属于几何概型.因为圆的半径为1,所以正方形EFGH 的边长是2,则正方形EFGH 的面积是2,又圆的面积是π,所以P (A )=2π. 9. 解析:选B 要使函数有零点,则Δ=(2a )2-4(-b 2+π2)≥0,a 2+b 2≥π2,又-π≤a ≤π,-π≤b ≤π,所以基本事件的范围是2π·2π=4π2,函数有零点所包含的基本事件的范围是4π2-π3.所以所求概率为4π2-π34π2=1-π4.故选B. 10. 解析:选C 设被污损的数字是x ,则x ∈{0,1,2,3,4,5,6,7,8,9}.甲的平均成绩为x 甲=15(88+89+90+91+92)=90,x 乙=15[83+83+87+(90+x )+99]=442+x 5,设甲的平均成绩超过乙的平均成绩为事件A ,则此时有90>442+x 5,解得x <8,则事件A 包含x =0,1,2,3,4,5,6,7,共8个基本事件,则P (A )=810=45. 11. 解析:选B 由古典概型的概率公式得P (A )=16,P (B )=36=12. 又事件A 与B 为互斥事件,由互斥事件的概率和公式得P (A ∪B )=P (A )+P (B )=16+12=23. 12. 解析:选C 由于两串彩灯第一次闪亮相互独立且4秒内任一时刻等可能发生,所以总的基本事件为如图所示的正方形的面积,而要求的是第一次闪亮的时刻相差不超过2秒的基本事件,即如图所示的阴影部分的面积,根据几何概型的计算公式可知它们第一次闪亮的时刻相差不超过2秒的概率是1216=34,故选C. 13. 解析:记“任取一球为白球”为事件A ,“任取一球为黑球”为事件B ,则P (A +B )=P (A)+P (B)。
高一数学必修三模块测试题(人教A版)

高一数学必修三模块测试题(人教A 版)限时:120分钟1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,第I 卷一、选择题(每小题5分,共50分) 1.下列给出的赋值语句中正确的是:A 、3=AB 、M=—MC 、B=A=2D 、x+y=0 2.把89化成五进制数的末位数字为 ( ) A 1 B 2 C 3 D 43.如右图,是某算法流程图的一部分,其算法的逻辑结构为 ( )A. 顺序结构B. 判断结构C.条件结构D. 循环结构4.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( ) A 、 分层抽样法,系统抽样法 B 、分层抽样法,简单随机抽样法 C 、系统抽样法,分层抽样法 D 、简单随机抽样法,分层抽样法 5.下列对一组数据的分析,不正确的说法是 ( ) A 、数据极差越小,样本数据分布越集中、稳定 B 、数据平均数越小,样本数据分布越集中、稳定 C 、数据标准差越小,样本数据分布越集中、稳定 D 、数据方差越小,样本数据分布越集中、稳定6.有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;②平均日学习时间和平均学习成绩;③某人每日吸烟量和其身体健康情况; ④正方形的边长和面积;⑤汽车的重量和百公里耗油量; 其中两个变量成正相关的是 ( ) A .①③B .②④C .②⑤D .④⑤7.计算机中常用16进制,采用数字0~9和字母A ~F 共16个计数符号与10进制得对应关系如下表: 例如用16进制表示D+E =1B ,则A ×B=( ) A 6E B 7C C 5F D B08.从一批产品中取出三件产品,设A =“三件产品全不是次品”,B =“三件产品全是次品”,C =“三件产品至少有一件是次品”,则下列结论正确的是( ) A . A 与C 互斥B . 任何两个均互斥 C .B 与C 互斥D . 任何两个均不互斥9.从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知 P (A )= 0.65 ,P(B)=0.2 ,P(C)=0.1。
人教版高中数学高一 必修3综合模块测试 1(人教A版必修3)
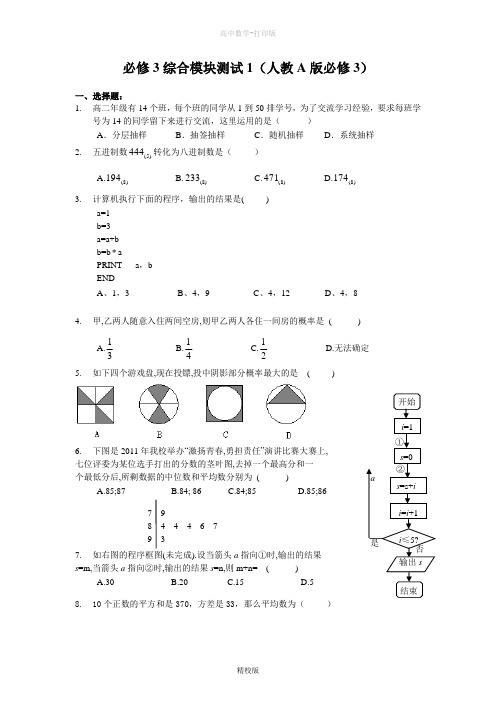
7 9 8 4 4 4 6 7 9 3 开始 i =1 s =0i =i +1s =s+ii ≤5? 输出s 结束① ②a是否 必修3综合模块测试1(人教A 版必修3)一、选择题:1. 高二年级有14个班,每个班的同学从1到50排学号,为了交流学习经验,要求每班学号为14的同学留下来进行交流,这里运用的是( )A .分层抽样B .抽签抽样C .随机抽样D .系统抽样2. 五进制数(5)444转化为八进制数是( )A.(8)194B.(8)233C.(8)471D.(8)1743. 计算机执行下面的程序,输出的结果是( )a=1 b=3 a=a+bb=b a PRINT a ,b ENDA 、1,3B 、4,9C 、4,12D 、4,8 4. 甲,乙两人随意入住两间空房,则甲乙两人各住一间房的概率是 ( )A.31B.41C.21 D.无法确定 5. 如下四个游戏盘,现在投镖,投中阴影部分概率最大的是 ( )6. 下图是2011年我校举办“激扬青春,勇担责任”演讲比赛大赛上, 七位评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的中位数和平均数分别为 ( )A.85;87B.84; 86C.84;85D.85;867. 如右图的程序框图(未完成).设当箭头a 指向①时,输出的结果 s =m,当箭头a 指向②时,输出的结果s =n,则m+n= ( )A.30B.20C.15D.5 8. 10个正数的平方和是370,方差是33,那么平均数为( )A .1B .2C .3D .49. 读程序 甲:INPUT i =1 乙:INPUT i =1000 S =0 S =0 WHILE i <=1000 DOS =S +i S =S +i i =i +l i =i 一1 WEND LOOP UNTIL i <1PRINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是( )A .程序不同,结果不同B .程序不同,结果相同C .程序相同,结果不同D .程序相同,结果相同 10. 已知点P 是边长为4的正方形内任一点,则P 到四个顶点的距离均大于2的概率是( )A.44π- B. 14 C. 34π- D. 1811. 甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b ,其中{},1,2,3,4,5,6a b ∈,若1a b -≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( ) A.19B.29C.718 D.4912. 如右的程序框图可用来估计圆周率π的值.设(1,1)CONRND -是产生随机数的函数,它能随机产生区间(1,1)-内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为 ( )A.3.144B.3.141C.3.142D.3.143二、填空题:13. 语句“PRINT 37 MOD 5 ”运行的结果是____. 14. 阅读右边的流程图,若0.30.322,2,log 0.8,a b c -===则输出的数是_____;15. 5280和2155的最大公约数是____. 16. 乙两艘轮船都要停靠同一个泊位,它们可以在一昼夜(零点至24点)的任意时刻到达,设甲、乙两艘轮船停靠泊位的时间分别是3小时和5小时,则有一艘轮船停靠泊位时必须等待一段时间的概率为____(用分数表示).0.030.01频率组距三.解答题:17. (本题满分12分)设数列{}{}111,n n n n a a a a n a +=-=满足,右图是求数列30前项和的算法流程图。
【人教A版】高中数学新课标必修三全册习题(含答案)

平均数分别是()A.91.5和91.5 B.91.5和92析,获得成绩数据的茎叶图如图所示.(1)计算样本的平均成绩及方差;C.25 D.27解析:该算法的运行过程是:i=1,i=1<10成立,i=1+2=3,S=2×3+3=9,i=3<10成立,i=3+2=5,S=2×5+3=13,i=5<10成立,i=5+2=7,S=2×7+3=17,i=7<10成立,i=7+2=9,S=2×9+3=21,i=9<10成立,i=9+2=11,S=2×11+3=25,i=11<10不成立,输出S=25.答案:C5.阅读如图所示的程序框图,运行相应的程序,输出的结果是()A.3 B.11C.38 D.123解析:根据框图可知第一步的运算为:a=1<10,满足条件,可以得到a=12+2=3.又因为a=3<10,满足条件,所以有a=32+2=11,因为a=11>10,不满足条件,输出结果a=11.答案:BA.A>0,V=S-T B.A<0,V=S-TC.A>0,V=S+T D.A<0,V=S+T解析:由条件结构及已知可得A>0,由已知总收入S和盈利V的值知:V=S+T,故C 项正确.答案:C12.执行如图所示的程序框图,若输出x的值为23,则输入的x值为()A.0 B.1C.2 D.11解析:设输入x的值为m,该程序框图的运行过程是:x=m,n=1n=1≤3成立x=2m+1n=1+1=2n=2≤3成立x=2(2m+1)+1=4m+3n=2+1=3n=3≤3成立x=2(4m+3)+1=8m+7n=3+1=4n=4≤3不成立输出x=8m+7,则有8m+7=23,解得m=2,即输入的x值为2.故选C.答案:C二、填空题:本大题共4小题,每小题5分,共20分.13.将258化成四进制数是________.解析:利用除4取余法.则258=10 002(4).答案:10 002(4)14.用秦九韶算法求多项式f(x)=3x6+12x5+8x4-3.5x3+7.2x2+5x-13在x=6时的值,v3=________.解析:f(x)=(((((3x+12)x+8)x-3.5)x+7.2)x+5)x-13,v0=3,v1=3×6+12=30,v2=v1x+8=30×6+8=188,v3=v2x-3.5=188×6-3.5=1 124.5.答案:1 124.515.阅读如图所示的程序框图,运用相应的程序,若输入m的值为2,则输出的结果i =________.解析:由程序框图,i=1后:A=1×2,B=1×1,A<B?否;i=2后:A=2×2,B=1×2,A<B?否;i=3后:A=4×2,B=2×3,A<B?否;i=4后:A=8×2,B=6×4,A<B?是,输出i=4.答案:416.输入8,下列程序执行后输出的结果是________.解析:∵输入的数据是8,t≤4不成立,∴c=0.2+0.1(8-3)=0.7.答案:0.7三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)阅读下列两个程序,回答问题.(1)上述两个程序的运行结果是:①________;②________.(2)上述两个程序中的第三行有什么区别?解析:(1)两个程序的运行结果是①44;②33;(2)程序①中的x=y是将y的值4赋给x,赋值后,x的值变为4,程序②中的y=x是将x的值3赋给y,赋值后y的值变为3.18.(本小题满分12分)利用秦九韶算法判断函数f(x)=x5+x3+x2-1在[0,2]上是否存在零点.解析:f(0)=-1<0,下面用秦九韶算法求x=2时,多项式f(x)=x5+x3+x2-1的值.多项式变形为f(x)=((((x+0)x+1)x+1)x+0)x-1,v0=1,v1=1×2+0=2,v2=2×2+1=5,v3=5×2+1=11,v4=11×2+0=22,v5=22×2-1=43,所以f(2)=43>0,即f(0)·f(2)<0,所以函数f(x)=x5+x3+x2-1在[0,2]上存在零点.19.(本小题满分12分)执行图中程序,回答下面问题:(1)若输入:m=30,n=18,则输出的结果为________.(2)画出该程序的程序框图.解析:(1)由程序知题目为用辗转相除法求两个正整数的最大公约数,所以30=1×18+12,18=1×12+6,12=2×6+0,即最大公约数为6.(2)程序框图:21.(本小题满分12分)在边长为4的正方形ABCD 的边上有一点P ,沿着折线BCDA 由点B(起点)向点A(终点)运动.设点P 运动的路程为x ,△APB 的面积为y ,且y 与x 之间的函数关系式用如图所示的程序框图给出.(1)写出程序框图中①,②,③处应填充的式子.(2)若输出的面积y 值为6,则路程x 的值为多少?并指出此时点P 在正方形的什么位置上.解析:(1)由题意,得y =⎩⎪⎨⎪⎧2x ,0≤x ≤4,8,4<x ≤8,24-2x ,8<x ≤12,故程序框图中①,②,③处应填充的式子分别为:y =2x ,y =8,y =24-2x.(2)若输出的y 值为6,则2x =6或24-2x =6,解得x =3或x =9,当x =3时,此时点P 在正方形的边BC 上,距C 点的距离为1;当x =9时,此时点P 在正方形的边DA 上,距D 点的距离为1.22.(本小题满分12分)已知某算法的程序框图如图所示,若将输出的(x,y)值依次为(x1,y1),(x2,y2),…,(x n,y n),…(1)若程序运行中输出的一个数组是(9,t),求t的值.(2)程序结束时,共输出(x,y)的组数为多少?(3)写出程序框图的程序语句.解析:(1)由程序框图知:当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 011时,输出最后一对,共输出(x,y)的组数为1 005.(3)程序框图的程序语句如下:第二章质量评估检测时间:120分钟满分:150分一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是()A.简单随机抽样B.系统抽样C.分层抽样D.抽签法解析:抽出的号码是5,10,15,…,60,符合系统抽样的特点:“等距抽样”.答案:B2.统计某校1 000名学生的数学测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是()A.20% B.25%C.6% D.80%解析:从左至右,后四个小矩形的面积和等于及格率,则及格率是1-10×(0.005+0.015)=0.8=80%.答案:D3.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是()A.x与y负相关,x与z负相关B.x与y正相关,x与z正相关C.x与y正相关,x与z负相关D.x与y负相关,x与z正相关解析:∵变量x和y满足关系y=0.1x-10,∴变量x和y是正相关关系. 又变量z与y图中可以得到这10位同学身高的中位数是()A.161 cm B.162 cm________,父亲的平均年龄比母亲的平均年龄多________岁.1A .求函数y =⎩⎪⎨⎪⎧x 2(x <0),-x 2(x ≥0)的函数值B .求函数y =⎩⎪⎨⎪⎧ x 2(x <0),2(x =0),-x 2(x >0)的函数值C .求函数y =⎩⎪⎨⎪⎧x 2(x >0),2(x =0),-x 2(x <0)的函数值D .以上都不正确解析:由算法知,当x <0时,y =x 2;当x =0时,y =2;当x >0时,y =-x 2.故选B.答案:B5.在用二分法求方程零点的算法中,下列说法正确的是( ) A .这个算法可以求方程所有的零点 B .这个算法可以求任何方程的零点 C .这个算法能求方程所有的近似零点D .这个算法并不一定能求方程所有的近似零点解析:二分法求方程零点的算法中,仅能求方程的一些特殊的近似零点.(满足函数零点存在性定理的条件)则D 正确.答案:D6.下列算法要解决的问题是( )第一步,比较a 与b 的大小,如果a <b ,则交换a ,b 的值. 第二步,比较a 与c 的大小,如果a <c ,则交换a ,c 的值. 第三步,比较b 与c 的大小,如果b <c ,则交换b ,c 的值. 第四步,输出a ,b ,c .A .输入a ,b ,c 三个数,比较a ,b ,c 的大小B .输入a ,b ,c 三个数,找出a ,b ,c 中的最大数C .输入a ,b ,c 三个数,按从大到小的顺序输出D .输入a ,b ,c 三个数,求a ,b ,c 的平均数解析:由这四个步骤可知算法要解决问题是输入a ,b ,c 三个数,按从大到小的顺序输出.答案:C7.如下算法:第一步,输入x 的值. 第二步,若x ≥0,则y =x . 第三步,否则,y =x 2. 第四步,输出y 的值,若输出的y 值为9,则x =________.解析:根据题意可知,此为分段函数y =⎩⎪⎨⎪⎧x ,x ≥0x 2,x <0的算法,当x ≥0时,x =9;当x <0时,x 2=9, 所以x =-3. 答案:9或-38.已知一个算法如下:第二步,如果a ≥4,则y =2a -1;否则,y =a 2-2a +3. 第三步,输出y 的值.问:(1)这个算法解决的是什么问题?(2)当输入的a 的值为多少时,输出的数值最小?最小值是多少?解析:(1)这个算法解决的是求分段函数y =⎩⎪⎨⎪⎧2a -1,a ≥4,a 2-2a +3,a <4的函数值的问题.(2)当a ≥4时,y =2a -1≥7;当a <4时,y =a 2-2a +3=(a -1)2+2≥2, ∵当a =1时,y 取得最小值2.∴当输入的a 值为1时,输出的数值最小为2.3.如图程序框图的运行结果是()534.如图程序框图中,若R=8,运行结果也是8,则程序框图中应填入的内容是()A.a=2b B.a=4b16.阅读如图所示程序框图.若输入x为9,则输出的y的值为()A.8B.3 C.2D.17.如图所示的是一个算法的程序框图,已知a1=3,输出的b=7,则a2等于()A.9B.10 C.11D.128.阅读如图的程序框图,若输出的结果为6,则①处执行框应填的是()A.x=1B.x=2 C.b=1D.b=2程序框图:B组能力提升则程序框图中①处应填________.a径的圆的面积,即a 2-π4a 2,故空白部分的面积S =a 2-2⎝⎛⎭⎫a 2-π4a 2=π2a 2-a 2. 答案:S =π2a 2-a 212.阅读如图所示的程序框图,根据该图和下列各小题的条件回答下面的问题.(1)该程序框图解决的是一个什么问题?(2)若当输入的x 值为0和4时,输出的值相等,则当输入的x 值为3时,输出的值为多大?(3)在(2)的条件下要想使输出的值最大,输入的x 值应为多大?解析:(1)该程序框图解决的是求二次函数f (x )=-x 2+mx 的函数值的问题. (2)当输入的x 值为0和4时,输出的值相等, 即f (0)=f (4).因为f (0)=0,f (4)=-16+4m , 所以-16+4m =0.所以m =4.所以f (x )=-x 2+4x . 于是f (3)=-32+4×3=3,所以当输入的x 值为3时,输出的f (x )值为3. (3)因为f (x )=-x 2+4x =-(x -2)2+4, 当x =2时,f (x )最大值=4,所以要想使输出的值最大,输入的x 值应为2.13.如图,是解决某个问题而绘制的程序框图,仔细分析各框内的内容及图框之间的关系,回答下面的问题:(1)图框①中x =2的含义是什么?(2)图框②中y 1=ax +b 的含义是什么? (3)图框④中y 2=ax +b 的含义是什么? (4)该程序框图解决的是怎样的问题?(5)当最终输出的结果是y 1=3,y 2=-2时,求y =f (x )的解析式. 解:(1)图框①中x =2表示把2赋值给变量x .(2)图框②中y 1=ax +b 的含义是:该图框在执行①的前提下,即当x =2时,计算ax +b 的值,并把这个值赋给y 1.(3)图框④中y 2=ax +b 的含义是:该图框在执行③的前提下,即当x =-3时,计算ax +b 的值,并把这个值赋给y 2.(4)该程序框图解决的是求函数y =ax +b 的函数值的问题,其中输入的是自变量x 的值,输出的是对应x 的函数值.(5)y 1=3,即2a +b =3. ⑤ y 2=-2,即-3a +b =-2. ⑥ 由⑤⑥,得a =1,b =1, 所以f (x )=x +1.课时作业(三) 条件结构A 组 基础巩固1.如图,是计算函数y =⎩⎪⎨⎪⎧-x ,x ≤-1,0,-1<x ≤2,x 2,x >2的值的程序框图,则在①,②,③处应分别填入的是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r=0
A 1 B 2 C 3 D 4 3.如右图,是某算法流程图的一部分,其算法的逻辑结构为 ( ) A. 顺序结构 B. 判断结构 C. 条件结构 D. 循环结构 4.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150 个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取 一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型 销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查 为(2)。则完成(1)、(2)这两项调查宜采用的抽样方法依次是 ( ) A、 分层抽样法,系统抽样法 B、分层抽样法,简 单随机抽样法 C、系统抽样法,分层抽样法 D、简单随机抽样法, 分层抽样法 5.下列对一组数据的分析,不正确的说法是 ( ) A、数据极差越小,样本数据分布越集中、稳定 B、数据平均数越小,样本数据分布越集中、稳定 C、数据标准差越小,样本数据分布越集中、稳定 D、数据方差越小,样本数据分布越集中、稳定 6.有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路
例如用16进制表示D+E=1B,则A×B=( A 6E B 7C C 5F D B0
)
8.从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产 品全是次品”,C=“三件产品至少有一件是次品”,则下列结论正确的是 ( ) A. A与C互斥 B. 任何两个均互斥 C. B与C互斥 D. 任何两个均不互斥 9.从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知 P(A)= 0.65 ,P(B)=0.2 ,P(C)=0.1。则事件“抽到的不是一等品”的概率为( ) A. 0.7 B. 0.65 C. 0.35 D. 0.3 10.先后抛掷质地均匀的硬币三次,则至少一次正面朝上的概率是 ( ) A. B. C. D. 二、填空题(每小题5分,共20分) 11.计算机的程序设计语言很多,但各种程序语言都包含下列基本的
16.(13分)下面是计算应纳税所得额的算法过程,其算法如下:
第一步 输入工资x(注x<=5000); 第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x800); 否则 y=25+0.1(x-1300) 第三步 输出税款y, 结束。 请写出该算法的程序框图和程序。(注意:程序框图与程序必须对 应)
山东省莱州一中高一数学必修三模块测试题(人 教A版)
限时:120分钟
第II卷
一、选择题(每小题5分,共60分) 1 2 3 4 5 6 7 8 9 10
二、填空题(每小题5分,共20分) 11. , , , 12. ,
,。Βιβλιοθήκη 。 14. 。13.
;
三、解答题: 甲 27 38 30 37 35 31 15.(12分)为了参加奥运会,对自 乙 33 29 38 34 28 36 行车运动员甲、乙两人在相同的条件下 进行了6次测试,测得他们的最大速度的数据如表所示: 请判断:谁参加这项重大比赛更合适,并阐述理由。
20.(本小题满分14分)给出50个数,1,2,4,7,11,…,其规律 是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4 个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面 给出的程序框图补充完整,再根据程序框图写出程序. 1. 把程序框图补充完整: (2)
算法语句: , , , , 。 12.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量 为60的样本(60名男生的身高,单位:cm),分组情况如下: 分组 151.5~ 158.5~ 165.5~ 172.5~ 则表中的 , 158.5 165.5 172.5 179.5 。 频数 6 2l
20.(本小题满分14分)给出50个数,1,2,4,7,11,…,其规律 是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4 个数比第3个数大3,…,以此类推. 要求计算这50个数的和. 先将下面 给出的程序框图补充完整,再根据程序框图写出程序. 1. 把程序框图补充完整: (2) 结束 i= i +1 (1) 开始
结束 i= i +1 (1) 开始
是
输出 s
否
i=1 P=1 S= 0 S= s + p (1)________________________ (3分) (2)________________________ (4分) 2. 程序:(7分)
山东省莱州一中高一数学必修三模块测试题(人 教A版)
参考答案
程; ②平均日学习时间和平均学习成绩; ③某人每日吸烟量和其 身体健康情况; ④正方形的边长和面积; ⑤汽车的重量和百公里 耗油量; 其中两个变量成正相关的是 ( ) A.①③ B.②④ C.②⑤ D.④⑤ 7.计算机中常用16进制,采用数字0~9和字母A~F共16个计数符号与 10进制得对应关系如下表: 16 0 1 2 3 4 5 6 7 8 9 A B C D E F 进 制 10 进 制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
17.(13分)为了调查甲、乙两个网站受欢迎的程度,随机选取了14
天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图, 根据统计图: 茎叶图 (1)甲、乙两个网站点击量的极差分别是多少? (4分) (2)甲网站点击量在[10,40]间的频率是多少? (5分) (3)甲、乙两个网站哪个更受欢迎?并说明理由。 (4分) 解:
山东省莱州一中高一数学必修三模块测试题(人 教A版)
限时:120分钟
1. 本试卷分第I卷(选择题)和第II卷(非选择题)两 部分,共150分, 第I卷
一、选择题(每小题5分,共50分) 1.下列给出的赋值语句中正确的是: A、3=A B、M=—M C、B=A=2 2.把89化成五进制数的末位数字为 n不是质数 n不是质数 是 否 D、x+y=0 ( )
13.如右图,在正
方形内有一扇形 频率 0.1 (见阴影部分), 扇形对应的圆心是 正方形的一顶点,半径为正方形的边长。在这个图形上随机撒一粒黄 豆,它落在扇形外正方形内的概率为 。(用分数表示) 14.下列说法中正确的有________ ①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据 影响; ②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝 上”、“恰好一枚硬币正面朝上”的概率一样大 ③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越 准确。 ④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等 可能的,则该随机试验的数学模型是古典概型。
17.(13分)为了调查甲、乙两个网站受欢迎的程度,随机选取了14
天,统计上午8:00—10:00间各自的点击量,得如下所示的统计图, 根据统计图: 茎叶图 (1)甲、乙两个网站点击量的极差分别是多少? (4分) (2)甲网站点击量在[10,40]间的频率是多少? (5分) (3)甲、乙两个网站哪个更受欢迎?并说明理由。 (4分)
18.(本小题满分14分)在人群流量较大的街道,有一中年人吆喝“送 钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球 (其体积、质地完成相同),旁边立着一块小黑板写道: 摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主 送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元 钱。 (1)摸出的3个球为白球的概率是多少? (2)摸出的3个球为2个黄球1个白球的概率是多少? (3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一 个月(按30天计)能赚多少钱?
限时:120分钟
第II卷
一、选择题(每小题5分,共60分) 1 2 3 4 5 6 7 8 B D C B B C A A 9 C 10 D
二、填空题(每小题5分,共20分) 11.输入语句 ,输出语句 , 赋值语句 , 条件语句 , 循环语句 。 12. 6 , 0.45
。 。
13.
14.
③
三、解答题: 甲 27 38 30 37 35 31 15.(12分)为了参加奥运会,对自 乙 33 29 38 34 28 36 行车运动员甲、乙两人在相同的条件下 进行了6次测试,测得他们的最大速度的数据如表所示: 请判断:谁参加这项重大比赛更合适,并阐述理由。 解: ( 4分) S甲=, S乙= (8分) ,S甲>S乙 (10分) 乙参加更合适 (12分)
16.(13分)下面是计算应纳税所得额的算法过程,其算法如下:
第一步 输入工资x(注x<=5000); 第二步 如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x800); 否则 y=25+0.1(x-1300) 第三步 输出税款y, 结束。 请写出该算法的程序框图和程序。(注意:程序框图与程序必须对 应) 解:框图7分,程序6分(不对应扣3-4分)
19.(14分)假设你家订了一份报纸,送报人可能在早上6点—8点之间 把报纸送到你家,你每天离家去工作的时间在早上7点—9点之间 (1)你离家前不能看到报纸(称事件A)的概率是多少?(8分, 须有过程) (2)请你设计一种随机模拟的方法近似计算事件A的概率(包括手 工的方法或用计算器、计算机的方法)(6分)
(1)甲网站的极差为:73-8=65; (2分) 乙网站的极差为:61-5=56 (4分) (2)甲网站点击量在[10,40]间的频率为4/14=2/7=0.28571 (9分) (3)甲网站的点击量集中在茎叶图的下方,而乙网站的点击 量集中在茎叶图的上方。从数据的分布情况来看,甲网站更受 欢迎。 (13分)
1
18.(本小题满分14分)在人群流量较大的街道,有一中年人吆喝“送 钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球 (其体积、质地完成相同),旁边立着一块小黑板写道: 摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主
