【人教版】七年级数学第二章《整式的加减》导学案
七年级数学《整式的加减》导学案
第二章整式的加减
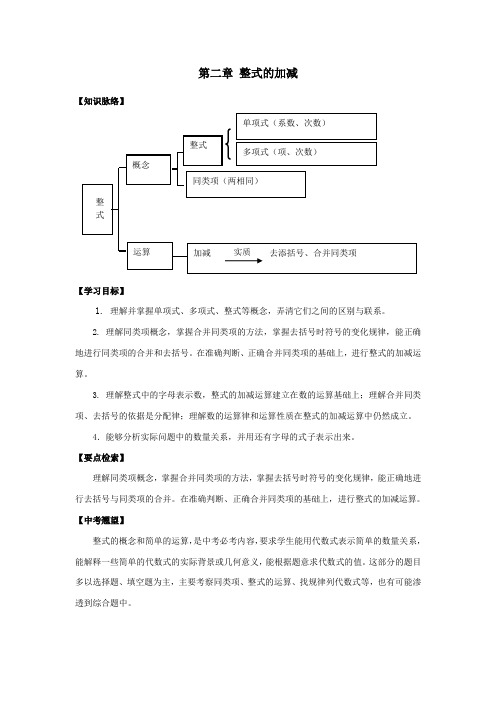
【知识脉络】
【学习目标】
1. 理解并掌握单项式、多项式、整式等概念,弄清它们之间的区别与联系。
2. 理解同类项概念,掌握合并同类项的方法,掌握去括号时符号的变化规律,能正确地进行同类项的合并和去括号。
在准确判断、正确合并同类项的基础上,进行整式的加减运算。
3. 理解整式中的字母表示数,整式的加减运算建立在数的运算基础上;理解合并同类项、去括号的依据是分配律;理解数的运算律和运算性质在整式的加减运算中仍然成立。
4.能够分析实际问题中的数量关系,并用还有字母的式子表示出来。
【要点检索】
理解同类项概念,掌握合并同类项的方法,掌握去括号时符号的变化规律,能正确地进行去括号与同类项的合并。
在准确判断、正确合并同类项的基础上,进行整式的加减运算。
【中考翘望】
整式的概念和简单的运算,是中考必考内容,要求学生能用代数式表示简单的数量关系,能解释一些简单的代数式的实际背景或几何意义,能根据题意求代数式的值。
这部分的题目多以选择题、填空题为主,主要考察同类项、整式的运算、找规律列代数式等,也有可能渗透到综合题中。
整式的加减导学案

整式的加减导学案一、课题:整式的加减二、学习目标1、在复习去括号以及合并同类项的基础上,进行整式加减运算。
2掌握整式加减的一般步骤,能熟练进行整式的加减运算。
3培养用代数的方法解决实际问题的能力。
三、教学重点1 理解整式的加减,实质就是去括号,合并同类项2掌握整式加减的一般步骤。
四、教学难点括号前面是一号,去括号时里面各项符号都改变。
五、学法指导通过例题讲解总结归纳出整式加减运算的一般步骤,并应用其熟练地进行整式的加减运算。
六、攻克重难点温故知新例1 计算(1)(2x- 3y)+(5x+4y) (2)(2x-3y)-(5x-4y)解:原式=2x-3y+5x+4y 去括号=2x+5x-3y+4y=7x+y 合并同类项尝试练习:1 、求多项式3x-5y和3x+5y的差。
整式的加减运算通常是先( ),再( )。
2一种笔记本的单价x元,圆珠笔的单价是y元。
小红买这种本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支。
问买这些笔记本和圆珠笔,小红和小明一共花费多少钱?学以致用例2 做大小两个长方形纸盒,尺寸如下(单位;cm):长宽高小纸盒abc大纸盒1.5a2b2c(1)做这两个纸盒共用料多少平方厘米?(2)做大纸盒比做小纸盒多用料多少平方厘米?解;小纸盒的表面积是(2ab+2bc+2ac)cm2大纸盒的表面积是(6ab+8bc+6ac)cm2(1)做这两个纸盒共用料(2ab+2bc+2ac)+(6ab+8bc+2ac)=2ab+2bc+2ac+6ab+8bc+6ac=8ab+10bc+8ac( cm2 )(2)做大纸盒比做小纸盒多用料(6ab+8bc+6ac)-(2ab+2bc+2ac)=6ab+8bc+6ac-2ab-2bc-2ac=4ab+6bc+4ac( cm2 )思考:整式加减的一般步骤是什么?归纳:整式加减运算法则一般地,几个证实相加减,如果有括号就先括号,然后再合并同类项。
练一练计算(1)3xy-4xy-(-2xy)(2)- ab - a2+ a2-(- ab)(3)(-x+2x2+5)+(4x2-3-6x)(4)(3a2-ab+7)-(-4a2+2ab+7)深化提高例3 求 x-2(x- y2)+(- x+ y2)的值,其中x=-2,y= 解:原式= x-2x+ y2- x+ y2 去括号=-3x+y2 合并同类项当x=-2,y= 时,原式=(-3)(-2)+( )2 再代入数值进行计算=6+ =七、构建知识体系整式加减的一般步骤:八、学习反馈化简求值:5(3a2b-ab2)-ab2+3a2b),其中a= ,b=九、作业:71页4、7题。
七年级数学上册 第2章《整式的加减》导学案(新版)新人教版

【课后作 业】 (一 )必做题 1.计算 (1)
1 1 1 2 ab a 2 a 2 ( ab ) 3 4 3 3
(2) (3a ab 7) (4a 2ab 7)
2 2
(3 ) ( 2 x
第 2 章《整式的加减》
学习目标: 1.进一步熟悉去括号、合并同类项法则. 2.熟练掌握整式的加减运算,并能进行化简求值. 学习重点:整式的加减. 学 习难点:化简求值. 【学前准备】 计算:①
2x 2 y 3xy 3x 2 y 2xy 1
②
a (2a b) 2(a 2b)
【评价】 准确程度评价 书写整洁程度评价 【课后反思】 优 优 良 良 中 中 差 差
【导入】 【自主学习,合作交流】 计算: (1) 2 x 3 y 5x 4 y (2) 8a 7b 4a 5b
3.求
2 1 1 3 1 x 2( x y 2 ) ( x y 2 ) 的值,其中 x=-2, y . 3 2 3 2 3
【当堂测试】
1.计算: (1) 3xy 4 xy (2 xy)
(2) ( x 2x 2 5) (4x 2 3 6x)
2.已知 A= 3x 2 4xy 2 y 2 , B x 2 2xy 5 y 2 ,求 A-B
3.先化简,再求值: 5(3x2 y xy 2 ) ( xy 2 3x2 y) ,其中 x
2
1 1 3 x ) 4( x x 2 ) 2 2
(4) 3x [7 x (4 x 3) 2 x ]
2 2
(二)选做题 1.已知多项式 a 2a 的值是 3,求 4 2a 4a 的值.
【最新】人教版七年级数学上册第二章《2.2整式的加减》导学案
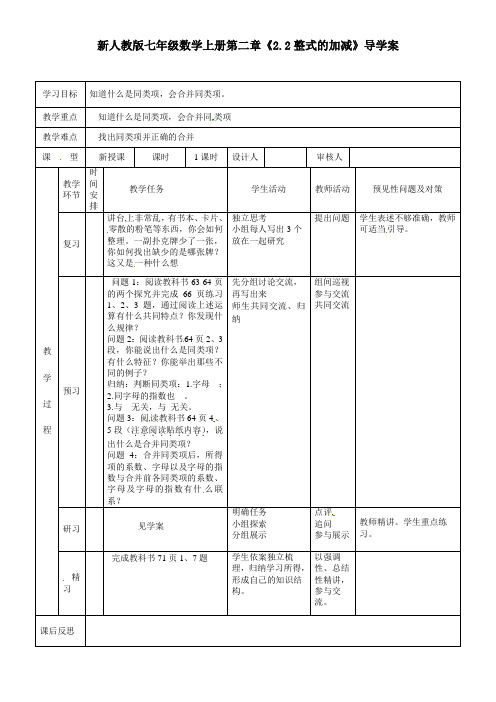
学习目标
知道什么是同类项,会合并同类项。
教学重点
知道什么是同类项,会合并同 类项
教学难点找出同类项并正确Fra bibliotek合并课 型
新授课
课时
1课时
设计人
审核人
教学过程
教学环节
时间安排
教学任务
学生活动
教师活动
预见性问题及对策
复习
讲台 上非常乱,有书本、卡片、 零散的粉笔等东西,你会如何整理。一副扑克牌少了一张,你如何找出缺少的是哪张牌?这又是 一种什么想
分组展示
点评
追问
参与展示
教师精讲。学生重点练习。
精习
完成教科书71页1、7题
学生依案独立梳理,归纳学习所得,形成自己的知识结构。
以强调性、总结性精讲,参与交流。
课后反思
3.与__无关,与_无关。
问题3:阅 读教科书64页4 、5段(注意阅读贴纸内容),说出什么是合并同类项?
问题4:合并同类项后,所得项的系数、字母以及字母的指数与合并前各同类项的系数、字母及字母的指数有什 么联系?
先分组讨论交流,
再写出来
师生共同交流、归纳
组间巡视
参与交流
共同交流
研习
见学案
明确任务
小组探索
独立思考
小组每人写出3个放在一起研究
提出问题
学生表述不够准确,教师可适当 引导。
预习
问题1:阅读教科书63-64页的两个探究并完成66页练习1、2、3题,通过阅读上述运算有什么共同特点?你发现什么规律?
问题2:阅读教科书 64页2、3段,你能说出什么是同类项?有什么特征?你能举出那些不同的例子?
七年级数学上册第二章整式的加减整式的加减导学案新人教版

课题 2.2.1整式的加减 (1)德育目标:、通过师生合作,体验教学活动充满着探索性和创造性,从而体会到学习中的成就感。
学习目的:1、理解同类项和合并同类项的概念2、掌握合并同类项的法则,并会运用该法则;学习重点:合并同类项、同类项的概念学习难点:根据同类项概念在多项式中找同类项学习过程:一、课堂引入: 运用有理数的运算律计算100×2+252×2=____________100×(-2)+252×(-2)=____________二、自学课本 P62-P63探究,小组探讨乘法分配律在计算中的运用由课本问题引出: 1、填空 (1)100t+252t=( )t(2)3x 2+2x 2= ( )x 2 (3)3ab 2—4ab 2=( )ab 2归纳: ___________________________________________,叫做同类项,几个常数项也是同类项。
__________________________,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的____,且___________ 不变。
理解同类项:两个相同①所含字母相同;②相同字母的指数分别相同;两者缺一不可;两个无关:(1)、同类项与系数大小无关;(2)、同类项与它们所含相同字母的顺序无关.三、例题讲解:例1:判断下列各组中的两项是否是同类项①-5ab 3与3a 3b , ②x 3与53, ③-xy 2z 与12zy 2x ,④3xy 与3x , ⑤53与35, ⑥3mn 与33mn例2:合并下列各式的同类项:(1)xy 2-51xy 2 (2)-3x 2y+2x 2y+3xy 2-2xy 2(3)4a 2+3b 2+2ab-4a 2-4b 2 (4)4x 2+2x+7+3x-8x 2-2例3、当K 取何值时,y x y xk 23-与是同类项? 分析:要使y x y x k 23-与是同类项,必须满足什么条件?四、当堂训练: (A 组) 1、下列两式是同类项的是( )A .32xyz 与32xy B. x1 与2x C.0.5x 3y 2和7x 2y 3 D.5m 2n 与-4 n m 22、下面计算正确的是( )A.3x 2-x 2=3B.3a 2+2a 3=5a 5C.3+x=3xD.-0.25ab+41ba=0 3、计算: (1)12x -20x ; (2)x+7x-5x ; (3)-5a+0.3a-2.7a ;(4)31y -32y +2y ; (5)-6ab+ba+8ab ; (6)10y 2-0.5y 2(B 组)4、请你在下面的横线上填上适当的内容,使两个单项式构成同类项。
新人教版初中数学七年级上册《第二章整式的加减整式的加减运算》优课导学案_0

七年级上册《整式的加减》教学设计1.理解同类项、合并同类项的概念。
2.掌握合并同类项法则,会应用该法则及运算律合并多项式的同类项,会应用同类项及合并同类项解决实际问题。
3.感受其中的“数式通性”和类比的数学思想。
【教学重点】理解同类项的概念;掌握合并同类项法则。
【教学难点】正确运用法则及运算律合并同类项。
【教学过程】一、知识链接1.运用运算律计算下列各题。
①6×20+3×20= ②6×(-20)+3×(-20)=2.口答。
8个人+5个人= 8只羊+5只羊=8个人+5只羊=[意图:①复习乘法分配律;②感受“同类”。
操作流程:幻灯片出示→学生口答(1)→分配律:ab+ac=a(b+c)→口答(2)→解释]二、探究新知探究一:一只蜗牛在爬一根竖立的竹竿,每节竹竿是a厘米,第1小时向上爬了6节,第2小时向上爬了2节,问这个蜗牛在竹竿上向上爬了多少厘米?(1)请列式表示:,你能对上式进行化简计算吗?(2)说说化简计算的依据。
[意图:联系生活情境,探究新知。
操作流程:幻灯片出示→学生独立思考并回答→师生小结方法]探究二:根据以上式子的运算,化简下列式子。
①100t-252t ②3x2+2x2②3ab2-4ab2 ④2m2n3-5m2n3(1)上述各多项式的项有什么共同特点?(2)上述多项式的运算有什么共同特点,有何规律?[意图:让学生经历动手、观察、猜想、归纳的学习过程,从而探究出新知。
操作流程:幻灯片出示→动手计算→回答并解释→观察(交流)→猜想→引导学生归纳新知]三、例题精炼例1.合并同类项。
4x2+2x+7+3x-8x2-2例2.求多项式-x2+4x+5x2-3x-4x2+3的值,其中x= 。
[意图:运用知识解决问题,突出重点。
操作流程:完成例1(3~4人演排)→学生质疑→师点评并规范格式、注意事项(例2处理方式同上)]四、课堂小结这节课你学到了哪些知识?[意图:养成总结反思的好习惯。
新人教版七年级数学上册第二章整式的加减导学案

新人教版七年级数学上册第二章整式的加减导学案学习目标、重点、难点【学习目标】1.会用字母表示数,并会列式表示数量关系.2.理解并掌握单项式、多项式和整式的概念,明确它们之间的区别与联系.3.会确定一个单项式的系数和次数,一个多项式的项数和次数.4.不断提高分析问题的能力,体会数学知识间具体与抽象的内在联系和统一性.【重点难点】1. 单项式、多项式、整式的概念及它们的联系.2. 单项式的系数和次数.知识概览图新课导引我们已会用字母表示数和表示加法、乘法的运算律,用字母表示未知数、列方程,求解问题时比用算术法有较大的优越性.如图所示.本节中,通过学习“整式”,将进一步感受到用字母表示数的广泛应用,归纳出运算的一般规律.体会数学美的内涵,解决生产、生活中的问题.教材精华知识点1列式表示数量关系用字母或含有字母的式子表示数和数量关系,为我们今后的学习和研究带来了极大的方便. ★列式时要注意:(1)数与字母相乘或字母与字母相乘,可省略乘号.(2)数与字母相乘,数写在字母前面.(3)除法运算要用分数线,如1÷a 写成1a. 知识点2单项式、多项式、整式的概念及它们的联系(重点)★单项式:由数或字母的乘积组成的式子叫做单项式.如:12ab ,m 2,-x 2y .特别地,单独的一个数或一个字母也是单项式.★多项式:几个单项式的和叫做多项式,如:x 2+2xy +y 2,a 2-b 2.★整式:单项式与多项式统称整式,它们的关系可以用图表示.知识点3单项式的系数和次数(重点)单项式的系数是指单项式中的数字因数,单项式的次数是指单项式中所有字母的指数的和.如:13-πa 2b 的系数是13-π,次数是3. 拓展:(1)圆周率π是常数。
(2)当一个单项式的系数是1或-l 时,“1”通常省略不写,如:a 2,-m 2;次数为“1”时,通常也省略不写,如x .知识点4多项式的项和次数在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项,多项式里次数最高项的次数,就是这个多项式的次数.拓展:(1)多项式的每一项包括它前面的符号.(2)像3n 4—2 n 2+ n +1,其中3 n 4叫四次项,类似地-2 n 2叫二次项,n 叫一次项, l 叫常数项.课堂检测基本概念题1、列式表示:(1)比a 的3倍小5的数;(2)数m 的一半与n 的平方的和;(3) a 与b 和的平方.基础知识应用题 2、指出下列各式中哪些是单项式;哪些是多项式.22227211210,61,,,25,,.37a b x y x xy m n x x a x x x++-+--+,,,综合应用题3、某市出租车的收费标准为:起步价为12.50元,3千米后每千米2.40元,某人乘坐出租车行驶x (x >3)千米.试用含x 的式子表示他应付的费用,并求当x =8时,这一式子的值.探索创新题4、有一个多项式为-a +2a 2-3a 3+4a 4-5a 5+…,按这样的规律加下去,第99项是 ,第2 010项是 ,第n 项是 .体验中考1、已知整式x 2-52x 的值为6,则2x 2-5x +6的值为( ) A .9 B .12 C .18 D .242、某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验:第1组取3粒,第2组取5粒,第3组取7粒,第4组取9粒,…,按此规律,请你推测第n 组应该取种子数是 粒.学后反思:附: 课堂检测及体验中考答案课堂检测1、分析:“和”用加法,“差”用减法,“倍”用乘法,“商”用除法.解:(1)3a -5;(2) 12m + n 2;(3)( a + b )2.2、分析:要分清哪些是单项式,哪些是多项式,关键要明确两者的概念,注意它们的联系与区别.解:单项式有:271,10,,.7x m n a - 多项式有:222161,,253a b x y xy x x x+++--,,. 点拨 单项式要包括它前面的“-”,多项式是n 个单项式的和,分母中含有字母的式子,如11,1x x +等都不是单项式或多项式.3、解:由题意,得此人应付的费用为[12.50+2.40(x -3)](x >3)元.当x =8时,12.50+2.40(x -3)=12.50+2.40×(8-3)=24.5(元).答:此人应付的费用可表示为[12.50+2.40(x -3)]元.当x =8时,他应付的费用为24.5元.提示 此题若没有给出x >3这一条件,则需分两种情况:一种是当x ≤3时,此人应付的费用为起步价12.50元;另一种就是本题的x >3时,此人应付的费用为起步价与超出3千米后的费用的和.4、答案:-99a 99 2 0l0a 2 010 (-1)n ·na n技巧 此题项的符号在第奇数个项时为“-”,第偶数个项时为“+”,特别要注意第n 项,要用(-1)n ·n 来确定它的系数,而不能直接写成n .体验中考1、C 解析:由x 2-52x =6,得2x 2-5x =12,代入得2x 2-5x +6=12+6=18.2、(2n +1) 解析:第1组取3粒,3=2×1+1,第2组取5粒,5=2×2+1,第3组取7粒,7=2×3-1,…,依此类推,第n 组取(2n +1)粒.2.2整式的加减学习目标、重点、难点【学习目标】1.理解同类项的概念,会合并同类项.2.掌握去括号的法则,会去括号.3.会用整式的加减运算法则,能熟练进行整式的加减运算、求值.【重点难点】1.同类项的概念,合并同类项.2.用整式的加减运算法则,能熟练进行整式的加减运算、求值.知识概览图新课导引前面我们学习了单项式、多项式和整式的概念,也学会了用字母表示实际生活中的一些数量关系,那么我们如何解决图中小明提出的问题呢?就让我们一起来学习整式的加减这一节吧!相信你通过这一节的学习,一定会帮助小明找到答案的.教材精华知识点1同类项(重点)★所含字母相同,并且相同字母的指数也相同的项叫做同类项.另外,所有的常数项都是同类项.★同类项要满足两个“同”,第一个“同”是所含字母相同,第二个“同”是相同字母的指数相同.注意:是不是同类项只与所含字母和字母的指数有关,而与该项系数无关(在系数不为零的前提下).如:-m2n与3m2n是同类项,x2y3与2y3x2是同类项.知识点2合并同类项(难点)★把多项式中的同类项合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母部分不变.为了更好地掌握合并同类项的法则,可记住以下口诀:合并同类项,法则不能忘,只求系数和,字母指数不变样.知识点3去括号(难点)★去括号的法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.★在去括号时需要注意:(1)去括号时,要将括号连同它前面的符号一起去掉;(2)在去括号时,首先要明确括号前是“+”还是“-”;(3)该变号时,各项都变号;不该变号时,各项都不变号.知识点4整式的加减(重点)★整式的加减的运算法则:一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.★应用整式的加减的运算法则进行化简求值时,一般先去括号、合并同类项,再代人字母的值进行计算,简记为“一化、二代、三计算”.课堂检测基本概念题1、若-5a3b m+1与13b2 a n+1是同类项,求(m-n)100的值.2、求下列代数式的值.(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=-3;(2)2x-y+(2y2-x2)-(x2+2y2),其中x=l,y=-2.基础知识应用题3、化简:(32)[5(2)3]--+---+-.x y z x x y z x综合应用题4、一列火车上原有乘客(6a-2b)人,中途有一半乘客下车,又有若干乘客上车,此时车上共有乘客(10a-6b)人,则中途上车的乘客有多少人?当a=200,b=100时,中途上车的乘客有多少人?探索创新题5、规定两种新运算:a*b=a+b,a#b=a-b,其中a,b为有理数.化简(a2b)*(3ab)+(5a2b)#(4ab),并求出当a=5,b=3时的值是多少?体验中考1、当a=1,b=2时,代数式a2-ab的值是.2、把3+[3a-2(a-1)]化简得.学后反思附: 课堂检测及体验中考答案课堂检测1、分析:解:因为-5a 3b m +1与13 b 2 a n +1是同类项,所以12,1 3.m n +=⎧⎨+=⎩解得1001001,()(12) 1.2.m m n n =⎧-=-=⎨=⎩则2、分析:此题属于化简求值题,应先去括号,再合并同类项,最后代入求值.解:(1)3(x 2-2x -1)-4(3x -2)+2(x -1)=3x 2-6x -3-12x +8+2x -2=3x 2-16x +3.当x =-3时,原式=3×(-3)2-16×(-3)+3=27+48+3=78.(2)2x -y +(2y 2-x 2)-(x 2+2y 2)=2x -y +2y 2-x 2-x 2 -2y 2=-2x 2+2x -y .当x =1,y =-2时,原式=-2×12+2×1-(-2)=-2+2+2=2.3、 分析:去括号时,可以由里向外去,也可以由外向里去.解:(32)[5(2)3x y z x x y z x --+---+- 32(523)32(2)3224.x y z x x y z x x y z x y z x y z x y z x=-+---+--=-+--+-=-+---+=- 规律对这类题目而言,化简就是先去括号,然后合并同类项.去括号时,一方面注意括号前是“-”时,去掉括号,括号里各项都要改变符号;另一方面是括号前的系数要与括号里的每一项相乘,防止漏乘.4、解:由题意可知,中途上车的乘客人数为(10a-6b)-12(6a-2b)=10a-6b-3a+b=7a-5b.当a=200,b=100时,中途上车的乘客有7×200-5×100=900(人);答:中途上车的乘客有(7a-5b)人.当a=200,b=100时,中途上车的乘客有900人.点拨此题要分清以下几个数量关系:(1)车上原有乘客人数;(2)中途下车的人数;(3)中途上车后车上现有人数;(4)中途上车的人数等于车上现有人数减去中途下车后车上剩余的人数.明确这几个数量关系是解决本题的关键.5、解:(a2b)*(3ab)+(5a2b)#(4ab)=a2b+3ab+5a2b-4ab=6a2b-ab.当a=5,b=3时,原式=6×25×3-5×3=450-15=435.说明读懂规则是解答此题的关键,根据不同的规则,正确列出常规算式.体验中考1、-1 解析:当a=1,b=2时,a2-ab=12-1×2=-1.2、a+5解析:3+[3a-2(a-1)]=3+(3a-2a+2)=3+3a-2a+2=a+5.。
人教版新课标数学七年级上册第二章整式的加减导学案

人教版新课标数学七年级上册第二章整式的加减导学案【学习目标】会用含有字母的式子表示数量关系,理解字母表示数的意义;【重点难点】用含有字母的式子表示数量关系;理解字母表示数的意义. 【创设情境】用含字母的式子填空⑴全校学生总数是x,其中女生占总数48%,则女生人数是,男生人数是 .⑵每包书有12册,n包书有册.⑶一辆汽车3小时行驶了S 千米,这辆汽车的平均速度是 .⑷产量由m千克增长10%,就达到千克.【自主、合作、展示】1.用字母表示数以后,字母和数一样可以,可以用式子把简明地表示出来.2.结合下列实际问题,总结用含有字母的式子表示数量关系的方法.⑴一条河的水流速度是2.5km/h,船在静水中的速度是v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度 .⑵买一个篮球需要x元,买一个排球需要y元,买一个足球需要y 元,用式子表示买3个篮球、5个排球、2个足球共需要的钱数 .⑶如图,用式子表示三角尺的面积(单位:cm) .⑷如图,用式子表示建筑平面图的面积(单位:m) .2.结合上述问题,思考用数字和字母表示式子的时候应该注意哪些问题?1.下列说法或书写是否正确,并在题上改正:①1x ②-1x ③a×3 ④a÷2 ⑤2411xy2.一台电视机的原价为a元,降价4%后的价格为元3.一三角形底为x厘米,高是底的一半,则此三角形面积是_平方厘米.4.李老师到文体商店为学校买篮球,篮球的单价为a元,商店规定:买10个或10个以上的篮球按8折优惠,请你表示:⑴购买30个篮球应付多少钱?⑵购买x个篮球要付多少钱?5.老师利用假期带学生外出浏览,已知每张车票50元,甲车车主说,如果乘我的车,师生全部可以享受八折优惠;乙车车主说,如果乘我的车,学生7折优惠,老师买全票,已知这个老师带了x名学生,分别写出乘甲、乙两车所需的车费.6.用字母表示图中阴影部分的面积.【学习目标】1.理解单项式及单项式系数、次数的概念;2.会准确确定一个单项式的系数和次数. 【重点难点】掌握单项式及单项式的系数、次数的概念;区别单项式的系数和次数. 【复习引入】1.列代数式⑴边长为a 的正方体的表面积为________,体积为;⑵铅笔单价是x 元,圆珠笔单价是铅笔的2.5倍,圆珠笔单价是元;⑶一辆汽车速度是v 千米/小时,行驶t 小时所走的路程是______千米;⑷设n 是一个数,则它的相反数是________;2.请学生观察所列代数式包含哪些运算,有何共同运算特征. (由小组讨论后,经小组推荐人员回答)【自主、合作、展示】1.通过上述特征的描述,概括单项式的概念.由________或______的乘积组成的代数式叫做单项式,单独的________或___________也是单项式.2.下列各代数式中,是单项式的有 .⑴21+x ;⑵abc ;⑶b 2;⑷-5ab 2;⑸y+x ;⑹-xy 2;⑺-5.3.单项式系数和次数.⑴在单项式31a 2h ,2πr ,abc ,-n 中,说出它们的数字因数和字母因数.⑵小结:一个单项式中,单项式中的称为这个单项式的系数,一个单项式中,叫做这个单项式的次数.⑶请指出下列单项式的系数和次数.①22a ②h 2.1- ③2xy ④2t - ⑤32vt- ⑥433r π1.在a 3,x +1, -2,3b-, 0.72xy 中,单项式的个数有() A. 2个 B.3个 C.4个 D.5个2.单项式-x 2yz 2的系数、次数分别是()A. 0,2B. 0, 4C. -1,5D.1,4 3.如果15--m xy 为四次单项式,则m=____;4.判断下列各代数式是否是单项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一学时 整式(1)学习内容:教科书第54—56页,2.1整式:1.单项式。
学习目标:1.理解单项式及单项式系数、次数的概念。
2.会准确迅速地确定一个单项式的系数和次数。
3.通过小组讨论、合作学习等方式,经历概念的形成过程,培养自主探索知识和合作交流能力。
学习重点和难点:重点:掌握单项式及单项式的系数、次数的概念,并会准确迅速地确定一个单项式的系数和次数。
难点:单项式概念的建立。
一、自主学习;1、先填空,再分析写出式子特点,与同伴交流。
(1)若正方形的边长为a ,则正方形的面积是 ;(2)若三角形一边长为a ,并且这边上的高为h ,则这个三角形的面积为 ;(3)若x 表示正方体棱长,则正方体的体积是 ;(4)若m 表示一个有理数,则它的相反数是 ;(5)小明从每月的零花钱中贮存x 元钱捐给希望工程,一年下来小明捐款 元。
2、观察以上式子的运算,有什么共同特点?3、单项式定义:由数与字母的乘积组成的代数式称为单项式。
[老师提示] 单独一个数或一个字母也是单项式,如a ,5,0。
4、练习:判断下列各代数式哪些是单项式? (1)21 x ; (2)a bc ; (3)b 2; (4)-5a b 2; (5)y ; (6)-xy 2; (7)-5。
5、单项式系数和次数:观察“1”中所列出的单项式,发现单项式是由数字因数和字母因数两部分组成。
单项式中的数字因数叫单项式的系数;单项式中所有字母指数的和叫单项式的次数。
说说四个单项式31a 2h ,2πr ,a bc ,-m 的数字因数和字母因数及各个字母的指数?二、合作探究:1、教材p56例1:阅读例题,体会单项式及系数次数概念。
2、判断下列各代数式是否是单项式。
如不是,请说明理由;如是,请指出它的系数和次数。
①x +1; ②x 1; ③πr 2; ④-23a 2b 。
3、下面各题的判断是否正确?①-7xy 2的系数是7; ②-x 2y 3与x 3没有系数; ③-a b 3c 2的次数是0+3+2;④-a 3的系数是-1; ⑤-32x 2y 3的次数是7; ⑥31πr 2h 的系数是31。
[老师提示]①圆周率π是常数;②当一个单项式的系数是1或-1时,“1”通常省略不写,如x 2,-a 2b 等;③单项式次数只与字母指数有关。
4、课堂练习:课本p56:1,2。
5、若单项式x m y 2的次数是5,则m= ;6、已知单项式2x m y n+2与3x m+2的次数相同,求n 的值。
7、写一个含m ,n 的3次单项式 ;8、有一串单项式:-x,2x 2, -3x 3,4x 4…, 10x 10…(1)、请写出第2010个单项式;(2)、请写出第n 个单项式。
三、学习小结:四、课堂作业: 课本p59习题第1,2题第二学时整式(2)学习内容:教科书第56—59页,2.1整式:2.多项式。
学习目标和要求:1.通过本节课的学习,掌握整式多项式的项及其次数、常数项的概念。
2.通过小组讨论、合作交流,经历新知的形成过程,培养比较、分析、归纳的能力。
由单项式与多项式归纳出整式,有利于知识的迁移和知识结构体系的更新。
3.初步体会类比和逆向思维的数学思想。
学习重点和难点:重点:掌握整式及多项式的有关概念,掌握多项式的定义、多项式的项和次数,以及常数项等概念。
难点:多项式的次数。
一、自主学习:1.列代数式:(1)长方形的长与宽分别为a、b,则长方形的周长是;(2)某班有男生x人,女生21人,则这个班共有学生人;(3)鸡兔同笼,鸡a只,兔b只,则共有头个,脚只。
2.观察以上所得出的三个代数式与上节课所学单项式有何区别。
[老师提示]上面这些代数式都是由几个单项式相加而成的。
几个单项式的和叫做多项式。
在多项式中,每个单项式叫做多项式的项。
其中,不含字母的项,叫做常数项。
如:多项式5-xx有32+2三项,它们是23x,-2x,5。
其中5是常数项。
一个多项式含有几项,就叫几项式。
多项式里,次数最高项的次数,就是这个多项式的次数。
例如,多项式5x是一个二次三项式。
-x32+2注意:(1)多项式的次数不是所有项的次数之和,是次数最高的项的次数;(2)多项式的每一项都包括它前面的符号。
(3)多项式不包含单项式单项式与多项式统称整式二、合作探究:1、教材p57例22、判断:①多项式a3-a2b+a b2-b3的项为a3、a2b、a b2、b3,次数为12;()②多项式3n4-2n2+1的次数为4,常数项为1。
()[注意]:多项式的次数为最高次项的次数。
3、指出下列多项式的项和次数:(1)3x -1+3x 2; (2)4x 3+2x -2y 2。
4、指出下列多项式是几次几项式。
(1)x 3-x +1; (2)x 3-2x 2y 2+3y 2。
5、已知代数式3x n -(m -1)x +1是关于x 的三次二项式,求m 、n 的条件。
6.课堂练习:课本p59:1,2。
7、填空:-45a 2b -34a b +1是 次 项式,其中三次项系数是 ,二次项为 ,常数项为 ,写出所有的项 。
8、下列代数式中哪些是整式?哪些是单项式?哪些是多项式?xy+z a x 2+bx -1 π21 x ; x y 1_三、学习小结:四、课堂作业: 课本p60:第3题第三学时整式(3)学习内容:课本p58例3及课本p64提到的一个内容学习目的和要求:1、通过用整式来表示事物间的关系,逐步掌握数学建模思想;2、理解多项式的升(降)幂排列的概念,会进行多项式的升(降)幂排列。
3、通过尝试和交流,体会多项式升(降)幂排列的可行性和必要性。
4、初步体验排列组合思想与数学美感,培养审美观。
学习重点和难点:重点:会进行多项式的升(降)幂排列,体验其中蕴含的数学美。
难点:会进行多项式的升(降)幂排列,体验其中蕴含的数学美。
一、自主学习:1、教材p58例3:我们知道船在河流中行驶时,船的速度需要分两种情况讨论:(1)顺水行驶:船的速度= ;(2)逆水行驶:船的速度= ;在上面两个关系式中若用字母V表示静水速度则船的顺水速度为船的逆水速度为当V=20时则甲船顺水速度甲船逆水速度乙船顺水速度乙船逆水速度2..请运用加法交换律,任意交换多项式x2+x+1中各项的位置,可以得到几种不同的排列方式?在众多的排列方式中,你认为那几种比较整齐?【提示】有六种不同的排列方式,像x2+x+1与1+x+x2这样的排列比较整齐。
这两种排列有一个共同点,那就是x的指数是逐渐变小(或变大)的。
我们把这种排列叫做升幂排列与降幂排列。
例如:把多项式5x2+3x-2x3-1按x的指数从大到小的顺序排列,可以写成-2x3+5x2+3x-1,这叫做这个多项式按字母x的降幂排列。
若按x的指数从小到大的顺序排列,则写成-1+3x+5x2-2x3,这叫做这个多项式按字母x的升幂排列。
二、合作探究1、请把卡片+3x2y2-7xy3+2y -11x7y5-35x3按x降幂排列2、把多项式2πr-1+3πr3-π2r2按r升幂排列。
【提示】:π是数字,不是字母,题目中一次项、二次项、三次项系数分别为2π、-π2、3π。
3、把多项式a3-b3-3a2b+3a b2重新排列。
(1)按a升幂排列;(2)按a降幂排列。
4、把多项式x4-y4+3x3y-2xy2-5x2y3用适当的方式排列。
(1)按字母x的升幂排列得:;(2)按字母y的升幂排列得:。
【注意】:(1)重新排列多项式时,每一项一定要连同它的符号一起移动;(2)含有两个或两个以上字母的多项式,常常按照其中某一字母升幂排列或降幂排列。
5.一个三位数百位数字是a,十位数字是b,个位数字是 c 则这个三位数表示为;6.课堂练习书P61习题8,9,10,11题三.学习小结四.作业。
书P60习题4,5,6,7,题第四学时 整式的加减(1)学习内容:教科书第63—64页,2.2整式的加减:(1)同类项。
学习目标和要求:1.理解同类项的概念,在具体情景中,认识同类项。
2.通过小组讨论、合作学习等方式,经历概念的形成过程,培养自主探索知识和合作交流的能力。
3.初步体会数学与人类生活的密切联系。
学习重点和难点:重点:理解同类项的概念。
难点:根据同类项的概念在多项式中找同类项。
一、自主学习1、问题;每本练习本x 元,小明买5本,小红买3本,两人一共花了多少钱?小明比小红多花多少钱?用代数式表示以上问题;(用两种表示方法)2、运用有理数的运算定律填空:100×2+252×2=( ) 100×(-2)+252×(-2)=( )100t+252t=( )你发现什么规侓了吗?与同伴交流一下。
3、用发现的规律填空:(1)100t-252t=( ) t (2)3x 2y+2x 2y=( ) x 2y(3)3mn 2--4mn 2=( ) mn 24.同类项的定义:我们常常把具有相同特征的事物归为一类。
比如多项式的项100t 和-252t 可以归为一类,3x 2y 、2x 2y 可以归为一类,3 mn 2、-4mn 2可以归为一类,5a 与9a 也可以归为一类,还有83、0与95也可以归为一类。
3x 2y 与2x 2y 只有系数不同,各自所含的字母都是x 、y ,并且x 的指数都是2,y 的指数都是1;同样地3mn 2、4mn 2,也只有系数不同,各自所含的字母都是m 、n ,并且m 的指数都是1,n 的指数都是2。
像这样,所含字母相同,并且相同字母的指数也分别相等的项叫做同类项。
另外,所有的常数项都是同类项。
比如,前面提到的83、0与95也是同类项。
二、合作探究1、判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x 与3mx 是同类项。
( ) (2)2a b 与-5a b 是同类项。
( )(3)3x 2y 与-31yx 2是同类项。
( ) (4)5a b 2与-2a b 2c 是同类项。
( ) (5)23与32是同类项。
( )2、指出下列多项式中的同类项:(1)3x -2y +1+3y -2x -5; (2)3x 2y -2xy 2+31xy 2-23yx 2。
3、k 取何值时,3x k y 与-x 2y 是同类项?4、若把(s +t)、(s -t)分别看作一个整体,指出下面式子中的同类项。
(1)31(s +t)-51(s -t)-43(s +t)+61(s -t); (2)2(s -t)+3(s -t)2-5(s -t)-8(s -t)2+s -t 。
三、学习小结:四、课堂作业:若2a m b 8与a 3b 2m+3n 是同类项,求m 与n 的值。
第五学时整式的加减(2)学习内容:教科书第64—66页,2.2整式的加减:2.合并同类项。
