牛头刨床,solidworks motion。仿真分析
牛头刨机构的运动分析
牛头刨机构运动仿真摘 要:本文中,主要阐述了牛头刨机构的位置、速度、加速度的理论分析,并通过UG 建模,adams 仿真分析,根据结果测得牛头刨机构的实际位置、速度、加速度,并与理论分析进行比较验证。
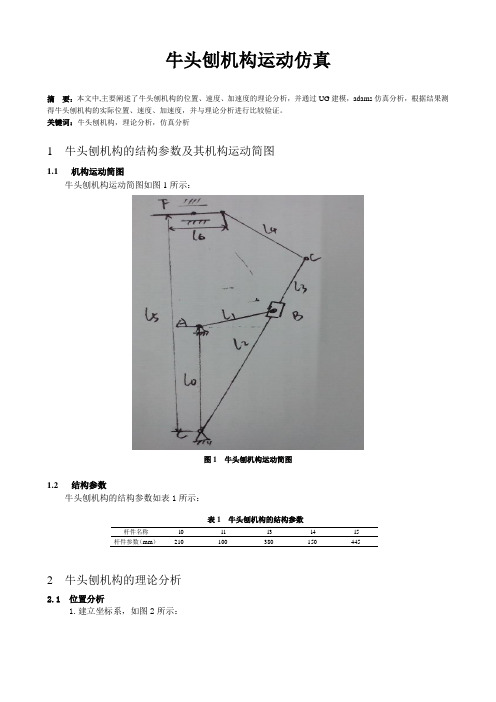
关键词:牛头刨机构,理论分析,仿真分析1 牛头刨机构的结构参数及其机构运动简图1.1 机构运动简图牛头刨机构运动简图如图1所示:图1 牛头刨机构运动简图1.2 结构参数牛头刨机构的结构参数如表1所示:表1 牛头刨机构的结构参数2 牛头刨机构的理论分析2.1 位置分析1.建立坐标系,如图2所示:杆件名称 l0 l1l3l4 l5 杆件参数(mm ) 210 100 380 150 445图2 牛头刨机构运动简图2.建立矢量方程由封闭图形ABCA 可写出机构一个封闭矢量方程:CA AB CB += (1-1)其分量形式为: 12121cos 2cos 01sin 2sin l l l l l θθθθ⋅=⋅⎧⎨+⋅=⋅⎩ (1-2)由封闭图形CDEFC 可写出机构另一个 封闭矢量方程:C D D EC F F E +=+ (1-3)其分量形式为:23233cos 4cos 63sin 4sin 5l l l l l l θθθθ⋅+⋅=⎧⎨⋅+⋅=⎩(1-4)3.求解未知参数2l (1-5) 21arccos(1cos /2)l l θθ=⋅ (1-6)32arcsin((53sin /)4)l l l θθ=-⋅ (1-7)2363cos 4cos l l l θθ=⋅+⋅ (1-8)2.2 速度分析将式(1-2)和式(1-4)对时间t 求一次导数,得速度关系:1122221122221sin 2sin cos 1cos 2cos sin l l l l θωθωνθθωθωνθ⋅⋅=⋅⋅-⋅⎧⎨⋅⋅=⋅⋅+⋅⎩ (1-9) 2233622333sin 4sin 3cos 4cos 0l l l l θωθωνθωθω⋅⋅+⋅⋅=-⎧⎨⋅⋅+⋅⋅=⎩(1-10) 若用矩阵形式来表示,则上式可写为:222122211233236cos 2sin 001sin sin 2cos 001cos 03sin 4sin 1003cos 4cos 00l v l l l l l l l θθθθθωθωθθωθθν--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (1-11)2.3 加速度分析将式(1-9)和(1-10)对时间t 求二次导数,可得加速度关系表达式。
SOLIDWORKSmotion运动仿真分析

SOLIDWORKSmotion运动仿真分析SOLIDWORKSmotion运动仿真分析SOLIDWROKSmotion是SOLIDWORKS中一个高性能的插件,能够帮助设计中完成
虚拟样机的仿真分析工具,motion既可以对众多的机械结构进行运动学和动力学仿真,同时也可以反馈机械设备的速度、加速度、作用力等,
在SOLIDWROKSmotion完成样机动画制作,图标信息的反馈。
在制作样机前就将可能存在的错误结构反馈到设计者,为后续的改进
提供借鉴与参考。
SOLIDWROKSmotion和运动算例集合是在一起的,在完成装配体之后,在不需要退出设计界面的情况下即可进入
motion界面,可以在该界面下添加约束和载荷,也可以对模型进行运动控制参数的设置。
例如我们需要完成齿轮运动的分析。
首先我们在装配
体中完成使用链整列来完成齿轮的装配配合启用motion插件,并选择运动算例,点击右下角来选择创建的算例类型为Motion分析在Mo
tion添加参数来模拟实际的运动受力状况。
添加三要素引力、接触、马达。
添加所有的要素后通过Motion来对马达的运动过程进行分析。
是否存在不合理之处,并进行修改调整。
也可以通过生成图标来进行检测数据结果。
第2-1节 牛头刨床运动仿真

第2讲牛头刨床运动仿真实例一、启动pro/e并设置工作目录1.点击【开始】→【所有程序】→【pro engineer】,启动pro/e软件,如图1所示。
图1 启动pro/e2.设置工作目录:选择【文件】→【设置工作目录】,选择桌面《运动仿真牛头刨床》文件夹为工作目录,点击该图框右下方的【确定】键,如图2、图3所示。
图2 设置工作目录图3 选择工作目录二、设置运动仿真文件1.点击【文件】→【新建】命令,选择类型为【组件】,子类型选择【设计】,将名称改为【niutoubaochuang】,将【使用缺省模板】前的对勾去掉,,如图4所示。
单击【确定】后弹出【新文件选项】对话框,【模板】选mmns asm design,单击【确定】完成任务的新建,如图5所示。
图4 新建文件图5 选择模板三、零件的装配1.预览整个机构效果图单击工作窗口右边工具栏中的【装配】命令,在【打开】命令中单击【niutoubaoch.asm】项。
单击【预览】可在框图中查看整个凸轮机构组装好后的效果图,如图6所示,后面的组装皆可按此标准来进行。
图6 机构效果图2. 安装基座(1)单击工作窗口右边的【装配】命令,在【打开】命令中选择ground.prt文件,即机座(也可以现【预览】确认一下),点击【打开】如图7所示。
图7 选择基座文件(2)导入机座后单击图8中所示【自动】命令右边小三角形,将机座设置为【缺省】模式,再点击面板右端的对勾,完成机座的放置,如图8所示。
图8 设置基座3. 安装圆盘(1)点击【装配】选中并打开打开第二个文件yuanpan.prt,即圆盘机构然后预览并单击【打开】,如图9所示,点击工具栏旁的【用户定义】下拉菜单,选择【销钉】连接类型,如图10所示。
图9 选择圆盘文件图10 设置约束类型(2)先进行轴对齐,即选择机座机架上矮圆柱的中心线A-2,再选择圆盘上圆孔的中心线A-1,完成轴对齐,如图11所示。
图11 轴对齐(3)再面匹配,光标移到圆盘上选中表面,然后选择矮圆柱的表面,点击工具栏上的对勾完成凸轮的装配,如图12所示。
机械原理大作业--牛头刨床仿真分析(matlab)全自动版本

牛头刨床机构运动分析一、设计小组人员构成二、设计任务1、机构结构分析2、机构运动分析建立数学模型,解析法进行运动分析;程序编写;上机调试程序;位移、速度和加速度运动曲线图与分析;三、设计参数四、设计分工五、 设计内容如右图,建立直角坐标系,并标出各杆矢量及方位角。
利用两个封闭图形ABCA 及CDEGC ,由此可得:l 6⃑⃑⃑ +l 3⃑⃑⃑ =s 3⃑⃑⃑ , l 3⃑⃑⃑ +l 4⃑⃑⃑ =l 6′⃑⃑⃑ +S E ⃑⃑⃑⃑投影方程式为:s 3 cos θ3=l 1 cos θ1 s 3sin θ3=l 6+l 1sin θ1 l 3cos θ3+l 4cos θ4−s E =0l 3sin θ3+l 4sin θ4=l 6′有以上各式即可求得s 3 、θ3 、θ4 四个运动那个变量,二滑块2的方位角θ2=θ3。
然后,分别将上式对时间去一次、二次导数,并写成矩阵形式,即得以下速度和加速度方程式:[cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3ω3ω4v E ]=ω1[−l 1sin θ1l 1cos θ100][cos θ3−s 3sin θ3sin θ3s 3cos θ30 00 00 −l 3sin θ30l 3cos θ3−l 4sin θ4−1l 4cos θ40] [s 3α3α4αE ] =- [−ω3sin θ3 −s 3sin θ3−s 3ω3sin θ3ω3cos θ3 s 3cos θ3−s 3ω3sin θ30 00 00 −l 3ω3cos θ30 −l 3ω3sin θ3−l 4ω4cos θ4 0−l 4ω4sin θ4 0] [s 3ω3ω4v E ]+ ω1[−l 1ω1cos θ1−l 1ω1sin θ100]而ω2=ω3 、α2=α3 。
基于SolidworksMotion的牛头刨床运动学分析
基于Solidworks Motion的牛头刨床运动学分析SolidWorks Motion是一个与SolidWorks完全集成的虚拟样机的仿真分析系统。
可以对复杂的机构进行运动学和动力学仿真,通过数据、图标、动画等表现出机构的速度、加速度、作用力等,可以反映机构的运动特性。
本例基于SolidWorks,通过对牛头刨床进行三维建模和运动仿真,分析刨头CD的位移、速度、加速度和机构的行程速度比。
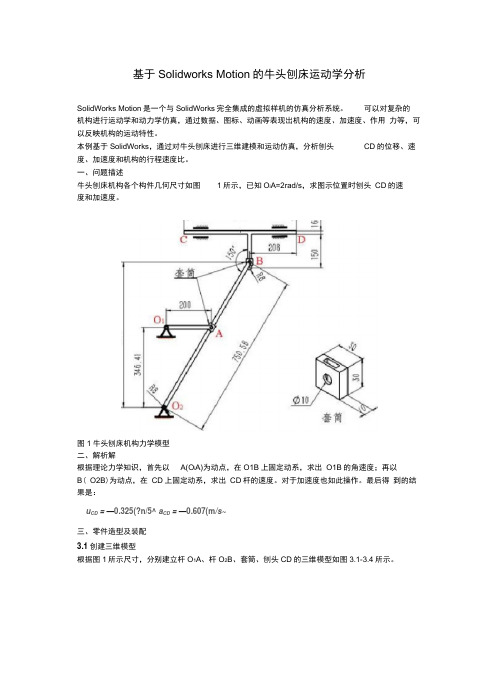
一、问题描述牛头刨床机构各个构件几何尺寸如图1所示,已知O i A=2rad/s,求图示位置时刨头CD的速度和加速度。
图1牛头刨床机构力学模型二、解析解根据理论力学知识,首先以A(O i A)为动点,在O1B上固定动系,求出O1B的角速度;再以B( O2B)为动点,在CD上固定动系,求出CD杆的速度。
对于加速度也如此操作。
最后得到的结果是:u CD= —0.325(?n/5^ a CD= —0.607(m/s~三、零件造型及装配3.1创建三维模型根据图1所示尺寸,分别建立杆O1A、杆O2B、套筒、刨头CD的三维模型如图3.1-3.4所示。
图3.4刨头CD依次导入杆O i A 、套筒、杆O 2B 、刨头CD,分别添加配合约束,3.5所示。
杆O l A图3.2杆O 2 B 套筒3.2装配牛头刨床 新建装配体命名为牛头刨床。
调整其相对位置后结果如图图3.5牛头刨床装配体注:在Solidworks Motion中,运动副是建立在装配关系约束的基础上的。
因此,正确选择装配约束,是运动仿真成功的重要一步。
四、仿真求解4.1新建运动算例在装配体界面,将"SolidWorks Motion ”插件载入,选择布局选项卡中的【运动算例1】在Motion Manager工具栏中【算例类型】下拉列表中选择【Motion分析】,如图4.1所示图4.1新建运动算例4.2添加马达单击"马达”按钮,弹出【马达】属性管理器,选择杆O1A圆孔为马达运动方向,大小设置为19.1RPM (已知O i A=2rad/s=19.1RPM),设置参数如图4.2所示:图4.2曲柄马达参数设置4.3仿真求解1)单击“运动算例属性”按钮,设置每秒帧数为40。
matlab对牛头刨床的仿真(速度,加速度,力,运动动画,matlab可运行程序)

北华航天工业学院牛头刨床主体机构的分析《机械原理》课程设计班级_______________姓名_______________序号_______________2015年1月摘要:文中建立了用解析法作牛头刨床的运动分析,基于机构的位置方程式,将位置方程对时间求一次和二次倒数,得到机构的速度和加速的方程,然后就得到位移、速度、加速度,并通过复数矢量法和矩阵法,并且借助Matlab等软件对牛头刨床进行运动分析,并对牛头刨床的运动学规律进行了仿真,画出牛头刨床的运动动画,使设计的机构更加直白,为该机床的优化设计提供了理论支撑。
目录摘要 (1)目录 (2)1.引言 (3)2.机构结构分析 (3)3.机构运动分及程序设计 (3)4.计算机仿真及结果 (4)5.图解法验证 (17)6.guide的制作 (22)7.参考文献 (30)8.研究感想 (30)1.引言:对牛头刨床进行运动分析的任务是在已知机构尺寸及原动件运动规律的情况下,确定机构中其他构件上某些点的轨迹、位移、速度、加速度和构件的角位移、角速度及角加速度。
而这些内容,不论是设计新的机器,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械动力性能的必要基础和前提。
对于牛头刨床来说,其刨刀在有效工作行程中应该接近等速运动,而回程速度却应高于前者速度,从而提高效率。
为了确定牛头刨床的设计是否满足要求,就必须对其进行运动分析。
本文建立了牛头刨床的力学模型,并推导了其运动微分方程,通过数值方法求得了牛头刨床的运动学规律并开发了一个用于牛头刨床的通用运动学分析程序。
2.机构结构分析:1.自由度计算:F=3n-2pl -phF=5*3-7*2=12.结构分析:5个可动构件,5个转动副2个移动副.3.机构运动分及程序设计3.1.如图先建立坐标系,已知l1=100mm, l3=500mm,l4=200mm,原动件1的方位角00~3600和等角速度w 1=2*pi rad/s 如图所示:解:3.1.1.位置分析:由于有四个位置量,为了求解需要建立两个封闭矢量方程。
基于Matlab的牛头刨床运动学分析及通用仿真软件开发(精)
参数名称L 1L 3L 5H G 准 3P 准 5S n 1准 1转向参数含义原动件 AB 的长度从动件 DE 的长度从动件 EF 的长度 AD 的长度刨头距离底座的竖直高度从动件 DE 的转角滑块 2到底座的距离从动件 EF 的转角滑块 6的位移原动件 AB 的转速原动件 AB 的转角原动件 AB 的转向表 1模型参数含义基于 Matlab 的牛头刨床运动学分析及通用仿真软件开发吴国祥(兰州交通大学教务处, 兰州 7300701引言机构运动分析的任务是在已知机构尺寸及原动件运动规律的情况下, 确定机构中其他构件上某些点的轨迹、位移、速度、加速度和构件的角位移、角速度及角加速度。
上述这些内容, 不论是设计新的机器, 还是为了了解现有机械的运动性能, 都是十分必要的, 而且它还是研究机械动力性能的必要基础和前提 [1]。
对于牛头刨床来说,其刨刀在有效工作行程中应该接近等速运动, 而回程速度却应高于前者速度, 从而提高效率。
为了确定牛头刨床的设计是否满足要求, 就必须对其进行运动分析 [2]。
本文建立了牛头刨床的力学模型,并推导了其运动微分方程,通过数值方法求得了牛头刨床的运动学规律并开发了一款用于牛头刨床的通用运动学分析软件 [3]。
2牛头刨床的数学模型图 1所示为牛头刨床的机构简图, 模型中各参数的物理意义如表 1所示。
设已知结构参数为 :L 1、 L 3、 L 5、 G H , 原动件的转角φ1和转速 n 1。
解:如图 1, 先建立一个直角坐标系, 并标出各杆矢及其方位角。
其中有四个未知变量φ3、φ5, P 及 S 。
为求解需建立两个封闭矢量方程,为此需利用两个封闭图形 ABDA 及 DEFD 。
为求这些未知量可以通过两种方法求解。
2.1用分析力学基础知识求解(1 求准 3、ω3及α3由封闭形 ABDA 可得L 1+H =P(1分别用 i 和 j 点积上式两端, 有L 1cos 准 1=P cos 准 3H +L 1sin 准 1=P sin 准 3联解上面两式可得:准3=arctan[(H +L 1sin 准 1 /L 1cos 准 1]H =L 1cos 准 1/cos准 3式 (1 对时间 t 求导数, 注意 P 为变量, 有准觶 1L 1e t 1=准 3Pe t 3+Pe3(2可用 e 3点积上式两端以消去准觶 3,并利用矢量方程解析法, 有P 觶 =V B 2B 3=-ω1L 1sin (准 1-准 3用 e t 3点积式 (2 两端可消去 P 觶 , 并注意到 e n 1·e t 3=-e 1·e t 3,则准觶3=ω3=ω1L 1cos (准 1-准 3 /P再将式 (2 对时间 t 求导, 则有准觶 21L 1e n 1=准咬 23Pe t 3+准觶 3Pe n 3+2准觶 3P 觶 e t 3+P 咬 e t3可分别用 e 3和 e t 3点积上式两端, 以消去准咬 3和 P 咬 , 注意e n 1·e t 3=-e 1·e t3,则 -准觶 1L 1cos (准 1-准 3 =-准觶 3P +P 咬准觶 21L 1sin(准 3-准 1 =准咬 3P +2准觶 3摘要:文中建立了牛头刨床的力学模型, 基于分析力学原理推导了牛头刨床的运动微分方程。
(完整版)牛头刨床运动分析实例
例: 如图所示为一牛头刨床的机构运动简图。
设已知各构件尺寸为:1125mm l =,3600mm l =,4150mm l =,原动件1的方位角1=0~360θ︒︒和等角速度1=1rad/s w 。
试用矩阵法求该机构中各从动件的方位角、角速度和角加速度以及E 点的位移、速度和家速度的运动线图。
解:先建立一直角坐标系,并标出各杆矢量及方位角。
其中共有四个未知量3θ、4θ、3s 及E s 。
为求解需建立两个封闭矢量方程,为此需利用两个封闭图形ABCA 及CDEGC ,由此可得,613346,'E l l s l l l s +=+=+(1-1)写成投影方程为: 331133611334433446cos cos sin sin cos cos 0sin sin 'E s l s l l l l s l l l θθθθθθθθ==++-=+= (1-2)解上面方程组,即可求得3θ、4θ、3s 及E s 四个位置参数,其中23θθ=。
将上列各式对时间取一次、二次导数,并写成矩阵形式,即可得以下速度和加速度方程式。
速度方程式:3331133331131334443344cos sin 00sin sin cos 00cos 0sin sin 1000cos cos 0E s l s s l w w l l w l l v θθθθθθθθθθ⎡⎤--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (1-3)机构从动件的位置参数矩阵:33333333443344cos sin 00sin cos 000sin sin 10cos cos 0s s l l l l θθθθθθθθ-⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎣⎦机构从动件的的速度列阵:334E s w w v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵:1111sin cos 00l l θθ-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1w :机构原动件的角速度加速度方程式:333333333344433443333333333333333344433344cos sin 00sin cos 000sin sin 10cos cos 0sin sin cos 00cos cos sin 000cos cos 00sin sin E s s s l l l l w s s w w s s w l w l w l w l w θθθθαθθαθθαθθθθθθθθθθ⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----=-----11131113144cos sin 000E l w s l w w w w v θθ⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦(1-4)机构从动件的位置参数矩阵求导:33333333333333333444333444sin sin cos 00cos cos sin 000cos cos 00sin sin 0w s s w w s s w l w l w l w l w θθθθθθθθθθ⎡⎤---⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥--⎢⎥⎣⎦机构从动件的的加速度列阵:334E s ααα⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵求导:111111cossinl wl wθθ-⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦主程序(matlab):%牛头刨床运动分析主程序s;%x(1)——代表3θ;%x(2)——代表构件3的转角3θ;%x(3)——代表构件4的转角4s;%x(4)——代表E点的线位移El;%x(5)——代表1l;%x(6)——代表3l;%x(7)——代表4l;%x(8)——代表6l;%x(9)——代表'6w。
SolidWorksMotion运动仿真教程
运动副:连接两个零件并定义其相对运动的机构
驱动:定义运动副的运动类型和参数,如旋转、平移等
创建运动副:在SolidWorks Motion中,选择要创建运动副的零件并定义其类型和参数
添加驱动:为运动副添加驱动,定义其运动类型和参数,以及运动范围和方向等
添加力和扭矩
在Motion分析中,选择“力和扭矩”选项
创建复杂运动副的方法:通过选择相应的运动副工具,如“旋转-旋转”、“滑块-滑块”等,并按照向导步骤进行操作,即可创建出所需的复杂运动副。
调整复杂运动副参数:在创建完复杂运动副后,可以通过调整其参数来改变运动副的运动特性,如旋转角度、滑块行程等。
注意事项:在创建和调整复杂运动副时,需要注意运动副的正确性、可行性和实际应用性,以确保仿真结果的准确性和可靠性。
案例描述:模拟一个机械手臂在生产线上的运动,实现抓取和放置物体的功能
仿真结果:展示优化后的机械手臂运动轨迹和关节角度,以及运动过程中的动态效果
应用价值:通过运动仿真优化机械手臂的设计,提高生产效率和降低生产成本
齿轮箱的运动仿真
齿轮箱运动仿真的目的和意义
齿轮箱运动仿真的建模过程
齿轮箱运动仿真的参数设置和优化
解决方案:检查模型定义、约束、驱动条件等是否正确
解决方案:检查模型是否存在几何问题、接触定义等,并尝试调整仿真参数
解决方案:检查模型中是否存在非线性因素,如摩擦、柔性连接等,并尝试调整仿真参数
解决方案:优化模型复杂度、调整仿真参数、使用更高效的求解器等
问题:仿真速度过慢 解决方案:优化模型复杂度、调整仿真参数、使用更高效的求解器等
汇报人:XX
XX,a click to unlimited possibilities
牛头刨床MATLAB运动仿真
l AB 133.72315102, lCD 702.92, l DE 210.88.
牛头刨床机构简图
二、运动方程的求解
(1)对如右图所示的矢量三角形
矢量方程为: R1
R2 R3 .
(*)
将上述矢量方程分别向水平、竖直方向投影,得:
r2 cos 2 r3 cos 3 ; r1 r2 sin 2 r3 sin 3 .
一、牛头刨床机构简介:
牛头刨床是一种常用的平面切削加工机床。电动机 经皮带传动、齿轮传动最后带动曲柄 1(见右图)转动。 刨床工作时,是由导杆机构 1-2-3-4-5 带动刨头和刨刀做 往复直线运动刨头 5 右行时,刨头切断,称为工作行程, 此时要求速度较低且均匀;刨头左行时,不进行切削, 称为空行程,此时速度较高,以节省时间提高生产率。 为此刨床采用有急回作用的导杆机构。 这里给出各构件的长度,以供下面的仿真使用。
5.
仿真: 仿真时间设置为 60/89 s,即一个周期。 在 MATLAB 的 Command Window 窗口输入命令:plot(tout,yout) 仿真输出结果如下图所示:
Results of simulition 3 2 1 r3 0 dotr3 -1 -2 -3 -4
3
3
3(rad)
alpha2 1 s 1 s
omega2 theta2
alpha2
omega2
theta5
omega3
theta3
omega_5 dot r7 1 s r7
r7
alpha3
r_7
theta2
omega2
alpha2
MATLAB Function
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab牛头刨床参数分析>> %Matlab源程序w1=1;l1=0.125;l3=0.6;l6=0.275;l61=0.575;l4=0.15;for m=1:3601o1(m)=pi*(m-1)/1800;o31(m)=atan((l6+l1*sin(o1(m)))/(l1*cos(o1(m))));if o31(m)>=0o3(m)=o31(m);else o3(m)=pi+o31(m);end;s3(m)=(l1*cos(o1(m)))/cos(o3(m));o4(m)=pi-asin((l61-l3*sin(o3(m)))/l4);se(m)=l3*cos(o3(m))+l4*cos(o4(m));if o1(m)==pi/2o3(m)=pi/2; s3(m)=l1+l6;endif o1(m)==3*pi/2o3(m)=pi/2; s3(m)=l6-l1;endA1=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),-l4*sin (o4(m)),-1;0,l3*cos(o3(m)),l4*cos(o4(m)),0];B1=w1*[-l1*sin(o1(m));l1*cos(o1(m));0;0];D1=A1\B1;E1(:,m)=D1;ds(m)=D1(1);w3(m)=D1(2); w4(m)=D1(3);ve(m)=D1(4);A2=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),-l4*sin (o4(m)),-1;0,l3*cos(o3(m)),l4*cos(o4(m)),0];B2=-[-w3(m)*sin(o3(m)),(-ds(m)*sin(o3(m))-s3(m)*w3(m)*cos(o3(m))),0,0;w3(m)*cos(o3(m)),( ds(m)*cos(o3(m))-s3(m)*w3(m)*sin(o3(m))),0,0;0,-l3*w3(m)*cos(o3(m)),-l4*w4(m)*cos(o4(m)) ,0;0,-l3*w3(m)*sin(o3(m)),-l4*w4(m)*sin(o4(m)),0]*[ds(m);w3(m);w4(m);ve(m)];C2=w1*[-l1*w1*cos(o1(m));-l1*w1*sin(o1(m));0;0];B=B2+C2;D2=A2\B;E2(:,m)=D2;dds(m)=D 2(1);a3(m)=D2(2);a4(m)=D2(3);ae(m)=D2(4);end;o11=o1*180/pi;y=[o3*180/pi;o4*180/pi];w=[w3;w4];a=[a3;a4];figure;subplot(221);h1=plotyy(o11,y,o11, se); axis auto ;grid minor;title('各机构位置曲线图');xlabel('\it\theta1');ylabel('\it\theta3,\theta4,Se');text(315,215,'SE');text(180,180,'θ4');text(70,105,'θ3');subplot(222);h2=plotyy(o11,w,o11,ve );grid minor;title('各机构速度曲线图');text(300,0.62,'VE');text(165,0.35,'ω3');text(90,0.1,'ω4');xlabel('\it\theta1');ylabel('\it\omega3,\omega4,Ve');subplot(212);h3=plotyy(o11,a,o11,ae);grid on;title('各机构加速度曲线图');text(185,-0.5,'α3');text(100,-0.3,'α4');text(100,0.7,'αE');xlabel('\it\theta1');ylabel('\it\alpha3,\alpha4,\alphaE');F=[o11;o3./pi*180;o4./pi*180;se;w3;w4;ve;a3;a4;ae]';G=F(1:100:3601,:)G =0 65.5560 168.9382 0.1011 0.1712 0.2888 -0.1018 0.2477 0.2927 -0.138710.0000 67.4668 172.0273 0.0814 0.2093 0.3239 -0.1227 0.1908 0.1172 -0.102620.0000 69.7125 175.3266 0.0585 0.2386 0.3320 -0.1383 0.1472 -0.0185 -0.078030.0000 72.2163 178.5980 0.0333 0.2612 0.3192 -0.1504 0.1132 -0.1241 -0.061440.0000 74.9188 181.6560 0.0062 0.2785 0.2900 -0.1601 0.0861 -0.2076 -0.050350.0000 77.7722 184.3541 -0.0225 0.2915 0.2477 -0.1681 0.0640 -0.2742 -0.042360.0000 80.7379 186.5757 -0.0524 0.3010 0.1951 -0.1749 0.0454 -0.3264 -0.035570.0000 83.7830 188.2297 -0.0835 0.3075 0.1346 -0.1805 0.0290 -0.3646 -0.028680.0000 86.8791 189.2495 -0.1154 0.3113 0.0687 -0.1848 0.0142 -0.3882 -0.020390.0000 90.0000 189.5941 -0.1479 0.3125 0.0000 -0.1875 0 -0.3962 -0.0099100.0000 93.1209 189.2495 -0.1807 0.3113 -0.0687 -0.1881 -0.0142 -0.3882 0.0030110.0000 96.2170 188.2297 -0.2134 0.3075 -0.1346 -0.1863 -0.0290 -0.3646 0.0183120.0000 99.2621 186.5757 -0.2456 0.3010 -0.1951 -0.1816 -0.0454 -0.3264 0.0357130.0000 102.2278 184.3541 -0.2766 0.2915 -0.2477 -0.1738 -0.0640-0.2742 0.0544140.0000 105.0812 181.6560 -0.3061 0.2785 -0.2900 -0.1626 -0.0861 -0.2076 0.0737150.0000 107.7837 178.5980 -0.3332 0.2612 -0.3192 -0.1481 -0.1132 -0.1241 0.0929160.0000 110.2875 175.3266 -0.3575 0.2386 -0.3320 -0.1302 -0.1472 -0.0185 0.1114170.0000 112.5332 172.0273 -0.3785 0.2093 -0.3239 -0.1092 -0.1908 0.1172 0.1289180.0000 114.4440 168.9382 -0.3955 0.1712 -0.2888 -0.0852 -0.2477 0.2927 0.1464(我的度数)190.0000 115.9198 166.3668 -0.4080 0.1217 -0.2190 -0.0580 -0.3229 0.5144 0.1669200.0000 116.8285 164.6992 -0.4155 0.0571 -0.1069 -0.0263 -0.4224 0.7754 0.1980210.0000 116.9955 164.3854 -0.4168 -0.0275 0.0518 0.0126 -0.5522 1.0375 0.2539220.0000 116.1941 165.8703 -0.4103 -0.1375 0.2504 0.0649 -0.7135 1.2133 0.3538230.0000 114.1449 169.4393 -0.3929 -0.2775 0.4619 0.1392 -0.8905 1.1564 0.5061240.0000 110.5470 174.9633 -0.3600 -0.4461 0.6286 0.2423 -1.0255 0.6624 0.6684250.0000 105.1832 181.5495 -0.3071 -0.6259 0.6559 0.3651 -0.9935 -0.4598 0.6995260.0000 98.1324 187.2640 -0.2337 -0.7742 0.4416 0.4682 -0.6461 -1.9991 0.4257270.0000 90.0000 189.5941 -0.1479 -0.8333 -0.0000 0.5000 -0.0000 -2.8172 -0.0704280.0000 81.8676 187.2640 -0.0639 -0.7742 -0.4416 0.4515 0.6461 -1.9991 -0.4435290.0000 74.8168 181.5495 0.0072 -0.6259 -0.6559 0.3598 0.9935 -0.4598 -0.5742300.0000 69.4530 174.9633 0.0612 -0.4461 -0.6286 0.2589 1.0255 0.6624 -0.5677310.0000 65.8551 169.4393 0.0980 -0.2775 -0.4619 0.1646 0.8905 1.1564 -0.5068320.0000 63.8059 165.8703 0.1194 -0.1375 -0.2504 0.0832 0.7135 1.2133 -0.4244330.0000 63.0045 164.3854 0.1279 -0.0275 -0.0518 0.0168 0.5522 1.0375 -0.3369340.0000 63.1715 164.6992 0.1261 0.0571 0.1069 -0.0348 0.4224 0.7754 -0.2561350.0000 64.0802 166.3668 0.1165 0.1217 0.2190 -0.0734 0.32290.5144 -0.1893360.0000 65.5560 168.9382 0.1011 0.1712 0.2888 -0.1018 0.2477 0.2927 -0.1387>>截图看不清楚可以放大,word限定篇幅。
