专题七第三讲直线平面平行判定与性质(61张)
合集下载
平行第三讲直线与平面平行的性质

求证:EF∥平面BCD.
B
A F D
C
判断下列命题的真假
(1)过直线外一点只能引一条直线与
这条直线平行.
()
(2)过平面外一点只能引一条直线与
这个平面平行.
()
(3)若两条直线都和第三条直线垂直, 则这两条直线平行.
()
(4)若两条直线都和第三条直线平行,
则这两条直线平行.
()
判断下列命题的真假
求证:EF∥RQ。
AERຫໍສະໝຸດ DSFB
Q
C
例1:有一块木料如图,已知棱BC平行于面A´C´. (1)要经过木料表面A´B´C´D´内的一点P和 棱BC将木料锯开,应怎样画线? (2)所画的线和面AC有什么关系?
已知:平面,,, l, m,
n,且l // m
求证: n // l, n // m
n
l
m
已知:平面,,, l, m,
ABCD是平行四边形,P是平面ABCD外一点,M是PC 的中点,在DM上取一点G,过G和AP作平面交平面 BDM于GH。 求证:AP∥GH。
P
M
D
G
C
H
A
B
S是空间四边形ABCD对角线BD上任意一点,E、F分 别是AD、CD上的点,且AE:AD=CF:CD,BE与AS交于R, BF与SC交于Q。
∴过直线a的某一个平面 ,若与平面 相交,
则直线a就平行于这一条交线
直线与平面平行性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这 个平面相交,那么这条直线和交线平行
条件
a , a , b
结论
a // b
a b
例1. 如图,空间四边形ABCD中,
直线、平面平行的判定与性质 课件
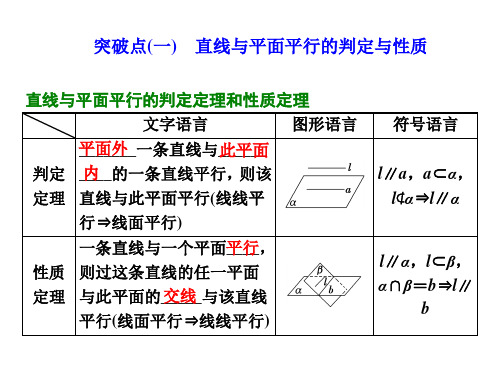
(2)GH∥平面 PAD. 证明:连接 FH,OH, ∵F,H 分别是 PC,CD 的中点, ∴FH∥PD,∴FH∥平面 PAD. 又∵O 是 AC 的中点,H 是 CD 的中点, ∴OH∥AD,∴OH∥平面 PAD. 又 FH∩OH=H, ∴平面 OHF∥平面 PAD. 又∵GH⊂平面 OHF,∴GH∥平面 PAD.
又因为点 H 为 BC 的中点, 所以 OH∥BD. 又因为 OH⊂平面 FGH,BD⊄平面 FGH, 所以 BD∥平面 FGH.
判定线面平行的四种方法 (1)利用线面平行的定义(无公共点); (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α); (3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β); (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
α∥β,α∩γ=a, β∩γ=b⇒a∥b
面面平行的判定与性质 [典例] 如图所示,在三棱柱 ABC-A1B1C1 中,E,F,G,H 分别是 AB,AC,A1B1,A1C1 的中点,求证: (1)B,C,H,G 四点共面; [证明] ∵G,H 分别是 A1B1,A1C1 的中点, ∴GH 是△A1B1C1 的中位线, ∴GH∥B1C1. 又∵B1C1∥BC,∴GH∥BC, ∴B,C,H,G 四点共面.
突破点(二) 平面与平面平行的判定与性质
平面与语言 符号语言
一个平面内的两条_相__交_ 判定 直__线__与另一个平面平 定理 行,则这两个平面平行
(线面平行⇒面面平行)
a∥β,b∥β, a∩b=P,a⊂α, b⊂α⇒α∥β
如果两个平行平面同时
性质 定理
和第三个平面_相__交__,那 么它们的_交__线__平行
(2)平面 EFA1∥平面 BCHG. [证明] ∵E,F 分别是 AB,AC 的中点, ∴EF∥BC. ∵EF⊄平面 BCHG,BC⊂平面 BCHG, ∴EF∥平面 BCHG.
专题37直线平面平行的判定与性质ppt课件

包括直线与平面平行和直线与平面相交两种情况,所以排除选项B;选项C中缺少直
线a不在平面α内这一条件;选项D正确.
第1轮 ·数学
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
立体几何
02 课堂互动·考点突破
自主 完成
1.(2019·山东日照月考)若m,n是两条不同的直线,α,β是两个不同的平面, 则下列命题正确的是( D )
解析 连接BD,设BD∩AC=O,连接EO,在△BDD1中,E为DD1的中点,O为BD的 中点,所以EO为△BDD1的中位线,则BD1∥EO,而BD1⊄平面ACE,EO⊂平面ACE,所以 BD1∥平面ACE.
第1轮 ·数学
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
解 析 对于 A , 若 α⊥β , m⊥β , 则 m∥α 或 m⊂α, 故 A 错误; 对 于 B,若 m∥α,n⊥m,则n⊥α或n⊂α或n与α相交,故B错误;对于C,若m∥α,n∥α, m⊂β,n⊂β,则α∥β或α、β相交,故C错误;对于D,若m∥β,m⊂α,α∩β =n,由线面平行的性质定理,可得m∥n,故D正确.
线平行(线面平行⇒线线平行)
第1轮 ·数学
图形语言
符号语言
l∥a,a⊂α, l⊄α⇒l∥α
l∥α,l⊂β, α∩β=b⇒l∥ b
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
立体几何
2.平面与平面平行的判定定理和性质定理
线a不在平面α内这一条件;选项D正确.
第1轮 ·数学
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
立体几何
02 课堂互动·考点突破
自主 完成
1.(2019·山东日照月考)若m,n是两条不同的直线,α,β是两个不同的平面, 则下列命题正确的是( D )
解析 连接BD,设BD∩AC=O,连接EO,在△BDD1中,E为DD1的中点,O为BD的 中点,所以EO为△BDD1的中位线,则BD1∥EO,而BD1⊄平面ACE,EO⊂平面ACE,所以 BD1∥平面ACE.
第1轮 ·数学
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
解 析 对于 A , 若 α⊥β , m⊥β , 则 m∥α 或 m⊂α, 故 A 错误; 对 于 B,若 m∥α,n⊥m,则n⊥α或n⊂α或n与α相交,故B错误;对于C,若m∥α,n∥α, m⊂β,n⊂β,则α∥β或α、β相交,故C错误;对于D,若m∥β,m⊂α,α∩β =n,由线面平行的性质定理,可得m∥n,故D正确.
线平行(线面平行⇒线线平行)
第1轮 ·数学
图形语言
符号语言
l∥a,a⊂α, l⊄α⇒l∥α
l∥α,l⊂β, α∩β=b⇒l∥ b
返回导航
第七章 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
立体几何
2.平面与平面平行的判定定理和性质定理
直线、平面平行的判定及其性质完整ppt课件

思考4:有一块木料如图,
E
P为面BCEF内一点,要求 过点P在平面BCEF内画一
F
P D
条直线和平面ABCD平行,
那么应如何画线?
A
整理版课件
C B
5
思考5:如图,设直线b在平面α内,直 线a在平面α外,猜想在什么条件下直线 a与平面α平行?
a
a//b
α
b
整理版课件
6
探究(二):直线与平面平行的判断定理
通过直线间的平行,推证直线与平面平 行,即将直线与平面的平行关系(空间 问题)转化为直线间的平行关系(平面 问题).
整理版课件
10
思考6:设直线a,b为异面直线,经过
直线a可作几个平面与直线b平行?过a,
b外一点P可作几个平面与直线a,b都
平行?
a
b
p
b a a
p
整理版课件
b
11
理论迁移
例1 在空间四边形ABCD中,E,F分别是 AB,AD的中点,求证:EF//平面BCD.
定理,分别用文字语言和符号语言可以
怎样表述?
γ
定理 如果两个平行
b
平面同时和第三个平 β
面相交,那么它们的
交线平行.
α
a
/ /, a ,整理版课件 b a / /b 48
思考2:上述定理通常称为平面与平面平 行的性质定理,该定理在实际应用中有 何功能作用?
/ / , a , b a / /b
整理版课件
41
2.2 直线、平面平行的判定及其性质 2.2.4 平面与平面平行的性质
整理版课件
42
问题提出
1.平面与平面平行的判定定理是什么?
直线、平面平行的判定与性质课件

考点一
直线与平面平行的判定与性质
考向基础
直线与平面平行的判定与性质
文字语言
平面外一条直线与此平面内的一
图形语言
符号语言
a⊄α,b⊂α,且a∥b⇒a∥α
条直线平行,则该直线与此平面
平行.简称:线线平行,则线面平行
一条直线与一个平面平行,则过
a∥α,a⊂β,
这条直线的任一平面与此平面的
α∩β=b⇒a∥b
别平行于另一个平面内的两条相交直线,那么这两个平面平行.
3.证明两个平面都垂直于同一条直线.(客观题可用)
4.证明两个平面同时平行于第三个平面.(客观题可用)
例2 如图所示,正方体ABCD-A1B1C1D1中,
M,N分别是A1B1,A1D1的中点,E,F分别是B1C1,C1D1的中点.
(1)求证:四边形BDFE为梯形;
∴PQ∥平面BCE.
证法二:如图,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∴PM∥平面BCE,且
AP AM
=
,
PE MB
易知AE=BD,又AP=DQ,∴PE=BQ,
∴
AP DQ
AM DQ
=
,∴
=
,
PE BQ
MB QB
∴MQ∥AD,又AD∥BC,
∴MQ∥BC,
∵BC⊂平面BCE,MQ⊄平面BCE,
∴OB∥平面EFC,
∵OB∩OG=O,∴平面OBG∥平面EFC.
方法技巧
方法1
证明直线与平面平行的方法
1.利用线面平行的定义(此法一般伴随反证法证明).
2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线
平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常
直线与平面平行的判定与性质
考向基础
直线与平面平行的判定与性质
文字语言
平面外一条直线与此平面内的一
图形语言
符号语言
a⊄α,b⊂α,且a∥b⇒a∥α
条直线平行,则该直线与此平面
平行.简称:线线平行,则线面平行
一条直线与一个平面平行,则过
a∥α,a⊂β,
这条直线的任一平面与此平面的
α∩β=b⇒a∥b
别平行于另一个平面内的两条相交直线,那么这两个平面平行.
3.证明两个平面都垂直于同一条直线.(客观题可用)
4.证明两个平面同时平行于第三个平面.(客观题可用)
例2 如图所示,正方体ABCD-A1B1C1D1中,
M,N分别是A1B1,A1D1的中点,E,F分别是B1C1,C1D1的中点.
(1)求证:四边形BDFE为梯形;
∴PQ∥平面BCE.
证法二:如图,在平面ABEF内,过点P作PM∥BE,交AB于点M,连接QM.
∴PM∥平面BCE,且
AP AM
=
,
PE MB
易知AE=BD,又AP=DQ,∴PE=BQ,
∴
AP DQ
AM DQ
=
,∴
=
,
PE BQ
MB QB
∴MQ∥AD,又AD∥BC,
∴MQ∥BC,
∵BC⊂平面BCE,MQ⊄平面BCE,
∴OB∥平面EFC,
∵OB∩OG=O,∴平面OBG∥平面EFC.
方法技巧
方法1
证明直线与平面平行的方法
1.利用线面平行的定义(此法一般伴随反证法证明).
2.利用线面平行的判定定理.应用此法的关键是在平面内找与已知直线
平行的直线.可先直观判断平面内是否已有,若没有,则需作出该直线,常
直线平面平行的判定与性质 课件
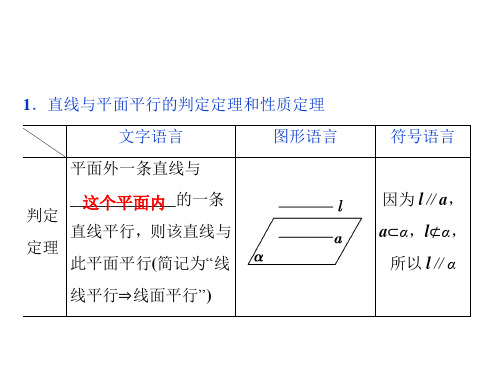
1.直线与平面平行的判定定理和性质定理
文字语言
图形语言
平面外一条直线与
__这__个__平__面__内___的一条 判定
直线平行,则该直线与 定理
此平面平行(简记为“线
线平行⇒线面平行”)
符号语言
因为 l∥a, a⊂α,l⊄α,
所以 l∥α
文字语言 一条直线与一个平面平 行,则过这条直线的任一 性质 平面与此平面的_交__线__与 定理 该直线平行(简记为“线 面平行⇒线线平行”)
2.如图所示,已知四边形 ABCD 是正方形, 四边形 ACEF 是矩形,AB=2,AF=1,M 是线段 EF 的中点. (1)求证:MA∥平面 BDE. (2)若平面 ADM∩平面 BDE=l,平面 ABM∩平面 BDE=m, 试分析 l 与 m 的位置关系,并证明你的结论.
解:(1)证明:如图,记 AC 与 BD 的交点为 O,连接 OE. 因为 O,M 分别是 AC,EF 的中点,四边形 ACEF 是矩形, 所以四边形 AOEM 是平行四边形,所以 AM∥OE. 又因为 OE⊂平面 BDE,AM⊄平面 BDE, 所以 AM∥平面 BDE.
【解析】 A 错误,n 有可能在平面 α 内;B 错误,平面 α 有 可能与平面 β 相交;C 错误,n 也有可能在平面 β 内;D 正确, 易知 m∥β 或 m⊂β,若 m⊂β,又 n∥m,n⊄β,所以 n∥β,若 m∥β,过 m 作平面 γ 交平面 β 于直线 l,则 m∥l,又 n∥m, 所以 n∥l,又 n⊄β,l⊂β,所以 n∥β.
线面平行的判定与性质(多维探究)
角度一 线面平行的证明 在正方体 ABCD-A1B1C1D1 中,E,F,G,H 分别是
BC,CC1,C1D1,A1A 的中点.求证: (1)BF∥HD1; (2)EG∥平面 BB1D1D.
文字语言
图形语言
平面外一条直线与
__这__个__平__面__内___的一条 判定
直线平行,则该直线与 定理
此平面平行(简记为“线
线平行⇒线面平行”)
符号语言
因为 l∥a, a⊂α,l⊄α,
所以 l∥α
文字语言 一条直线与一个平面平 行,则过这条直线的任一 性质 平面与此平面的_交__线__与 定理 该直线平行(简记为“线 面平行⇒线线平行”)
2.如图所示,已知四边形 ABCD 是正方形, 四边形 ACEF 是矩形,AB=2,AF=1,M 是线段 EF 的中点. (1)求证:MA∥平面 BDE. (2)若平面 ADM∩平面 BDE=l,平面 ABM∩平面 BDE=m, 试分析 l 与 m 的位置关系,并证明你的结论.
解:(1)证明:如图,记 AC 与 BD 的交点为 O,连接 OE. 因为 O,M 分别是 AC,EF 的中点,四边形 ACEF 是矩形, 所以四边形 AOEM 是平行四边形,所以 AM∥OE. 又因为 OE⊂平面 BDE,AM⊄平面 BDE, 所以 AM∥平面 BDE.
【解析】 A 错误,n 有可能在平面 α 内;B 错误,平面 α 有 可能与平面 β 相交;C 错误,n 也有可能在平面 β 内;D 正确, 易知 m∥β 或 m⊂β,若 m⊂β,又 n∥m,n⊄β,所以 n∥β,若 m∥β,过 m 作平面 γ 交平面 β 于直线 l,则 m∥l,又 n∥m, 所以 n∥l,又 n⊄β,l⊂β,所以 n∥β.
线面平行的判定与性质(多维探究)
角度一 线面平行的证明 在正方体 ABCD-A1B1C1D1 中,E,F,G,H 分别是
BC,CC1,C1D1,A1A 的中点.求证: (1)BF∥HD1; (2)EG∥平面 BB1D1D.
直线与平面平行的性质ppt课件
举例 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
例4. 设平面α、β、γ两两相交,且 a , b , c 若a∥b,求证:b∥c .
a
c
b
α
β
γ
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
证明:因为 b,所以 b 因 为 a // b 所 以 a // , 又因为 a,所以 a 又因为 c 所 以 a // c, 因 为 a // b 所 以 b // c
小结
1. 复习直线与平面的位置关系 2. 复习直线与平面平行的判定 3. 学习并掌握直线与平面平行的性质
b (√)
a
举例 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
例2.在四面体ABCD中,E、F分别是 AB、AC的中点,过直线EF作平面α,分别 交BD、CD于M、N,求证:EF∥MN.
A
E
F
BM
D
N C
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
直线与平面平行的性质定理:
如果一条直线和一个平面平行,经 过这条直线的平面和这个平面相交,那 么这条直线和交线平行.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)【证明】因为BC∥平面GEFH,BC⊂平面PBC,且平面 PBC∩平面GEFH=GH,
所以GH∥BC.同理可证EF∥BC, 因此GH∥EF.
(2)【解】如图,连接AC,BD交于点O,BD交EF于点K,连接 OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC.同理可得PO⊥BD. 又BD∩AC=O,且AC,BD都在底面ABCD内,所以PO⊥底面 ABCD. 又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,所以PO∥ 平面GEFH.
【证明】∵CD∥AB,AB⊂平面SAB,CD⊄平面SAB,∴CD∥平 面SAB.又平面CDEF∩平面SAB=EF,∴CD∥EF.
(2)【解】∵CD⊥AD,平面SAD⊥平面ABCD,平面SAD∩平面 ABCD=AD,∴CD⊥平面SAD.又SD⊂平面SAD,∴CD⊥SD,同理 AD⊥SD.
由(1)知EF∥CD,∴EF⊥平面SAD. ∵EC=AC,∠ADC=∠EDC=90°, ∴△ADC≌△EDC,∴ED=AD.
又易知AO= 2,S矩形BDEF=3×2 2=6 2, 所以四棱锥A-BDEF的体积V1=13·AO·S矩形BDEF=4. 同理可得四棱锥C-BDEF的体积V2=4. 所以多面体ABCDEF的体积V=V1+V2=8.
平行关系的综合应用
(2018河南开封模拟)如图,ABCD与ADEF均为平行四边形,M, N,G分别是AB,AD,EF的中点.
第八章 立体几何
第38节 直线、平面平行的 判定与性质
考纲呈现 1.掌握线线、 线面、面面平行的判定定理和性质定理,并能应 用它们证明有关空间图形的平行关系的简单命题. 2.高考的重点考查内容之一,主要以几何体为载体考查线线、 线面、面面平行的判定和性质.
诊断型·微题组
课前预习·诊断双基
1.直线与平面平行的判定定理和性质定理
微技探究 利用线面平行的性质,可以实现与线线平行的转化,尤其在截 面图的画法中,常用来确定交线的位置,对于最值问题,常用函数 思想来解决.
如图所示,平面α∥平面β,点A∈α,点C∈α,点B∈β,点D ∈β,点E,F分别在线段AB,CD上,且AE∶EB=CF∶FD.
(1)求证:EF∥平面β; (2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD 所成的角为60°,求EF的长.
4.(必修2P56练习T2改编)在正方体ABCD—A1B1C1D1中,点E是 DD1的中点,则BD1与平面ACE的位置关系为________.
【答案】平行
【解析】连接BD,设BD∩AC=O,连接EO,在△BDD1中,点 E,O分别是DD1,BD的中点,则EO∥BD1,又因为EO⊂平面ACE, BD1⊄平面ACE,所以BD1∥平面ACE.
(2019四川乐山一中调研)如图,在多面体ABCDEF中,底面 ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面 ABCD,BF=3,G和H分别是CE和CF的中点.
(1)求证:平面BDGH∥平面AEF; (2)求多面体ABCDEF的体积.
(1)【证明】在△CEF中,因为G,H分别是CE,CF的中点,所 以GH∥EF.又因为GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面 AEF.
又G,E分别为A1B1,AB的中点,A1B1綊AB.
∴A1G綊EB,∴四边形A1EBG是平行四边形.
∴A1E∥GB. ∵A1E⊄平面BCHG,GB⊂平面BCHG, ∴A1E∥平面BCHG.又A1E∩EF=E, ∴平面EFA1∥平面BCHG.
微技探究 证明面面平行的方法 (1)面面平行的定义. (2)面面平行的判定定理:如果一个平面内有两条相交直线都平 行于另一个平面,那么这两个平面平行. (3)利用垂直于同一条直线的两个平面平行. (4)两个平面同时平行于第三个平面,那么这两个平面平行. (5)利用“线线平行”“线面平行”“面面平行”的相互转化.
2.平面与平面平行的判定定理和性质定理
3.必记结论 (1)两个平面平行,其中一个平面内的任意一条直线平行于另一 个平面. (2)夹在两个平行平面间的平行线段长度相等. (3)经过平面外一点有且只有一个平面与已知平面平行. (4)两条直线被三个平行平面所截,截得的对应线段成比例. (5)如果两个平面分别和第三个平面平行,那么这两个平面互相 平行. (6)如果两个平面分别垂直于同一条直线,那么这两个平面互相 平行.
1.直线与平面平行的判定中易忽视“线在面内”这一关键条 件.
2.面面平行的判定中易忽视“面内两条相交线”这一条件. 3.如果一个平面内有无数条直线与另一个平面平行,易误认为 这两个平面平行,实质上也可以相交.
1.下面四个正方体图形中,A,B为正方体的两个顶点,M, N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
3.(必修2P58练习T3改编)平面α∥平面β的一个充分条件是( ) A.存在一条直线a,a∥α,a∥β B.存在一条直线a,a⊂α,a∥β C.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α D.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α
【答案】D
【解析】若α∩β=l,a∥l,a⊄α,a⊄β,a∥α,a∥β,故排除A.若 α∩β=l,a⊂α,a∥l,则a∥β,故排除B.若α∩β=l,a⊂α,a∥l,b ⊂β,b∥l,则a∥β,b∥α,故排除C.故选D.
∴四边形ABCE是平行四边形.∴O为AC的中点.又∵F是PC的 中点,∴FO∥AP.
又FO⊂平面BEF,AP⊄平面BEF,∴AP∥平面BEF. (2)如图,连接FH,OH,∵F,H分别是PC,CD的中点,∴FH ∥PD. 又PD⊂平面PAD,FH⊄平面PAD,∴FH∥平面PAD. ∵O是BE的中点,H是CD的中点, ∴OH∥AD. ∵AD⊂平面PAD,OH⊄平面PAD,∴OH∥平面PAD. 又FH∩OH=H,∴平面OHF∥平面PAD. ∵GH⊂平面OHF,∴GH∥平面PAD.
行四边形,∴C1D1綊DA,
∴四边形ADC1D1为平行四边形,∴AD1∥C1D, 又AD1⊄平面BDC1,C1D⊂平面BDC1, ∴AD1∥平面BDC1. (2)连接D1D,∵BB1∥平面ACC1A1,BB1⊂平面BB1D1D,平面 ACC1A1∩平面BB1D1D=D1D, ∴BB1∥D1D. 又D1,D分别为A1C1,AC的中点, ∴BB1=DD1. 故四边形BDD1B1为平行四边形, ∴BD∥B1D1. 又BD⊄平面AB1D1,B1D1⊂平面AB1D1, ∴BD∥平面AB1D1.
1 2
BC=
4.
由已知可得OB=4 2 ,PO= PB2-OB2 = 68-32 =6,所以
GK=3.
故四边形GEFH的面积S=GH+2 EF·GK=4+2 8×3=18.
微技探究 判断或证明线面平行的常用方法 (1)利用线面平行的定义(无公共点). (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α). (3)利用面面平行的性质(α∥β,a⊂α⇒α∥β). (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒α∥β).
求证: (1)B,C,H,G四点共面; (2)平面EFA1∥平面BCHG.
【证明】(1)∵G,H分别是A1B1,A1C1的中点, ∴GH是△A1B1C1的中位线,则GH∥B1C1. 又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面. (2)∵E,F分别为AB,AC的中点,∴EF∥BC. ∵EF⊄平面BCHG,BC⊂平面BCHG, ∴EF∥平面BCHG.
(1)求证:BE∥平面DMF; (2)求证:平面BDE∥平面MNG.
【证明】(1)如图,连接AE,则AE必过DF与GN的交点O,连接 MO,则MO为△ABE的中位线,所以BE∥MO.
又BE⊄平面DMF,MO⊂平面DMF, 所以BE∥平面DMF. (2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以 DE∥GN. 又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG. 又因为M为AB的中点,所以MN为△ABD的中位线, 所以BD∥MN. 又BD⊄平面MNG, MN⊂平面MNG. 所以BD∥平面MNG, 又DE与BD为平面BDE内的两条相交直线, 所以平面Bห้องสมุดไป่ตู้E∥平面MNG.
1.(2018河北故城期中)在四棱锥P-ABCD中,AD∥BC,AB =BC=12AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交 于O点,G是线段OF上一点.
(1)求证:AP∥平面BEF; (2)求证:GH∥平面PAD.
【证明】(1)如图,连接EC,
∵AD∥BC,BC=12AD,E为AD的中点, ∴BC綊AE.
连接AC,设AC与BD的交点为O,连接OH,如图.
在△ACF中,因为O,H分别是AC,CF的中点,所以OH∥AF. 又因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF. 因为OH∩GH=H,OH,GH⊂平面BDGH, 所以平面BDGH∥平面AEF.
(2)【解】因为四边形ABCD是正方形,所以AC⊥BD.平面 ABCD∩平面BDEF=BD,AC⊂平面ABCD,且平面ABCD⊥平面 BDEF,所以AC⊥平面BDEF,
2.已知m,n表示两条不同直线,α表示平面.下列说法正确的 是( )
A.若m∥α,n∥α,则m∥n B.若m⊥α,n⊂α,则m⊥n C.若m⊥α,m⊥n,则n∥α D.若m∥α,m⊥n,则n⊥α
【答案】B
【解析】若m∥α,n∥α,则m与n可能平行、相交或异面,故A错 误;B正确;若m⊥α,m⊥n,则n∥α或n⊂α,故C错误;若m∥α,m ⊥n,则n与α可能平行、相交或n⊂α,故D错误.因此选B.
形成型·微题组
归纳演绎·形成方法
直线与平面平行的判定与性质 命题角度1 直线与平面平行的判定
(2018甘肃张掖模拟)如图所示,斜三棱柱ABC-A1B1C1中,点 D,D1分别为AC,A1C1的中点.
(1)证明:AD1∥平面BDC1; (2)证明:BD∥平面AB1D1. 【证明】(1)∵D1,D分别为A1C1,AC的中点,四边形ACC1A1为平
所以GH∥BC.同理可证EF∥BC, 因此GH∥EF.
(2)【解】如图,连接AC,BD交于点O,BD交EF于点K,连接 OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC.同理可得PO⊥BD. 又BD∩AC=O,且AC,BD都在底面ABCD内,所以PO⊥底面 ABCD. 又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH,所以PO∥ 平面GEFH.
【证明】∵CD∥AB,AB⊂平面SAB,CD⊄平面SAB,∴CD∥平 面SAB.又平面CDEF∩平面SAB=EF,∴CD∥EF.
(2)【解】∵CD⊥AD,平面SAD⊥平面ABCD,平面SAD∩平面 ABCD=AD,∴CD⊥平面SAD.又SD⊂平面SAD,∴CD⊥SD,同理 AD⊥SD.
由(1)知EF∥CD,∴EF⊥平面SAD. ∵EC=AC,∠ADC=∠EDC=90°, ∴△ADC≌△EDC,∴ED=AD.
又易知AO= 2,S矩形BDEF=3×2 2=6 2, 所以四棱锥A-BDEF的体积V1=13·AO·S矩形BDEF=4. 同理可得四棱锥C-BDEF的体积V2=4. 所以多面体ABCDEF的体积V=V1+V2=8.
平行关系的综合应用
(2018河南开封模拟)如图,ABCD与ADEF均为平行四边形,M, N,G分别是AB,AD,EF的中点.
第八章 立体几何
第38节 直线、平面平行的 判定与性质
考纲呈现 1.掌握线线、 线面、面面平行的判定定理和性质定理,并能应 用它们证明有关空间图形的平行关系的简单命题. 2.高考的重点考查内容之一,主要以几何体为载体考查线线、 线面、面面平行的判定和性质.
诊断型·微题组
课前预习·诊断双基
1.直线与平面平行的判定定理和性质定理
微技探究 利用线面平行的性质,可以实现与线线平行的转化,尤其在截 面图的画法中,常用来确定交线的位置,对于最值问题,常用函数 思想来解决.
如图所示,平面α∥平面β,点A∈α,点C∈α,点B∈β,点D ∈β,点E,F分别在线段AB,CD上,且AE∶EB=CF∶FD.
(1)求证:EF∥平面β; (2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD 所成的角为60°,求EF的长.
4.(必修2P56练习T2改编)在正方体ABCD—A1B1C1D1中,点E是 DD1的中点,则BD1与平面ACE的位置关系为________.
【答案】平行
【解析】连接BD,设BD∩AC=O,连接EO,在△BDD1中,点 E,O分别是DD1,BD的中点,则EO∥BD1,又因为EO⊂平面ACE, BD1⊄平面ACE,所以BD1∥平面ACE.
(2019四川乐山一中调研)如图,在多面体ABCDEF中,底面 ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面 ABCD,BF=3,G和H分别是CE和CF的中点.
(1)求证:平面BDGH∥平面AEF; (2)求多面体ABCDEF的体积.
(1)【证明】在△CEF中,因为G,H分别是CE,CF的中点,所 以GH∥EF.又因为GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面 AEF.
又G,E分别为A1B1,AB的中点,A1B1綊AB.
∴A1G綊EB,∴四边形A1EBG是平行四边形.
∴A1E∥GB. ∵A1E⊄平面BCHG,GB⊂平面BCHG, ∴A1E∥平面BCHG.又A1E∩EF=E, ∴平面EFA1∥平面BCHG.
微技探究 证明面面平行的方法 (1)面面平行的定义. (2)面面平行的判定定理:如果一个平面内有两条相交直线都平 行于另一个平面,那么这两个平面平行. (3)利用垂直于同一条直线的两个平面平行. (4)两个平面同时平行于第三个平面,那么这两个平面平行. (5)利用“线线平行”“线面平行”“面面平行”的相互转化.
2.平面与平面平行的判定定理和性质定理
3.必记结论 (1)两个平面平行,其中一个平面内的任意一条直线平行于另一 个平面. (2)夹在两个平行平面间的平行线段长度相等. (3)经过平面外一点有且只有一个平面与已知平面平行. (4)两条直线被三个平行平面所截,截得的对应线段成比例. (5)如果两个平面分别和第三个平面平行,那么这两个平面互相 平行. (6)如果两个平面分别垂直于同一条直线,那么这两个平面互相 平行.
1.直线与平面平行的判定中易忽视“线在面内”这一关键条 件.
2.面面平行的判定中易忽视“面内两条相交线”这一条件. 3.如果一个平面内有无数条直线与另一个平面平行,易误认为 这两个平面平行,实质上也可以相交.
1.下面四个正方体图形中,A,B为正方体的两个顶点,M, N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是( )
3.(必修2P58练习T3改编)平面α∥平面β的一个充分条件是( ) A.存在一条直线a,a∥α,a∥β B.存在一条直线a,a⊂α,a∥β C.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α D.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α
【答案】D
【解析】若α∩β=l,a∥l,a⊄α,a⊄β,a∥α,a∥β,故排除A.若 α∩β=l,a⊂α,a∥l,则a∥β,故排除B.若α∩β=l,a⊂α,a∥l,b ⊂β,b∥l,则a∥β,b∥α,故排除C.故选D.
∴四边形ABCE是平行四边形.∴O为AC的中点.又∵F是PC的 中点,∴FO∥AP.
又FO⊂平面BEF,AP⊄平面BEF,∴AP∥平面BEF. (2)如图,连接FH,OH,∵F,H分别是PC,CD的中点,∴FH ∥PD. 又PD⊂平面PAD,FH⊄平面PAD,∴FH∥平面PAD. ∵O是BE的中点,H是CD的中点, ∴OH∥AD. ∵AD⊂平面PAD,OH⊄平面PAD,∴OH∥平面PAD. 又FH∩OH=H,∴平面OHF∥平面PAD. ∵GH⊂平面OHF,∴GH∥平面PAD.
行四边形,∴C1D1綊DA,
∴四边形ADC1D1为平行四边形,∴AD1∥C1D, 又AD1⊄平面BDC1,C1D⊂平面BDC1, ∴AD1∥平面BDC1. (2)连接D1D,∵BB1∥平面ACC1A1,BB1⊂平面BB1D1D,平面 ACC1A1∩平面BB1D1D=D1D, ∴BB1∥D1D. 又D1,D分别为A1C1,AC的中点, ∴BB1=DD1. 故四边形BDD1B1为平行四边形, ∴BD∥B1D1. 又BD⊄平面AB1D1,B1D1⊂平面AB1D1, ∴BD∥平面AB1D1.
1 2
BC=
4.
由已知可得OB=4 2 ,PO= PB2-OB2 = 68-32 =6,所以
GK=3.
故四边形GEFH的面积S=GH+2 EF·GK=4+2 8×3=18.
微技探究 判断或证明线面平行的常用方法 (1)利用线面平行的定义(无公共点). (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α). (3)利用面面平行的性质(α∥β,a⊂α⇒α∥β). (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒α∥β).
求证: (1)B,C,H,G四点共面; (2)平面EFA1∥平面BCHG.
【证明】(1)∵G,H分别是A1B1,A1C1的中点, ∴GH是△A1B1C1的中位线,则GH∥B1C1. 又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面. (2)∵E,F分别为AB,AC的中点,∴EF∥BC. ∵EF⊄平面BCHG,BC⊂平面BCHG, ∴EF∥平面BCHG.
(1)求证:BE∥平面DMF; (2)求证:平面BDE∥平面MNG.
【证明】(1)如图,连接AE,则AE必过DF与GN的交点O,连接 MO,则MO为△ABE的中位线,所以BE∥MO.
又BE⊄平面DMF,MO⊂平面DMF, 所以BE∥平面DMF. (2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以 DE∥GN. 又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG. 又因为M为AB的中点,所以MN为△ABD的中位线, 所以BD∥MN. 又BD⊄平面MNG, MN⊂平面MNG. 所以BD∥平面MNG, 又DE与BD为平面BDE内的两条相交直线, 所以平面Bห้องสมุดไป่ตู้E∥平面MNG.
1.(2018河北故城期中)在四棱锥P-ABCD中,AD∥BC,AB =BC=12AD,E,F,H分别为线段AD,PC,CD的中点,AC与BE交 于O点,G是线段OF上一点.
(1)求证:AP∥平面BEF; (2)求证:GH∥平面PAD.
【证明】(1)如图,连接EC,
∵AD∥BC,BC=12AD,E为AD的中点, ∴BC綊AE.
连接AC,设AC与BD的交点为O,连接OH,如图.
在△ACF中,因为O,H分别是AC,CF的中点,所以OH∥AF. 又因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF. 因为OH∩GH=H,OH,GH⊂平面BDGH, 所以平面BDGH∥平面AEF.
(2)【解】因为四边形ABCD是正方形,所以AC⊥BD.平面 ABCD∩平面BDEF=BD,AC⊂平面ABCD,且平面ABCD⊥平面 BDEF,所以AC⊥平面BDEF,
2.已知m,n表示两条不同直线,α表示平面.下列说法正确的 是( )
A.若m∥α,n∥α,则m∥n B.若m⊥α,n⊂α,则m⊥n C.若m⊥α,m⊥n,则n∥α D.若m∥α,m⊥n,则n⊥α
【答案】B
【解析】若m∥α,n∥α,则m与n可能平行、相交或异面,故A错 误;B正确;若m⊥α,m⊥n,则n∥α或n⊂α,故C错误;若m∥α,m ⊥n,则n与α可能平行、相交或n⊂α,故D错误.因此选B.
形成型·微题组
归纳演绎·形成方法
直线与平面平行的判定与性质 命题角度1 直线与平面平行的判定
(2018甘肃张掖模拟)如图所示,斜三棱柱ABC-A1B1C1中,点 D,D1分别为AC,A1C1的中点.
(1)证明:AD1∥平面BDC1; (2)证明:BD∥平面AB1D1. 【证明】(1)∵D1,D分别为A1C1,AC的中点,四边形ACC1A1为平
