2019年深国交G1入学考试数学专题复习(十二)新定义题(含答案)
2019年广东省深圳市招生入学数学试卷

2019年广东省深圳市招生入学数学试卷一、比眼力,你能把每题中正确答案的序号都写在()里(14分)1. 一个三角形,三个内角度数的比为2:5:3,则此三角形为()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定2. 一批水泥,用去49,剩下的是用去的()A.5 9B.45C.54D.1093. 一台电冰箱的原价是2400元,现在按七折出售,求便宜了多少元?列式是()A.2400÷70%B.2400×70%C.2400×(1−70%)D.2400÷(1−70%)4. 已知:a×23=a×135=a÷23,且a、a、a都不等于0,则a、a、a中最小的数是()A.aB.aC.a5. 用100个盒子装杯子,每盒装的个数都不相同,并且每盒不空,那么至少要用()杯子。
A.100B.500C.1000D.50506. 一个小数的小数点向右移动一位,比原数大5.4,原来的这个小数是()A.0.6B.5.4C.0.54D.0、457. 张师傅以1元钱4个苹果的价格买进苹果若干个,又以2元钱5个苹果的价格把这些苹果卖出,如果他要赚得15元钱的利润,那么他必须卖出苹果()个。
A.10B.100C.20D.160二、细心填一填,你一定行(共22分,每小题2分)8. 四川汶川特大地震发生以来,全国共接收国内外社会各界捐赠款物(截至2008年9月25日12时)总计(五百九十四亿六千万零八十元),括号里的数写作________,省略亿后面的尾数约是________.9. 水是由氢气和氧气按1:8的质量比反应生成的。
如果要生成54千克的水,需要氢气________千克。
10. 一个正方形的边长增加2aa,面积增加20aa2,扩大后正方形面积为36aa2.11. 工地上有a吨水泥,每天用去a吨,用了2天。
用式子表示剩下的吨数是________.如果a=20,a=4,那么剩下的是________吨。
2019年深国交G1入学考试数学:二次函数的性质01(选择题)

二次函数的性质01(选择题)一.选择题(共30小题)1.(2015•益阳)若抛物线y=(x﹣m)2+(m+1)的顶点在第一象限,则m的取值范围为()A.m>1 B.m>0 C.m>﹣1 D.﹣1<m<02.(2015•常州)已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()A.m=﹣1 B.m=3 C.m≤﹣1 D.m≥﹣13.(2015•南昌)已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴()A.只能是x=﹣1B.可能是y轴C.可能在y轴右侧且在直线x=2的左侧D.可能在y轴左侧且在直线x=﹣2的右侧4.(2015•梅州)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为()A.1 B.2 C.3 D.45.(2015•甘孜州)二次函数y=x2+4x﹣5的图象的对称轴为()A.x=4 B.x=﹣4 C.x=2 D.x=﹣26.(2015•新疆)抛物线y=(x﹣1)2+2的顶点坐标是()A.(﹣1,2)B.(﹣1,﹣2)C.(1,﹣2)D.(1,2)7.(2016•重庆模拟)在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1,y2中的较大值记为N;当y1=y2时,N=y1=y2.则下列说法:①当0<x<2时,N=y1;②N随x的增大而增大的取值范围是x<0;③取y1,y2中的较小值记为M,则使得M大于4的x值不存在;④若N=2,则x=2﹣或x=1.其中正确的有()A.1个B.2个C.3个D.4个8.(2015•台州)设二次函数y=(x﹣3)2﹣4图象的对称轴为直线l,若点M在直线l上,则点M的坐标可能是()A.(1,0)B.(3,0)C.(﹣3,0)D.(0,﹣4)9.(2015•贵阳)已知二次函数y=﹣x2+2x+3,当x≥2时,y的取值范围是()A.y≥3 B.y≤3 C.y>3 D.y<310.(2015•福州)已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是()A.正比例函数B.一次函数 C.反比例函数D.二次函数11.(2015•玉林)如图,反比例函数y=的图象经过二次函数y=ax2+bx图象的顶点(﹣,m)(m>0),则有()A.a=b+2k B.a=b﹣2k C.k<b<0 D.a<k<012.(2015•南开区二模)二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y <0;那么当x=a﹣1时,函数值()A.y<0 B.0<y<m C.y>m D.y=m13.(2015•深圳模拟)若(2,5)、(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是()A.x=﹣B.x=1 C.x=2 D.x=314.(2015•潍坊模拟)若函数y=的自变量x的取值范围是全体实数,则c的取值范围是()A.c<1 B.c=1 C.c>1 D.c≤115.(2015•巴中模拟)抛物线y=x2﹣8x+m的顶点在x轴上,则m等于()A.﹣16 B.﹣4 C.8 D.1616.(2015•大庆模拟)若点A(2,y1),B(﹣3,y2),C(﹣1,y3)三点在抛物线y=x2﹣4x﹣m的图象上,则y1、y2、y3的大小关系是()A.y1>y2>y3B.y2>y1>y3C.y2>y3>y1D.y3>y1>y22时,y随x的增大而增大;⑤方程ax2+bx+c=0有两个不相等的实数根.其中正确的是()A.①②③ B.①③⑤ C.①③④ D.①④⑤18.(2015•巴中模拟)若直线y=ax+b(a≠0)在第二、四象限都无图象,则抛物线y=ax2+bx+c ()A.开口向上,对称轴是y轴B.开口向下,对称轴平行于y轴C.开口向上,对称轴平行于y轴D.开口向下,对称轴是y轴19.(2015•鄄城县三模)关于二次函数y=3x2﹣kx+k﹣3,以下结论:①抛物线交x轴有两个不同的交点;②不论k取何值,抛物线总是经过一个定点;③设抛物线交x轴于A、B两点,若AB=1,则k=9;④抛物线的顶点在y=﹣3(x﹣1)2图象上.中正确的序号是()A.①②③④B.②③C.②④D.①②④20.(2015•山西模拟)已知二次函数y1=﹣3x2,,,它们的图象开口由小到大的顺序是()A.y1<y2<y3B.y3<y2<y1C.y1<y3<y2D.y2<y3<y121.(2015•亭湖区校级模拟)若二次函数y=(x﹣k)2+m,当x≤2时,y随x的增大而减小,则k的取值范围是()A.k=2 B.k>2 C.k≥2 D.k≤222.(2015•平阴县二模)下列函数中,在0≤x≤2上y随x的增大而增大的是()A.y=﹣x+1 B.y=x2﹣4x+5 C.y=x2D.y=23.(2015•石家庄校级模拟)已知二次函数y=ax2+bx+c的x、y的部分对应值如表:则该二)y 5 1 ﹣1 ﹣1 1A.y轴B.直线x= C.直线x=2 D.直线x=﹣224.(2015•海宁市模拟)二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部+(b ﹣1)x+c=0的一个根;(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.其中正确的个数为()A.1个B.2个C.3个D.4个25.(2015•岱岳区二模)已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(﹣1,﹣2)、B(2,1)和C(,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论错误的是()A.当x<﹣1时,M=Y1B.当﹣1<x<0时,Y2<Y3<Y1C.当0≤x≤2时,M的最大值是1,无最小值D.当x≥2时,M最大值是1,无最小值26.(2015•牡丹江二模)抛物线y=ax2+bx+c经过点(4,﹣5)且对称轴是直线x=2,则代数式c﹣2的值为()A.25 B.﹣25 C.D.﹣27.(2015•彭州市校级模拟)已知二次函数y=x2+bx+c过点(0,﹣3)和(﹣1,2m﹣2)对于该二次函数有如下说法:①它的图象与x轴有两个公共点;②若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0;③若将它的图象向左平移3个单位后过原点,则m=﹣1;④若当x=2时的函数值与x=2012时的函数值相等,则当x=20时的函数值为﹣3.其中正确的说法的个数是()A.1 B.2 C.3 D.428.(2015•杭州模拟)如图,已知二次函数的解析式为y=x2﹣1,其图象上有一个动点P,连接OP(O为坐标原点),并以OP为半径作圆,则该圆的最小面积是()A.πB.πC.πD.π29.(2015•杭州模拟)如图,已知点A(﹣1,0),B(7,0),P是线段AB上任意一点(不含端点A,B),过A、P两点的二次函数y1和过P、B两点的二次函数y2的图象开口均向上,它们的顶点分别为C、D,射线BD与AC相交于点E.当AE=BE=5时,这两个二次函数的最小值之和等于()A.﹣1 B.﹣2 C.﹣3 D.﹣430.(2015•岱岳区二模)若不等式组(x为未知数)无解,则对二次函数y=ax2﹣2x+1的图象的下列叙述:(1)开口向上;(2)与x轴没有交点;(3)顶点在第二象限;(4)当x>﹣时,y随x的增大而增大.其中正确的有()A.4个B.3个C.2个D.1个。
2019年深国交G1入学考试数学复习资料:创新题1(含答案)

答案:D
【9】在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是( )
A. B. C. D.
答案:D
【10】小强拿了张正方形的纸如图(1),沿虚线对折一次如图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是()
答案:D
五.折叠后得结论
【15】亲爱的同学们,在我们的生活中处处有数学的身影.请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于_______°.”
答案:180
【16】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则与之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是()
【20】同学们肯定天天阅读报纸吧?我国的报纸一般都有一个共同的特征:每次对折后,所得的长方形和原长方形相似,问这些报纸的长和宽的比值是多少?
答案: ∶1.
【21】用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
整理得9x2-9x+2=0.
解得x1= ,x2= .
当AA1= 时,AD1= ,
当AA1= 时,AD1= .
∴当AA1=BB1=CC1=DD1= 或 时,
四边形A1B1C1D1仍为正方形且面积是原面积的 .
答案:C
【2】如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
2019年深国交G1入学考试复习专题:二次函数的最值(试题版)

2019年深国交G1入学考试复习专题:二次函数的最值一.选择题(共15小题)22或C或或2.已知二次函数的图象y=ax2+bx+c(0≤x≤3)如图.关于该函数在所给自变量取值范围内,下列说法正确的是()22﹣D﹣22225.二次函数y=﹣x2+6x﹣7,当x取值为t≤x≤t+2时,y最大值=﹣(t﹣3)2+2,则t的取值范27.如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于()C210.小聪、小明、小伶、小俐四人共同探究代数式2x2﹣4x+6的值的情况.他们作了如下分工:小聪负责找值为0时x的值,小明负责找值为4时x的值,小伶负责找最小值,小俐负11.y=x2+(1﹣a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取22222C15.正实数x,y满足xy=1,那么的最小值为()C二.填空题(共8小题)16.二次函数y=x2+2ax+a在﹣1≤x≤2上有最小值﹣4,则a的值为.17.已知实数x、y满足x2﹣2x+4y=5,则x+2y的最大值为.18.若的最大值为a,最小值为b,则a2+b2的值为.19.正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN.当BM=时,四边形ABCN的面积最大.20.如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是.21.若二次函数y=x2+2x﹣3(0≤x≤3)的最小值为,最大值为.22.函数y=﹣+的最大值为.23.已知二次函数y=(x﹣1)2+(x﹣3)2,当x=时,函数达到最小值.。
2020年深国交G1入学考试数学复习资料:填空综合训练-12(30题)

填空综合训练-121.如图,数轴上有六个点,且EF DE CD BC AB ====,则与点C 所表示的数最接近的整数是。
2.因式分解:=+++611623x x x 。
3.方程1252-=+x x 的解是4.(1)计算:=++⨯20202020202020202018638443(.(2)如n 8333444422666666555555555555555=+++++⨯++++++,那么n =.5.若322255(21)()3x ax x x ax x b --+=+--+,其中a ,b 为整数,则ab 的值为6.已知不等式⎩⎨⎧+><14a x x ,满足不等式的所有整数解之和为5,则实数a 的取值范围是7.已知一元二次方程02=++c bx x ,且c b ,在5,4,3,21,中取值(可重复),使得组成的方程有实数根的概率为8.若方程a x x =-|24|2有且只有三个不同实根,则=a9.若m 为实数,关于x 的方程0162=-+-m x x 的两个非负实数根为a 、b ,则代数式)2)(2(22b a --的最大值为.10.已知20201+=x a ,19201+=x b ,21201+=x c ,则=---++ac bc ab c b a 22211.已知一元二次方程01)6(322=-+--+a x a a x 的两个根互为相反数,则=a 12.如图是一组密码的一部分。
为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”。
目前,已破译出“今天考试”的真实意思是“努力发挥”。
若“今”所处的位置为),(y x ,你找到的密码钥匙是(,),破译“正做数学”的真实意思是“”。
13.如图,已知9321A A A A 是一个正九边形,a A A =21,b A A =31,则51A A 的值为。
14.已知直线:l 12-=x y 与y 轴交于点A ,若将直线l 绕点A 旋转090,则得到的直线的解析式为15.如图,用3个边长为1的正方形组成一个对称图形,则能将其完全覆盖的圆的最小半径为.16.如图,已知在ABC RT ∆中,90C ∠= ,D 是BC 边上一点,AD =,CAD ABC α∠=∠=,且1tan 2α=,则BD 的长为.17.如图,在直角坐标系中,矩形OABC 的顶点A 、B 在双曲线)0(>=x x k y 上,BC 与x 轴交于点D .若点A 的坐标为(1,2),则点B 的坐标为.。
深国交测试题及答案

深国交测试题及答案一、选择题(每题2分,共20分)1. 以下哪个选项是正确的描述?A. 地球是平的B. 太阳是银河系的中心C. 月亮是地球的卫星D. 火星上存在液态水2. 根据题目分析,选项C是正确的描述,因为月亮确实是地球的卫星。
其他选项描述错误,地球是圆的,太阳不是银河系的中心,火星上尚未发现液态水。
3. 以下哪个历史事件标志着第二次世界大战的结束?A. 珍珠港事件B. 诺曼底登陆C. 广岛原子弹爆炸D. 日本投降4. 选项D是正确的,因为1945年8月15日,日本宣布无条件投降,标志着第二次世界大战的结束。
5. 以下哪个公式是计算圆的面积的公式?A. A = πr²B. A = 2πrC. A = r²D. A = πd6. 选项A是正确的,圆的面积公式是A = πr²,其中r是圆的半径。
7. 以下哪个国家不是联合国安全理事会的常任理事国?A. 中国B. 法国C. 德国D. 俄罗斯8. 选项C是正确的,因为联合国安全理事会的五个常任理事国是中国、法国、俄罗斯、英国和美国,不包括德国。
9. 以下哪个元素是人体必需的微量元素?A. 氢B. 氧C. 铁D. 碳10. 选项C是正确的,铁是人体必需的微量元素,对血红蛋白的形成至关重要。
二、填空题(每空1分,共10分)11. 光合作用是植物通过______吸收太阳能,将______和水转化为葡萄糖和氧气的过程。
答案:叶绿体;二氧化碳12. 牛顿的第二定律表明,力等于______乘以______。
答案:质量;加速度13. 英语中的“Hello”在中文中通常翻译为______。
答案:你好14. 世界上最深的海沟是______。
答案:马里亚纳海沟15. 国际标准时间的起点是______经线。
答案:本初子午线三、简答题(每题5分,共20分)16. 请简述牛顿的三大定律。
答案:牛顿的三大定律是经典力学的基础。
第一定律(惯性定律)指出,物体会保持静止或匀速直线运动状态,除非受到外力作用。
2019年深国交G1入学考试资料:二元一次方程组

2019年深国交G1入学考试资料:二元一次方程组一.填空题(共30小题)1.已知三个非负实数a,b,c满足:3a+2b+c=5和2a+b﹣3c=1,若m=3a+b﹣7c,则m的最小值为.2.在关于x1,x2,x3的方程组中,已知a1>a2>a3,那么将x1,x2,x3从大到小排起来应该是.3.如图,正方形是由k个相同的矩形组成,上下各有2个水平放置的矩形,中间竖放若干个矩形,则k=.4.蔬菜种植专业户王先生要办一个小型蔬菜加工厂,分别向银行申请甲、乙两种贷款,共13万元,王先生每年须付利息6075元,已知甲种贷款的年利率为6%,乙种贷款的年利率为3.5%,则甲、乙两种贷款分别是万元和万元.5.若关于x、y的二元一次方程组的解是,那么关于x、y的二元一次方程组的解是x=,y=.6.一支科学考察队前往某条河流的上游去考察一个生态区,他们以每天17km的速度出发,沿河岸向上游行进若干天后到达目的地,然后在生态区考察了若干天,完成任务后以每天25km的速度返回,在出发后的第60天,考察队行进了24km后回到出发点,那么科学考察队的生态区考察了天.7.一次数学比赛,有两种给分方法:一种是答对一题给5分,不答给2分,答错不给分;另一种是先给40分,答对一题给3分,不答不给分,答错扣1分,用这两种方法评分,某考生都得81分,这张试卷共有题.8.甲乙两人到特价商店购买商品,已知两人购买商品的件数相等,且每件商品的单价只有8元和9元,若两人购买商品一共花费了172元,则其中单价为9元的商品有件.9.若4x﹣3y﹣6z=0,x+2y﹣7z=0(xyz≠0),则的值等于.10.方程x+3y=6的正整数解是.11.小亮解方程组的解为由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则这两个数分别为.12.若|a﹣b+1|与互为相反数,则(a﹣b)2005=.13.把面值为1元的纸币换为1角或5角的硬币,则换法共有种.14.已知方程组与有相同的解,则m=,n=.15.若方程组的解满足x+y=,则m=.16.已知二元一次方程组的解也是方程7mx﹣4y=﹣18x的解,那么m=.17.当k=时,方程组中x与y互为相反数.18.若x m﹣2y n﹣3=1为含x,y的二元一次方程,是m=,n=.19.某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有种租车方案.20.方程组==4的解为.21.若关于x,y方程组的解为,则方程组的解为.22.在方程组中,若未知数x、y满足x+y>0,则m的取值范围是.23.设x,y都是有理数,且满足方程,那么x﹣y 的值是.24.m为正整数,已知二元一次方程组有整数解,即x,y均为整数,则m2=.25.已知等式(2A﹣7B)x+(3A﹣8B)=8x+10对一切实数x都成立,则A=,B=.26.如果2x2a﹣b﹣1﹣3y3a+2b﹣16=10是一个二元一次方程,则ab=.27.已知:,且3a+2b﹣4c=9,则a+b+c的值等于.28.方程mx+3y=4x﹣1是关于x、y的二元一次方程,则m的取值范围为.29.“鸡兔同笼”是我国古代《孙子算经》上的一道名题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.运用方程的思想,我们可以算出笼中有鸡只.30.对任意两个正整数x、y,定义一个运算“★”为x★y=(x+2xy+y),若正整数a、b满足a★b=1154,则有序正整数对(a,b)共有对.。
2019年深国交G1入学考试复习专题:相似三角形以及锐角三角函数(试题版)
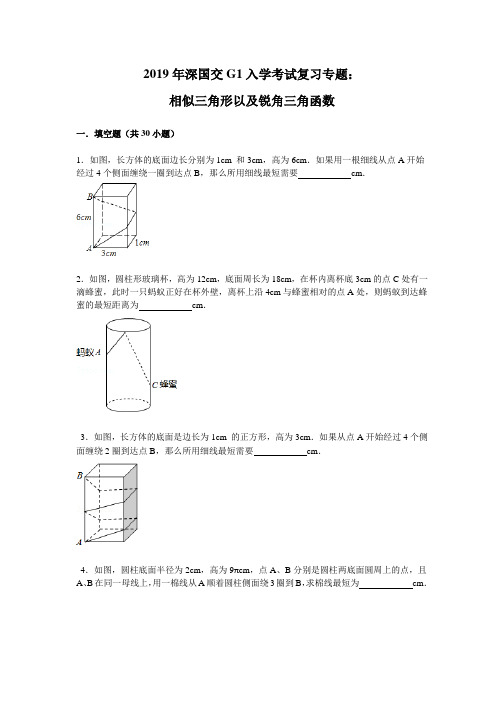
2019年深国交G1入学考试复习专题:相似三角形以及锐角三角函数一.填空题(共30小题)1.如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.2.如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为cm.3.如图,长方体的底面是边长为1cm 的正方形,高为3cm.如果从点A开始经过4个侧面缠绕2圈到达点B,那么所用细线最短需要cm.4.如图,圆柱底面半径为2cm,高为9πcm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一棉线从A顺着圆柱侧面绕3圈到B,求棉线最短为cm.5.如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是m.(结果不取近似值)6.如图,将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1.若AB=3,图中阴影部分面积为2,则BB1=.7.在直角坐标系中,已知点P(﹣3,2),点Q是点P关于x轴的对称点,将点Q向右平移4个单位得到点R,则点R的坐标是.8.如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,OP n(n为正整数),则点P6的坐标是;△P5OP6的面积是.9.如图,△DEF是由△ABC绕某点旋转得到的,则这点的坐标是.10.如图,边长为6的正方形ABCD绕点B按顺时针方向旋转30°后得到正方形EBGF,EF 交CD于点H,则FH的长为(结果保留根号).11.如图,点A在反比例函数的图象上,点B在反比例函数的图象上,且∠AOB=90°,则tan∠OAB的值为.12.如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为.13.如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B n+1D n C n的面积为S n,则S n=(用含n的式子表示).14.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为.15.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影长度在A处为米,在B处为米.16.如图,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,且AD=AB,则△ADE的周长与△ABC的周长的比为.17.小亮和他弟弟在阳光下散步,小亮的身高为1.75米,他的影子长2米.若此时他的弟弟的影子长为1.6米,则弟弟的身高为米.18.李老师从拉面的制作受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段AB,对折后(点A与B重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段AB上的,均变成,变成1,等).那么在线段AB上(除A,B)的点中,在第二次操作后,恰好被拉到与1重合的点所对应的数之和是.19.如图,在△ABC中DE∥BC,若DE=2,BC=3,则S三角形ADE:S四边形DBEC.20.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为.21.若,则=.22.如图,在平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果,那么=.23.在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,,则AC 的长是.24.观察下列等式①sin30°=cos60°=②sin45°=cos45°=③sin60°=cos30°=…根据上述规律,计算sin2a+sin2(90°﹣a)=.25.因为cos30°=,cos210°=﹣,所以cos210°=cos(180°+30°)=﹣cos30°=﹣;因为cos45°=,cos225°=﹣,所以cos225°=cos(180°+45°)=﹣cos45°=﹣;猜想:一般地,当a为锐角时,有cos(180°+a)=﹣cosa,由此可知cos240°的值等于.26.如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,,则tan∠B 的值为.27.如图,∠AOB=30°,过OA上到点O的距离为1,3,5,7,…的点作OA的垂线,分别与OB相交,得到如图所示的阴影梯形,它们的面积依次记为S1,S2,S3,….则:(1)S1=;(2)通过计算可得S2009=.28.如图,在正方形网格中,∠AOB的正切值是.29.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为海里(结果保留根号).30.⊙O的半径OA=2,弦AB、AC的长分别为一元二次方程x2﹣(2+2)x+4=0的两个根,则∠BAC的度数为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年深国交G1入学考试数学专题复习(十一)
新定义题含答案
1.在平面直角坐标系xOy中的某圆上,有弦MN,取MN的中点P,我们规定:点P到某点(直线)的距离叫
做“弦中距”,用符号“d
”表示.
中
以(3,0)
W-为圆心,半径为2的圆上.
(1)已知弦MN长度为2.
的长度;
①如图1:当MN∥x轴时,直接写出到原点O的d
中
的取值范围.
②如果MN在圆上运动时,在图2中画出示意图,并直接写出到点O的d
中
(2)已知点(5,0)
y x
=-,求到直线2
=-的d
M-,点N为⊙W上的一动点,有直线2
y x
中Array
的最大值.
1
2
2.研究发现,抛物线2
14
y x =上的点到点F (0,1)的距离与到直线l :1y =-的距离相等.如图1所示,若点P 是抛物线2
14
y x =
上任意一点,PH ⊥l 于点H ,则PH PF =. 基于上述发现,对于平面直角坐标系x O y 中的点M ,记点M 到点P 的距离与点P 到点F 的距离之和的最小值为d ,称d 为点M 关于抛物线214y x =
的关联距离;当24d ≤≤时,称点M 为抛物线21
4
y x =的关联点.
(1)在点1(20)M ,
,2(12)M ,,3(45)M ,,4(04)M -,中,抛物线2
14
y x =的关联点是______ ; (2)如图2,在矩形ABCD 中,点(1)A t ,,点(13)A t +,C ( t .
①若t =4,点M 在矩形ABCD 上,求点M 关于抛物线2
14
y x =的关联距离d 的取值范围; ②若矩形ABCD 上的所有点都是抛物线2
14
y x =
的关联点,则t 的取值范围是__________.
3
3.对于平面直角坐标系xOy 中的点(,)Q x y (x ≠0),将它的纵坐标y 与横坐标x 的比
y
x
称为点Q 的“理想值”,记作Q L .如(1,2)Q -的“理想值”2
21
Q L =
=--. (1)①若点(1,)Q a 在直线4y x =-上,则点Q 的“理想值”Q L 等于_________;
②如图,C ,⊙C 的半径为1. 若点Q 在⊙C 上,则点Q 的“理想值”
Q L 的取值范围是 . (2)点D
在直线+3y x =上,⊙D 的半径为1,点Q 在⊙D 上运动时都有 0≤L Q
,求点D 的横坐标D x 的取值范围;
(3)(2,)M m (m >0),Q 是以r 为半径的⊙M 上任意一点,当0≤L Q
≤并直接写出相应的半径r 的值.(要求画图位置准确,但不必尺规作图)
4
答案:
1.解: (1)①
. ……………………………………………2分
②示意图正确 …………………………………3分
33d +中≤……………………………4分
(2)由于PW 是⊙W 的弦心距 所以PW MN ⊥
所以点N 在运动过程中,点P 在以MW
由图可知直线与点P 的运动轨迹形成的圆相切时,且 弦中距d 中过圆心时,距离最大………………6分 ∵2y x =-的图象与x 轴夹角是45° ∴由图可得6DE =
在等腰直角三角形DFM 中 可得DE =1PL = 即:d 中的最大值为1PL =
2. (1) 12M M ,; -----------------------------------------------------------------2分
(2)①当4t =时,()41A ,,()51B ,,()53C ,,()43D ,, 此时矩形ABCD 上的所有点都在抛物线2
14
y x =的下方, ∴.d MF = ∴.AF d CF ≤≤ ∵=4AF CF ,
∴d 4≤ ---------------------------------------------------------------------------------- 5分 ② 1.t ≤ ------------------------------------------------------------------------8分
3.(1)①3-. ………………………………………………………………………… 1分
② 0≤
Q
L .……………………………………………………………… 2分
(2)设直线
+3
y =与x 轴,y 轴的交点分别为点A ,点B ,可得
A ,
5
(0,3)B .
∴
OA =3OB =,30OAB ∠=︒. 由0≤
Q
L
y =.
①如图,当⊙D 与x 轴相切时,相应的圆心1D 满足题意, 其横坐标取到最大值.作11D E x ⊥轴于点1E ,
可得11D E ∥OB ,
111
D E AE BO AO =
. ∵ ⊙D 的半径为1, ∴ 111D E =.
∴
1AE =
11OE OA AE =-=. ∴
1D x =
②如图,当⊙D
与直线y =相切时, 相应的圆心2D 满足题意,其横坐标取到 最小值.
作22D E x ⊥轴于点2E ,则22D E ⊥OA .
设直线
y =
与直线+3y =的
交点为F .
可得60AOF ∠=︒,OF ⊥AB .
则
9
cos 2AF OA OAF =⋅∠==.
∵ ⊙D 的半径为1, ∴ 21D F =.
∴
227
2AD AF D F =-=
.
∴ 22cos AE AD OAF
=⋅
∠72=
=,
6
22OE OA AE =-=
.
∴
2D x =
.
由①②可得,D x
的取值范围是≤D x
≤.
………………………………………… 5分
(3)画图.
.…………………………………………… 7分。
