奥数知识点图形计数完整版
第一讲 图形计 数-小学奥数

第一讲 图形计数告诉你本讲的重点、难点小学阶段我们认识了很多图形,数出某种图形的个数是一类有趣的数学问题,我们称之为“图形计数”,由于雷形千变万化,错综复杂,通过本讲掌握分类计数的方法.看老师画龙点晴,教给像解题诀窍【例1】数出下图中共有多少条线段。
分析与解 我们可以按照线段的左端点的位置分为五类,以A 为左端点的线段有5条,AB (,,,,)AF AF AD AC 以B 为左端点的线段有4条),,,,(BF BE BD BC 以C 为左端点的线段有3条 ),,,(CF CE CD 以D 为左端点的线段有2条),,(DF DE 以E 为左端点的线段有1条).(EF 所以共有 1512345=++++(条).答:图中共有15条线段.【例2】数一数,图中共有多少个角?分析与解 仔细观察,我们可以看出,图中包含的所有角都是以0点为 角的顶点的,如果我们按照一定的顺序数,就会发现:以射线OA 为角的一边的角有:AOF AOE AOD A AOB ∠∠∠∝∠∠,,,.,共5个;以射线OB 为角的一边的角有:BOF BOE BOD BOC ∠∠∠∠,,,共4个;(已经数过的BOA ∠不要再数.)以射线OC 为角的一边的角有:COF COE COD ∠∠∠,,共3个;以射线OD 为角的一边的角有:DOF DOE ∠∠,共2个;以射线OE 为角的一边的角有:EOF ∠共1个.角的总数:1512345=++++(个).答:图中共有15个角,当直线上有n A A A A n ,,,,32 个点时,则有;2)1(-n n 条线段,类似地,角和三角形也有同样的数数结果.【例3】一个正三角形的边长为5厘米,取每边5等分,作出许多边长为l 厘 米的小正三角形,如图.那么图中共有多少个正三角形?分析与解按边长分类计数边长为1厘米的正三角形有25个,边长为2厘米的正三角形有13个,边长为3厘米的正三角形有6个,边长为4厘米的正三角形有3个,边长为5厘米的正三角形有1个答:图中共有正三角形481361325=++++个.【例4】求图中共有多少个长方形?解法1 先看以1AA 为宽的长方形有多少?也就是在AE 上以A 为左端点的线段有几条,我们知道有4条,也就是以1AA 为宽的长方形有4个,再看以BBi 为宽的长方形有几个,相当于以B 点左端点的线段有几条,已知有3条,所以有3个长方形;以1CC 为宽的长方形有2个,以1DD 为宽的长方形有1个,所以在11A AEE 中有101234=+++个长方形.同理,在3//323321221,,E E A A E E A A E E A A 中也各有10个长方形,这样共有40个长方形.但 是还需考虑宽为A A A A A A AA AA AA 213132,,,,,中也各有10个长方形.所以,共有100个长方形.解法2 因为长方形由长和宽决定,在图中,长方形的长有,,,,,,,BE BD BC AE AD AC AB DE CE CD ,,共10种可能,它的宽也有10种可能,,,,,,,(3213121321A A A A A A A A AAAA AA AA ),32A A A A 对每一种长都有10种宽可以与之相配,构成10个长方形,所以共有1001010=⨯个长方形.在长方形的一边上取m-l 个点,而在与之相邻的另一边上取1-n 个点,过各个点分别作长方形边的平行线,可得到)321()321(n m ++++⨯++++ 个长方形.快来试一斌你的身手吧!1.下图中有多少条线段?又有多少个三角形?2.有一块木板上钉了16个钉子,横竖都是4个,横竖相邻的两个钉子间的距离都相等.用皮筋能套出多少个正方形和长方形?做题也有小窍门噢!数图形的个数时,适当分类,然后逐类计数,才能做到不重复、不遗漏,正确地数出图形的个数,通往初中名校的班车1.图中共有多少个梯形?2.数出图中正方形的个数.3.图中共有多少个三角形?4.图中共有几个三角形?答案。
四年级奥数—几何中的计数问题
几何中的计数问题
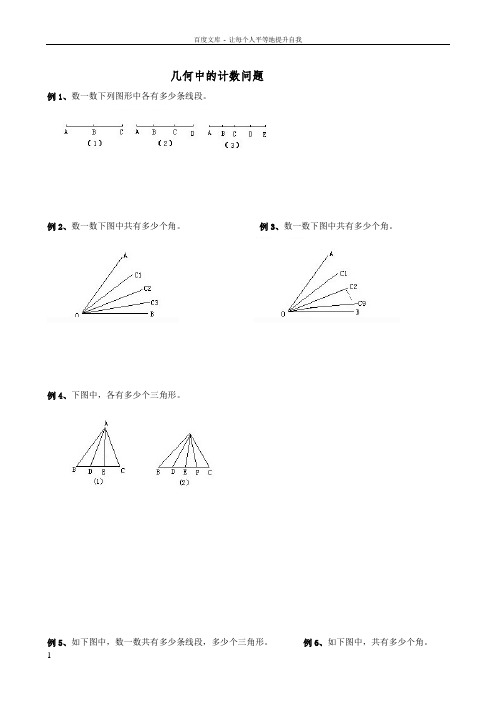
例1、数一数下列图形中各有多少条线段。
例2、数一数下图中共有多少个角。
例3、数一数下图中共有多少个角。
例4、下图中,各有多少个三角形。
例5、如下图中,数一数共有多少条线段,多少个三角形。
例6、如下图中,共有多少个角。
例7、如下图,数一数共有多少个长方形。
例8、数一数下图中长方形的个数。
例9、数一数下面各图中所有正方形的个数。
例10、数一数下图中有多少个正方形。
例11、数一数下图三角形的个数。
例12、数一数下图中三角形的个数。
例13、数一数下图中三角形的个数。
例14、数一数下图中三角形的个数。
练:1、数一数下面各图中有多少条线段。
2、数一数下面各图中有多少个角。
3、数一数下面各图中,各有多少条线段。
4、数一数下面各图中,各有多少条线段,各有多少个三角形。
5、下面图中有多少个正方形。
6、下图中有多少个长方形。
7、下图中有多少个三角形。
8、下图中有多少个长方形。
9、下图中各有多少个三角形。
五年级奥数-数图形.

练习2.数一数,下图中有多少个三角形?
12 3 4
1 234 5
(4+3+2+1)×2=20 个
(5+4+3+2+1)×3=45 个
例4.数一数,下图中有多少个角?
1
11
2
3
4
2
4+3+2+1=10 个
拓展1. 数一数,下图中有几个三角形?
拆除2条红线和蓝绿线后有三角 形 14个 2条红线返回后增加6个三角形
绿线返回后增加10个三角形
蓝线返回后增加14个三角形
还可以这样数: 单个三角形 16个 2个三角形组合16个 4个三角形组合8个
8个三角形组合4个
总共16+16+8+4=44 个
总共14+6+10+14= 44个
拓展2、数出下面图形中分别有多少个三 角形?
红线退出后有3个三角形。 红线返回后有增2个三角形。
20 16 8
20+16+8+4= 48 个
数一数,图中有多少个正方形?
51
5+4+1= 10 个
数一数,图中有多少个长方形?
3 13 3
20 3+3+3+1=
个
设想大 长方形消失 则有15+10-1=24个
还原大长方形则增4
个
总共24+4总= 共282个8个
数一数,下图中有多少个三角形?
还可以这样数:
线段总数=端点数×基本线段数÷2
数线段:方法二
31542
共5+4+3+2+1= 15条线段
小学奥数~平面图形计数-数正方形--不规则图形
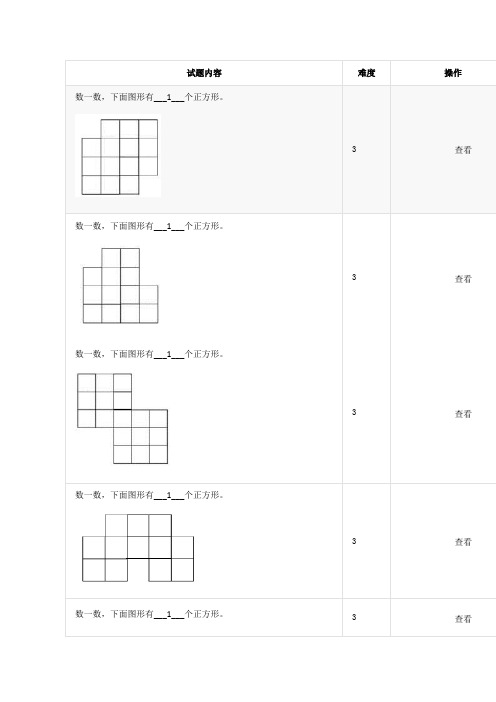
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看
数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看数一数,下面图形有___1___个正方形。
查看
查看
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
数一数,下面图形有___1___个正方形。
一年级奥数-图形的计数

céngfǎ
层法
fāngfǎ yīcéngyīcéngshùqīngchǔ zuòhǎo jì suàn
方 法 :一hìguānjiàn
是关 键
qǐngláojì yìxiēchángyòngdejìsuànjiéguǒ ò
都 要 分 到 糖 ,但 分 到 的 糖 块 数 又
bùnéngyíyàngduō shuíhuìfēn jiéguǒxiǎohuǒbàn
不 能 一 样 多 , 谁 会 分 ?” 结 果 小 伙 伴
mendōubúhuìfēn wèishénmene rúguǒyàogòufēn
们 都 不 会 分 , 为 什 么 呢?如 果 要 够 分 ,
课 堂 小结
lì tǐ túxíngshùfāngkuài cóngshàngwǎngxiàfēn
1.立体 图 形 数 方 块 : 从 上 往 下 分
céngfǎ
层法
kǒujué shùtóudǐngjiālóushàng
口 诀:数 头 顶 加 楼 上
píngmiàntúxíng jì shùfǎ cóngshàngwǎngxiàfēn
有 一 天 小 猴 子 和 7 个 小 伙 伴 一起 出 去 玩 ,
xiǎohóuzináchūyībāotáng duìxiǎohuǒbànmenshuō
小 猴 子拿 出 一 包 糖 , 对 小 伙 伴 们 说 :
wǒmenláifēntángchība zhè lǐ miànyígòngyǒu kuài
“ 我 们 来 分 糖 吃 吧 , 这 里 面 一 共 有 35 块
táng xiànzàiwǒmenyígòngyǒu gèxiǎohuǒbàn měigè
小学奥数~平面图形计数-数三角形(二)--复杂图形

第1步数一数,下面图形有___1___个三角形。
一个三角形:4个二个三角形组合:2个三个三角形组合:2个4+2+2=8(个)故答案为:8第1步数一数,下面图形有___1___个三角形。
一个三角形:4个二个三角形组合:4个4+4=8(个)故答案为:8第1步数一数,下面图形有___1___个三角形。
一个三角形:5个二个组合三角形:6个三个组合三角形:2个四个组合三角形:1个5+6+2+1=14(个)故答案为:14数一数,下面图形有___1___个三角形。
一个三角形:12个二个三角形组合:2个三个三角形组合:2个四个三角形组合:2个五个三角形组合:2个六个三角形组合:2个十二个三角形组合:1个12+2×5+1=23(个)故答案为:23第1步数一数,下面图形有___1___个三角形。
红线上方的有10个添加红线下方的三角形增加了5个三角形共10+5=15(个)故答案为:15数一数,下面图形有___1___个三角形。
第1步一个三角形:8个二个三角形组合:4个四个三角形组合:4个8+4+4=16(个)故答案为:16一个三角形:4个二个三角形组合:6个三个三角形组合:3个四个三角形组合:3个所有三角形组合:1个4+6+3+3+1=17(个)故答案为:17数一数,下面图形有___1___个三角形。
第1步一个三角形:8个二个三角形组合:8个四个三角形组合:2个8+8+2=18(个)故答案为:18数一数,下面图形有___1___个三角形。
第1步1、大三角:4个2、三角形与直线形成的三角形:5个3、大三角型之间形成的三角形:3个4+5+3=12(个)故答案为:12数一数,下面图形有___1___个三角形。
第1步三角形分别有:①、②、④、⑤、①+③+④、②+③+⑤、③+④+⑤共7个故答案为:7第1步一个三角形:9个二个三角形组合:6个三个三角形组合:4个六个三角形组合:2个共9+6+4+2=21(个)故答案为:21第1步数一数,下面图形有___1___个三角形。
小学奥数 图形计数 知识点+例题+练习 (分类全面)

一、图形计数
要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数,从中发现规律,以便得到正确的结果。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
例1、数出下图中有多少条线段?
巩固、数出下图中有几个长方形?
例2、数出图中有几个角?
D A B
C O
D C
B
A
巩固、数出图中有几个角?
例3、数出下图中共有多少个三角形?
巩固、数出图中共有多少个三角形?
例4、数出下图中有多少个长方形?
O C B A
P
C B A K G I H G F E A
D C B A
巩固、数出下图中有多少个正方形?
课后练习:
1、数出下图中有多少条线段?
2、数出图中有几个角?
E
A B C D E D
O
C B A
3、数出图中共有多少个三角形?
4、数出下图中有多少个长方形?
A
B A D
C B A。
(完整版)四年级奥数第一讲_图形的计数问题

第一讲图形的计数问题一、知识点:几何图形计数问题常常没有不言而喻的次序,并且要数的对象往常是重叠交织的,要正确计数就需要一些智慧了.实质上,图形计数问题,往常采纳一种简单原始的计数方法-一列举法.详细而言,它是指把所要计数的对象一一列举出来,以保证列举时无一重复、.无一遗漏,而后计算其总和.正确地解答较复杂的图形个数问题,有助于培育同学们思想的有序性和优秀的学习习惯.二、典例解析:例( 1)数出右图中总合有多少个角解析:在∠ AOB内有三条角分线 OC1、OC2、OC3,∠ AOB被这三条角分线分红 4 个基本角,那么∠ AOB内总合有多少个角呢?第一有这 4 个基本角,其次是包括有 2 个基本角构成的角有 3 个(即∠ AOC2、∠ C1OC3、∠ C2OB),而后是包括有 3 个基本角构成的角有 2 个(即∠ AOC3、∠C1OB),最后是包括有 4 个基本角构成的角有 1 个(即∠ AOB),因此∠ AOB内总合有角:4+3+2+1=10(个)解:4+3+ 2+ 1=10(个)答:图中总合有10 个角。
方法 2:用公式计算:边数×(边数—1)÷ 25 ×( 5-1 )÷ 2=10练一练:数一数右图中总合有多少个角?例( 2 )数一数共有多少条线段?共有多少个三角形?解析:①要数多少条线段:先看线段 AB、AD、AE、AF、AC纵向线段,再看 BC、MN、 GH 这 3 条横向线段:(4×3÷2)×5+(5×4÷2)×3=60(条)②要数有多少个三角形,先看在△ ABC中,被 GH和 MN分红了三层,每一层的三角形同样多,因此只需算出一层三角形个数就能够了。
(5 ×4÷2)×3=30(个)答:在△ ABC中共有线段60 条,共有三角形30 个。
练一练:图中共有多少个三角形?例( 3)数一数图中长方形的个数解析:长边线段有:6× 5÷ 2=15宽边线段有: 4 ×3÷2=6共有长方形: 15×6 = 90(个)答:共有长方形90 个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数知识点图形计数 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】
巧数图形
例1、数出下图中共有多少条线段。
分析与解:对于基础图形,用最小线段为单位,按序递增。
单拼:3(段),双拼:2(段),三拼:1(段)
通过以上的计数方法可以发现:开小火车的方式解决。
最小线段(基础线段)的数量为火车头
火车头为基础线段数3段:3+2+1=6(段)
或者,线段个数=基础线段数×端点÷2(高阶)
基础线段要求:手拉手,肩并肩
对于相交的线段,分别计算各个方向,然后加总
例2、数出下页左上图中锐角的个数。
分析与解:对于基础图形,可以使用开小火车的方式解决。
最小线段的数量为火车头。
或者,角的个数=最小角个数×(最小角个数+1)÷2
又,角的个数=射线的个数×(射线个数-1)÷2
例3、下列各图形中,三角形的个数各是多少?
分析与解:对于基础图形,可以使用开小火车的方式解决,最小线段的数量为火车
头。
所以,三角形个数=底边线段个数(每个底边基础线段构成一个基础三角形)
或者,三角形的个数=最小三角形个数×(最小三角形个数+1)÷2(高
阶)
以上的内容基本是单层规整图形:数线段(数角,数三角形),解决方法:开小火
车!
对于多层规整的图形,应该以单层规整图形为基础,运用技术,算出多层规整图形的
数量。
例4、下列图形中各有多少个三角形?
分析与解:方法(1)使用分层计数法:
方法(2)公式法:第一层三角形的总数×层数
例5、下列图形中各有多少个三角形?
小TIPS:吹泡泡法
例6、右图中有多少个三角形?
例7、右图中有多少个三角形?
分析与解:对于不规则的图形,
数之前,先将每个图形编号,
编好后,先数单拼三角形1、4、3号,共3个。
再数两个图形合成的(双拼)三角形,1+2号,2+3号,
3+4号,4+1号,按顺序两个两个合并,共4个三角形。
最后数由1+2+3+4号组成的(四拼)大三角形,有1个。
所以3+4+1=8,共8个三角形。
例8、下列各图形中,长方形的个数各是多少?
分析与解:对于(单层)基础图形,可以使用开小火车的方式解
决。
每个长方形相当于最小线段。
所以数单层的基础长
方形,就是数基础线段数。
对于多层的长方形的个数=单层长方形的数量×层数(个)
单层长方形的数量=长边上的线段数(个),层数=宽边上线段的个数(层)
例9、下列图形中,长方形的个数是多少个
分析与解:对于基础图形,可以使用开小火车的方式解决。
单层长方形的数量=长边线段数=4+3+2+1=10(个),
层数=宽边线段数=3+2+1=6(层)
总数=(4+3+2+1)×(3+2+1)=60(个)
例10、下列图形中,长方形的个数是多少个?
分析,先将<格1>与<格2>隐去,剩下的格
3,
就是一个多层规整长方形=10×6=60(个)
格1带来的长方形=4(个)(吹泡泡法)
格2带来的长方形=5(个)
总数=60+4+5=69(个)
例11、下列图形中,长方形的个数是多少个
分析与解:了解正方形的构成特点:四边相等。
方法(1)数格子:一格,四格,九格,十六格……
方法(2)开小火车法:最小正方形的个数为“火车头”,
后面的“车厢”中的每个乘数都减-1,直至出现1为止(0
乘任何数都等于0)
解:3×3+2×2+1×1=14(个)
例12、下列图形中,正方形的个数是多少个
分析与解:利用开小火车法:
火车头为最小9正方形数量:6×5
正方形个数=6×5+5×4+4×3+3×2+2×1=70(个)
例13、数下列图形中共有21个三角形,一共需要多少个小棒:
例10、在下图中,包含“*”号的长方形和正方形共有多少个?
分析与解:对于不规整的图形,进行分类讨论。
左图中,应先进行分类:正正方形与斜正方形
正正方形=5+5=10(个)
斜正方形= 5(个)
总数=10+5=15(个)
例11、如下图是由小立方体构成的塔,数一数有多少个小立方体?
分析与解:数立方体时,先从顶层数起。
公式:本层可见数+上层数
本题:1+(3+1)+(5+4)+(7+9)=30(个)
例12、数一数,下列图形中有多少个长方形?
方法(1):小讨厌法:
不包含小讨厌的多层规整图形:10×6=60(个)
小讨厌□1+□2+□12:4+4+4=12,共:60+12=72(个)
*方法(2):重叠法(三年级):
横:10×6=60(个),竖:3×10=30(个)
中(重叠):3×6=18(个),共:60+30-18=72(个)
例13、数一数,第10个图形应该有多少圆圈组成?
1 2 3 (10)
2 2+4+2 2+4+6+4+2 ……2+4+…+20…+4+2
2 8 18 (200)
例13、数一数,第10个图形应该有多少条线段?
1 2 3 4 (10)
1×2+2 3×2+3 6×2+4 10×2+5 55×2+11 22=4 32=9 42=16 52=25 112=121 例14、数一数,下列图形中包含★长方形有多少个?
方法(1)勾对角线法:将★的左上角的点和右下角的
点相连:
通过加标字母A、B和a、b、c、d、e、f,帮助我们
数图形:
Aa、Ab、Ac、Ad、Ae、Af、
Ba、Bb、Bc、Bd、Be、Bf、
*方法(2)公式法:经过★划十字线,左侧、右侧、上面、下面焦点数相乘:2×2×1×3=12(个)
例15、数一数,下列图形中有多少条线段有多少个三角形
(1)数线段:分方向:共:6×5+5=35(条)
(2)数三角形:分方向
中间五角星(不用①③③④⑤):共10个三角形。
仅使用①③③④⑤中一条:每一条有4个三角形,共4×5=20
(条)
使用①③③④⑤中的两条:共4个三角形。
共:10+20+5=35(个)。
