信号与线性系统分析试题2004——期末试卷.
信号与系统期末考试复习题及答案(共8套)
信号与系统考试题及答案（一）1． 系统的激励是)t (e ，响应为)t (r ，若满足dt)t (de )t (r =，则该系统为 线性、时不变、因果。
（是否线性、时不变、因果？） 2． 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3． 当信号是脉冲信号f(t)时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。
4． 若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。
5． 信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。
6． 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7． 若信号的3s F(s)=(s+4)(s+2)，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8． 为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9． 已知信号的频谱函数是））00(()j (F ωωδωωδω--+=，则其时间信号f(t)为01sin()t j ωπ。
10． 若信号f(t)的211)s (s )s (F +-=，则其初始值=+)(f 0 1 。
二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。
（每小题2分，共10分）1.单位冲激函数总是满足)()(t t -=δδ （ √ ）2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。
（ × ） 3.非周期信号的脉冲宽度越小，其频带宽度越宽。
（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。
（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。
（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分， 6题15分，共60分）1.信号)t (u e )t (f t-=21，信号⎩⎨⎧<<=其他，01012t )t (f ，试求)t (f *)t (f 21。
信号与系统期末试卷及答案
四、实验思考题
1.既然可直接由DTFT定义计算序列DTFT，为何利用DFT分析序列的频谱？答：通过DFT可以求出确定性信号相应的离散频 谱或频谱的样值，变换到有限频谱序列，这样就可以用计算机实现对信号进行分析，数字化计算速度快，故提出了DFT来分析 序列的频谱
2.若序列持续时间无限长，且无解析表达式，如何利用DFT分析其频谱？答：当原始的非周期信号为无限长或比较长，可截取 一段时间内的序列值，长度为L，作N点的DFT变换，NL。而截取的长度有限或不等于原始信号的 长度，则需考虑频谱泄露引 起的不良影响。为了减少泄露的影响，一般可适当增加长度To，也可以通过试探法，先取长度L1（To=L1*T），然后取 L2=2*L1,进行运算。若两者计算的结果很接近，则可取N1作为截取长度，否则继续去L3=2*L2,直至相邻两个长度的计算结果 相近，取长度较小的L为好。
时60附：当n取n=0:60;x=(0.8).^n;subplot(2,1,1);stem(n,x); ');subplot(2,1,2); 杨婕婕title('朱艺星w=n-15;plot(w,abs(fftshift(fft(x))));
读书破万卷下笔如有神 （2）进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。n x(n)?0.8u(n)为离散非周期信号，且为无限 长的信号。根据理答：信号论分析，一个时间有限的信号其频谱宽度为无限，一个时间无限的信号其频带宽度则为有限，因 此，对一个时间有限的信号，应用DFT进行分析，频谱混叠难以避免。对一个时间无限的信号虽然频带有限，但在时间运算 中，时间长度总是取有限值，所以频谱泄露难以避免。当原始信号事有限长，截取的长度等于原始信号的长度，则可以不考虑 泄露的影响。当原始的非周期信号为无限长或比较长，而截取的长度有限或不等于原始信号的长度，则需考虑频谱泄露引起的 不良影响。 为了减少泄露的影响，一般可适当增加长度To，也可以通过试探法，先取长度N1（To=N1*T），然后取N2=2*N1,进行运算。 若两者计算的结果很接近，则可取N1作为截取长度，否则继续去N3=2*N2,直至相邻两个长度的n x(n)?0.8u(n) 为计算结果相近，取长度较小的N为好。本题中，因为信号离散非周期信号，且为无限长的信号，用试探法：取n为30和60， 进行比较，发现两者的频谱基本相似，所以取n为30较好。因为n取过大，fs提高，要求存贮单元增加，硬件速度提高，其结果 势必在经济上和技术上带来新的问题。 3.有限长脉冲序列，利用FFT分析其频 谱。],50,1332?nx()[,,,?N=6;n=0:N-1;x=[2,3,3,1,0,5]; subplot(3,1,1);stem(n,x);title('朱艺星杨婕婕'); subplot(3,1,2);w=n;plot(w,abs(fftshift(fft(x)))); subplot(3,1,3);plot(w,angle(fftshift(fft(x)))); 读书破万卷下笔如有神
解：由零极点图知系统函数：
2004级自动化专业信号与系统期末考试参考答案与评分标准一、填空题（每空2分，共20分）1．非线性 时变 因果 稳定2．离散性 谐波性 收敛性3．)()(0t t k t h -=δ 0)()()(ωωϕωωj j j Ke e e H -==j H4．)()(11nT t f t f n T -∑+∞-∞=或二、计算题1．解：)()(00)()(t t t t t t δδδδ'-='-+='+2．解：5|)243()1()122(1223=-+-=-'+-+=+∞∞-⎰t t t dt t t t t δ 3．解：令11)()1(1+-=+-s e s F S 因为)1()(1--⇔--t t se Sεε 所以)()]1()([11)(1)1(1t f e t t s e s F t S =--⇔+-=-+-εε S e s F s F 211)()(--=+---+--=∴---)]3()2([)]1()([)()2(t t e t t e t f t t εεεε4．解： )3)(2)(1(12611612)(232323++++++=++++++=s s s s s s s s s s s s s F 6116)595(1)(232+++++-+=s s s s s s F 56116)595(lim )(lim )0(2320-=+++++-==∞→→++s s s s s s t f f s t 0)(lim )(lim )(0===∞→∞→s F s t f f s t 三、综合题：1．解：如图所示：2．解：(1)此题用戴维南定理求U2(s)U0C(s)=E(s)/2; R0=6Ω. 故有：)(205.02)(3.063.0)(2s E s s s E s s s U +=⋅+= (2分) 20105.0205.0)()()(2+-=+==s s s s E s U s H …………………………………………………. (2分) )(10)(5.0)(20t et t h t εδ--=∴冲激响应为…………………………………………...…... (3分) 205.01205.0)()(2+=⋅+==s s s s s U s R ε…………………………………… . )(5.0)(20t e t r t εε-=∴阶跃响应为 …………………………………………………....…(3分)(2) )1()()(1-+=t t t e εε………………… ……………………………………(2分) )1(5.0)(5.0)1()()()1(20202--=--=∴---t e t e t r t r t u t t εεεε… ………………. .(2分)（3）)1()1()()1()(2--+-=t t t t t e εε………………. .(1分))1(11111)(2222s s e s s e ss s s E ----=+-=∴………………. .(2分) )20()1(5.0205.0)1(11205.0)()()(222+--+=⎥⎦⎤⎢⎣⎡--⋅+==--s s e s e s s s s s E s H s U s s …… .(1分) )1()1(401)()211(401)()1(20202--+--=∴---t e t e t u t t εε………………. .(2分) 3．解：由零极点图：3466)53)(53(6)(2+++=++-++=s s s K j s j s s K s Z …………. .(2分)-15 24 -24 15 ω0 -6 -9 69由Z(0)=3, 得K=17。
2004级自动化专业信号与系统期末考试参考答案与评分标...
2004级自动化专业信号与系统期末考试参考答案与评分标准一、填空题（每空2分，共20分）1．非线性 时变 因果 稳定2．离散性 谐波性 收敛性3．)()(0t t k t h -=δ 0)()()(ωωϕωωj j j Ke e e H -==j H4．)()(11nT t f t f n T -∑+∞-∞=或二、计算题 1．解：)()(00)()(t t t t t t δδδδ'-='-+='+2．解：5|)243()1()122(1223=-+-=-'+-+=+∞∞-⎰t t t dt t t t t δ 3．解：令11)()1(1+-=+-s e s F S 因为)1()(1--⇔--t t se Sεε 所以)()]1()([11)(1)1(1t f e t t s e s F t S =--⇔+-=-+-εε S e s F s F 211)()(--=+---+--=∴---)]3()2([)]1()([)()2(t t e t t e t f t t εεεε4．解： )3)(2)(1(12611612)(232323++++++=++++++=s s s s s s s s s s s s s F 6116)595(1)(232+++++-+=s s s s s s F 56116)595(lim )(lim )0(2320-=+++++-==∞→→++s s s s s s t f f s t 0)(lim )(lim )(0===∞→∞→s F s t f f s t 三、综合题：1．解：如图所示：2．解：(1)此题用戴维南定理求U2(s)U0C(s)=E(s)/2; R0=6Ω. 故有： )(205.02)(3.063.0)(2s E s s s E s s s U +=⋅+= (2分) 20105.0205.0)()()(2+-=+==s s s s E s U s H …………………………………………………. (2分) )(10)(5.0)(20t et t h t εδ--=∴冲激响应为…………………………………………...…... (3分) 205.01205.0)()(2+=⋅+==s s s s s U s R ε…………………………………… . )(5.0)(20t e t r t εε-=∴阶跃响应为 …………………………………………………....…(3分)(2) )1()()(1-+=t t t e εε………………… ……………………………………(2分) )1(5.0)(5.0)1()()()1(20202--=--=∴---t e t e t r t r t u t t εεεε… ………………. .(2分)（3）)1()1()()1()(2--+-=t t t t t e εε………………. .(1分))1(11111)(2222s s e s s e ss s s E ----=+-=∴………………. .(2分) )20()1(5.0205.0)1(11205.0)()()(222+--+=⎥⎦⎤⎢⎣⎡--⋅+==--s s e s e s s s s s E s H s U s s …… .(1分) )1()1(401)()211(401)()1(20202--+--=∴---t e t e t u t t εε………………. .(2分) 3．解：由零极点图：3466)53)(53(6)(2+++=++-++=s s s K j s j s s K s Z …………. .(2分)-15 24 -24 15 ω0-6-99由Z(0)=3, 得K=17。
信号与系统期末考试试题有标准答案的.doc
信 号与系统 期 末 考 试 试 题一、选择题（共10 题，每题 3 分 ，共30 分，每题给出四个答案，其中只有一个正确的）1、 卷积 f 1(k+5)*f2 (k-3)等于。
（ A ） f 1 (k)*f 2(k)（ B ） f 1(k)*f 2(k-8) （ C ） f 1(k)*f 2 (k+8) （D ） f 1(k+3)*f 2 (k-3)2、 积分(t 2) (1 2t )dt 等于。
（ A ）（ B ）（ C ） 3（ D ） 53、 序列 f(k)=-u(-k) 的 z 变换等于。
（ A ）z z （ B ） - z （ C ） 1 （ D ） 11 z 1 z 1z 14、 若 y(t)=f(t)*h(t), 则 f(2t)*h(2t) 等于。
（ A ）1y( 2t ) （ B ） 1 y(2t ) （ C ） 1 y( 4t ) （ D ） 1 y(4t)4 2 4 25、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+(t ) ,当输入 f(t)=3e — t u(t) 时，系统的零状态响应 y f (t) 等于（A ） (-9e -t +12e -2t )u(t)（ B ）(3-9e -t +12e -2t )u(t)（C ） (t) +(-6e -t +8e -2t )u(t)（D ）3 (t )+(-9e -t +12e -2t)u(t) 6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （ C ）离散性、周期性（D ）离散性、收敛性7、 周期序列 2COS (1.5 k 45 0 ) 的 周期 N 等于（A ） 1（ B ）2（ C ）3（D ）48、序列和k 1 等于k（ A ） 1 (B) ∞ (C)u k 1 (D) ku k19、单边拉普拉斯变换 F s2s 1e 2s 的愿函数等于s 210、信号 f tte 3t u t 2 的单边拉氏变换 F s 等于二、填空题（共 9 小题，每空 3 分，共 30 分）1、卷积和 [ （）k+1u(k+1)]* (1 k) =________________________、单边 z 变换 F(z)= z 的原序列 f(k)=______________________2 2z 1s、已知函数f(t) 的单边拉普拉斯变换F(s)=，则函数 y(t)=3e-2t ·f(3t)的单边拉普3s 1拉斯变换 Y(s)=_________________________4、频谱函数 F(j )=2u(1-)的傅里叶逆变换 f(t)=__________________5、单边拉普拉斯变换 F (s)s23s 1的原函数 f(t)=__________________________s 2s6、已知某离散系统的差分方程为 2y(k) y(k 1) y(k 2)f (k ) 2 f ( k 1) ，则系统的单位序列响应 h(k)=_______________________ 7、已知信号 f(t) 的单边拉氏变换是 F(s),则信号 y(t )t 2f ( x)dx 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为该系统的冲激响应 h(t)=9、 写出拉氏变换的结果 66u t， 22t k三、 （ 8 分）四、（ 10 分）如图所示信号f t，其傅里叶变换F jw F f t ，求（ 1） F 0 （ 2）F jw dw六、（ 10 分）某 LTI系统的系统函数H ss 2，已知初始状态y 00, y2, 激s 2 2s1励 f tu t , 求该系统的完全响应。
信号与系统期末考试6(含答案)
101G06A信号与系统一、已知某连续时不变系统的微分方程为)(14)(10)(2)(6)(5)(2222t e dt t de dt t e d t y dt t dy dt t y d ++=++。
（14分） ⑴ 求该系统的系统函数H (s )和单位冲激响应h (t )； ⑵绘出该系统的仿真框图(要求用尽量少的积分器)。
二、求下列信号的傅里叶变换。
（10分）⑴()()10()sin t f t e t u t αω-=⋅⋅，用傅里叶变换性质计算 ⑵()()20()sin f t t u t ω=⋅，用拉氏变换与傅氏变换的关系计算101G06A信号与系统三、如图所示的因果反馈系统，问K 取何值时系统稳定？（10分）四、某线性时不变连续系统，具有两个初始条件，分别为r 1(0)和r 2(0)。
（12分）⑴ 当r 1(0)=1, r 2(0)=0时，其响应为：()()2tte eu t --+⑵ 当r 1(0)=0, r 2(0)=1时，其响应为())(22t u e e t t --+； ⑶ 当r 1(0)=1, r 2(0)=-1，输入为e (t )时，其响应为：()()2teu t -+。
试求：当1(0)r =3, r 2(0)=2，输入为2e (t )时，其响应为多少？101G06A信号与系统五、设有二阶系统方程)()()(11)(2)(22t e dt t de t y dt t dy dtt y d +=++，试求其稳态响应)(3sin 5)(t tu t y =所对应的激励信号e (t )。
（10分）六、已知一线性时不变系统的单位样值响应)(n h 除在10N n N ≤≤区间之外都为零。
而输入)(n x 除在32N n N ≤≤区间之外均为零。
这样，响应)(n y 除在54N n N ≤≤区间之外均被限制为零。
试用N 0，N 1，N 2，N 3，来表示N 4与N 5。
(8分)七、设有差分方程()()()312(2)y n y n y n f n +-+-=，已知()()10.5,2 1.25y y -=--=，)()(n u n f =。
信号与线性系统分析试卷
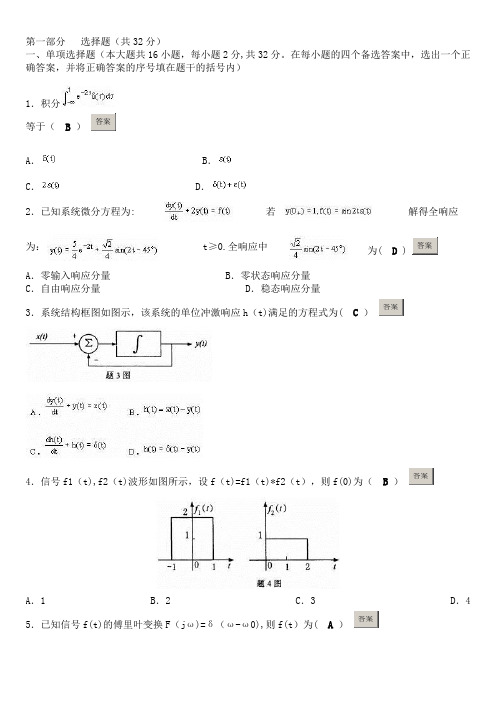
第一部分选择题（共32分）一、单项选择题（本大题共16小题，每小题2分,共32分。
在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内）1．积分等于（B）答案A． B．C． D．2．已知系统微分方程为: 若解得全响应为：t≥0.全响应中为( D ) 答案A．零输入响应分量 B．零状态响应分量C．自由响应分量 D．稳态响应分量3．系统结构框图如图示，该系统的单位冲激响应h（t)满足的方程式为( C）答案4．信号f1（t),f2（t)波形如图所示，设f（t)=f1（t)*f2（t），则f(0)为（B）答案A．1 B．2 C．3 D．4 5．已知信号f(t)的傅里叶变换F（jω)=δ（ω-ω0),则f(t）为( A）答案6．已知信号f（t）如图所示，则其傅里叶变换为（C）答案7．f（t）=ε(t）-ε(t—1)的拉氏变换为（A）答案8. 的拉氏反变换为（D）答案9．图（a）中ab段电路是某复杂电路的一部分，其中电感L和电容C都含有初始状态，请在图(b）中选出该电路的复频域模型。
（B ) 答案10．离散信号f(n)是指（B）答案A．n的取值是连续的，而f（n)的取值是任意的信号B．n的取值是离散的，而f(n)的取值是任意的信号C．n的取值是连续的，而f(n)的取值是连续的信号D．n的取值是连续的,而f（n）的取值是离散的信号11．若序列f（n）的图形如图(a)所示,那么f（—n+1）的图形为图(b)中的( D）答案12．差分方程的齐次解为，特解为，那么系统的稳态响应为( B ) 答案13．已知离散系统的单位序列响应和系统输入如图所示，f（n)作用于系统引起的零状态响应为,那么序列不为零的点数为（C）答案A．3个 B．4个C．5个 D．6个第二部分非选题（共68分）二、填空题(本大题共9小题，每小题2分，共18分）14．=（)。
答案15．GLC并联电路发生谐振时，电容上电流的幅值是电流源幅值的（Q）倍。
信号与系统信号与线性系统期末考试试卷
信号与系统信号与线性系统期末考试试卷1、已知某连续信号()f t 的傅⾥叶变换为21()23F j j ωωω=-+，按照取样间隔1T =对其进⾏取样得到离散时间序列()f k ，序列()f k 的Z 变换。
解法⼀：f(t)的拉普拉斯变换为2111)2)(1(1321)(2+-+=++=++=s s s s ss s F ，2111)(Re )(--===---=-=?-=∑∑e z z e z z e z z K e z z s F s z F ni T s i s s ni sT i i解法⼆：f(t)=L -1{F(jw)}=(e -t - e -2t)ε(t)f(k)= (e -k - e-2k)ε(k)=)())()((21k e ekk ε---F(z)=Z[f(k)]= 21-----ez zez z2、求序列{}10()1,2,1k f k ==和2()1cos ()2f k k k πε??=+的卷积和。
解：f 1(k)={1,2,1}=δ(k)+2δ(k -1)+ δ(k -2)f 1(k)* f 2(k)= f 2(k)+ 2f 2(k -1)+ f 2(k -2)3、已知某双边序列的Z 变换为21()1092F z z z =++，求该序列的时域表达式()f k 。
解：5.014.01)(+-+=z z z F ，两个单阶极点为-0.4、-0.5 当收敛域为|z|>0.5时，f(k)=(( -0.4)k -1-( -0.5)k -1)ε(k -1)当收敛域为0.4<|z|<0.5时，f(k)= ( -0.4)k -1ε(k -1)+( -0.5)k -1ε( -k)当收敛域为|z|<0.4时，f(k)= - ( -0.4)k -1ε(-k)+( -0.5)k -1ε( -k)点评：此题应对收敛域分别讨论，很多学⽣只写出第⼀步答案，即只考虑单边序列。
信号与系统期末考试试卷(有详细答案).doc
格式《信号与系统》考试试卷（时间 120 分钟）院 / 系专业姓名学号题号一二三四五六七总分得分一、填空题（每小题 2 分，共 20 分）得分1．系统的激励是 e(t) ，响应为 r(t) ，若满足de(t)r ( t) ，则该系统为线性、时不变、因果。
dt（是否线性、时不变、因果？）2 的值为 5。
2．求积分 (t1)(t2)dt3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。
4．若信号f(t)的最高频率是2kHz，则 f(2t)的乃奎斯特抽样频率为8kHz。
5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为 _一过原点的直线（群时延）。
6．系统阶跃响应的上升时间和系统的截止频率成反比。
．若信号的F(s)=3s j37。
，求该信号的 F ( j)(s+4)(s+2) (j+4)(j+2)8．为使LTI 连续系统是稳定的，其系统函数H(s ) 的极点必须在S 平面的左半平面。
1。
9．已知信号的频谱函数是0）(）F(( ，则其时间信号f(t)为0j)sin(t)js110．若信号 f(t)的F ( s ) ，则其初始值f(0)1。
2(s1 )得分二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。
（每小题 2 分，共 10 分）《信号与系统》试卷第1页共 7页专业资料整理格式1.单位冲激函数总是满足 ( t )( t ) （√）2.满足绝对可积条件 f ( t ) dt 的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。
（×）3.非周期信号的脉冲宽度越小，其频带宽度越宽。
（√）4.连续 LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。
（√）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。
（×）得分三、计算分析题（1、 3、 4、 5 题每题 10 分， 2 题 5 分，6 题15 分，共 60 分）t 10t11.信号f(t)2eu(t) ，1，信号 f ，试求 f 1 (t)*f 2 (t)。
信号与线性系统分析试题及答案(10套)
标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。
3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。
4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。
5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。
信号与线性系统分析复习题及答案
信号与线性系统复习题单项选择题;1. 已知序列3()cos()5f k k π=为周期序列,其周期为 C A ． 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 B图题2A ．()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+-3.已知sin()()()t f t t dt t πδ∞-∞=⎰,其值是 AA ．π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 AA ． 1 B. 2 C. 3 D. 45.为了使信号无失真传输,系统的频率响应函数应为 D A ． ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 B A ．13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 AA ．0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ,则(3)f t +的傅里叶变换为 C A ．()jwF jw e B. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f kεα=,)2()(-=k k h δ,则()()f k h k *的值为 BA ．)1(1--k k εαB. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα10.连续时间系统的零输入响应的“零”是指 A A. 激励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列kjek f 3)(π=为周期序列,其周期为A ． 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为A ．)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ,则 12()()f t f t *的值是 A ．)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(,则其对应的原函数为A ．)(t δ B. )('t δ C. )(''t δ D. )('''t δ15.连续因果系统的充分必要条件是 A ． 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为A ．1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=,则其单位冲激响应()h t 为A ．)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ,则)5(t f 的拉普拉斯变换为tA ．)5(s F B. )5(31s F C. )5(51s F D. )5(71s F 19.已知)2()(2-=-k k f k εα,)2()(-=k k h δ,则()()f k h k *的值为A ．)1(1--k k εα B. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为 A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 下列微分或差分方程所描述的系统是时变系统的是 A ． )(2)()(2)(''t f t f t y t y -=+B. )()(sin )('t f t ty t y =+C. )()]([)(2't f t y t y =+D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==,则)()(21t f t f *的值是 A ．)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 A ．ωj 1 B. ωj 2 C. ωj 3 D. ωj 424.连续系统是稳定系统的充分必要条件是 A ． M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ,则原函数)(t f 的初值为A ． 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ,则该系统的单位冲激响应为 A ．)(t e tε- B.)(2t e tε- C.)(3t e tε- D. )(4t e tε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα,则)()(k h k f *的值为A ．)(k kεα B.)1(1--k k εα C.)2(2--k k εα D. )3(3--k k εα28. 系统的零输入响应是指 A.系统无激励信号 B. 系统的初始状态为零C. 系统的激励为零,仅由系统的初始状态引起的响应D. 系统的初始状态为零,仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中A ．只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形,则)2(t f 的波形为 A ．将()f t 以原点为基准,沿横轴压缩到原来的12B. 将()f t 以原点为基准,沿横轴展宽到原来的2倍C. 将()f t 以原点为基准,沿横轴压缩到原来的14D. 将()f t 以原点为基准,沿横轴展宽到原来的4倍 填空题1. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________;2.()(2)t e t t dt δ∞--∞++=⎰____________________________;3.当LTI 离散系统的激励为单位阶跃序列()k ε时,系统的零状态响应称为_________________;4.已知函数4()23F s s =+,其拉普拉斯逆变换为____________________; 5.函数()f t 的傅里叶变换存在的充分条件是________________________;6. 已知11()10.5X z z -=+(0.5)z >,则其逆变换()x n 的值是______________;7.系统函数(1)(1)()1()2z z H z z -+=-的极点是___________________________;8.已知()f t 的拉普拉斯变换为()F s ,则00()()f t t t t ε--的拉普拉斯变换为_________________; 9.如果系统的幅频响应()H jw 对所有的ω均为常数,则称该系统为__________________________; 10. 已知信号)(t f ,则其傅里叶变换的公式为______________; 11. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________; 12.()(2)t e t t dt δ∞--∞++=⎰____________________________;13.当LTI 离散系统的激励为单位阶跃序列()k ε时,系统的零状态响应称为_________________;14.已知函数4()23F s s =+,其拉普拉斯逆变换为____________________; 15.函数()f t 的傅里叶变换存在的充分条件是________________________;16. 已知11()10.5X z z-=+(0.5)z >,则其逆变换()x n 的值是______________; 17.系统函数(1)(1)()1()2z z H z z -+=-的极点是___________________________;18.已知()f t 的拉普拉斯变换为()F s ,则00()()f t t t t ε--的拉普拉斯变换为_________________; 19.如果系统的幅频响应()H jw 对所有的ω均为常数,则称该系统为__________________________; 20. 已知信号)(t f ,则其傅里叶变换的公式为______________; 21.)(63t e tε-的单边拉普拉斯变换为_________________________;22.=-⎰∞∞-dt t t t f )()(0δ ____________________________;23.)(5t δ的频谱函数为______________________;24.一个LTI 连续时间系统,当其初始状态为零,输入为单位阶跃函数所引起的响应称为__________响应; 25.序列)()21()(k k f kε=的z 变换为___________________________;26.时间和幅值均为______________的信号称为数字信号; 27.系统函数)6.0)(4.0()1()(+-+=z z z z z H 的极点是___________________________;28.LTI 系统的全响应可分为自由响应和__________________;29. 函数)(1t f 和)(2t f 的卷积积分运算=*)()(21t f t f _______________________; 30. 已知函数23)(+=s s F ,其拉普拉斯逆变换为____________________; 简答题．;1．简述根据数学模型的不同,系统常用的几种分类;2．简述稳定系统的概念及连续时间系统时域稳定的充分必要条件; 3．简述单边拉普拉斯变换及其收敛域的定义; 4．简述时域取样定理的内容; 5.简述系统的时不变性和时变性; 6.简述频域取样定理;7.简述-0时刻系统状态的含义;8. 简述信号拉普拉斯变换的终值定理;9.简述LTI 连续系统微分方程经典解的求解过程; 10.简述傅里叶变换的卷积定理;11.简述LTI 离散系统差分方程的经典解的求解过程;12.简述信号z 变换的终值定理;13.简述全通系统及全通函数的定义; 14.简述LTI 系统的特点; 15.简述信号的基本运算 计算题1.描述离散系统的差分方程为1)1(,0)1(9.0)(=-=--y k y k y ,利用z 变换的方法求解)(k y ; 2．描述某LTI 系统的微分方程为)(3)()(3)(4)(''''t f t f t y t y t y -=++ ,求其冲激响应)(t h ;3．给定微分方程 )(3)()(2)(3)(''''t f t f t y t y t y +=++,1)0(),()(==-y t t f ε,2)0('=-y ,求其零输入响应;4．已知某LTI 离散系统的差分方程为),()1(2)(k f k y k y =--)(2)(k k f ε=, y-1=-1,求其零状态响应;5．当输入)()(k k f ε=时,某LTI 离散系统的零状态响应为)(])5.1()5.0(2[)(k k y k k zs ε-+-=,求其系统函数;6．描述某LTI 系统的方程为),(3)()(3)(4)(''''t f t f t y t y t y -=++求其冲激响应)(t h ;7．描述离散系统的差分方程为 )1()(2)2(43)1()(--=---+k f k f k y k y k y ,,求系统函数和零、极点; 8． 已知系统的微分方程为)()(3)(4)('''t f t y t y t y =++,1)0()0('==--y y )()(t t f ε=,求其零状态响应;9．用z 变换法求解方程2)1(),(1.0)1(9.0)(=-=--y k k y k y ε的全解10．已知描述某系统的微分方程)(4)()(6)(5)(''''t f t f t y t y t y +=++,求该系统的频率响应).(jw H11.已知某LTI 系统的阶跃响应)()1()(2t e t g tε--=,欲使系统的零状态响应)()1()(22t te e t y t t zs ε--+-=,求系统的输入信号)(t f ;12.利用傅里叶变换的延时和线性性质门函数的频谱可利用已知结果,求解下列信号的频谱函数;13.若描述某系统的微分方程和初始状态为 )(4)(2)(4)(5)(''''t f t f t y t y t y -=++5)0(,1)0('==--y y ,求系统的零输入响应;14.描述离散系统的差分方程为 )2()()2(21)1()(--=-+--k f k f k y k y k y , 求系统函数和零、极点;15.若描述某系统的差分方程为)()2(2)1(3)(k k y k y k y ε=-+-+,已知初始条件5.0)2(,0)1(=-=-y y ,利用z 变换法,求方程的全解;信号与线性系统分析复习题答案单项选择题1. C2.B3.A4.A5.D6.B 7 .A 8.C 9.B 10.A 11. C 12.A 13. D 14.B 15.B 16. D17. A 18.C 19. D 20.C 21.B 22.C 23. B 24.A 25.B 26.C 27. D 28.C 29. B 30. B填空题1. 22. 22e - 3. 单位阶跃响应/阶跃响应 4. )(223t et ε- 5.()f t dt ∞-∞<∞⎰6.)()5.0(k k ε- 7.128. 0()st F s e - 9. 全通系统 10. dt e t f jw F jwt⎰∞∞--=)()( 11.卷积和 12. 1 13.)()(d t t kf t y -= 14. )()()()(3121t f t f t f t f *+* 15.齐次解和特解16. 系统函数分子 17. 2 18.63-z z 19.)(2w πδ 20.齐次 21.36+s 22.)(0t f - 23. 5 24. 单位阶跃响应 25. 122-z z26. 离散 27. 0.4,-0.6 28. 强迫响应 29.τττd t f f )()(21-⎰∞∞- 30. )(32t e t ε-简答题1．答：1加法运算,信号1()f ⋅与 2()f ⋅之和是指同一瞬时两信号之值对应相加所构成的“和信号”,即12()()()f f f ⋅=⋅+⋅2乘法运算,信号1()f ⋅与 2()f ⋅之积是指同一瞬时两信号之值对应相乘所构成的“积信号”,即12()()()f f f ⋅=⋅⋅3反转运算：将信号()f t 或()f k 中的自变量t 或k 换为t -或k -,其几何含义是将信号()f ⋅以纵坐标为轴反转;4平移运算：对于连续信号()f t ,若有常数00t >,延时信号0()f t t -是将原信号沿t 轴正方向平移0t 时间,而0()f t t +是将原信号沿t 轴负方向平移0t 时间；对于离散信号()f k ,若有整常数00k >,延时信号0()f k k -是将原序列沿k 轴正方向平移0k 单位,而0()f k k +是将原序列沿k 轴负方向平移0k 单位; 5尺度变换：将信号横坐标的尺寸展宽或压缩,如信号()f t 变换为()f at ,若1a >,则信号()f at 将原信号()f t 以原点为基准,将横轴压缩到原来的1a倍,若01a <<,则()f at 表示将()f t 沿横轴展宽至1a 倍2．答：根据数学模型的不同,系统可分为4种类型. 即时系统与动态系统； 连续系统与离散系统； 线性系统与非线性系统 时变系统与时不变系统3．答：1一个系统连续的或离散的如果对任意的有界输入,其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统;2连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰4．信号的单边拉普拉斯正变换为：dt e t f s F st ⎰∞-=)()(逆变换为：ds e s F j t f jwjwst ⎰+-=δδπ)(21)(收敛域为：在s 平面上,能使0)(lim =-∞→tt et f δ满足和成立的δ的取值范围或区域,称为)(t f 或)(s F 的收敛域;5．答：一个频谱受限的信号)(t f ,如果频谱只占据m m w w ~-的范围,则信号)(t f 可以用等间隔的抽样值唯一表示;而抽样间隔必须不大于mf 21m m f w π2=,或者说,最低抽样频率为m f 2; 6.答：如果系统的参数都是常数,它们不随时间变化,则称该系统为时不变或非时变系统或常参量系统,否则称为时变系统; 描述线性时不变系统的数学模型是常系数线性微分方程或差分方程,而描述线性时变系统的数学模型是变系数线性微分或差分方程;7．答：一个在时域区间),(m m t t -以外为零的有限时间信号)(t f 的频谱函数)(jw F ,可唯一地由其在均匀间隔)21(m s s t f f <上的样点值)(s jnw F 确定;)()()(ππn wt Sa t n j F jw F m n m -=∑∞-∞=,sm f t 21=8．答：在系统分析中,一般认为输入)(t f 是在0=t 接入系统的;在-=0t 时,激励尚未接入,因而响应及其导数在该时刻的值)0()(-j y与激励无关,它们为求得0>t 时的响应)(t y 提供了以往的历史的全部信息,故-=0t 时刻的值为初始状态;9．答：若)(t f 及其导数dt t df )(可以进行拉氏变换,)(t f 的变换式为)(s F ,而且)(lim t f t ∞→存在,则信号)(t f 的终值为)(lim )(0lim s sF t f s t →∞→=;终值定理的条件是：仅当)(s sF 在s 平面的虚轴上及其右边都为解析时原点除外,终值定理才可用;10.答：1列写特征方程,根据特征方程得到特征根,根据特征根得到齐次解的表达式 2 根据激励函数的形式,设特解函数的形式,将特解代入原微分方程,求出待定系数得到特解的具体值. 3 得到微分方程全解的表达式, 代入初值,求出待定系数 4 得到微分方程的全解11.答：1时域卷积定理:若)()(),()(2211ωωj F t f j F t f ↔↔,则)()()()(2121ωωj F j F t f t f ↔* 2 频域卷积定理:若)()(),()(2211ωωj F t f j F t f ↔↔,则)()(21)()(2121ωωπj F j F t f t f *↔12..答：1列写特征方程,得到特征根,根据特征根得到齐次解的表达式 2 根据激励函数的形式,设特解的形式,将特解代入原差分方程,求出待定系数, 得到特解的具体值. 3 得到差分方程全解的表达式, 代入初始条件,求出待定系数, 4 得到差分方程的全解 13.答：终值定理适用于右边序列,可以由象函数直接求得序列的终值,而不必求得原序列;如果序列在M k < 时,0)(=k f ,设∞<<↔z z F k f α),()(且10<≤α,则序列的终值为)(1lim)(lim )(1z F zz k f f z k -==∞→∞→或写为)()1(lim )(1z F z f z -=∞→上式中是取1→z 的极限,因此终值定理要求1=z 在收敛域内10<≤α,这时)(lim k f k ∞→存在;14.答 全通系统是指如果系统的幅频响应)(jw H 对所有的w 均为常数,则该系统为全通系统,其相应的系统函数称为全通函数;凡极点位于左半开平面,零点位于右半开平面,且所有的零点与极点为一一镜像对称于jw 轴的系统函数即为全通函数;15.答：当系统的输入激励增大α 倍时,由其产生的响应也增大α倍,则称该系统是齐次的或均匀的；若两个激励之和的响应等于各个激励所引起的响应之和,则称该系统是可加的;如果系统既满足齐次性又满足可加性,则称系统是线性的；如果系统的参数都是常数,它们不随时间变化,则称该系统为时不变系统或常参量系统;同时满足线性和时不变的系统就称为线性时不变系统LTI 系统;描述线性时不变系统的数学模型是常系数线性微分差分方程;线性时不变系统还具有微分特性;计算题1解：令)()(z Y k y ↔,对差分方程取z 变换,得 0)]1()([9.0)(1=-+--y z Y z z Y将1)1(=-y 代入上式并整理,可得 9.09.09.019.0)(1-=-=-z zz z Y 取逆变换得 )()9.0()(1k k y k ε+=2．解：令零状态响应的象函数为)(s Y zs ,对方程取拉普拉斯变换得：)(3)()(3)(4)(2s F s sF s Y s sY s Y s zs zs zs -=++于是系统函数为343)()()(2++-==s s s s F s Y s H zs )()23()(3t e e t h t t ε---=3.系统的特征方程为0232=++λλ特征根为：1,221-=-=λλ 所以,零输入响应为t zi tzi zi e C e C t y --+=221)(所以：22)0(1)0(21'21=--==+=++zi zi zi zi zi zi C C y C C y故：4321=-=zi zi C C所以：t t zi e e t y --+-=43)(24.解：零状态响应满足：2)1(2)(=--k y k y zs zs ,且0)1(=-zs y 该方程的齐次解为：kzs C 2设特解为p,将特解代入原方程有：22=-p p从而解得2)(-=k y p所以22)(-=k zs zs C k y 将2)0(=zs y 代入上式,可解得4=zs C故,)()224()(k k y k zs ε-⋅=5．解：1)(-=z z z F )5.1)(5.0)(1()5.02()(2+--+=z z z z z z Y zs 75.05.02)()()(22-++==z z z z F z Y z H zs 6.解：令零状态响应的象函数为)(s Y zs ,对方程取拉普拉斯变换得：)(3)()(3)(4)(2s F s sF s Y s sY s Y s zs zs zs -=++ 系统函数为：3312)()()(+++-==s s s F s Y s H zs 故冲激响应为)()23()(3t e e t h t t ε---=7． 解：对差分方程取z 变换,设初始状态为零;则：)()2()()431(121z F z z Y z z ----=-+于是系统函数)21)(23()12()()()(-+-==z z z z z F z Y z H 其零点为21,021==ζζ, 极点为21.2321=-=p p 8． 解： 方程的齐次解为：t zs t zs e C e C 321--+方程的特解为：31 于是：31)(321++=--t zs t zs zs e C e C t y 031)0(21=++=+zs zs zs C C y 03)0(21'=--=+zs zs zs C C y得61,2121=-=zs zs C C 于是：)()312161()(3t e et y t t zs ε+-=--9． 解：令)()(z Y k y ↔,对差分方程取z 变换,得11.0)]1()([9.0)(1-=-+--z z y z Y z z Y 将2)1(=-y 代入上式,并整理得 )9.0)(1()8.19.1()(---=z z z z z Y )(])9.0(1[)(1k k y k ε++=10．解：令)()(),()(jw Y t y jw F t f ↔↔,对方程取傅里叶变换,得 )(4)()()(6)()(5)()(2jw F jw F jw jw Y jw Y jw jw Y jw +=++ 654)()()(2++-+==jw w jw jw F jw Y jw H 11. 解：)(2)()(2t e dtt dg t h t ε-==22)(+=s s H 2)2(43)(++=s s s s Y zs 2211)()()(++==s s s H s Y s F zs )()211()(2t e t f t ε-+= 12 解：)(t f 可看作两个时移后的门函数的叠合;)2()2()(22-++=t g t g t f因为)(2)(2w Sa t g ↔所以由延时性和线性性有： )2cos()(4)(2)(2)(22w w Sa e w Sa e w Sa jw F w j w j =+=- 13.解：特征方程为：0452=++λλ 4,121-=-=λλt zi t zi zi e C e C t y 421)(--+=t zi t zi zi e C e C t y 421'4)(----=令,0=t 将初始条件代入上式中,得1)0(21=+=+zi zi zi C C y 54)0(21'=--=+zi zi zi C C y 可得： 2,321-==zi zi C C0,23)(4≥-+=--t e e t y t t zi14.解：对差分方程取z 变换,设初始状态为零,则 )()1()()211(221z F z z Y z z ----=+- 211)()()(22+--==z z z z F z Y z H 其零点1,121-==ζζ；极点21212,1j p ±= 15. 解：令)()(z Y k y ↔,对差分方程取z 变换,得112111)]2()1()((2)]1()([3)(----+=-+-++-++zy y z z Y z y z Y z z Y)1)(23()(22-++=z z z z z Y )(])2(32)1(2161[)(k k y k k ε---+=。
信号与系统期末考试试卷(有详细答案)
《信号与系统》考试试卷（时间120 分钟）院/系专业姓名学号题号一二三四五六七总分得分一、填空题（每小题 2 分，共20 分）得分1．系统的激励是e(t ) ，响应为r( t ) ，若满足de( t )r(t ) ，则该系统为线性、时不变、因果。
dt（是否线性、时不变、因果？）2 的值为5 。
2．求积分( t 1) ( t 2 )dt3．当信号是脉冲信号f(t) 时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。
4．若信号f(t) 的最高频率是2kHz，则f( 2t) 的乃奎斯特抽样频率为8kHz 。
5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为_一过原点的直线（群时延）。
6．系统阶跃响应的上升时间和系统的截止频率成反比。
7．若信号的F(s)= 3s(s+4)(s+2) ，求该信号的F( j )j3(j +4)(j +2)。
8．为使LTI 连续系统是稳定的，其系统函数H ( s)的极点必须在S平面的左半平面。
19．已知信号的频谱函数是0）( ）F( ( ，则其时间信号f(t) 为0j ) sin( t)j。
10．若信号f(t) 的s 1F(s)，则其初始值 f ( 0 ) 1 。
2( s 1)得分二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。
（每小题 2 分，共10 分）《信号与系统》试卷第 1 页共7 页1. 单位冲激函数总是满足( t) ( t) （√）2. 满足绝对可积条件f(t)dt的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。
（×）3. 非周期信号的脉冲宽度越小，其频带宽度越宽。
（√）4. 连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。
（√）5. 所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。
（×）得分三、计算分析题（1、3、4、5 题每题10 分，2 题5 分，6 题15 分，共60 分）t1. 信号f ( t ) 2e u( t )1 ，信号1 0 t 1，f ，试求f1( t )* f2( t ) 。
信号与线性系统期末考试试题与答案
信号与系统期末考试试题6课程名称： 信号与系统一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。
（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。
（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=kt 22三、（8分）已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
[VIP专享]信号与系统期末试卷-含答案全
![[VIP专享]信号与系统期末试卷-含答案全](https://img.taocdn.com/s3/m/059203627375a417866f8ff1.png)
e(t1) (t 1) (t) e (t2) (t 2) (1 t) .
y(t) et (t) (1 t) ；则 f (t) (t 1) (t 2) 时，输出 y f (t) ＝
某因果线性非时变（LTI）系统，输入 f (t) (t) 时，输出为：
7.
4 3m
max
Tmax
Tmax 为
根据时 2) 取样时，其频谱不混迭的最大抽样间隔
m
3 4
m 2
m 4
max
int level(BinTreeNodlesevt}r*Beutsl,icnBt(rtrTuiontrcaoTetgtert,_eyapNnpetg)oy;oeN_pddinoeeodtd;fde*esreafc*ttrphsB*au{l)ti;cilrn/duh/tT;ciB/lr/tdo1eiTt;u1ea//NcnrNgoto_loiu(fdn(dtnbe*oetpivdlt{(roe(e}TbidpEititrcfrl(ero!-pbmu>tintrTvritgaey-l(>hlpbulteeie,rtrf=xdt)e,=apr{xkextta,)rt;ru{;k,kr)sd+n;tra+;u1t;ac}0txyBpieTNxv},ooidi{ndet&m*lkac)hi}nil(de)}l;s/e/ js+tr}+uj;cBf+BtoB.+Bid.r.L(;+adikTe+taanN=;t[agojB]e[tdkh=l.se+L+eA1e*+]nr.i;dfc=g(d.-[d;{aiB]1a/it;f/a.;t(dkaA[}ia[]>.kBtdB<}=a];aii.T[BLjt+;aNke.+d[Loni;-]aed-g>t)netahg,B[jt*]+h.)wBd+]{avhi;T=otilareiAedi[n(Be.i{dtm;.<Laive=etAoarngi.0[dLgie],e;jt2Ch=n(o{Sg-0ut9q1h,n/kAL])/t)/iL/[;2s1/e1AtA…aABBmf"…,.S(h+Bq"mniLT6m+irsnet8]e&mhBTen),amidn+dtn&a2Ot*acx(7o10u)n+t)0x{11*ixf=0( nT+o1)d*{ex2i_1f c(+(o!uT2/xn/-*10>tx+l2+cxh=1il;+dnx)o&2/d/h&e=tt_(pn!c:To0o//-duw>1enrw*_c2t/wchx-oi0.1ldu;xon)/)1c*t;cinx6o42.1ucleonfmtt+d/+5ap;t-a5//r7iLg9Cihs4ot8lNuet5nmof9ttdreLp4iegme.=h*ap3tMfAmBol(a[aTrTlit]ex(-;(><i2)nAlccetl[ha0i]}ise=l=ds1,0}A…Tc;[yoine2pu<-nT6ein=-yH>12tp)(]Te;v;enn[Co1-A-ti1o3m1d[u]nA)pHin-[/;in(tv-kL21]ene;]1reyais=A+)nef=[+(t-nm(k1Ta])eAT-p){y>nyA;r-p%c2eh…1iAld3e[2,1]3c,2e1oi20Vn0(u3e=bt×n4i{)n3t1a5)B0);,5b20A}{7,B(2ce[2a150,(l0)ds0cn(a20e,a)]×ie[13j1)1cnr2,a17Af2e0A4,i58g2jtB]b1u(B03}(a5r4,21[En)]06a1B;=07A51([}{0]b937S<A/3)56/HaL([06C0c,sT1b3)]uo[A.>81A0c5u,493]cBn<B0.]=taC5H[L8(0,A1De(4g]k/,Aa5>2EBef0,[)Fy,<]*4C[G)G]b[=2B1,,DHk)g+[]e>,I1AEJy,/[<(,81%C1c]-[8,a5bD1)]C>3C]B,D1<[D1]2Bd62,GFc3E>=41A,V5</1I5EdH475,Gf1231>01+0*J5,91<420G4+0e*30G241,7W1d+*787>13P031,4*9<1L74=41f=0+,515a24953>**/546,17<5+15=0g37413,2*0c5572>/4+517,5<6451*g524,0d+3>956,*5<0315f9+2,3e5W12>14P,12*<3L157g+=56,52f13053>105*693}64*1,{73+80217+9596510*77046873+1*71249264+*9503182+79012*176208590=*2092+8123169831731237*793}W2+531P352L5*0313173+s3T3125158*,21T2052=5,2…915W063…303P5,LTS Tini k1i(2i={a1b,2c,d…e…fg}S0)1,1k10in1i011k11k10n+1kk1Pn21>r+0ikm…00…11+1k0s1=0n11+n21K…ru…snkas1l ns,s=nk,nk a11a121a02K1)aru2s2kaa=2l203*:9(a1i+03/1jA2-03aB(3a131+Aa12=3B+42[…0+]3A…+a3aij1+n3inn149-+iH10-41au+jnfi84+fnm4+16a5B8n+58F1544):52=5706305306.986,2T76:0150,D811:00148110683171,F10ST6:06D413S024H515,1H12:007412101402H*1291u60+22f{f7m4*63a2+n58307*71836+21102*72306+722774*0674128+493}*()4+86*312=513219 5:13/5671(130+7822+6261+p03a1+341352+401143,41)p0=83,21a.8425,913,,p66331:121,0A1a24B13G,,CP4pJ9AD3KG21EHD12AFDaJ3GBH,EPaDHKBApGIBM3J2HEKIF1AJMCKCAEFCMFIIM
04级信号与系统期末考试试卷.doc
南昌大学2005〜2006学年第二学期期末考试试卷试卷编号：______ (B)卷课程编号：___________ 课程名称：信号与系统考试形式:闭卷适用班级：04级电子系各班姓名: _____________ 学号： _________ 班级：_______ 学院：信息工程学院专业: _____________________ 考试日期：________________考生注意事项：1、本试卷共匕页，请查看试卷屮是否有缺页或破损。
如有立即举手报告以便更换。
2、考试结束后，考生不得将试卷、答题纸和草稿纸带出考场。
一、填空题(每空2分，共20分)1、理想模拟低通滤波器为非因果物理上 __________ 的系统(填“不可实现”或“可实现” )o2、已知连续时间信号f(t)=S「(l()()；r/) + S“(50;z7),如果对f(t)进行取样，则奈奎斯特抽样频率£为____________ -3、已知某一因果信号，/⑴的拉普拉斯变换为FG),则/(/ + *))*%⑴，心＞0的拉氏变换为_______________ o4、如某一因果线性时不变系统为稳定系统，其单位序列响应为h{n),则£|/?(«)|应满//=()足________ 的条件。
5、若信号/⑴通过某线性时不变系统的零状态响应为y(t) =(K, t0为常数) 则该系统的频率响应H(jco) = ______________ ,单位冲激响应力⑴= ______________ - 56、J (z — 30(-2/ + 4)dr = _____________ 。
-57、连续时间信号/(/) = sin 2m的周期T= __________ ,若对/⑴以f s = \Hz进行抽样,所得离散序列f(n) ___________ ,该离散序列_________ 周期序列(填“是”或“不是”)。
选择题(每空2分，共20分)1、 离散时间信号x(n) = sin(——令)，则x(n)是( )A 、周期性信号，周期N=4B 、非周期性信号C 、周期性信号，周期N=0.8D 、周期性信号，周期N =271 2、 已知f(t),为求f(t ()-at),下列哪种运算顺序求得正确结果(式中t 。
《信号与系统》期末测验试题及答案(P)
《信号与系统》测验一、单项选择题 ................................................. 1 二、简答题 ..................................................... 4 三、计算题 .. (9)一、单项选择题1．设系统的初始状态为()0t x ，输入为()t f ，完全响应为()t y ，以下系统为线性系统的是 D 。
(A) ()()()[]t f t x t y lg 02∙= (B) ()()()t f t x t y 20+= (C) ()()()ττd f t x t y tt ⎰+=00 (D) ()()()()ττd f dtt df t x e t y tt t ⎰++=-00 2．一个矩形脉冲信号，当脉冲幅度提高一倍，脉冲宽度扩大一倍，则其频带宽度较原来频带宽度 A 。
（A ）缩小一倍 （B ） 扩大一倍 （C ） 不变 （D ）不能确定 3. 某系统的系统函数为)2)(5.0()(--=z z zz H ，若该系统是因果系统，则其收敛区为B 。
（A ）|z|<0.5 （B ）|z|>2 （C ）0.5<|z|<2 （D ）以上答案都不对 4. 下面关于离散信号的描述正确的是 B 。
(A) 有限个点上有非零值，其他点为零值的信号。
(B) 仅在离散时刻上有定义的信号。
(C) 在时间t 为整数的点上有非零值的信号。
(D) 信号的取值为规定的若干离散值的信号。
5．下列信号中为周期信号的是 D 。
t t t f 5s i n 3s i n)(1+= t t t f πc o s 2c o s )(2+=k k k f 2s i n 6s i n )(3ππ+= )(21)(4k k f kε⎪⎭⎫⎝⎛=()A )(1t f 和)(2t f ())(),(21t f t f c 和)(3k f())(2t f B 和)(3k f ())(1t f D 和)(3k f6. 连续周期信号的频谱具有 D 。
信号与系统期末考试试题有答案
信号与系统期末考试试题有答案信号与系统期末考试试题一、选择题（共10题，每题3分，共30分，每题给出四个答案，其中只有一个正确的）1、卷积f1(k+5)*f2(k-3)等于。
（A）f1(k)*f2(k)（B）f1(k)*f2(k-8)（C）f1(k)*f2(k+8)（D）f1(k+3)*f2(k-3)2、积分等于。
（A）1.25（B）2.5（C）3（D）53、序列f(k)=-u(-k)的z变换等于。
（A）（B）-（C）（D）4、若y(t)=f(t)*h(t),则f(2t)*h(2t)等于。
（A）（B）（C）（D）5、已知一个线性时不变系统的阶跃相应g(t)=2e-2tu(t)+,当输入f(t)=3e—tu(t)时，系统的零状态响应yf(t)等于（A）(-9e-t+12e-2t)u(t)（B）(3-9e-t+12e-2t)u(t)（C）+(-6e-t+8e-2t)u(t)（D）3+(-9e-t+12e-2t)u(t)6、连续周期信号的频谱具有（A）连续性、周期性（B）连续性、收敛性（C）离散性、周期性（D）离散性、收敛性7、周期序列2的周期N等于（A）1（B）2（C）3（D）48、序列和等于（A）1(B)∞(C)(D)9、单边拉普拉斯变换的愿函数等于10、信号的单边拉氏变换等于二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*=________________________2、单边z变换F(z)=的原序列f(k)=______________________3、已知函数f(t)的单边拉普拉斯变换F(s)=，则函数y(t)=3e-2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j)=2u(1-)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换的原函数f(t)=__________________________6、已知某离散系统的差分方程为，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为该系统的冲激响应h(t)=9、写出拉氏变换的结果，三、（8分）四、（10分）如图所示信号，其傅里叶变换，求（1）（2）六、（10分）某LTI系统的系统函数，已知初始状态激励求该系统的完全响应。
信号与线性系统分析试题2004——期末试卷
f1(t)
-2 1 3
s 1 x1 s 1
3 题19图 x2 -3 8
y1(t)
1 1
f2(t)
y2(t)
第0-11页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
（10分）20、已知一离散因果系统框图如题20图所示。 求：（1）系统函数H(z); （2）系统稳定时常量K的值取值范围； （3）当K = 0时，系统的输入f(k) = 1+ 5cos(0.5kπ)，求 系统的稳态响应yS(k)。
信号与系统 电子教案
2004期末考试试题 120 分钟
说明：（1）请将答卷全部写在本题册内（如某题不 够书写，可写在背面，并请在该题处注明）。在其它 纸张上的答卷内容一律无效。 （2）符号(t)、(k)分别为单位阶跃函数和单位 阶跃序列。LTI表示线性时不变。
Ⅰ、选择题（共10小题，每小题3分，共30分）
___ 3、设系统的初始状态为x(0)，各系统的全响应 y(· )与激励f (· )和初始状态的关系如下。下列系统为 线性系统的是 (A) y(t) = e
–t x(0)
i
i 0
+
t
cos(x) f ( x) d x
0
t
(B) y(t) = f (t) x(0) +
f ( x) d x
0
(C) y(k) = k x(0) + f (k) f (k–1)
第0-2页
■
(D) y(k) = e x(0) k + f (i )
i
k
©西安电子科技大学电路与系统教研中心
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X1(z)
∑
z 1
F(z)
0.5
X2(z)
∑
z 1
Y(z)
0.5
K
题20图
第0-12页
■
©西安电子科技大学电路与系统教研中心
___ 5、信号f (t)= e –2 t (t+1) 的傅里叶变换F (jω)等于
(A) e j 2
j 2
e j2
(B) j 2 (C)
e j
j 2
(D) e 2 j
j 2
第0-3页
■
©西安电子科技大学电路与系统教研中心
信号与系统 1 z
z 0.5 z 2
(A) (k) = k (i)
(B)
(k)
=
(k
i)
i0
i
(C) (k) = (–k) – (–k–1) (D) δ(k)= (k–1) – (k)
___ 3、设系统的初始状态为x(0)，各系统的全响应 y(·)与激励f (·)和初始状态的关系如下。下列系统为 线性系统的是
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
___ 4、信号f1(t)和f2(t)的波形如题4图所示，设
y(t)=f1(t)*f2(t)，则y(4)等于
f1(t)
f2(t)
(A) 2 (B) 3 (C) 4 (D) 5
2 -1 0 2
2 1
4 t 0 123 t
? 4?
(C) –(0.5)k–1 (–k) + (–2) k (– k–1) (D) (0.5)k–1 (k–1) + (–2) k (– k–1)
第0-4页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
_则__电9容、C如等题于9图所示电路，其系统函数H(s)=UU12
(s) (s)
s 2，1s
1
(A) 0.5F (B) 1F (C) 2F (D) 3F
L
u1(t)
2Ω u2(t)
C
题9图
___ 10、已知某LTI连续因果系统的冲激响应h(t)满足 h(t) +3 h(t) = 2δ (t) +δ(t) ，则h(t)在t=0+时的初始值 h(0+)等于
(A) 0 (B) 5 (C) –5 (D) 2
每题给出四个答案，其中只有一个是正确的，请将正确答案的 标号（A或B或C或D）写在题号前的横线 上。
___ 1、积分
(1 2t) d t 等于
0
(A) 2 (B) 1 (C) 0.5 (D) 0
第0-1页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
___2、下列等式不成立的是
d
=d t
f(t)，试画
f(2t-1)
f (t)
g(t)
1
01
t
0
t
0 1 2t
题12图
第0-6页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
13、函数f (t) = 1 + sin(t) 的单边拉普拉斯变换
F(s) =
。
14、已知f(t)
=
e
jt
0
请你写出简明解题步骤；只有答案得0分。非通用符号请 注明含义。
（10分）16、某LTI因果连续系统，初始状态为x(0–)。 已知，当x(0–) =1，输入因果信号f1(t)时，全响应y1(t) = e – t + cos(πt)，t≥0；当x(0–) =2，输入因果信号f2(t)=3f1(t) 时，全响应y2(t) = –2e – t +3 cos(πt)，t≥0；求输入f3(t) = +2f1(t–1)时，系d 统df1t(t)的零状态响应y3zs(t)。
,,|否t |则1，其频谱函数F(jω) =
。
15、已知f1 (k) = {…0，5， 6， 7，0，…}，f2 (k) = {…，0，4， 5， 0，…}，则
f1 (k) *f2 (k) =
。
第0-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
Ⅲ、计算题（共5小题，50分）
信号与系统 电子教案
2004期末考试试题 120 分钟
说明：（1）请将答卷全部写在本题册内（如某题不 够书写，可写在背面，并请在该题处注明）。在其它 纸张上的答卷内容一律无效。
（2）符号(t)、(k)分别为单位阶跃函数和单位 阶跃序列。LTI表示线性时不变。
Ⅰ、选择题（共10小题，每小题3分，共30分）
电子教案
___ 6、信号f (t)= sin t
t
2004期末考试试题
的能量为
(A) 2 (B) (C) 2 (D) 22
___ 7、已知因果函数f (t)的象函数为F (s)，则e –3 t f (0.5t–1)的象函数为
(A) e–2s F (s+3)
(B) 2e–2(s+3) F(2s+6)
第0-8页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
（10分）17、周期信号 f(t) = 1 1 cos t 2 1 sin t
2 4 3 4 2 6
（1）试求该周期信号的基波周期T和基波角频率，
并画出它的单边振幅频谱图An~n和相位频谱图n~ n；
（2） 若该信号f(t)通过一理想低通滤波器
H(j)=
2 0
,| |1，求其响应y(t)。
,| | 1
第0-9页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
（10分）18、描述某因果系统输出y(t)与输入f(t)的微分 方程为
y(t) + 3 y (t) + 2y(t) = f (t) + 4 f(t) （1）已知f(t) = (t)，y(0–) = 0，y (0–) = 1， 求系统的零输入响应yzi(t)和零状态响应yzs1(t)；(t≥0) （2）画出该系统直接形式的信号流图； （3）若f(t) = (–t)，求系统的零状态响应yzs2(t)。(t>–∞)
(A) y(t) = e –t x(0) +
t
cos(x) f (x) d x
0
(B) y(t) = f (t) x(0) +
t
f (x) d x 0
(C) y(k) = k x(0) + f (k) f (k–1)
k
(D) y(k) = e x(0) k + f (i) i
第0-2页
(C) 2e–2(s+3)F (s+3) (D) 2e–(2s+3)F (2s+3)
___
8、已知象函数F(z) =
z
1 0.5
z
z
2，其收敛域包含单位园，
则原序列f(k)等于
(A) (0.5)k–1 (k–1) – (–2) k (k) (B) (0.5)k–1 (k–1) – (–2) k (– k–1)
第0-5页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
Ⅱ、填空题（共5小题，每小题4分，共20分）
请将你算得的正确答案写在各题所求的
上。
11、信号f(t)的傅里叶变换的定义式和序列f(k)的单边z
变换的定义式分别为
F(jω) =
； F(z) =
；
12、已知f(2t–1)波形如题12图所示，g(t) 出f (t)和g(t)的波形。
（2）试列出该系统的输出y1(t)与输入f1(t)、f2(t2
4
1
f1(t)
-2
s 1 x1
y1(t)
1
13
f2(t)
s 1 8
1
y2(t)
3
x2
-3
题19图
第0-11页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
（10分）20、已知一离散因果系统框图如题20图所示。 求：（1）系统函数H(z); （2）系统稳定时常量K的值取值范围； （3）当K = 0时，系统的输入f(k) = 1+ 5cos(0.5kπ)，求 系统的稳态响应yS(k)。
第0-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2004期末考试试题
（10分）19、题19图所示连续因果系统的信号流图，状
态变量x1(t)、x2(t)如图所标，f1(t)、f2(t)为输入，y1(t)、 y2(t)为输出。 （1）试列出该系统的状态方程与输出方程，并判断该
系统是否稳定？