2018年高考数学选择、填空题精华练习
最新-2018高考数学填空题型精选精练41 精品

2018高考数学填空题型精选精练1、过点()1,1总可以向圆22222280x y kx y k ++++-=作两条切线,则实数k 的取值范围为__________.2、已知圆()221:21C x y ++=,圆222:4770C x y x +--=,动圆P 与圆1C 外切,与圆2C 内切,则动圆圆心P 的轨迹方程是__________.3、已知椭圆()222210x y a b a b +=>>的中心为O ,右焦点为F 、右顶点为A ,右准线与x 轴交点为H ,则FAOH的最大值为__________.4、已知抛物线28y x =上一动点M ,圆22430x x y -++=上一动点N ,定点()5,4T 则线段,MN MT 之和的最小值为__________.5、已知函数()()321332m f x x x m x n =-+-+,若()f x 有6个不同的单调区间,则实数m 的取值范围为__________.6.执行以下语句后,打印纸上打印出的结果应是__________.7.在数轴上区间[]3,6-内,任取三个点,,A B C ,则它们的坐标满足不等式:()()0A B B C x x x x --<的概率为__________. 8.P 为抛物线24y x =上任意一点,P 在y 轴上的射影为Q ,点M (4,5),则PQ 与PM 长度之和的最小值为__________.9. 定义在R 上()f x 满足:(2)()1f x f x +=,当(0,2)x ∈时,()f x =1()2x ,则(2011)f =__________.10.过平面区域202020x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩内一点P 作圆22:1O x y +=的两条切线,切点分别为,A B ,记APB α∠=,则当α最小时cos α=__________.11.如图所示的数阵叫“莱布尼兹调和三角形”,他们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1(2)n n≥,每个数是它下一行左右相邻两数的和,如:111111111,,1222363412=+=+=+…,则第(3)n n ≥行第3个数字是__________.12. 已知正方形A B C D 的坐标分别是(1,0)-,(0,1),(1,0),(0,1)-,动点M 满足:12M B M D k k =- 则MA MC +=__________.13. “18a ≥”是“对∀正实数x ,2ax c x+≥”的充要条件,则实数c =__________.14.函数()f x 的定义域为D ,若满足①()f x 在D 内是单调函数,②存在[],a b D ⊆,使()f x 在[],a b 上的值域为[],b a --,那么()y f x =叫做对称函数,现有()f x k 是对称函数, 那么k的取值范围是__________.参考答案1、2-;2、2212521x y +=;3、14;4、6;5、()2,36. 28; 7.13 ; 1; 9.2; 10.910; 11.2(1)(2)n n n ⨯-⨯- ; 12.设点M 的坐标为(,)x y ,∵12MB MD kk =-, 整理,(0x ≠),发现动点M 的轨迹方程是椭圆,其焦点恰为,A C 两点,所以MA +13. 若0,c <则0,a ≥不符合题意,若0,c >则2,8c a ≥于是21188c c =⇒=,亦可转化为二次函数22a x cx ≥-+恒成立展开讨论。
【高考复习】2018年高考数学 数列 综合题专项练习(含答案)

2018年高考数学 数列 综合题专项练习一、选择题:1.在等差数列{a n }中,S n 为其前n 项和,若34825a a a ++=,则9S =( ) A.60 B.75 C.90 D.1052.已知数列{a n }为等差数列,其前n 项和为S n ,7825a a -=,则11S 为( ) A.110 B.55 C.50 D.不能确定3.若数列{a n },{b n }的通项公式分别为a a n n ∙-=+2016)1(,nb n n 2017)1(2+-+=,且n n b a <,对任意*∈N n 恒成立,则实数a 的取值范围是( )A.)21,1[- B.[-1,1) C.[-2,1) D.)23,2[- 二、填空题:4.已知等差数列{a n }的公差d ≠0,若a 21+a 2=1,a 22+a 3=1,则a 1=________.5.已知{a n }是等差数列,S n 是其前n 项和.若a 1+a 22=-3,S 5=10,则a 9的值是 . 三、解答题:6.已知等差数列{a n }的前n 项和为S n ,a 1=1+2,S 3=9+32. (1)求数列{a n }的通项公式及其前n 项和; (2)设b n =nS n,求证:数列{b n }中任意不同的三项都不可能成等比数列.7.已知数列{a n }的前n 项和1n n S a λ=+,其中λ错误!未找到引用源。
0. (1)证明{a n }是等比数列,并求其通项公式. (2)若53132S =,求λ.8.已知数列{a n }的前n 项和为S n ,a 1=1,且3S n =a n+1﹣1. (1)求数列{a n }的通项公式;(2)设等差数列{b n }的前n 项和为T n ,a 2=b 2,T 4=1+S 3,求的值.9.已知各项都为正数的数列{a n }满足a 1=1,211(21)20n n n n a a a a ++---=.(1)求23,a a ;(2)求{}n a 的通项公式.10.已知数列{a n }中,a 1=4,a n =a n ﹣1+2n ﹣1+3(n ≥2,n ∈N *).(1)证明数列{a n ﹣2n}是等差数列,并求{a n }的通项公式;(2)设b n =,求b n 的前n 和S n .11.已知{a n }是各项均为正数的等比数列,且a 1+ a 2 =6, a 1a 2= a 3 (1)求数列{a n }通项公式;(2){b n }为各项非零的等差数列,其前n 项和为S n 。
浙江2018年高考数学选择题+填空题解析
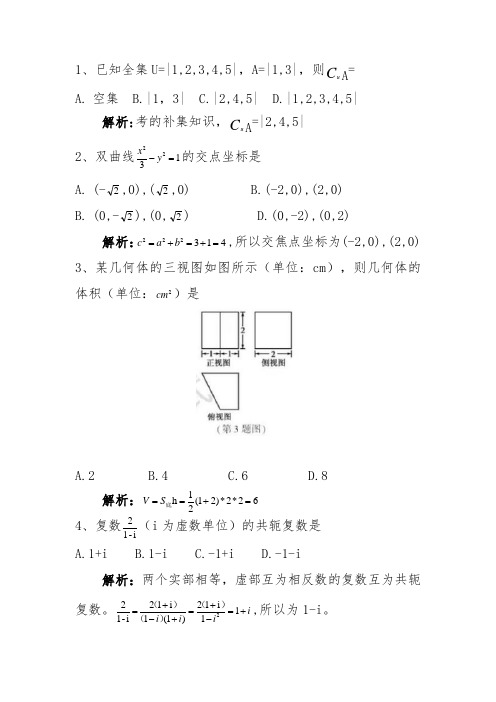
1、已知全集U=|1,2,3,4,5|,A=|1,3|,则C u A = A. 空集 B.|1,3| C.|2,4,5| D.|1,2,3,4,5|解析:考的补集知识,C u A =|2,4,5|2、双曲线1322=-y x 的交点坐标是A. (-2,0),(2,0)B.(-2,0),(2,0) B. (0,-2),(0,2) D.(0,-2),(0,2)解析:413222=+=+=b a c ,所以交焦点坐标为(-2,0),(2,0) 3、某几何体的三视图如图所示(单位:cm ),则几何体的体积(单位:2cm )是A.2B.4C.6D.8解析:62*2*)21(21h =+==底S V4、复数i-12(i 为虚数单位)的共轭复数是A.1+iB.1-iC.-1+iD.-1-i解析:两个实部相等,虚部互为相反数的复数互为共轭复数。
i ii i +=-+=+-+=11i 12)1(1i 12i -122)()()(,所以为1-i 。
5、函数x y x 2sin 2=的图像可能是解析:x 在【0,π】时,有两个零点,又x x x x 2-sin 2-2sin 2-=为奇函数,所以选D 。
6、已知平面a ,直线m ,n 满足a m ⊄,a n ⊂,则“m//n ”是“m//a ”的A. 充分不必要条件B.必要不充分条件C.充分必要条件 D 既不充分也不必要条件解析:“m//n ”->“m//a ”,“m//a ”-/>“m//n ”,所以为“m//n ”是“m//a ”的充分不必要条件。
7、设0<p<1,随机变量的分布列是则当p 在(0,1)内增大时,A. )(εD 减小B.)(εD 增大C.)(εD 先减小后增大D.)(εD 先增大后减少解析:41)22121021(22121021))(()()(2222312+-=*+*+*--*+*+*-=-=∑=p p pp p p E p D i i i εεε 开口向下,对称轴为1/2,所以是先增大后减少 8、已知四棱准S-ABCD 的地面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点),设SE 与BC 所成的角为1θ,SE 与平面ABCD 所成的角为2θ,二面角S-AB-C 的平面角为3θ,则1θ2θ3θA. 1θ≤2θ≤3θB.3θ≤2θ≤1θC.1θ≤3θ≤2θD.2θ≤3θ≤1θ解析:如图SE SF =1sin θ,SE SS 'sin 2=θ,''sin 3SE SS =θ又SF ≥SS ’,所以1sin θ≥2sin θ,1θ≥2θ; SE ≥SE ’,所以2sin θ≤3sin θ,2θ≤3θ; 又SEEF =1cos θ,'''cos 3SE S E =θ,EF =''S E ,所以1cos θ≤3cos θ,1θ≥3θ 所以2θ≤3θ≤1θ。
2018年高考数学—概率统计(选择+填空+答案)

A.p1=p2
B.p1=p3
C.p2=p3
D.p1=p2+p3
9.(18 江苏 3)已知 5 位裁判给某运动员打出的分数的茎叶图如图所示,那么这 5 位裁判打出
的分数的平均数为 ▲ .
2
10.(18 江苏 6)某兴趣小组有 2 名男生和 3 名女生,现从中任选 2 名学生去参加活动,则恰 好选中 2 名女生的概率为 ▲ .
13.(18 全国三文 14)某公司有大量客户,且不同龄段客户对其服务的评价有较大差异.为了 解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层 抽样和系统抽样,则最合适的抽样方法是________.
参考答案:
1.D
2.C
9.90
10. 3
10
3.B 4.A 11.16
5.D 6.D 7.B 8. A 12.1260 13.分层抽样
2018 高考数学——概率统计选填
1.(18 北京理(4))“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出 半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份, 依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都 等于 12 2 .若第一个单音的频率为 f,则第八个单音的频率为
A. 1 12
B. 1 14
C. 1 15
D. 1 18
3.(18 全国三理 8)某群体中的每位成员使用移动支付的概率都为 p ,各成员的支付方式相互
独 立 , 设 X 为 该 群 体 的 10 位 成 员 中 使 用 移 动 支 付 的 人 数 , DX 2.4 ,
P X 4 P X 6 ,则 p
建设后经济收入构成比例
2018年高考数学试题及答案word版

2018年高考数学试题及答案word版一、选择题(每题4分,共40分)1. 若函数f(x) = x^2 - 4x + 3的零点为x1和x2,则x1 + x2等于多少?A. 1B. 2C. 3D. 4答案:B2. 已知向量a = (1, 2),向量b = (3, 4),向量a与向量b的点积为多少?A. 5B. 6C. 7D. 8答案:C3. 在一个等差数列中,首项为3,公差为2,第10项的值是多少?A. 23B. 24C. 25D. 26答案:A4. 已知函数f(x) = sin(x) + cos(x),求f(π/4)的值。
A. √2B. √3C. 2D. 3答案:A5. 一个圆的半径为5,圆心到直线x + y - 7 = 0的距离为多少?A. 3B. 4C. 5D. 6答案:B6. 若复数z = 1 + i,则|z|等于多少?A. √2B. 2C. √3D. 3答案:A7. 已知函数f(x) = x^3 - 3x^2 + 2,求f'(x)。
A. 3x^2 - 6xB. x^2 - 6x + 2C. 3x^2 - 6x + 2D. x^3 - 3x^2答案:A8. 已知双曲线方程为x^2/9 - y^2/16 = 1,其渐近线方程为多少?A. y = ±(4/3)xB. y = ±(3/4)xC. y = ±(4/3)x + 1D. y = ±(3/4)x + 1答案:A9. 已知正方体的体积为8,求其表面积。
A. 12B. 16C. 24D. 32答案:C10. 已知函数f(x) = ln(x),求f'(1)。
A. 0B. 1C. -1D. 2答案:A二、填空题(每题4分,共20分)11. 已知等比数列的首项为2,公比为3,求第5项的值。
答案:48612. 已知三角形的三边长分别为3, 4, 5,求其面积。
答案:613. 已知函数f(x) = x^2 - 6x + 8,求其对称轴方程。
2018年高考数学选择填空专项训练(第二轮)
2018年高考数学选择填空专项训练(第二轮)一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在复平面内,复数12ii+对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 2、从集合{1,1,2}A =-中随机选取一个数记为k ,从集合{2,1,2}B =-中随机选取 一个数记为b ,则直线y kx b =+不经过第三象限的概率为( )A .29 B. 13 C. 49D. 593、已知函数()()()f x x a x b =--(其中a b >)的图象如下图所示,则函数()x g x a b =+的图象是A .B .C . D.4.已知双曲线2215x y m -=(0m >)的右焦点与抛物线212y x =的焦点相同,则此双曲线的离心率为A .6 BC .32D .345、.跳格游戏:如图,人从格子外只能进入第1个格子,在格子中每次可向前跳1格或2格,那么人从格外跳到第8个格子的方法种数为( )A .8种B .13种C .21种D .34种6、已知)0,(),0,(21c F c F -为椭圆12222=+b y a x 的两个焦点,P 为椭圆上一点且221c PF PF =⋅,则此椭圆离心率的取值范围是( )A. B .11[,]32 C. D. 7. 曲线1x y xe -=在点(1,1)处切线的斜率等于( )A .2eB .eC .2D .18.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )A .814πB .16πC .9πD .274π9. 已知双曲线C 的离心率为2,焦点为1F 、2F ,点A 在C 上,若12||2||F A F A =,则21cos AF F ∠=( )A .14B .13 C.4 D.310、已知函数1)(+-=mx e x f x的图像为曲线C ,若曲线C 存在与直线xy 21=垂直的切线,则实数m 的取值范围是A 、2≤mB 、2>mC 、21-≤m D 、21->m二、填空题:本大题共5小题,每小题4分,共20分。
最新-2018高考数学填空题型精选精练2 精品

2018高考数学填空题型精选精练1.{}{}222,0A x y c c R B x y r r =+=∈=+=>,则AB 的子集个数为 .2.若函数()23k kh x x x =-+在()1,+∞上是增函数,则实数k 的取值范围是 . 3.锐角ABC ∆中,若2A B =,则ab的取值范围是 .4.若ABC ∆的周长等于20,面积是060A =,则BC = .5.已知,,a b c 为ABC ∆的三个内角,,A B C 的对边,向量()3,1m =-,()cos ,sin n A A =,若m n ⊥,且cos cos sin a B b A c C +=,则角B = .6.定义在R 上的奇函数()f x ,当0x ≥时,()()[)[)12log 1,0,113,1,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩,则方程()12f x =的所有解之和为 . 7.已知()f x 是R 上的减函数,(0,2),(3,2)A B --是图象上的两点,那么不等式|(2)|2f x ->的解集为 .8.在∆ABC中,若1,b c ==23C π=,则a = .9.设含有集合{}1,2,4,8,16A =中三个元素的集合A 的所有子集记为123,,,,n B B B B …(其中*n N ∈),又将(1,2,,)k B k n =…的元素之和记为k a ,则1nk k a ==∑ .10.设函数()f x 的定义域为R ,若存在常数0k >,使()2010kf x x ≤对一切实数x 均成立,则称()f x 为“海宝”函数.给出下列函数:①2()f x x =;②()sin cos f x x x =+;③2()1xf x x x =++;④()31x f x =+ 其中()f x 是“海宝”函数的序号为 .11.在ABC ∆中,角A B C ,,所对的边分别为,,a b c ,11tan ,tan 23A B ==,且ABC ∆最短边的长为1,则ABC S ∆= .12.设不等式组1103305390x y x y x y +-⎧⎪-+⎨⎪-+⎩≥≥≤表示的平面区域为D ,若指数函数x y a =的图象上存在区域D上的点,则a 的取值范围是 .13.若x >1,则函数21161x y x x x =+++的最小值为 .14.()f x 是定义在(0,)+∞上的非负可导函数,且满足()()0xf x f x '->,对任意的正数a b 、,若a b >,则必有 .15.已知椭圆C :2212x y +=的两焦点为12,F F ,点00(,)P x y 满足2200012x y <+<,则12PF PF +的取值范围为_______;直线0012x xy y +=与椭圆C 的公共点个数为_______.参考答案1、1;2、[)2,-+∞;3、;4、7;5、6π;6、17、(,1)(2,)-∞-+∞ 8、1;9、解析:五个元素中,每个元素都出现246C =次,1nkk a==∑6×(1+2+4+8+16)=186,填186.10、③;11、12;12、(]3,1;13、8;14、()()af b bf a <;15、)22,2[;0。
2018年全国统一高考数学试卷(文科)(新课标ⅰ)(含解析版)

关注公众号”一个高中僧“获取更多高中资料
第 3 页(共 28 页)
18.(12 分)如图,在平行四边形 ABCM 中,AB=AC=3,∠ACM=90°,以 AC 为 折痕将△ACM 折起,使点 M 到达点 D 的位置,且 AB⊥DA.
(1)证明:平面 ACD⊥平面 ABC; (2)Q 为线段 AD 上一点,P 为线段 BC 上一点,且 BP=DQ= DA,求三棱锥
A.12 π
B.12π
C.8 π
D.10π
【考点】LE:棱柱、棱锥、棱台的侧面积和表面积. 菁优网版权所有
【专题】11:计算题;35:转化思想;49:综合法;5F:空间位置关系与距离.
【分析】利用圆柱的截面是面积为 8 的正方形,求出圆柱的底面直径与高,然后
求解圆柱的表面积.
【解答】解:设圆柱的底面直径为 2R,则高为 2R,
(2)估计该家庭使用节水龙头后,日用水量小于 0.35m3 的概率; (3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按 365 天计算,
同一组中的数据以这组数据所在区间中点的值作代表)
20.(12 分)设抛物线 C:y2=2x,点 A(2,0),B(﹣2,0),过点 A 的直线 l 与 C 交于 M,N 两点.
参考答案与试题解析
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选 项中,只有一项是符合题目要求的。
1.(5 分)已知集合 A={0,2},B={﹣2,﹣1,0,1,2},则 A∩B=( )
A.{0,2}
B.{1,2}
C.{0}
D.{﹣2,﹣1,0,1,2}
【考点】1E:交集及其运算. 菁优网版权所有
问题解决问题的能力.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年高考选择题和填空题专项训练(1)一. 选择题:(1)25(4)(2)i i i +=+( )(A )5(1-38i ) (B )5(1+38i ) (C )1+38i (D )1-38i (2)不等式|2x 2-1|≤1的解集为( )(A ){|11}x x -≤≤ (B ){|22}x x -≤≤ (C ){|02}x x ≤≤ (D ){|20}x x -≤≤(3)已知F 1、F 2为椭圆22221x y a b +=(0a b >>)的焦点;M 为椭圆上一点,MF 1垂直于x 轴,且∠F 1MF 2=600,则椭圆的离心率为( )(A )12(B (C (D(4)235(2)(23)lim(1)n n n n →∞-+=-( ) (A )0 (B )32 (C )-27 (D )27(5)等边三角形ABC 的边长为4,M 、N 分别为AB 、AC 的中点,沿MN 将△AMN 折起,使得面AMN 与面MNCB 所处的二面角为300,则四棱锥A -MNCB 的体积为( )(A )32(B (C (D )3(6)已知数列{}n a 满足01a =,011n n a a a a -=+++(1n ≥),则当1n ≥时,n a =( )(A )2n (B )(1)2n n + (C )2n -1 (D )2n -1 (7)若二面角l αβ--为1200,直线m α⊥,则β所在平面内的直线与m 所成角的取值范围是( ) (A )00(0,90] (B )[300,600] (C )[600,900] (D )[300,900] (8)若(sin )2cos2f x x =-,则(cos )f x =( )(A )2-sin 2x (B )2+sin 2x (C )2-cos 2x (D )2+cos 2x (9)直角坐标xOy 平面上,平行直线x =n (n =0,1,2,……,5)与平行直线y =n (n =0,1,2,……,5)组成的图形中,矩形共有( )(A )25个 (B )36个 (C )100个 (D )225个(10)已知直线l :x ―y ―1=0,l 1:2x ―y ―2=0.若直线l 2与l 1关于l 对称,则l 2的方程是( ) (A )x ―2y +1=0 (B )x ―2y ―1=0 (C )x +y ―1=0 (D )x +2y ―1=0 二. 填空题:(11)已知向量集合{|(1,2)(3,4),}M a a R λλ==+∈,{|(2,2)(4,5),}N a a R λλ==--+∈,则M N=____________.(12)抛物线26y x =的准线方程为 .(13)在5名学生(3名男生,2名女生)中安排2名学生值日,其中至少有1名女生的概率是 .(14)函数y x =(0x ≥)的最大值为 . (15)若1(2)n x x+-的展开式中常数项为-20,则自然数n = .2018年高考选择题和填空题专项训练(2)一、选择题: 1.复数10)11(ii +-的值是 ( ) A .-1 B .1 C .-32 D .32 2.tan15°+cot15°的值是( ) A .2 B .2+3 C .4 D .334 3.命题p :若a 、b ∈R ,则|a |+|b|>1是|a +b|>1的充分而不必要条件;命题q :函数y=2|1|--x 的定义域是(-∞,-1]∪[3,+∞).则 ( )A .“p 或q ”为假B .“p 且q ”为真C .p 真q 假D .p 假q 真4.已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2是正三角形,则这个椭圆的离心率是( )A .33B .32C .22D .23 5.已知m 、n 是不重合的直线,α、β是不重合的平面,有下列命题:①若m ⊂α,n ∥α,则m ∥n ;②若m ∥α,m ∥β,则α∥β;③若α∩β=n ,m ∥n ,则m ∥α且m ∥β;④若m ⊥α,m ⊥β,则α∥β. 其中真命题的个数是( ) A .0 B .1 C .2 D .36.某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为( )A .2426C A B .242621C A C .2426A AD .262A7.已知函数y=log 2x 的反函数是y=f —1(x ),则函数y= f —1(1-x )的图象是( )11(A)xOy11(B)xOy11( C )_x_ Oy11(D)xOy8.已知a 、b 是非零向量且满足(a -2b ) ⊥a ,(b -2a ) ⊥b ,则a 与b 的夹角是 ( ) A .6π B .3π C .32π D .65π9.若(1-2x )9展开式的第3项为288,则2111lim()nn x x x →∞+++的值是 ( )A .2B .1C .21 D .5210.如图,A 、B 、C 是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O 为球心,则直线 OA 与截面ABC 所成的角是( ) A .arcsin 63B .arccos 63 C .arcsin 33 D .arccos33二、填空题:11.如图,B 地在A 地的正东方向4 km 处,C地在B 地的北偏东30°方向2 km 处,河流 的沿岸PQ (曲线)上任意一点到A 的距离 比到B 的距离远2 km.现要在曲线PQ 上 选一处M 建一座码头,向B 、C 两地转运 货物.经测算,从M 到B 、M 到C 修建公 路的费用分别是a 万元/km 、2a 万元/km ,那么修建这两条公路的总费用最低是:________________.12.直线x +2y=0被曲线x 2+y 2-6x -2y -15=0所截得的弦长等于 . 13.设函数11()x f x a+-=⎪⎩(0)(0)x x ≠= 在x =0处连续,则实数a 的值为 . 14.某射手射击1次,击中目标的概率是0.9.他连续射击4次,且各次射击是否击中目标相互之间没有影响.有下列结论:①他第3次击中目标的概率是0.9;②他恰好击中目标3次的概率是0.93×0.1; ③他至少击中目标1次的概率是1-0.14.其中正确结论的序号是 (写出所有正确结论的序号). 15.如图1,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器.当这个正六棱柱容器的底面边长为 时,其容积最大.2018年高考选择题和填空题专项训练(3)一.选择题1.已知平面向量a =(3,1),b =(x ,–3),且a b ⊥,则x= ( ) A. –3 B. –1 C. 1 D . 32.已知{}213|||,|6,22A x x B x x x ⎧⎫=+>=+≤⎨⎬⎩⎭则A B = ( )A.[)(]3,21,2-- B.(]()3,21,--+∞ C. (][)3,21,2-- D.(](],31,2-∞-3.设函数 2322,(2)()42(2)x x f x x x a x +⎧->⎪=--⎨⎪≤⎩在x=2处连续,则a= ( )A.12-B.14-C.14D.134.123212lim 11111n n nn n n n n →∞--+-+-+++++()的值为 ( ) A. –1 B.0 C.12D.1 5.函数22sin sin 44f x x x ππ=+--()()()是 ( ) A.周期为π的偶函数 B.周期为π的奇函数C. 周期为2π的偶函数D..周期为2π的奇函数6.一台X 型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这种型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 ( )A.0.1536B. 0.1808C. 0.5632D. 0.97287.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 ( )A. 23B. 76C. 45D. 568. 若双曲线2220)x y k k -=>(的焦点到它相对应的准线的距离是2,则k= ( ) A. 6 B. 8 C. 1 D. 49.当04x π<<时,函数22cos ()cos sin sin x f x x x x =-的最小值是 ( ) A. 4 B. 12 C.2 D. 1410. 变量x 、y 满足下列条件:212,2936,2324,0,0.x y x y x y x y +≥⎧⎪+≥⎪⎨+=⎪⎪≥≥⎩ 则使z=3x+2y 的值最小的(x ,y )是 A. ( 4.5 ,3 ) B. ( 3,6 ) C. ( 9, 2 ) D. ( 6, 4 ) 二.填空题11. 如右下图,定圆半径为a ,圆心为 ( b ,c ), 则直线ax+by+c=0与直线 x –y+1=0的交点在第______象限.12. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 (用分数作答)____________.13. 已知复数z 与 (z +2)2-8i 均是纯虚数,则 z = . 14. 由图(1)有面积关系: PA B PAB S PA PB S PA PB''∆∆''⋅=⋅,则由(2) 有体积关系: .P A B C P ABC VV '''--=15.函数10)f x In x =>())(的反函数1().f x -=16、不等式log sin 2(01)a x x a a >>≠且对任意(0,)4x π∈都成立,则a 的取值范围为 .2018年高考选择题和填空题专项训练(4)一、选择题:1.与直线240x y -+=的平行的抛物线2y x =的切线方程是 ( )A .230x y -+=B .230x y --=C .210x y -+=D .210x y --=2的值是 ( )A .-16B .16C .14-D.14-3.已知2211(),()11x x f f x x x --=++的解析式可取为 ( )A .21x x +B .221x x -+ C .221xx + D .21xx -+ 4.已知,,a b c 为非零的平面向量. 甲:,:,a b a c b c ⋅=⋅=乙 ( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件图(2)图(1)C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件 5.若110a b <<,则下列不等式①a b ab +<;②||||;a b >③a b <;④2b aa b +>中,正确的不等式有( )A .1个B .2个C .3个D .4个6.已知椭圆221169x y +=的左、右焦点分别为F 1、F 2,点P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为 ( )A .95B .3C .977D .947.函数()log (1)[0,1]x a f x a x =++在上的最大值和最小值之和为a ,则a 的值为( )A .14B .12C .2D .48.已知数列{n a }的前n 项和1111[2()][2(1)()](1,2,),22n n n S a b n n --=---+=其中a 、b 是非零常数,则存在数列{n x }、{n y }使得( ) A .,{}n n n n a x y x =+其中为等差数列,{n y }为等比数列 B .,{}n n n n a x y x =+其中和{n y }都为等差数列C .,{}n n n n a x y x =⋅其中为等差数列,{n y }都为等比数列D .,{}n n n n a x y x =⋅其中和{n y }都为等比数列9.函数3()1f x ax x =++有极值的充要条件是 ( )A .0a >B .0a ≥C .0a <D .0a ≤10.设集合2{|10},{|440P m m Q m R mx mx =-<<=∈+-<对任意实数x 恒成立},则下列关系中成立的是( )A .P QB .Q PC .P=QD .PQ=二、填空题:11.已知平面αβ与所成的二面角为80°,P 为α、β外一定点,过点P 的一条直线与α、β所成的角都是30°,则这样的直线有且仅有____________条.12设随机变量ξ的概率分布为(),,1,2,,5k aP k a k a ξ====常 .13.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 种.(以数字作答)14.设A 、B 为两个集合,下列四个命题:①A ⊄B ⇔对任意,x A x B ∈∉有 ②A⊄ B ⇔AB =φ ③A ⊄B ⇔A B ④A ⊄ B ⇔存在,x A x B ∈∉使得其中真命题的序号是 .(把符合要求的命题序号都填上) 15.某日中午12时整,甲船自A 处以16km/h 的速度向正东行驶,乙船自A 的正北18km 处以24km/h的速度向正南行驶,则当日12时30分时两船之间距离对时间的变化率是 _________________km/h.16.若函数f (x )=2cos(312kx π-)的周期为T ,且T ∈(23, 34),则正整数k 的值为 .2018年高考选择题和填空题专项训练(5)一、选择题:1.复数41(1)i +的值是( )A .4iB .-4iC .4D .-42.如果双曲线2211312x y -=上一点P P 到右准线的距离是 ( )A .135B .13C .5D .5133.设1()f x -是函数2()log (1)f x x =+的反函数,若11[1()][1()]8f a f b --++=,则()f a b +的值为( ) A .1B .2C .3D .2log 34.把正方形ABCD 沿对角线AC 折起,当A 、B C 、D 四点为顶点的三棱锥体积最大时,直线BD与平面ABC 所成的角的大小为 ( )A .90°B .60°C .45°D .30°5.某公司甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其收入和售后服务等情况,记这项调查为②则完成①、②这两项调查宜采用的抽样方法依次是 ( ) A .分层抽样法,系统抽样法 B .分层抽样法,简单随机抽样法C .系统抽样法,分层抽样法D .简单随机抽样法,分层抽样法6.设函数2,0,()(4)(0),(2)2,2,0.x bx c x f x f f f x ⎧++≤=-=-=-⎨>⎩若则关于x 的方程()f x x =解的个数为 ( ) A .1B .2C .3D .4 7.设0,0,a b >>则以下不等式中不恒成立....的是 ( )A .11()()4a b a b++≥B .3322a b ab +≥C .22222a b a b ++≥+D 8.数列{}1112116,,,*,lim()55n n n n n n a a a a n N a a a ++→∞=+=∈+++=中则( )A .25 B .27 C .14 D .4259.设集合{(,)|,},{(,)|20},{(,)|0}U x y x R y R A x y x y m B x y x y n =∈∈=-+>=+-≤,那么 点P (2,3)(U C B )的充要条件是 ( ) A .1,5m n >-< B .1,5m n <-<C .1,5m n >->D .1,5m n <->10.从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为( )A .56B .52C .48D .40二、填空题:11.设(),()f x g x 分别是定义在R 上的奇函数和偶函数,当0x <时,()()()()0,f x g x f x g x ''+>且(3)0,g -=则不等式()()0f x g x <的解集是________________________.12.已知向量a =(cos ,sin )θθ,向量b =1)-,则|2a -b |的最大值是 .13.同时抛两枚相同的均匀硬币,随机变量ξ=1表示结果中有正面向上,ξ=0表示结果中没有正面向上,则E ξ= . 14.若3(n x的展开式中的常数项为84,则n= .15.设F 是椭圆22176x y +=的右焦点,且椭圆上至少有21个不同的点P i (i =1,2,3,…),使|FP 1|,|FP 2|,|FP 3|,…组成公差为d 的等差数列,则d 的取值范围为 . 16.将正方形ABCD 沿对角线BD 折成直二面角A BD C --,有如下四个结论: ①AC BD ⊥ ②ACD ∆是等边三角形 ③AB 与平面BCD 成60的角 ④AB 与CD 所成的角为60其中真命题的编号是 (写出所有真命题的编号)2018年高考选择题和填空题专项训练(6)一、选择题:1.设集合P={1,2,3,4},Q={2,x x x R ≤∈},则P ∩Q 等于 ( ) (A){1,2} (B) {3,4} (C) {1} (D) {-2,-1,0,1,2}2.函数y=2cos 2x+1(x ∈R )的最小正周期为 ( ) (A)2π(B)π (C)2π (D)4π0.5 时间(小时)0 1.0 1.5 2.03.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( ) (A)140种 (B)120种 (C)35种 (D)34种4.一平面截一球得到直径是6cm 的圆面,球心到这个平面的距离是4cm ,则该球的体积是 ( ) (A)31003cm π (B) 32083cm π (C) 35003cm π(D)3 5.若双曲线22218x y b-=的一条准线与抛物线28y x =的准线重合,则双曲线离心率为 ( )(B) (C) 4(D)6.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用右侧的条形图表示. 根据条形图可得这50名学生这一天平均每人的课外阅读时间为 ( ) (A)0.6小时 (B)0.9小时 (C)1.0小时 (D)1.5小时7.4(2x 的展开式中x 3的系数是( )(A)6 (B)12 (C)24 (D)488.若函数log ()(0,1)a y x b a a =+>≠的图象过两点(-1,0)和(0,1),则 ( ) (A)a=2,b=2,b=2 (C)a=2,b=19.将一颗质地均匀的骰子(它是一种各面上分别标有点数1,2,3,4,5,6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是 ( )(A)5216 (B)25216 (C)31216 (D)9121610.函数3()31f x x x =-+在闭区间[-3,0]上的最大值、最小值分别是 ( )(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19 二、填空题:11.设k>1,f(x)=k(x-1)(x ∈R ) . 在平面直角坐标系xOy 中,函数y=f(x)的图象与x 轴交于A 点,它的反函数y=f -1(x)的图象与y 轴交于B 点,并且这两个函数的图象交于P 点. 已知四边形OAPB 的面积是3,则k 等于____________________.12.二次函数y=ax 2+bx+c(x ∈R )的部分对应值如下表:则不等式ax 2+bx+c>0的解集是_______________________.13.以点(1,2)为圆心,与直线4x+3y-35=0相切的圆的方程是________________.14.设数列{a n }的前n 项和为S n ,S n =1(31)2n a -(对于所有n ≥1),且a 4=54,则a 1的数值是_______.15.平面向量,a b 中,已知a =(4,-3),b =1,且a b ⋅=5,则向量b =__________. 16.有下列命题:① G G ≠0)是a ,G ,b 成等比数列的充分非必要条件;②若角α,β满足cos αcos β=1,则sin (α+β)=0;③若不等式|x -4|+|x -3|<a 的解集非空,则必有a ≥1;④函数y =sin x +sin |x |的值域是[-2,2].其中错误命题的序号是 .(把你认为错误的命题的序号都填上)2018年高考选择题和填空题专项训练(7)一、选择题:1.若cos 0,sin 20,θθθ><且则角的终边所在象限是( ) A .第一象限 B .第二象限 C .第三象限D .第四象限2.对于01a <<,给出下列四个不等式①1log (1)log (1)a a a a +<+;②1log (1)log (1)a a a a+>+;③111a a a a ++<;④111a a a a ++>其中成立的是( ) A .①与③ B .①与④ C .②与③ D .②与④3.已知α、β是不同的两个平面,直线,a b αβ⊂⊂直线,命题:p a b 与无公共点;命题 ://q αβ. 则p q 是的( )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分也不必要的条件4.设复数z 满足1,|1|1zi z z -=+=+则( )A .0B .1CD .25.甲、乙两人独立地解同一问题,甲解决这个问题的概率是p 1,乙解决这个问题的概率是p 2,那么恰好有1人解决这个问题的概率是( )A .12p p B.1221(1)(1)p p p p -+- C .121p p - D .121(1)(1)p p ---6.已知点(2,0)A -、(3,0)B ,动点2(,)P x y PA PB x ⋅=满足,则点P 的轨迹是( )A .圆B .椭圆C .双曲线D .抛物线7.已知函数()sin()12f x x ππ=--,则下列命题正确的是( )A .()f x 是周期为1的奇函数B .()f x 是周期为2的偶函数C .()f x 是周期为1的非奇非偶函数D .()f x 是周期为2的非奇非偶函数 8.已知随机变量ξ的概率分布如下:AC 1A .923B .1023C .913 D .10139.已知点1(F 、2F ,动点P 满足21||||2PF PF -=. 当点P 的纵坐标是12时,点P 到坐标原点的距离是( ) AB .32C .D .210.设A 、B 、C 、D 是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到该平面的距离是球半径的一半,则球的体积是( )A .B .C .D .二、填空题:11.有两排座位,前排11个座位,后排12个座位,现安排2人就座,规定前排中间的3个座位不能坐,并且这2人不.左右相邻,那么不同排法的种数是_____________________. 12.若经过点P (-1,0)的直线与圆224230x y x y ++-+=相切,则此直线在y 轴上的截距是 . 13.x π→= .14.如图,四棱柱ABCD —A 1B 1C 1D 1的底面ABCD 为正方形,侧棱与底面边长均为2a ,且1160A AD A AB ∠=∠=︒,则侧棱AA 1和截面B 1D 1DB 的距离是 .15.口袋内装有10个相同的球,其中5个球标有数字0,5个球标有数字1,若从袋中摸出5个球,那么摸出的5个球所标数字之和小于2或大于3的概率是 .(以数值作答)16.定义运算a b *为:()(),a a b a b b a b ≤⎧⎪*=⎨>⎪⎩例如,121*=,则函数f (x )=sin cos x x *的值域为 .2018年高考选择题和填空题专项训练(8)一、选择题 :1.(1-i)2·i= ( ) A .2-2i B .2+2i C .-2D .22.已知函数1()lg .().()1xf x f a b f a x-==-=+若则( )A .bB .-bC .1bD .-1b3.已知a 、b 均为单位向量,它们的夹角为60°,那么|a +3b |= ( )A B C D .44.函数1(1)y x =≥的反函数是( ) A .y=x 2-2x +2(x <1) B .y=x 2-2x +2(x ≥1)C .y=x 2-2x (x <1)D .y=x 2-2x (x ≥1)5.37(2x的展开式中常数项是( )A .14B .-14C .42D .-42 6.设A 、B 、I 均为非空集合,且满足A ⊆B ⊆I ,则下列各式中错误..的是 ( )A .(I C A)∪B=IB .(IC A)∪(I C B)=I C .A ∩(I C B)=φD .(I C A)(I C B)= I C B7.椭圆2214x y +=的两个焦点为F 1、F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则2||PF =( )A B C .72D .48.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是( )A .[-12,12] B .[-2,2] C .[-1,1] D .[-4,4]9.为了得到函数sin(2)6y x π=-的图象,可以将函数cos2y x =的图象( )A .向右平移6π个单位长度 B .向右平移3π个单位长度C .向左平移6π个单位长度D .向左平移3π个单位长度10.已知正四面体ABCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H.设四面体EFGH 的表面积为T ,则TS等于( )A .19B .49 C .14 D .13二、填空题:11.从数字1,2,3,4,5,中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为________________. 12.不等式|x +2|≥|x |的解集是 .13.由动点P 向圆x 2+y 2=1引两条切线PA 、PB ,切点分别为A 、B ,∠APB=60°,则动点P 的轨迹方程为 .14.已知数列{a n },满足a 1=1,a n =a 1+2a 2+3a 3+…+(n -1)a n -1(n ≥2),则{a n }的通项1___n a ⎧=⎨⎩12n n =≥ 15.已知a 、b 为不垂直的异面直线,α是一个平面,则a 、b 在α上的射影有可能是 .①两条平行直线 ②两条互相垂直的直线 ③同一条直线 ④一条直线及其外一点 在上面结论中,正确结论的编号是 (写出所有正确结论的编号).16、若函数2()log (3)k f x x kx =-+在区间,2k ⎛⎤-∞ ⎥⎝⎦上是减函数,则实数k 的取值范围是 。
