凉城县宏远中学七下数学试题(全等三角形周考2)
2021版七年级数学下册 4.3 探索三角形全等的条件评测练习2(全国通用版)人教版
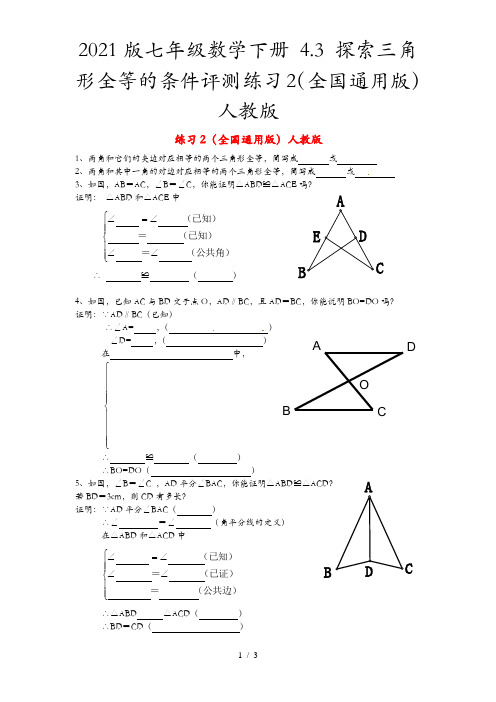
人教版1 / 3练习2(全国通用版)人教版1、两角和它们的夹边对应相等的两个三角形全等,简写成 或2、两角和其中一角的对边对应相等的两个三角形全等,简写成 或3、如图,AB =AC ,∠B =∠C ,你能证明△ABD ≌△ACE 吗? 证明: △ABD 和△ACE 中⎪⎪⎩⎪⎪⎨⎧∠∠∠=∠(公共角)=(已知)=(已知)∴ ≌ ( )4、如图,已知AC 与BD 交于点O ,AD ∥BC ,且AD =BC ,你能说明BO=DO 吗? 证明:∵AD ∥BC (已知)∴∠A= ,( ) ∠D= ,( )在 中,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧∴ ≌ ( ) ∴BO=DO ( )5、如图,∠B =∠C ,AD 平分∠BAC ,你能证明△ABD ≌△ACD ? 若BD =3cm ,则CD 有多长?证明:∵AD 平分∠BAC ( )∴∠ =∠ (角平分线的定义) 在△ABD 和△ACD 中⎪⎪⎩⎪⎪⎨⎧∠∠∠=∠(公共边)=(已证)=(已知) ∴△ABD △ACD ( ) ∴BD =CD ( )A BCDOBCDCD E人教版2 / 3∵BD =3cm (已知)∴C D = = (等量代换)6、如图,在△ABC 中,BE ⊥AD 于E ,CF ⊥AD 于F ,且BE =CF ,那么BD 与DC 相等吗?你能说明理由吗? 解:BD =DC 。
∵BE ⊥AD 于E ,CF ⊥AD 于F∴∠ =∠ =90°(垂直的定义) 在 中,⎪⎪⎪⎩⎪⎪⎪⎨⎧ ∴ ≌ ( )∴BD =DC ( ) (第6题)7、如图,已知AB =CD ,∠B =∠C ,你能说明△ABO ≌△DCO 吗?8、如图,A B ∥CD ,∠A =∠D ,BF =CE ,∠AEB =110°,求∠DCF 的度数。
9、如图,在Rt △ACB 中,∠C =90°,BE 是角平分线,ED ⊥AB 于D , 且BD =AD ,试确定∠A 的度数。
七年级下数学全等三角形试题

..七年级下数学全等三角形测试题(5月24日)一、选择(每题3分,共30分) 1、下列说法正确的是( )A 全等三角形是指形状相同的两个三角形B 全等三角形的周长和面积分别相等C 全等三角形是指面积相等的两个三角形D 所有的等边三角形都是全等三角形2、如下图:若△ABE ≌△ACF ,且AB=5,AE=2,则EC 的长为( )A :2B :3C :5D :2.53.如图,AC、BD相交于点O,OA=OC,OB=OD,则图中全等三角形有( ) (A)2对 (B)3对 (C)4对 (D)5对 4、如图:EA ∥DF ,AE=DF ,要使△AEC ≌△DBF ,则只要( ) A :AB=CD B :EC=BF C :∠A=∠D D :AB=BC 5、根据下列条件,能唯一画出△ABC的是( )A。
AB=3,BC=4,AC=8 B。
AB=4,BC=3,∠A=30° C。
∠A=60°,∠B=45°,AB=4 D。
∠C=90°,AB=66、能确定△ABC ≌△DEF 的条件是 ( )A .AB =DE ,BC =EF ,∠A =∠E B .AB =DE ,BC =EF ,∠C =∠E C .∠A =∠E ,AB =EF ,∠B =∠D D .∠A =∠D ,AB =DE ,∠B =∠E 7、如下左图所示,在△ABC 中,D 、E 分别是边AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数为( )A. 15°B. 20°C. 25°D. 30°8、如图:在△ABC 中,AB=AC ,∠BAD=∠CAD ,则下列结论:①△ABD≌△ACD ,②∠B=∠C ,③BD=CD ,④AD ⊥BC 。
其中正确的个数有( )A :1个B :2个 C :3个 D :4个ABCDE 第3题9、如上右图,已知在△,D 为BC 上一点,BF =CD ,CE =BD ,那么∠EDF 等于( )A 、90°-∠AB 、90°-21∠A C 、180°-∠A D 、45°-21∠A 10、已知△ABC 与△DEF 全等,∠A=∠D=90°,∠B=37°,则∠E 的度数是( )A 、37°B 、53°C 、37°或63°D 、37°或53° 二、填空(每题3分,共30分)1、如下左图AB ,CD 相交于点O ,AD =CB ,请你补充一个条件,使得△AOD ≌△COB ,你补充的条件是 ;2.如下中图,若△ABC ≌△ADE ,∠EAC=35°,则∠BAD=_________度. 3、如下右二图:AB=AC ,BD=CD ,若∠B=28°则∠C= ;(第11题)DCBAABCDMN 图2O(第19题)DCBAABCDE图1(第2题)F EC BA OC A B (第7题)F E D C BA FE(第6题)B A.4.如上右图,沿AM 折叠,使D 点落在BC 上的N 点处,如果AD=7cm ,DM=5cm ,∠DAM=300,则AN= cm ,NM= cm , ∠NAM= .5.AD 是△ABC 的边BC 上的中线,AB =12,AC =8,则边BC 的取值范围是____;中线AD 的取值范围是____.6.如下左一图,△ABC ≌△AED ,∠C=85°,∠B=30°,则∠EAD= . 7、如下左二图:在△ABC 中,AD=AE ,BD=EC ,∠ADB=∠AEC=105°,∠B=40°,则∠CAE= ;8、如上右二图:在∠AOB 的两边截取OA=OB ,OC=OD ,连接AD ,BC 交于点P ,则下列结论中①△AOD ≌△BOC ,②△APC ≌△BPD , ③点P 在∠AOB 的平分线上。
七年级(下册)_全等三角形证明经典题

七年级数学下册《全等三角形》专题练习1、 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2、已知:D 是AB 中点,∠ACB=90°,求证:12CD AB =3、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,证21∠=∠4、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=ACBA CDF2 1 EADB C5、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C6、已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE7、已知:AB=6,AC=2,D 是BC 中线,求AD 的取值围。
8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
9、已知:AB//ED ,∠EAB=∠BDE ,AF=CD ,EF=BC ,求证:∠F=∠CDCBA FECDB ADBCA10、已知:AB=CD ,∠A=∠D ,求证:∠B=∠C11、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE12.如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .13.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,A 、B 为垂足,AB 交OM 于点N .求证:∠OAB =∠OBA14.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP于D .求证:AD +BC =AB .15.如图,△ABC 中,AD 是∠CAB 的平分线,且∠C =2∠B,求证:AB=AC+CD 16.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立AB C D请给予证明;若不成立请说明理由.17.已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):18.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.19、如图:DF=CE,AD=BC,∠D=∠C。
七年级下册数学三角形全等练习题

七年级下册数学三角形全等练习题一、选择题1.下列三角形不一定全等的是 A.有两个角和一条边对应相等的三角形 B.有两条边和一个角对应相等的三角形C.斜边和一个锐角对应相等的两个直角三角形 D.三条边对应相等的两个三角形.下列说法:①所有的等边三角形都全等②斜边相等的直角三角形全等③顶角和腰长对应相等的等腰三角形全等④有两个锐角相等的直角三角形全等其中正确的个数是A.1个 B.2个 C.3个 D.4个3.如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是A.BC=BDB.CE=DEC.BA平分∠CBDD.图中有两对全等三角形4.AD是△ABC的角平分线,自D向AB、AC两边作垂线,垂足为E、F,那么下列结论中错误的是 A.DE=DFB.AE=AF 角对应的角是.A.∠A B.∠B C.∠C D.∠B或∠C6.如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=.A.25° B.27° C.30° D.45°.如右图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,且AB=10 cm,则△BED 的周长为 A.cm B.10 cm; C.1cm D.20 cmCOE;③点O在∠BAC的角平分线上,其中正确的结论有A.3个 B.2个 C.1个 D.0个C.BD=CDD.∠ADE=∠ADF5.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是130°,那么△ABC中与这个A8.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,则①△ABE≌△ACFABE二、填空题9.如图,在△ABC中,AD平分∠BAC,过B作BE过E作EF∥AC交AB于F,则A、AF=2BF;B、AF=BF;C、AF>BF;D、AF 1.如果△ABC≌△A’B’C’,若AB=A’B’,∠B=50°,∠C=70°,则∠A’=°2.如图,若BD⊥AE于B,DC⊥AF于C,且DC=DC,∠BAC=40°,∠ADG=130°,则∠DGF=________。
七年级下册全等三角形题型

数学七年级下册《全等三角形》典型例题例1如图,ABC ∆≌ADE ∆,写出其对应顶点、对应边、对应角.例2如图,已知ABC ∆≌C B A '''∆,且C C B B ''、、、在同一直线上,(1)B B '和C C '相等吗?试说明理由;(2)如果︒=∠50A ,求A '∠和DC B '∠的度数.例3下列各题的全等三角形经过怎样的运动后能完全重合?(1)ABC ∆≌ADE ∆;(2)ABC ∆≌ADC ∆;(3)ABC ∆≌ADE ∆.例4如图,ABC ∆≌CDA ∆,求证:CDAB //例5如图,ABC ∆与DCB ∆全等,你能找出其中相等的线段和相等的角吗?参考答案例1分析:找对应元素,有一简便方法:先结合图形判断已知条件中的“ABC ∆≌ADE ∆”是否按照对应顶点的顺序写的,如果确认顺序正确,则可以按照以下顺序:写出它们的对应边:AB 与AD ,BC 与DE ,AC 与AE ,类似地,可以写出它们的对应顶点、对应角.解:对应顶点:A 与A ,B 与D ,C 与E对应边:AB 与AD ,BC 与DE ,AC 与AE对应角:ABC ∠与ADE ∠,ACB ∠与AED ∠,BAC ∠与DAE∠例2分析:(1)因为ABC ∆≌C B A '''∆,所以C C C B C B C B BC B B C B BC '='-''='-='''=,.(2)因为ABC ∆≌C B A '''∆,︒=∠='∠50A A ,又因为C B A B '''∠=∠,所以B A AB ''//.所以︒=∠='∠50A DC B .解:(1)C C B B '=',因为ABC ∆≌C B A '''∆,所以C B BC ''=,所以C C C B BC B B '='-='.(2)︒=∠='∠='∠50A DC B A 因为ABC ∆≌C B A '''∆,所以,︒=∠='∠50A A 所以C B A B '''∠=∠,所以B A AB ''//,所以︒=∠='∠50A DC B .说明:该题主要是应用“全等三角形对应边相等,对应角相等”,在找相等的边和角时,应注意“对应”.例3分析:这样的题关键是先找到对应边和对应角,即哪个边和哪个边重合,哪个角和哪个角重合就可以找到运动的办法.解:(1)把三角形ADE 顺时针旋转45°;(2)把三角形ABC 沿AC 对折过去;(3)把三角形ABC 沿A 、F 所在的直线对折过去.说明:(1)要找准对应边、对应角;(2)运动是相对的,所以两个三角形中移动哪个都可以.例4分析:本题是全等三角形与平行线的综合应用,由三角形全等可推出对应角相等,而由角相等可推出直线(或线段)平行.同学们,数学知识是前后贯通的,你体会到了吗?解:ABC ∆ ≌CDA∆∴DCA BAC ∠=∠(全等三角形对应角相等)∴CD AB //(内错角相等,两直线平行)例5分析:观察图形可知,公共边BC 与CB 、最长边BD 与CA 、最短边AB 与DC 是对应边.然后根据“对应边所对的角是对应角”或“两条对应边所夹的角是对应角”可以识别对应角.解:由全等三角形的对应边相等,对应角相等,得DB AC CB BC DC AB ===,,DBCACB DCB ABC D A ∠=∠∠=∠∠=∠,,。
七年级数学下册三角形周周测(全章)北师大版

第四章 三角形 周周测10一、细心选一选(每小题3分,共36分)1.下列说法正确的是……………………………………( )A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等 2.下列各组线段能组成三角形的是……………………( )A.3cm ,3cm ,6cmB.7cm,4cm,5cmC.3cm,4cm,8cmD.4.2cm,2.8cm,7cm 3.下列图形中,与已知图形全等的是……………………( )4.如图,已知△ABC ≌△CDE,其中AB=CD,那么下列结论中, 不正确的是……………………… ( )A.AC=CEB.∠BAC=∠CDEC.∠ACB=∠ECDD.∠B=∠D5.下列条件中,不能判定三角形全等的是……………………………………( ) A.三条边对应相等 B.两边和一角对应相等 C.两角和其中一角的对边对应相等 D.两角和它们的夹边对应相等6. 如图,把图形沿BC 对折,点A 和点D 重合,那么图中共有全等三角形…………………( )A.1对B.2对C.3对D.4对7.在△ABC 和△A ′B ′C ′中,已知AB= A ′B ′,∠B=∠B ′要保证△ABC ≌△A ′B ′C ′,可补充的条件是………………………………………………………………………………………………(A) (B) (C)(D)第3题图DE第4题ABDCE( )A.∠B+∠A=900B.AC= A ′C ′C.BC=B ′C ′D. ∠A+∠A ′=9008.已知在△ABC 和△A ′B ′C ′中,AB= A ′B ′,∠B=∠B ′,补充下面一个条件,不能说明△ABC≌△A′B′C′的是……………………………………………………………………………………( )A. BC=B ′C ′B. AC= A ′C ′C. ∠C=∠C ′D. ∠A=∠A ′9.如图,已知AE=CF,BE=DF.要证△ABE ≌△CDF,还需添加的一个条件是………( ) A.∠BAC=∠ACD B.∠ABE=∠CDF C.∠DAC=∠BCA D.∠AEB=∠CFD10.如图AD 是△ABC 的角平分线,DE 是△ABD 的高,EF 是△ACD 的高,则…( ) A.∠B=∠C B.∠EDB=∠FDC C.∠ADE=∠ADF D. ∠ADB=∠ADC 11.如图AC 与BD 相交于点O ,已知AB=CD,AD=BC,则图中全等三角形有………( ) A.1对 B.2对 C.3对 D.4对 12.如图,D 、E 分别是AB,AC 上一点,若∠B=∠C ,则在下列条件中,无法判定△ABE ≌△ACD 是………………………………( ) A.AD=AE B.AB=ACC.BE=CDD.∠AEB=∠ADC二、专心填一填:(每小题3分,共24分)13.如图,△ABC ≌△DEF,点B 和点E, 点A 和点D 是对应顶点, 则AB= ,CB= , ∠C= ,∠CAB= . 14.若已知两个三角形有两条边对应,则要视这两个三角形全等, 还需增加的条件可以是 或 .15.如图已知AC 与BD 相交于点O ,AO=CO,BO=DO,则AB=CD 请说明理由. 解:在△AOB 和△COD 中A B C D F E第9题AA AA 第10题A BCDO第11题ABCE第12题D第13题ABC DEFA BO(BO DO(AO CO ==⎧⎪⎨⎪⎩已知)(对顶角相等已知) ∴△AOB ≌△COD ( ) ∴AB=DC ( ) 16.如图,已知AO=OB,OC=OD,AD 和BC 相交于点E , 则图中全等三角形有 对.17.在△ABC 和△DEF 中,AB=4, ∠A=350, ∠B=700,DE=4, ∠D= , ∠E=700,根据 判定△ABC ≌△DEF.18.如图,在△ABC 和△DEF 中AB=DC(BC=DA(=⎧⎪⎨⎪⎩已知)已知)()∴△ABC ≌△DEF( )19.如图∠B=∠DEF,AB=DE,要证明△ABC ≌△DEF ,(1)若以“ASA ”为依据,需添加的条件是 ; (2)若以“SAS ”为依据,需添加的条件是 .20.如图,△ABC 中,AB=AC=13cm ,AB 的垂直平分线交AB 于D, 交AC 于E,若△EBC 的周长为21cm,则BC= cm.三、耐心答一答:(本题有6小题,共40分)21.(本题4分)已知∠α、∠β和线段a, 如图,用直尺和圆规作△ABC ,使∠A=∠α,∠B=∠β,BC=a.OABD第16题CE第19题B CAECD第18题ADAB CE D第20题22.(本题6分)已知AD 平分∠CAB,且DC ⊥AC, DB ⊥AB ,那么AB 和AC 相等吗?请说明理由.23.(本题6分)如图,已知BD=CD ,∠1=∠2. 说出△ABD ≌△ACD 的理由.24.(本题8分)如图,已知AB=DC ,AD=BC,说出下列判断成立的理由: (1) △ABC ≌△CDA (2) ∠B=∠D25.(本题8分) 如图,把大小为4×4的正方形方格图形分别分割成两个全等图形,例如图DCABABC12DB D①,请在下图中,沿着须先画出四种不同的分法,把4×4的正方形分割成两个全等图形26.(本题8分)如图,△ABC 中,AD 垂直平分BC,H 是AD 上一点,连接BH,CH.(1)AD 平分∠BAC 吗?为什么?(2)你能找出几堆相等的角?请把他么写出来(不需写理由)第四章 三角形 周周测10参考答案与解析一、细心选一选:(每小题3分,共36分)图①画法1画法2画法3画法4ACBHD二、专心填一填(每小题3分,共24分)13.DE,FE,∠F, ∠FED. 14.3第三边相等,这两边的夹角相等15. ∠AOB=∠COD,SAS,全等三角形的对应边相等 16.4 17.350, AAS 18.AC,CA,公共边,SSS 19.∠A=∠D 20.8三、耐心答一答(本题有六小题,共40分)21.图略 22.AB=AC 23.略 24.略25.26.(1)由△ADB≌△ADC(SAS)得∠BAD=∠CAD (4)4对,∠BHD=∠CHD, ∠ABD=∠ACD, ∠HBD=∠HCD, ∠BDA=∠CDA画法1 画法2 画法3 画法4。
北师大版数学七年级下册《全等三角形》练习题含答案

北师⼤版数学七年级下册《全等三⾓形》练习题含答案全等三⾓形练习题含答案⼀、选择题(每⼩题3分,共30分)1.在△ABC 中,∠B =∠C ,与△ABC 全等的三⾓形有⼀个⾓是100°,那么在△ABC 中与这100°⾓对应相等的⾓是()A.∠AB.∠BC.∠CD.∠B 或∠C2.如图,在CD 上求⼀点P ,使它到OA ,OB 的距离相等,则P 点是()A.线段CD 的中点B.OA 与OB 的中垂线的交点C.OA 与CD 的中垂线的交点D.CD 与∠AOB的平分线的交点3.如图所⽰,△ABD ≌△CDB ,下⾯四个结论中,不正确的是()A.△ABD 和△CDB 的⾯积相等B.△ABD 和△CDB 的周长相等C.∠A +∠ABD =∠C +∠CBDD.AD ∥BC ,且AD =BC4.如图,已知AB =DC ,AD =BC ,E ,F 在DB 上两点且BF =DE ,若∠AEB =120°,∠ADB =30°,则∠BCF =() A.150° B.40° C.80° D.90°5.所对的⾓的关系是()A.相等B.不相等C.互余或相等 6,如图,AB ⊥BC ,BE ⊥AC ,∠1=∠2,AD A.∠1=∠EFD B.BE =EC C.BF =DF =7.如图所⽰,BE ⊥AC 于点D ,且AD =CD ,BD A.25° B.27° C.30°A D A CB O DC B A8.如图,在△ABC 中,AD 平分∠BAC ,过B 作BE ⊥AD 于E ,过E 作EF ∥AC 交AB于F ,则()A.AF =2BFB.AF =BFC.AF >BFD.AF <BF9.如图所⽰,亮亮书上的三⾓形被墨迹污染了⼀部分,很快他就根据所学知识画出⼀个与书上完全⼀样的三⾓形,那么这两个三⾓形完全⼀样的依据是()A.SSSB.SASC.AASD.ASA10.将⼀张长⽅形纸⽚按如图4所⽰的⽅式折叠,BC BD ,为折痕,则CBD ∠的度数为() A .60° B .75° C .90° D .95°⼆、填空题(每⼩题3分,共24分)11. (08牡丹江)如图,BAC ABD ∠=∠,请你添加⼀个条件:,使OC OD=(只添⼀个即可).12.如图,在△ABC 中,AB =AC ,BE13.如图,AB =CD ,AD =BC ,O 为F ,若∠ADB =60°,EO =10,则∠DBCDOC B AFED C B A A EC B A ′ E ′D14.已知Rt △ABC 中,∠C =90°,AD 平分∠BAC 交BC 于D ,若BC =32,且BD ∶CD =9∶7,则D 到AB 边的距离为___.15.如果两个三⾓形的两条边和其中⼀条边上的⾼对应相等,那么这两个三⾓形的第三边所对的⾓的关系是__________.16.如图,AB ∥CD ,AD ∥BC ,OE =OF ,图中全等三⾓形共有______对.17.在数学活动课上,⼩明提出这样⼀个问题:∠B =∠C =90°,E 是BC 的中点,DE 平分∠ADC ,∠CED =35°,如图,则∠EAB 是多少度?⼤家⼀起热烈地讨论交流,⼩英第⼀个得出正确答案,是______.18.如图,AD ,A ′D ′分别是锐⾓三⾓形ABC 和锐⾓三⾓形A ′B ′C ′中BC ,B ′C ′边上的⾼,且AB =A ′B ′,AD =A ′D ′.若使△ABC ≌△A ′B ′C ′,请你补充条件________.(填写⼀个你认为适当的条件即可)三、解答题(第19-25每题8分,第26题10分,共60分)19.已知:△DEF ≌△MNP ,且EF =NP ,∠F =∠P ,∠D =48°,∠E =52°,MN =12cm ,求:∠P 的度数及DE 的长.20. 如图,∠DCE=90o ,CD=CE ,AD ⊥AC ,BE ⊥AC ,垂⾜分别为A 、B ,试说明AD+AB =BE.21.如图,⼯⼈师傅要检查⼈字梁的∠B 和∠C 是否相等,但他⼿边没有量⾓器,只有⼀个刻度尺.他是这样操作的:①分别在BA 和CA 上取BE =CG ;②在BC 上取BD =CF ;③A B C D A ′ B ′ D ′ C ′量出DE 的长a ⽶,FG 的长b ⽶.如果a =b ,则说明∠B 和∠C 是相等的.他的这种做法合理吗?为什么?22.要将如图中的∠MON 平分,⼩梅设计了如下⽅案:在射线OM ,ON 上分别取OA =OB ,过A 作DA ⊥OM 于A ,交ON 于D ,过B 作EB ⊥ON 于B 交OM 于E ,AD ,EB 交于点C ,过O ,C 作射线OC 即为MON 的平分线,试说明这样做的理由.23.如图所⽰,A ,E ,F ,C 在⼀条直线上,AE =CF ,过E ,F 分别作DE ⊥AC ,BF ⊥AC ,若AB =CD ,可以得到BD 平分EF ,为什么?若将△DEC 的边EC 沿AC ⽅向移动,变为图时,其余条件不变,上述结论是否成⽴?请说明理由.24.如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC 的平⾏线BG 于G 点,DE ⊥DF ,交AB 于点E ,连结EG 、EF .(1)求证:BG =CF . (2)请你判断BE +CF 与EF 的⼤⼩关系,并说明理由.25.(1)如图1,△ABC 的边AB 、AC 为边分别向外作正⽅形ABDE 和正⽅形ACFG ,连结EG ,试判断△ABC 与△AEG ⾯积之间的关系,并说明理由.(2)园林⼩路,曲径通幽,如图2所⽰,⼩路由⽩⾊的正⽅形理⽯和⿊⾊的三⾓形理⽯铺成.已知中间的所有正⽅形的⾯积之和是a 平⽅⽶,内圈的所有三⾓形的⾯积之和是b 平⽅⽶,这条⼩路⼀共占地多少平⽅⽶?A D E CB F G G D F AC B E GD FA CB E F E DC B AGFBD图1 图2参考答案:⼀、选择题1.A2.D3.C 提⽰:∵△ABD ≌△CDB ,∴AB =CD ,BD =DB ,AD =CB ,∠ADB =∠CBD ,∴△ABD 和△CDB 的周长和⾯积都分别相等.∵∠ADB =∠CBD ,∴AD ∥BC .4.D5.A6.D7.B 解析:在Rt △ADB 与Rt △EDC 中,AD =CD ,BD =ED ,∠ADB =∠EDC =90°,∴△ADB ≌△CDE ,∴∠ABD =∠E .在Rt △BDC 与Rt △EDC 中,BD =DE ,∠BDC =∠EDC =90°,CD =CD ,∴Rt △BDC ≌Rt △EDC ,∴∠DBC =∠E.∴∠ABD =∠DBC =12∠ABC ,∴∠E =∠DBC =12×54°=27°.提⽰:本题主要通过两次三⾓形全等找出∠ABD =∠DBC =∠E. 8.B 9.D 10. C⼆、填空题11. C D ∠=∠或ABC BAD ∠=∠或AC BD =或OAD OBC ∠=∠ 12.SAS 13.60°,10 14. 14提⽰:⾓平分线上的⼀点到⾓的两边的距离相等.15.互补或相等 16.5 17.35° 18.答案不惟⼀三、解答题19.解:∵△DEF ≌△MNP ,∴DE =MN ,∠D =∠M ,∠E =∠N ,∠F =∠P ,∴∠M =48°,∠N =52°,∴∠P =180°-48°-52°=80°,DE =MN =12cm.20. 解:因为∠DCE=90o (已知),所以∠ECB+∠ACD=90o ,因为EB ⊥AC ,所以∠E+∠ECB=90o (直⾓三⾓形两锐⾓互余).所以∠ACD=∠E(同⾓的余⾓相等).因为AD ⊥AC ,BE ⊥AC(已知),所以∠A=∠EBC=90o (垂直的定义).在Rt △ACD 和Rt△BEC 中,A EBC ACD E CD EC ∠=∠??∠=∠??=?,所以Rt △ACD ≌Rt △BEC(AAS).所以AD=BC ,AC=BE(全等三⾓形的对应边相等),所以AD+AB=BC+ AB=AC.所以AD+AB=BE.21.解:DE =AE .由△ABC ≌△EDC 可知.22.证明∵DA ⊥OM ,EB ⊥ON ,∴∠OAD=∠OBE=90°.在△OAD 和△OBE 中,,,(),OAD OBE AOD BOE OA OB ∠=∠??∠=∠??=?公共⾓∴△OAD ≌△OBE (ASA ),∴OD=OE ,∠ODA=∠OEB ,∴OD-OB=OE-OA .即BD=AE .在△BCD 和△ACE 中,,,(),ODA OEB BCD ACE BD AE ∠=∠??∠=∠??=?对顶⾓∴△BCD ≌△ACE (AAS ),∴BC=AC .在Rt △BOC 和Rt △AOC 中,,,B C A C O B O A =??=?∴△BOC ≌△AOC (HL ),∴∠BOC=∠AOC .23.∵DE ⊥AC 于点E ,BF ⊥AC 于点F ,∴∠DEF =∠BFE =90°.∵AE =CF ,∴AE +EF =CF +FE ,即AF =CE .在Rt△ABF 与Rt △CDE 中,AB =CD ,AF =CE ,∴Rt △ABF ≌Rt △CDE ,∴BF=DE.在Rt△DEG≌Rt△BFG中,∠DGE=∠BGF,DE=BF,∴Rt△DEG≌Rt△BFG,∴EG=FG,即BD平分EF.若将△DEC的边EC沿AC⽅向移动到图2时,其余条件不变,上述结论仍旧成⽴,理由同上.提⽰:寻找AF与CE的关系是解决本题的关键.24.(1)∵AC∥BG,∴∠GBD=∠C,在△GBD与△FCD中,∠GBD=∠C,BD=CD,∠BDG=∠CDF,∴△GBD≌△FCD,∴BG=CF.(2)BE+CF>EF,⼜∵△GBD≌△FCD(已证) ,∴GD=FD,在△GDE与△FDE中,GD =FD,∠GDE=∠FDE=90°,DE=DE,∴△GDE≌△FDE(SAS) ,∴EG=EF,∵BE+BG>GE,∴BE+CF>EF.25.(1)解:△ABC与△AEG⾯积相等.理由:过点C作CM⊥AB于M,过点G作GN ⊥EA交EA延长线于N,则∠AMC=∠ANG =90°,∵四边形ABDE和四边形ACFG都是正⽅形,∴∠BAE=∠CAG=90°,AB=AE,AC=AG,∴∠BAC+∠EAG=180°,∵∠EAG+∠GAN=180°,∴∠BAC=∠GAN,∴△ACM≌△AGN,∴CM=GN.∵S△ABC=12AB×CM,S△AEG=12AE×GN,∴S△ABC=S△AEG.(2)解:由(1)知外圈的所有三⾓形的⾯积之和等于内圈的所有三⾓形的⾯积之和,∴这条⼩路的⾯积为(a+2b)平⽅⽶.BD。
初一数学全等三角形测试题

这篇关于初⼀数学全等三⾓形测试题,是特地为⼤家整理的,希望对⼤家有所帮助!⼀、选择题(每⼩题3分,共30分)1.△ABC、△DEF中给出下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=EF ,∠C=∠F;④AB=DE, AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有( )A.1组B.2组C.3组D.4组2.已知图中的两个三⾓形全等,则∠α度数是( )A.72°B.60°C.58°D.50°第2题图第4题图第5题图第8题图3.下列结论正确的是( )A.有两个锐⾓相等的两个直⾓三⾓形全等;B.⼀条斜边对应相等的两个直⾓三⾓形全等;C.顶⾓和底边对应相等的两个等腰三⾓形全等;D.两个等边三⾓形全等.4.如图,△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )A.△ABD≌△ACDB.∠B=∠CC. AD是 BAC的平分线D.△ABC是等边三⾓形5.如图在△ABC中,AB=AC,⾼AD、BE、CF相交于O,如图所⽰,图中全等三⾓形的对数是( )A.4B.5C.6D.76.在△ABC内部取⼀点P使得点P到△ABC的三边距离相等,则点P是△ABC的哪三条线交点( )A.⾼B.⾓平分线C.中线D.垂直平分线7.不能确定两个三⾓形全等的条件是( )A.三边对应相等B.两边及夹⾓相等C.两⾓和任⼀边对应相等D.三⾓对应相等8.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E且AB=6 cm,则△DEB的周长为 ( )A.40 cmB.6 cmC.8 cmD.10 cm9. 下列命题中,错误的是( )A.全等三⾓形对应边上的中线相等B.⾯积相等的两个三⾓形是全等三⾓形C.全等三⾓形对应边上的⾼线相等D.全等三⾓形对应⾓的平分线相等10.下列条件能判定两个三⾓形全等的是( )A.有两边和第三边上的⾼对应相等B.有两边和其中⼀边的对⾓对应相等C.有两边和其中⼀边上的⾼对应相等D.有两边和第三边上的中线对应相等⼆、填空题(每题3分,共30分)11.如图,根据SAS,如果AB=AC, = ,即可判定ΔABD≌ΔACE.第11题图第13题图第17题图第19题图第20题图12.△ABC中,∠BAC∶∠ACB∶∠ABC=4∶3∶2,且△ABC≌△DEF,则∠DEF=________.13.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的⾯积是________.14.△ABC中,∠BAC=100°,D、E分别AB、AC的延长线上,∠DBC、∠BCE的⾓平分线交于点P,连接AP,则∠DAP=______.15.⼀个三⾓形的三边为2、5、x,另⼀个三⾓形的三边为y、2、6,若这两个三⾓形全等,则x+y= .16.在△ABC中,AB=AC,∠A=80°,将△ABC绕点B旋转,使点A落在BC上,点C落在点C’,那么∠BCC’的⼤⼩是______________.17.如图,AE=AF,AB=AC,∠A=60°,∠B=24°,则∠BOC= .18. △ABC内⼀点O到三边的距离都相等,且∠A=60°,则∠BOC= .19.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF.②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论序号是 .20. 如图,宽为50cm的长⽅形图案由20个全等的直⾓三⾓形拼成,其中⼀个直⾓三⾓形的⾯积为 .三、解答题(共60分)21.如图,AC⊥CB,DB⊥CB,AB=DC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学(周考)试题
时间:60分钟 满分:100分
一. 择题题(把正确答案填入表格内,每小题3分,共30分)
A .AB=DE ,BC=EF ,∠A=∠D
B .∠A=∠D ,∠C=∠F ,AC=EF
C .AB=DE ,BC=EF ,△ABC 的周长= △DEF 的周长
D .∠A=∠D ,∠B=∠
E ,∠C=∠F
2. 在△ABC 与△DEF 中,给出下列六个条件: (1)AB =DE ;(2)BC =EF ;(3)AC =DF ;(4)∠A =∠D ;(5)∠B =∠E ;(6)∠C =∠F ,以其中三个条件为已知,不能判断△ABC 与△DEF 全等 的是( ) A.(1)(5)(2) B.(1)(2)(3) C.(4)(6)(1) D.(2)(3)(4)
3.下列几种说法 ①全等三角形的对应边相等;②面积相等的两个三角
形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等。
其中正确的是( )
A. ①②
B. ②③
C. ③④
D. ①④
4. △ABC 和△DEF 中,∠B =∠E 、∠C =∠F,添加下列条件不能得
出△ABC ≌△DEF 的是( )
A. BC =EF
B. AB =DE
C. AC =DE
D. AC =DF
5.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=
∠D,④ ∠B=∠E,其中能使ΔABC ≌ΔAED 的条件有( )个.
A.4
B.3
C.2
D.1
6 .如图所示,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )
A B C D E F
2
A .80°
B .100°
C .60°
D .45°.
7. 如图, AD 是ABC △的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF ,连结BF ,CE .下列说法:①CE =BF ;②△ABD 和△ACD 面积相等; ③BF ∥CE ;④△BDF ≌△CDE .其中正确的有( ) A .1个 B .2个 C .3个 D .4个
8. 直角三角形两锐角的角平分线所交成的角的度数是( ) A .45° B .135° C .45°或135° D .都不对 9. 如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是( )
A .甲和乙
B .乙和丙
C .只有乙
D .只有丙
10. 已知:如图10,在△ABC 中,AB =AC
,D 是BC 的中点,DE ⊥AB 于E ,
DF ⊥AC 于F ,则图中共有全等三角形( )
A .5对
B .4对
C .3对
D .2对
二.填空题:(每空4分,共48分)
1. 如图,∠1=∠2,∠3=∠4,则图中全等三角形有____________对。
21
E
D
C B
A
第5题
A
D C
B
E
F
第6题 第7题
A D
E C B 第10题
F
G 第9题 E
第1题
第2题
第3题
3
2. 如图,已知在△ABC 中,∠A=90°,AB=AC,CD 平分∠
ACB ,DE ⊥BC 于E ,若15cm BC =,则DEB △的周长为 cm .
3.如图,ΔABC 的三边AB 、BC 、CA 的长分别是20、30、40、其中三条角平分线将ΔABD 分为三个三角形,则S ABO ∆:S BCO ∆:S CAO ∆等于______.
4.已知,△ABC ≌△DEF, BC =EF =6cm ,△ABC 的面积为18cm 2 ,则EF 边上的高的长是__________。
5 .一个三角形三边长分别为3、4、5,另一个三角形的三边为a 、b 、c ,且满足 a =b +1,b =c +1,a +c =8,那么这两个三角形的关系是_________________________。
6.如图,直线a.b.c 表示三条相互交叉 的公路,现在拟建一个货物中转站,要求它到 三条公路的距离都相等,刚可供选择的地址 有: 处;
7.如图:在四边形ABCD 中,点E 在边CD 上,连接AE 、BE 并延长AE 交BC 的延长线于点F ,给出下列5个关系式::①AD ∥BC ,②,DE=EC ③∠1=∠2,④∠3=∠4,⑤AD+BC=AB 。
将其中三个关系式作为已知,另外两个作为结论,构成正确的命题。
请用序号写出两个正确的命题:(书写形式:如果……那么……)(1) ;(2) ;
8. 如图,△ABC 中,∠C=90°,CD ⊥AB 于点D ,AE 是∠BAC 的平分线, 点E 到AB 的距离等于3cm ,则CF=_____cm 。
9. 如图,在Rt ΔABC 中,∠C=90°,BD 是∠ABC 的平分线,交于点D ,若CD=n ,AB=m ,则ΔABD 的面积是_______
a b
c
B
第8题
A
第9题
10. AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是____;中线AD的取值范围是____.
三、解答题:(每小题11分,共22分)
1.如图,已知AB∥DE,AB=DE,AF=DC,
请问图中有哪几对全等三角形?
并任选其中一对给予证明.
2.已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点
Q在CE上,CQ=AB。
判断线段AP和AQ的位置.大小关系,并证明.
3 4
E
4。
