物理化学课件多相平衡
合集下载
物理化学课件第五章 多相平衡
d ln p sub H m 2 dT RT
当温度变化不大时，subHm可看作常数
p2 sub H m 定积分: ln p1 R
1 1 T T 2 1
C-C方程
山东理工大学
25
三、固－液平衡 dp
dT
fus H m T fusVm
-----Clapeyron方程
克拉贝龙方程 克劳修斯-克拉贝龙方程
Trouton规则
山东理工大学
19
克拉贝龙方程 设某物质在一定T，p时达两相平衡： T, p平衡 相()
G=0
相()
dG()
T+dT, p+dp 平衡 所以dG()=dG()
相()
G=0
dG()
相()
当n=1mol时，即dGm()=dGm()
上式两边分别代入基本公式 dGm= – SmdT + Vmdp
山东理工大学
20
得 –Sm()dT + Vm()dp = –Sm()dT + Vm()dp
移项: [Vm()－Vm()]dp =[Sm()–Sm()]dT 整理为: dp /dT=Sm/ Vm 对于可逆相变Sm=Hm(可逆相变焓)/T
第五章 多相平衡
克 相 克 律 方 程
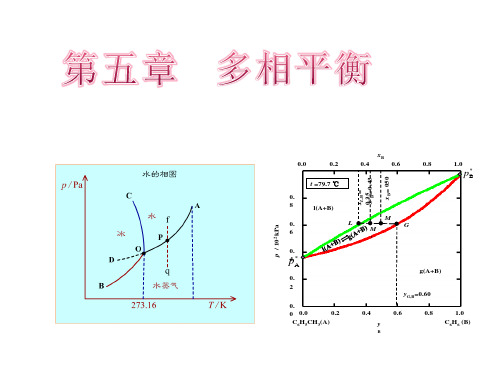
水 的 相 图
二 组 分 系 统
完 全 互 溶 双 液 系 统
部 分 互 溶 双 液 系 统
完 全 不 互 溶 双 液 系 统
低 共 熔 混 合 物
有 化 合 物 的 固 液 系 统
三 角 坐 标 图 表 示 法
习 题 课
引 言
相平衡是热力学在化学领域中的重要应用之一 研究多相系统的平衡在化学、化工的科研和生产 中有重要的意义，例如：溶解、蒸馏、重结晶、萃取、
物理化学第五章 多相平衡
f ( K 1) 2 K ( 1) K 2
F = K – Φ + 2 吉布斯相律
f=自由度，K=独立组分数，Φ=相数
一定条件下，f=K-Φ+1（凝固相系统或指定一个变量）
如果考虑电场、磁场，则f=K-Φ+n
例1 (1) 仅由 NH4Cl(s) 部分分解，建立如下反应平衡： NH4Cl (s) =NH3(g)+HCl(g) (2) 由任意量的 NH4Cl (s) 、NH3(g)、HCl(g) 建立如下反应 平衡： NH4Cl (s) =NH3(g)+HCl(g) 试求(1) 、(2)两种情况下，系统的 组分数 K=？自由度数f =? 解： (1) K = S - R - R´= 3 - 1 - 1=1 f = K - Φ + 2= 1 - 2 + 2 = 1 (2) K = S - R - R´= 3 - 1 - 0 =2 f =K-Φ+2= 2-2+2=2
xB 0.0 0.2 t =79.7 ℃ 0. 8 p / 102 kPa 0. 6 0. 4 p* 0. 2 yG,B=0.60 0. 0.2 0 0.0 C6H5CH3(A) 0.4 y
B
0.4 xL,B= 0.35 0.43 x' = xB= 050
0.6
0.8
1.0
* pB
l(A+B) L M ' M G
K=S-R=3-1=2
要注意独立二字：
C ( s) H 2O( g ) CO( g ) H 2 ( g ) C (s) C O2 (g) 2 C O(g) C O (g) H2O (g) C O2 ( g) H2 (g) (1) (2) (3)
物理化学：第四章 相平衡
NH4Cl(s)
∴ f＝1－2＋2＝1
b)若在上述体系中额外再加入少量NH3 反应产生的CNH3反＋CNH3加≠CHCl R’＝0 C＝S－R－R’＝3－1－0＝2 f＝2－2＋2＝2
NH3(g) NH3(g)、HCl(g)
NH4Cl(s)
c)NH4Cl(s)和任意量的NH3(g)和HCl(g)达平衡 C＝S－R－R’＝3－1－0＝2 f＝2－2＋2＝2
∑χB＝1。每一相的组成只要指定（S－1）个浓度变量就够了， 另一个已固定。总的浓度变量数是Φ（S－1）。
看看温度、压力有几个： 研究的是平衡体系，平衡体系的各相温度及压力都相等。
Tα = Tβ = Tγ = …… = TΦ Pα = Pβ = Pγ = …… = PΦ 总变量数 = Φ（S－1）+ 2
设某多组分多相平衡体系，其中含有S种物质，分布在Φ 个相中，要描述这个状态，需要指定独立变量数（即自由度 数）是多少？
根据数学原理： 自由度数（独立变量数）＝ 描述平衡体系的总变量数 －
平衡时变量之间的关系式的数目
总变量数是多少？ 通常一个体系的状态用温度、压力、浓度 这三种强度性质
的变量来描述，不考虑电场、磁场的影响。 有多少个浓度变量？
当Φ＝2时，f＝3－2＝1 单变量体系 图上的线
当Φ＝3时，f＝3－3＝0 不变体系 图上的点
对于单组分体系，f最大为P2/，Pa 有两个变量，所以可用平面
图来表示。
P/Pa
C
以水的相图为例说明：
A 水
①用相律分析水的相图上
冰
的点、线、面的意义
D
O 水蒸气
B
273.16
T/K
P/Pa
P/Pa
C A
第五章 多相平衡PhaseEquilibrium 物理化学课件
故系统中共有5种化学物种，2个独立反应， 则 C=5–2=3。设固体不互溶，即共4相，故F=3–4+2=1 。系统强度变量为T, p, p(CO), p(CO2), p(Zn)，5个强 度变量中只有1个是独立的。
(2) 相律的推导
现设该独立变量为温度，则根据纯液态锌的克拉佩 龙－克劳休斯方程，p(Zn)=f (T)， 在一定温度下有确 定的p(Zn)，上面第一个方程表示如下的平衡
ZnO(s) + C(s) = Zn(g) +CO(g) 因其平衡常数在定温下为定值，有K1=p(Zn)·p(CO) 于是p(CO)有定值。再根据第二个化学平衡，其平衡 常数在定温下为另一定值K2=p(CO2)/p2(CO)，因此 p(CO2)也有定值。故一个强度变量的值可确定其它四 个强度变量的值，F=1，同样若先确定另一强度变量 的值，例如p(CO)为某值，同样可推论出其它强度变 量的值。
(2) 相律的推导
设有 S 种物质在 P 个相中， 描述一个相的状态要 T，p，(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= P(S –1) + 2
(2) 相律的推导
在一个封闭的多相系统中，相与相之间可以有热的 交换、功的传递和物质的交流。对具有P个相系统的 热力学平衡，实际上包含了如下四个平衡条件： (1)热平衡条件：设系统有、Ⅱ······P 个相，达到平 衡时，各相具有相同温度
2c(NH3) = c(H2S) 但如果分解产物在不同相则不然，如反应：
CaCO3(s) = CO2(g) + CaO(s) c(CO2, g)和c(CaO, s)无关，则无浓度限制条件。 设浓度限制条件的数目为R′，则又有R′个关于浓度的 方程式。
(2) 相律的推导
(2) 相律的推导
现设该独立变量为温度，则根据纯液态锌的克拉佩 龙－克劳休斯方程，p(Zn)=f (T)， 在一定温度下有确 定的p(Zn)，上面第一个方程表示如下的平衡
ZnO(s) + C(s) = Zn(g) +CO(g) 因其平衡常数在定温下为定值，有K1=p(Zn)·p(CO) 于是p(CO)有定值。再根据第二个化学平衡，其平衡 常数在定温下为另一定值K2=p(CO2)/p2(CO)，因此 p(CO2)也有定值。故一个强度变量的值可确定其它四 个强度变量的值，F=1，同样若先确定另一强度变量 的值，例如p(CO)为某值，同样可推论出其它强度变 量的值。
(2) 相律的推导
设有 S 种物质在 P 个相中， 描述一个相的状态要 T，p，(x1, x2, …xs)
(S–1)种独立变量 所以总变量数= P(S –1) + 2
(2) 相律的推导
在一个封闭的多相系统中，相与相之间可以有热的 交换、功的传递和物质的交流。对具有P个相系统的 热力学平衡，实际上包含了如下四个平衡条件： (1)热平衡条件：设系统有、Ⅱ······P 个相，达到平 衡时，各相具有相同温度
2c(NH3) = c(H2S) 但如果分解产物在不同相则不然，如反应：
CaCO3(s) = CO2(g) + CaO(s) c(CO2, g)和c(CaO, s)无关，则无浓度限制条件。 设浓度限制条件的数目为R′，则又有R′个关于浓度的 方程式。
(2) 相律的推导
物理化学课件第4章_相平衡
上一内容 下一内容 ²回主目录
O返回
2021-3-12
Clausius-Clapeyron方程
对于气-液两相平衡，并假设气体为1mol理想气
体，将液体体积忽略不计，则
dp H vap m H vap m dT TVm (g) T (RT / p)
d ln p vap Hm
dT
RT 2
这就是Clausius-Clapeyron 方程，vapH m是摩尔气化热。
4.1 引言
相平衡是热力学在化学领域中的重要应用之一。 研究多相体系的平衡在化学、化工的科研和生产中有 重要的意义，例如：溶解、蒸馏、重结晶、萃取、提 纯及金相分析等方面都要用到相平衡的知识。
相图（phase diagram）表达多相体系的状态如何随 温度、压力、组成等强度性质变化而变化的图形， 称为相图。
OA 是气-液两相平衡线，即水的蒸气压曲线。它 不能任意延长，终止于临界点。临界点T 647 K , p 2.2107 Pa ，这时气-液界面消失。高于临界温
度，不能用加压的方法使气体液化。
OB 是气-固两相平衡线，即 冰的升华曲线，理论上可延长
至0 K附近。
OC 是液-固两相平衡线，当C点延长至压力大于 2108 Pa 时，相图变得复杂，有不同结构的冰生成。
•
=2260×18.02×(T2－
373)/(8.314×373×T2)
•
=40725(T2－373)/3101T2
• 解得:
•
T2=376.4K=103.7℃
上一内容 下一内容 ²回主目录
O返回
2021-3-12
例题
• 例2： 试计算在－0 .5℃下,欲使冰溶化所需施加的压力为多少? 已知: 冰的熔化热为333.5 J.g-1; 水=0.9998g.cm-3; 冰 =0.9168g.cm-3.
工科大学物理化学课件第十二章 相平衡1
§1 相 律
气体物质：不论有多少种气体混合，一般只有一个相。 液体物质： 按互溶程度可以组成单相（完全互溶）或多
相共存（完全不互溶或部分互溶）。
固体物质： 一般不互溶，因此一种固体便成为一个相；
但若两种以上固体物质形成固溶体（固体溶液），则该固
溶体为一个相。 2. 物种数 体系中所含化学物质的数目，用N表示。 工科大学化学
C= 、相数Φ = 、和自由度数f = 。
(a) C=3, Φ=2, f =3;
(c) C=1, Φ=2, f =1;
(b) C=2, Φ=2, f =2;
(d) C=2, Φ=1, f =3.
[例2] 由CaCO3、 CaO和CO2组成的体系，存在一 个化学反应： CaCO3(s) = CaO(s) + CO2(g) 问：体系的自由度数是多少？
水蒸气
工科大学化学
四、两相平衡线的斜率
三条两相平衡线的斜率均可由Clausius-Clapeyron方 程或Clapeyron方程求得。 p
OA线斜率为正，因为：
C
水 冰
A
trs H m vap H m 0 trsVm Vm,g Vm,l 0
vap H m dp ( )OA 0 dT T vapVm
因素 · · · · · · · · · · · · · · · · · · · · n个，等式· · · · · · · · · · · · · · · · · 共n(Φ –1)个 ▲ 化学势 μ1(α) = μ1(β) = μ1(γ) = μN(α) = μN (β) = μN (γ) =
……
= μ1(Φ) ， （Φ –1）个
工科大学化学
三条两相平衡线： 压力与温度只能改 变一个，指定了压力， 则温度由体系自定。 OA线： 液(水)-气(水蒸气) 平衡线，水蒸气压曲线
物理化学：相平衡
第五章 相平衡
相平衡是热力学在化学领域中的重要应用之一。研究 多相体系的平衡在化学、化工的科研和生产中有重要的 意义，例如：溶化、蒸馏、重结晶、萃取、提纯及金相 分析等方面都要用到相平衡的知识。
一、基本概念
第一节 相律
1、 相（phase） 体系内部物理和化学性质完全均匀的 部分称为相。相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。体系中相的总数 称为相数，用Φ表示。
三、自由度数（f）
自由度: 确定平衡体系的状态所必须的独立强度变量的
数目称为自由度，用字母 f 表示。这些强度变量通常是
压力、温度和浓度等。
以水为例〔注意是商量平衡态〕∶ a. 当φ=1时，例如液态水的T、p可在肯定范围内改变， φ不变 ∴ f=2 b. 当φ=2时，例如气－液平衡，指定p外，则Tb确定； 而指定T，则水有确定的平衡蒸气压p，∴ f=1 c. 当φ=3时，即气－液－固三相平衡共存时〔三相点〕，T、 p是确定的〔273.16K、6.1×102Pa、由水的性质所决定〕， ∴ f=0，如果变化T或p，则不可能三相共存〔即φ≠3〕。
一、水的相图 水的相图是依据实验绘制的。图上有：
水 的 相 图
(1) 气、液、固单相区∶f=1－1＋2=2
(2) 两相平衡线∶
f=1－2＋2=1
OC线∶气－液平衡
T与液态水的饱和蒸气压p蒸气的关系
或沸点Tb与p外的关系
OA线∶液－固平衡 凝固点Tf与p外的关系
OB线∶气－固平衡
T与冰的饱和蒸气压p蒸气的关系
dp/dT=ΔHm / T·ΔVm 此方程适合于任何纯物质的两相平衡
2、对于气－液或气－固两相平衡体系 近似处理∶a. 假设蒸气遵守理想气体状态方程
相平衡是热力学在化学领域中的重要应用之一。研究 多相体系的平衡在化学、化工的科研和生产中有重要的 意义，例如：溶化、蒸馏、重结晶、萃取、提纯及金相 分析等方面都要用到相平衡的知识。
一、基本概念
第一节 相律
1、 相（phase） 体系内部物理和化学性质完全均匀的 部分称为相。相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。体系中相的总数 称为相数，用Φ表示。
三、自由度数（f）
自由度: 确定平衡体系的状态所必须的独立强度变量的
数目称为自由度，用字母 f 表示。这些强度变量通常是
压力、温度和浓度等。
以水为例〔注意是商量平衡态〕∶ a. 当φ=1时，例如液态水的T、p可在肯定范围内改变， φ不变 ∴ f=2 b. 当φ=2时，例如气－液平衡，指定p外，则Tb确定； 而指定T，则水有确定的平衡蒸气压p，∴ f=1 c. 当φ=3时，即气－液－固三相平衡共存时〔三相点〕，T、 p是确定的〔273.16K、6.1×102Pa、由水的性质所决定〕， ∴ f=0，如果变化T或p，则不可能三相共存〔即φ≠3〕。
一、水的相图 水的相图是依据实验绘制的。图上有：
水 的 相 图
(1) 气、液、固单相区∶f=1－1＋2=2
(2) 两相平衡线∶
f=1－2＋2=1
OC线∶气－液平衡
T与液态水的饱和蒸气压p蒸气的关系
或沸点Tb与p外的关系
OA线∶液－固平衡 凝固点Tf与p外的关系
OB线∶气－固平衡
T与冰的饱和蒸气压p蒸气的关系
dp/dT=ΔHm / T·ΔVm 此方程适合于任何纯物质的两相平衡
2、对于气－液或气－固两相平衡体系 近似处理∶a. 假设蒸气遵守理想气体状态方程
物理化学课件05章 相平衡
根据偏摩尔量加和公式
dG dGB dGB B dnB B dnB
因为 dnB dnB
dG B dnB B dnB (B B )dnB
平衡时 dG 0
B B
同理，可以推广到多相平衡系统
(4) 化学平衡条件
在达到化学平衡时，反应物的化学势等于生 成物的化学势，化学势的代数和可表示为
相图（phase diagram） 研究多相系统的状态如何随温度、压力和组成 等强度性质变化而变化，并用图形来表示，这种图 形称为相图。
§5.1 引 言
相律（phase rule）
研究多相平衡系统中，相数、独立组分数与描 述该平衡系统的变数之间的关系。它只能作定性的 描述，而不能给出具体的数目。
相（phase） 系统内部物理和化学性质完全均匀的部分称 为相。
f * C 1
若除温度、压力外，还要考虑其他因素（如磁 场、电场、重力场等）的影响，则相律可表示为
f C n
§5.4 单组分系统的相平衡
单组分系统的两相平衡——Clapeyron方程
外压与蒸气压的关系—— 不活泼气体对液体蒸气压的影响
水的相图 *硫的相图
超临界状态
在 界面上宏观性质的改变是飞跃式的。
§5.1 引 言
系统中相的总数称为相数，用 表示。
气体，不论有多少种气体混合，只有一个气相。
液体，按其互溶程度可以组成一相、两相或三 相共存。
固体，一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀，仍是两个相（固体溶液 除外，它是单相）。
设 相膨胀了 dV 相收缩了 dV
当系统达平衡时 dA dA dA 0
dA p dV p dV 0
dV dV
p p
dG dGB dGB B dnB B dnB
因为 dnB dnB
dG B dnB B dnB (B B )dnB
平衡时 dG 0
B B
同理，可以推广到多相平衡系统
(4) 化学平衡条件
在达到化学平衡时，反应物的化学势等于生 成物的化学势，化学势的代数和可表示为
相图（phase diagram） 研究多相系统的状态如何随温度、压力和组成 等强度性质变化而变化，并用图形来表示，这种图 形称为相图。
§5.1 引 言
相律（phase rule）
研究多相平衡系统中，相数、独立组分数与描 述该平衡系统的变数之间的关系。它只能作定性的 描述，而不能给出具体的数目。
相（phase） 系统内部物理和化学性质完全均匀的部分称 为相。
f * C 1
若除温度、压力外，还要考虑其他因素（如磁 场、电场、重力场等）的影响，则相律可表示为
f C n
§5.4 单组分系统的相平衡
单组分系统的两相平衡——Clapeyron方程
外压与蒸气压的关系—— 不活泼气体对液体蒸气压的影响
水的相图 *硫的相图
超临界状态
在 界面上宏观性质的改变是飞跃式的。
§5.1 引 言
系统中相的总数称为相数，用 表示。
气体，不论有多少种气体混合，只有一个气相。
液体，按其互溶程度可以组成一相、两相或三 相共存。
固体，一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀，仍是两个相（固体溶液 除外，它是单相）。
设 相膨胀了 dV 相收缩了 dV
当系统达平衡时 dA dA dA 0
dA p dV p dV 0
dV dV
p p
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
线上出现一转折：当物系点通过三相线时，步冷曲 线上出现平台；(三相线的两端点除外)。
6
三组分相图
f32 Φ 5 Φ
保持温度和压力都不变 等边三角形坐标表示法
等边三角形坐标表示法
在等边三角形上，沿
A
反时针方向标出三个顶点。
三个顶点分别表示纯 组分A，B 和 C。
三条边上的点表示相
wB
b' c
ob
wA
5
3)凡是曲线都是两相平衡线。线上的一点为相点，表 示一个平衡相的状态。
4)凡是垂直线都可看成单组分纯物质。 如果是稳定化合物： 垂线顶端与曲线相交，为极大点； 若是不稳定化合物： 垂线顶端与水平线相交，为“T”形
5)凡是水平线基本上都是“三相线”。三相线上f = 0 6)冷却时，当物系点通过(两相平衡)曲线时，步冷曲
态解。： t/℃
l xB= 0.5
65℃
6℃ 1℃ A+AB2
14
B+l A+l
l+ B+ AB2 AB2
A xB= 0.x2B AB2
30℃ B
例4 已知A 、 B二组分系统的相图如下： (1) 画出a、 b、c三个系统冷却时的步冷曲线; (2) 标出各相区的相态，指出自由度为零的地方； (3) 使系统p降温，说明系统状态变化情况；
subHm= vapHm+ fusHm=51 kJmol-
1
lnp2 p1
s
uRH b mT11 T12
克-克方程
lnp2 51103 1 1 609 R 273263
p2 25P9a
12
例2 丙烯单体以液体状态存放较好。若储存场地 夏天最高气温为313K。试估计储液罐至少耐多大
压力？丙烯正常沸点225.7K 解：本题要求的是最高气温时丙烯的蒸气压为多少 ，根据克-克方程可求出。题目缺少气化热数据，根
B+A B2
α+β α+ B
A+B
稳定化合物
不稳定化合物
有共轭溶液
2
四、二组分系统相图基本特征：
1）单相区： A，B两组分能形成溶液或固溶体的部分。 相区内的一点既代表系统的组成和温度； 又代表该相的组成和温度。
2）两相区： 处于两个单相区或单相线之间。 相区内的一点只代表系统的组成和温度； 结线两端点代表各相的组成和温度。 两相区内适用杠杆规则。
2 下列化学反应，同时达平衡时(900—1200K)，
CaCO3(s) = CaO(s) + CO2(g)
CO2(g) + H2(g) = CO(g) + H2O(g)
CO(g) + H2O(g) + CaO(s) = CaCO3(s) +
H2(g)
4
3
3
其独立组分数C =__, 相数 =__，和自由度数f =__
lnaAfuR H s m,AT1f,AT1f
180301 1 R 600 500
aA= 0.485 = xA = (1-xB ) = 1.21
18
Na2CO3溶液，一相是Na2CO3(s)，一相是
______N__a_2C__O_3__H_2_O____ 。
11
7 水在三相点附近的蒸发热和熔化热分别为45kJmol1和6kJm____ kJmol-1。–10C时冰的蒸气压 =_2_5_9_P_a___ 。 计算依据是什么？
据特鲁顿规则： H 88.0JK1 Tb
lnp p1 28.0 8 R Tb212 .7 5311 32.952p2 19.1p
13
例3 苯(A)和二苯基甲醇(B)的熔点分别为6℃和65 ℃
A和B可形成不稳定化合物AB2，它在30℃时分解为B
和xB=0.5的熔液。低共熔点为1℃, 低共熔液组成
xB=0.2根据以上数据绘出其二元相图，并指出各区相
(4) 已知纯A的凝固热为-18.03J·mol-1（设不随温度变 化）。低共熔液组成 xB =0.6，当把A作为非理想溶
液中的溶剂时，求该溶液中组分A的活度系数。
解：从图上可知A的熔点和低共熔点分别为337ºC、 237ºC，低共熔液组成 xB =0.6。根据非理想溶液中 溶剂的凝固点下降公式：
多相平衡习题课
周利鹏
（一）总结
一、相律：f = K – + 2 二、克拉贝龙方程 三、二组分系统基本相图： 1.两种固态物质完全不互溶的相图
dp Hm dT TVm
l
np2 p1
v
R aH p mT11T12
l+AB2
β +B
A+l
l+ B
A+ B
低共熔点
l+AB A+AB B+AB
A+AB2
9
3 AlCl3溶液完全水解后，此系统的独立组分数=_3_ ，自由度数=__3___。
4 完全互溶双液系统xB=0.6处，平衡蒸气压有最高 值，那么组成xB=0.4的溶液在气液平衡时，xB(g), xB(l), xB(总)大小顺序为_x_B_(_l)_<_x_B_(_总__)<__x_B_(g_)___， 将该溶液完全分馏，塔顶将得到 __恒__沸__点__混__合_物____ 。
a
a'
应两个组分的质量分数， B c '
C
对应顶点的含量为零
wC
wAwBwC1
三角形内任一点都代表三组分系统
a ' b ' c ' a b c 1
（二）例题
例1 1 固体Fe, FeO, Fe3O4与气体CO, CO2达到平衡时，其 独立组分数C =__3_, 相数 =_4__，和自由度数f =_1___
a bc
p
337ºC
237ºC
0.6
A
xB
15
0.8 B
解: (1), (2)
a bc
ab
c
l l+ AB4 l+B
l+A
A+AB4
B+ AB4
f=0：三相线处，两个纯物质的熔点处
16
p
q
r E
s
A
xB
B
17
(3) pq: =1, f=2 q r:析出固体,
=2 (A+sln) , f=1 液相组成q E移动 r: A+AB4+E(sln) , f=0 rs: A+AB4
10
5 A, B双液系的相图如下，将 s
点所代表的物系分馏，并将馏液
T
和残液分别冷却到温度T1，残液
的相数为___2__ ，相点是_a_,_b___
l1+l2
。
sa
b
6 Na2CO3(s)可形成三种水合物Na2CO3 H2O,
Na2CO3 7H2O, Na2CO3 10H2O 。常压下将
Na2CO3(s)投入其水溶液中，待三相平衡时，一相是
6
三组分相图
f32 Φ 5 Φ
保持温度和压力都不变 等边三角形坐标表示法
等边三角形坐标表示法
在等边三角形上，沿
A
反时针方向标出三个顶点。
三个顶点分别表示纯 组分A，B 和 C。
三条边上的点表示相
wB
b' c
ob
wA
5
3)凡是曲线都是两相平衡线。线上的一点为相点，表 示一个平衡相的状态。
4)凡是垂直线都可看成单组分纯物质。 如果是稳定化合物： 垂线顶端与曲线相交，为极大点； 若是不稳定化合物： 垂线顶端与水平线相交，为“T”形
5)凡是水平线基本上都是“三相线”。三相线上f = 0 6)冷却时，当物系点通过(两相平衡)曲线时，步冷曲
态解。： t/℃
l xB= 0.5
65℃
6℃ 1℃ A+AB2
14
B+l A+l
l+ B+ AB2 AB2
A xB= 0.x2B AB2
30℃ B
例4 已知A 、 B二组分系统的相图如下： (1) 画出a、 b、c三个系统冷却时的步冷曲线; (2) 标出各相区的相态，指出自由度为零的地方； (3) 使系统p降温，说明系统状态变化情况；
subHm= vapHm+ fusHm=51 kJmol-
1
lnp2 p1
s
uRH b mT11 T12
克-克方程
lnp2 51103 1 1 609 R 273263
p2 25P9a
12
例2 丙烯单体以液体状态存放较好。若储存场地 夏天最高气温为313K。试估计储液罐至少耐多大
压力？丙烯正常沸点225.7K 解：本题要求的是最高气温时丙烯的蒸气压为多少 ，根据克-克方程可求出。题目缺少气化热数据，根
B+A B2
α+β α+ B
A+B
稳定化合物
不稳定化合物
有共轭溶液
2
四、二组分系统相图基本特征：
1）单相区： A，B两组分能形成溶液或固溶体的部分。 相区内的一点既代表系统的组成和温度； 又代表该相的组成和温度。
2）两相区： 处于两个单相区或单相线之间。 相区内的一点只代表系统的组成和温度； 结线两端点代表各相的组成和温度。 两相区内适用杠杆规则。
2 下列化学反应，同时达平衡时(900—1200K)，
CaCO3(s) = CaO(s) + CO2(g)
CO2(g) + H2(g) = CO(g) + H2O(g)
CO(g) + H2O(g) + CaO(s) = CaCO3(s) +
H2(g)
4
3
3
其独立组分数C =__, 相数 =__，和自由度数f =__
lnaAfuR H s m,AT1f,AT1f
180301 1 R 600 500
aA= 0.485 = xA = (1-xB ) = 1.21
18
Na2CO3溶液，一相是Na2CO3(s)，一相是
______N__a_2C__O_3__H_2_O____ 。
11
7 水在三相点附近的蒸发热和熔化热分别为45kJmol1和6kJm____ kJmol-1。–10C时冰的蒸气压 =_2_5_9_P_a___ 。 计算依据是什么？
据特鲁顿规则： H 88.0JK1 Tb
lnp p1 28.0 8 R Tb212 .7 5311 32.952p2 19.1p
13
例3 苯(A)和二苯基甲醇(B)的熔点分别为6℃和65 ℃
A和B可形成不稳定化合物AB2，它在30℃时分解为B
和xB=0.5的熔液。低共熔点为1℃, 低共熔液组成
xB=0.2根据以上数据绘出其二元相图，并指出各区相
(4) 已知纯A的凝固热为-18.03J·mol-1（设不随温度变 化）。低共熔液组成 xB =0.6，当把A作为非理想溶
液中的溶剂时，求该溶液中组分A的活度系数。
解：从图上可知A的熔点和低共熔点分别为337ºC、 237ºC，低共熔液组成 xB =0.6。根据非理想溶液中 溶剂的凝固点下降公式：
多相平衡习题课
周利鹏
（一）总结
一、相律：f = K – + 2 二、克拉贝龙方程 三、二组分系统基本相图： 1.两种固态物质完全不互溶的相图
dp Hm dT TVm
l
np2 p1
v
R aH p mT11T12
l+AB2
β +B
A+l
l+ B
A+ B
低共熔点
l+AB A+AB B+AB
A+AB2
9
3 AlCl3溶液完全水解后，此系统的独立组分数=_3_ ，自由度数=__3___。
4 完全互溶双液系统xB=0.6处，平衡蒸气压有最高 值，那么组成xB=0.4的溶液在气液平衡时，xB(g), xB(l), xB(总)大小顺序为_x_B_(_l)_<_x_B_(_总__)<__x_B_(g_)___， 将该溶液完全分馏，塔顶将得到 __恒__沸__点__混__合_物____ 。
a
a'
应两个组分的质量分数， B c '
C
对应顶点的含量为零
wC
wAwBwC1
三角形内任一点都代表三组分系统
a ' b ' c ' a b c 1
（二）例题
例1 1 固体Fe, FeO, Fe3O4与气体CO, CO2达到平衡时，其 独立组分数C =__3_, 相数 =_4__，和自由度数f =_1___
a bc
p
337ºC
237ºC
0.6
A
xB
15
0.8 B
解: (1), (2)
a bc
ab
c
l l+ AB4 l+B
l+A
A+AB4
B+ AB4
f=0：三相线处，两个纯物质的熔点处
16
p
q
r E
s
A
xB
B
17
(3) pq: =1, f=2 q r:析出固体,
=2 (A+sln) , f=1 液相组成q E移动 r: A+AB4+E(sln) , f=0 rs: A+AB4
10
5 A, B双液系的相图如下，将 s
点所代表的物系分馏，并将馏液
T
和残液分别冷却到温度T1，残液
的相数为___2__ ，相点是_a_,_b___
l1+l2
。
sa
b
6 Na2CO3(s)可形成三种水合物Na2CO3 H2O,
Na2CO3 7H2O, Na2CO3 10H2O 。常压下将
Na2CO3(s)投入其水溶液中，待三相平衡时，一相是