数据结构:第七章 查找
数据结构 查找

用二次探测再散列技术处理冲突
再哈希法
当发生冲突时,用另一个哈希函数计算出 另—个哈希地址,如果还发生冲突,再使 用另一个哈希函数,直至不发生冲突为止。 这种方法要求预先设置一个哈希函数的序 列。
链地址法
链地址法解决冲突的做法是将所有关键字为同义 词的结点链接在同一个单链表中。若哈希函数的 值域为0~m-1,则可将散列表定义为一个由m 个头指针组成的指针数组HT[m],凡是散列地址 为i的结点,均插入到以HT[i]为头指针的单链表 中。
7.4.4 哈希表查找的性能分析
由于冲突的存在,产生冲突后的查找仍然是给定值与 关键码进行比较的过程。
在查找过程中,关键码的比较次数取决于产生冲突的 概率。而影响冲突产生的因素有: (1)散列函数是否均匀
(2)处理冲突的方法
(3)散列表的装载因子 α =表中填入的记录数/表的长度
几种不同处理冲突方法的平均查找长度
查找算法的性能
平均查找长度:查找算法进行的关键码的比较 次数的数学期望值。计算公式为:
ASL = pi ci i =1
其中:n:问题规模,查找集合中的记录个数; pi:查找第i个记录的概率; ci:查找第i个记录所需的关键码的比较次数。
n
结论:ci取决于算法;pi与算法无关,取决于具体应用。如果 pi是已知的,则平均查找长度只是问题规模的函数。
使用条件: 线性表中的记录必须按关键码有序; 必须采用顺序存储。 基本思想: 在有序表中,取中间记录作为比较对象,若给定值与 中间记录的关键码相等,则查找成功;若给定值小于 中间记录的关键码,则在中间记录的左半区继续查找; 若给定值大于中间记录的关键码,则在中间记录的右 半区继续查找。不断重复上述过程,直到查找成功, 或所查找的区域无记录,查找失败。
数据结构7 查找

折半法算法分析
假设:查找关键字为0-6的数据
查找的过程形成二叉判定树
3
5 2 4 6
ASL=1/7(1+2×2+4×3)
1
=2.43
0
假设:有序表长度为n,且n≤2h-1 二叉判定树 若n=2h-1 则:查找过程为一棵深度为h的满二叉树,
2014-7-4 第7章 查找 18
则满二叉树的第 i 层有2i-1个结点。
分块[17,8,21,19],[31,33,25,22], [43,37,35,40], [61,73,78,55] 索引表:21 33 43 78
数据表
17 8 21 19 31 33 25 22 43 37 35 40 61 73 78 55 … … … … … … … … … … … … … … … …
(2)key与R[mid].key比较
若key=R[mid].key则查找成功; 若key<R[mid].key ,则high=mid-1,转(3)。 若key>R[mid].key ,则low=mid+1,转(3)。 (3)若low≤high, 则重复(1) 否则:查找不成功,结束。
2014-7-4
关键字 地址 21 33 43 78
2014-7-4
第7章 查找
22
表结构说明:
typedef struct {KeyType key; int link; } indextype; indextype Lr[m] typedef struct {char name[10]; KeyType key; } DataType; DataType r[Max];
ASL=∑[(1/n)×2i-1 ×i]
《数据结构(C语言版 第2版)》(严蔚敏 著)第七章练习题答案

《数据结构(C语言版第2版)》(严蔚敏著)第七章练习题答案第7章查找1.选择题(1)对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为()。
A.(n-1)/2B.n/2C.(n+1)/2D.n答案:C解释:总查找次数N=1+2+3+…+n=n(n+1)/2,则平均查找长度为N/n=(n+1)/2。
(2)适用于折半查找的表的存储方式及元素排列要求为()。
A.链接方式存储,元素无序B.链接方式存储,元素有序C.顺序方式存储,元素无序D.顺序方式存储,元素有序答案:D解释:折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
(3)如果要求一个线性表既能较快的查找,又能适应动态变化的要求,最好采用()查找法。
A.顺序查找B.折半查找C.分块查找D.哈希查找答案:C解释:分块查找的优点是:在表中插入和删除数据元素时,只要找到该元素对应的块,就可以在该块内进行插入和删除运算。
由于块内是无序的,故插入和删除比较容易,无需进行大量移动。
如果线性表既要快速查找又经常动态变化,则可采用分块查找。
(4)折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
若查找表中元素58,则它将依次与表中()比较大小,查找结果是失败。
A.20,70,30,50B.30,88,70,50C.20,50D.30,88,50答案:A解释:表中共10个元素,第一次取⎣(1+10)/2⎦=5,与第五个元素20比较,58大于20,再取⎣(6+10)/2⎦=8,与第八个元素70比较,依次类推再与30、50比较,最终查找失败。
(5)对22个记录的有序表作折半查找,当查找失败时,至少需要比较()次关键字。
A.3B.4C.5D.6答案:B解释:22个记录的有序表,其折半查找的判定树深度为⎣log222⎦+1=5,且该判定树不是满二叉树,即查找失败时至多比较5次,至少比较4次。
(6)折半搜索与二叉排序树的时间性能()。
王道数据结构 第七章 查找思维导图-高清脑图模板
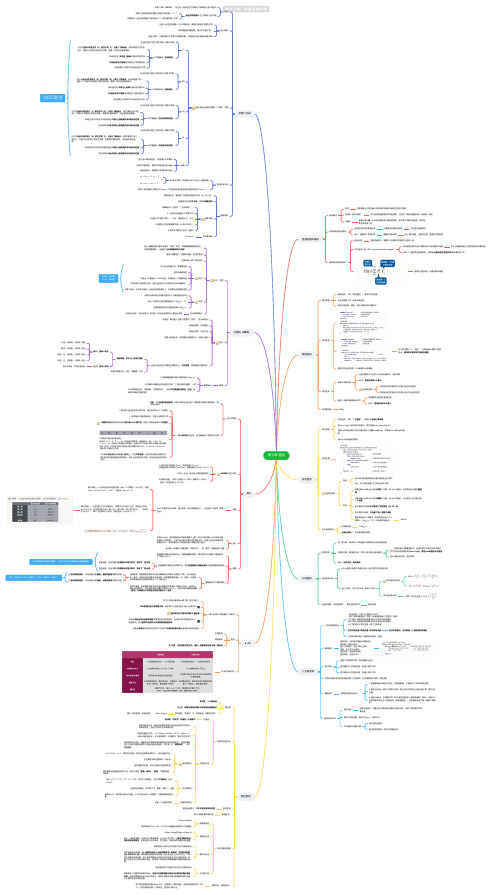
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
第1.7章 数据结构——查找

若对此算法进行一些改进, 若对此算法进行一些改进,在表尾增加一个关键字为 指定值K的记录 可避免每“比较”一次, 的记录, 指定值 的记录,可避免每“比较”一次,就要判别查找 是否结束。 很大时, 是否结束。当n很大时,大约可节省一半的时间。 很大时 大约可节省一半的时间。
The College of Computer Science and Technology
性能分析
折半查找成功的平均查找长度为: 折半查找成功的平均查找长度为: ASLbs=[log2n]+1 (求解过程从略 求解过程从略) 求解过程从略 折半查找的优点是比较次数少,查找速度快, 折半查找的优点是比较次数少,查找速度快,但只能 对有序表进行查找。 对有序表进行查找。它适用于一经建立就很少变动而又经 常需进行查找的有序表。 常需进行查找的有序表。
改进算法
#define MAXLEN n+1 int seqsearch2(DATATYPE A[],int k) { int i; i=0; A[MAXLEN−1].key=k;
The College of Computer Science and Technology
while (A[i].key!=k) i++; if (i<MAXLEN−1) return i; else return –1; } 称作监视哨, 将A[MAXLEN−1]称作监视哨,这个增加的记录起 称作监视哨 到了边界标识的作用。 到了边界标识的作用。
第一篇 数据结构
第7章 查找 章
章节分布
1 2 3 4
查找的基本概念
顺序查找
数据结构:第七章 查找

索引表
22 48 86 1 7 13
查38
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 22 12 13 8 9 20 33 42 44 38 24 48 60 58 74 57 86 53
查找方法比较
ASL 表结构 存储结构
顺序查找 最大
折半查找 最小
关键字输入顺序:45,24,53,12,28,90
45
24
53
12
28
90
9.4 哈希查找
基本思想:在记录的存储地址和它的关键字之间建立一 个确定的对应关系(函数关系);这样,不经过比较, 直接通过计算就能得到所查元素。
一、定义
❖哈希函数——在记录的关键字与记录的存储地址之间 建立的一种对应关系叫哈希函数。
high low
1 2 3 4 5 6 7 8 9 10 11 5 13 19 21 37 56 64 75 80 88 92
6
56
3
9
19
80
1
4
7
10
5 21 64 88
比较1次 比较2次 比较3次
2
13
5
8
37 75
11
92
比较4次
判定树(二叉排序树):描 述查找过程的二叉树
把当前查找区间的中间位 置上的结点作为根,左子表 和右子表中的结点分别作 为根的左子树和右子树
适用条件:采用顺序存储结构的有序表。 算法实现
❖设表长为n,low、high 和 mid分别指向待查元素所 在区间的上界、下界和中点,k为给定值
❖初始时,令low=1, high=n, mid=(low+high)/2 ❖让k与mid指向的记录比较
数据结构实验七 查找

数据结构实验七查找在计算机科学中,数据结构是组织和存储数据的方式,而查找则是在给定的数据结构中寻找特定元素的操作。
本次实验七的重点就是深入研究查找这一重要的数据处理操作。
查找操作在我们日常生活和计算机程序中无处不在。
想象一下在电话簿中查找一个朋友的号码,或者在图书馆的书架中寻找一本书,这都是查找的实际应用场景。
在计算机程序中,当我们需要从大量数据中快速找到所需的信息时,高效的查找算法就显得至关重要。
常见的查找算法有顺序查找、二分查找、哈希查找等。
顺序查找是最简单直接的方法,它从数据结构的起始位置开始,依次比较每个元素,直到找到目标元素或者遍历完整个数据结构。
这种方法适用于数据量较小或者数据未排序的情况。
让我们通过一个简单的示例来理解顺序查找。
假设有一个整数数组5, 3, 8, 2, 9,我们要查找数字 8。
从数组的第一个元素 5 开始,依次与8 进行比较。
当比较到第三个元素时,找到了目标数字 8,查找结束。
虽然顺序查找的思路简单,但在数据量较大时,它的效率相对较低。
与顺序查找不同,二分查找则要求数据是有序的。
它通过不断将待查找的区间一分为二,逐步缩小查找范围,从而提高查找效率。
还是以整数数组为例,比如 2, 4, 6, 8, 10 要查找数字 6。
首先,比较中间元素 6 和目标数字 6,正好相等,查找成功。
如果要查找的数字小于中间元素,则在左半区间继续查找;如果大于中间元素,则在右半区间查找。
二分查找的效率在有序数据中表现出色。
然而,如果数据经常变动,需要频繁进行插入和删除操作,维护数据的有序性可能会带来较大的开销。
哈希查找则是另一种常见的查找方法。
它通过一个哈希函数将关键字映射到一个特定的位置,从而实现快速查找。
哈希函数的设计至关重要,如果设计不当,可能会导致大量的冲突,影响查找效率。
在实际应用中,选择合适的查找算法取决于多种因素,如数据的规模、数据的分布特征、查找的频繁程度以及对时间和空间复杂度的要求等。
《数据结构(C语言)》第7章 查找

教学要求
❖ 建议学时:6学时 ❖ 总体要求
掌握顺序查找、折半查找的实现方法; 掌握动态查找表(二叉排序树、二叉平衡树)的构造
和查找方法; 掌握哈希表、哈希函数a structures
教学要求
❖ 相关知识点
顺序查找、折半查找的基本思想、算法实现和查找效 率分析
Data structures
静态查找表
❖ 顺序查找
❖1. 一般线性表的顺序查找
(2) 静态查找表的顺序存储结构
静态查找表采用顺序存储结构,其类型定义如下:
typedef struct
{ ElemType *elem; 建表时按实际长度分配*/
/*元素存储空间基址,
int TableLen;
/*表的长度*/
Data structures
静态查找表
❖ 分块查找
索引表的类型定义如下:
typedef struct{
Elemtype key;
/*块内最大关键字值*/
int stadr; 的位置*/
/*块中第一个记录
}indexItem;
typedef struct{
indexItem elem[n];
int length;
Data structures
静态查找表
❖ 折半查找
4.折半查找算法 算法7.2 折半查找算法
else if(L.elem[mid].key>key)high=mid-1; 前半部分继续查找*/
else low=mid+1; /*从后半部分继续查找*/
}
return -1; /*顺序表中不存在待查元素*/
(1) 基本思想 从线性表的一端开始,逐个检查关键字是否满足给定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iii
比较次数:
查找第n个元素: 1
查找第n-1个元素:2
……….
查找第1个元素: n
查找第i个元素: n+1-i
查找失败:
n+1
ii
比较次数=5
数据结构定义:
因一般不对查找表做修改,表长不变,所以可将其 作为常量。以顺序表为例:
#define n 100
typedef struct
{ keytype key;
1、 顺序查找
查找过程:从表的一端开始逐个进行记录的关键字和给 定值的比较。若相等则成功;若扫描结束仍未找到,则 失败。
找64
例 0 1 2 3 4 5 6 7 8 9 10 11 64 5 13 19 21 37 56 64 75 80 88 92
监视哨:设置在两 端r[0]或r[n+1], 使其关键字值为给 定值k。避免每次 的越界判断。
第七章 查 找
➢线性表的查找 ➢树上的查找 ➢散列技术
7.1 基本概念
查找——也叫检索,是根据给定的某个值,在表(指查找表) 中确定一个关键字等于给定值的记录或数据元素。
关键字——是数据元素中某个数据项的值,它可以标识一 个数据元素。
平均查找长度ASL——由于查找运算的关键操作是关键字的 比较。通常以查找过程中对关键字执行的平均比较次数, 即平均查找长度(ASL),作为衡量一个查找算法效率优劣的 标准。
high low
1 2 3 4 5 6 7 8 9 10 11 5 13 19 21 37 56 64 75 80 88 92
6
56
3
9
19
80
1
4
7
10
5 21 64 88
比较1次 比较2次 比较3次
2
13
5
8
37 75
11
92
比较4次
判定树(二叉排序树):描 述查找过程的二叉树
把当前查找区间的中间位 置上的结点作为根,左子表 和右子表中的结点分别作 为根的左子树和右子树
1 n
则ASL
n i 1
pi ci
1 n
n i 1
(n i 1)
n 1 2
顺序查找的优缺点:
优点:简单且适用面广,对表的结构没有要求, 无论记录是否按关键字有序都可应用。
缺点:效率低。
2、 折半查找(二分查找)
查找过程:以中间位置记录关键字与给定值比 较。相等则成功;不等,则缩小查找范围,继 续查找。每次将待查记录所在区间缩小一半。
查找方法的确定:首先取决于使用的数据结构(线性表、 图);其次是表的有序性(有序、无序)。主要分为:顺 序查找、折半查找和分块查找,这3种属于静态查找(查找 过程不修改原结构),一般以线性表做为数据结构。另一 类是二叉排序树查找,属于动态查找(即动态生成查找结 构,在查找同时,对原结构做修改)。
7.2 线性表的查找——静态查找
return 0;
// 顺序表中不存在待查元素
} // Search_Bin
算法评价
❖折半查找过程恰好是走了一条从根结点到被查结点的 路径.比较次数为路径上结点个数(被查结点在树上的 层数),在查找过程中进行的比较次数最多不超过其判 定树的深度.
算法描述
找21 例 1 2 3 4 5 6 7 8 9 10 11
5 13 19 21 37 56 64 75 80 88 92
low
mid
123456 7 5 13 19 21 37 56 64
high
8 9 10 11 75 80 88 92
low
mid
high
1 2 3 4 5 6 7 8 9 10 11
5 13 19 21 37 56 64 75 80 88 92
lowmid high
找70 例 1 2 3 4 5 6 7 8 9 10 11
5 13 19 21 37 56 64 75 80 88 92
low
mid
123456 7
5 13 19 21 37 56 64
high 8 9 10 11 75 80 88 92
{ mid = (low + high) / 2;
if(k= = r[mid].key ) return mid; //找到
if ( k < r[mid].key ) high = mid - 1;
// 继续在前半区间内进行查找
else low = mid + 1; // 继续在后半区间内进行查找
} //while
折半查找算法:
int Search_Bin ( Seqlist r, KeyType k )
{// 在有序表ST中折半查找其关键字等于kval的数据元素。 // 若找到,则函数值为该元素在表中的位置,否则为0。
int low = 1, high = n, mid; // 置区间初值
while (low <= high)
low
mid
high
1 2 3 4 5 6 7 8 9 10 11
5 13 19 21 37 56 64 75 80 88 92
low mid high 1 2 3 4 5 6 7 8 9 10 11 5 13 19 21 37 56 64 75 80 88 92
low high mid
1 2 3 4 5 6 7 8 9 10 11 5 13 19 21 37 56 64 75 80 88 92
若找到则返回该元素在表中的位置,否则为0。
int i=n;
r[0].key == k;
// 设置"哨兵“
while(r[i].key != k) i--; // 从后往前查找
return i; // 成功则返回位置不成功返回0
} // Search_Seq
顺序查找方法的ASL
设表中每个元素的查找概率相等pi
适用条件:采用顺序存储结构的有序表。 算法实现
❖设表长为n,low、high 和 mid分别指向待查元素所 在区间的上界、下界和中点,k为给定值
❖初始时,令low=1, high=n, mid=(low+high)/2 ❖让k与mid指向的记录比较
若k==r[mid].key,查找成功 若k<r[mid].key,则high=mid-1 若k>r[mid].key,则low=mid+1 ❖重复上述操作,直至low>high时,查找失败
//关键字
infotype otherinfo; //其他数据项
} NodeType;
Typedef NodeType Seqlist[n+1]; //多一个设置哨兵
顺序查找算法:
int Search_Seq (Seqlist r, KeyType k)
{ // 在顺序表ST中顺序查找其关键字等于kval的数据元素,
