组合图形的面积练习题
小学五年级数学《组合图形的面积》试题及答案

五年级数学(上册):《组合图形的面积》试题1、求图形的面积(单位:厘米)梯形面积:三角形面积:(8+12)×8.5÷2 12×3÷2= 20×8.5÷2 = 36÷2= 170÷2 = 18(cm2)= 85(cm2)图形面积= 梯形面积–三角形面积:85-18=67(cm2)2、校园里有两块花圃(如图),你能计算出它们的面积吗?(单位:m)图形面积=长方形面积6×(5-2)+ 正方形面积(2×2)图形面积=长方形面积 - 梯形面积6×(5-2)+ 2×2 10×6 –[(3+6)×2÷2 ]= 6×3 + 4 = 60 -[ 9×2÷2 ]= 18 + 4 = 60 - 9= 22(m2)= 51(m2)3、下图直角梯形的面积是49平方分米,求阴影部分的面积。
直角梯形的高=直角三角形的高(阴影部分面积)直角梯形的高= 49÷(6+8)×2 直角三角形面积= 6×7÷2= 49÷14× 2 = 42÷2= 3.5× 2 = 21(dm²)= 7(dm²)4、图中梯形中空白部分是直角三角形,它的面积是45平方厘米,求阴影部分面积。
直角梯形的高=直角三角形的高梯形面积=(5+12)×7.5÷2= 45÷12×2= 17×7.5÷2= 3.75×2 = 127.5÷2= 7.5(cm2)= 63.75(cm2)阴影部分面积=梯形面积–空白部分面积:63.75 - 45 = 18.75(cm2)5、阴影部分面积是40平方米,求空白部分面积。
(单位:米)梯形的高=三角形的高(阴影部分三角形)梯形面积=(6+10)×8÷2= 40÷10× 2 = 16×8÷2= 4× 2 = 128÷2= 8(m2)= 64(m2)空白部分面积=梯形面积–阴影部分面积:64–40 = 24(m2)6、如图,平行四边形面积240平方厘米,求阴影部分面积。
六年级组合图形面积的计算

六年级组合图形面积的计算(一) 说明:1题中A组的题,中等以上学生能全部写出,注意公式的正确运用。
B组的题,三个图形有联系。
C组的题,有一定难度,可以指导后完成。
4、5、6题较难,注意思考。
1. 求阴影部分的面积(单位:厘米)。
ABC2. 求周长和面积.(单位:米)3. 已知A是正方形的边上的中点,求阴影部分的面积。
4. 下图正方形的面积是8平方厘米,求阴影部分的面积。
5. 在正方形ABCD中,AC=6厘米。
求阴影部分的面积。
6. 两圆的半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO1O的面积。
六年级组合图形面积的计算(二)1.根据左下图中条件,求阴影部分的面积。
(单位:厘米)2.右上图中阴影部分的面积是40厘米,那么环形的面积是多少平方厘米?3.已知O是圆心,求图中阴影部分的面积。
(单位:厘米)4.求下左图阴影部分的面积。
(单位:厘米)5.求右上图阴影部分的面积。
(单位:厘米)6.如下左图(单位:米),三个圆的周长都是25.12厘米,求阴影部分的面积。
7.如上右图,有一个平行四边形,它的一个角是60°,两条边分别是4厘米和6厘米,高3.4厘米,求图中阴影部分的面积。
(得数保留两位小数)8.右图中△①比△②的面积小6平方厘米,求a边的长。
(单位:厘米)9.平行四边形ABCD的面积是24平方厘米。
以平行四边形底边AB为直径,AB的中点O 为圆心,画一个周长为25.12厘米的圆,恰好过点D,连接OD,量得∠DOB为45°,求图中阴影部分的面积。
五年级组合图形的面积精选32题
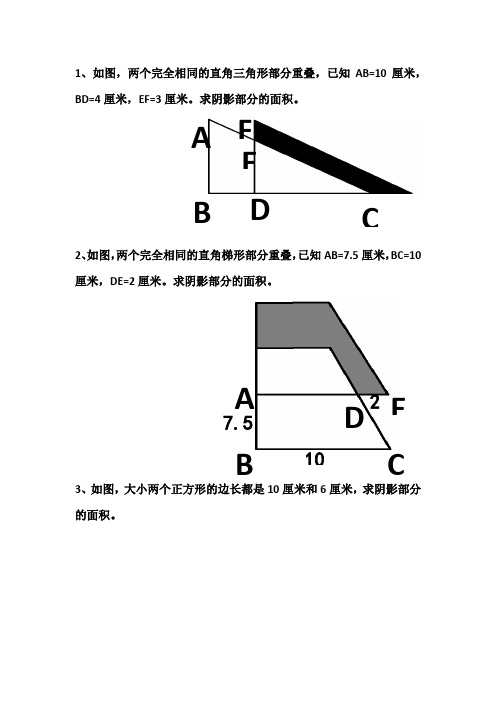
1、如图,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4厘米,EF=3厘米。
求阴影部分的面积。
2、如图,两个完全相同的直角梯形部分重叠,已知AB=7.5厘米,BC=10厘米,DE=2厘米。
求阴影部分的面积。
3、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
ABCDEFADEBC107.524、如图,大小两个正方形的边长都是10厘米和6厘米,求阴影部分的面积。
5、如图,由长方形ABCD 和直角梯形BEFC 组成,其中阴影部分的面积是36.5平方厘米,CD 是5厘米。
求长方形ABCD 的面积。
6、如图,平行四边形ABCD 的底BC 长12厘米,线段EF 长8.3厘米,求图中阴影部分的面积总和是多少平方厘米?ABCDEFABCDFEG7、如图,梯形上底长5.4厘米,下底长8.6厘米,高长4厘米,求三角形甲的面积比三角形乙的面积小多少平方厘米?8、如图,ABCD 是长方形,AB=8厘米,BC=6厘米,三角形ABF 的面积比三角形DEF 的面积大12平方厘米,求DE 长多少厘米?9、如图,平行四边形ABCD 的底BC 长10厘米,直角三角形FBC 的直角边FC 长8厘米。
已知阴影部分的总面积比三角形EFG 的面积大10平方厘米。
求EF 的长度。
甲乙ABCDEF8681010、如图,△ABC 和△DCB 都是直角三角形,已知AB=3.4厘米,BC=7.2厘米,且甲比乙的面积大3.6平方厘米,求CD 的长。
11、如图,CA=AB=4厘米,三角形ABE 的面积比三角形CDE 的面积小2平方厘米,求CD 的长。
12、如图,甲的面积比乙的面积大36平方厘米,已知AB 长8厘米,BC 长12厘米,CD 长6厘米,求DE 的长。
ABCD甲乙7.23.4ABCDE4ABCDE 甲乙812613、如图,D 是AC 的中点,E 、F 是BC 边上的三等分点,已知阴影部分的面积为20平方厘米,求三角形ABC 的面积。
(完整版)五年级组合图形的面积典型例题

五年级上册组合图形面积计算题1:一个等腰直角三角形,最长的边是10 厘米,这个三角形的面积是多少平方厘米?【巩固练习1】:如图正方形中套着一个长方形,正方形的边长是12 厘米,长方形的四个角的顶点把正方形的四条边各分成两段,其中长的一段是短的 2 倍。
求中间长方形的面积。
2:求右面平行四边形的周长。
5412巩固练习2】:求右面三角形的AB上的高典型例题3:求右图等腰直角三角形中阴影部分的面积。
单位:厘米)10巩固练习3】:求四边形ABCD的面积。
(单位:厘米)典型例题4:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?巩固练习4】:有一种将正方形内接于等腰直角三角形。
已知等腰直角三角形的面积是72 平方厘米,正方形的面积分别是多少?典型例题5:图中两个正方形的边长分别是10厘米和 6 厘米,求阴影部分的面积。
【巩固练习5】:图中两个正方形的边长分别是阴影部分的面积。
巩固练习6】求右图等腰直角三角形中阴影部分的面积。
(单位:厘米)典型例题7:在一个直角三角形铁皮上剪下一块正方形,剩三角形,已知AD=3cm,DB=4cm,两个三角形面积和是多少?2、已知正方形ABCD的边长是7 厘米,求正方形EFGH的面积A下两个3、求下图长方形ABCD的面积(单位:厘米)4、如图,用48m长的篱笆靠墙围了一个梯形养鸡场,求养鸡场的面积?5、在一个直角三角形铁皮上剪下一块正方形,剩下两个三角形,已知AD=4cm,DB=6cm,两个三角形面积和是多少?A【练一练】如果用铁丝围成如下图一样的平行四边形,需要用多少厘米铁丝?(单位:厘米)例2 】下图中甲和乙都是正方形,求阴影部分的面积。
单位:厘米)【练一练】平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长8厘米,已知阴影部分的面积比三角形EFG 的面积大10 平方厘米。
求CF 的长。
【例4】两条对角线把梯形ABCD 分割成四个三角形。
组合图形的面积练习题

三、应用 1、右图是两个相同的直角三角形叠在一起,求阴影部分的面积。(单 位:厘米)
2、如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求 长方形内阴影部分的面积。
3、
右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2 米的道路,求草地(阴影部分)的面积。
4、
如图长方形,长18厘米,宽12厘米,AE、AF两条线段把长方形面积三 等分,求三角形AEF的面积。
组合图形的面积练习题 姓名: 一、计算下列组合图形的面积
⑴
⑵
18
12
⑶
⑷
二、计算下面图形中阴影部分的面积。 30dm
12dm
3m
25dm
5m 5m
求S阴。
13cm 16cm 8dm 3dm已知S平=48dm2,
24平方厘米, 4dm 8dm
12cm 7cm
已知:阴影部分的面积为 求梯形的面积。
5、图中三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米,求阴 影部分的面积(ADFC不是正方形)。
(完整版)五年级组合图形的面积练习题.docx

组合图形的面积一、计算下面图形的面积(单位:cm)203104560 38306680二、计算图中阴影部分的面积。
(单位: cm)604053三、解决问题1、新风小学有一块菜地,形状如图,这块菜地的面积是多少平方米?35m12m33m50m2、一张指示牌的形状是一个组合图形,求它的面积。
201020108 米的正方形花圃,其余铺草坪。
草坪的2. 一块长 20 米,宽 18 米的空地中间建一个边长为面积是多少平方米?( 6 分)3.如图,这个长方形的长是 9 厘米,宽是 8 厘米, A 和 B 是宽的中点,求长方形内阴影部分的面积。
( 7 分)A B4. 梯形面积是 48 平方厘米,阴影部分比空白部分12 平方厘米,求阴影部分面积。
25. 阴影部分比空白部分大6cm,求 S 阴26. 平行四边形的面积是30cm,求阴影部分的面积。
组合图形的面积综合测试A一、填空。
(18 分)1.一个梯形,它的下底是 8 厘米,如果将他的上底增加 3 厘米,正好变成一个平行四边形,这时面积增加 15 平方厘米,原来的梯形面积是()平方厘米。
2. 如图,平行四边形的底是10 厘米,高是 6 厘米,阴影部分的面积和是()平方厘米。
3. 1d㎡ =()c ㎡5公顷 =()㎡200d㎡ =()㎡12k㎡ =()公顷1000公顷 =()k ㎡ 1400c㎡=()d ㎡1k㎡=()㎡ =()公顷2㎡ =() c ㎡4.在○里填上“>”“小于”“等于”。
5 公顷○ 5 平方米800平方厘米○8 平方分米9平方米○ 90 平方分米588 平方分米○6 平方米400公顷○ 4000平方米1平方千米○ 100000平方米5.如图,两个两个大三角形等底等高,有部分重叠在一起,甲、乙两个图形的面积相比,甲()乙。
(填“大于”“小于”“=”)甲乙二、估计下面图形的面积。
(每个小方格的面积表示 1 厘米)(9 分)面积约为()面积约为()面积约为()三、求下面组合图形的面积。
六年级数学《组合图形面积》经典习题
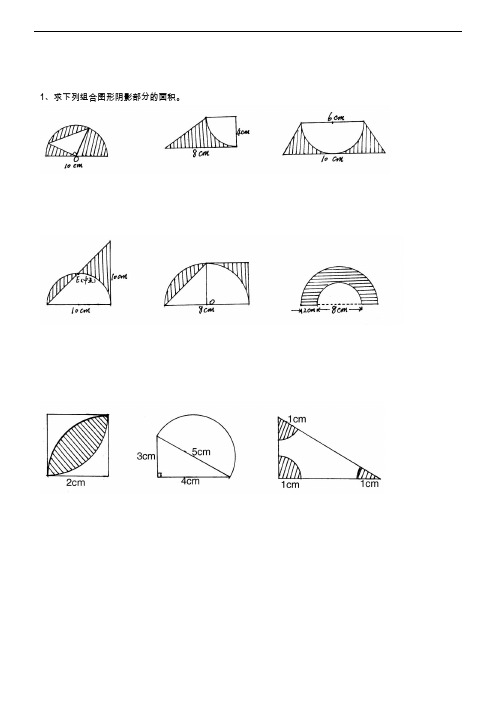
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF 的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
Welcome To Download !!!
欢迎您的下载,资料仅供参考!。
六年级数学组合图形的面积试题

六年级数学组合图形的面积试题1.如下图,长方形和长方形拼成了长方形,长方形的长是20,宽是12,则它内部阴影部分的面积是多少?【答案】120【解析】根据面积比例模型可知阴影部分面积等于长方形面积的一半,为.2.的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是()平方厘米.【答案】23.5【解析】为了使这7个点围成最大的面积,这7个点应尽量在正方形的边或顶点上,如图选取7个点,围成面积最大.最大面积为(平方厘米).3.图中正六边形ABCDEF的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ的面积.【答案】31【解析】如图,将正六边形ABCDEF等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积,面积,面积,四边形ABQP面积.上述三块面积之和为.因此,阴影四边形CEPQ面积为.4.把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【答案】200【解析】图1中阴影部分占整个三角形面积的,图2中阴影部分占整个三角形面积的,故图2中阴影部分的面积为294÷=200(平方分米).5.如图所示,矩形的面积为36平方厘米,四边形的面积是3平方厘米,则阴影部分的面积是多少平方厘米?【答案】12【解析】因为三角形面积为矩形的面积的一半,即18平方厘米,三角形面积为矩形的面积的,即9平方厘米,又四边形的面积为3平方厘米,所以三角形与三角形的面积之和是平方厘米.又三角形与三角形的面积之和是矩形的面积的一半,即18平方厘米,所以阴影部分面积为(平方厘米).6.如图,长方形的面积是36,是的三等分点,,则阴影部分的面积为多少?【答案】2.7【解析】如图,连接.根据蝴蝶定理,,所以;,所以.又,,所以阴影部分面积为:.7.如图所示,在四边形中,,,,分别是各边的中点,求阴影部分与四边形的面积之比.【答案】1【解析】(法1)设,,,.连接知,,,;所以;同理.于是;注意到这四个三角形重合的部分是四块阴影小三角形,没算的部分是四边形;因此四块阴影的面积和就等于四边形的面积.(法2)特殊值法(只用于填空题、选择题),将四边形画成正方形,很容易得到结果.8.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.9.如图,ABCD为平行四边形,EF平行AC,如果ADE的面积为4平方厘米.求三角形CDF的面积.【答案】4【解析】连结AF、CE.∴;;又∵AC与EF平行,∴.∴(平方厘米).10.在边长为6厘米的正方形内任取一点,将正方形的一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分的面积.【答案】15【解析】(法1)特殊点法.由于是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上图所示,图中的两个阴影三角形的面积分别占正方形面积的和,所以阴影部分的面积为平方厘米.(法2)连接、.由于与的面积之和等于正方形面积的一半,所以上、下两个阴影三角形的面积之和等于正方形面积的,同理可知左、右两个阴影三角形的面积之和等于正方形面积的,所以阴影部分的面积为平方厘米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的面积练习题 Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998
组合图形的面积练习题
一、填空
(1)两个完全一样的梯形可以拼成一个()形。
(2)一个梯形上底与下底的和是15厘米,高是厘米,面积是()平方厘米。
(3)平行四边形的底是2分米5厘米,高是底的倍,它的面积是()平方厘米。
(4)有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有()根。
二、判断题
(1)平行四边形的面积大于梯形面积。
()
(2)梯形的上底下底越长,面积越大。
()
(3)任何一个梯形都可以分成两个等高的三角形。
()
(4)两个形状相同的三角形可以拼成一个平行四边形。
()三、计算下列组合图形的面积
五、有一块青菜地,中间是有两个小池塘,如右图,平均每平方米菜地能生产
出8千克的青菜,这块地的面积是多少平方米这块地能产出多少千克的青菜。
